Initial development of goCMC: a GPU-oriented fast cross-platform Monte Carlo engine for carbon ion therapy

Abstract

Monte Carlo (MC) simulation is considered as the most accurate method for calculation of absorbed dose and fundamental physics quantities related to biological effects in carbon ion therapy. To improve its computational efficiency, we have developed a GPU-oriented fast MC package named goCMC, for carbon therapy. goCMC simulates particle transport in voxelized geometry with kinetic energy up to 450 MeV/u. Class II condensed history simulation scheme with a continuous slowing down approximation was employed. Energy straggling and multiple scattering were modeled. δ-electrons were terminated with their energy locally deposited. Four types of nuclear interactions were implemented in goCMC, i.e., carbon-hydrogen, carbon-carbon, carbon-oxygen and carbon-calcium inelastic collisions. Total cross section data from Geant4 were used. Secondary particles produced in these interactions were sampled according to particle yield with energy and directional distribution data derived from Geant4 simulation results. Secondary charged particles were transported following the condensed history scheme, whereas secondary neutral particles were ignored. goCMC was developed under OpenCL framework and is executable on different platforms, e.g. GPU and multi-core CPU. We have validated goCMC with Geant4 in cases with different beam energy and phantoms including four homogeneous phantoms, one heterogeneous half-slab phantom, and one patient case. For each case 3 × 10⁷ carbon ions were simulated, such that in the region with dose greater than 10% of maximum dose, the mean relative statistical uncertainty was less than 1%. Good agreements for dose distributions and range estimations between goCMC and Geant4 were observed. 3D gamma passing rates with 1%/1 mm criterion were over 90% within 10%) isodose line except in two extreme cases, and those with 2%/1 mm criterion were all over 96%. Efficiency and code portability were tested with different GPUs and CPUs. Depending on the beam energy and voxel size, the computation time to simulate 10⁷ carbons was 9.9–125 sec, 2.5–50 sec and 60–612 sec on an AMD Radeon GPU card, an NVidia GeForce GTX 1080 GPU card and an Intel Xeon E5-2640 CPU, respectively. The combined accuracy, efficiency and portability make goCMC attractive for research and clinical applications in carbon ion therapy.

1. Introduction

Radiotherapy plays an important role in cancer treatment. During recent years, radiation therapy with light ion beams (protons and carbon ions) has been increasingly used in clinic (Schardt et al., 2010; Durante and Loeffler, 2010). Comparing with an X-ray beam that delivers dose almost homogeneously over the entire beam path, an ion beam deposits most of its energy at the very end of its finite range (Bragg peak). Therefore a more favorable ratio between dose to the tumor target and healthy tissues can be achieved. Carbon ion therapy is particularly attractive due to its sharp lateral beam penumbra, biological benefits such as enhanced relative biological effectiveness (RBE) in the Bragg peak region (Amaldi and Kraft, 2005), tissue activation and secondary radiation production that allow in vivo range verification (Poenisch et al., 2004; Enghardt et al., 2004; Testa et al., 2008; Testa et al., 2009), and potential to overcome tumor hypoxia (Staab et al., 2004; Furusawa et al., 2000).

Monte Carlo (MC) simulation is an essential tool for carbon ion therapy for several reasons. First, experimentally validated MC is acknowledged as the most accurate tool to predict dose distributions that are highly sensitive to treatment geometry and patient anatomy (Lomax, 2008b, a; Soukup et al., 2009; Unkelbach et al., 2009). Because of the sharp distal dose fall-off of a carbon ion beam, its range must be predicted as accurately as possible in the treatment planning process to fully utilize the potential of tumor targeting. MC method has been shown to be an important dose calculation tool to reduce the range uncertainty and hence improve treatment precision (Paganetti, 2012; Bauer et al., 2014). Second, biological effectiveness is an important aspect of carbon ion therapy. MC simulation can accurately calculate fundamental physics quantities, e.g., particle spectra, that are essential for the assessment of biologically related quantities (Frese et al., 2012; Taleei et al., 2016). Third, MC simulation also plays a critical role in treatment verification. Its capability of predicting secondary radiation, such as positron emitting nuclei and prompt gamma rays, offers a feasible approach to assess delivery accuracy by comparing the calculated and measured data (Bauer et al., 2013; Robert et al., 2013).

Computational efficiency is a major issue hindering clinical adoption of MC method as well as its applications in research. Being a statistical method, an MC simulation requires transporting a large number of particles to yield a satisfactory level of precision, causing a high computational burden. Although acceleration could be achieved with computer clusters (Jiang and Paganetti, 2004; Paganetti et al., 2008; Vadapalli et al., 2011), this is not a clinically favorable way due to the efforts of facility deployment and maintenance. Recently, accelerated MC computation using graphics processing units (GPUs) has been employed in radiotherapy research and clinical applications due to GPU’s tremendous parallel processing capability at a low cost (Jia et al., 2014). Substantial acceleration factors over conventional CPU-based computations have been reported for photon, electron and proton dose calculations (Jia et al., 2010a; Jia et al., 2011; Hissoiny et al., 2011; Jahnke et al., 2012; Townson et al., 2013; Bol et al., 2012; Hissoiny et al., 2012; Jia et al., 2012a; Yepes et al., 2010; Badal and Badano, 2009; Ma et al., 2014; Tseung et al., 2015).

Aiming at extending the success of GPU-based MC simulation to the carbon ion therapy regime, we have started developing an MC engine for this treatment modality. In addition to employing GPU-friendly parallel processing schemes developed previously by many groups, the current study also focused on solving computational challenges associated with nuclear interactions. Hadronic models in the carbon ion radiotherapy energy range, such as quantum molecular dynamics model, pre-compound model, Bertini cascade, etc., are numerically complicated (Agostinelli et al., 2003). Implementing these models will inevitably increase computational burden, as well as the chance of thread divergence, which is unfavorable for GPU-based parallel simulation (Jia et al., 2014). To overcome the thread divergence issue, it is possible to design novel code workflow to synchronize nuclear interaction calculations among GPU threads. This approach has been employed previously in proton MC simulation problems (Tseung et al., 2015). However, in carbon ion therapy, due to the large number of secondary particles, this method would lead to simultaneous writing of a large amount of secondary particles to a common stack from many GPU threads. These writing operations have to be serialized, impairing overall efficiency. To mitigate these problems, in this study we developed a GPU-friendly data-driven approach to sample secondary particles based on pre-generated data tables.

Our carbon MC engine was developed under a programming framework called Open Computing Language (OpenCL). At present, the majority of the existing GPU-based MC packages are implemented under NVidia’s Compute Unified Device Architecture (CUDA) environment (NVIDIA, 2011), which supports exclusively NVidia GPUs. While great success has been achieved, these packages are not compatible with other computing devices such as CPUs and GPUs from other manufacturers. In 2009, OpenCL was released, which specified a C-based programming language and a standard interface for parallel computing on a variety of platforms consisting of CPUs, GPUs, and other processors or hardware accelerators. This provided a solution to the portability problem and eliminated the extra efforts when running programs on different platforms. It thus could potentially facilitate adoption of the developed code to radiotherapy research and clinical practice (Ammazzalorso et al., 2014; Zhou et al., 2012; Tian et al., 2015).

This paper reports our initial achievements in developing a GPU-oriented fast cross-platform MC engine under the OpenCL framework, named goCMC (GPU OpenCL Carbon Monte Carlo). A complete MC engine for carbon ion therapy should include many features such as source modeling and RBE calculation. As the initial step towards developing such a MC engine, this study only focuses on the the modeling of particle transport, which is the basis for all other advanced functions. In section 2, we will describe the employed physics, transport algorithm and parallelization scheme. Dose calculation results in different testing cases, as well as performance tests on a variety of computing devices will be presented in section 3. Finally we will conclude our study and discuss some further works in section 4.

2. Methods

2.1 Physics

goCMC simulates carbon ion transport in voxelized geometry with kinetic energy up to 450 MeV/u. Each voxel is defined with its mass density and elemental composition. Charged particle transport in goCMC follows the standard class II condensed history scheme (Berger, 1963) using the continuously slowing down approximation (CSDA). Each particle is tracked along a path consisting of a number of steps, till its residual range is smaller than the distance to the next voxel boundary. Carbon CSDA range as a function of energy is tabulated to estimate the residual range. For other charged particles, the range is estimated using the carbon range table with appropriate scaling to account for charge and mass difference (Deasy, 1994).

2.1.1 Sampling step size

The simulation of a carbon ion starts with the sampling of the step size δx, i.e., the distance before undergoing a hard interaction event. In goCMC, Coulomb interaction with δ-electron production (ionization) and nuclear interactions are considered as hard events. Therefore, δx is determined by the total cross section of nuclear interactions and ionization. Woodcock method is employed to consider the variation of cross-section within a step due to energy loss (Kawrakow, 2000). The total cross section data of nuclear interactions are extracted from Geant4 (Agostinelli et al., 2003) and the total ionization cross section was computed by (Olive et al., 2014)

$$\sigma (E)={\int }_{T_{\mathrm{e},\text{min}}}^{T_{\text{max}}}\mathit{\text{dT}}\frac{2\pi r_e^2{m}_e{c}^2{n}_e{z}^2}{{\beta }^2{T}^2}[1-\frac{{\beta }^{2}T}{T_{\text{max}}}],$$ (1)

Here r_e is the classical electron radius, m_e is the electron mass, n_e is the number of electrons per volume, z and E are the charge number and kinetic energy of the incident particle, β is the particle velocity relative to the speed of light c. The integration is from the electron production cut-off energy T_e,min to the maximum transferable energy T_max, which is given by

$$T_{\text{max}}=\frac{2m_e{c}^2({\gamma }^2-1)}{1+2\gamma (m_e/m)+{(m_e/m)}^2},$$ (2)

where m is the incident particle rest mass and γ is the Lorentz factor. All these cross section data are tabulated in goCMC database. The sampled step size δx is limited by the distance to the next voxel boundary. We also restrict the maximal step size, such that the fractional energy loss per step is less than a predefined threshold value. The default threshold value is 0.25.

After moving a step, if the carbon ion does not reach the voxel boundary, a hard event will be sampled. The production of δ-electrons, as well as the energy loss and angular deflection along the step are described below in Sec. 2.1.2. The nuclear interaction modeling is presented in Sec. 2.1.3.

2.1.2 Electromagnetic process

Electromagnetic process in goCMC is modeled by the standard class II condensed history simulation scheme (Berger, 1963) with a continuous slowing down approximation. The mean energy loss of carbon ions is calculated via its equivalent step length in water (Fippel and Soukup, 2004). Specifically, for a carbon ion with kinetic energy E transport in material type i, once the step length δx is sampled as introduced above, its equivalent length in water δx_w is calculated accordingly as

$$\delta x_w=\delta x{f}_s(E,i)\frac{{\rho }_i}{{\rho }_w},$$ (3)

where f_s(E, i) is the mass stopping power relative to water for the i’th material at energy E. ρ_i and ρ_w are mass densities of the considered material and water, respectively. f_s(E,i) for different materials and energies are precomputed via Bethe-Bloch equation, and are tabulated in goCMC database. In the calculation, the mean ionization energy of each material except water is computed via

$$\text{ln}I=\sum p_i{Z}_i\text{ln}{I}_i$$ (4)

where p_i is the stoichiometric percentage of the i’th element with an atomic number Z_i and mean ionization energy I_i. For water, we used the ionization energy 69.2 eV, so that the simulated range in water agrees with that from Geant4.

The mean energy loss $\overline{\Delta E}$ in a step δx is calculated by numerically solving the equation (Kawrakow, 2000)

$$\delta x_w=-{\int }_E^{E-\overline{\Delta E}}\frac{1}{L(E)}dE,$$ (5)

where the restricted stopping power in water, L(E), is also precomputed following the standard procedure (Agostinelli et al., 2003). The total energy loss is a stochastic quantity with a distribution described in terms of a straggling function. As a good approximation, this energy straggling is modeled as a random fluctuation around the mean energy loss $\overline{\Delta E}$. The fluctuation follows Gaussian distribution with Bohr’s variance (Bohr, 1948).

Besides energy loss, a carbon ion traversing a medium is also deflected due to many small-angle scatters. According to the central limit theorem, the net effect is a Gaussian distribution (Bethe, 1953) with mean 0 and standard deviation given by (Highland, 1975; Lynch and Dahl, 1991)

$${\theta }_0=\frac{E_s}{\beta cp}\delta x\sqrt{\delta x/X_0}[1+0.038\text{ln}(\delta x/X_0)].$$ (6)

Here p is the momentum of the carbon ion and X₀ is the radiation length of the material. The parameter E_s is usually regarded as a constant of 13.6 MeV. However, we found this choice led to large deviations in the deflection angle distribution when validating goCMC with Geant4 (Agostinelli et al., 2003; Allison et al., 2006). To solve this problem, we have calibrated E_s for different energies and obtained an empirical energy-dependent form as

$$E_s=19.8+0.0023E(\mathit{\text{MeV}}),$$ (7)

which provided good agreement between goCMC and Geant4 on calculated dose. Note that although E_s increases with energy, θ₀ still decreases with energy because of the 1/βcp term, as the high-energy carbon ions are harder to be deflected than low-energy carbon ions. Lateral displacement of the carbon ion position is ignored in our simulation. This approximation was found to be valid for proton MC simulation (Fippel and Soukup, 2004). Hence, we expect it is also acceptable for carbon ions due to the larger mass.

Elastic Coulomb interactions with production of δ-electrons over user-specified cut-off energy T_e,min are simulated. In goCMC the default value of T_e,min is 0.1 MeV. Kinetic energy of δ-electrons is sampled using a standard rejection method (Agostinelli et al., 2003). For low energy carbon ion beams (e.g., 100 MeV/u), the maximal energy of δ-electrons is ~0.3 MeV, corresponding to ~0.5 mm range in water. For high energy beams (e.g., 400 MeV/u), the maximal energy of δ -electrons is around 1.0 MeV, corresponding to ~4.0–5.0 mm range in water. Because carbon ions intensively interact with matters, electron equilibrium is built shortly after a beam enters a phantom. Hence, current version of goCMC terminates δ -electrons once they are generated and their energy is deposited locally.

2.1.3 Nuclear interactions

Four types of nuclear interactions are implemented in goCMC, i.e., carbon-hydrogen, carbon-carbon, carbon-oxygen and carbon-calcium inelastic collisions, because these four elements constitute more than 90% of human body weight. Elastic interactions are not included, similar to Geant4 which ignores elastic hadronic interactions for projectiles heavier than alpha particle. The cross section data extracted from Geant4 are used to sample the interaction type.

Once a carbon ion encounters a certain nuclear event, secondary particles are produced. In Geant4, a large variety of hadronic models are provided for simulating such nuclear collisions. These models describe physics processes in detail and provide good agreement with experiments (Wenzel et al., 2015). Due to the complicated calculations involved, simulating these models is time consuming. To accelerate the simulation without sacrificing the accuracy, we use precomputed data table to achieve secondary particle sampling in goCMC. Specifically, to prepare these data, we repeatedly ran simulations of each of the four nuclear interactions with Geant4 using the Binary Light Ion Reaction model. The energy of carbon ions ranged from 10 MeV/u to 450 MeV/u with an interval of 10 MeV/u. For each energy level and each interaction type, we first determined all of the possible types of secondary particle. Note that each specific type of secondary particle may be produced from multiple reaction channels. For instance, in a carbon-oxygen interaction, ¹¹C could be produced through different channels (¹²C + ¹⁶O →¹¹C+¹⁶O + n, ¹²C + ¹⁶O → ¹¹C + ¹⁵N + ²H etc.). For each type of secondary particle, we performed statistical analysis to obtain the yield of this particle type per nuclear interaction event, as well as the tables of cumulative probability distributions for its energy and scattering angle. These data were tabulated in goCMC database.

With these data available, we are able to sample secondary particles in goCMC simulation. Here we briefly introduce the sampling procedures. When a primary carbon with certain kinetic energy collides with a nucleon, the corresponding yields of all secondary particle types are determined from interpolation of the yields data table. For each secondary particle type, we generate a given number of particles accordingly. Note that the number of particles determined from the yield table may not be an integer. This issue is solved via a statistical approach. For example, if the yield of ¹¹C is 1.2, one ¹¹C would be produced and with 20% chance another ¹¹C would be produced. For each of the secondary particle, its energy and direction are sampled from the tabulated cumulative probability distributions. We would like to remark that such a sampling method does not satisfy momentum and energy conservation for each single event. However, when enough events are sampled, the conservation laws are satisfied in the statistical sense.

We also ignore all electrically neutral particles generated in nuclear interactions. Majority of the neutral particles are secondary neutrons. We have conducted studies using Geant4 to investigate the impact of secondary neutrons on physical dose. Dose distributions from simulation with and without neutron transport were compared. Deviations smaller than 0.5% relative to maximum dose were observed. Normalizing to the maximum dose is one typical approach in radiotherapy, as only the high dose region is of clinical interest. Hence, we expect that neglecting simulations of those neutral secondary particles is a clinically acceptable approximation for treatment planning purposes. Similar approach has also been employed previously in proton MC simulations (Fippel and Soukup, 2004).

The produced secondary charged particles are transported via electromagnetic process in a similar way as primary carbon ions. Because of the large number of particle types, it is infeasible to precompute and tabulate all the stopping power data. Therefore restricted stopping power is calculated on the fly. Energy straggling, multiple scattering and ionization are also included. Since there were more than 300 types of secondary particles considered in goCMC, it is not practical to implement their nuclear interactions in the same manner as described above for the primary carbon. Hence, the nuclear interactions of these secondary particles are ignored in goCMC. In the validation cases we studied, goCMC and Geant4 dose calculations agreed well with each other, indicating that such an approximation is acceptable.

2.2 OpenCL implementation

goCMC is developed under OpenCL framework, which provides efficiency as well as portability on various platforms and devices. To achieve high efficiency, single precision floating-point variables are used, because GPUs have much higher processing power on single precision than double precision. In addition, the image objects and their associated fast hardware interpolation on GPU are only available for single precision. To address potential precision loss due to the use of single precision (Magnoux et al., 2015), we used an additional memory buffer to store the scored quantities after each batch of simulation (Qin et al., 2016).

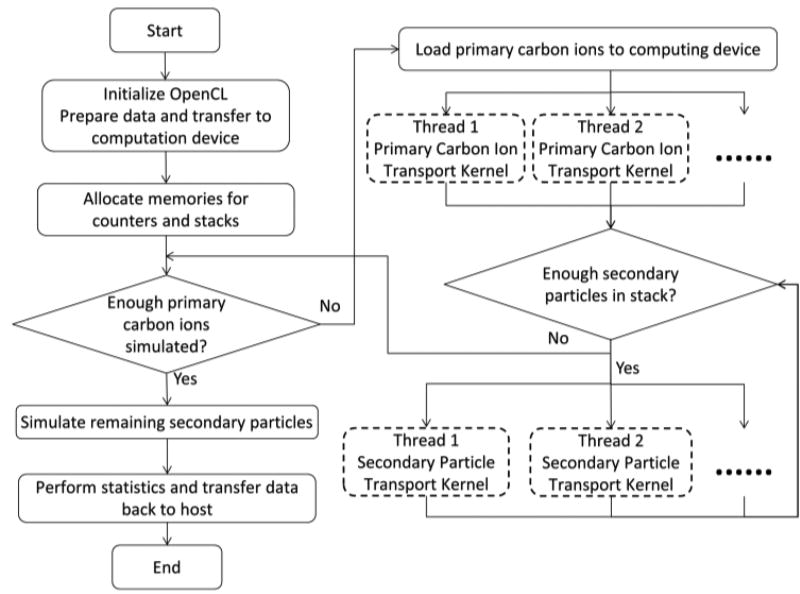
The structure of goCMC is illustrated in Figure 1. The solid boxes performing configuration and scheduling works constitute the outer control logic of goCMC, which is called host program in OpenCL. The host program usually runs on a general purpose CPU. The dashed boxes indicate the parallel execution of OpenCL kernels. Kernels are C-based functions simulating particle transport and scoring physics quantities, which run on processing cores of a computing device, e.g., a GPU. There are two simulation kernels in goCMC, one for primary carbon transport and the other for secondary charged particle transport.

Figure 1.

Flow chart of goCMC simulation. The dashed boxes indicate threads in the primary carbon ions and secondary particle transport kernels which are distributed to multiple processing cores.

At initialization stage of goCMC, all physics data and patient data are loaded to the memory of the computing device. A stack to store secondary particles and the scoring counters for dose and other physical quantities are also allocated on the computing device. We would like to mention that the small lateral scattering of carbon ions cause memory writing conflict issue during paralleled MC simulation. Specifically speaking, the direction changes of the primary carbon ions are very small, so they deposit energy primarily to voxels along a straight beam path. Therefore, multiple threads concurrently simulating many carbon ions will try to update the same voxels simultaneously, which become serialized and hence degraded the simulation efficiency (Jia et al., 2012b). To alleviate this issue, multiple scoring counters are implemented in goCMC (Qin et al., 2016).

After initialization, the primary carbon transport kernel is distributed to multiple processing cores performing the simulation. Because the maximal number of threads is restricted by the device’s computational power, primary carbons are loaded and simulated in a batched fashion. During transport simulation, quantities of interest are scored and the produced secondary particles are pushed into the aforementioned stack. Since the stack size is restricted by the device’s memory size, after each batch of primary carbons, we preferably simulate secondary particles, as long as there are enough of them to fully utilize the device’s processing power. As mentioned in 2.1.3, we implement nuclear interactions for primary carbons but not for secondary particles. The simulation time for transport of primary carbon ions is hence longer than that of secondary particles. Therefore, the transport of primary carbon ions and secondary particles are separated to avoid wasting computation powers, since otherwise those short secondary particle transport threads would wait for the primary particle transport threads. After all the primary and secondary particles are simulated, statistical analysis is performed on the multiple counters to calculate the mean and standard deviation of the scoring quantities in each voxel.

2.3 Testing scenarios

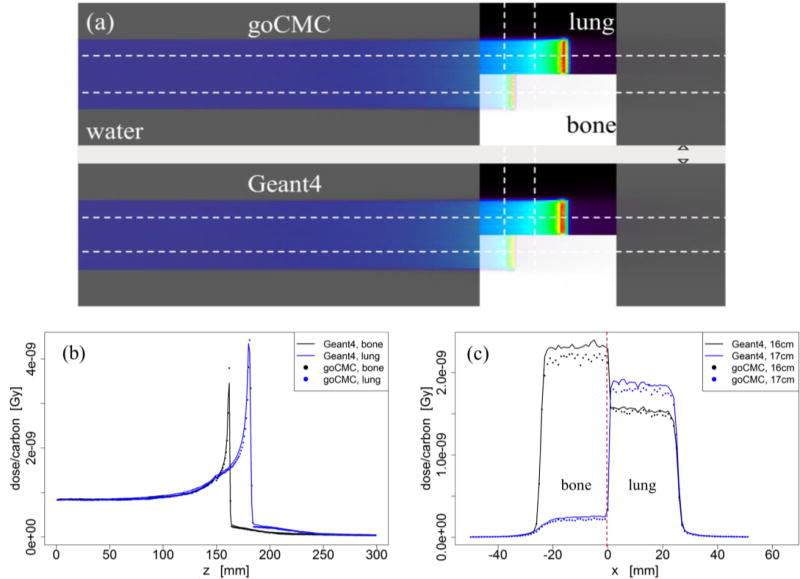
We have performed comprehensive dose calculation studies to validate goCMC. In this initial development study, we focused on the accuracy of physical dose calculation. Calculations of other quantities of interest, e.g., biological effectiveness will be investigated in future works. As such, four homogeneous phantom cases, i.e., pure water, lung (−500HU), soft tissue (40HU) and bone (600HU), an inhomogeneous phantom, and a patient case were used, and the doses calculated by our goCMC were compared with dose computed by the general purpose MC code Geant4 10.01 (Agostinelli et al., 2003). The same Geant4 version and physics settings were used to get the physics data described in Section 2.1. In all the phantom cases except lung, the phantom dimensions were 10.2 × 10.2 × 45 cm³ (x × y × z) with a voxel size 0.1 × 0.1 × 0.1 cm³. Because the range of carbon ions in lung is much longer than others, we used a 10.2 × 10.2 × 75 cm³ lung phantom with a voxel size 0.1 × 0.1 × 0.1 cm³. In these cases, mono-energetic mono-directional beams with initial energy of 100 MeV/u, 250 MeV/u and 400 MeV/u were studied. In the water phantom case, we simulated both broad beams (a 5.0 × 5.0 cm² square beam) and infinitesimal pencil beams with zero initial beam size. The reason to use an infinitesimal pencil beam is that compared to the broad beam dose distribution, pencil beam dose distribution is more sensitive to primary carbon ion angular deflection and secondary particle angular distributions. In other homogeneous cases, only the broad beam was simulated. The inhomogeneous phantom was a water phantom with a half-lung half-bone slab of 5.0 cm thickness inserted with their proximal edges at z = 15 cm depth, as indicated in Figure 6(a). A 300 MeV/u broad beam was used in this case to have the Bragg peaks inside the slab. The incident beam in all the phantom cases was along z direction. We also tested goCMC on a patient case. We selected a patient head CT scan with a resolution of 512 × 512 × 128 and a voxel size 0.075 × 0.075 × 0.125 cm³. A 250 MeV/u broad beam impinged laterally on the patient. The material composition for each voxel was derived from the CT images using the calibration method from Schneider et al., 2000.

Figure 6.

(a) Configuration of the inhomogeneous phantom and dose distributions calculated by goCMC and Geant4 of a 300 MeV/u broad beam. (b) Depth dose curves through the bone and lung inserts. (c) Lateral profiles at the depths of 16.0 and 17.0 cm.

As mentioned in Section 2.1, neutral particles and electrons were not transported in goCMC. We thus disabled transport of these particles in Geant4 simulations for all the phantom cases. To confirm that the contribution from these particles is negligible, we performed two Geant4 simulations for the patient case. One was the simplified simulation without transport of secondary electrons and neutral particles in analogy to goCMC. The other one was the full simulation with all of these considered.

To test the efficiency and portability of goCMC, we ran simulations on different computing devices: 1) an NVidia GeForce GTX TITAN GPU card with 2688 cores, 876 MHz clock frequency, 6.0 GB memory and 288.4 GB/sec memory bandwidth; 2) an AMD Radeon R9 290x GPU card with 2816 cores, 980 MHZ clock frequency, 4.0 GB memory and 320 GB/sec memory bandwidth; 3) an NVidia GeForce GTX 1080 GPU card with 2560 cores, 1607 MHZ clock frequency, 8.0 GB memory and 320 GB/sec memory bandwidth; 4) an Intel i7-3770 CPU processor with 4 cores, 3.4 GHz clock frequency, 32 GB memory and 25.6 GB/sec memory bandwidth; 5) an Intel Xeon E5-2640 CPU processor with 6 cores, 2.5 GHz clock frequency, 384 GB memory and 42.6 GB/sec memory bandwidth.

3. Results

3.1 Dose distributions

Dose distributions in different cases are shown in Figures 2–7. For all cases, both goCMC and Geant4 simulated 3 × 10⁷ primary carbon ions. The precision of our simulation was quantified by the relative uncertainty σ/D. At each voxel, σ is the uncertainty estimated by the dose results from all dose counters and D is the calculated dose value. The mean relative uncertainty $\overline{\sigma /D}$ in the region with dose greater than 10% of the maximum dose was found less than 1%. For visualization purposes, error bars are not drawn in the figures.

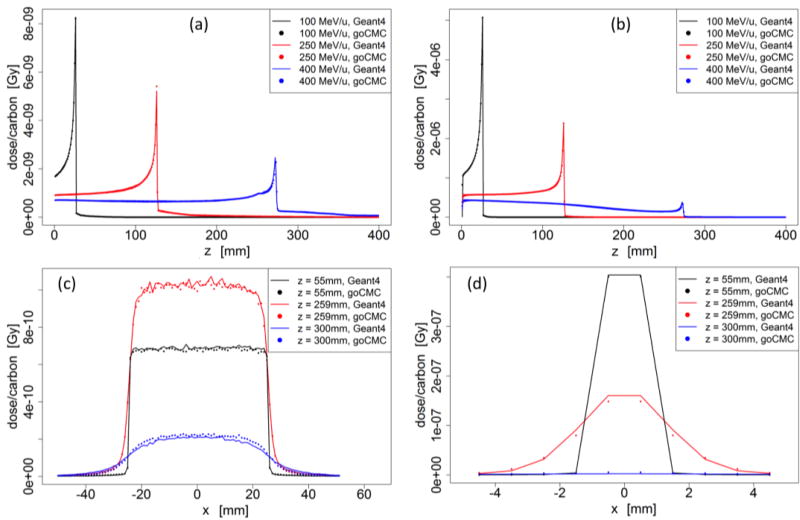
Figure 2.

Water phantom case: (a) Depth dose curve of a broad beam. (b) Depth dose curve of a pencil beam. (c) Lateral profile of the 400 MeV/u broad beam at entrance, close to Bragg Peak and beyond Bragg Peak. (d) Lateral profile of the 400 MeV/u pencil beam at entrance, close to Bragg Peak and beyond Bragg Peak.

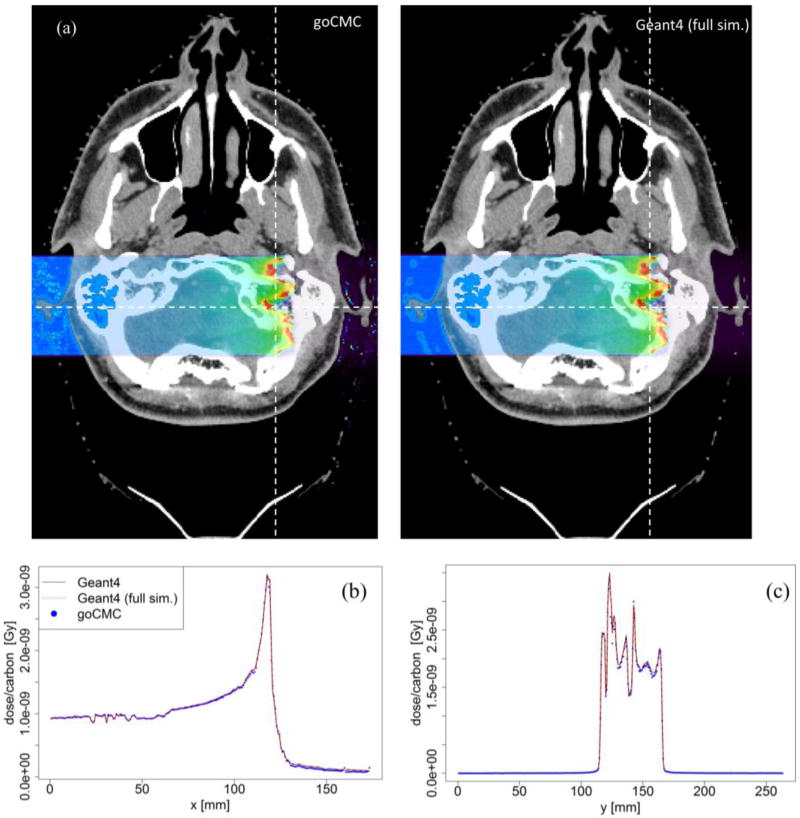
Figure 7.

(a) Dose distributions in a patient case calculated by goCMC and Geant4 full simulation, (b), (c) Dose profiles along a horizontal and a vertical line as indicated by the dashed lines in (a).

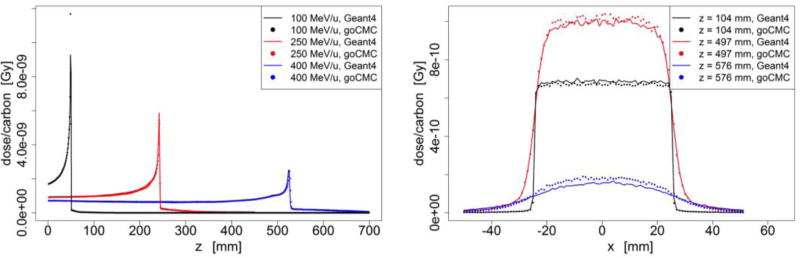
As described in section 2.1.2, energy loss of carbon ions within a step was calculated via its equivalent step length in water. Therefore the accuracy of simulation in water is of particular importance. We thus first examined dose distribution in a homogeneous water phantom with a broad beam as well as an infinitesimal pencil beam. Figure 2 shows the depth dose curves and lateral profiles in the water phantom. The left column corresponds to the broad beam and the right column is for the pencil beam. The three lateral profiles are taken from the 400 MeV/u beam case at the entrance region (z = 55 mm), right in front of Bragg peak (z = 259 mm), and beyond the Bragg peak (z = 300 mm). Depth dose of the 100 MeV/u and 250 MeV/u beams matched well, whereas small discrepancies existed for the 400 MeV/u beam in front of the peak region. Quantified discrepancies for all cases will be presented later. Both goCMC and Geant4 produced a small bump in front of the Bragg peak in depth dose curves of the 400 MeV/u beam. The bump was found to be the Bragg peak of secondary ¹¹C, which had a shorter range than primary ¹²C (Pshenichnov et al., 2007). There was also discrepancy when comparing the profile beyond the Bragg peak, as indicated by the blue line and dots in Figure 2(c). These discrepancies were mainly due to the fact that goCMC ignored nuclear interactions for secondary particles that contributed to dose beyond the Bragg peak.

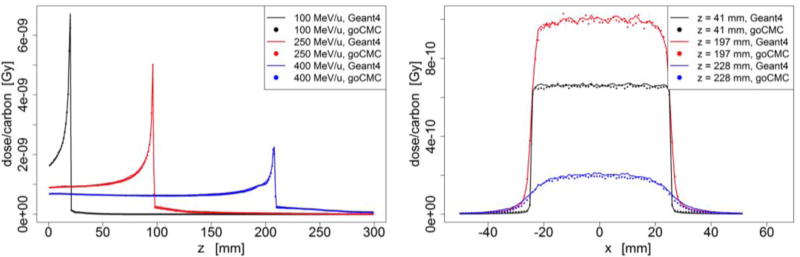
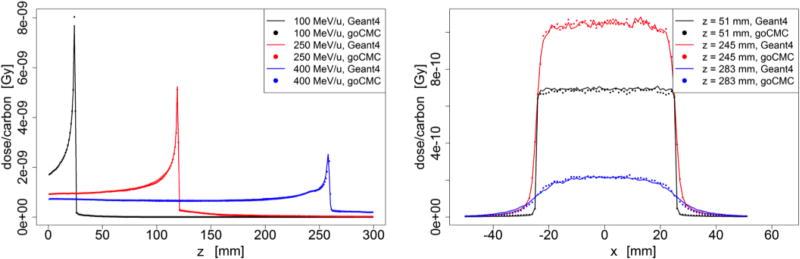
Dose distributions in other homogeneous phantoms are presented in Figure 3–5. In most of the cases, goCMC and Geant4 were in good agreement. However, a relatively big difference of 28% of the peak value appears in the low energy lung case as shown in Figure 3. This can be ascribed to a small shift (less than a voxel) of the peak locations between goCMC and Geant4 results.

Figure 3.

Lung phantom case: (Left) Depth dose curve of broad beam in lung. (Right) Lateral profile of the 400 MeV/u broad beam at entrance, close to Bragg Peak and beyond Bragg Peak.

Figure 5.

Bone phantom case: (Left) Depth dose curve of broad beam in bone. (Right) Lateral profile of the 400 MeV/u broad beam at entrance, close to Bragg Peak and beyond Bragg Peak.

To validate goCMC simulation in heterogeneous media, we used an inhomogeneous phantom and a patient case. Figure 6(a) illustrates the geometry of the phantom, along with the dose distribution of a 300 MeV/u mono-energetic square beam overlaid on the phantom for display. Figure 6(b) depicts the depth dose curves along the two horizontal lines in Figure 6(a) and Figure 6(c) plots lateral profiles along the two vertical lines in Figure 6(a). A small shift was observed in depth dose curves, which made difference in lateral profiles obvious due to the sharp dose gradient along the depth direction.

The results of the patient case are illustrated in Figure 7. A 250 MeV/u mono-energetic square beam impinged on the patient from the right side. In addition to Geant4 simulation without neutral particles and electron transport, we also performed a full Geant4 simulation. Figure 7(a) shows the dose distributions calculated by goCMC and Geant4 full simulation at one axial slice. Figure 7(b) and (c) illustrate the good agreement of dose profiles between goCMC and the two Geant4 simulations along the two straight lines indicated in Figure 7(a).

3.2 Quantitative analysis

We have computed the voxel-by-voxel dose difference between goCMC and Geant4 in regions that received a dose greater than 10% of the maximal dose for all testing cases. The mean difference relative to the maximal dose, ∊̅_{D 10%} ≡ | D_goCMC − D_Geant4|/D_max is listed in Table 1, where |.| denotes standard L2 vector norm and D is a vector of calculated dose in voxels within 10% isodose line. ∊̅_{D 10%} was small for all the cases (~<1%) except the lung case with 100 MeV/u beam. The relatively large difference of 1.6% in the latter case was due to the difference of peak dose. As discussed above, it is mainly caused by a small range difference and binning effects.

Table 1.

Average relative dose difference ∊̅_D10%, range difference ∊_R, γ-test passing rates P_γ for all testing cases.

Phantom	Beam setup	Energy (MeV/u)	∊̅D10% (%)	∊R (mm)	Pγ (1%/1mm) (%)	Pγ (2%/1mm) (%)
Water	Pencil beam	100	0.7	<0.1	99.0	99.0
		250	0.5	<0.1	99.8	99.8
		400	0.9	<0.1	68.6	99.6
	Broad beam	100	0.5	<0.1	99.9	100
		250	0.4	<0.1	99.8	99.9
		400	0.8	<0.1	93.8	98.2
Lung	Broad beam	100	1.6	0.8	99.9	100
		250	0.6	0.6	99.1	99.8
		400	0.9	1.4	93.0	97.5
Soft tissue	Broad beam	100	1.0	<0.1	99.9	100
		250	0.5	<0.1	99.1	99.7
		400	0.9	0.7	91.5	96.4
Bone	Broad beam	100	1.0	<0.1	95.9	97.1
		250	0.6	<0.1	99.7	99.9
		400	0.9	<0.1	79.1	99.3
Slab	Broad beam	300	0.8	NA	96.0	99.8
Patient	Broad beam	250	0.5	NA	99.6	99.8

From the depth dose curves, beam ranges in homogeneous phantoms were estimated as the distal position where dose dropped to 80% of the peak value. The corresponding range difference ∊_R between goCMC and Geant4 is also listed in Table 1. Most of the range differences were very small (less than 1 mm). The only large value of ∊_R is 1.36 mm for 400 MeV/u beam in lung, which corresponds to over 50 cm range. This is an extreme case and is probably not of clinical relevance.

We also performed a 3D γ-test (Gu et al., 2011) on the doses calculated by goCMC with the corresponding ones calculated by Geant4 as reference. With 1%/1mm criterion, the passing rate in regions that receive a dose higher than 10% maximum dose was over 90% for all the cases, except 68.6% for 400 MeV/u pencil beam in water and 79.1% for 400 MeV/u broad beam in bone. The first one was caused by the small peak value in the dose distribution, which was the reference dose used for γ index calculation. The second one was due to a small difference in the location of the ¹¹C bump (~2 mm), as well as the dose difference beyond the Bragg peak that can be ascribed to the lack of nuclear interactions of secondary particles in goCMC. When using a less strict criterion, i.e., 2%/1mm, these two cases got over 99% passing rate. The passing rates of all other cases were over 96%.

3.3 Efficiency and code portability

One of the motivations of this study is to achieve high computational efficiency using the GPU platform. We also employed OpenCL for code portability consideration. We have tested goCMC on different GPUs and CPUs and resulting dose distributions were consistent with each other. Table 2 lists particle transport simulation time and GPU/CPU data transfer time in various cases. Difference in performance among the devices was mainly due to the distinct computing ability of the devices at the hardware level (Tian et al., 2015).

Table 2.

Simulation time of 10⁷ carbon ions in a water phantom with different energies and computing devices. For all cases, voxel size was 1 × 1 × 1 mm³ and phantom size was 102 × 102 × 450 mm³. All time are in unit of sec, except noted otherwise.

Device	Simulation time			CPU/GPU transfer time
	100MeV/u	250 MeV/u	400 MeV/u
NVidia GeForce GTX TITAN GPU	11.1	68.1	162.6	0.3
AMD Radeon R9 290x GPU	9.9	60.5	125.6	0.3
NVidia GeForce GTX 1080 GPU	2.5	20.4	50.4	0.3
Intel i7-3770 CPU	245.9	1596.6	2316.2	NA
Intel XeonE5-2640 CPU	60.1	332.2	612.5	NA
Geant4, Intel i7-4770 CPU	64 h	84 h	90 h	NA

The computation time for Geant4 on a 3.40GHz Intel i7-4770 CPU is also presented in Table 2. This is not a fair comparison because goCMC ignored the nuclear interactions for secondary particles, whereas Geant4 simulated nuclear interactions of all particles with sophisticated hadronic models, and the produced tertiary and further generations of particles were simulated as well. Here, we would only like to emphasize that goCMC can achieve a clinically acceptable dose calculation accuracy within 3–200 seconds on a single GPU, depending on the beam energy and GPU type.

4. Discussion and conclusions

We have successfully developed a GPU-oriented fast cross-platform MC engine for carbon ion therapy, goCMC. Both electromagnetic and nuclear interactions were simulated in goCMC based on physics laws and/or reliable tabulated data. Various testing cases have been studied and good agreement between goCMC and Geant4 was observed. The Geant4 version and physics settings used in this study was validated against published experimental data (Schwaab et al., 2011; Parodi et al., 2013) and another experimentally validated code FLUKA (Parodi et al., 2012). If desired, users can always use other physics data as the code input. By using parallel computing devices such as GPUs, goCMC could reach very high efficiency. Depending on the beam energy and voxel size, it took 16–200 seconds to simulate 10⁷ carbon ions on a single GPU card. The corresponding CPU time for Geant4 with the same setup was 60–100 hours. Besides accuracy and efficiency, goCMC was also portable among different computing devices.

The evaluation studies in this paper were performed in cases with mono-energetic mono-directional beams. A realistic case typically contains source particles with initial energies and directions in a wide range. goCMC is able to simulate particles with different initial states in parallel and properly accumulate physics quantities e.g. physics dose, fluence, spectra from all threads. For biological dose calculation, in addition to physics dose, dose-averaged α and β (linear-quadratic model (Kellerer and Rossi, 1978) parameters) should also be scored. After transporting all the input particles, the final biological dose can be computed using the scored physical dose, and dose averaged α and β. In this process, the OpenCL kernel scheduling and data distribution approach reported in this paper are still valid. Regarding efficiency, in a parallel execution of a transport kernel, the number of concurrently simulated particles depends on the available hardware resources, mainly the number of available processing cores. It is desired to have the execution time among cores close to each other to avoid the situation that some cores finish sooner and wait for others. Since simulation time of a particle is mainly determined by its initial energy, in a case with input particles of different energies, it is desired to arrange the particles, such that the concurrently transported particles are close in initial energy. A practical approach is to first sort and group source particles by initial energy and then to perform simulations group-by-group. For each kernel execution, the particles being transport together are close in energy. Hence, the simulation time and acceleration factor is approximately the same as the mono-energetic case. Thus, we expect that the acceleration reported in Table 2 will still hold in realistic cases.

Despite the success, there are a few issues to be addressed in future studies. First, for clinical applications, the overall dose calculation accuracy is determined by two components, i.e., carbon ion transport inside the patient body and the input source particle information. Analytical beam model or phase space files are usually used to provide the information of source particles. One of our future works is to implement the function of such beam models. Second, the validation presented in this paper only covers some simple setups. Comprehensive investigation of robustness and accuracy of goCMC in various patient cases will be conducted. Third, secondary electrons were simply terminated in the current version of goCMC with their energy locally deposited. While this was expected to be accurate enough in most scenarios, electron transport may be necessary in some cases, e.g., in lung or in the boundary between two tissues of very different density and/or compositions where electron disequilibrium may occur. In future versions of goCMC, electron transport will be included by using modules from our existing photon-electron MC package (Tian et al., 2015; Jia et al., 2010b). Similarly, transport of neutron was not included in goCMC. If neutron transport is found necessary in some applications, we will implement this in future versions. Last, but not least, to further boost efficiency, especially for some computational intensive tasks such as repeated spot dose calculations in inverse treatment planning, it is likely that GPUs/CPUs in a cluster will be needed. Currently, OpenCL does not support working with clusters. It is our plan to enable acceleration on clusters by using a framework called VirtualCL (Barak and Shiloh, 2014), a wrapper for OpenCL that allows most unmodified applications to transparently utilize multiple OpenCL devices in a cluster.

In carbon ion therapy, relative biological effectiveness (RBE) calculation is an important issue (Hall and Giaccia, 2012) since it determines the photon-equivalent dose for biological treatment planning. In contrast to proton therapy where a single RBE value of 1.1 is usually used (Paganetti et al., 2002), RBE varies largely throughout the radiation field for heavier ions. There are several factors affecting RBE values, including projectile type, energy, linear energy transfer (LET) and radiosensitivity of the tissue. It is complicated to calculate RBE for carbon ions using deterministic algorithms due to the large number of nuclear fragments. MC simulation has the potential for RBE calculations, because it explicitly simulates the production and propagation of secondary particles. Incorporation of RBE models into goCMC is currently under development. Upon completion, goCMC could serve as a module in biological treatment planning systems.

Positron-emitting nuclei (PEN) produced in nuclear interactions could be used for treatment verifications (Bauer et al., 2013; Knopf et al., 2008; Parodi et al., 2008a; Parodi et al., 2008b, c; Parodi and Enghardt, 2000). For carbon ion therapy, ¹¹C, ¹⁰C, ¹⁵O and ¹³N are dominant contributions. MC simulation is an important tool to compute their distributions, which will be compared with measurements for treatment verification. The current version of goCMC is able to score the distribution of these PENs. This paper focuses on presenting our initial development of goCMC and its validation in terms of physical dose. It is our next step to perform a more comprehensive validation study to investigate its accuracy in other aspects including the computation of PEN distributions.

Figure 4.

Soft tissue phantom case: (Left) Depth dose curve of broad beam in soft tissue. (Right) Lateral profile of the 400 MeV/u broad beam at entrance, close to Bragg Peak and beyond Bragg Peak.