Entrained delta oscillations reflect the subjective tracking of time

ABSTRACT

The ability to precisely anticipate the timing of upcoming events at the time-scale of seconds is essential to predict objects' trajectories or to select relevant sensory information. What neurophysiological mechanism underlies the temporal precision in anticipating the occurrence of events? In a recent article,¹ we demonstrated that the sensori-motor system predictively controls neural oscillations in time to optimize sensory selection. However, whether and how the same oscillatory processes can be used to keep track of elapsing time and evaluate short durations remains unclear.

Here, we aim at testing the hypothesis that the brain tracks durations by converting (external, objective) elapsing time into an (internal, subjective) oscillatory phase-angle. To test this, we measured magnetoencephalographic oscillatory activity while participants performed a delayed-target detection task. In the delayed condition, we observe that trials that are perceived as longer are associated with faster delta-band oscillations. This suggests that the subjective indexing of time is reflected in the range of phase-angles covered by delta oscillations during the pre-stimulus period. This result provides new insights into how we predict and evaluate temporal structure and support models in which the active entrainment of sensori-motor oscillatory dynamics is exploited to track elapsing time.

We recently demonstrated that participants' accuracy at determining whether an auditory target occurred at the predicted time depends on the pre-stimulus alignment of oscillations in the delta-band.¹ In this initial magnetoencephalographic study, we tested the ability of 19 participants with normal hearing to perform a delayed target detection task. Participants were required to listen to isochronous sequences of 4 or 5 tones (400 Hz, 150 ms duration per tone, average beat rate: 1 Hz). The occurrence of the last tone of the sequence was manipulated so that it occurred either at the right time (Δt₀: no delay) or too late (Δt+: delayed by 75 ms or 150 ms). The task was to detect whether the last tone was delayed or not with regards to the beat. We primarily showed that before target occurrence, coupled delta (1–3 Hz) and beta (18–22 Hz) oscillations temporally align with upcoming targets and bias decisions toward correct responses. Consistent with earlier hypotheses,^2,3 this suggests that the brain predictively aligns ongoing neural activity so that incoming sensory events occur during an ideal neuronal excitability phase. Such an effect, however, was insufficient to provide a neurophysiologically plausible mechanism to explain how the brain evaluates durations in the time-order of seconds.

Because of their implication in the predictive tracking of temporal regularities,^1,2,4-7 we conjectured that neural delta oscillations (1–3 Hz) could further be exploited to measure durations at the seconds time-scale (in the order of 0.3–1 second). According to this idea, the entrained delta-band phase-course might be used as an “internal chronograph” to derive a subjective measure of duration.⁸ In other words, elapsing time can be tracked through the accumulation of phase-information (i.e. the measure of a trigonometric distance) across time. Therefore, for a given physical duration preceding the target, trials that are associated with longer perceived durations should be associated with increased phase-evidence build-up (i.e., a larger range of phase-angles covered during the pre-stimulus period). When averaging trials, this should result in slightly faster (i.e., higher-frequency) oscillations within the same frequency-band for trials that are perceived as longer. To test this hypothesis, we measured whether different subjective reports of the same duration (for instance physically delayed Δt+ trials reported as ‘normal’ vs. ‘delayed’) were associated with distinct peak frequency within the (delta) frequency-band of interest. For each frequency within the band of interest (delta 1–3 Hz, 0.5 Hz increments), we primarily averaged the prestimulus power (−300 to −100 ms; estimated using wavelet transforms on a 2 seconds time-window, see¹) in functionally defined auditory sensors across trials. We then extracted the individual peak frequency (i.e., the frequency at which the power is maximal in the time window of interest) and measured the difference between frequency peaks distributions between correct vs. incorrect conditions across participants (Fig. 1A). To assess the statistical difference between experimental conditions while controlling for multiple comparisons, and accounting for the non-normality of some variables' distribution (e.g. peak frequency), all statistical comparisons used non-parametric permutations tests. For each statistical test (paired t-tests), we compared the statistic to the same statistic computed on randomly permuted data. The non-parametric statistic was performed by repeating 1000 times the calculation of a permutation test where the experimental conditions are randomly intermixed within each subject. This provided corrected p-values, reported as Pcorr.

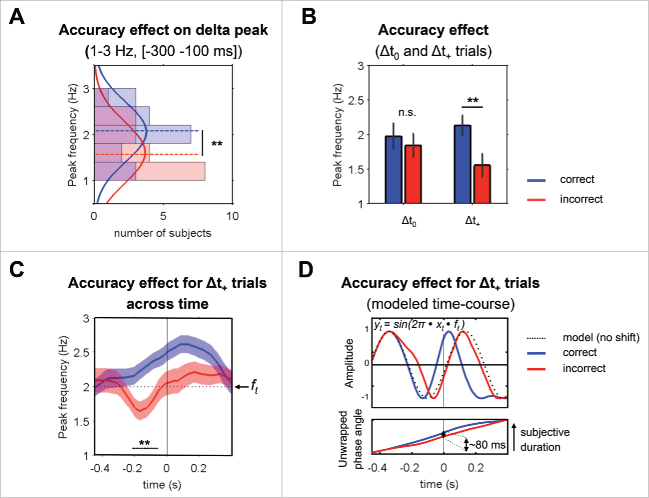
Figure 1.

Pre-stimulus delta (1–3 Hz) phase-angle ranges account for subjective percepts in the ∆t+ conditions. (A) Histogram of delta peak frequencies extracted per subject on prestimulus [−300 −100 ms] delta band activity between correct and incorrect conditions. Dashed horizontal lines indicate the mean frequency of correct (blue) and incorrect (red) distributions. ** indicate significance of the difference between peak frequency distributions at the p < 0.01 level. (B) Mean peak frequency differences between correct and incorrect conditions assessed separately for Δt₀ and Δt+ trials. ** indicate significance of the difference between the mean of peak frequency distributions at the p < 0.01 level; n.s. indicates non-significant difference. (C) Mean delta-band peak frequency across time (f_t) for Δt+ correct (blue) vs. Δt+ incorrect (red) trials. The procedure of individual frequency peak extraction used in Fig. 1A was repeated at each time point using a 200 ms sliding window for each condition. The horizontal dotted black line indicates the center frequency of the frequency band of interest (1–3 Hz). Shaded error bars indicate SEM and the thick black line shows significance of the difference between correct and incorrect conditions, after correction for multiple comparisons. Note that the apparent frequency up- or downward shifting does not reflect single-trial dynamics. This metric rather reflects that the proportion of higher frequency peak trials was larger in correct than in incorrect trial pools during the prestimulus time-window. (D) Top panel: Accuracy effect on the modeled time-course of oscillations. Oscillation models were drawn using the instantaneous frequencies provided by the mean peak frequency curves (f_t) in Fig. 1C applied at each time point t, according to the formula y_(t) = sin(2π • x_(t) • f_(t)). The black dotted line indicates the time-course of an ideal oscillation at the stationary frequency of 2 Hz (center frequency of the frequency band of interest). Blue and red lines represent the time-course of correct and incorrect conditions respectively. Bottom panel: unwrapped delta phase-angles during pre-stimulus time period are larger for correctly (blue, perceived ‘longer’) than incorrectly (red, perceived ‘normal’) detected delayed trials. Consistent with our to our hypothesis, at the target's occurrence, the phase-angle difference between correct and incorrect conditions in the ∆t₊ condition corresponds to a 80 ms subjective time-lag.

By comparing the distributions of peak frequencies across subjects during the pre-stimulus time window of interest (−300 to −100 ms), we found that the peak frequency of delta oscillations was higher for correct than incorrect trials (Fig. 1A, Pcorr = 0,02). When computing this measure separately for non-delayed (Δt₀) and delayed trials (Δt+), we found that the peak frequency was significantly higher for correct than incorrect trials only in the delayed conditions (Fig. 1B, Δt_0: Pcorr = 0.28; Δt_+: Pcorr = 0.005). This primarily suggests that the delta peak-frequency was slightly shifted in those delayed trials that were associated with longer subjective percepts. Using a sliding time-window of 200 ms, we also applied this measure across time to test for a potential build-up of phase-accumulation (Fig. 1C). We found that the delta-band peak frequency varies in an opposite manner between correct and incorrect (Δt₊) trials across time, speeding-up over time before the occurrence of the target only in correct trials (Fig. 1C). In other words, on average, correctly detected delayed-trials were associated with a slightly higher oscillatory frequency (i.e., larger delta phase-angles covered) during the pre-stimulus time-window than when the same duration was perceived as shorter.

Using the resulting time-course of instantaneous frequencies (designated as f_t in Fig. 1C), we modeled the corresponding oscillatory-course to provide a measure of subjective time difference between compared conditions (Fig. 1D). We found that the averaged phase angle difference between correct and incorrect trials roughly corresponds to an 80 ms difference in subjective duration (see double black arrow in Fig. 1D). This value is consistent with the minimal delays that the subject had to detect in this experiment (75 ms) and supports the notion that the instantaneous phase of delta oscillations could potentially be exploited to precisely measure elapsed time.

Building on evidence showing that (i) the motor system is recruited during rhythmic perception,^6,9,10 and (ii) that motor efferent signals directly modulate activity in the auditory cortex,¹¹ we recently conjectured that the sensori-motor system predicts upcoming events by “simulating” movement synchronized with external events.^1,4,10 Consistent with other findings showing that the motor system is involved in duration perception at the seconds time-scale,^9,12-14 we speculated that evaluating short durations could be achieved through motor simulation. According to this idea, short durations (on the order of seconds) can be accurately evaluated by deriving the length of the trajectory simulated during this duration, i.e., by converting time elapsed into a (simulated) distance. Crucially, it was recently shown that delta oscillations predictively entrain to periodic sequences in the motor system.⁶ By analogy with the notion that the phase of theta-band (4–8 Hz) oscillations indexes spatial distance in the rat hippocampus,^15,16 we propose that the phase of ongoing delta oscillations might reflect the course of a simulated (motor) trajectory. In this context, phase-evidence accumulation could be used to keep track of the simulated distance, which in turn would provide a subjective index of duration.

While such a mechanism provides an appealing explanation to predict whether delayed targets will be detected or not, it is insufficient to explain why non-delayed targets are falsely detected as delayed in our data. It is possible that the rather small proportion of incorrect trials in the Δt₀ condition (< 5% of all trials, less than 10 trials per participant on average) does not permit us to reliably assess this effect. While partially consistent with our results, the notion that time is converted into a simulated motor trajectory remains highly speculative and requires further investigation. We believe however that it offers a simple and efficient potential mechanism to explain how the brain accurately measures duration at the seconds time-scale.

Disclosure of potential conflicts of interest

No potential conflicts of interest were disclosed.

Funding

This work was supported by the Fondation Louis Jeantet (L. H. A. and A. K.), and NIH 2R01DC05660 (to David Poeppel, NYU; L. H. A. worked at NYU at time of data collection).