Chronic Stress Alters Striosome-Circuit Dynamics, Leading to Aberrant Decision-Making

SUMMARY

Effective evaluation of costs and benefits is a core survival capacity that in humans is considered as optimal, ’rational’ decision-making. This capacity is vulnerable in neuropsychiatric disorders and in the aftermath of chronic stress, in which aberrant choices and high-risk behaviors occur. We report that chronic stress exposure in rodents produces abnormal evaluation of costs and benefits resembling non-optimal decision-making in which choices of high-cost/high-reward options are sharply increased. Concomitantly, alterations in the task-related spike activity of medial prefrontal neurons correspond to increased activity of their striosome-predominant striatal projection neuron targets and to decreased and delayed striatal fast-firing interneuron activity. These effects of chronic stress on prefronto-striatal circuit dynamics could be blocked, or be mimicked, by selective optogenetic manipulation of these circuits. We suggest that altered excitation-inhibition dynamics of striosome-based circuit function could be an underlying mechanism by which chronic stress contributes to disorders characterized by aberrant decision-making under conflict.

Graphical Abstract

INTRODUCTION

The ability to perform integration of costs and benefits is essential for resolution of motivational conflict during value-based decision-making (Glimcher and Fehr, 2013). Abnormal decision-making, including risky or irrational choices leading to negative outcomes, can emerge as a symptom in neurologic and neuropsychiatric disorders, including anxiety and depression, bipolar disorder, Huntington’s disease, schizophrenia, and suicidality (Amemori and Graybiel, 2012; Aupperle and Paulus, 2010; Gleichgerrcht et al., 2010; Szanto et al., 2015). The development of such disorders can be facilitated by exposure to chronic stress (Pittenger and Duman, 2008; Selye, 1936); and prolonged stress can itself induce aberrant decision-making (Schwabe and Wolf, 2009; Soares et al., 2012; Sousa and Almeida, 2012). These findings and other pioneering work demonstrates that the induction of dysfunctional neuronal circuitry due to prolonged environmental stress can deleteriously affect mental health (Lucassen et al., 2014; Pittenger and Duman, 2008; Selye, 1936; Sousa and Almeida, 2012). Within the brain, widespread effects of chronic stress have been reported (Dias-Ferreira et al., 2009; Lucassen et al., 2014; Sousa and Almeida, 2012), but the cell- and circuit-level mechanisms underlying these effects still are not fully understood (Dias-Ferreira et al., 2009; Lucassen et al., 2014; Sousa and Almeida, 2012).

Here, we examined the effects of chronic stress on a prefrontal corticostriatal circuit that has been implicated in evaluation of cost, effort and reward (Amemori and Graybiel, 2012; Friedman et al., 2015; Rushworth et al., 2011) and is related to cortical regions that in humans are affected in individuals suffering from anxiety, depression and related problems (Aupperle and Paulus, 2010). This circuit preferentially targets the neurochemically specialized striosomes in the rodent dorsomedial ’associative’ striatum, a striatal region affected by chronic stress along with the prefrontal cortex itself (Arnsten, 2015; Dias-Ferreira et al., 2009). We earlier found that this prefronto-striosomal circuit selectively modulates decision-making under conditions of motivational conflict in which cost-benefit decisions must be made (Amemori and Graybiel, 2012; Friedman et al., 2015). Optogenetic disconnection of the prelimbic region of the prefrontal cortex (PFC-PL) from its putative striosomal targets in the dorsomedial striatum provoked rats to make abnormal choices in which they increased their choices of high-cost/high-reward options, mimicking abnormal decision-making and reflecting abnormal utility functions (Friedman et al., 2015). Within the striatum, both projection neurons (SPNs) and fast-spiking interneurons (FSIs) (Gage et al., 2010; Tepper et al., 2004) were impacted by this circuit disconnection.

We trained rats and mice on the same cost-benefit conflict (CBC), benefit-benefit (BB) and cost-cost (CC) tasks, and then exposed them to chronic stress and re-tested their performance. To our surprise, the behavioral effects of the chronic stress were nearly indistinguishable from those that we had found by optogenetically disconnecting the medial prefrontal cortex from its striosomal targets in the dorsomedial striatum (Friedman et al., 2015). Behavioral performance was abnormal in the CBC task but not in the other decision-making tasks. This striking similarity suggested that we might be able to identify specific prefronto-striatal circuit malfunctions induced by chronic stress. We therefore combined electrophysiological recording with optogenetic manipulations to compare cohorts of unstressed and chronically stressed rats and engineered mice in which we had preferential access to putative FSIs.

We demonstrate that chronic stress radically alters the dynamic functioning of this prefronto-striosomal circuit by altering feed-forward inhibition in parallel with the induction of aberrant CBC decision-making. We show that we could block these effects of stress by optogenetically exciting striatal FSIs, that we could mimic these effects by optogenetically inhibiting striatal FSIs, and that we could model these effects in Hodgkin-Huxley models. These findings provide causal evidence that a prefronto-striatal circuit engaging striosomes is targeted specifically by chronic stress so as to produce a functional phenocopy of a prefronto-striosome disconnection syndrome.

RESULTS

Chronic Stress Selectively Impairs Cost-Benefit Conflict Decision-Making

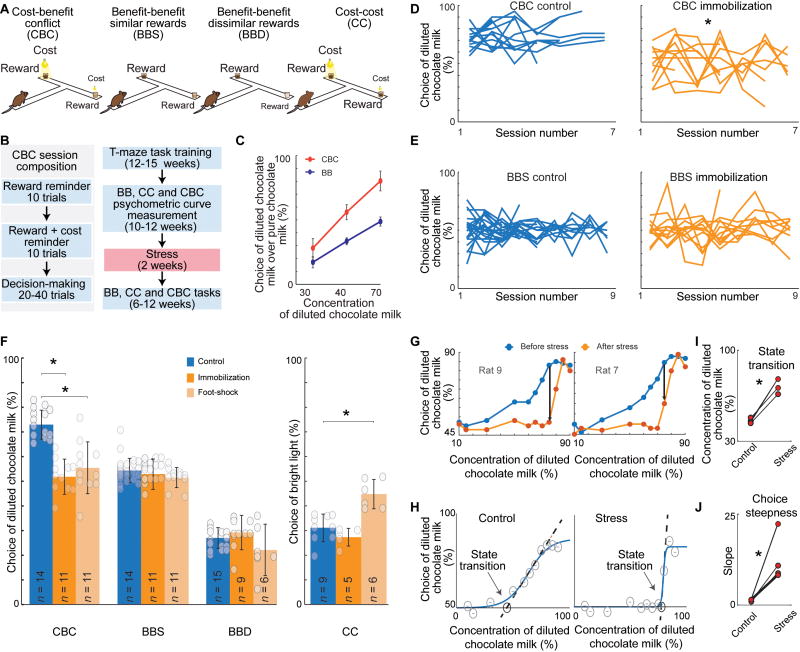
We compared groups of control and chronically stressed rats and mice for four different types of decision-making in T-maze tasks (Figure 1A, Method Details). The main CBC decision-making task presented a conflict between the choice of pure chocolate milk (high reward) paired with aversive strong light (high cost) and the choice of diluted chocolate milk (low reward) paired with dim light (low cost). We further introduced two BB decision-making (BB) tasks and a CC decision-making (CC) task. Animals were trained in stages and over-trained to minimize choice variability (Figure 1B). For each rat and mouse, we measured the psychometric function that related choice to concentration of chocolate milk and light intensity, and calibrated the concentration of diluted chocolate milk and strong light intensity to achieve similar decision-making boundaries for each rodent for each task (Figures 1C, S1A and S1B). We then exposed cohorts of animals to 14 days of constraint or shock stress (Method Details), with control cohorts not exposed to stress, and then measured performance in the four decision-making tasks (n = 22 rats, n = 23 mice).

Figure 1. Chronic Stress Selectively Affects CBC Decision-Making.

(A) The four decision-making tasks.

(B) Single session diagram (left) and experimental timeline (right). For immobilization stress, rats and mice were immobilized, respectively, for 4 and 1 hr/day. For foot-shock stress, rats received 50 shocks, each lasting 3 s, over 1 hr. Both stress protocols were repeated on 14 consecutive days.

(C) Mean (± SD) psychometric function for a single rat performing CBC and BB tasks. See also Figures S1A and S1B.

(D and E) Performance in CBC (D) and BBS (E) tasks by individual control (left) and immobilization stressed (right) rats over 6–12 weeks. *p < 0.001 (CBC control vs. CBC immobilization, ANOVA repeated measures with Bonferroni correction). Intervals between two consecutive sessions were 1–2 weeks. See also Figure S1C.

(F) Decision-making by control and stressed rats performing the 4 tasks. Mean was calculated for each rat (dots), then mean and SD were calculated for each group. *p < 0.001 (one-way ANOVA with Bonferroni correction). See also Figure S1D.

(G) Psychometric functions of two rats for CBC task before (blue) and after (orange) stress. See also Figures S1G and S1H.

(H) Single rat’s psychometric function before (left) and after (right) chronic stress, modeled using a four-parameter sigmoid. The concentration of diluted milk was varied across sessions (circles), and a logistic curve was fitted to the data. Arrows show the onset of linear cost-benefit integration. The dashed lines show the linear trend of the choice behavior.

(I and J) Stress delayed the onset (I) and increased the slopes (J) of linear cost-benefit integration. *p < 0.05 (paired t-test).

The effect of chronic stress on decision-making was strikingly selective. The stressed animals were significantly more likely to choose high-cost/high-reward options than matched controls in the CBC task (Figures 1D–1F, S1C–S1F), yet they performed like the control animals in the BB and CC tasks after restraint stress, and differed from controls only in the CC task after foot-shock stress. The choice variability in the CBC sessions was also increased in the stressed animals (Figure S1E and S1F). The penetrance of the effects was high across gender, stress protocol and mouse strain (Figure S1F).

These effects coincided with marked shifts in the psychometric functions measured in the rats by incrementally changing the concentration of reward across sessions (Figures 1G, S1G and S1H). We modeled these psychometric functions to parameterize the condition in which the choice behavior exhibited four- and two-parameter sigmoidal curves (Figures 1H–1J and S1I–S1L, Detailed Methods). The range of options in which the choice behavior could be characterized by the psychometric curves was markedly different between control and stressed animals. As the concentration of the diluted chocolate milk of the low-cost side increased, the control rats began to choose that option, following a linear function paralleling the increasing utility (Train, 2002) of the low-cost/low-reward option. However, the stressed rats began responding to increases in utility only after large increases in chocolate concentration of the diluted chocolate milk, and when they did so, suddenly began to choose the low-cost/low-reward side, following a step function. These results indicate that the animals exposed to chronic stress failed to exhibit normal integration of cost and benefit over most of the large range of cost-benefit options.

The fact that we observed no clear effect of the chronic stress on decisions made in the BB and CC tasks was surprising, given evidence that links chronic stress with anxiety and anhedonia (Ampuero et al., 2015). Therefore, we tested for these symptoms in the rats using two-bottle task tests. In a two-bottle sucrose-preference test, the previously stressed rats exhibited diminished choices of sucrose over water, but in a test with chocolate milk, the pure chocolate milk preference was not affected (Figures S1M and S1N). We also found no difference in light avoidance behavior between the control and stressed groups (Figures S1O and S1P). We found no significant difference in run times or in previous choices on subsequent decisions across choice sequences for stressed and non-stressed rats (Figures S1Q–S1S).

A Prefronto-Striatal Pathway Preferentially Targeting Striosomes Causally Affects Decision-Making

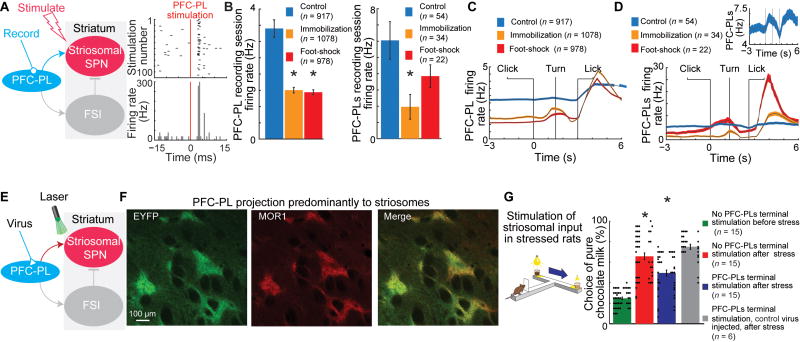
To examine the potential cellular effects of chronic stress on neurons in this prefronto-striatal circuit, we recorded the spike activity in the PFC-PL cortex (Figure S2A), and we also identified a sub-population of the PFC-PL neurons that project to the striatum (PFC-PLs neurons) (Figure 2A, and Method Details). The average firing rates over the entire recording window were reduced for both PFC-PL and PFC-PLs units in the stressed animals (Figure 2B). Chronic stress affected activity in three sub-periods: activity during the pre-click baseline and click-to-turn periods was reduced after stress, whereas the lick sub-period had higher activity after stress (Figures 2C–D and S2B–F). There was no change in PFC-PLs firing rate during the BB task with similar rewards (BBS, Figure S2G).

Figure 2. Effect of Chronic Stress and Optogenetic Manipulation of the PFC-PLs.

(A) Antidromic stimulation to identify PFC-PL neurons that project to the striatum (PFC-PLs neurons, left), and raster plot (top) and histogram (bottom) for an identified PFC-PLs neuron (right).

(B) PFC-PL (left) and PFC-PLs (right) firing rates in control and stressed rats. *p < 0.01 (Kolmogorov–Smirnov test and t-test). Error bars, SEM.

(C and D) PFC-PL (C) and PFC-PLs (D) activity in stressed and control rats during CBC task. Inset, magnified activity of control group.

(E) Manipulating PFC-PLs terminals in dorsomedial striatum.

(F) PFC-PL corticostriatal projections virally labeled with enhanced yellow fluorescent protein (EYFP, green), striosomes immunostained for mu-opioid receptor 1 (MOR1, red), and a merged image (yellow). In targeted dorsomedial striatal region, the EYFP signal intensity was 4.71 ± 0.68 fold higher in MOR1⁺ striosomes than in matrix.

(G) Optogenetic excitation of PFC-PLs terminals normalizes CBC choice of stressed rats. Dots show choice in each session. *p < 0.001 (one-way ANOVA with Bonferroni correction).

We tested for a causal relationship between the aberrant choices and the function of the prefrontal projection preferentially targeting striosomes by injecting the PFC-PL region with either AAV5-CaMKIIa-eNpHR3.0-EYFP for optogenetic inhibition, AAV5-CaMKIIa-C1V1(E122T/E162T)-TS-EYFP for optogenetic excitation or a control virus (AAV5-CaMKIIa-EYFP) and, after 5–8 weeks, applying laser light (590 nm or 532 nm wavelengths, respectively) to the dorsomedial striatum for 3 s after a click cue signaling trial start (Figures 2E and 2F). In the chronically stressed rats, optogenetic inhibition of PFC-PL terminals had no effect on CBC decision-making beyond that found after stress alone (n = 4, Figure S2H). By contrast, optogenetic excitation of the intrastriatal PFC-PL terminals led to partial normalization of performance in the stressed rats (n = 15, Figures 2G and S2I). These results suggest that optogenetic boosting of activity in the striosome-targeting PFC-PL pathway can help to block the effects of prior chronic stress on choice behavior.

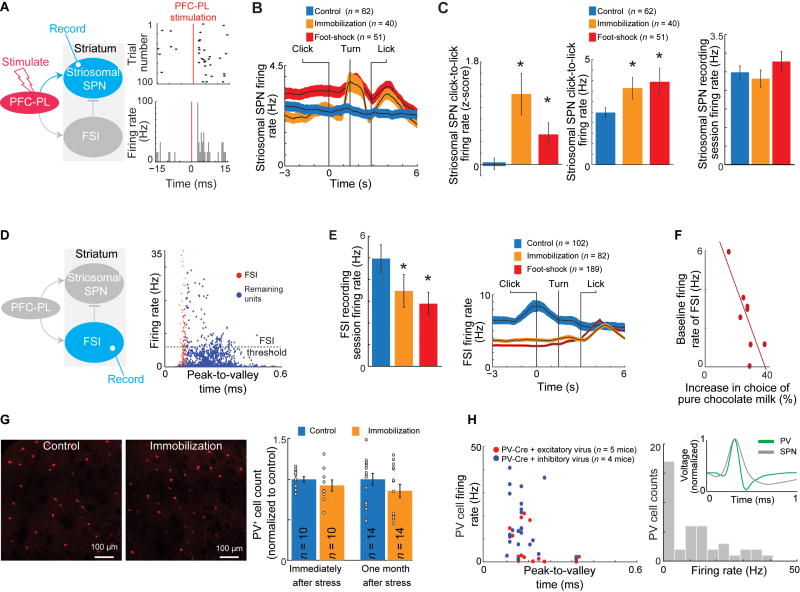
Chronic Stress Strongly Increases Firing Rates of Striosomal SPNs during CBC Performance

We identified putative striosomal SPNs in the dorsomedial striatum (Figure S2J) by orthodromic stimulation of the PFC-PL through chronically implanted tetrodes and measured the activity of responding striosomal SPNs (Figures 3A and S3A–S3P; Method Details; Friedman et al., 2015). During the click-to-lick period, the PFC-PL-recipient putative striosomal SPNs were strikingly more active in the stressed rats than in controls (Figures 3B, 3C and S3Q–S3T). Yet firing rates over the entire recording window were similar in both groups (Figure 3C). We found no consistent effect of stress on putative matrix SPNs, identified by an absence of response to PFC-PL stimulation (Figures S3Q–S3U). Striosomal SPN firing rates were similar in stressed and control rats in the BBS task (Figure S3V). These findings suggest temporally selective effects of the prior stress on striosomal SPNs during the critical click-to-lick period in the CBC task.

Figure 3. Striatal Activity after Chronic Stress.

(A) Orthodromic stimulation to identify striosomes (left) and an identified striosomal SPN (right).

(B) Mean (± SEM) firing rates of striosomal SPNs during CBC task.

(C) Stress significantly increased normalized (left) and raw (middle) firing rates of striosomal SPNs during click-to-lick period, but not over full recording session (right) *p < 0.01 (Kolmogorov–Smirnov test and t-test).

(D) FSI recording (left) and classification (right).

(E) FSI activity during the entire session (left) and click-to-turn period (right). *p < 0.01 (Kolmogorov–Smirnov test and t-test).

(F) FSI firing rates were inversely correlated with increases in choice of pure chocolate milk in CBC task (p < 0.01, Pearson correlation).

(G) PV-immunostained striatal sections from control and stressed (immobilization) mice (left), and numbers of PV⁺ neurons (right).

(H) Peak-to-valley times (left) and firing rate distribution (right) of optogenetically identified PV⁺ neurons. Inset, spike waveforms.

Chronic Stress Strongly Decreases the Activity of FSIs during CBC Performance

We previously found in normal rats that striatal FSIs can influence CBC decision-making (Friedman et al., 2015). We therefore asked whether diminished FSI activity could contribute to the striosomal hyperactivity and behavioral effects that we observed in the chronically stressed animals. We initially classified units with narrow spike widths and high firing rates as FSIs (control rats: n = 6496; immobilization stress: n= 7463; foot-shock stress: n = 8787) (Figures 3D and S4A–S4F; Methods Details). Prior stress produced a reduction in the number of putative FSIs and a significant inverse correlation between the proportion of FSIs encountered and the individual effect of stress in each animal (Figures S4G and S4H).

To determine whether the reduction of identified FSIs reflected a real reduction of FSI numbers or a misclassification because of low firing rates, we followed three approaches: First, we identified FSIs as narrow width units (Gage et al., 2010; Kawaguchi, 1993) and found a wide range of firing rates among them. Identified FSIs with high and low firing rates had indistinguishable peak-to-valley and valley widths (Figures S4D–S4F). Prior exposure to stress strongly reduced these FSI firing rates, but did not affect the proportion of units identified as FSIs out of all neurons recorded in the dorsomedial striatum (Figures 3E, S4I and S4J). Strikingly, the stress-induced change in CBC performance of each rat was strongly correlated with its FSI firing rate, but not with FSI proportion (Figures 3F and S4K). We also found a significant reduction in FSI firing rate during the BBS task (Figure S4L), but not in firing rates of PFC-PLs neurons or putative striosomal SPNs so that not all circuit elements could be identified as abnormal in this task, in which behavior was also not abnormal.

Second, because of the known overlap of parvalbumin-immunoreactive (PV⁺) cells and FSIs (Kawaguchi, 1993; Szydlowski et al., 2013), we used histology to analyze the number of PV⁺ cells in control mice and chronically stressed mice immediately (n = 10 per group) or one month (n = 14 per group) after immobilization stress. The PV⁺ cell count decreased only slightly and insignificantly at both time points (Figure 3G), suggesting that the primary stress effect was not neuronal death, but a reduction in FSI firing rates.

Finally, we verified that the FSIs indeed reflected PV⁺ cells by determining the electrophysiological properties of the PV⁺ cells identified optogenetically in PV-Cre mice. We injected 5 PV-Cre transgenic mice with excitatory opsin (AAV5-EF1a-DIO-C1V1(E122T/E162T)-TS-EYFP) and 4 with inhibitory opsin (AAV5-EF1a-DIO-eArch3.0-EYFP) viruses. Over 90% of the optogenetically identified neurons (92%, 39 out of 42) exhibited narrow waveforms and a wide spectrum of firing rates, indicating that indeed striatal FSIs overlap strongly with PV⁺ neurons (Kawaguchi, 1993; Kim et al., 2016; Szydlowski et al., 2013) (Figures 3H, S4M and S4N).

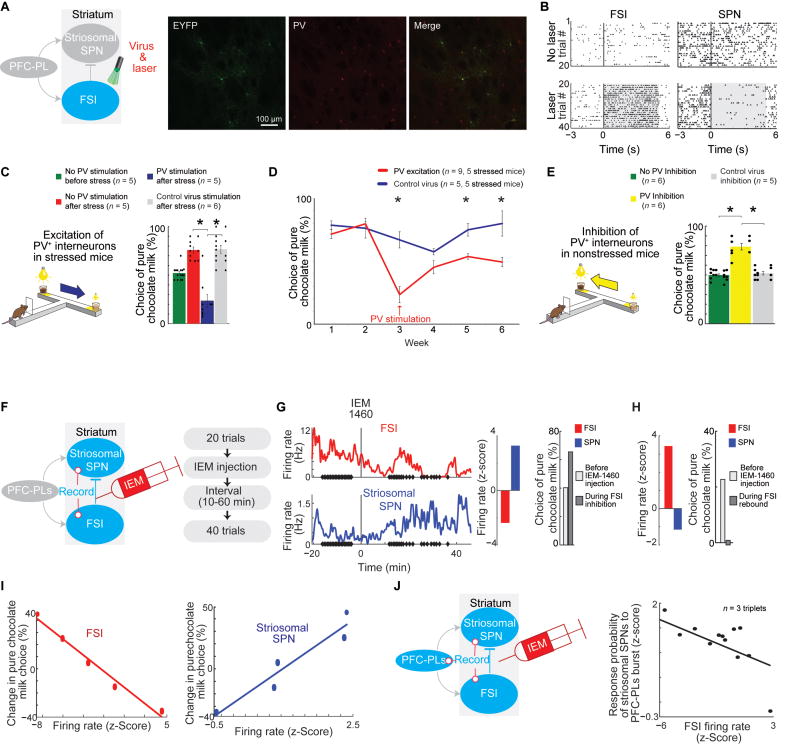
Bidirectional Optogenetic Control of PV⁺ Neurons Can Mimic or Rescue CBC Choice Behavior

If the reduced FSI firing rates were causally related to the increased preference for risky high-cost/high-reward CBC options after chronic stress, then manipulations of these neurons in stressed animals should at least partially rescue the behavioral abnormality. This was the case. We injected inhibitory (AAV5-EF1a-DIO-eArch3.0-EYFP) or excitatory (AAV5-EF1a-DIO-C1V1(E122T/E162T)-TS-EYFP) virus into the dorsomedial striatum of PV-Cre transgenic mice (Figure S4O), and optogenetically manipulated PV⁺ neurons (532 nm wavelength, 25-Hz pulses for 5 s for excitation, 1 pulse for 3.5 s for inhibition) beginning at the click (Figure 4A), thereby putatively exciting SPNs through PV inhibition, or inhibiting SPNs through PV stimulation (Figures 4B and S4P).

Figure 4. Causal Relationship between PV⁺ Neuron Activity and Stress.

(A) Optogenetic manipulation experiment (left), and, from left to right, virus-expressing (green, EYFP) and PV⁺ (red) neurons in PV-Cre mice, and merged image (yellow).

(B) A PV⁺ neuron (left) and SPN (right) recorded during 20 CBC trials without (top) and with (bottom) optogenetic PV excitation (shading).

(C) Optogenetic excitation of PV⁺ neurons in stressed mice reverses the effects of stress. *p < 0.001 (one-way ANOVA with Bonferroni correction). Error bars, SEM.

(D) Long-term effect of optogenetic PV excitation in stressed mice (p < 0.001, repeated measures ANOVA with Bonferroni correction). *p < 0.001 (post hoc Tukey’s).

(E) Optogenetic inhibition of PV⁺ neurons in non-stressed mice mimics the stress effects. *p < 0.001 (one-way ANOVA with Bonferroni correction).

(F) Intrastriatal IEM-1460 injections to test the causal relationship between FSI and striosomal SPN activity.

(G) IEM-1460 injection reduced FSI activity (top) and increased striosomal SPN activity (bottom). Dots show trial start. Z-score quantification of the firing rate changes (middle). Choice of pure chocolate milk (right).

(H) FSI activity rebound and striosomal SPN activity reduction (left), and choice of pure chocolate milk (right) about 40–120 min after IEM-1460 injection.

(I) FSI (left) and striosomal SPN (right) firing rates after IEM-1460 injection correlated with choice of pure chocolate milk (p < 0.01, Pearson correlation test).

(J) Simultaneous recordings of a PFC-PL, FSI and striosomal SPN after IEM-1460 injection (left), and probability that PFC-PLs bursts evoke striosomal SPN bursts, given FSI firing rates (right, p < 0.01, Pearson correlation test).

PV⁺ neuron excitation in stressed mice rescued the effects of the prior stress: this manipulation sharply increased the frequency of low-cost/low-reward choices (Figure 4C), and this partial restoration lasted for up to one month without additional stimulation (Figure 4D). Moreover, optogenetic inhibition of PV⁺ neurons applied to non-stressed mice increased high-cost/high-reward choices to the levels seen in paired chronically stressed mice (Figure 4E). Thus increasing or decreasing the firing rates of striatal PV⁺ neurons can drastically affect CBC decision-making, and can rescue the effects of prior exposure to chronic stress or, conversely, mimic them.

Pharmacologic FSI Inhibition during CBC Performance Causally Affects FSI-SPN Firing Rate Balance and Behavioral Choice in CBC Task

To test the potential causal relationship between FSI firing rates, striosomal SPN firing rates, and decisions made in the CBC task, we injected IEM-1460 (1 mg/kg), an inhibitor of GluA2-lacking AMPARs that blocks synaptic excitation of striatal FSIs (Gittis et al., 2011), into the dorsomedial striatum. We tested the performance of the rats on the CBC task (Figure 4F) and recorded the activity of putative striosomal SPNs and FSIs. During the first ~40 min post-injection, the FSI activity decreased, whereas SPN activity increased (Figures 4G and S4Q). In the later, apparently rebound, phase (~40–120 min post-injection), FSI firing rates significantly increased, and the SPNs were inhibited (Figure 4H). Thus in both phases, we found an inverse relationship between the FSI and striosomal SPN firing rates. Changes in activity after saline injections were nil (Figure S4R).

In the IEM-1460 injection group, we found very strong correlations between the changes in firing rates of striosomal SPNs and FSIs and the changes in CBC choices (Figures 4I and S4S). Further, there was a strong correlation between the FSI firing rates and the probability of a PFC-PLs burst to be followed by a striosomal SPN burst (Figures 4J and S4T). This evidence further supports a causal relation between alterations in the prefronto-striosomal circuit and CBC choice.

Dynamics in the PFC-PLs Circuit Targeting Striosomes Are Altered after Chronic Stress

In control rats, the PFC-PLs-striosomal circuit activity formed a temporal PFC-PLs → FSI → striosomal SPN cascade during performance of the CBC task. Shortly after PFC-PL activation, striosomal SPNs were inhibited, whereas FSIs were activated. Strikingly, prior exposure to chronic stress produced a delay up to seconds in FSI activity, relative to their peak firing in controls (Figures 5A, 5B, S5A and S5B). When FSIs were relatively active, activity occurred after the turn, thus too late to inhibit the earlier striosomal activation (Figures 5C, 5D and S5C–S5H). We tested whether this post-stress FSI late firing could be accounted for by a reduction in the number of co-active PFC-PLs neurons among the CBC task-responsive prefrontal neurons. We also performed a population analysis of the PFC-PLs virtual population and found that during the click-to-turn period, prior stress exposure reduced temporally coordinated PFC-PLs activity (Figure S5I). However, this count of co-active PFC-PLs neurons was increased during the turn-to-lick period, potentially triggering late FSI activity (Figure S5I). Thus, the dynamics of the circuit during the maze runs were fundamentally altered in the chronically stressed animals, with late or even absent FSI activity accompanied by strong, abnormal activation of striosomal SPNs that, in the control animals, exhibited little activity.

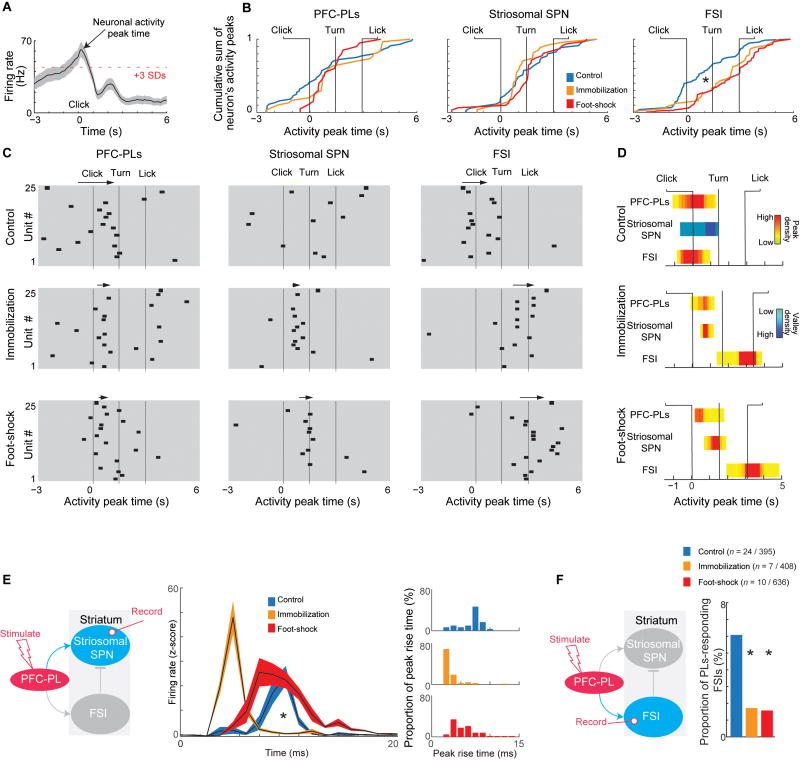
Figure 5. Stress Effect on Corticostriatal Circuit Dynamics.

(A) Activity peak (> 3 SDs) identified for each neuron.

(B) Cumulative sum of activity peak times. FSI activity peaks were significantly delayed after stress. *p < 0.001 (Kolmogorov–Smirnov test). See also Figure S5B.

(C) Dynamics of PFC-PL-striosomal circuit components. Individual neurons are shown horizontally. Black squares, activity peak time. Arrows, high-activity periods (see Figure S5C). See also Figures S5E and S5G.

(D) Relative activity (high: yellow to red; low: blue) of PFC-PLs neurons, striosomal SPNs and FSIs measured by concentration of maxima or minima across time windows. See also Figure S5C.

(E) Recording of striosomal SPN and FSI responses to PFC-PL microstimulation (left), striosomal SPN responses (middle) and earlier striosomal peak times in stressed animals (right). See also Figures S5J and S5K. *p < 0.001 (Kolmogorov–Smirnov test and t-test). Shading, SEM. See also Figures S5J and S5K.

(F) Stress significantly reduces the number of FSIs that respond to PFC-PL stimulation. *p < 0.01 (chi-square test).

Chronic Stress Strengthens Striosomal Responses to PFC-PL Microstimulation and Weakens FSI Responses

To test for a potential change in functional connectivity between PFC-PL, striosomal SPNs and FSIs, we measured the responses of putative striosomal SPNs and FSIs to electric microstimulation applied to the PFC-PL in chronically stressed and control rats (Figure 5E, Method Details). After chronic stress, the number of responsive striosomal SPNs was unchanged, but the peak firing of these SPNs in response to PFC-PL stimulation occurred earlier and was stronger than in the unstressed animals (Figures 5E, S5J and S5K). By contrast, far fewer FSIs responded to PFC-PL stimulation, even though, as outlined above, the numbers of FSIs and PV⁺ neurons were unchanged (Figures 5F and 3G). Thus, chronic stress reduces the FSI activation by the PFC-PL, reducing feed-forward inhibition of the SPNs and shifting the balance of excitation-inhibition in striosomes toward excitation.

Chronic Stress Increased the Interaction between PFC-PLs and Striosomal SPN Bursts, but Decreased Interaction between PFC-PLs and FSI Bursts

We earlier found that a focus on spike bursts provided a clearer picture of the interaction between elements of the prefronto-striosomal circuit than did a focus on spike rates alone (Friedman et al., 2015). We tested for this feature in chronically stressed (n = 9) and control (n = 14) rats. In the stressed rats, we detected more pairs of PFC-PLs neurons and SPNs with significant short-time interaction starting immediately after PFC-PL burst (control: 2/30, immobilization stress: 13/36, foot-shock stress: 7/30), suggesting an increased interaction between the PFC-PLs neurons and striosomal SPNs or common source influence (Figures 6A and S6A–S6D). With the same methods, we measured the timing relations of spike bursts of PFC-PLs neurons and FSIs and found fewer PFC-PLs-FSI interacting pairs in stressed than control rats (Figure 6B), consistent with the effects found by direct cortical microstimulation.

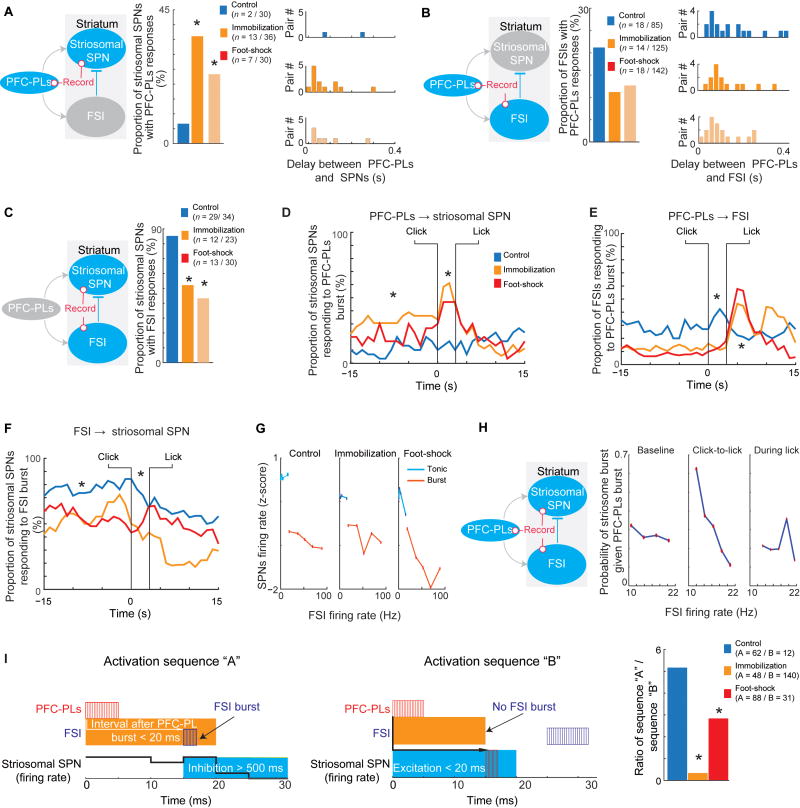
Figure 6. Stress Effect on the Relationships between PFC-PLs neurons, FSIs and Striosomal SPNs.

(A) Simultaneous recording of PFC-PLs neuron and striosomal SPN to measure delays between PFC-PLs and striosomal bursts (left), proportion of PFC-PLs-striosomal interacting pairs (middle) and delays between striosomal SPN and PFC-PLs bursts (right). *p < 0.01 (chi-square test).

(B) Simultaneously recorded PFC-PLs neuron and FSI, shown as in A.

(C) Simultaneous recording of striosomal SPNs and FSI (left), and proportion of FSI-striosomal SPN interacting pairs (right). *p < 0.01 (chi-square test).

(D–F) Stress increased interaction (see Figures S6C–S6E) between PFC-PLs and striosomal SPN bursting during the baseline and click-to-lick periods (D), but decreased interaction between PFC-PLs neurons and FSIs during the baseline and click-to-turn periods, with an increase during the licking period (E). Striosomal SPN inhibition by FSIs was smaller after stress (F). *p < 0.05 (Kolmogorov–Smirnov and chi-square tests).

(G) Burst FSI activity inhibited striosomal SPNs more than tonic FSI activity (p < 0.001, bootstrap vs. shuffled time recordings) in both control and stressed rats (p = 0.1).

(H) Triplets of PFC-PLs neuron, striosomal SPN, and FSI simultaneously recorded in a control rat. Probability of striosomal burst given PFC-PLs burst depended on FSI firing rate only during the click-to-lick period (p < 0.01, Pearson correlation test).

(I) Two firing sequences identified by Granger causality in triplets recorded in control and stressed rats performing CBC task. In sequence A, an FSI burst succeeded a PFC-PLs burst by <20 ms, reducing striosomal activity for >500 ms, ending with a striosomal burst, suggesting feed-forward inhibition (left). In sequence B, a PLC-PLs burst was succeeded by a striosomal burst by <20 ms, leading to an FSI burst, suggesting an absence of feed-forward inhibition (middle). Stress reduced feed-forward inhibition (the ratio of sequences A to B, right). *p <0.001 (chi-square test).

Effective FSI Inhibition of Striosomal SPN Spiking during CBC Performance Is Decreased after Chronic Stress

We next estimated the potential connectivity of the putative striatal FSIs and striosomal SPNs by determining the duration of the interval in which FSI activity induced a reduction in SPN firing rate (Figures 6B and S6E, Methods Details). As reported before (Friedman et al., 2015; Gage et al., 2010), there was in controls no apparent inhibition of SPNs during tonic FSI activity, but a pronounced inhibition when FSIs fired in bursts. In stressed animals, the numbers of interacting FSI-striosomal SPN pairs were significantly reduced (control: 29/34, immobilization stress: 12/23, foot-shock stress: 13/30) (Figure 6C). The number of FSI pairs with non-striosomal (putative matrix) SPNs was unaffected (Figure S6F).

We conducted an analysis of putative PFC-PLs neuron, FSI and striosomal SPN pairs and triplets in order to clarify the mechanism and dynamics of interactions between neurons in the circuit. A pair analysis at each time point during CBC task performance showed that during the click-to-lick period, there were more PFC-PLs-responding putative striosomal SPNs in stressed animals, but fewer responding FSIs (Figures 6D–6F). To examine the mechanism behind this reduction in PFC-PLs-to-FSI interaction, we measured PFC-PLs synchronous burst activity prior to FSI bursts during the click-to-lick interval. We found that during this period both augmented activity and synchronous firing of PFC-PLs neurons before FSI activation was necessary to evoke an FSI burst (Figure S6G). Additionally, PFC-PLs and FSI firing rates were correlated in simultaneously recorded neurons (Figure S6H). We examined the mechanism behind FSI-SPN interaction by measuring the influence of FSI tonic and burst activity on SPN activity (Figure S6I), but failed to find an effect of chronic stress on the ability of FSI tonic and burst activity to inhibit striosomal and matrix SPNs (Figures 6G and S6J). After chronic stress, the effective PFC-PLs-to-SPN activity significantly increased, and the effective PFC-PLs-to-FSI activity decreased. Our correlation analysis indicates that ability of FSIs to inhibit SPNs was unchanged despite a reduction in detected pairs after stress.

We identified 4 triplets of PFC-PLs neuron, striosomal SPN, and FSI that had frequent and significant short-time interactions (Figures S6C and S6E). We found that the FSIs influenced the probability of SPN bursts following PFC-PLs bursts only during the click-to-lick interval (Figure 6H). This result supports the task-related interaction among elements of the PFC-PLs-FSI-striosomal SPN circuit. We also applied the Granger causality method to identify functionally connected triplets during the click-to-turn interval (n = 14 for control, 18 for immobilization stressed and 14 for foot-shock stressed). We focused on two activation sequences: sequence A in which the PFC-PLs burst preceded the FSI burst, which led to striosomal SPN inhibition; and sequence B where the PFC-PLs burst was followed by a striosomal SPN burst either without an FSI burst or with a delayed FSI burst (Figure 6I). After stress, we observed a significant reduction of the sequence A and an increase of the sequence B.

Hodgkin-Huxley Circuit Modeling Suggests That Chronic Stress Alters Excitation-Inhibition (E–I) Balance in the Cortico-Striosomal Circuit

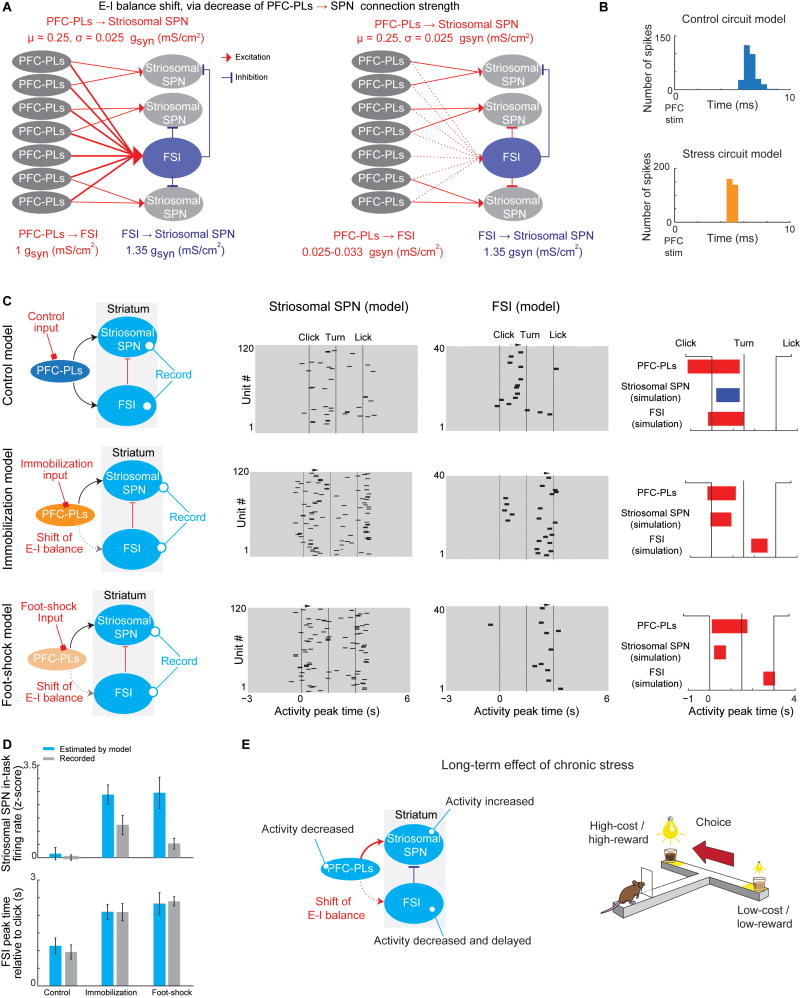
Our experimental findings raised the possibility that a shift in E–I balance in the cortico-striosomal circuit could be a dominant effect of prior exposure to chronic stress. To test this view, we created Hodgkin-Huxley models of a normal circuit and a circuit exposed to stress (Destexhe et al., 1994), implementing a simplified version of the network consisting of seven excitatory PFC-PLs neurons, three striosomal SPNs, and one FSI (Figure 7A and Methods Details). We adjusted functional connectivity strengths among neurons in the circuit so that synchronous input to PFC-PLs would cause SPN spikes with delays similar to those observed in our PFC-PL microstimulation experiment (Figures 5E and 7B). The decrease of PFC-PL-to-FSI connectivity, which was found in stressed animals in our experiment (Figures 5F and 6B) and modeled here, replicated the early onset of response to PFC-PL stimulation (Figure 7B). We then initiated both control and stressed models using PFC-PLs neuronal recording data. The model successfully reflected key changes in circuit behavior that we observed experimentally during CBC task performance after stress; a strong increase in striosomal SPN activity, and a delayed FSI activity peak, occurring after the main striosomal response (Figures 7C and 7D).

Figure 7. Modeling the Stress Effect on E–I Balance of the Cortico-Striosomal Circuit.

(A) The cortico-striosomal E–I balance modeled by the Hodgkin-Huxley method. Seven PFC-PLs neurons excite an FSI and 3 striosomal SPNs, and the FSI inhibits the striosomal SPNs (left). After stress, the FSI and PFC-PLs neurons have weaker connection, causing a shift in E–I balance (right).

(B) Connectivity values between circuit elements were calibrated so that synchronous input to PFC-PLs would cause an SPN to spike with a delay observed in PFC-PL microstimulation experiment (see Figure 5E).

(C) Model successfully reproduces the dynamics of the PFC-PLs-striosomal pathway components, as shown in Figures 5B and 5C.

(D) Model reproduced the increased striosomal response (top) and FSI activity peak times (bottom) after stress (mean ± SEM).

(E) Summary of major findings.

This modeling approach also enabled us to investigate the relative importance of abnormal PFC-PL activity vs. a shift in E–I balance in accounting for the stress-induced changes in the activity of striatal SPNs and FSIs. We inserted control PFC-PLs activity into the stress-shifted E–I model and observed heightened striosomal activity, similar to what we found experimentally (Figure S7A). However, when PFC-PLs activity recorded following either immobilization or foot-shock stress was inserted into the control model, the model did not consistently reproduce the experimental results, suggesting that E–I balance is crucial to account for striosomal activity levels, and that deficits in PFC-PLs activity alone were insufficient to produce the electrophysiological phenotype (Figure S7B). However, insertion of control PFC-PLs activity to the stressed model produced an early FSI peak, and insertion of stressed PFC-PLs activity into the control model produced a delayed FSI peak, suggesting that PFC-PLs activity is the primary factor accounting for the timing of FSI activity.

We then tested whether a symmetrical degradation of the PFC-PLs connection to striosomal SPNs and FSIs could produce high striosomal activity. We decreased the strengths of connectivity from PFC-PLs neurons to SPNs and from PFC-PLs neurons to FSIs by a factor of 40. This model did not predict high striosomal activity consistently across stress groups (Figure S7C), suggesting that dendritic degradation observed after stress (Dias-Ferreira et al., 2009) is unlikely to account for striosomal hyperactivity without an E–I shift.

Optogenetic stimulation of PV⁺ neurons was 3.6 times stronger than the PFC-PLs intrastriatal terminal stimulation in changing choice behavior, producing an over-correction of choice. This effect lasted up to a month. These results suggested that decreased FSI/PV⁺ firing rate is a more potent contributor to aberrant post-stress CBC choice than is decreased PFC-PLs firing rate (Figure S7D). We then modeled a shift of E–I balance through decrease of an FSI-to-striosome connection. We observed high striosomal activity suggesting a possible mechanism for the experimental results of PV inhibition (Figures 4E and S7E).

We further tested the relation between stress-induced reduction of simultaneous PFC-PLs activity and delayed FSI activity. We found that only many simultaneously active PFC-PLs neurons could elicit FSI firing (Figure S7F). Thus, after chronic stress, the reduction in the number of ‘coactive’ neurons during the click-to-turn interval likely led to the delayed FSI activity (Figure S5I). We created a model that included this population factor, and found that it could account for the observed shift of E–I balance via different thresholds for the effectiveness of degradation of the PFC-PLs-to-FSI connection. In the model, there are many connections between PFC-PLs neurons and FSIs, but these connections are weak compared to those between PFC-PLs neurons and SPNs, or between FSIs and SPNs. We suggest by this model that the weakest connections are most vulnerable to chronic stress, while strong connections initially survive (Figure S7G). This model successfully reproduces our experimental results, providing support for our hypothesis that a shift in the E–I balance of the prefronto-striosomal circuit dynamics toward excitation of striosomes accounts for the predominant effects of stress on the cortico-striosomal circuit.

DISCUSSION

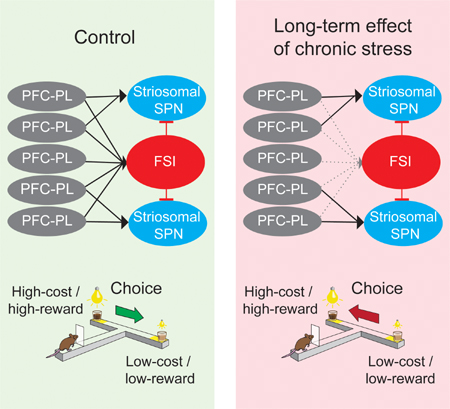
Our findings demonstrate that chronic stress can powerfully and selectively affect decision-making involving judgments of relative cost and benefit under conditions of conflict. We show that these changes in choice behavior are causally related to shifts in the dynamic balance of excitation and inhibition in a prefronto-striosomal circuit resulting in excitation of striosomes in the associative striatum (Figure 7E). These effects were strikingly selective for decisions in the face of motivationally conflicting choices, and affected neurons of the medial prefrontal cortex and their putative targets in the dorsomedial striatum, including both putative projection neurons and interneurons. As a result, there were radically altered dynamics in this prefronto-striosomal circuit, with major abnormalities in the timing and level of FSI activity, and abnormally strong activity of putative striosomal SPNs in animals engaged in CBC choices. Thus, chronic exposure to stress can induce changes that leave the circuit components active but no longer capable of normal circuit dynamics.

These findings identify the prefronto-striosomal circuit as part of the large forebrain network implicated in the behavioral effects of stress (Arnsten, 2015; Sousa and Almeida, 2012). The selectivity of the circuit we identify, and of the stress-induced behavioral abnormality in cost-benefit behavior, is particularly interesting given what is known about the circuit connectivity of striosomes, which, despite their location within the dorsal striatum, are strongly linked to the limbic system. Striosomal SPNs receive cortical inputs from regions that in humans have been related to mood states control, including regions influenced by stress (Amemori and Graybiel, 2012; Arnsten, 2015; Eblen and Graybiel, 1995; Friedman et al., 2015; Kalivas and Volkow, 2005; Rushworth et al., 2011). Striosomes, in turn, project directly to subsets of dopamine-containing neurons in the substantia nigra pars compacta (Crittenden et al., 2016; Fujiyama et al., 2011; Watabe-Uchida et al., 2012), whose neuronal populations respond variously to rewarding, aversive or salient stimuli (Lak et al., 2014). Striosomes also project via the pallidum to the lateral habenula (Rajakumar et al., 1993; Stephenson-Jones et al., 2016), which contains neurons sensitive to aversive stimuli and is strongly affected by stress (Hikosaka, 2010; Sousa and Almeida, 2012). Thus elements of cost and benefit are embedded in the outflow from the prefronto-striosomal circuit. The stress-induced cortico-striosomal circuit alterations documented here could have major effects on neural networks crucially implicated in the control of mood states, movement, and decision-making made under conditions of motivational conflict.

Stress Shifts the E–I Balance of the Prefronto-Striosomal Circuit toward Excitation

Both our experimental and modeling findings suggest that a primary long-term effect of chronic stress is a shift in circuit dynamics, leading to a shift in the E–I balance of the cortico-striosomal circuit towards abnormal excitation of striosomes. E–I balance is a critical computational feature in the brain, controlled by intrinsic conductance of neurons (Gjorgjieva et al., 2016; Vogels and Abbott, 2009). Here, we implicate circuit-level changes in inhibitory FSI firing in such E–I control. Striatal FSIs were selectively activated during CBC decision-making in unstressed rats and were selectively suppressed in chronically stressed rats. Optogenetic experiments pointed to the FSIs as causally responsible for both circuit E–I changes and behavioral changes induced by chronic stress, as selective manipulations of PV⁺ FSIs could both mimic and block these effects. Our modeling work further suggests that aberrant PFC-PLs signals alone cannot account for the alteration of striosomal SPN activity after stress and that shifts in E–I balance are necessary. Changes in the active PFC-PLs population can, however, account for the delayed timing of FSI activity.

We found reduced numbers of FSI-striosomal SPN pairs in the chronically stressed animals. This decline could result from reduced FSI firing rates, but paired recordings showed that when FSI firing rates were high, the FSIs successfully inhibited simultaneously recorded striosomal SPNs. Therefore, the observed reduction of feed-forward inhibition likely was related to a reduction of PFC-PLs-to-FSI connectivity, but we cannot make a firm conclusion about the FSI-striosomal SPN connection at a population level. This issue is important to resolve, given evidence that striatal PV⁺ neurons, putative FSIs, have been implicated in neuropsychiatric as well as motor disorders (Gittis et al., 2011; Lee et al., 2017a).

Chronic Stress Produces a Functional Phenocopy of a Prefronto-Striatal Disconnection Syndrome

The abnormal behavior of the chronically stressed rats and mice during CBC performance, and its selectivity for the CBC task, were strikingly similar to the effects induced by optogenetic disconnection of the prefrontal cortex from striosomal targets in the dorsomedial striatum (Friedman et al., 2015). Our findings here give this similarity biologic validation. The reduced responsiveness of FSIs to PFC-PL microstimulation and the reduction in FSI activity during CBC performance suggest that chronic stress releases striosomal SPNs from the inhibitory influence of FSIs. Optogenetic inhibition of striatal PV⁺ neurons in unstressed animals itself produced behavioral effects similar to those of chronic stress (Friedman et al., 2015). Multiple other effects surely co-occurred with those found here, as evidenced by a large body of work on neural changes induced by stress (Amat et al., 2005; Chaouloff et al., 1999; Jacinto et al., 2017; Lucassen et al., 2014; Sousa and Almeida, 2012). Our findings strongly suggest that abnormal intrastriatal microcircuit function involving decreased striatal FSI function and increased striosomal SPN activity as a major causal contributor to the aberrant choice behavior following chronic stress exposure.

Stress-Induced Striosomal Hyperactivity Could Alter Dopaminergic System and Related Limbic Circuits

The hyperactivity of striosomes after chronic stress could have a profound effect on related network function. The normally low activity of striosomal SPNs during the motivationally challenging CBC context could lead to increased or otherwise altered dopaminergic activity in the striatum, promoting resolution of motivational conflict in coordination with corticostriatal and thalamic inputs. After chronic stress, however, this mechanism could be altered, as the striosomes become extremely active. Chronic stress might lead to lowered levels of striatal dopamine release, as have been reported (Hollon et al., 2015), possibly via a striosome-nigral pars compacta-striatal loop. Additionally, decreased striatal dopamine, reported to occur after chronic stress, could reduce FSI activity, as dopamine can excite FSIs (Bracci et al., 2002). In parallel, changes in striosomal activity could affect lateral habenular pathways related to motivation via dopaminergic and serotonergic systems (Hikosaka, 2010).

Long-Term Stress Effects Include a Switch from Seemingly Rational to Seemingly Irrational Cost-Benefit Integration

Chronic stress selectively affected choices in the CBC task. The utility functions of the animals were profoundly affected, so that the stressed rats and mice maintained approaches to high-cost/high-reward choices over a wide range of options, seemingly failing to make a normal, ’rational’ transition away from approaching the normally avoided option. This behavior suggests aberrant integration of cost and benefit under conditions of conflict, but we could not determine whether stressed animals had reduced sensitivity to cost or augmented sensitivity to reward.

Neuroeconomic theories suggest estimates of utility as a fundamental feature of such rational decision-making (Glimcher and Fehr, 2013). The abnormal cost-benefit integration indicated by the abnormal utility functions we observed suggests a parallel to human irrational choice behavior such as seen in choices of high risk (Aupperle and Paulus, 2010; Szanto et al., 2015), but the increase in high-cost/high-reward choices could have reflected a beneficial adaptation associated with surviving in extreme environments that previously evoked stress. ’Rational’ linear integration, as we saw in the non-stressed controls, could entail computational time and energy resources not required in sticking to the high-cost/high-reward decisions. The seemingly irrational decision-making, by this view, was not necessarily a sign of dysfunction, but an adaptive state (Sih et al., 2015).

A diminished ability to resolve motivational conflict is a symptom not only of prior chronic stress, but also of neurological and psychiatric disorders including anxiety and depressive states (Aupperle and Paulus, 2010; Gleichgerrcht et al., 2010; Szanto et al., 2015). There are only hints as to how these behavioral problems relate to the circuit that we examined here in rodents, but evidence in non-human primates suggests that the prefronto-striosomal circuit could be differentially involved in approach-avoidance decision-making and likely in anxiety states (Amemori and Graybiel, 2012). Our evidence on the effects of stress on the PFC-PLs-striosomal circuit may be valuable in understanding other disorders including anxiety and depressive states that also affect this circuit and produce a similar change in behavior.

Experimental Limitations and Opportunities for Future Work

Our procedures carry several limitations. Although we observed similar circuit and behavioral abnormalities following two different, canonical stress protocols, others might produce different effects. The PFC-PL pathway to the dorsolateral striatum, though targeting striosomes most densely, also weakly labels the matrix. Our optogenetic experiments are subject to the current problems with this methodology, including the introduction of synchronous activity and secondary effects. In the engineered PV mouse model studied, not all PV⁺ neurons expressed Cre, so that we only manipulated a subgroup of PV⁺ putative FSIs, and manipulation of PV⁺ interneurons likely affects other striatal interneurons (Lee et al., 2017b). Our observations on the matrix were also limited to putative ‘non-striosomal neurons’ defined as non-responsive to the PFC-PL microstimulation. Finally, our experiments were confined to a circuit related to the dorsomedial striatum and PFC-PL; other striatal (Dias-Ferreira et al., 2009) and cortical and subcortical regions could be involved, including, for example, parts of the orbitofrontal cortex (Eblen and Graybiel, 1995; Padoa-Schioppa and Cai, 2011).

Despite these and other caveats, our findings demonstrate that a cortico-striosomal circuit linking the medial prefrontal cortex to the dorsomedial striatum is severely disrupted by chronic exposure to stress, and that its selective abnormal functioning could be critical for the induction of aberrant cost-benefit evaluation caused by chronic stress. Our work points to a need for future research to study changes in this circuit in other disorders in which aberrant cost-benefit decision-making is a feature.

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for data and reagents should be directed to and will be fulfilled by the Lead Contact, Ann M. Graybiel (graybiel@mit.edu)

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Rodents

All animal procedures were approved by the Committee on Animal Care at the Massachusetts Institute of Technology and were carried out in accordance with the U.S. National Research Council Guide for the Care and Use of Laboratory Animals. Male Long-Evans rats (n = 84, 380–600 g, 2–8 month), male C57BL/6J mice (n = 85, 25–35 g, 2–8 month) and transgenic parvalbumin-Cre (n = 32, PV-Cre in following text, B6.129P2-Pvalb^tm1(cre)Arbr/J, genotyping at Transnetyx for PV-IRES-Cre; 25–35 gram, 2–8 month, Jackson Laboratory) heterozygous mice were individually caged and were maintained under conditions of constant temperature (25°C) and humidity (50%), a 12:12 h light/dark cycle, food restriction to maintain 95% of body weight, and free access to water. Animals were randomly assigned to control and stress experimental groups

METHOD DETAILS

T-Maze Based Decision-Making Tasks

To determine experimentally the effects of chronic stress on decision-making ability, animals were sorted into groups of pre-stressed and unstressed animals and trained in a T-maze apparatus on three different decision-making contexts: benefit-benefit (BB), cost-cost (CC) and cost-benefit conflict (CBC) (Figure 1A).

T-Maze Apparatus

All behavioral tests were performed in a T-maze composed of an initial running track (stem) with two end-arms and were configured to limit bumping of the headstages implanted on animals against the walls. Each end-arm possessed wells where a chocolate milk reward was presented. Licking of the chocolate milk reward was detected by an infrared photobeam (Panasonic Sunx EX31A). Two light devices were connected to the walls at the top of the end-arms so as to be focused on the reward-delivery feeders and served as the costs involved in the task. A clicking sound was used to indicate the beginning of each trial. This click triggered the onset of the laser stimulation during behavioral optogenetic studies using custom-designed hardware. An overhead CCD camera allowed detection of the position of the animals in the maze throughout each trial, including the timing of turning events. Two T-maze configurations were used for this study, one for rats and one for mice.

The rat maze had a 33 cm long stem and 33 cm long end-arms with 61 cm high surrounding walls and included a 23 cm elevated track with a distance of 12.5 cm from the surrounding walls. Each arm of the maze had either white or black walls that were switched randomly from day to day.

The mouse maze had a non-elevated track comprised of 36 cm long stem and 23 cm long end-arms with 23 cm high surrounding walls slanted at a 40° angle. The right arm of the maze was marked with vertical black stripes on the walls of the arm, and the left arm was marked with horizontal black stripes on the walls.

Experimental Timeline

Each animal was habituated to and pre-trained in the T-maze for 3 weeks (Figure 1B, also see Habituation and Training). Immediately following, each animal was trained for 6 weeks on the BB decision-making task, and preferences were recorded to determine the chocolate milk concentration necessary to achieve a similar reward preference (see Benefit-Benefit Task). Next, animals were trained for 3 weeks on the CC task to determine the brightness of light necessary to achieve a similar cost aversion (see Cost-Cost Task). Once both the concentration and brightness had been determined and stabilized, animals were trained for another 3 weeks on the CBC decision-making task (see Cost-Benefit Conflict Task), with a BB task session in between each CBC task session to check for bias development (see Potential Training Problems). After this training phase was complete and baseline preference data were collected, animals were randomly assigned to the stressed and non-stressed groups. Each stressed group was subjected to one of the stress paradigms for 2 weeks, whereas the non-stressed group remained unstressed during this time (see Stress Procedure). Following this 2-week period, we collected data from each animal in the BB and CBC tasks again for 6–12 weeks. Each experimental session on a given day consisted of one of these decision-making tasks (BB, CC or CBC), and animals’ behavior was recorded using the CCD camera.

Habituation and Training

Animals were habituated to and trained in the T-maze apparatus in order to find baseline decisions. Task training was divided into several steps (Figure 1B). In the first step, mice and rats were habituated to the experimenter, to chocolate milk and to the T-maze. In the next step, animals learned how to receive the chocolate milk reward in the maze. This was accomplished by blocking the running track of the T-maze so the animals were forced to alternate between both arms where they received pure chocolate milk as a reward. We gradually decreased the rewards presented at the end of each arm to get the minimum amount of reward necessary for the animals to run (0.2 ml of milk for rats and 0.05 ml of milk for mice). This step was completed when animals were consistently able to run 20 forced-choice trials.

Benefit-Benefit Task

BB tasks consisted of decisions where a reward was present in both choices with no costs associated. This task was used to gauge how reward preferences of each animal were affected by chronic stress. The two rewards were pure chocolate milk located at the end of one arm of the maze and chocolate milk solution diluted with whole milk at the end of the other arm. The location of these rewards was alternated daily between the two arms.

There were two types of BB tasks. The BB task with similar rewards (BBS) consisted of a pure chocolate milk reward at the end of one arm and a chocolate milk reward diluted at high (60–80%) concentrations at the other end. The BB task with dissimilar rewards (BBD) consisted of a pure chocolate milk reward at the end of one arm and a chocolate milk reward diluted at a low (15–60%) concentrations at the other end.

As each animal had different reward preferences for chocolate milk, the concentration of the diluted milk was adjusted in both the BBS and BBD tasks to have each animal achieve similar preferences toward the pure chocolate milk reward in at least four consecutive sessions (Figures 1C and S1A). This preference in animals resulted in a 50–62.5% choice of pure chocolate milk in the BBS task, and a 62.5–75% choice in the BBD task.

Cost-Cost Task

The CC tasks consisted of pure chocolate milk rewards at the ends of both arms of the maze with a dim light (5–9 lux) in one arm and a brighter light (0.6 – 2 klux) in the other. This task was used to determine the effects of chronic stress on light avoidance for each animal. Costs were alternated between the arms on each experimental day. Much like milk preferences, each animal showed different light tolerance, and the brightness of the lights was adjusted so that each animal performed the task with similar choice preferences (avoiding the brighter light in 16.6–33.3% of trials) in at least three consecutive sessions.

Cost-Benefit Conflict Task

In order to determine the effects of chronic stress on cost-benefit integration, we introduced the cost-benefit decision-making task. The CBC task consisted of a pure chocolate milk reward at the end of one arm of the maze paired with a bright light (high-cost/high-reward), whereas the other arm had a diluted milk reward paired with a dim light (low-cost/low-reward). The concentrations of chocolate milk and brightness of light used in this task were adjusted per animal based on the results obtained from the BB and CC tasks performed by each animal (Figures 1C and S1A–B).

For the rat version of the CBC task, we used diluted chocolate milk concentrations as identified in the BBS task. We calibrated the concentration for each rat to have diluted chocolate milk preference of 75% in the CBC task. For the mouse version of the CBC task, we used diluted chocolate milk concentrations estimated in the BBD task. We calibrated so that each mouse had a diluted chocolate milk preference of 50%.

Session Composition

Training sessions were given once per day, 5–7 days a week. Each session began with the running track of the maze blocked (Figure 1B). Animals participated in 10–20 forced-choice reminder trials to be familiarized with the costs and benefits associated with each choice. Next, the animals ran 20–80 trials in which they were allowed to choose freely which arm to visit. Rewards and costs remained in the same end-arm during each daily session but randomly varied from day to day.

Stress Procedures

Two stress paradigms, described below, were used to test for the consistency of generalized chronic stress on decision-making behavior and neural activity. Animals were randomly divided into three groups: one that remained unstressed and the others that underwent one of the two stress paradigms. All animals were exposed to the same conditions with the exception of exposure to stress. These stress procedures were performed in rooms with regular indoor lighting (400–600 lux).

Rat and Mouse Immobilization

Animals were placed in a Decapicone bag with a hole for the snout (model DC200 for rats and model DC M200 for mice, Braintree Scientific, Inc.). The size of the bag was large enough not to impede animals’ breathing but small enough to limit their mobility. Animals were carefully placed in the bags to minimize the chance of injury and to ensure that breathing was unobstructed. The bags were taped shut so that the animals’ tails protruded and animals were secured in an upright position to an empty acrylic cage. Animals were monitored every 15 min to ensure that they remained upright, unharmed, and fully contained and were able to breathe. The rats were immobilized in this manner for 4 hr a day for 14 consecutive days, whereas mice were immobilized for 1 hr a day for 14 consecutive days.

Chronic Electric Shock

Rats were placed in an apparatus containing a small chamber with a hole for the tail. The tail of the rat was attached to a cable that delivered a mild electric shock (1–2 mA) whenever a tone was played. The rat received 50 shocks, each shock lasting 3 s, during 1-hr daily sessions on 14 consecutive days.

Potential Training Problems

Spatial Biases

As some animals could be spatially biased toward one side of the T-maze regardless of the rewards or costs presented on each side of the T-maze, they were checked regularly for their spatial bias using the BBS task. In the cases where biases had developed (more than 65% choice of one of the sides), the animals were given bias-breaking sessions in which a low concentration (10–40%) of diluted chocolate milk was provided on the side toward which the animal was biased and a pure chocolate milk reward on the other side. These sessions were continued until the animal returned to choosing each side with equal likelihood.

Aversive Nature of Light

Because rodents show high aversion to light, tasks that used lights as costs were introduced slowly, and sessions that involved light were limited to one type of such task per week. Prior to and following each session with these tasks, rodents were given a BBS task session with equal rewards to confirm absence of biases.

Exclusion Criteria

Animals were excluded from experimental participation if they failed to achieve certain goals within each timeframe. In the training phase, animals that were unable to achieve 20 consistent back-and-forth runs of the end arms (10 rewards collected from each side) in the 2-week timeframe were excluded from the study. Next, during the BB training period, animals were excluded if they were unable to achieve stable BBS and BBD preferences in the 6-week time-period. These stable preferences were defined in BBS as choosing the pure chocolate milk reward 50–62.5% of the trials in at least four consecutive sessions. In BBD, stability was defined as choosing the pure chocolate milk reward 62.5–75% of the trials in at least four consecutive sessions. In total, 30% of rats and 20% of mice were excluded from experimentation in this manner.

Behavior Modeling

In order to examine the effect of stress on cost-benefit decision-making, we systematically varied the concentration of diluted chocolate milk in one arm of the maze while maintaining a constant concentration of pure chocolate milk in the other arm. We also maintained a constant low cost (dim light) associated with the diluted chocolate milk and a constant high cost (bright light) associated with the pure chocolate milk. We measured the preference before and after chronic stress in four rats (Figures 1G and S1G–S1H). We found that rat preference in a psychometric function appeared to show a sigmoid with three distinct sections. In the first section, we found that at a lower concentration of chocolate milk in the diluted mixture, rats chose the mixture around 50% of the time, indicating a lack of linear integration of cost and benefit. With increasing concentration of chocolate milk, we found an increase in preference for the diluted mixture up until it reached its plateau. The sigmoid property of the function suggests that, after a distinct quality of reward, the rodents began to make their choices by integrating cost and benefit.

To quantitatively model this gradual shift in choice behavior, we introduced the four-parameter logistic regression (4PLR) (Figures 1H–1J) and two-state threshold (2ST) (Figures S1I–S1L) models. The 4PLR model produced the best-fit sigmoid curve, and the 2ST model produced parameters that give us more intuitive explanations. First, we compared the conditional logit model and the 4PLR model using Bayesian information criteria, and confirmed that 4PLR model was suitable to model these choice behaviors. The 4PLR model was formulated by p(x) = a + (b−a)/(1+exp(c+dx)), where p is the probability of choosing diluted mixture and x is the concentration of the diluted mixture. Nonlinear least square algorithm (MATLAB, function nlinfit) was applied to derive the four parameters (a, b, c and d) that produced best-fit sigmoid curve for the choice behavior of each animal. The transition point from lack of linear cost-benefit integration to linear cost-benefit integration was defined by the extrapolation of the linear trend modeled by the tangential line of the 4PLR model (Figure 1H). The transition from lack of linear cost-benefit integration to linear cost-benefit integration was represented by the intersection between the tangential line (Figure 1H) and lack of linear cost-benefit integration lines (p = p(0)). We performed paired t-test to examine whether the lack of linear integration choice condition was significantly extended for four rats (Figure 1I). The choice steepness was characterized by the slopes of the tangential line in four rats, which exhibited significant increase in stress condition (paired t-test, P < 0.05) (Figure 1J).

Secondly, we introduced the 2ST model to derive parameters corresponding to two behavioral features: threshold to start of linear cost-benefit integration and utilities of choices in cost-benefit integration (Figure S1I). To derive the threshold for the 2ST model, we used a two-term Gaussian function and extracted the behavioral property when the animal chose both sides without integrating cost and benefit linearly (Figure S1J). With the choice behavior accumulated for four rats, nonlinear least square algorithm was applied to derive the parameters of the two-term Gaussian function. Each distinctive state was then characterized by either of the two Gaussian terms of the function (Figure S1J). The state with lack of linear integration of cost and benefit (random choice state) could be characterized by the left Gaussian term with the mean frequency to choose the diluted side (m = 49.5%) and the standard deviation (SD, s = 2.1%). The threshold to determine the state change from the random choice state could thus be defined by the 95% confidence interval of the left Gaussian term. We set the threshold to the value which was significantly deviated from the mean, i.e., m + 1.96s (= 53.6%). When the choices were consecutively above the threshold, we considered that the state had shifted to linear integration of cost and benefit. The choice behavior during the state of linear integration of cost and benefit was characterized by conditional logit model (Train, 2002) that gave us choice utilities. The choice behavior during this phase was modeled as p(x) = 1/(1+exp(−f(x)), where p is the probability of choosing diluted mixture and x is the concentration of the diluted mixture. The function f(x) was formulated by a linear function as f(x) = Bx + C, representing the difference in utilities of two goals. The parameter B corresponds to the steepness of the sigmoid curve, representing the degree between linear cost-benefit integration and sharply splitting choices.

Similarly to the results obtained by 4PLR model, we confirmed that the transition point (Figure S1K) and the choice steepness (Figure S1L) were both increased significantly in the stress condition. The transition point was defined by the intersection between segment without linear cost-benefit integration line (p(x) = d) (red line in Figure S1I) and segment with the conditional logit model (blue line in Figure S1I). We examined whether the transition point was extended in the stress condition by paired t-test (Figure S1K). In comparison to control, we found that the first segment of the stressed rats was significantly elongated, and the second segment has a strikingly steeper slope. In the region in which the behavior was characterized by conditional logit model, rats made choices based on the difference in total utilities of the two sides. The choice steepness was represented by the best-fit B parameter in the conditional logit model, which was also increased significantly in the stress condition (paired t-test, p < 0.05) (Figure S1L). The parameter B represents the inverse temperature parameter in the softmax function, corresponding to the degree of steepness of the sigmoidal curve. The sharper slope of the second section indicates that stress increases tendency to make a sharply splitting choice, suggesting an excessive sensitivity in difference in utility.

Anhedonia and Light Avoidance Tests

Sucrose and Chocolate Milk Preference Tests

We introduced three types of preferences tests to determine the effects of chronic stress on benefit-benefit decision-making (n = 8 per group). One of these tests was a sucrose preference test comparing sucrose preference to water, and the other two were modified preference tests comparing pure chocolate milk to diluted chocolate milk. For each test, two bottles were randomly placed into each cage, one containing a high reward and the other containing a lower reward or no reward as described below:

1. Water vs. 2.5% sucrose solution in water (no value vs. value) (Figure S1M)

2. Pure chocolate milk vs. 70% mixture of chocolate milk (value vs. value, similar to BBS task) (Figure S1N).

3. Pure chocolate milk vs. 50% mixture of chocolate milk (similar to BBD task) (Figure S1N).

Prior to testing, rats were first habituated for 2 hr/day for two weeks to the presence of two leak-proof drinking bottles that were to be used in testing. Bottles were placed randomly in the cages to prohibit spatial biases from developing. Testing was limited to 2 hr/day to prevent the chocolate milk from spoiling. Due to the short duration of the test, each test was repeated 3 times. Animals were given at least one day off between bottle tests.

Light Avoidance Tests

We observed a very small difference in the performance of the CC task between stressed and non-stressed rats. However, in order to disentangle the perceived value of rewards from the perceived costs, we conducted new light avoidance tests in which no rewards were present. Additionally, these new tests consisted of cost vs. cost situations and cost vs. no-cost situations to determine the inflation of value of costs caused by stress.

An additional three groups of rats (n = 8 per group) were habituated to the experimenter and to an apparatus for seven sessions. For the light avoidance task, we used a linear maze with 66-cm long running track that was elevated by 23 cm. The track was 12.5 cm from the 61-cm high surrounding walls. Two lights were present, one on each end of the maze. After this habituation, they were exposed to one of the following conditions:

1. 2 klux vs. 7 lux (cost vs cost) (Figure S1O)

2. 600 lux vs. 0 lux (cost vs no-cost) (Figure S1P)

3. 2 klux vs. 0 lux (cost vs no-cost) (Figure S1P)

After habituation, rats were placed in the maze for 5 min during which we recorded the time that the rat’s head was in the illuminated spot. The brightness of the light was assigned randomly to each side of the maze on each experimental day to prevent spatial biases, causing a preference of sides regardless of costs associated with that side, from developing. Each animal went through the light avoidance test only once a day.

Limitations of T-Maze Based Tasks

Limited Sensitivity of BB Task for Measuring Preference

Chronic stress is often reported to cause anhedonia or devaluation of rewards (Ampuero et al., 2015). However, in our experiments, we observed no distinguishable difference after chronic stress on the performance of the BB tasks (Figure 1F). Modified preference tests showed that stressed and control rats made similar choices when shown two types of chocolate milk varying in concentration, but significantly different choices when shown sucrose solution and water (Figures S1M and S1N). These observations suggest that BBS tasks are less sensitive for measuring animal’s preference of pure chocolate over mixture. On the other hand, the psychometric curve of CBC task was evidently shifted from that of CC tasks (Figure S1B), demonstrating that the CBC task sensitively measures animals’ preference based on both reward and cost value.

Limitation of CC Task for Measuring Aversion

Because the light can be not only aversive but also fearful or anxiogenic to rats and mice, our CC task and CBC task may not be purely measuring aversion. However, as we previously documented (Friedman et al., 2015), our behavioral protocol involved extensive overtraining that mitigate the fear- and anxiety-related behavior (e.g., freezing and delayed response), while the animals still strongly avoid light. Consistently, in our current experiments, we did not observe a significant difference in decision-making in the T-maze based CC task between stressed and control animals, while chronic stress reportedly induce anxiety or enhance fear-related behavior. Additionally, using place-preference light avoidance tests, we did not find a significant difference in rat’s avoidance of light (Figures S1O and S1P). These observations suggest that our CC task may not be sensitive for measuring light-induced fear or anxiety, but capable of measuring animals’ aversion to light in quantitative manner.

Surgical Procedures

After successful training on the CBC task, rats and mice received virus injection for optogenetic manipulation and head-stage implantation for electrophysiological recordings, and electrical, optogenetic and chemical manipulations.

Anesthesia and Analgesia

Prior to surgery, animals were given an injection of meloxicam (1 mg/kg for rats and 0.5 mg/kg for mice) as a pre-surgical analgesic. Animals were anesthetized through either an injection (IP) of ketamine and xylazine (rats: 100 mg/kg ketamine + 10 mg/kg xylazine, with 30 mg/kg of ketamine as booster; mice: 120 mg/kg ketamine + 16 mg/kg xylazine, with 40 mg/kg of ketamine as booster) or application of isoflurane (1.0–2.0%, at an input flow rate of 1 l/min). Meloxicam (2 mg/kg for rats and 1 mg/kg for mice, SC) was also administered to both mice and rats once a day for three post-surgical days, including the day of surgery.

Implantation and Viral Injection for Rat Electrophysiology and Optogenetic Manipulation of PFC-PL Terminals in the Striatum

Rats were injected with 0.2 µl of one of three viruses: AAV5-CaMKIIa-eNpHR3.0-EYFP (University of North Carolina Vector Core), AAV5-CaMKIIa-C1V1(E122T/E162T)-TS-EYFP, or AAV5-CaMKIIa-EYFP. Injections were made in the PFC-PL (AP: +3 mm; ML: ±1 mm; DV: 3.2 mm from dura mater) through a 35 gauge needle attached to a Hamilton syringe at a rate of 0.02 µl/min. After each injection, the injection needle remained in place for 10 min to allow full dispersion of the virus.

For electrophysiological recordings, we implanted headstages comprised of 24 recording tetrodes and four bipolar stimulation electrodes. The tetrodes targeted the PFC-PL (Figure S2A, AP: 2.8–3.4 mm; ML: ±0.3–0.9 mm; DV: 3.3–4.5 mm) and the dorsomedial striatum (AP: 2.0–1.4 mm; ML: ±1.5–2.1 mm; DV: 3.6–5.0 mm). For optogenetic experiments, two optical fibers (Doric Lenses) were implanted into the dorsomedial striatum (Figure S2J, AP: + 1.7 mm; ML: ±1.8 mm; DV: 3.6 mm from dura mater). All recording and stimulation tetrodes were manufactured from 0.02 mm diameter tungsten wire (California Fine Wire) with an impedance of 150–400 kΩ per tetrode wire.

Identification of PFC-PLs Neurons

In order to determine the identity of the putative neurons recorded during behavioral sessions, we applied electrical microstimulation in the dorsomedial striatum and recorded antidromic responses in the PFC-PL at the end of each behavioral session (Figure 2A).

Electrical Microstimulation in Dorsomedial Striatum

We used one of the tetrodes placed in the dorsomedial striatum for electrical microstimulation using two channels as anodes and two as cathodes. This tetrode was connected to ISO-Flex and Master 9 systems (A.M.P.I.) to control stimulations (0.5 ms square pulse, 15 µA, 2 s gap between pulses; 100 pulses) delivered to the dorsomedial striatum.

Spike Sorting and Antidromic Stimulation Response Analysis

Extracellular spikes were recorded using one of the tetrode channels as reference. The signal was band-pass filtered (600–6000 Hz) and recorded with a Cheetah Data Acquisition System (Digital Lynx 16 SX, Neuralynx) at 33-kHz sampling rate. Recorded spikes were sorted by a custom-developed algorithm and were confirmed manually using Offline Sorter (Plexon, Inc.).

Statistical Analysis of PFC-PL Response to Striatal Microstimulation

Spike activity for each PFC-PL unit was analyzed over a 1–10 ms window aligned at the onset of stimulation. We counted the number of spikes evoked by 100 stimulations in a 10-ms post-stimulation window. If more than 10 spikes were generated in this window, the PFC-PL unit was classified as a candidate striosome-projecting neuron. Units with less than 10 spikes were excluded due to low stimulation-evoked activity. The mean and SD of firing rate for each PFC-PL unit were calculated both over this window and over a baseline period 1 s prior to stimulation. If the mean firing rate of the PFC-PL unit during the window was at least 4 SDs above the baseline window, the unit was classified putatively as a striatum-projecting PFC-PL neuron.

Neuronal Activity Aligning

To analyze the activity of neuronal populations, we aligned the activity of recorded neurons relative to three task events: the click, which coincides with the opening of the door to the maze; the turn, which coincides with the rodent’s choice; and the lick, which coincides with receiving reward. We found that the duration of trials became similar with overtraining (Figure S1Q). In all, 83% of trials lasted under 5 s.

We leveraged the similarity of trial duration to align each trial based on the time of click, turn, and lick. In our binning strategy, each trial was split into 600 time bins of equal length. The bins are aligned such that the click occurs between bins 300 and 301 and the lick occurs between bins 360 and 361.

We determined baseline activity in two ways: first, as the mean activity during pre-task period from bins 60 to 240. During this interval, the animal had been in the starting box for at least 40 s since the end of the previous trial, making influence from the previous trial unlikely, and the next trial has not yet begun. Second, we defined another measure of baseline as the mean activity during the full recording session.

Task-Related Neuronal Activity Analysis

Our next task was to measure the activity differences of PFC-PL neurons across control and stressed groups. Among groups, we compared baseline firing rate, firing rate during in-task peak activity period (bins 316 to 330), and normalized (z-score) firing rate in the in-task period relative to baseline. We tested each difference statistically in two ways. First, we compared mean firing rates across control and stressed groups by performing two-sample t-tests (MATLAB) (Figure 2E). Second, we performed a cumulative density analysis between groups. In this test, after building cumulative density functions from the entire population of neurons for each group, we determined significance through a two-sample Kolmogorov-Smirnov test (MATLAB). Additionally, we calculated a cumulative density function for each rat, and then formed an average cumulative density function for each group with an associated standard error. High significance was marked by little overlap between the standard errors of the average cumulative density functions. The activities of striatal neurons were also aligned and analyzed as above.

Optogenetic Manipulation of PFC-PLs Terminals

In order to determine the causal role of the PFC-PL projections to the striatum in cost-benefit decision-making, we optogenetically manipulated these terminals in the dorsomedial striatum. Three groups of rats were injected in the PFC-PL with excitatory (AAV5-CaMKIIa-C1V1(E122T/E162T)-TS-EYFP or a AAV5-CaMKIIa-EYFP), inhibitory (AAV5-CaMKIIa-eNpHR3.0-EYFP (UNC)) and control viruses and implanted with two optical fibers in the dorsomedial striatum. Rats were habituated to the maze and trained on various decision-making tasks. After baseline data collection, rats underwent sessions with optogenetic manipulation. Each session began with 10 forced-choice reminder trials with lights (cost) off and then 10 forced-choice reminder trials with lights on to familiarize each rat to the costs and benefits located at each end-arm. Following these reminder trials, rats performed 20 trials without optogenetic manipulation and then 20 trials with optogenetic manipulation. In trials with optogenetic manipulation, light (wavelength: either 590 nm for inhibitory virus or 532 nm for excitatory virus, 2 mW per hemisphere) was delivered from the click to signal trial start. The light from a laser source (OEM Laser Systems) was controlled by a Master 9 pulse generator (A.M.P.I.) and a shutter (LS2 Uniblitz). In optogenetic inhibition trials, manipulation persisted for 3 s and consisted of 1 pulse. In optogenetic excitation trials, manipulation persisted for 3 s and consisted of 46 pulses 30 ms in length with a 36 ms interval between each pulse. Fiber cords, a rotary joint and a beam splitter (Thorlabs; Doric Lenses) were used to allow free movement of rats in the maze.

Potential Problems and Limitations of Optogenetic Manipulation

We observed that some rats can develop a side bias after optogenetic manipulation, causing them to prefer either the left or right side regardless of the rewards and costs presented. Therefore, before and after each optogenetic manipulation session, rats were presented with two pure chocolate milk rewards and no costs on each side of the T-maze to check for potential side biases. If a preference to one of the sides was greater than 62%, we determined that a side bias existed, and animals were given bias breaking sessions (see above) until this bias was reversed. Only animals that had no side biases were allowed to participate in optogenetic manipulation sessions.

We note that optogenetic manipulation has problems related to introduction of unnatural synchronous activity and also could cause secondary circuit effects. Additionally, PFC-PLs neurons have many fibers of passage through the dorsomedial striatum to other brain regions. It is possible that optogenetic manipulations in the dorsomedial striatum also affected the activity of these fibers near the manipulation sites.

Immunohistochemistry

Perfusion

Animals were perfused using a 0.9% saline solution followed by 4% paraformaldehyde in 0.1 M phosphate buffer (PB). Brains were dissected out, cryoprotected, and blocked before being frozen in dry ice. Using a sliding microtome, 40-µm thick coronal sections were made. Sections were stored at 4°C in 0.02% sodium azide in 0.1 M PB until use.

Immunofluorescent Staining

For visualizing striatal terminals of PFC-PL neurons infected with AAV vector (Figure 2E), sections were rinsed for 10 min in 0.01 M phosphate buffered saline (PBS) with 0.2% Triton X-100 (Tx) 3 times and were then pre-treated for 30 min using 3% H₂O₂ in PBS-Tx. After rinse in PBS-Tx for 10 min, sections were blocked with tyramid signal amplification (TSA) blocking solution for 20 min at room temperature, and then incubated with primary antibodies, goat anti-mu opioid receptor (MOR1) antibody (1:500) and rabbit anti-GFP antibody (1:2000, for detecting enhanced yellow fluorescent protein (EYFP) encoded in AAVs), in TSA blocking solution for 48 hr at 4°C. Sections were again rinsed with PBS-Tx for 3 × 10 min, and incubated with anti-goat or anti-rabbit secondary antibodies (1:300, Invitrogen) conjugated with Alexa Fluor 546 or 488 in TBS-Tx. For identification of electrode tracks and tips (Figures S3A–S3F and S3I–S3N), serial sections were processed as above using anti-MOR1 antibody and anti-glial fibrillary acidic protein (GFAP) antibody (1:1000, ab4674, Abcam). For confirmation of viral expression in PV-Cre mice (Figure 4A), sections were stained using guinea pig anti-PV antibody (1:5000) and rabbit anti-GFP antibody (1:2000). Rest of staining protocol is the same as above.

After staining, sections were mounted with ProLong Gold antifade reagent with 4′,6-diamidino-2-phenylindole (DAPI) (Invitrogen) and subjected to imaging.

Imaging and Image Analysis

The compartment selectivity for PFC-PLs axon terminals was estimated as follows: EYFP, MOR1 and DAPI images were collected with Zeiss LSM 510 confocal microscope (EC Plan-NEOFLUAR; Hamamatsu Orca Flash 4.0 V2 digital CMOS camera C11450-22CU). The pixels in the striatal region in 0.5 mm × 0.5 mm square field around targeted brain coordinates were categorized into striosomes, matrix, and internal capsule bundle according MOR1 and DAPI images, and EYFP signal of each compartment was calculated.

To identify the tip of electrodes, the tiled images for MOR1, GFAP, and DAPI were taken by TissueFAXS Whole Slide Scanning System. The end of DAPI-positive cluster was defined as a tip, and its compartment identity (i.e., striosomes or matrix) was defined by MOR1 channel (Figures S3A–S3F and S3I–S3N).

Classifying Putative Striosomal SPNs

Identifying Striosomes Based on Orthodromic Response

In order study the striosomal response to chronic stress, we developed a method for identifying striosomal neurons (Friedman et al., 2015). We applied electrical microstimulation in the PFC-PL (15 µA, 2 s interval between 100 pulses, 0.5 ms pulse) via implanted microelectrode (AP: 3.1 mm; ML: ±0.7 mm; DV: 3.4 mm), and simultaneously recorded striatal response using a tetrode arrays implanted in the dorsomedial striatum (AP: 2.0–1.4 mm; ML: ±1.5–2.1 mm; DV: 3.6–5.0 mm). We observed a range of responses to PFC-PL stimulation among dorsomedial striatal neurons. One group of neurons exhibited biphastic responses, beginning with a period of short-latency excitation 3–15 ms after stimulation that was followed by a prolonged period of inhibition that lasted up to 250 ms. A second group of neurons exhibited triphastic responses, which included a rebound after the period of excitation or inhibition. A third group of neurons demonstrated only inhibition after PFC-PL stimulation.

Based on these results, we developed an algorithm to differentiate striosomal SPNs from other neurons in the dorsomedial striatum by identifying dorsomedial striatal SPNs with significant responses to PFC-PL stimulation. The algorithm determined, for each dorsomedial striatal SPN, intervals of excitation and inhibition. To measure the excitation strength that occurred during an interval, the algorithm calculated firing rate. Inhibition strength was calculated similarly, but then subtracted from firing rate in the pre-stimulation baseline period (1000–0 ms before stimulation). The significance of short-latency excitation and inhibition was calculated by bootstrapping the shuffled baseline spike data. Responses to PFC-PL stimulation that fell 2 SDs above the bootstrapped mean were considered significant.

Using the algorithm, we classified dorsomedial striatal SPNs based on response to PFC-PL stimulation. The SPNs fell into three groups: SPNs that exhibited significant excitation and inhibition, those that exhibited either significant excitation or inhibition, and those that exhibited neither excitation nor inhibition. In our previous work in which we identified tetrode tip position histologically (Friedman et al., 2015), we found that 31 of 35 tetrodes with units that exhibited both excitation and inhibition were in striosomes. We also reconfirmed these results in a pilot study here and found that tetrodes identified to be in striosomes (n = 2) demonstrate sharp response to PFC-PL stimulation, whereas tetrodes identified to be in matrix (n = 2) do not respond to PFC-PL microstimulation (Figures S3G, S3H, S3O and S3P).

Therefore, we classified SPNs that responded significantly with both excitation and inhibition as putative striosomal SPNs, and SPNs that showed neither excitation nor inhibition as putative matrix SPNs.

Limitations of Our Method for Identifying Striosomes

A limitation of our identification method lies in the fact that we identify only striosomal SPNs that respond to microstimulation of the PFC-PL, which make up only a subset of all SPNs in striosomes. The high rate of false negatives is reflected in our rates of identification of striosomes; out of 6065 SPNs recorded during the CBC task, we found 153 to be striosomal (2.5%), compared to the actual ~10–20% volume of striosomes in the anterior dorsomedial striatum.

This limitation is also reflected in our classification of matrix SPNs. Because we classify SPNs that did not respond significantly to microstimulation of the PFC-PL as matrix SPNs, our population of putative matrix SPNs include those striosomal SPNs that do not respond to the microstimulation. However, the vast majority of classified matrix SPNs are likely, in fact, matrix SPNs, because it is estimated that 80–90% of striatal neurons are matrix SPNs. Additionally, we remove from this population SPNs that remained unclassified because they either exhibited significant excitatory or inhibitory response to stimulation.

Classifying Fast-Spiking Interneurons

Pre-Processing of Recorded Spike Waveforms

Neuronal spikes were recorded from the dorsomedial striatum using tetrode bundles and sorted by identifying individual clusters using custom-developed software. Because recorded spike waveform had low temporal resolution (32000 points/s), we interpolated waveforms to 600 points/s and calculated a mean waveform for each putative unit. In order to account for possible effects of spike amplitude on measurements of spike width, we restricted our analysis to neurons with spike amplitude of at least 80 µV.

Measuring Key Features of Spike Waveforms for Classification

After the pre-processing, we used a custom-developed algorithm to estimate the features of the neuronal spike waveforms. For each putative neuronal cluster, we calculated the mean spike waveform across all the recorded spikes, and the velocity of the waveform, determined as the rate of voltage change over time. Then we found local and global extrema of voltage and velocity over time (Figure S4A). We estimated the peak-to-valley time as the time from the global maximum to the global minimum of the spike waveform. We estimated the half-peak width as the time from the first local maximum that occurs before the global maximum to the first local minimum that occurs after the global maximum. We estimated the velocity-based valley recovery time as the time from the global minimum to the first local maximum that occurs after the global minimum.

Feature Combination for FSI classification

We constructed histograms of peak-to-valley time, half-peak width, and velocity-based valley recovery time across all recorded dorsomedial striatal neurons (n = 6496 for control, n = 7463 for immobilization stress and n = 8787 for foot-shock stress groups). The resulting distributions were each bimodal, with the left mode encapsulating what we define as FSIs, and the right mode encapsulating non-FSI neurons (Figure S4B). We separated FSIs and non-FSIs in each distribution using thresholds, determined separately for each distribution to provide clean separation (Figure S4B).

Sub-Classification of FSIs

We also classified FSIs based on their firing rates. Many of the identified FSIs exhibited firing rates above 6 Hz, which we designated as high firing. On the other hand, most SPNs had firing rates below 6 Hz. Firing rate, therefore, became a metric, along with peak-to-valley time, half-peak width, and velocity-based valley recovery time, to separate FSIs from other neuronal types. By analyzing firing rates, we were able also to identify a subgroup in FSI distribution that exhibited both high firing rates and narrow spike widths (Figure 3D; n = 103 for control, n = 57 for immobilization stress and n = 79 for foot-shock stress groups). All FSIs had similar waveform features (Figures 3D and S4D–S4F).

We found a potential advantage of classifying FSIs based on both firing rate and spike widths in that classification on both metrics led to a lower rate of false positives in our neuron identification process. A limitation of the classification method based on firing rates, in the case of our experiment, is due to the effect of stress on FSIs. After stress, we observed significantly fewer neurons classified as FSIs that exhibited high firing rates (Figures S4G and S4H). This change could occur because stress reduces the firing rate of striatal neurons or because stress reduces the number of FSIs. Therefore, in this manuscript, we present results using both methods of classification.

Counting PV-Expressing Interneurons

To examine the effect of chronic stress on the number of PV⁺ striatal interneurons, we conducted a histological experiment (Figure 3G). Forty-eight male C57BL/6J mice were randomly split into the stress and control groups. The stress group was stressed using an immobilization procedure (14 day one hr per day), whereas the control group did not receive such treatment. Twenty mice were perfused on the day after the completion of the chronic stress or control procedures, and another twenty-eight mice were perfused one month later. Mice were anesthetized with pentobarbital (100 mg/kg, i.p.) and transcardially perfused with 50 ml saline (0.9% NaCL), followed by 50 ml PFA (4% paraformaldehyde in 0.1 M PB). After this, the brains were removed and post-fixed for 16 hr in PFA at 4°C before transferring them to sinking solution (25% glycerol in TBS). Next, the brains were frozen in dry ice and cut in 40-µm coronal sections using a freezing microtome. Per animal, 4–6 sections were used for staining for PV⁺ neurons and for peri-neuronal nets and striosomes (data not presented). Sections were first rinsed 3 × 10 min in PBS-Tx (0.01M PBS + 0.2% Triton X-100), 10 min in the PBS-Tx with 3% H2O2, rinsed in PBS-Tx again, after which they were incubated in blocking buffer (Perkin Elmer TSA Kit) for 20 min, and 2 days in blocking solution with primary PV antibody (polyclonal guinea pig anti-PV, 1:5000, Synaptic systems 195004) and MOR1 antibody (polyclonal rabbit anti-MOR-1, 1:500, Abcam ab134054) at 4°C. Two days later, the slices were rinsed, incubated in biotinylated Wisteria floribunda lectin (1:10000, Vector, B-1355) for 30 min, rinsed, incubated in ABC (Elite Kit, Vector, PK-6100) for 60 min, rinsed, incubated in TSA-Plus Fluorescein (1:500, PerkinElmer) for 5 min, rinsed, and incubated with secondary antibodies (Goat anti-guinea pig AF 546, Invitrogen, 1:300 and goat anti-rabbit AF 647, Invitrogen, 1:300) for 120 min, after which they were rinsed 3 × 10 min in 0.1M PB and mounted on slides and coverslipped in antifade solution (ProLong Gold Antifade Mountant with DAPI, ThermoFisher). All rinsing steps were 3 × 10 min in PBS-Tx unless otherwise indicated. Next, z-stacks were made from the dorsomedial striatal sections of both hemispheres using a Zeiss LSM 510 confocal microscope. The number of PV⁺ neurons in every stack, excluding the first and last slices, was counted manually using the ZEN software by people unaware of the experimental conditions. After quantification, the data were normalized to the average of the control group, and differences were tested using ANOVA and t-tests.

Characterization of PV⁺ Interneurons

Characterizing PV⁺Interneurons Based on Spike Waveform and Firing Rate

To link our classification method to anatomical and optogenetic experiments, we determined the correlation between our FSI designations for interneurons and their PV expression through an experiment on genetically engineered mice expressing Cre in PV⁺ neurons. In this experiment, we injected the mice with the excitatory AAV5-EF1a-DIO-C1V1(E122T/E162T)-TS-EYFP virus or the AAV5-EF1a-DIO-eArch3.0-EYFP inhibitory virus (0.2 µl at 0.05 µl/min). All injections were made in the dorsomedial striatum (AP: +0.6 mm; ML: ±1.25 mm; DV: −2.0, −2.7 and −3.4 mm from dura mater). After 4–12 weeks to allow the virus to express fully, we implanted a custom-developed headstage containing 16 recording tetrodes that surround two optical fibers (100 µm, Doric Lenses). One week after surgery, we performed optogenetic manipulation (300 pulses, 30 ms, 2-s interval between pulses for excitatory virus; and 300 pulses, 500 ms, 3-s interval between pulses for inhibitory virus) and conducted electrophysiological recordings. We moved the tetrodes and the optical fibers systematically to search for units that responded to optogenetic manipulation. Spike activity of each recorded unit was aligned to the onset of optogenetic perturbation to examine the significance of neuronal response to the manipulation. We also calculated the z-scores to normalize neuronal activity relative to baseline (1 s before to the onset of stimulation). The probability that stimulation caused a significant response (p < 0.01) was calculated by shuffling 1000 times the spike times in the baseline interval and by using a bootstrap method on those shuffled data. We examined the spike waveform properties of the responding PV⁺ neurons and found that they had narrow spike waveforms as we found in FSIs (Figures 3H, S4M and S4N) and had a wide distribution of firing rates, supporting idea that PV⁺ interneurons could be categorized as FSIs.

It is important to note that only 30% of Cre-positive neurons express PV, and we cannot draw a conclusion about waveform properties of other 70% of PV⁺ interneurons population. We also observed that SPNs (n = 25) responded to laser delivery but in the opposite direction of PV manipulation (i.e., using inhibitory virus, PV⁺ neurons were inhibited but SPNs were excited).

Optogenetic Manipulation of PV⁺ Interneurons

To determine the role of PV⁺ neurons in the causal relationship between stress and abnormal decision-making, we optogenetically manipulated the activity of PV⁺ neurons in genetically engineered PV-Cre mouse models. These mice were injected with Cre-dependent viruses and were implanted with headstages containing two fibers aimed to the dorsomedial striatum. The mice were trained on the CBC decision-making task prior to receiving optogenetic manipulation sessions. These sessions consisted of 10 reminder trials to familiarize the mice with the costs and benefits associated with each end-arm and 20–40 CBC decision-making trials during which laser was applied from the click sound that signaled the trial start to reward licking.

Injection and Implantation of PV-Cre Mouse Models

Three groups of PV-Cre mice were injected with 0.6 µl of either AAV5-EF1a-DIO-eArch3.0-EYFP virus for inhibition, AAV5-EF1a-DIO-C1V1(E122T/E162T)-TS-EYFP virus for excitation, or AAV5-CaMKIIa-EYFP virus for control optogenetic manipulation. The virus was injected into the dorsomedial striatum (AP: +0.6 mm; ML: ±1.25 mm; DV: 2.7 mm from dura mater for one group and AP: +0.6 mm; ML: ±1.25 mm; DV: 2.35 mm from dura mater for other group) at a rate of 0.06 µl/min. One pair of optical fibers (Doric Lenses, length: 5.0 mm) was implanted in the dorsomedial striatum (AP: +0.6 mm; ML: ±1.25 mm; DV: 2.5 mm from dura mater; and AP: +0.6 mm; ML: ±1.25 mm; DV: 1.7 mm from dura mater).

Laser Manipulation Parameters for PV-Cre Mice

For each PV optogenetic experiment, light (532 nm in wavelength, 2–4 mW per hemisphere) was delivered from a laser source (OEM Laser Systems). In optogenetic inhibition trials, 1 light pulse was applied for 3.5 s, and in optogenetic excitation trials, 125 10-ms light pulses were delivered, with a 30-ms intervals between them, for 5 s.

Limitation of Optogenetic Manipulation in PV-Cre Mice

In addition to the limitations listed in the “Potential Problems and Limitations of Optogenetic Manipulation” section, several other limitations result from our procedure for optogenetic manipulation in PV-Cre mice. Importantly, it is known that not all PV⁺ neurons express Cre in the PV-Cre mouse line that we used. In our histological examination, ~30% of PV⁺ neurons expressed PV-Cre, indicating that the Cre-targeted behavioral optogenetic experiments successfully manipulated only a subgroup of PV⁺ interneurons.

Additionally, our histological examination demonstrates that PV⁺ neurons in several cortical regions may also express the virus at their terminals in the striatum. Their observed infection may occur due to anterograde terminal labeling of the AVV5 virus. Therefore, we performed another experiment to manipulate PV⁺ interneuron predominantly by IEM-1460 (selective AMPA receptor blocker) injection in the dorsomedial striatum (see below), which turned out to be consistent to PV optogenetic experiment.

Striatal Microinjections of IEM-1460

In order to test the causal relationship found between FSIs and SPNs, we performed a chemical manipulation of FSIs during cost-benefit decision-making. Rats were first implanted with headstages containing 24 recording tetrodes and 2 guide cannulas for drug delivery aimed to the dorsomedial striatum. This headstage also contained 2 stimulation tetrodes aimed at the PFC-PL for the identification of striosomal neurons. Rats were trained to perform the CBC decision-making task. After successful training, rats underwent CBC sessions with IEM-1460 administration. Before performing the CBC task, rats were placed in a plastic cage, and baseline FSI and SPN firing rates were measured for 15 min. After this, rats were placed in the T-maze, and sessions began with 20 reminder trials and continued with 20 baseline CBC decision-making trials. After these trials, we performed electrical stimulations of the PFC-PL to identify striosomal SPNs (described above). Thereafter rats were placed in the plastic cage, and we injected 0.5 ul per hemisphere of a freshly diluted IEM-1460 solution (0.25 mg E-1460 per 1 ml saline, 1 mM concentration) through the cannula (PlasticOne) with a speed of injection of 0.05 µl/min. After a 10–70 min interval after the injection, we collected an additional 40 trials of the CBC decision-making task (Figure 4F).

Effect of IEM-1460 Microinjections on FSI and SPN Firing Rates

To determine the effect of IEM-1460 microinjections on the activity of FSIs and SPNs, we compared their firing rates before and after IEM-1460 injection. During the task, we observed a large variation of firing rates. Therefore, as a baseline, we selected the 15-min interval before the task started when the animal rested in the plastic cage.

Correlation between Chocolate Milk Preference and Striatal Neuron Firing Rates

We measured the correlation between chocolate milk preferences and the firing rates of FSIs or striosomal SPNs after IEM-1460 injection for each session. Chocolate milk preference and mean FSI or SPN firing rate were calculated per individual windows of 5 consecutive trials in a session (40 trials) after IEM-1460 injection and compared to preference and firing rates before the injection. We correlated chocolate milk preference to FSI (n = 92) or SPN (n = 47) firing rates using the linear regression (regression function in MATLAB). Significance of the correlation was determined using Pearson correlation coefficient (corrcoeff function in MATLAB) (Figures 4I and S4S).

Correlation between FSI Firing Rates and Probability of PFC-PLs Burst Followed by SPN Burst

In order to determine the correlation between FSI firing rates and the likelihood of a PFC-PL burst followed by an SPN burst, we identified session that have simultaneous recordings of a PFC-PLs neuron, a striosomal SPN and an FSI (n = 3). For each neuron in the triplets, we isolated the burst signal (described in PFC-PLs-Striosomal SPN/FSI Interactions). For each trial after IEM-1460 injection, we calculated the probability of a PFC-PLs burst response followed by a striosomal SPN burst. These probabilities and FSI firing rates were normalized using the z-score calculation with the 20 trials prior to injection as the baseline. We correlated FSI firing rates to this probabilities using linear regression (regression function in MATLAB). Significance was determined using the Pearson correlation coefficient (corrcoeff function in MATLAB) (Figures 4J and S4T).

PFC-PLs-Striosomal Circuit Dynamics

Understanding how stress affects the PFC-PLs-striosomal circuit requires examining the dynamics of the circuit during the CBC task before and after stress. In this effort, we examined when periods of high and low activity occur for different neuron types in the circuit, in previously stressed and control animals.

Defining Neuronal Activity Peak and Valley Time

We determined high and low activity based on the spike distribution of individual neurons. High activity was defined as activity 3 SDs above the mean activity of an individual neuron. Low activity was defined as 1.5 SDs below its mean activity. We also identified times of the first minima or maxima in activity for each neuron (Figures 5A and S5A). Local minima or maxima are identified by concentrating on the first period of high or low activity in the recording window. The first local maximum or minimum for the recording window is defined as the maximum or minimum over this first period of high or low activity.

Determining the Relative Activity of Populations of Neurons

We calculated, for each neuron recorded during CBC task performance, the time of the first relative maximum (peak) or minimum (valley) in activity, as defined in the previous section and illustrated as black dots in Figure S5C. Over each time window beginning at the maximum/minimum of one neuron and ending at the maximum/minimum of another, we calculated the density of extrema across all the neurons in the virtual population (i.e., group of units not recorded simultaneously). Density was defined as the count of extrema in the time window divided by the window duration. We then calculated a distribution of peak densities across all possible windows and determined a ‘high-activity period’ defined as a window that contains 80% of the peaks/valleys during the click-to-lick period.

PFC-PLs-Striosomal SPN/FSI Interactions

In order to analyze PFC-PLs and striatal task-related activity dynamics, we focused on pairs of PFC-PLs and striatal neurons simultaneously recorded during CBC task sessions (striosomal SPN shown in Figure 6A and FSIs shown in Figure 6B). First, we isolated bursts in neuronal activity of the PFC-PLs and striatal neurons by calculating the distribution of inter-spike intervals (ISIs) and then extracting the spike pairs corresponds to lower 35% percentile of ISIs (Figures S6A and S6B).

By isolating bursts in neuronal activity in the PFC-PLs and striatal neurons, we can determine how bursts in PFC-PLs neurons affect the activity of the striatal neurons. We concentrated on bursts that occurred over the interval from 3 s before click to the lick (Figures 6A–6C) and on bursts during 15 s before to 15 s after click (Figure 6D–6F). After each PFC-PLs burst, we assigned a time window of 1.5 s to search for an excitatory response in a striatal neuron. For each burst in this 1.5-s time window, we found the time delay between the PFC-PLs burst and the striatal bursts (Figure S6C). The time delays for this 1.5-s window were compiled into a histogram. We iterated this process for each PFC-PLs burst, forming a histogram of all striatal burst delays for that pair of neurons (Figure S6D).

From this distribution of time delays, we determined the significance of the interaction between PFC-PLs and striatal neurons through a one-sample Kolmogorov-Smirnov test (MATLAB). We also confirmed that the distribution was different from random using a bootstrap technique to calculate the difference between PFC-PLs bursts and shuffled striatal neuron spike times.

We also used the distribution of time delays to search for the CBC task ‘connection’ time between PFC-PLs neurons and striatal neurons. We measured this by determining, for each PFC-PLs-striatal neuron pair, the earliest response of the striatal neuron after a burst in PFC-PLs neurons. To ensure significance, we calculated a histogram of time delays, and created a threshold above which responses were considered significant. The first bin above this significance threshold was considered the earliest response. The significance threshold was determined by taking the mean and SD of the counts across bins of the histogram. The threshold, for each distribution, was one SD above the mean of the counts. We calculated the distribution of first peak delay for all significantly interacting pairs (Figures 6A and 6B, right panels).

FSI-Striosomal SPN Functional Connectivity

We also examined the inhibitory effect of individual FSIs on individual SPNs. As we did for PFC-PLs and striatal neurons, we determined, from intervals between spikes, neuronal bursts in both the FSIs and SPNs. Our process for determining functional connection was different from that for PFC-PLs and striatal neurons, because the relationship between SPNs and FSIs is inhibitory, rather than excitatory. Rather than examining whether a PFC-PL burst induced a burst in a striatal neuron, we determined whether FSI activity induced a reduction of bursts in an SPN over a time window. For this inhibitory case, we set the start of the time window as the mid-point of the preceding FSI burst. The end of the time window was set as the onset time of the next SPN spike with an ISI less than or equal to the mean ISI. If the SPN firing rate does not recover from inhibition before the next FSI burst, the end of the inhibition was set as the start of the next FSI burst (Figure S6E).

We then looked for significant changes in the length of the period of SPN inhibition following an FSI burst. Similar to our test of excitation, we created, for each pair, a histogram of the length of inhibitory time windows. With a one-sample Kolmogorov-Smirnov test (MATLAB), we compared the distribution to a uniform distribution. We also used a bootstrap technique on shuffled SPN spike times with an identical optimization procedure to test for significance from shuffled recordings.

Inhibition of Striosomal SPNs from FSIs

To expand on our tests that showed that FSI activity induces SPN inhibition, we then tested whether the ability of FSIs to inhibit SPNs was affected by stress. This is particularly important because stress affects many aspects of the corticostriatal circuit, including the activity of FSIs and SPNs. Yet we found no significant decrease in the ability of FSIs to inhibit SPNs after stress.

We first separated the tonic and burst activity of FSIs (Figure S6I). Burst activity was determined based on ISIs, as in our determination for functional connection, and tonic activity was defined as spikes during intervals between 200 ms after the previous burst and 200 ms before the next burst. We correlated SPN firing rates to tonic and burst FSI firing rates.

Effect of Temporally Coordinated PFC-PLs Activation

We identified triplets and quadruplets of simultaneously recorded neurons consisting of 2–6 PFC-PLs neurons and one FSI. We defined the PFC-PLs neurons and FSI to be connected if, during click-to-turn interval, 90% PFC-PLs neurons bursts preceded an FSI burst in a 100 ms window prior to the FSI burst. We calculated the levels of the PFC-PLs activation using a z-score and measured a proportion of PFC-PLs neurons connected to FSIs.

Model of the PFC-PLs-Striosomal SPN Circuit

We modeled all neurons in the PFC-PLs-striosomal SPNs circuit as single compartments obeying the equations and parameters of Hodgkin and Huxley (Destexhe et al., 1994). Using this simple model demonstrates that the results do not depend on conductances besides sodium and potassium. Such Hodgkin–Huxley neurons were connected to each other using conductance-based model synapses. Seven model PFC-PLs neurons were connected to one model FSI and three model SPNs via model excitatory (AMPA) synapses, and the FSI was connected to the SPNs via a model inhibitory (GABA_A) synapse. Synapses were modeled by the following equations (Destexhe et al., 1994):

$$I_{\mathit{syn}}(t)=g_{\mathit{syn}}r(t)\left[V_{\mathit{post}}(t)-E_{\mathit{rev}}\right]$$

$$\frac{dr(t)}{dt}=\alpha T(t)[1-r(t)]-\beta r(t)$$

$$T(t)=\frac{T_{\mathit{max}}}{1+exp\left\{-\left[V_{\mathit{pre}}(t)-V_p\right]/Kp\right\}}$$

Here, I_syn(t) is the synaptic current, g_syn is the maximal synaptic conductance, r(t) is the fraction of the receptors in the open state, V_pre(t) and V_post(t) are the membrane potentials of the presynaptic and postsynaptic neurons shifted by −70 mV, E_rev is the synaptic reversal potential, α and β are the forward and backward rate constants, T(t) is the neurotransmitter concentration in the synaptic cleft, and T_max = 1.5 mM is the maximal neurotransmitter concentration. When calculating synaptic currents, the membrane potentials of the neurons are shifted by −70 mV, because the resting membrane potential in Hodgkin and Huxley’s model is 0 mV. For excitatory synapses, E_rev = 0 mV, α = 1.1 mM⁻¹ms⁻¹, and β = 0.19 ms⁻¹. For inhibitory synapses, E_rev = −80 mV, α = 5.0 mM⁻¹ms⁻¹, and β = 0.18 ms⁻¹. The maximal synaptic conductance g_syn. We used MATLAB’s ode45 solver to integrate the system of differential equations.

Each time the cortico-striosomal circuit model is initiated, 7 PFC-PLs neurons, 1 FSI, and 3 striosomal SPNs are simulated. The spike pattern of each model PFC-PLs neuron followed the pattern of PFC-PLs neurons recorded during one trial of the CBC task, drawn pseudorandomly from the full set of trials run by rats. Each PFC-PLs spike is converted into a T = 1.5 mM neurotransmitter pulse of duration 1 ms, driving synaptic dynamics. The FSI receives a synapse from each of the 7 PFC-PLs neurons. The maximal conductance of these synapses is g_syn = 1 mS/cm² in the unstressed condition (Figure 7A) and 0.025–0.033 mS/cm² in either of the two stressed conditions. Each striosomal SPN receives synapses from the FSI neuron (g_syn = 1.35 mS/cm²), and two pseudorandomly selected PFC-PLs neurons with connection strength randomly selected from a normal distribution (distribution mean g_syn = 0.25 mS/cm², and distribution SD σ = 0.025 mS/cm²).

For the simulation of PFC-PL microstimulation summarized in Figure 7C, we activated all 7 PFC-PLs neurons simultaneously with a T = 1.5 mM pulse of duration 1 ms. For simulations of in-task FSI and SPN activity, the PFC-PLs spike patterns were drawn from 54 neurons in unstressed, 34 in immobilization-stressed, or 22 in foot-shock-stressed rats. The model was initiated many times for each of these 3 conditions, each time selecting the spike pattern from one trial for each of a set of 7 PFC-PLs neurons. For Figures 7C, S7A–S7C, S7E and S7G, the model was initiated 40 times. Thus, in effect for each condition, we simulated 40 FSIs and 120 SPNs driven by 4087 PFC-PLs neurons.

QUANTIFICATION AND STATISTICAL ANALYSIS

In order to measure the effect of chronic stress on decision-making and to determine the significance of optogenetic manipulation effects on choices made by rats and mice (Figures 1F, 2G, 4C, 4E and S2H), we used one-way ANOVA with Bonferroni correction. We used repeated measures ANOVA with Bonferroni correction and also applied Tukey’s test to detect differences between sessions (Figures 1D and 4D). We used two-sample t-tests and two-sample Kolmogorov-Smirnov tests (Matlab statistic toolbox) to measure significant differences in firing rates (Figures 2B, 3C, 3E, 5B, S2B–S2D, S3Q, S3R, S4J, S4L, S5B, S5H and S5J). The statistical differences of counts in histograms (Figures 5F, 6A–F and 6I) were determined by chi-square test (Matlab statistic toolbox). Significance of the correlations (Figures 3F, 4I, 4J, S2F, S2I, S4H, S4S and S4T) was determined using Pearson correlation coefficient (corrcoeff function in MATLAB). In order to distinguish significant effect of stress on striosomal SPN response to PFC-PL electrical stimulation (Figures 5E and S5J), we used two-sample t-test (MATLAB statistic toolbox). We verified the absence of significant difference between the groups (Figures 4G and 7D) by two-sample t-test (Matlab statistic toolbox). For data presentation, we used mean as a center, and used standard error of mean (all Figures) or SD (Figures 1F, S1A, S1B, S1Q–S1S, S4E and S5J) as confidence intervals.

In each figure that describes behavioral, optogenetic and anatomical experiments, we indicate number of animals that we used for each group (Figures 1F, 2G, 3G, 4C–4E, S1M–S1P and S2H). In each figure that describes electrophysiological and modeling experiments, we indicate number of recorded units (Figures 2B–2D, 3B–3E, 3H, 4J, 5C, 5E, 5F, 6A–6C, 6I, S2A–S2D, S3G–S3U, S4D–S4R, S5D, S5E, S5G, S5H, S5J, S5K and S6F). We indicated statistical tests and p values in the figure legends. Details of data analysis were indicated in detailed methods. Codes that were used for data analysis were deposit into github.

For identification of the stress effect on cost-benefit decision-making mediated by the prefronto-striosomal circuit, we conducted 11 experiments:

1. Long-Evans rats used for assessment of chronic stress effect on cost-benefit decision-making

   1. Rats chronically stressed using immobilization procedure (n = 11)

   2. Rats chronically stressed using electric foot-shock procedure (n = 8)

   3. Control rats (n = 14)

2. C57BL/6J mice used for assessment of chronic stress effect on cost-benefit decision-making

   1. Mice chronically stressed using immobilization procedure (n = 23)

   2. Control mice (n = 14)

3. Long-Evans rats used for assessing anhedonia effects of chronic stress using various preference tests and light avoidance tests

   1. Rats chronically stressed using immobilization procedure (n = 8)

   2. Rats chronically stressed using chronic electric foot-shock procedure (n = 8)

   3. Control rats (n = 8)

4. Long-Evans rats used for electrophysiological recordings in PFC-PL and dorsomedial striatum during behavioral task and neuronal targeting

   1. Rats chronically stressed using immobilization procedure (n = 5)

   2. Rats chronically stressed using chronic electric foot-shock procedure (n = 4)

   3. Control rats (n = 14)

5. Long-Evans rats used for optogenetic manipulation of PFC-PL projection to striosomes

   1. Rats injected with AAV5-CaMKIIa-EYFP (control) virus in PFC-PL (n = 4)

   2. Rats injected with AAV5-CaMKIIa-eNpHR3.0-EYFP (inhibitory) virus in PFC-PL (n = 4)

   3. Rats injected with AAV5-CaMKIIa-C1V1(E122T/E162T)-TS-EYFP (excitatory) virus in PFC-PL (n = 15)

6. Long-Evans rats used for 3D reconstruction of striatum and identification of tetrode location in striosomes or matrix (n =2).

7. C57BL/6J mice used for testing effect of chronic stress on the number of PV⁺ neurons

   1. Mice chronically stressed using immobilization procedure (n = 24)

   2. Control mice (n = 24)

8. PV-Cre mice used for optogenetic manipulation of PV⁺ neurons during cost-benefit decision-making

   1. Mice injected with Cre-dependent opsin-lacking construct virus (n = 6)

   2. Mice injected with Cre-dependent AAV5-EF1a-DIO-C1V1(E122T/E162T)-TS-EYFP virus for excitation of PV⁺ neurons (n = 5)

   3. Mice injected with Cre-dependent AAV5-EF1a-DIO-eArch3.0-EYFP virus for inhibition of PV⁺ neurons (n = 6)

9. PV-Cre mice used for measurement of physiological waveform features of PV⁺ interneurons

   1. Mice injected with AAV5-EF1a-DIO-C1V1(E122T/E162T)-TS-EYFP (excitatory) virus (n = 5)

   2. Mice injected with AAV5-EF1a-DIO-eArch3.0-EYFP (inhibitory) virus (n = 4)

10. Long-Evans rats used for electrical microstimulation in PFC-PL and recording of striosomal SPNs and FSIs in the dorsomedial striatum

    1. Rats chronically stressed using immobilization procedure (n = 5)

    2. Rats chronically stressed using chronic electric foot-shock procedure (n = 4)

    3. Control rats (n = 13)

11. Long-Evans rats used for intrastriatal microinjections of IEM-1460 for FSI manipulation during the CBC task (n = 3)

DATA AND SOFTWARE AVAILABILITY

All data that were used for this project have been deposited at Mendeley. All codes that were used for this project have been deposited at Github.

Mendeley databases include:

1. Spike recordings in the dorsomedial striatum and PFC-PL of control rats, rats that underwent immobilization stress, and rats that underwent foot-shock stress: http://dx.doi.org/10.17632/z9jd8xhj84.1#file-01cffc75-3075-40fb-8c92-20e1c635abb0

2. Spike recordings in the dorsomedial striatum and PFC-PL before and after IEM-1460 injection: http://dx.doi.org/10.17632/z9jd8xhj84.1#file-9b92b939-9983-44b1-ac75-a6d4d784163b

3. Spike recordings in the dorsomedial striatum during PV-targeted optogenetic manipulation: http://dx.doi.org/10.17632/z9jd8xhj84.1#file-27e45bba-96eb-4961-868a-ecf0f9e340f4

4. Effect of chronic stress on rat decision-making: http://dx.doi.org/10.17632/z9jd8xhj84.1#file-74fcf2e3-6f97-4450-92af-d2b3aa34435c

5. Effect of chronic stress on mouse decision-making: http://dx.doi.org/10.17632/z9jd8xhj84.1#file-74fcf2e3-6f97-4450-92af-d2b3aa34435c

6. Effect of optogenetic manipulation on rat and mouse decision-making: http://dx.doi.org/10.17632/z9jd8xhj84.1#file-74fcf2e3-6f97-4450-92af-d2b3aa34435c

7. Chronic Stress Penetration Analysis http://dx.doi.org/10.17632/z9jd8xhj84.1#file-22c9e600-18d2-4737-bb48-a86996a1abcc

Custom developed codes that were used for data base analysis listed above were deposit at - https://github.com/timt51/Corticostriosomal-Circuit-Stress-Experiment

The codes are organized as follows:

1. Data analysis code reused from (Friedman et al., 2015): https://github.com/timt51/Corticostriosomal-Circuit-Stress-Experiment/tree/master/Cell%20Codes

2. Data analysis code comparing control and stress groups: https://github.com/timt51/Corticostriosomal-Circuit-Stress-Experiment/tree/master/Stress%20Paper%20Codes/Control%20and%20Stress%20Group%20 Comparisons

3. Code for analyzing model of corticostriatal circuit: https://github.com/timt51/Corticostriosomal-Circuit-Stress-Experiment/tree/master/Stress%20Paper%20Codes/Model

4. Code for analyzing orthodromic and antidromic stimulation experiments: https://github.com/timt51/Corticostriosomal-Circuit-Stress-Experiment/tree/master/Stress%20Paper%20Codes/Orthodromic%20and%20Antridromic%20St imulation

5. Code for visualization algorithms: https://github.com/timt51/Corticostriosomal-Circuit-Stress-Experiment/tree/master/Stress%20Paper%20Codes/Algorithm%20Visualization

6. Data analysis helper functions: https://github.com/timt51/Corticostriosomal-Circuit-Stress-Experiment/tree/master/Stress%20Paper%20Codes/Helper%20Functions

7. Master script running all of the above code: https://github.com/timt51/Corticostriosomal-Circuit-Stress-Experiment/tree/master/Stress%20Paper%20Codes/Helper%20Functions

Supplementary Material

1

Figure S1. Effect of Chronic Stress on Behavior of Rats and Mice, Related toFigure 1

(A) An example of a psychometric function of a mouse performing CBC and BB tasks, with preference measured across concentrations, as in Figure 1C. Error bars show SD.

(B) Psychometric functions of rats performing CBC and CC tasks. *p < 0.001 (CBC vs. CC, repeated measures ANOVA with Bonferroni correction). Error bars indicate SEM.

(C) Performance in the CBC (left) and BBS (right) tasks by rats that were exposed to foot-shock stress (related to Figures 1D and 1E). Each line represents the choices of an individual rat across sessions.

(D) Effect of immobilization stress on mouse decision-making. *p < 0.001 (CBC control vs. CBC immobilization, one-way ANOVA with Bonferroni correction). Dots represent choice in each session. Error bars show SEM.

(E) Variability (left) and coefficient of variation (right) of choice increased after stress. Dots indicate choice variance or coefficient of variance of each rat. *p < 0.01 (two-sample t-test). Error bars show SD.

(F) The CBC performance was similar between foot-shock and immobilization stress groups (left), between strains of mice (middle) and between genders (right). The top of the bar indicates the mean before stress, red lines indicate levels of 1, 2, and 3 SDs below the mean, and black dots indicate the preferences of each animal after chronic stress.

(G) The CBC task psychometric functions for two additional rats before and after stress (related to Figure 1G).

(H) CBC task psychometric functions for two control rats before and after two weeks of no-stress period (related to Figure 1G).

(I) A second model of the psychometrical functions. We split the psychometrical functions into two states: a state without cost and benefit integration (red) and a state with linear integration of cost and benefit (blue). A two-parameter sigmoid is fit to the second state.

(J) The frequency of choice behavior (gray) was modeled by two-term Gaussian function (red line), suggesting the fit of a two-state model. The dashed line indicates the location of the state transition in I.

(K) Stress extended the length of the random choice state. *p < 0.01 (paired t-test).

(L) Stress also increased the inverse temperature parameter B for the conditional logit model, representing the choice function steepness. *p < 0.05 (paired t-test).

(M) A sucrose preference test on control and stressed rats demonstrates stress-induced anhedonia. In the test, rats were given a choice between 2.5% sucrose solution and water. *p < 0.01 (two-sample t-test). Error bars show SEM.

(N) A modified preference test on control and stressed rats. Rats were given a choice between pure chocolate milk and diluted chocolate milk, either with a concentration of 70%, similar to the concentration used for BBS tasks (left), or a concentration of 30%, similar to the concentration used for BBD tasks (right). Error bars show SEM.

(O) A light avoidance test on a linear maze with bright and dim light. Time spent in brighter half of linear maze area was measured for 5 min. Error bars show SEM.

(P) A light avoidance test on a linear maze with a bright light at one end.

(Q) Mean (± SD) running times from click to the first lick were comparable across tasks.

(R) Choice in the current session was not influenced by previous sessions. For each task type, we calculated the change in probability of choice between unconditional and conditional probability due to previous task type. Error bars show SD.

(S) Choice in the current trial was influenced by previous choices made within the same session. For each task and stress type, conditional probability of choosing pure chocolate milk in current trial (t) given choice of pure chocolate milk in previous trial (t–1), two trials before (t–2), three trials before (t–3), four trials before (t–4), or five trials before (t–5) was calculated. Change in probability was calculated by subtracting the unconditional probability of choosing pure chocolate milk and expressed as a percentage (mean ± SD). *p < 0.001 (two-sample z-test comparing the conditional probability given choice in previous trial (t−1) with that given choice in two to five trials before (i.e., t–2, t–3, t–4 and t–5)).

2

Figure S2. Effect of Chronic Stress on the PFC-PL Neuronal Population, Related toFigure 2

(A) Cresylecht violet stained sections, showing tetrode tracks (orange dotted lines) and lesions marking tetrode tips (arrows). Numbers indicate anterior-posterior coordinates (mm). Scale bars represent 1 mm.

(B) Baseline activities of the PFC-PL (left) and PFC-PLs (right) neurons were significantly decreased after stress. *p < 0.01 (Kolmogorov–Smirnov test and two-sample t-test). Error bars show SEM.

(C) Average firing rate of PFC-PL neurons was significantly lower in stressed rats than in controls during the click-to-lick period of the CBC task (left), but firing rate of PFC-PLs neurons was not different between the groups (right). *p < 0.01 (Kolmogorov–Smirnov test and two-sample t-test).

(D) Firing rates of PFC-PL (left) and PFC-PLs (right) neurons was altered in stressed rats during the period of reward licking. *p < 0.01 (Kolmogorov–Smirnov test and two-sample t-test).

(E) Firing rates of PFC-PLs neurons recorded in control (left) and stressed (middle and right) rats. Related to Figure 2D.

(F) Reduction in PFC-PLs firing rate was linearly and inversely correlated with increased preference for pure chocolate milk after stress (p < 0.05, Pearson correlation).

(G) Stress had little effect on the firing rate of PFC-PLs neurons during the BBS task.

(H) Optogenetic inhibition had no effect on CBC choice of previously stressed rats. Dots correspond to choice in individual CBC sessions.

(I) Magnitude of intrastriatal optogenetic stimulation of PFC-PLs terminals was linearly correlated with increased preference for pure chocolate milk after chronic stress. Dots indicate individual rats (p < 0.01, Pearson correlation).

(J) Location of tetrode tracks (orange dotted lines) and tips (arrows) in the dorsomedial striatum (DMS) of a rat.

3

Figure S3. Effect of Chronic Stress on Striatal Neurons, Related toFigure 3

(A–H) Example of a tetrode tip identified in a striosome. Rats were implanted with a headstage containing 24 tetrodes arranged in rows. We performed a 3D brain reconstruction and aligned each section to white matter bundles and blood vessels. We then identified the location of this tetrode tip as in a striosome based of observed tetrode track through consecutive brain sections (A–C). Magnification of the tetrode tip (arrows) with staining for striosomes (D, MOR1) and DAPI staining (F), and a merged image (E, MOR1, red and DAPI, blue). Electrophysiological recordings from this tetrode demonstrated a sharp response to PFC-PL stimulation, as shown in a raster plot (G) and firing rate histogram (H).

(I–P) Example of tetrode tip identified in matrix, shown as in A–H. No response was recorded by this tetrode following PFC-PL stimulation.

(Q) Mean (± SEM) baseline firing rate of putative striosomal (left) and matrix (right) SPNs recorded during CBC task performance showed no difference between the control and stress groups.

(R) Stress-induced increase in the activity of matrix SPNs was detected in normalized (z-scores, left) and raw (right) firing rates during the click-to-lick period. *p < 0.01 (Kolmogorov–Smirnov test and two-sample t-test).

(S) Activity of striosomal (left) and matrix (right) SPNs was not different among stressed and control groups during the period of reward licking.

(T) Spike activity of striosomal SPNs recorded in control (left), immobilization stressed (middle) and foot-shock stressed (right) rats performing the CBC task. Inner T-maze outline indicates the period from the click to first lick (i.e., in-run period), and outer outline includes 3 s before and after runs. Activity shown as mean z-scores in color scale from blue (low) to red (high).

(U) Stressed rats exhibited no significant change in matrix SPN firing rate over the full recording session.

(V) Stress had no effects on the firing rate of striosomal SPNs recorded during the BBS task.

4

Figure S4. Classification and Activity of FSIs, Related toFigure 3 and 4

(A) For each putative unit, we calculated a mean (blue) and velocity (orange) of waveform. We found local peaks and valleys to estimate peak-to-valley time, half-peak widths, and velocity-based valley recovery time (dotted lines).

(B) Distribution of peak-to-valley times (left), half-peak widths (middle), and velocity-based valley recovery time (right) for all recorded striatal units. Two Gaussian functions were fitted for each distribution. The red lines indicate the Gaussian function used for classification of FSIs, and the orange lines represent that used for the remaining units.

(C) Mean spike waveform of FSIs (red) and SPNs (blue).

(D) Spike features of FSIs (red), FSIs that had high firing rates (black) and remaining units (blue).

(E) FSIs were distinct from the majority of striatal neurons in exhibiting a much larger spectrum of firing rates.

(F) Scatter dot plots showing the relationship between inter spike intervals (ISI, in log scale) and peak-to-valley times for FSIs and SPNs recorded in control and stressed rats.

(G) Proportion (mean ± SEM) of putative FSIs exhibiting high firing rates among all recorded striatal units. Each dot represents the proportion for an individual rat. *p < 0.01 (Kolmogorov– Smirnov test and t-test).

(H) The proportion of FSIs with high firing rates among total recorded striatal units was inversely correlated with increases in behavioral preferences for pure chocolate milk in the CBC task (p < 0.05, Pearson correlation).

(I) Stress did not alter proportion of FSIs identified among all units recorded in the striatum.

(J) Stress caused a reduction in FSI firing rates during the baseline (left), click-to-lick (middle) and reward-licking (right) periods of the CBC task. *p < 0.01 (Kolmogorov-Smirnov test and t-test).

(K) Percentages of FSIs among all recorded striatal units for individual rats were not correlated with behavioral preferences for pure chocolate milk in the CBC task.

(L) FSI firing rate was significantly lower in stressed animals performing the BBS task. *p < 0.01 (Kolmogorov-Smirnov test and t-test).

(M) Examples of optogenetic inhibition (left) and excitation (right) of PV⁺ neurons recorded in PV-Cre mice injected with opsin-expressing viruses for optogenetic targeting.

(N) A histogram of peak-to-valley times of PV⁺ neurons, demonstrating their narrow spikes. Red dashed line indicates a threshold that was used for classification (Figure S4B).

(O) Location of the track (orange dotted line) and tip (arrow) of an optical fiber in the dorsomedial striatum (DMS) of a mouse.

(P) Changes in the activity of PV⁺ neurons (left) and SPNs (right) simultaneously recorded during 20 CBC trials without optogenetic inhibition of PV⁺ neurons and during 20 trials with inhibition, shown in z-scores. The laser was applied for 3.5 s beginning at the click.

(Q) Intrastriatally injected IEM-1460 inhibited FSIs (left) and excited SPNs (right) during the 10–25 min post-injection period.

(R) FSI and SPN firing rates (left), z-score normalization of the firing rate changes (top right), and choice of pure chocolate milk (bottom right) before and after saline injection. Dots in left plots represent beginning of each trial.

(S) Correlation between changes in firing rate of FSIs (n = 92) and SPNs (n = 157) after IEM-1460 injection and choice of pure chocolate milk across 14 sessions. Firing rates and pure chocolate milk choice were calculated in windows of five consecutive trials. Z-scores were calculated relative to the pre-injection baseline firing rate.

(T) The probability of PFC-PLs bursts to evoke striosomal bursts, given FSI firing rates, calculated for a PFC-PLs-FSI-SPN triplet.

5

Figure S5. Effect of Stress on SPNs and FSIs, Related toFigure 5

(A) Detection of activity valley (1.5 STD below mean firing rate). Shading indicates SEM.

(B) Cumulative sum of activity peak times for FSIs that fired at high rates. Activity peaks were significantly delayed in stressed rats. *p < 0.001 (Kolmogorov–Smirnov test). See Figure 5B for all FSIs.

(C) Algorithm to determine relative activity. The recording interval was first broken into multiple time windows between extrema. Each window began and ended at a neuronal activity peak (small black rectangles). Three time windows between extrema are shown, one that filled the entire trial window (gray, below 50th percentile), another that encapsulated activity greater than mean (yellow, 50th to 70th percentile), and a third that had very high activity (red, above 30th percentile). High activity periods were indicated by arrows in Figures 5C and S5D–S5F.

(D) Dynamics of corticostriatal pathway components, related to Figure 5C. Individual neurons (stacked horizontally) showed periods of activity that rose above 3 SDs from baseline. Black squares indicate activity maxima.

(E) Activity peaks of FSIs that exhibited high firing rates.

(F) By determining the location of the minima and maxima across neurons (black squares in D and E), we identified when components of the PFC-PL-striosomal circuit had relatively high activity (red) or relatively low activity (blue). FSIs with high firing rates showed a delay or deletion in signaling after chronic stress (related to Figure 5D).

(G) Dynamics of striosomal activity, related to Figure 5C. Red indicates periods of activity above 3 SDs from baseline, and blue indicates periods of activity below 1.5 SDs. Black squares indicate activity maxima (for excitation) or minima (for inhibition). The left panels show inhibition of striosomal SPNs in control and stressed groups, and the right panels show their inhibition and excitation.

(H) Chronic stress causes a significant delay in the peak activity of FSIs (left) and FSIs with high firing rates (right) in the CBC task. *p < 0.001 (t-test). Error bars show SEM. Related to Figures 5B–5D.

(I) Temporary coordinated firing of the PFC-PLs neurons. Percentage of active (>25 Hz) PFC-PLs neurons calculated for each time bin (100 ms) during the task. In the control group, activity followed a step function, rising with the click. In stress groups, activity increases were delayed (immobilization) or irregular (foot-shock).

(J) Chronic stress caused a faster rise in striosomal SPN firing rates after PFC-PLs electrical microstimulation. *p < 0.001 (t-test). Related to Figure 5E.

(K) No significant difference in the proportion of SPNs that responded to PFC-PLs stimulation after stress.

6

Figure S6. Relationships among PFC-PLs neurons, FSIs, and Striosomal SPNs, Related toFigure 6

(A and B) Burst extraction algorithm. Spikes times were recorded (A, top), and ISIs were calculated (A, middle). Purple and red lines indicate, respectively, ISIs above and below the mean, shown as the vertical line in the ISI histogram (B). Groups of spikes with shorter than average ISIs are considered bursts (A, bottom).

(C and D) Algorithm for analyzing coincident bursts. Bursts in striosomal SPNs or FSIs were identified (C) after a burst in paired PFC-PLs neurons (yellow), and measured time delay (arrows) between the SPN/FSI and PFC-PLs bursts. A histogram of time delays shows whether the PFC-PLs-SPN pair had significant connection (D, top) or not (D, bottom). Significant difference from a uniform distribution was determined by performing the Kolmogorov–Smirnov test. Significance was also measured by applying the bootstrap technique to PFC-PLs-SPN pairs after randomly shuffling SPN burst times.

(E) Algorithm for identifying SPN inhibition by FSIs. We measured SPN firing rate after a burst in paired FSIs (top). If SPN ISIs were greater than mean ISI over the interval, we considered the firing rate reduced (bottom). Purple and red lines indicate, respectively, ISIs above and below the mean. As in C and D, histograms of inhibition times were constructed, and significance was determined.

(F) Stress did not affect the proportion of matrix SPN-FSI pairs in which FSI bursts were followed by SPN inhibition.

(G) Correlation between PFC-PLs activity strength and population temporal coordination measured during the 100-ms window 100 ms prior to FSI burst (p < 0.05, Pearson correlation).

(H) Firing rates of simultaneously recorded PFC-PLs neurons and FSIs were significantly correlated in control and stressed rats performing the CBC task (p < 0.01, Pearson correlation, Pearson correlation coefficient = 0.4).

(I) Algorithm to separate tonic and burst activity of FSIs. As described in A and B, FSI bursts were identified (rectangles). We measured the tonic firing rate in the window from 200 ms after a burst to 200 ms before the next burst (yellow).

(J) FSI burst activity had a significantly larger impact than tonic FSI activity on matrix SPNs. The ability of FSI bursts to inhibit matrix SPNs was similar after stress (p = 0.1).

7

Figure S7. Measuring the Effect of Shifts in E–I Balance after Stress, Related toFigure 7

(A) PFC-PLs recordings from control animals were entered into the immobilization and foot-shock models. Striosomes were more active in the model that takes into account shift of E–I balance even with control PFC-PLs inputs (A′). FSI activity peaks happened earlier in the control model than in stress models (A″). Therefore, the increase in striosomal SPN activity after stress is likely a product of a shift in E–I balance. Error bars indicate SEM.

(B) PFC-PLs recordings from stressed animals were entered into the control model. Striosomal SPN activity was inconsistent across stress models (A′). However, FSIs peaked early in the control model and with a delay in stress models (A″). These results suggest that the delay of FSI peaks after stress may be caused by abnormal PFC-PL signals.

(C) We symmetrically decreased connectivity between PFC-PLs neurons and SPNs and between PFC-PLs neurons and FSI. Symmetrical model did not produce consistent high striosomal activity across stress groups (C′). FSI activity peak was delayed (C″).

(D) The effect of intrastriatal optogenetic stimulation of PFC-PLs was significantly lower than that of PV optogenetic stimulation.

(E) We shifted the E–I balance of the circuit by decreasing connectivity between the FSI and SPNs (E). Model produced a high striosomal activity (E′).

(F) We fed PFC-PLs spike trains (top 8 rows) from control (left) and stressed (right) animals to the Hodgkin-Huxley model. Each row is an input neuron, and each vertical line is a spike. There was overlap between four spikes of PFC-PLs neurons in the control model, leading to an FSI spike (bottom row). However, in the stressed model, there was not enough PFC-PLs overlap to lead to an FSI spike. This example demonstrates that simultaneous PFC-PLs activity leads to FSI activation.

(G) Model taking into account that chronic stress equally decreases connectivity strength between all circuit elements, thereby inducing greater changes to weak connections as compared to strong connections. We connected 70 PFC-PLs neurons to one FSI and 3 striosomal SPNs. We modeled the stress effects on circuit by equally decreasing the connectivity strength among all circuit elements. We fed PFC-PLs activity of control and chronically stressed rats into the model. The model successfully reproduced striosomal hyperactivity (G′) and delayed FSI activity (G″).