Estimate your dose: RADDOSE‐3D

Abstract

We present the current status of RADDOSE‐3D, a software tool allowing the estimation of the dose absorbed in a macromolecular crystallography diffraction experiment. The code allows a temporal and spatial dose contour map to be calculated for a crystal of any geometry and size as it is rotated in an X‐ray beam, and gives several summary dose values: among them diffraction weighted dose. This allows experimenters to plan data collections which will minimize radiation damage effects by spreading the absorbed dose more homogeneously, and thus to optimize the use of their crystals. It also allows quantitative comparisons between different radiation damage studies, giving a universal “x‐axis” against which to plot various metrics.

Introduction

Radiation damage inflicted during X‐ray diffraction experiments has plagued macromolecular crystallography (MX) since the early days of the field. Tracking its effects, either in reciprocal space from the diffraction images or in real space from the final electron density maps, requires a generally used and reproducible “x‐axis” against which to plot the various metrics used to monitor radiation damage. Parameters such as time, image number, or goniometer angle are neither useful for comparative studies between experiments, nor for obtaining knowledge on the radiation damage progression rates under different experimental conditions and data collection protocols.

A quantity that can fulfil the need for a universally applicable x‐axis for this purpose is the absorbed dose D. This is defined as the energy absorbed per unit mass of sample during irradiation, in SI units of gray (Gy = J kg⁻¹). It is generally accepted that the rate of damage in a protein crystal is proportional to the dose (with certain caveats—see later) as first observed in 1962 by Blake and Phillips1 at room temperature (RT): the absorbed X‐ray energy is dissipated in the protein and solvent, causing ionisation of atoms and sometimes bond breakage. Dose cannot be measured, but it can be estimated using knowledge of the incident beam characteristics (energy, flux, size, and two‐dimensional profile) and of the crystal characteristics (volume, morphology, unit cell size, protein atomic contents, number of amino acids, and solvent composition) as well as the exposure time per image and number of images. The crystal parameters allow the absorption coefficients for X‐rays to be calculated, permitting the estimation of the absorbed dose.

Having defined the x‐axis as dose, D, various radiation damage indicators can be defined to plot on the y‐axis. In reciprocal space, the two most commonly used metrics are: the diffraction intensity of the nth dataset, or wedge of data divided by the summed mean intensity of the first dataset or wedge, I _n/I ₁, which decreases with dose, with higher resolution reflections fading first,2 and secondly B _rel, defined as the B‐factor of the 1st dataset subtracted from the B‐factor of the nth dataset, B _n‐B ₁. The gradient of this plot gives a sensitivity measure, s _AD = ΔB _rel/8π²ΔD, typically around 0.012 Ų/MGy for cryocooled crystals held at around 100 K during data collection.3 Among other possible y‐axis metrics is R _d,4 which is defined as the R‐factor between symmetry related reflections plotted not against the dose, but against the difference in the dose at which the reflections were recorded, ΔD. The R‐factor tends to increase with ΔD if the crystal is suffering radiation damage. Note that the three metrics described above do not necessarily give the same results when comparing, for example, the efficacy of scavengers in reducing radiation damage rates.5

Mosaicity also tends to increase with dose, as does the unit cell volume, whereas I/σ(I) decreases. However, it has been shown that none of these are robust or reproducible metrics, and thus they do not tend to be commonly used.6, 7

At the X‐ray beam energies, E _x, routinely used in MX (7 keV to 15 keV), the basic interaction processes which occur on irradiation of a protein crystal can be divided into three mechanisms (see Fig. 1). The first is diffraction (the Thomson effect), involving elastic scattering events during which no energy is lost in the crystal and thus no dose is absorbed. The second is the Compton effect resulting in inelastic scattering events in which the outgoing photon has a longer wavelength (and lower energy) than the incident one, with the residual energy being deposited in the crystal. The third one is the photoelectric effect in which the photon is totally absorbed by an atom, and a so‐called ‘photoelectron’ is ejected, carrying with it the incident photon energy minus the binding energy of the electron to the atom. For a 12.4 keV (1 Å) absorbed X‐ray, as many as 500 ionisation events in the crystal can be subsequently initiated by each original photoelectron.8 On ejection of the photoelectron, the atom is left in an excited state with a vacancy in one of its electron orbitals. The de‐excitation occurs by an electron dropping from an outer shell to fill the hole, with the accompanying release of the difference in binding energy either by emission of an Auger electron or a fluorescent X‐ray. For light elements the Auger process dominates, but the probability of fluorescent escape increases markedly with atomic number, being for example 30% for iron atoms. At E _x = 12.4 keV, ∼98% of the beam passes through a 100‐µm‐thick crystal (if it contains no nonorganic atoms) without any interaction occurring, and of the 2% that does interact, 8% diffracts, 8% undergoes Compton scattering and 84% causes photoelectric emission: thus this latter effect accounts for >90% of the energy absorption, and thus of the dose.9

Figure 1.

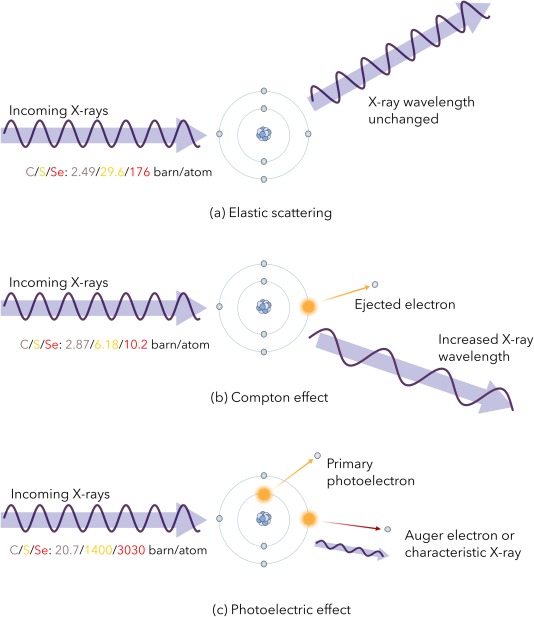
Interaction processes of incident X‐ray photons with atoms in the crystal. The photon cross‐sections for each interaction (in units of barn/atom: 1 barn = 10⁻²⁸ m²) have been provided for C, S, and Se, for an incident 12.4 keV (1 Å) X‐ray beam, as reported in the XCOM Photon Cross Section Database (http://physics.nist.gov/PhysRefData/Xcom/html/xcom1.html).

There is a limit to the dose that can be tolerated by biological samples before their integrity is compromised. For instance, radiotherapy for human glioblastoma multiforme brain tumours is 60 Gy at 2 Gy/day for 30 days directed to the affected area, and this is the maximum dose ever medically delivered to humans. Small rodents will die in minutes if they absorb 1 kGy in a single dose. For protein crystals, Henderson10 postulated a dose limit for MX from observations made in electron diffraction experiments at 77 K, and considered the relative energy loss in organic material when irradiated with 100 keV electrons compared with 8 keV photons. He suggested that protein crystals in MX would lose half their diffraction intensity following absorption of 20 MGy, the so‐called “Henderson limit.” This dose to half intensity, D _1/2, for MX was experimentally measured to be 43 (±0.3) MGy by Owen et al.11 who using a homogeneous (“top‐hat”) profile beam, monitored diffraction intensity loss between 20 and 2.2 Å in holo‐ (1 iron atom/2 amino acids) and apo‐ (no iron) ferritin crystals, whose absorption coefficients vary by more than a factor of 2 (1.113 mm⁻¹ compared to 0.406 mm⁻¹, respectively at E _x = 12.7 keV). However, it was found that at D _1/2, the final electron density maps derived for the data exhibited significant damage to particular amino acids (“specific damage”) and a more conservative experimental limit of 30 MGy, corresponding to a diffraction intensity of 0.7 × I ₁, was recommended.11 To plan an MX experiment below this dose limit, the dose must be estimated, and it was to facilitate this conveniently for crystallographers that the original RADDOSE programme was conceived and designed.

Note that the dose is a metric which takes account of the physical processes pertinent when X‐rays traverse a crystal but does not include possible chemical effects related to the true atomic environment, and these may result in the crystal not reaching the dose limit. For example, certain amino acids such as aspartates and glutamates are known to be particularly susceptible to specific damage, and if they are present at crystal contacts, the lattice may break down well before the dose limit is reached (as reported in Ref. 12). In addition, in principle radical scavengers can be either co‐crystallized with, or soaked into the crystal to modify the radiation chemistry taking place, and a number of studies have tested this method of extending macromolecular crystal lifetime both at 100 K and RT. The results from various research groups disagree, with conflicting publications as to the efficacy of this strategy (see e.g., the results in Ref. 13 compared with Ref. 14 for sodium nitrate at 100 K, and those in Ref. 15 vs. Ref. 16 for nicotinic acid). However, none of the tested scavengers has resulted in more than a factor of 2 increase in dose tolerance, with the exception of 1,4‐benzoquinone which improved the dose lifetime of RT lysozyme crystals by a factor of >9.17 Table I and the Supporting Information Table of Ref. 18 summarize all the results on scavengers for MX up to 2013, and to the authors knowledge, there have been no additional studies since then apart from that of Ref. 19 on uridine as a radical scavenger for both MX and SAXS.

RADDOSE v1–3

RADDOSE v120 was written at a time when typical X‐ray beams were larger than most protein crystals. It could thus take the incident flux (photons/sec) multiplied by the data collection time as the total flux impinging on the crystal, and treat the crystal as static in the beam to calculate the absorbed dose. The FORTRAN77 code was dependent on parts of the CCP4 software suite21 for space group information, and reported the maximum dose absorbed. The Thomson (elastic), Compton (inelastic) and photoelectric effect cross sections were obtained from those compiled in Ref. 22, and accessed from the “mucal” subroutine23 incorporated into RADDOSE. All three processes were used to calculate the attenuation cross section (μ _att), but the Compton cross section was not included in the absorption coefficient (μ _abs) for the dose calculation. Additionally, fluorescent X‐rays emitted by heavier mass atoms were assumed to be absorbed within the crystal, so were all included in the energy loss computation.

The dose, D, was calculated according to the following formula:

$$D\propto \frac{I_0}{\lambda V}[1-\exp ({-\mu }_{abs }t)] \mathrm{a}\mathrm{n}\mathrm{d}\hspace{0.17em} {\mu }_{abs}= \frac{1}{V} \sum _{j=1}^N{\sigma }_{pe}$$

where $I_0$ is the incident beam flux, λ is the wavelength of the beam, V is the irradiated crystal volume, t is the crystal thickness, and ${\sigma }_{\mathrm{p}\mathrm{e}}$ is the photoelectric cross section summed over the various atomic constituents of the crystal in the correct proportions (1…N). DNA and RNA as well as protein could be included in the calculation.

For the convenience of the user, solvent concentrations could be entered as mM quantities. The beam could be either a Gaussian with user defined horizontal and vertical full width half‐maxima (FWHM), or a homogeneous “top‐hat” in profile. To improve the cross section accuracy for heavier atoms, RADDOSE v1 could read in a fluorescent scan collected over an absorption edge at a synchrotron beamline: this scan was pre‐processed with the software program CHOOCH.24 Crystal morphology could only be specified as cuboid.

The program was distributed on request and the necessary information for running the program, in particular the flux, gradually became more available at MX beamlines. It was incorporated into the beamline programs BEST25 and Web‐Ice26 to assist experimenters to design optimum data collection strategies. An analysis of the parameters affecting the absorbed dose using RADDOSE concluded that the dose was almost independent of the crystal thickness, since the beam attenuation at the incident energies usually employed is negligible. However, reliable values for the beam area, profile and flux are a prerequisite for obtaining accurate dose estimates.12 Systematic flux calibration procedures were thus also established.27 Typical fluxes on modern synchrotron beamlines used for MX are, for example, 3 × 10¹² ph/s on MASSIF‐1 at the ESRF in Grenoble into a 100 µm (h) × 65 µm (v) FWHM Gaussian beam, and 2 × 10¹¹ ph/s for P14 at PETRA III in Hamburg, for a defocused “top‐hat” shaped beam of 140 µm × 140 µm. At microbeam lines, the flux density is higher, for instance 3 × 10¹² ph/s at I24 at the Diamond Light Source (DLS), UK for a 6 µm (h) × 9 µm (v) FWHM Gaussian beam. At XFELs, there are typically 10¹² photons in around a 2 µm diameter beam pulse lasting 50 fs.

In the next iteration of the program, RADDOSE v2,28 the probability of any fluorescent X‐rays escaping from the crystal following photoelectron emission from a heavier atom (see above) was included in the code, by including the ionisation probabilities for all atomic K, L, and M shells, and the values for proportions of Auger and fluorescence production for all elements. To simplify the estimation of how many fluorescent photons were likely to escape, it was assumed that they were all produced in a plane perpendicular to the beam half way through the crystal. As an example, for a crystal of a 45 kDa protein with 10 Se‐substituted methionines, the calculated dose at the Se edge (12.6634 keV) was reduced by 27% when fluorescent escape from the selenium was taken into account. This in turn extends the time taken to reach the dose limit of 30 MGy by 27%. Additionally, in RADDOSE v2, the dependence on the CCP4 suite was removed. This version of the code was widely distributed to over 150 different researchers, and was also incorporated into a new version of BEST29 and into EDNA.30

In Version 3 (v3) of RADDOSE,31 the Compton cross section was included in the absorption coefficient and the average Compton electron energy was computed by integration of the formula for their angular distribution. It was assumed that the inelastically scattered X‐ray escapes from the crystal and the Compton electron is absorbed. The results showed that inclusion of this effect had negligible impact on dose values for incident X‐ray energies below 20 keV. The Compton scattering cross section rises with incident energy, and the diffraction cross section decreases, as does that of the photoelectric effect. The relevant quantity for MX is the diffracted intensity per absorbed dose, which changes very little as the incident photon energy is increased. This version of the code was only distributed to experimenters using high incident energies, since at low energies the dose values were unchanged by the inclusion of Compton scattering.

Need for RADDOSE‐3D

As the X‐ray beams used for MX became smaller and microbeams became available at many synchrotrons (e.g., FWHM Gaussian beams at ID23‐2, ESRF of 10 µm (h) × 4 µm (v) and as mentioned above, at I24, DLS of 6 µm (h) × 9 µm (v) with fluxes of 1.1 × 10¹² ph/s and 3 × 10¹² ph/s respectively), crystals were routinely larger than incident beams and were thus no longer completely bathed in it. Thus the dose values computed via the treatment used in RADDOSE v1–3 became increasingly unsuitable, since as the crystal was rotated, new unexposed volume was being brought into the beam. It was clear that a completely new approach was required which would give temporal and spatial information of the absorbed dose in order to aid experimental protocol optimization.

Concomitant with this issue was the question of which dose value should be quoted, since for a crystal rotated in a Gaussian beam, the maximum dose absorbed at the peak of the beam can be as much as 2 orders of magnitude greater than in parts of the crystal nearer to the tails of the beam. For example, for a cuboid shaped protein crystal (μ_abs = 2.37 mm⁻¹) with 100 µm sides in an uncollimated 12.4 keV beam with a 20 × 20 µm² FWHM and flux of 5 × 10¹¹ ph/s, for a 90° wedge with a total of 60 s exposure, the maximum dose is 30.3 MGy (i.e., above the dose limit), but the average dose (whole crystal) is only 1.5 MGy.

Thus quoting the maximum dose did not give a realistic picture of how damaged the crystal was likely to be at the end of the experiment. It was then beneficial to develop a metric that is more intimately linked to the diffraction pattern as the data collection proceeds (see below).

As mentioned above, a minor issue with RADDOSE v1–3 was that the calculation of the beam attenuation as the beam traversed the crystal used the absorption coefficient, μ_abs, rather than the attenuation coefficient, μ_att, so did not account for the decrease in beam intensity due to the diffracted component of the interaction with the crystal. The effect of this assumption is only slight, since the majority of beam attenuation is due to the absorption component rather than diffraction (typically 92% vs. 8% at 12.4 keV beam energy for a 100 µm thick heavy atom free protein crystal).

RADDOSE‐3D

The new RADDOSE‐3D code32 was designed to allow easy extendibility so that new experimental scenarios can be included as they arise. It is highly modular so that future contributions from the community can be easily integrated into it. The language chosen for RADDOSE‐3D was Java, and the code follows an object‐oriented programming architecture. In this programming paradigm, concepts are described by classes and their attributes. Objects are instances of such classes, which can be used to represent a part of the actual experiment, such as the crystal, the X‐ray beam, and angular wedges of X‐ray exposure. The crystal volume is partitioned into a set of evenly spaced three‐dimensional voxel coordinates, each of finite volume, at which X‐ray fluence (photons/second) and dose values are stored during the simulation. The granularity of the crystal can be user‐defined to ensure that the simulation resolution is appropriate for the dimensions of the irradiated crystal. The distribution of dose within the crystal volume is calculated for a number of iterations in small angular steps across one or more data collection wedges, thus providing a three dimensional and time‐resolved simulation of the dose state of the crystal. Multi‐wavelength anomalous dispersion experiments can be specified, as usually the same crystal is used for the data collections at different incident energies.

A flow chart for RADDOSE‐3D is shown in Figure 2, and a representative input file is given in Figure 3. The program contains over 17,000 lines of functional Java code, and the job defined by the Figure 3 input file would take ∼2 s to run on a 2 GHz Intel Core i5 processor.

Figure 2.

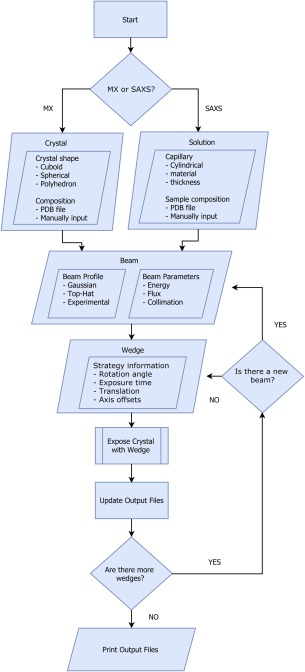
Flow chart outlining the structure of RADDOSE‐3D.

Figure 3.

The structure of a typical RADDOSE‐3D input file. The crystal geometry and composition is first described by a “Crystal” block (in orange). The three‐dimensional geometry of the crystal has been approximated as a polyhedron (as a collection of vertices and faces) and this information has been supplied to RADDOSE‐3D using the “ModelFile” flag. A “Beam” block (in blue) followed by a “Wedge” block (in green) describe the strategy by which the specified beam will interact with the crystal. Multiple beam and wedge parameters can be implemented in the same RADDOSE‐3D input file; and each exposure strategy will be run sequentially by the program. Whereas in the first beam block the beam profile will be approximated as a 2D Gaussian with FWHMs of 20 µm × 20 µm, in the second beam block, the beam profile has been extracted directly from the beamline and supplied to RADDOSE‐3D as an experimentalBeamProfile.pgm.

Since the original publication describing RADDOSE‐3D, there have been a number of additions and improvements made to the code. Among these is the ability to input real experimental beam shapes for use in the calculation. The example input shown in Figure 3 uses different beam profiles for the two wedges of data (multiple wedges can be specified) defined by the user: a Gaussian shaped beam for the first and an experimentally measured beam profile for the second (a homogeneous “top‐hat” profile can also be specified). Beam profiles can be measured experimentally at a beamline using a variety of methods (scintillator images, aperture or line scans etc.). These measurements can be processed and transformed into portable graymap (.pgm) files, which can be input and interpreted by RADDOSE‐3D for the simulation of the experiment.

A further major extension to the code has been the incorporation of a way to specify an irregular crystal shape: previously the shapes that could be specified were confined to a cuboid or a sphere. For this, the three‐dimensional geometry of the crystal is defined by its vertices and connecting edges in the OBJ geometry definition format. The generated polyhedron shape can be input into RADDOSE‐3D, and the program performs ray‐tracing operations to determine the crystal interior and thus to define positions where voxels should be assigned. An external open‐source software program, Blender (https://www.blender.org), provides an easy interface for creating arbitrary crystal shapes and generates geometry files that can be read directly into RADDOSE‐3D.

For convenience, if the protein structure for the irradiated crystal is already known, the PDB code can now be entered by the user and read into RADDOSE‐3D directly.

Other minor modifications have included firstly a better calculation of the volume in the unit cell occupied by RNA and DNA by setting their average densities to be the same as that of protein (1.3 mg mL⁻¹), secondly the absorption calculation subroutine “mucal” has been converted from Fortran into Java code to end any dependence of RADDOSE‐3D on RADDOSE v2, and thirdly the attenuation coefficient (which includes the diffraction cross section) is now used to calculate the incident flux on the face of a voxel, rather than using the absorption coefficient (see above).

Using RADDOSE‐3D, the dose distributions for various data collection protocols can be usefully explored33 in order to spread the absorbed dose as homogeneously as possible over the full crystal volume. It is important to note here that inhomogeneous irradiation results in the crystal having a range of site specific damage states at any instant, and thus the electron density derived from the data will be an average of all these states. Thus it is highly desirable to irradiate the crystal as evenly as possible. For example, for beams smaller than the crystal, the crystal can be rotated in the beam around a single axis as is traditionally employed [Fig. 4(A)], or it can be translated after a certain angular wedge has been collected resulting in a dose map that is colloquially referred to as a “Newton's cradle” [Fig. 4(B)], or it can be simultaneously translated and rotated [Fig. 4(C)], the so called ‘helical data collection’,34 resulting in a spiral path along a needle shaped crystal. Another possible strategy is to deliberately displace the center of the crystal from the spindle rotation axis, giving a “doughnut”‐shaped dose contour [Fig. 4(D)] which reduces the maximum dose and has been experimentally shown to give better quality data and a longer crystal lifetime in the beam.35 This latter approach can be combined with the helical strategy to further spread the dose [Fig. 4(E)]. An intrinsic assumption in the discussion above is that the rate of radiation damage in MX is proportional to the absorbed dose and is not dose rate dependent. This relationship is still believed to be true for experiments carried out at cryo‐temperatures, but has been questioned for high dose rate RT measurements, where a ∼100 ms “lag period” has been observed before a decrease in diffraction intensity becomes apparent.36 In addition, at low dose rates, damage rates at RT that are inversely proportional to the dose rate have been documented.37 Thus there is current debate concerning the relationship between dose rate and damage rates at RT.

Figure 4.

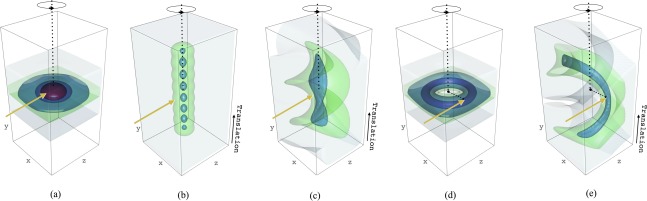
Effect of the dose distribution on the chosen exposure strategy modelled in RADDOSE‐3D. Dose contouring levels have been shown at 0.0001 MGy (grey), 5 MGy (green), 10 MGy (light blue), 20 MGy (dark blue) and 30 MGy (red), using R (www.r-project.org). In each simulation, the crystal rotation axis (in black) and incident beam direction (in yellow, coincident with the z axis) are shown. Unless otherwise stated, each dose distribution is generated following a 360° rotation over a total exposure time of 100 s. In (a) the crystal rotation axis and incident beam direction intersect. In (b) the crystal undergoes a series of eight 360° rotations, each lasting 100/8 = 12.5 s, intersected by a series of 20 µm translations of the crystal parallel to the rotation axis to spread the dose across the crystal volume. In (c) the crystal rotation axis and incident beam direction intersect, however the crystal is continuously translated along the rotation axis at a rate of 0.2 µm/°. In (b) the crystal rotation axis has been offset by 30 µm relative to the incident beam direction. In (e) the rotation axis is offset by 30 µm relative to the beam direction, and the crystal is also continuously translated along the rotation axis at 0.2 µm/°. In all simulations a cuboid crystal has been modelled with dimensions x = 100 µm, y = 200 µm and z = 100 µm. The beam has been modelled as Gaussian shaped (FWHM: 20 µm × 20 µm), with energy 12.4 keV, flux 5 × 10¹¹ ph/s, and a large 1 mm × 1 mm rectangular collimation in order to ensure the full crystal is continuously bathed in the beam for each simulation.

The effect on the dose distributions of using various Gaussian FWHM beam profiles with the same flux (but thus different flux densities) is illustrated for an irregular shaped crystal of volume 10⁶ μm³ in Figure 5. As expected, it can be seen that the 20 µm × 20 µm profile gives the biggest dose contrast, and it is clear that parts of the crystal are not used at all, whereas data collection with the 60 µm × 60 µm beam results in a more even dose distribution. The most homogeneous distribution is achieved with a “top‐hat” beam [Fig. 5(D)].

Figure 5.

The effect of varying the incident beam profile on the dose distribution for an irregular polyhedron shaped crystal formed by distorting a cube of dimension (100 µm)3 leaving the total volume the same at 10⁶ µm³. In (a)–(c) the beam has been modelled as Gaussian shaped, and the FWHM has been varied as: (a) 20 µm × 20 µm, (b) 40 µm × 40 µm and (c) 60 µm × 60 µm. In (d) a uniform “top‐hat” shaped beam distribution has been modelled. All other beam parameters have been kept constant (energy: 12.4 keV, flux 5 × 10¹¹ ph/s, rectangular collimation: 200 µm × 200 µm). In all simulations the crystal has been exposed for 100 s throughout a 360° rotation about the y‐axis (shown in each plot). The direction of the incident beam with respect to the initial orientation of the crystal has been shown (green arrow). The crystal morphology has been specified with the “Type Polyhedron” flag in the RADDOSE‐3D input file. Visualization has been produced using the open source Paraview software package (https://www.paraview.org).

As can be seen from Figure 4, there is usually a large range of absorbed doses within a crystal by the end of an MX experiment. RADDOSE v1–3 quoted the maximum dose (MD) in the sample, which for a Gaussian shaped beam incident on a centred crystal is usually in the center. This value does not give an indication of the average dose absorbed by the irradiated part of the crystal, or an idea of the current state of the diffracting power. Thus we proposed the Diffraction Weighted Dose (DWD) metric, which combines information on the cumulative dose within each volume element of the crystal up to a given time, weighted by the fluence through that voxel at that instant. This metric has been described in detail previously, and experimentally validated by showing that for three very different sized inhomogeneous beams, the DWD gave consistent results for the intensity decay and scaling B‐factor rise for data collections on cubic insulin crystals at 100 K.35 The dose values on the x‐axis of all the figures shown here are diffraction weighted dose (DWD), calculated by RADDOSE‐3D.

The DWD metric has already been used to good effect in a mechanistic study of a cofactor free oxidase using a combination of on‐line Raman and MX38 and in an enzyme catalysis study of copper nitrite reductase.39 The necessity for the DWD metric is clear from the irradiation regimes shown in Figure 4(A), where there is a significant difference between the MD (78.9 MGy) and the average dose (1.98 MGy) calculated over the entire crystal volume. The DWD is 10.0 MGy, demonstrating how the MD and average dose significantly over‐ and underestimate the relevant accumulated dose, respectively, which propagates through to the recorded diffraction data.

In addition, whereas the average dose for both strategies in Figure 4(A,C) is 1.98 MGy (as calculated over the whole crystal volume) the DWD is considerably lower for the crystal shown in Figure 4(C) compared with 4(A) (2.9 MGy vs. 10 MGy), indicating the positive effect that crystal translation parallel to the rotation axis has to more efficiently spread the dose throughout the crystal volume. Again, in Figure 4(C), the MD (11.6 MGy) overestimates the relevant accumulated dose, but to a lesser extent than in 4(A), as anticipated.

RADDOSE‐3D for SAXS

RADDOSE‐3D was recently extended40 to estimate the dose in a Small Angle X‐ray Scattering (SAXS) experiment which uses an arrangement as illustrated in Figure 6 to determine the overall shape of macromolecules. The liquid protein solution in buffer is irradiated at room temperature in a cylindrical capillary made of glass or quartz. RADDOSE‐3D takes account of this experimental setup allowing doses to be calculated for many SAXS experiments.

Figure 6.

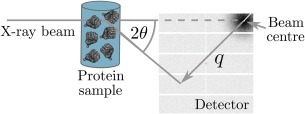
Diagram of a basic SAXS experiment. An X‐ray beam (typical energies range between 7 and 12.5 keV) is incident on a protein SAXS sample. Commonly the sample volume exposed to the beam is between 15 and 30 $\mathrm{\mu }\mathrm{L}$, with a protein concentration that usually ranges from 0.5 to 10 mg mL⁻¹. The scattered radiation is collected on a detector. The symbol, $q$ in the figure, is termed the momentum transfer and is defined as $q=4\pi \sin \theta /\lambda$ where $\theta$ is half the scattering angle, and $\lambda$ is the wavelength of the incident X‐ray beam. The detector images that are generated from the experiment can be processed and analysed to determine the overall shape and size of the protein molecule in the SAXS sample.

The module that allows RADDOSE‐3D to model arbitrary crystal shapes has been used to implement cylindrical shapes for a SAXS sample. The X‐ray beam has to travel through the capillary material before it interacts with the protein sample. The capillary thus attenuates the X‐ray beam; hence the measured flux value at the sample position is slightly higher than the true flux on the sample. RADDOSE‐3D now allows the user to specify parameters for the capillary such as its material and thickness, so that the code can calculate the attenuation of the X‐ray beam before it reaches the sample.

The final major modification allows RADDOSE‐3D to calculate the absorption coefficients given a description of the liquid sample composition. The simulation defines a volume of liquid and estimates its contents given the protein concentration (provided by the user in mg mL⁻¹) and buffer composition. The molecular mass of the molecule is calculated either from the protein sequence file (the sample can also contain DNA and RNA) by summing the molecular mass of each residue in the file, or alternatively, an average molecular weight is used for each residue (110.0 Da for protein residues, 339.5 Da for RNA nucleotides and 327.0 Da for DNA nucleotides). The number of molecules in the volume can then be calculated and hence the absorption coefficient can be computed.

Using the resulting dose values, sample lifetimes can be compared across different facilities, and sample aggregation avoided by suitable experimental design. For instance, evaluation of putative scavengers can be quantitative rather than qualitative. In a recent such study,40 a range of threshold doses (above which the SAXS data were determined to be compromised) ranged between 2.37 and 51.24 kGy, much lower than typical values for the dose required to reduce the diffraction to half of its initial intensity (D _1/2) determined for RT MX.

However, the program cannot yet handle cases where the sample is continuously flowed through the capillary during X‐ray irradiation, a common strategy in SAXS to avoid radiation damaged data being collected.

Other Contributions to the Absorbed Dose Value

Several other physical effects must be taken into account to obtain true estimates of the dose absorbed by a protein crystal, and a number of these have recently been incorporated into the RADDOSE‐3D code.

First, RADDOSE‐3D has been modified to take into account the energy deposited in the crystal by electrons produced by the inelastic scattering of X‐rays, the Compton effect. As mentioned above, this was taken into account in RADDOSE v3, and found to make negligible difference to the dose values obtained for incident X‐ray energies below 20 keV and very little difference below 40 keV. The Compton cross section increases only slowly in this energy region, concomitant with a steeper decrease in the photoelectric cross section. The parameterization of the electron energy distribution implemented in RADDOSE‐3D is identical to that detailed previously.31

Figure 7 shows a plot of DWD against X‐ray energy for the same sample (sample smaller than beam) and data collection conditions with and without consideration of the Compton electron energy loss (CEEL). It can be seen that the results from RADDOSE‐3D concur with the conclusions drawn previously from the RADDOSE v3 results,31 that is, the effect is negligible for incident energies below 20 keV. Thus this modification of the code will only make a noticeable difference to DWD when higher energy incident beams are used, as noted by Cowan and Nave41 from their analysis of CASINO simulations including the CEEL.

Figure 7.

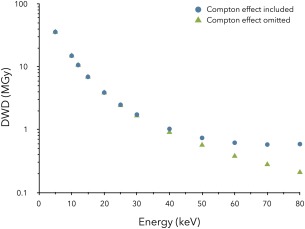
The effect of Compton scattering on the calculated DWD (MGy) values for a 100 µm × 100 µm × 100 µm cuboid crystal in RADDOSE‐3D with varying incident photon energy, E_x (keV). In all simulations, the beam has been modelled as Gaussian shaped with energy: 12.4 keV, flux: 5 × 10¹¹ ph/s, FWHM: 20 µm × 20 µm and with a rectangular collimation size of 100 µm × 100 µm. In all simulations the crystal has been exposed for 100 s over a 360° rotation. Note the y‐axis logarithmic scale.

Second, as pointed out over a decade ago by Nave and Hill,42 for small crystals (less than around 10 μm in size), there is a significant probability that the ejected photoelectron will escape from the crystal rather than depositing all of its energy within it. This effect will reduce the dose, and this implies that smaller crystals will have an extended lifetime in the beam compared with larger ones. Clearly, to take this effect into account, the range of the photoelectrons produced by different incident beam energies must be known, as well as some parameterization of their energy loss as a function of penetration depth through the sample. We are currently incorporating this effect into RADDOSE‐3D, and following extensive simulations with CASINO (`monte CArlo SImulation of electroN trajectory in sOlids') [http://www.gel.usherbrooke.ca/casino/What.html], we are now able to model these distributions analytically. The path length of photoelectrons of energy E has been found to approximately follow a Gumbel distributed random variable, X _pe, with Probability Density Function (PDF), for incident beam energies up to 20 keV:

$$PDF=\frac{1}{\beta } \mathrm{e}\mathrm{x}\mathrm{p}[-\left(z+\exp \left(-z\right)\right)] \mathrm{a}\mathrm{n}\mathrm{d} z=\frac{(x-\mu )}{\beta }$$

where μ is the mean path length of a photoelectron of a given energy, and β is an energy dependent scale parameter determined by a polynomial fitting to the results of CASINO simulations run for different incident energies. The validity of the Gumbel distribution was tested up to a beam energy of 30 keV, and up to E_x = 20 keV the β parameter of the Gumbel distribution approximately followed the quadratic relationship:

$$\beta =0.002 {E_{\mathrm{x}}}^2+0.0096 E_{\mathrm{x}}$$

This quadratic relationship is implemented in RADDOSE‐3D, and thus our code can be used for beam energies up to 20 keV.

In RADDOSE‐3D, for each crystal voxel, photoelectrons are then modelled to spread their kinetic energy along linear tracks of a randomly assigned length, X _pe(voxel), extending uniformly in all directions from the original voxel. If the linear track of a photoelectron exits the crystal boundary, all its remaining kinetic energy is then lost from the crystal. The effect of any beam polarization on the preferential direction in which photoelectrons travel is not currently taken into account.

Experimentally, the range of photoelectrons produced by an 18.7 keV beam has been measured through radiation damage studies with a 1 μm sized beam, and found to be 4 μm.43 Figure 8 shows the effect on the DWD at E _x = 12.4 keV of taking the probability of photoelectron escape into account for isolated crystals of various dimensions. It can be seen that for a 20 μm crystal there is a dose reduction of about 3% whereas this rises to over 20% for a 10 μm crystal. As the incident energy is increased, the probability of photoelectron escape will increase. An important caveat for the dose reduction described here is that for a crystal held within a cryoloop completely surrounded by vitrified cryobuffer which is also in the beam path, as many photoelectrons will enter the crystal from the buffer as will leave it, so there will be no concomitant reduction in the dose at all. Thus photoelectron escape modelling is only valid if the effects of the surrounding buffer are assumed to be negligible.

Figure 8.

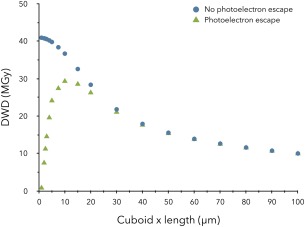
The effect of accounting for photoelectron escape in RADDOSE‐3D on the calculated DWD (MGy) values for various sized cubic shaped crystals. In all simulations, the beam has been modelled as Gaussian shaped with energy: 12.4 keV, flux: 5 × 10¹¹ ph/s, FWHM: 20 µm × 20 µm and with a rectangular collimation size of 100 µm × 100 µm, and the crystal has been exposed for 100 s over 360°. The PixelsPerMicron parameter in RADDOSE‐3D has been varied for the x‐dimension of each crystal (between 0.5 and 10 pixels/µm) to account for the diminishing size of the crystal.

The effect described above is especially relevant when calculating the dose absorbed during X‐ray Free Electron Laser serial crystallography experiments, where generally micro‐ or nano‐crystals are utilized.

Future Developments Planned for RADDOSE‐3D

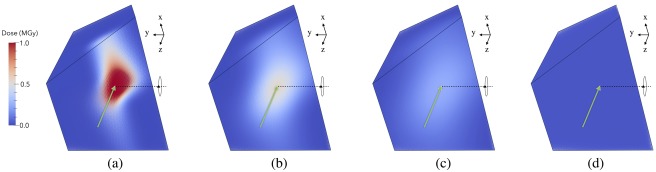
Several further refinements of RADDOSE‐3D are planned, with the eventual aim of being able to use it to determine an optimum data collection strategy given information about the beamline geometry, the 2D beam profile and the crystal shape. In particular, development of better protocols for imaging real experimental X‐ray beam profiles and incorporation of online methods for determining the physical shape of macromolecular crystals would be beneficial. If these could be conveniently input directly into RADDOSE‐3D, dose estimates could be more reliable and thus useful. A question is often asked regarding the importance of knowing the exact crystal shape and size when running RADDOSE‐3D, and the effect on the resulting calculated dose if they are not accurately known. Figure 9 illustrates the variation in DWD when irregular crystal shapes [Fig. 8(A,B)] are approximated by either a cuboid [Fig. 8(C)] or a sphere [Fig. 8(D)], for 4 very different crystal shapes all having the same volume (of 10⁶ µm³), and it can be seen that it lies between 9.4 and 10.3 MGy. Given other uncertainties in the experiment, these simulations show that knowing the exact crystal shape is not pivotal in obtaining a reasonable dose estimate.

Figure 9.

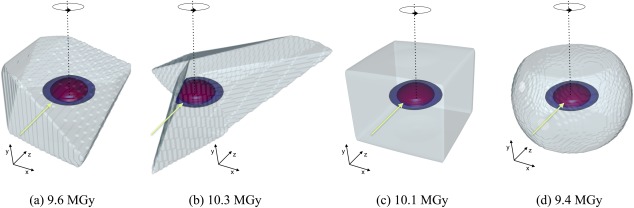
The effect of modelled crystal geometry on the calculated DWD (MGy) values has been illustrated for four crystal shapes, each with a total volume of 10⁶ µm³. Dose isosurfaces are contoured at 0.001 MGy (light blue), 20 MGy (dark blue) and 30 MGy (red), using R (www.r-project.org). In (a) and (b), two irregular polyhedron‐shaped crystals were generated using the open‐source three‐dimensional graphics software called Blender. In (c) and (d) the “Type cuboid” and “Type spherical” input file parameters to RADDOSE‐3D have been used to model the crystal as a 100 µm × 100 µm × 100 µm cuboid, and a 124.2 µm diameter sphere, respectively. In all simulations, a Gaussian beam (12.4 keV, 1e11 ph/s) was modelled with FWHM of 20 µm × 20 µm, in order to obtain the infamous “fried egg” effect.

As aforementioned, the probability of fluorescence rather than Auger electron emission following photoelectron ejection rises as the atomic number of the sample constituent increases: it is ∼7% for sulfur, rising to 60% for selenium. These fluorescent X‐rays then have a finite chance of escaping from the sample, carrying with them the binding energy of the photoelectron. This has the effect of reducing the dose for samples containing heavier atoms, and was taken into account in RADDOSE v2.28 It has yet to be incorporated into RADDOSE‐3D.

There is renewed interest in using pink beams (Δλ/λ>0.5%) for MX (e.g., see Ref. 44) and also for performing Laue experiments. Additionally, the band width of XFEL beams tends to be (Δλ/λ∼1.0%). Incorporating an energy spectrum for the incident beam into RADDOSE‐3D would thus allow dose calculations for these scenarios.

A very useful extension of RADDOSE‐3D would be to adapt it to give doses during electron microscopy (EM) experiments. Recent advances in this field have allowed far higher resolution macromolecular structural models than previously possible with EM, and have resulted in site‐specific radiation damage effects being observed (R. Henderson, private communication). There is thus now interest in tracking this as a function of dose.

Code Availability

RADDOSE‐3D is an open source software tool which can be freely accessed at www.raddo.se along with the User Guide, and the source code is also available for download at https://github.com/GarmanGroup/RADDOSE-3D.