Prediction of nearest neighbor effects on backbone torsion angles and NMR scalar coupling constants in disordered proteins

Abstract

Using fine‐tuned hydrogen bonding criteria, a library of coiled peptide fragments has been generated from a large set of high‐resolution protein X‐ray structures. This library is shown to be an improved representation of ϕ/ψ torsion angles seen in intrinsically disordered proteins (IDPs). The ϕ/ψ torsion angle distribution of the library, on average, provides good agreement with experimentally observed chemical shifts and ³J _HN‐Hα coupling constants for a set of five disordered proteins. Inspection of the coil library confirms that nearest‐neighbor effects significantly impact the ϕ/ψ distribution of residues in the coil state. Importantly, ³J _HN‐Hα coupling constants derived from the nearest‐neighbor modulated backbone ϕ distribution in the coil library show improved agreement to experimental values, thereby providing a better way to predict ³J _HN‐Hα coupling constants for IDPs, and for identifying locations that deviate from fully random behavior.

Introduction

The torsion angles ϕ and ψ define the backbone conformation of a polypeptide chain and the ϕ/ψ distribution of intrinsically disordered proteins (IDPs) remains the focus of considerable interest. An accurate, residue‐specific representation of the random coil Ramachandran map is important as it provides an empirical calibration for the residue dependence of the energies associated with each pair of ϕ/ψ angles. Equally important, an accurate representation will facilitate identification of residues in a dynamically disordered protein where the angular distribution deviates from what is expected for a fully disordered chain, i.e., to identify transient conformations that may be important for target binding.1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 Of course, a key problem in such work is finding an optimal “baseline” of coil behavior, and much effort has been devoted to developing an optimal ϕ/ψ distribution of such an ideal coil, which lacks any significant long range interactions other than steric occlusion by the peptide chain itself, but includes nearest neighbor effects.12, 13, 14, 15, 16, 17, 18, 19, 20, 21 In principle, analysis of long molecular dynamics trajectories of intrinsically disordered systems could provide this information.22 However, in practice, the ϕ/ψ distributions generated in this manner are highly sensitive to the water model used and to the parameterization of the empirically developed force fields,16, 23, 24 sometimes resulting in formation of secondary structure for sequences that are known from experiment to be disordered. Although adjustment terms can be introduced to prevent the formation of such elements,25 in practice they do not yet yield the exquisite balance that is needed to properly represent the Boltzmann distribution across the entire Ramachandran space. Instead, coil distributions therefore have mostly relied on a compilation of segments void of secondary structure that are taken from crystallographically determined protein structures,13, 26, 27 where the lengths of such segments that can be observed with good electron density are often relatively short.

NMR spectroscopy is another widely used method for characterizing dynamic systems, where the observable parameters — chemical shifts and J couplings, sometimes supplemented by residual dipolar couplings9, 24 — report on the time or ensemble average of ϕ/ψ angles sampled by the polypeptide. However, the limited number of NMR observables per residue is clearly insufficient to uniquely define its entire Ramachandran map distribution. An additional requirement, minimizing the deviation from a database distribution, was therefore introduced by the MERA program to resolve this under determined problem.21, 28 More commonly, chemical shifts and J couplings of short linear peptides have been used to define a “baseline” for random coil values of such parameters.29, 30, 31, 32, 33 However, it was clear that effects of neighboring residues are not negligible, and a calibration using the increasingly growing library of values recorded for highly disordered systems, which permits the effect of nearest neighbors to be taken into account, provides a better reference for values representative of complete disorder.13, 14, 34, 35, 36 In order to gain mechanistic insights into the relation between nearest neighbors and ϕ/ψ distributions, the distribution of a given amino acid may be compared to that of the residue embedded in a sequence of Gly residues.37, 38 The impact of nearest neighbors on ³ J _HN‐Hα values, relative to Gly‐embedded residues, correlates reasonably well with nearest neighbor effects measured in a series of blocked dipeptides, with small systematic differences attributed to the effect of the adjacent blocking groups.39 However, when we applied such an analysis to our experimental data recorded for a series of disordered proteins, the RMSD relative to predicted values remained rather high (0.46 Hz), comparable to what was obtained with the neighbor corrections proposed by Griffiths‐Jones et al.15

Our current study aims to predict ³ J _HN‐Hα values by analyzing the impact of residue type and that of its neighbors on the ϕ/ψ distributions of coil regions in the protein data bank while using a previously parameterized Karplus equation. Evaluation of the effect of nearest neighbors on the Ramachandran distribution follows the insightful analysis by Ting et al.19 but uses different, H‐bond based criteria for identifying coil residues. The analysis relies on the assumption that effects beyond those from its nearest neighbors are averaged to zero when considering a sufficiently large set of database triplets of any given residue composition. Our curated library of coiled protein fragments is relatively large (> 20,000 fragments) and is generated strictly on the basis of the absence of both intra‐ and intermolecular nonsequential H‐bonding in the X‐ray structure coordinates, using a generous cut‐off in a previously developed potential of mean force for such interactions. Although, by the very nature of the X‐ray structures from which they were derived, the segments are subject to large numbers of steric interactions with other intra‐ or intermolecular residues, we again assume that the effect of these nonspecific interactions averages to zero when the library is sufficiently large. This assumption is validated by the observation that our library shows good consistency with experimental chemical shifts and ³ J _HN‐Hα values measured for a set of five highly disordered proteins, thereby allowing generation of improved “random coil” values for ³ J _HN‐Hα. Because IDPs can be sensitive to oligomer formation, care was taken to ensure that the NMR spectra of these five proteins were insensitive to sample concentration, thereby ensuring that the experimental values correspond to their monomeric states.

Methods

Generation of the coil library

Analysis of the ϕ/ψ angle distributions of residues in coil regions of protein structures has been widely used to probe the intrinsic, sequence‐based preferences to populate any given region of Ramachandran space. Such an analysis requires (1) determination of the ϕ/ψ propensities of each residue type free from stabilizing interactions associated with secondary structure, including β‐strands and α‐helices, or other H‐bond interactions to nonimmediate neighboring residues and (2) examination of the effects of immediately neighboring residues in modulating sterically or otherwise the coil propensities.

In a previous study,28 we used the coil library of Fitzkee et al.,18 which simply excluded residues in regions of α‐helical or β‐sheet secondary structure based on a “mesostate” evaluation. However, this type of coil library then includes a substantial fraction of residues in the α‐region of Ramachandran space, resulting from H‐bonded β‐turns, and exclusion of turn residues as well as residues immediately adjacent to α‐helix or β‐sheet has been shown beneficial for removing bias in a coil library.17 For the subsequent development of the MERA program,21 which aims to generate a “maximum entropy” ϕ/ψ distribution from NMR restraints, an updated “H‐bond free” coil library was generated. For this purpose, a simple intramolecular H‐bond energy cut‐off criterion of E _HB < −0.7 kcal/mol was used, where the energy was calculated by the DSSP program.40

Here, we use a more elaborate H‐bond potential with stricter H‐bond partner criteria for generating the coil library. Specifically, inclusion in the new coil library requires that a fragment (1) is at least 3 residues in length; (2) that there are no intra‐ or inter‐molecular H‐bonds to the carbonyl immediately preceding a fragment or the N‐H group immediately following the fragment; (3) that all its residues lack both intra‐ and inter‐molecular H‐bonding including partners belonging to the chains related by crystallographic symmetry. Here, the presence of a H‐bond is defined by a potential of mean force “HBDB” energy cut‐off of 2.4 kcal/mol above the minimum for backbone‐backbone H‐bonds to any intra‐ or intermolecular residue.41 Residues involved in backbone‐sidechain H‐bonds and an energy below −0.5 kcal/mol as defined by the DSSP program40 are also excluded. An exception to rule (3) is that we do allow backbone‐backbone (i–1 to i + 1) and sidechain‐backbone H‐bonding within a three‐residue fragment, as such (lowly populated) conformations ostensibly could be part of their natural coil conformational distribution.

As input for generating the coil library, we used all PDB X‐ray structures solved at a resolution ≤ 2.0 Å, with an R factor lower than 23%, and a maximum pairwise sequence identity of 90%. The new coil library contains 20,136 fragments, yielding ϕ/ψ torsion angles for 96,240 residues. The populations observed in the five standard regions, comprising polyproline‐II (PPII), β, α_R, type I β‐turn (β‐I) and α_L, are ca 25%, 25%, 10%, 5%, and 1%, respectively [Fig. 1(A)]. The remaining, ca one third of residues are simply grouped together as “other.” A comparison between the newly generated coil library and the MERA library shows a small fractional decrease of residues in the α_R and β‐I regions, but a similar distribution in the β and PPII regions (Supporting Information Fig. S1). An increased ϕ/ψ density is also observed for several sparsely populated regions, such as the region around 60°/–90°, which contains ten 3‐residue fragments with a backbone‐backbone H‐bond between the first and last residues. The modest shift in our newly generated coil library distribution relative to the previous H‐bond based MERA coil library (Supporting Information Fig. S1) is not surprising, considering that the new coil library eliminates more structured elements such as H‐bonded turns, identified with the more sophisticated H‐bond potential, whereas H‐bonds previously identified solely on the basis of donor‐acceptor distance now also include an angular term that can remove them from being counted as valid.

Figure 1.

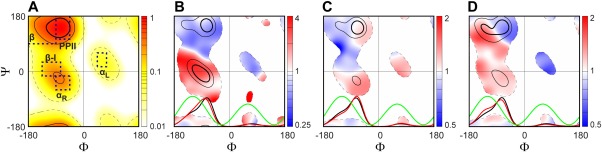
Backbone torsion angles distributions observed in our newly generated coil library, illustrated for (A) all residues, (B) 963 residues neighbored by two Gly (or subset {G‐X‐G}), (C) 11,938 residues followed by a Lys, Gln or Arg ({X‐K|Q|R}), and (D) 7,122 residues next to a Phe, Trp or Tyr ({F|W|Y‐X}). For each plot, three different φ/ψ conformational regions are marked as those with a normalized residue density d(ϕ,ψ)/d _max above thresholds of 60%, 30%, and 3%, respectively, in the newly generated coil library or its subsets. Their boundaries are marked by dark solid, light solid and light dashed lines, respectively. The residue density, d(ϕ,ψ), is derived by convolution of each of the ϕ_k/ψ_k coil library entries with a Gaussian function, exp(–((ϕ – ϕ_k)² + (ψ – ψ_k)2))/450).42 (A) Ramachandran density map of all residues in the coil library, d(ϕ,ψ)/d _max; (B‐D) for each of the three subsets, the ratio of d(ϕ,ψ)/Σd(ϕ,ψ) between the subset and all other residues (center residue X ≠ Gly, Pro and Xaa‐Pro) is plotted from blue to red (B‐D). To illustrate the impact of different nearest‐neighbors on the ϕ torsion angle distribution, the normalized ϕ torsion angle distribution is also plotted (red) at the bottom of each plot (B‐D), together with the normalized ϕ angle distribution observed for all other residues in the coil library (black) and the scaled ³ J _HN‐Hα Karplus equation curve (green). Dashed boxes mark secondary structure regions: β (–180°<ϕ<–90°, 90°<ψ<180°), PPII (–90°<ϕ<–45°, 105°<ψ<180°), α_R (–90°<ϕ<–45°, −60°<ψ<−15°), type I β‐turn (β‐I) (–135°<ϕ<–75°, −15°<ψ<30°), and α_L (45°<ϕ<75°, 15°<ψ<60°) (see labels in A).

Validation of the coil library by NMR chemical shifts

If the backbone ϕ/ψ torsion angle distribution observed in our newly derived coil library is representative of a random coil, the NMR chemical shift calculated for any given type of residue averaged over the coil library should agree well with its empirically calibrated random coil value. For this purpose, we use the SPARTA+ program43 to predict the chemical shifts for each coil residue in the context of its original crystal structure. While the value for each predicted chemical shift would deviate substantially from random coil, the agreement should be much improved after averaging over the many residues of any given type in the coil library, provided that our newly derived Ramachandran distribution mimics the one sampled in solution by an IDP. The impact of neighboring residues on the ϕ/ψ torsion angle distribution sampled by a disordered peptide, and thereby on its chemical shifts, has been accounted for by neighbor correction factors.44 For example, as discussed below, for a VAV tripeptide the center Ala residue is expected to sample α_R torsion angles less frequently than what is expected for Ala residues, resulting in negative correction parameters for its 13C^α chemical shift.44 For this reason, it is preferred to consider the difference between the SPARTA+ calculated values for each coil library residue and its neighbor‐corrected random coil value when calculating the average difference for a given type of residue. On the other hand, since these correction factors are small, and can have either a positive or negative sign, the impact on the average difference tends to be even smaller, in particular when the residue type composition of the neighbors in the library is broadly distributed.

The average difference between SPARTA+ and neighbor‐corrected random coil values for 13C^α, 13C′, and backbone 15N was calculated for each residue type in the four different coil libraries considered in our study (Supporting Information Table S1). With a mean difference of 0.09 ppm (¹³C^α), 0.12 ppm (¹³C′), and 0.49 ppm (¹⁵N) over the 20 residue types, these agreements are somewhat better for our newly generated coil library than for earlier ones and indicative of an absence of bias in population of helical over sheet regions. In fact, the differences are smaller than the RMSD between predicted coil values and experimentally measured random coil chemical shifts in α‐synuclein, which exhibits chemical shifts closest to Poulsen random coil values of any IDP for which extensive chemical shift values have been reported.45

ANN analysis of nearest‐neighbor effects

The nearest‐neighbor effects on the ϕ/ψ distribution of coil residues are first evaluated by using a single‐level, feed‐forward, multi‐layer artificial neural network (ANN). This neural network has an architecture very similar to that used by the program SPARTA+.43 The input signals to the first layer consist of the tripeptide sequences for all residues in the coil library, with each residue coded by its amino acid type similarity score taken from the 20 × 20 BLOSUM62 matrix.46 Therefore, each tripeptide input is represented by 60 nodes. In the hidden layer of the network, where each node receives the weighted sum of the input layer nodes as a signal, 20 such nodes (or hidden neurons) are used. The output of a hidden layer node is obtained through a nodal transformation function.

For the purpose of evaluating the impact of nearest neighbors on the ϕ/ψ distribution of coil residues, the ϕ/ψ space is grouped into six different regions, comprising PPII, β, α_R, β‐I, and α_L with the remainder assigned to “other” [Fig. 1(A)]. For a given input tripeptide, a Boolean number [1 or 0] is used to indicate the region in which the center residue resides; i.e., a six‐dimensional Boolean vector is used as the training target of the network. For example, a vector of [0 1 0 0 0 0] is used as the training target for a tripeptide with its center residue in the β region.

Each output value has one node with a linear activation function f ₂(x). The empirical relationship between the ϕ/ψ torsion angle distribution of the center residue and the tri‐peptide sequence data, received by the network, is given by

$$P_{1\times 6}^{ANN}=f_2(f_1(X_{1\times 60}\times W_{60\times 20}^{(1)}+b_{1\times 20}^{(1)})\times W_{20\times 6}^{(2)}+b_{1\times 6}^{(2)})$$ (1)

with f ₁(x) = (1 − e^{−2 x})/(1 + e^{−2 x}), and f ₂(x) = x. X _1×60 is the input data vector consisting of 60 elements; W ⁽¹⁾ and b ⁽¹⁾ are the weight matrix and bias, respectively, for the connection between the nodes in the input and the hidden layer; W ⁽²⁾ and b ⁽²⁾ are the weight matrix and bias for the connection between the nodes in the hidden and output layer; P _1×6 is the training target or output vector, consisting of the normalized probabilities that its center residue is located in any of the six regions.

The weight and bias terms were determined by training the artificial neural network on our new coil library. To prevent over training, a standard three‐fold jackknifing procedure was employed for the neural network model by dividing the input–output training dataset into three separate subsets, followed by separate training of the corresponding neural networks on two thirds of the data and evaluation of the trained ANN performance on the remaining one third. Training of the network was terminated when its performance on the validation dataset, represented by the mean squared errors between the predicted and target values began to degrade. This procedure was repeated three times, each time with a different one‐third of the library proteins assigned to the validation set.

The likelihood of a given tripeptide center residue residing in each of the six ϕ/ψ regions, $P_i^{\mathrm{ANN}}$ [i = 1 to 6], is taken from the ANN‐predicted values using the weights and biases obtained from the above training steps, averaged over the outputs from the three separately trained networks. The 6‐region $P_i^{\mathrm{ANN}}$ score is then calculated for the center residue of all 8,000 possible tri‐peptides, with results available at https://spin.niddk.nih.gov/bax/nmrserver/rc_3Jhnha/ann_results.txt

Training of the ANN also was repeated by using the simple residue types, rather than their BLOSUM62 representation as input, with each input residue type described by a 20‐dimensional unit vector containing a single one and 19 zeroes. Training of this network yielded a matrix very similar to the one derived from the BLOSUM62 representation, but with slightly worse statistics in terms of validation parameters. Similarly, repeating the calculations with different matrix representations of the amino acid similarities (RBLOSUM64, BLOSUM45, and BLOSUM80) resulted in slightly (0.5–2%) lower Q6 cross validation statistics.

Results and Discussion

Nearest‐neighbor effects on the ϕ/ψ distribution

Although the above neural network training approach yields an optimized predictor for the placement of the center residue of any given tri‐peptide fragment into any of the six target regions, it does not provide an intuitive picture of which factors dominate this distribution. Therefore, we here also evaluate the impact of residue type for all three positions in tri‐peptides. Because statistically the α_L region is poorly sampled, and the region designated as “other” consists of a wide range of very different, sparsely sampled conformations, we only focus on the standard regions: PPII, β, α_R, and β‐I.

As expected, the type of the center residue strongly impacts its ϕ/ψ probability [Table 1; Fig. 2(A); Supporting Information Fig. S2]. For example, Ile and Val are nearly twice as likely to be located in the β region than Asp or Asn, and much less likely to be found in the α_R region. Gly residues show below average propensities for any of the four selected regions [Fig. 2(A)], but this can be explained by the fact that our partitioning of ϕ/ψ space is not suitable for the nonchiral Gly residue, causing its majority to fall outside of the β, PPII, α_R and β‐I regions. Gln, Met, and Lys show closest to average backbone angle distributions, as viewed by the pairwise Hellinger distance map [Fig. 2(D)]. The Hellinger distance is a convenient parameter to represent how similar two probability distributions are, and in our case is used to compare two Ramachandran map distributions.19, 38 Two distributions that are identical have a Hellinger distance of zero, while two distributions without overlap have a distance of one. As is commonly done, we have scaled the Hellinger distances up by a factor of 100.

Table 1.

Center Residue and Nearest‐Neighbor Effects on the Backbone Conformational Distribution

	< $d\left\{X_i\right\}$/ $d\left\{X\right\}$>a				< $d\{Z-\underset{¯}{X}\}$/ $d\{X-\underset{¯}{X}\}$>b				< $d\{\underset{¯}{X}-Z\}$/ $d\{\underset{¯}{X}-X\}$>b
	PPII	β	αR	β‐I	PPII	β	αR	β‐I	PPII	β	αR	β‐I
A	1.48	0.84	1.28	0.53	0.99	0.94	1.09	0.96	1.02	1.06	0.88	0.86
C	0.93	1.35	0.71	0.75	0.72	0.73	1.48	2.25	0.98	1.01	0.79	1.04
D	0.75	0.57	1.37	1.95	0.86	1.17	0.90	1.03	0.85	0.99	1.18	1.23
E	1.22	0.92	1.29	0.68	1.16	1.07	0.76	0.65	0.91	0.98	1.30	1.00
F	1.02	1.36	0.57	0.87	0.76	1.22	1.07	1.18	0.80	1.15	1.17	0.99
G	0.50	0.45	0.37	0.39	0.99	0.88	1.12	1.42	0.92	0.91	1.03	1.55
H	0.86	1.28	0.67	0.90	1.07	1.06	0.97	0.96	1.02	0.91	1.14	1.11
I	1.19	1.73	0.65	0.52	1.02	1.06	0.95	1.14	1.20	1.12	0.72	0.78
K	1.05	0.93	1.25	0.82	1.19	1.08	0.70	0.70	1.15	0.99	1.04	0.79
L	1.38	1.16	0.94	0.76	0.79	1.05	1.21	1.05	1.13	1.13	0.67	0.63
M	1.06	1.13	0.85	0.86	1.12	0.94	1.00	0.90	1.18	1.00	0.90	0.84
N	0.58	0.66	0.98	1.87	0.96	1.12	0.90	0.96	0.86	0.98	1.23	1.10
P	3.21	0.97	1.19	0.75	1.11	0.90	1.24	0.92	1.28	1.23	‐	‐
Q	1.05	1.09	0.97	0.80	1.19	0.98	0.90	0.73	1.05	0.98	1.03	0.96
R	0.96	1.19	0.90	0.77	1.11	0.96	0.93	0.94	1.14	0.94	1.15	0.84
S	0.90	0.97	1.39	1.18	0.92	1.00	1.07	1.06	0.96	1.04	1.04	1.11
T	0.77	1.07	1.09	2.01	1.00	1.05	0.91	1.00	1.13	0.99	0.91	1.03
V	1.10	1.74	0.54	0.55	1.11	1.09	0.88	1.01	1.25	1.03	0.80	0.73
W	1.06	0.96	1.36	1.17	0.64	1.15	1.34	1.29	0.84	1.16	0.98	1.02
Y	1.03	1.32	0.68	0.79	0.75	1.28	1.03	0.99	0.80	1.12	1.13	0.96

^aFractional change in populations of four regions in ϕ/ψ space: PPII, β, α_R, and type I β‐turn (β‐I), defined in the legend to Fig. 1. For each residue, the ratio between the population of subset {X _i} is compared to the average population of that region in the coil library (excluding residues preceding Pro). Jackknife uncertainties are given in Supporting Information Table S3.

^bSame as above, but comparing residues preceded by Z to the average coil population of that region. Gly, Pro and residues preceding Pro are excluded from the reference set.

Figure 2.

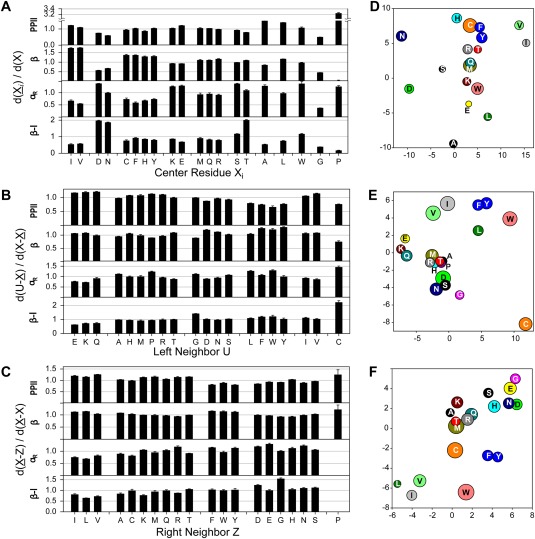
Effects on the backbone conformational distribution from (A,D) the residue itself, (B,E) preceding, and (C,F) following residue. Populations of four regions with characteristic backbone torsion angles are evaluated: PPII, β, α_R, and type I β‐turn (β‐I) [marked in Fig. 1(A)]. (A) For each residue type X_i in the coil library, its impact on the backbone ϕ/ψ conformational distribution is evaluated by using the ratio of the normalized residue density (black bars) between subsets $\left\{X_i\right\}$ and all data {X} in the coil library. (B‐C) For each residue type Z, the ratio of the normalized residue density d, d(ϕ,ψ)/Σd(ϕ,ψ), between subsets $\{Z-\underset{¯}{X}\}$ (or $\{\underset{¯}{X}-Z\}$) and all data in the coil library $\{X-X\}$ are firstly calculated for its neighbor residue $\underset{¯}{X}$. The weighted averaged ratio < $d\{Z-\underset{¯}{X}\}$/ $d\{X-\underset{¯}{X}\}$> and < $d\{\underset{¯}{X}-Z\}$/ $d\{\underset{¯}{X}-X\}$> is then calculated and plotted (black bars) for each of the four ϕ/ψ regions, visualizing the impact of the preceding (B) and following residue (C) on the ϕ/ψ region populated by the center residue. The calculation is performed for five randomly selected two‐half subset of the random coil library, the average pairwise RMS deviation observed among these 10 sets of calculated density ratios is calculated and plotted (as error bars). Xaa‐Pro, Gly and Pro are excluded from the center residue set X. (D‐F) Multi‐dimensional scaling plots of average Hellinger distances between (D) any two center residues, (E) any pair of preceding, or (F) any pair of following residues. Hellinger distance maps (upscaled by a factor of 100) were derived as described by Ting et al.19 The radius of each bubble in the 2D map corresponds to half the positional uncertainty, as derived from jackknife analysis. Locations of Pro (at x,y = −34, 5) falls outside the box shown in (F), and Gly (at x,y = −52, 6) and Pro (at x,y = −2, −45) fall outside the box shown in (D). Clustering of the 20 residue types in the Hellinger maps is used to aid grouping of residues in (A‐C). Full sets of pairwise Hellinger distances are given in Supporting Information Table S7

For evaluating the effect of a residue of type Z in position i – 1 on the ϕ/ψ propensities of X in position i, residues preceded by Z, $\{Z-X\}$, are compared to the full set $\left\{X\right\}$. Similarly, for the effect of Z in position i + 1, $\{X-Z\}$ is compared to $\left\{X\right\}$. For all these comparisons, Gly and Pro are excluded when calculating the average for residue set X because their ϕ/ψ distributions deviate strongly from other residue types. Comparison of the ϕ/ψ torsion angle distribution of $\{Z-X\}$ and $\left\{X\right\}$, viewed as the ratio of their respective densities in the Ramachandran map, is used for an initial evaluation of the effect of the preceding residue (Supporting Information Fig. S3), and similarly comparison of $\{X-Z\}$ and $\left\{X\right\}$ for the effect of the residue following X (Supporting Information Fig. S4). Such analyses assume that the effects of both preceding and following residues on the backbone torsion angles of the center residue are independent of the center residue type. Although we will show that this assumption accounts to first order for the effect of neighbors, the interaction between nearest neighbors also plays a role.

The effect of neighbor residue type on the Ramachandran distributions (Supporting Information Figs. S3 and S4) can be summarized by the fractional population change they cause for the four most populated Ramachandran map regions, β, PPII, α_R and β‐I. It is seen, for example, that an aromatic residue in the i‐1 position increases the β propensity of residue i, at the expense of PPII [Fig. 2(B), Table 1, Supporting Information Table S2]. Ala, Ser, Thr, Ile, Asn, and Pro have only small effects on the backbone ϕ/ψ distribution of the following residue, while those from Phe, Trp, Tyr, Gly, Asp, Glu, and Lys are relative large. Although the statistical uncertainty in these fractional changes is substantial for less common residues such as Trp and Cys, for the majority of residues the average effect is well determined with an uncertainty of less than ca 3% for the β and PPII regions, but slightly higher for the less populated α_R and β‐I regions (Supporting Information Table S3). Based on the data shown in Figure 2(B) and the corresponding Hellinger map [Fig. 2(E)], the left neighbor effects of the 20 residue types can be consolidated into six groups of residues with similar impact on their neighbor: {EKQ} (L1), which increases P _PPII and P _β of the following residue while decreasing P _αR and P _β‐I, {AHMPRT} (L2), {GDNS} (L3), {LFWY} (L4), which tend to reduce P _PPII and increase P _β, {IV} (L5), {C} (L6). Consolidating different residue types into a single, similarly behaving group is desirable because it provides some insight into which chemical property of a residue is responsible for modulating the torsion angles of its neighbor. For example, the similar effects imposed by the L3 group suggest that it is the polarity of this residue, and the short (or absent) sidechain; and the observation that L5 contains both Ile and Val, but not Thr, indicates that not only the Cβ‐branched nature of the sidechain but also its polarity is a contributing factor.

When evaluating the effect of the i + 1 residue type on the backbone torsion angles of i [Fig. 2(C), Table 1], one finds again that the presence of an aromatic residue decreases PPII propensity of i while increasing β, but to a lesser extent than is seen when the aromatic residue is located in the i – 1 position. Ile, Val and Leu in position i + 1 increase the PPII population of i by about 20%, at the expense of a decrease in α_R, whereas the highly polar Asp and Asn residues have the opposite effect. Thr, Met, Arg, Lys, Ala, and Gln in the i + 1 position have relatively small effects, while larger effects are observed for Gly [Fig. 2(C), Supporting Information Fig. S4, Table 1, Supporting Information Tables S2 and S3]. Due to the pronounced effect of Pro on the backbone conformation of its preceding residue and its relatively large population in the coil library, we opted to exclude it from the “control” subsets, $\left\{X\right\}$. The effect of the following residue Z on the backbone conformation of X is consolidated into five groups: {ILV} (R1), which increases P _PPII/P _β (∼10–20%) while lowering P _αR/P _β–I (∼20–40%); {ACKMQRT} (R2), which has the smallest overall impact; {FWY} (R3), which decreases P _PPII (by ∼20%) and increases P _β and P _αR (∼10–20%); {DEGHNS} (R4), which modestly lowers P _PPII and raises P _αR and P _β–I; and {P} (R5) which effectively removes population of α_R and β‐I.

Considering the effects of residue type in positions i – 1, i, and i + 1 on the ϕ/ψ angles of i independently, as done above, ignores the impact of interactions between specific types of residues. Indeed, it is plausible that it is the interaction between residues i – 1, i, and i + 1 that modulate the torsion angle propensity of residue i. For example, like charges in the i – 1 and i + 1 residues have been proposed to promote extended backbone angles for i, whereas opposite charges would promote turn formation.15 However, analysis of our library suggests that such electrostatic effects are essentially undetectable (Supporting Information Table S4). Nevertheless, as discussed below, our data confirm that the effect of nearest neighbors on the backbone angles of the center residue of a coil triplet depends on the type of the center residue.

Effect of inter‐residue interactions on Ramachandran distribution

If the effect of residue types of the left, center, and right residue of a triplet on the torsion angles of the center residue are assumed to be independent of one another, the fractional probability factors of Table 1 (left neighbor and right neighbor) and Supporting Information Table S2 (center residue) could simply be multiplied to calculate the likelihood that the center residue of a given triplet falls in any of the selected regions. For example, the probability for the ϕ/ψ angles of Ala in a Gln‐Ala‐Val fragment to locate in the PPII region to a first approximation then is given by 1.19 × 0.31 × 1.25. The correctness of such predictions was evaluated as described below, using an additional 17,600 coil residues (validation library) taken from more recent PDB depositions, not used for deriving the probabilities of Table 1.

First, for all residues X in the validation library, the 6‐state ϕ/ψ distribution P(X,r) is generated from the observed 6‐state ϕ/ψ distribution probability in the training coil library, ignoring neighboring residue type. Thus, P(X,r) = N(X,r)/N(X), where N(X,r) is the number of type X residues residing in region r, and N(X) is the total number of X residues, with r = PPII, β, α_R, β‐I, α_L and other. The average scalar product between the predicted P(X,r) and the observed P(X,r)^obs for a given region r in the validation coil library is then calculated as Σ{P(X,r)×P(X,r)^obs/<P(r)>}/N(X,r)^obs, where the summation extends over all residues of type X in the validation library, with numbers larger than one indicative of an improved prediction relative to simply using the fractional library population of r to make the prediction. <P(r)> is the average P(X,r) value for region r over all residues in the validation library, N(X,r)^obs is the number of X residues residing in region r in the validation library, and P(X,r)^obs is coded as a Boolean number to indicate if the residue resides in r.

Only taking the type of the center residue into account already significantly improves the prediction (top row in Table 2). Additionally taking into account the residue type of the left neighbor, or right neighbor, further improves the prediction (rows 2 and 3 in Table 2). Taking the effect of center residue, as well as left and right neighbor into account, but assuming these effects are independent of one another, further improves the prediction outcome (row 4). However, when simultaneously taking into account the center residue type as well as that of the left and right neighbor, i.e. using only tripeptides of the same L‐X‐R composition in the training library to make the prediction, accuracy decreases (row 5). This effect results from the increased statistical uncertainty in P(L‐X‐R,r), as for many residue types there are insufficient numbers of L‐X‐R tripeptides in the training library. This statistical deficiency can be mitigated somewhat by using the above grouping of left and right neighbor residue types (row 6), but remains slightly below what can be achieved when treating these effects independently. As expected, the best prediction accuracy is obtained when using the output of the trained ANN algorithm (row 7).

Table 2.

Relative Accuracies of Backbone Conformational Distribution Predicted from Sequence^a

	All	PPII	β	αR	β‐I	αL	other
P(X,r)b	1.15	1.06	1.10	1.11	1.33	2.82	1.12
P(L‐X,r)c	1.19	1.08	1.12	1.17	1.43	3.25	1.13
P(X‐R,r)d	1.21	1.09	1.13	1.21	1.48	3.34	1.13
P(L‐X,r)×P(X‐R,r)/P(X,r)e	1.25	1.12	1.15	1.27	1.59	3.91	1.14
P(L‐X‐R,r)f	1.19	1.10	1.13	1.16	1.44	2.87	1.12
P({L}‐X‐{R},r)g	1.22	1.11	1.14	1.20	1.51	3.57	1.13
PANN(L‐X‐R,r)h	1.28	1.11	1.15	1.30	1.70	4.59	1.13

^aAccuracy of the prediction P for residue X to be located in region r of the Ramachandran map, with r = PPII, β, α_R, type I β‐turn (β‐I), α_R and other. The reported value is relative to the probability that any residue, regardless of type or neighbors, is found in that region.

^b P(X,r) is the predicted probability of X being located in r when taking the residue type of X into account, compared to the fractional population of r, regardless of residue type.

^c P(L‐X,r) prediction based on left and center residue.

^d P(X‐R,r) prediction based on center and right neighbor residue.

^ePrediction accuracy when effect of left, center and right residue are considered independently. Note that the denominator term, P(X,r), is needed for normalization.

^f P(L‐X‐R,r) prediction based on fractional occurrence of L‐X‐R tripeptides in region r of the training library.

^g P({L}‐X‐{R},r) prediction based on fractional occurrence of {L}‐X‐{R} tripeptides in region r of the training library, using grouping of left and right neighbor residues.

^h P^ANN(L‐X‐R,r) prediction based on trained artificial neural network.

Calculation of ³J_HN‐Hα coupling constants from database analysis

As in prior studies,12, 15, 34 we also used the ϕ distributions from the coil library to predict coil ³ J _HN‐Hα values using a Karplus relationship:

$$〈{}^{3}J(X)〉={\displaystyle \sum _{i\subset coil}^{i=X}\left[A\times {\cos }^2\left({\varphi }_i-60\right)+B\times \cos \left({\varphi }_i-60\right)+C\right]}/N_X$$ (2)

where X is the residue type, N_X is the number of residues of type X observed in our coil library, and Karplus coefficients are A = 7.97 Hz, B = −1.26 Hz, and C = 0.63 Hz, respectively.47

Using eq (2), the average ³ J _HN‐Hα for different residue types in our coil library (Table 3, Supporting Information Table S5) are, on average, somewhat higher than those by Smith et al.34 and Serrano,12 which in part results from the use of more recent Karplus parameters for coupling constant calculation. On the other hand, our average ³ J _HN‐Hα are slightly lower compared to those measured for a series of Ac‐GGXGG‐NH₂ peptides,33 a difference caused by the increased population of more negative ϕ angles (i.e., larger ³ J _HN‐Hα) for residues neighbored by Gly residues in these peptides [Fig. 1(B)].

Table 3.

Average ³J_HN‐Hα Couplings and Nearest‐Neighbor Corrections

X	<3J(X)>a [Hz]	<δ3J(X‐)>b [Hz]	<δ3J(‐X)>c [Hz]	<3J(X)>ANN d [Hz]
A	5.81	−0.07	0.00	5.83
C	7.02	0.17	0.01	7.15
D	6.89	0.02	0.04	6.98
E	6.55	−0.15	−0.10	6.57
F	7.23	0.50	0.34	7.11
G	‐	0.04	0.18
H	7.24	−0.01	0.00	7.34
I	7.60	0.17	0.03	7.26
K	6.70	−0.14	−0.24	6.71
L	6.86	0.25	0.05	6.89
M	6.88	−0.03	−0.22	6.94
N	7.33	−0.03	−0.04	7.32
P	‐	−0.22	0.02
Q	6.99	−0.24	−0.15	6.73
R	6.96	−0.09	−0.23	6.66
S	6.83	−0.05	−0.03	6.40
T	7.59	0.01	−0.10	7.22
V	7.73	0.06	−0.08	7.16
W	6.81	0.41	0.38	6.44
Y	7.17	0.44	0.30	6.74

^aAverage ³J _HN‐Hα couplings calculated from Eq (2) over all residues of type X in the coil library.

^bAverage correction from the preceding residue to ³J _HN‐Hα couplings (Eq. (3)) for all residues in the coil library which have a preceding residue of type X.

^cAverage correction from the following residue to ³J _HN‐Hα couplings (Eq. (3)) for all residues in the coil library which have a following residue of type X.

^dCalculated average ³J _HN‐Hα coupling constant A_X in Eq (4). Coefficients used for Eq. (4) are c_PPII = −1.13, c_β = 1.28, c_αR = −0.16, c_β‐I = 0.92, c_αL = −0.97, and c_other = 0.07.

Nearest‐neighbors effects on ³ J _HN‐Hα coupling constants

As discussed above, the Ramachandran map distribution of a coil residue depends both on its own residue type and that of its neighbors [Fig. 1(B–D), Supporting Information Figs. S2–S5], giving rise to sequence‐dependent variations of ³ J _HN‐Hα. Accounting for the nearest‐neighbors effects therefore is expected to yield a more accurate prediction of ³ J _HN‐Hα for disordered residues. For a residue X preceded by U and followed by Z, a secondary scalar coupling constant term δ ³ J can then be introduced to account for the deviation caused by the neighbors to the “random coil” ³ J _HN‐Hα value of X:

$$\delta {}^{3}J(X|U-X-Z)={}^{3}J(U-X-Z)-〈{}^{3}J(X)〉$$ (3)

where ${}^{3}J(U-X-Z)$ is the calculated ³ J _HN‐Hα coupling constant for X in the tri‐peptide U‐X‐Z and $〈{}^{3}J(X)〉$ is the average calculated value without taking neighbors into account. Originally we had anticipated that the effect of the neighbors on the ³ J _HN‐Hα coupling would depend on the type of the center residue, with potential synergy between the left and right neighbors making their effects nonadditive.15 However, after exhaustive searching, including the grouping of residues and residue pairs that are closest in their Ramachandran map distribution as evaluated by their Hellinger distance, we were unable to find any statistically meaningful improvement over simply considering the effects of left and right neighbor on ³ J _HN–Hα of the center residue independently of one another, and independent of the center residue type. Therefore, the neighbor effects can simply be summarized by small positive or negative adjustment to $〈{}^{3}J(X)〉$ of the center residue (Table 3). The largest neighbor effects are seen for an aromatic residue in the i – 1 or i + 1 position, increasing $〈{}^{3}J(X)〉$ by nearly 0.5 Hz, whereas smaller effects in the opposite direction are observed for residues with C^γ methylene groups (Lys, Arg, Glu, Gln, Met).

³ J _HN‐Hα coupling constants from ANN prediction

As discussed above, we were unable to identify nonlinear interactions when searching for the effect of sequence of a tripeptide on the ³ J _HN‐Hα of its center residue, meaning that the contributions of preceding and following residue to ³ J _HN‐Hα simply were additive. Although this outcome was perhaps not surprising, considering that the effect of sequence on secondary structure propensity also showed at most limited nonlinear contributions, it was conceivable that we could have missed a given specific type of interaction between the preceding and following residues that could impact ³ J _HN‐Hα of the center residue. We therefore also employed a more advanced method to predict ³ J _HN‐Hα for the center residue of a given tripeptide sequence, using again the ANN algorithm.

As demonstrated above, the ANN is very robust for predicting the probability, $P_i^{\mathrm{ANN}}$, for a center residue X of a given tripeptide U‐X‐Z to reside in each of the six ϕ/ψ regions of Ramachandran space. As these probabilities are strongly correlated to the respective ϕ angle distribution, the correction term to ³ J _HN‐Hα can be written as a linear sum over these probabilities:

$${}^{3}J(X|U-X-Z)={\displaystyle \sum _i^{}{c}_i\times P_i^{ANN}(U-X-Z)}+A_X$$ (4)

where c_i is the weight given to each ϕ/ψ region i (i = PPII, β, α_R, β‐I, α_L and other), and A_X (X ≠ Gly&Pro) is a residue‐specific, average coupling constant. Using Eq. (4) requires optimization of 24 parameters (18 A_X values and 6 c_i coefficients), a linear problem most easily solved by singular value decomposition (SVD). With 332 experimental ³ J _HN‐Hα values available (Table 4), this suffices to determine these parameters.

Table 4.

Accuracy of Predicting Coil ³J_HN‐Hα Values for Disordered Peptides and Proteins

Protein	N a	RMS deviationsb [Hz]
		<3J>	3Jna	3JANN	<(3Jna+3JANN)/2>	3JSearle
Aβ(1–40)	30	0.45	0.38	0.37	0.37	0.42
α‐synuclein	111	0.39	0.29	0.29	0.29	0.50
Protease	64	0.44	0.38	0.42	0.38	0.43
Integrase‐N	44	0.47	0.41	0.36	0.37	0.58
Ubiquitinc	65	0.45	0.41	0.38	0.38	0.42
GGXGGd	18	0.43	0.43	0.28	0.31	0.37
All	332	0.43	0.37	0.36	0.35	0.47

^aNumber of experimental ³J _HN‐Hα couplings for each test set; for N‐terminally acetylated α‐synuclein, the first six residues have partial helical character and were excluded; temperature correction48 was applied to experimental data if not measured at 20°C, including a +0.16 Hz correction for Aβ (measured at 4°C) and a −0.10 Hz correction for denatured ubiquitin data (measured at 30°C); pressure correction of +0.08 Hz/kbar49 is applied to the experimental data not acquired at 1 bar, including a +0.20 Hz correction for both pressure‐denatured HIV‐1 Protease and the N‐terminal DNA‐binding domain of HIV‐1 Integrase (both collected at 2500 bar).

^bRMSD between experimental and predicted ³J _HN‐Hα coupling constants; <³J> is the difference relative to the average ³J _HN–Hα value calculated using Eq. (2) for residues of type X in the newly generated coil library, ³J_na is calculated relative to <³J> plus the neighbor adjustments of Table 3; ³J_ANN is the RMSD relative to values predicted by the ANN‐based Eq. (4). ³J_ANN values for each of the 8000 triplets are also available at https://spin.niddk.nih.gov/bax/nmrserver/rc_3Jhnha/ann_results.txt; ³J_Searle is the RMSD relative to the neighbor‐corrected coil values of Searle and co‐workers.15

^cFrom Peti et al.50

^dFrom Shi and Kallenbach.33

To prevent over‐fitting, and to exclude residue types for which less than 10 experimental values were available, a similar three‐fold jackknifing procedure as used above for training the ANN algorithm was employed: the subset of 306 (out of 332) experimental ³ J _HN‐Hα data, with ≥ 10 experimental ³ J _HN‐Hα for each residue type (excl. Cys, Trp, His, Met, and Phe), was split into three even subsets of 102 residues each, followed by three separate SVD fittings. For each of these three SVD fits, one of the subsets was excluded from the input data but then used to evaluate the fitting performance on the other two subsets plus the remaining set of 26 sparse residues. This procedure was repeated three times, each time with a different one‐third of the experimental ³ J _HN‐Hα dataset assigned to the validation set. With this procedure, the RMSD to the calculated ³ J _HN‐Hα coupling constants [Eq. (4)] was 0.34 and 0.36 Hz for the fitting and validation datasets (Table 4) [Fig. 3(B)], with the average weights and A_X values listed in Table 3.

Figure 3.

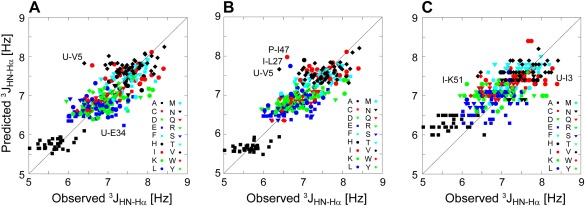
Correlation plot between predicted ³ J _HN‐Hα couplings for six sets of experimental values obtained for disordered peptides and proteins (Table IV). (A) Predicted using the newly derived nearest‐neighbors effects (Eq. 3). (B) Predicted using the ANN algorithm. (C) Predicted using the nearest‐neighbor‐specific values of Searle and co‐workers.15 RMSD values for the three plots are 0.37, 0.36, and 0.47 Hz, respectively. Some outlying residues are labeled by their one‐letter code and residue number, preceded by a letter designating the protein (I: HIV‐1 integrase; P: HIV‐1 protease; U: ubiquitin)

Comparison of predicted and experimentally observed ³ J _HN‐Hα

For disordered proteins, the rapid, large amplitude chain dynamics yields narrow ¹H NMR line widths, and consequently ³ J _HN‐Hα couplings can be measured at very high precision simply by recording 2D TROSY‐HSQC spectra, with some minor adaptations to the pulse sequence to minimize phase distortions.51 These measurements were previously demonstrated for α‐synuclein, an intrinsically disordered protein of 140 residues,49 and the Aβ1 ^– 40 and Aβ1 ^– 42 peptides.51, 52 High precision values for ubiquitin, denatured in 8M urea at pH 2.0, have been reported by Peti et al.50 Additionally, we have used the 2D TROSY‐HSQC method to measure high precision values for two pressure‐denatured proteins: HIV‐1 protease and the C‐terminal DNA‐binding domain of HIV‐1 integrase (Supporting Information Table S8). These data were collected at 2.5 kbar, and were adjusted to 1 bar by using the known, rather uniform pressure dependence of −0.08 Hz/kbar measured previously for α‐synuclein.49 Additionally, we used the high precision set of ³ J _HN‐Hα couplings reported by Kallenbach and co‐workers for a series of G‐G‐X‐G‐G peptides.33 These systems yielded a total set of 332 high‐precision experimental ³ J _HN‐Hα coupling constants for highly disordered residues.

When ignoring the effect of neighboring residues, the RMSD between observed and predicted 3 J_HN‐Hα values equals 0.43 Hz, but simply adding the neighbor adjustment terms of Table 3 decreases this RMSD to 0.37 Hz [Fig. 3(A); Table 4]. Essentially the same level of agreement [Fig. 3(B); Table 4] is obtained by using the above described ANN method to predict 3 J_HN‐Hα (Table 4). This result confirms that indeed the prediction method is not limiting the accuracy at which random coil ³ J _HN‐Hα values can be predicted. With both the linear and ANN prediction methods being somewhat independent of one another, the output error can be reduced slightly by averaging their predictions, decreasing the RMSD from experimental values to 0.35 Hz (Table 4).

Concluding remarks

Identifying the perfect “random coil” distribution remains a serious challenge. Most solutions proposed to date, including ours, simply identify segments in crystal structures that lack commonly observed elements of secondary structure. Our exclusion criteria are strictly based on the absence of H‐bonding to nonimmediate neighbors, as these could bias the distribution of backbone torsion angles. Although our H‐bond criteria are perhaps overly restrictive, the increased size of today's protein databank yields a sufficiently large set of coil residues for statistical analysis. Averaged chemical shift predictions for the residues in our coil library agree very well with empirically derived random coil values.

Predictions for random coil values of ³ J _HN‐Hα derived from our new coil library also show improved agreement with experimental values, but by a modest fraction of ca 25% relative to the best prior method for predicting these values, proposed by Searle and co‐workers,15 However, if their method is applied using our new coil library as input, that prediction method also improves, albeit by only ca 12%. Therefore, it appears that about half the improvement may be attributed to the more stringent H‐bond criteria used for identifying coil regions in crystal structures, whereas the other half results from how the effect of neighboring residues is accounted for. Although Griffiths‐Jones et al.15 postulated electrostatic interactions between residues i – 1 and i + 1 to significantly affect the torsion angles of i, we were unable to confirm such effects. Instead, we find that only interactions between immediate neighbors are sufficiently large to permit statistical analysis.

Even after extensive efforts to improve the prediction accuracy for ³ J _HN‐Hα of coil residues, our results reach a lower limit of ca 0.35 Hz for the residual RMSD between predicted values and experimentally measured ones for a range of disordered peptide and protein systems. Considering that the experimental uncertainty is well below 0.35 Hz, the residual discrepancy likely results from effects that perturb the coil backbone torsion angles originating from nonimmediate neighbors. Indeed, the largest outliers in our experimental validation analysis were observed for residues that appeared to have some degree of residual order, as judged by RCI‐S² ≥0.6, where RCI‐S² is an empirically derived, chemical‐shift‐based “order parameter,” which ranges from 0 when backbone chemical shifts are at random coil values, to 1 when they strongly differ.53 When excluding the ca 20 residues in our experimental data set for which RCI‐S² ≥ 0.6, the RMSD between observed and predicted ³ J _HN‐Hα decreases to 0.30 Hz. It is likely that variations of this magnitude must be attributed to residual interactions in disordered systems with residues other than immediate neighbors. In this respect, it is interesting to note substantial variations in our set of experimentally measured values for triplets of residues that have multiple occurrences (Supporting Information Table S6). For example, for the four occurrences of the tri‐peptide Lys‐Glu‐Gly, a 0.43 Hz RMSD from average was observed, and comparable differences for other tripeptides with multiple occurrences are seen.

Analysis of coil regions in crystal structures using the stringent H‐bond cut‐off criteria used in our study appears to yield a library of fragments that agrees very well with empirically determined random coil chemical shifts and ³ J _HN‐Hα couplings. However, the difference between individual chemical shifts and ³ J _HN‐Hα values predicted for a given sequence and experimentally measured ones often exceeds both measurement error and the uncertainty in the prediction. This result suggests that even in highly disordered polypeptides, interactions with residues outside of the triplet of residues considered often impacts backbone torsion angles to a degree that is reflected in the observed NMR parameters.

Software availability

The program, together with the coil library used in this work, is available at http://spin.niddk.nih.gov/bax/nmrserver/rc_3Jhnha as a webserver.

Supporting information

Supporting Information