MMM: A toolbox for integrative structure modeling

Abstract

Structural characterization of proteins and their complexes may require integration of restraints from various experimental techniques. MMM (Multiscale Modeling of Macromolecules) is a Matlab‐based open‐source modeling toolbox for this purpose with a particular emphasis on distance distribution restraints obtained from electron paramagnetic resonance experiments on spin‐labelled proteins and nucleic acids and their combination with atomistic structures of domains or whole protomers, small‐angle scattering data, secondary structure information, homology information, and elastic network models. MMM does not only integrate various types of restraints, but also various existing modeling tools by providing a common graphical user interface to them. The types of restraints that can support such modeling and the available model types are illustrated by recent application examples.

Introduction

For decades molecular and structural biology was inspired by Anfinsen's dogma, which states that under ambient conditions the amino acid sequence encodes a unique, stable, and accessible conformation of the peptide chain that corresponds to a minimum of free energy.1 According to this dogma, the task of structural biology is determination of the unique structures of as many proteins as possible at atomic resolution. Such structure determination for a single protein or protein complex is usually accomplished by relying on data of one of three techniques: x‐ray diffraction, NMR spectroscopy, or cryoelectron microscopy. Quite a few proteins and protein complexes do not crystallize, are too large for structure determination solely by high‐resolution NMR, and are also difficult to prepare in states that allow for atomic resolution cryoelectron microscopy. More important, proteins and their complexes are dynamic entities and in many cases their function depends on transitions between different conformations. Often Anfinsen's dogma applies only to domains of a protein, while other domains are intrinsically disordered and cannot be described by a single conformation at atomic resolution. Relative domain arrangement may change by large‐scale conformation transitions upon interaction with small ligands, other proteins, or nucleic acids. Even if the individual functional states can be specified at atomic resolution, not all of them may be accessible under conditions that allow for application of one of the three major techniques for structure determination at such resolution.

Almost a decade ago, Steven and Baumeister2 argued that understanding especially of large, dynamic macromolecular machines requires the integration of experimental data from different methodologies, in other words, hybrid or integrative structure modeling. The experimental data may be augmented by information from computational approaches. Although it is clear that integrative structure modeling is a promising—and possibly the only viable—approach for understanding macromolecular machinery in living cells, it is often hard to estimate reliability and uncertainty of the models. The problem arises mainly from a discrepancy between the amount of required and the amount of available restraints. On the one hand, specification of a set of conformations in terms of an ensemble of atomistic models requires more restraints than specification of a single conformation. On the other hand, it is usually much harder to obtain a large number of restraints if more than a single conformation is present. In this situation it may be difficult to decide which conclusions can be safely drawn from a model. Hybrid structure modeling thus needs to strive for quantification of uncertainty. This in turn is also difficult, since the width of a modeled conformational ensemble represents both intrinsic disorder and uncertainty from the lack of restraints. The two contributions can be distinguished if not only the mean values but also the distributions are available for at least some of the restraints. Such distance distribution restraints can be measured in the nanometre range between spin labels by pulsed dipolar electron paramagnetic resonance (EPR) spectroscopy.3, 4, 5 This type of information on length scales between about 1.5 and 10 nm complements shorter‐range information on internal structure of ordered domains and low‐resolution information from small‐angle scattering techniques on the global shape of a protein or protein complex. Distance distribution information has revealed that the RmsZ/RmsE protein‐RNA complex populates two distinct conformations,6, 7 has provided a model for the conformation distribution of the N‐terminal residues 3–13 of trimeric major plant light‐harvesting complex LHCII,8 and indicates that the piercing domain of the pro‐apoptotic protein Bax in its active, membrane‐bound form features intrinsic disorder beyond helix α6.9

Measurements between labels pose the problem that the conformation distribution of the label must be considered during modeling. Furthermore, distribution widths are foreign to structure determination software that aims to explain the data in terms of a single conformation or at least in terms of a minimally distributed set of conformations. From my point of view, hybrid structure modeling should aim for the ensemble with maximum width that is consistent with experimental and computational uncertainty as well as intrinsic disorder. These considerations led to the development of the modeling toolbox MMM (Multiscale Modeling of Macromolecules). In its current version, MMM can build models based on domain structure information from PDB files, different types of EPR restraints, selected types of NMR restraints, small‐angle x‐ray scattering (SAXS) and small‐angle neutron scattering curves. By interacting with MODELLER,10 MMM can also generate models based on sequence homology, experimental distance restraints, and experimental restraints on secondary structure. In addition to building models, MMM can also be used for testing whether a given model is consistent with EPR restraints.

This article is structured as follows. First, I describe the general concept of MMM and its use together with other software for structure modeling and visualization. Second, I explain how spin labels are treated in the various analysis and modeling modules. Third, I briefly illustrate the capabilities of the modeling modules by examples. Restraint files for the examples are included in the current distribution of MMM (2017.2) and protocols for reproducing these examples are provided as Supplementary Material. All visualization was performed in MMM. MMM is an open‐source Matlab program that runs on Windows, MacOS, and Linux systems. Interaction with third‐party software is currently supported only on Windows. The program can be freely downloaded at www.epr.ethz.ch/software.

General Concept of MMM

MMM is an open‐source toolbox implemented in Matlab (The MathWorks Inc., Natick, MA) that features a graphical user interface (GUI) for easier use and for specialized visualization. Such specialized visualization includes spin label conformation distributions, localization of labels or other paramagnetic centers, models of conformation transitions, and a coarse lipid bilayer model. Structures and ensembles thereof can be loaded and saved in PDB format. In addition, an internal data format can be used to save a session including information that is foreign to the PDB format. A small set of commands allows for accessing MMM functions via a command line or via simple scripts. MMM communicates diagnostic information, warnings, and error messages via a message board integrated into the GUI. This output is also written to a log file of the session. Some modeling modules create separate log files with diagnostic information. Modeling is generally controlled by restraint files. Runtime limits can be specified for some of the modeling modules.

MMM makes use of other freely available software (third‐party software) for tasks that can be solved by an established, well‐tested program with a clearly defined interface. Hence, the full functionality is only available after obtaining licenses and installing all third‐party software. In my view, this disadvantage is outweighed by the advantage that these tasks are thus solved by very well tested and maintained software, which is widely used in the structural biology community. In particular, MMM relies on DSSP11 for secondary structure assignment, on MODELLER10 for homology modeling, on SCWRL4¹² for side group modeling of native amino acids, on MSMS13 for computing solvent‐accessible surfaces, on the ATSAS package14 for simulation and fitting of small‐angle scattering curves, and on some TINKER15 modules for force‐field computations. A large part of the functionality of MMM is accessible without any of these programs being installed. The program MUSCLE16 for sequence alignment is included in the MMM distribution, courtesy of Robert C. Edgar.

With Matlab being a cross‐platform compatible interpreter language available for Windows, MacOS, and Linux systems, the core part of MMM is also cross‐platform compatible. Interfacing with third‐party software is currently implemented for Windows only.

I recognize the need for a new format for specifying models in which various domains differ in resolution and in the extent of intrinsic disorder. The PDB format is neither intended nor practical for such specification. However, a better format is not yet available and, in my view, it is not yet established how restrained conformation ensembles should be best represented. Therefore, MMM still specifies conformation ensembles by a set of individual conformations at atomic resolution. This allows for saving them in PDB format and processing them by other software that uses this format. In MMM, any part of an atomic‐resolution structure has its unique hierarchical address. As an example, [2ADC](B){7}533.P specifies the phosphorous atom of uracil 533 in model 7 of chain B of the NMR structure with PDB identifier 2ADC of Polypyrimidine Tract Binding protein RBD34 complexed with the oligonucleotide CUCUCU. This MMM address format is also used to specify sites in restraint files, usually at residue level.

MMM has a set of on‐line help files with the help for particular modules being accessible via tool buttons in the corresponding GUI windows. The manual is compiled from the help files and is available as a separate PDF document.

Spin Labels in Structure Modeling

By the use of spin labels it is possible to address biomolecules and their complexes irrespective of their size and in a broad range of environments. In particular, membrane proteins can be addressed after reconstitution into lipid bilayers.4, 17 EPR spectroscopy, which is used for detection, is less sensitive to signal quenching than fluorescence techniques. Natively paramagnetic proteins are relatively rare, so that there are usually no background signals. Furthermore, site‐directed spin labeling (SDSL)17 is possible, so that usually assignment of the signals is straightforward. The typically employed nitroxide labels are only slightly larger than native amino acid side groups. In the context of NMR structure determination spin labels can provide valuable long‐range distance restraints by paramagnetic relaxation enhancement18 and, in case of very fast relaxing paramagnetic metal ions, by pseudo‐contact shifts.19

In such SDSL studies, the structure of interest is the structure in the absence of the labels, but restraint information relates to the spatial distribution of the unpaired electron of the label. A similar problem is encountered in integrative structure modeling based on fluorescence resonance energy transfer (FRET) measurements.20 The problem is aggravated by the necessity for a semi‐flexible linker between the protein backbone and the label in order to minimize structural perturbation by the label. With pulsed dipolar EPR spectroscopy techniques, accuracy of distance restraints, as well as their precision in the case of well‐defined backbone structure, are limited by the uncertainty in predicting the spatial distribution of the electron spin for given backbone coordinates.5, 21 This problem has been addressed by accessible volume22, 23, 24 and rotamer library25, 26 approaches. The rotamer library approach combines physical realism of the set of spin label conformations, high computational efficiency that allows applying it on‐the‐fly in modeling runs, and an accuracy that is on par with other approaches.21, 24, 27 Briefly, the set of rotamers of the sterically unrestricted spin label is precomputed once for all together with estimates for their relative free energy f _{0, i}. For a given structure model, all rotamers i are consecutively attached in silico and their interaction energy Δu_i with the macromolecule or complex is computed, taking into account only repulsion and van‐der‐Waals interaction by a Lennard‐Jones potential. Populations p_i of each rotamer are then computed assuming a Boltzmann distribution with f _{0, i} + Δu_i as an estimate for their free energies. The spatial distribution of the electron spin is modeled by a cloud of centers of spin density of all rotamers, taking into account the populations p_i. The centers can be visualized by spheres with a volume proportional to the p_i and the individual rotamers can be visualized by ball & stick models with an opaqueness proportional to the p_i.

In MMM, libraries exist for the most common nitroxide spin labels with thiol‐reactive groups, for three Gd(III) labels with maleimido linkers, for a methanethiosulfonate‐substituted trityl label,28 and for an unnatural amino acid label.29 For RNA, libraries exist for attachment to thiouracil7 or to 5′‐thiophosphate groups.30 Further libraries can be generated on request. Note that none of the existing approaches for in silico spin labeling takes into account interactions of the label with the solvent or with lipid bilayers.

Localization of Spin Sites

Localization of an unknown site with respect to a known structure may be of interest in the context of ligand or cofactor binding,31 assignment of paramagnetic metal centers,32 or coarse‐grained modeling of disordered domains of a protein.9 If the structure is assumed to be rigid, the problem can be solved by an approach akin to the global positioning system (GPS). Spin label reference sites in the known part of the structure take the role of the GPS satellites and the position of the unknown site is computed from distances to at least three such sites in an approach called trilateration.33 With three reference sites, the unknown site is the top of a pyramid whose base is the triangle formed by the reference sites. The ambiguity of locating the unknown site either above or below the base triangle may be resolved by the structural context of the macromolecule or can be resolved by adding a fourth reference site that is not located in the same plane as the three existing reference sites. With more than three reference sites, multilateration needs to be solved in a least‐squares sense if the distances are not known exactly. In the case at hand, uncertainty inevitably arises from the computation of the mean spin label positions at the reference sites and from the width of the experimental distance distributions. MMM visualizes this uncertainty by a probability density isosurface with a user‐selected total probability for finding the unknown site inside the surface (default 0.5).

Figure 1(A) shows a multilateration exercise for spin‐labeled residue 131 in T4 Lysozyme, based on eight distances to reference sites at residues 68, 72, 75, 76, 79, 86, 89, and 109 and on the crystal structure 2LZM. Due to all reference sites being situated in a relatively narrow cone on the same side of residue 131, uncertainty is significantly larger perpendicular to the cone axis than parallel to it. The eight distances have a root mean square inconsistency of 1.26 Å with respect to the least‐squares position computed for the spin label at residue 131.

Figure 1.

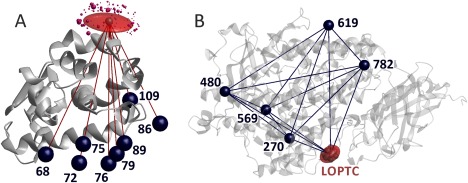
Localization of paramagnetic centers by distance distribution measurements. (A) MTSL at residue 131 in T4 Lysozyme (PDB 2LZM) is localized by multilateration using eight distances to other spin‐labeled residues and the standard deviations of their distributions. Underlying data courtesy H. Mchaourab34 and C. Altenbach (unpublished). Dark blue spheres visualize the mean position of the reference spin sites, the red semi‐transparent surface includes 50% of the probability for finding the spin at site 131, and purple spheres the spin density centers of MTSL rotamers predicted by MMM with sphere volume proportional to their predicted population. (B) LOPTC in soybean seed lipoxygenase‐1 (PDB 1YGE) is localized by distance geometry, taking into account distances and their standard deviations to five reference sites labeled with MTSL as well as the ten distances between the reference sites.31 The red semi‐transparent surface includes 50% of the probability for finding the spin of the labeled lipid

Such uncertainty can be reduced if experimental distance restraints are also available between reference sites. Obtaining such restraints is of particular importance if the domain containing the reference sites may itself be somewhat flexible and may thus undergo some conformation change on ligand binding. In this situation, the problem is best solved by distance geometry.31 Figure 1(B) shows the localization of lysooleoylphosphatidyl‐TEMPO‐choline (LOPTC) in soybean seed lipoxygenase‐1 based on ten distance restraints between five reference sites and the five distance restraints from the reference site to the spin‐labeled ligand and the crystal structure 1YGE. The primary output is a polyhedron with the reference sites and unknown site as vertices. MMM allows for specifying the approximate location of the reference sites in the restraint file, so that the polyhedron can be superimposed onto the known domain structure.

Restraint‐Augmented Homology Modeling

Distance restraints on the nanometer scale can be used to test whether a homology model of a protein is realistic. Additional restraints on secondary structure can be obtained from SDSL site scans by continuous‐wave EPR17 or from NMR spectroscopy. In comparative modeling, where homology information is implemented in terms of spatial restraints,10 the additional experimental restraints can be directly included in model building. MMM does this by serving as a front end for MODELLER,10 which eases setup of the MODELLER job and processes the information related to spin labeling. As an option, MMM uses SCWRL412 for replacing spin‐labeled residues by native residues and for repacking native side chains. MMM allows for ensemble computations and selection of the final ensemble by combined evaluation of the GA341³ 5 and Discrete Optimized Protein Energy (DOPE)36 scores of the models. The GA341 score combines a Z‐score from a statistical potential function, a measure for target‐template sequence identity and a measure for compactness of the structure. It should exceed 0.7 for a model to be considered reliable. The DOPE score is a probability measure for the modeled structure to be native‐like and refers to an atomic distance‐dependent potential. It is used to rank models, since it correlates to the root mean square deviation of Cα atom coordinates between decoys and native structure.36 Fulfilment of distance distribution restraints in the template structure and in the final models is monitored.

As an example, modeling of the extracellular loop 4 (eL4) (residues 294–324) of the Na⁺/proline symporter (PutP) based on secondary structure restraints for two short helices in this loop domain and on eight distance restraints from DEER measurements37 is shown in Figure 2. The alignment was taken from an earlier homology modeling study of the same protein.38 The PDB structure 2XQ2 of the related Na⁺/glucose transporter vSGLT of Vibrio parahaemolyticus with only about 20% sequence identity was used as a template. In this structure, five residues of the corresponding loop are not resolved and the loop has a different length and very low sequence identity. All models of the ensemble fulfil the DEER restraints within experimental uncertainty and have a GA341 score larger than 0.75. The loop is reasonably well defined by the secondary structure and distance restraints. This model allowed for forming a hypothesis on the interaction between eL4 and the core helices that was later tested and confirmed.39

Figure 2.

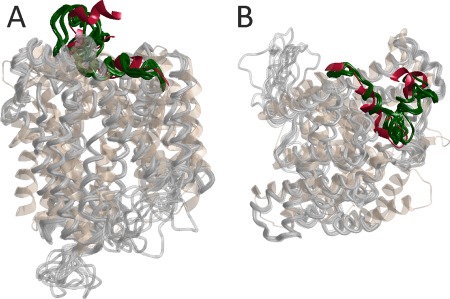
Restraint‐augmented homology modeling of eL4 of the Na⁺/proline symporter PutP.37 Short helices 296–306 and 312–321 were specified based on SDSL site scan information and eight distance restraints between spin labels were provided to MODELLER. An ensemble of 10 models (lightgray, eL4 darkgreen) is superimposed on the template structure of the Na⁺/glucose transporter vSGLT (PDB 2XQ2, peachpuff, corresponding loop crimson). (A) View parallel to the lipid bilayer. (B) View perpendicular to the lipid bilayer

Rigid‐Body Docking by a Full Grid Search

Relative position and orientation of two rigid bodies are defined by three translation parameters and three Euler angles. For symmetric oligomers with known multiplicity the number of degrees of freedom reduces to four, two translation parameters within the plane perpendicular to the symmetry axis and two polar angles that orient the symmetry axis with respect to the protomer structure.40 In any case, sufficient information can be obtained from a small number of long‐range distance restraints. The rigid‐body docking algorithm of MMM does not consider any further information, such as favourable interaction energy or avoidance of clashes. It is intended for exploring all solutions that fulfil the experimental restraints. Other software can be used for refining the models if necessary.40

Even if the number of distance restraints is larger than the number of degrees of freedom, the solution is not necessarily unique. This is because of uncertainties in the restraints and because the reference points in the two bodies may not be optimally placed for solving the problem. Therefore, a solution is not guaranteed to be the correct one even if it fulfils all restraints. It is thus advantageous to scan all six (or four) free parameters in a full grid search, so that all acceptable solutions are found. The MMMdock module allows for automatic refinement of the best solution on the grid by minimizing the root mean square deviation (RMSD) of the distance restraints and for manual refinement of any other significantly different solution.

As an example, consider the relative position and orientation of the FnIII‐3,4 domains of integrin α6β4, a problem that was originally solved with a separate program.41 Although the problem is overdetermined by 13 distance restraints for six degrees of freedom, several slightly different solutions fulfil the restraints within experimental uncertainty. In Figure 3 the twelve models are superimposed on the first domain and the second domain is shown with opaqueness of 0.25. The 12 unique models resulted from RMSD‐based refinement starting from the 20 grid points with lowest RMSD and cover an RMSD range from 0.498 to 0.510 Å. Modeling of the 21‐residue flexible linker between the domains and scoring of the models by SAXS data is discussed below in the section of RigiFlex modeling.

Figure 3.

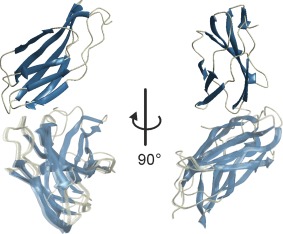
Rigid‐body docking of the FnIII‐3,4 domains of integrin α6β4 (crystal structures PDB 4WTW and 4WTX) based on 13 distance distribution restraints. All models are superimposed on the FnIII‐3 domain (fully opaque) and the second domains are shown with opaqueness of 0.25

Rigid‐body docking has two caveats. First, the assumption of the domains or protomers to behave as rigid bodies may be wrong or a poor approximation. We encountered this problem with respect to a β‐sheet in the dimeric Na⁺/H⁺ antiporter NhaA of Escherichia coli 38 that was deformed by a crystal packing artefact and was later found in a different conformation in a cryo‐EM structure of the dimeric antiporter.42 Second, each additional rigid body adds six more degrees of freedom, unless symmetry restraints apply. A full grid search with the necessary resolution is not feasible for more than two rigid bodies. Problems with three or more rigid domains or protomers are better solved with the RigiFlex approach (vide infra) that relies on distance matrix geometry for directly solving the problem of rigid‐body arrangement.

Elastic Network Modeling of Conformational Change

For ligand‐binding proteins, a structural model is often available for either the ligand‐bound or apo state, but not for both of them. The conformational change between the two states is frequently a hinge motion or a combination of hinge motion with a slight rotation of one domain with respect to the other one. Such conformational changes proceed approximately along one or a few normal modes of the protein backbone. The normal modes in turn can be surprisingly well approximated by residue‐level coarse‐grained elastic network models (ENMs).43 Such models consist of beads at the Cα atom positions and springs that connect bead pairs up to a cutoff Cα‐Cα distance. The springs have distance‐dependent force constants. Conformational change can be modeled by deforming an ENM along its soft modes. The known conformation of the protein defines the initial state of the ENM and distance restraints can be translated into forces that deform the network.44 An adaptation of this Zheng‐Brooks algorithm to distances between spin labels45 with a modification that weighs the modes according to the equipartition theorem46 is implemented in MMM.

Such modeling has been applied to the release of 3′,5′‐cyclic adenosine monophosphate (cAMP) from the C‐terminal cyclic nucleotide‐binding domain of HCN ion channel.47 Six distances between the C‐terminal helix and the β‐roll were found to change between the apo and cAMP‐bound form. Figure 4 shows a model of the transition from the apo state to the cAMP‐bound state that was obtained by reverse ENM‐modeling, using the cAMP‐bound crystal structure (PDB 3ETQ) as the initial state and six distance restraints for the apo state for deformation forces. The golden coil model in Figure 4(A) corresponds to the apo state while the green cones point from the Cα positions in the apo state to the Cα positions in the cAMP‐bound state. In Figure 4(B), the cAMP‐bound state is shown as a green coil model and depth cueing is used. The red arrow denotes the movement of the C‐terminal helix upon cAMP binding.

Figure 4.

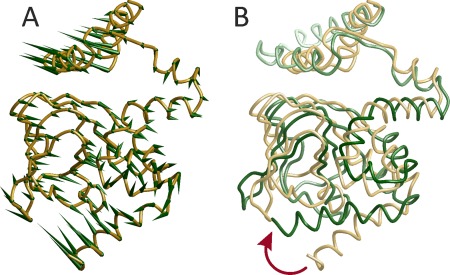
Conformational change of the nucleotide‐gated HCN ion channel upon binding of cAMP modeled from six distance restraints on the basis of an ENM and the structure of the cAMP‐bound state (PDB 3ETQ).47 (A) Green cones point from Cα positions of the modeled apo conformation (golden coil model) to the Cα positions in the cAMP‐bound state. (B) The cAMP‐bound state is visualized by the green coil model. The red arrow marks motion of the C‐terminal helix

Ensemble Modeling of Flexible Domains

Conformation space increases exponentially with the length of a flexible section of a macromolecule. To cope with such growth and ensure sufficient sampling, conformers that violate experimental restraints should be rejected as early as possible during their modeling. Such a strategy is enabled by distance distribution restraints, which allow for computing the probability that the current conformer is consistent with the restraints.48 In MMM, conformers are generated from pseudo‐random backbone torsion angles whose statistics is consistent with residue‐specific Ramachandran plots.49 Mean spin label positions for restraint testing are approximated from the mean position of a sterically unrestrained label in the local residue frame. This leads to very fast rejection of conformers that violate restraints by a large margin. More elaborate clash tests and side chain generation by SCWRL4 are performed only for conformers that have passed all fast tests.

The algorithm can implement secondary structure restraints or propensities. Furthermore, it can test for beacon restraints between a reference site in the structured part of the macromolecule and a label in the flexible section, for distance distributions restraints between two residues in the same flexible section, for oligomer restraints between a site in the flexible section and its symmetry‐related counterparts in other protomers of the same homooligomer, and for bilayer immersion depth restraints.48 Flexible sections that connect two residues in the structured parts are modeled starting from their N‐terminal residue and are steered towards their C‐terminal anchor residue by a Monte Carlo Metropolis approach.

Figure 5 shows modeling of residues 3–13 in the N‐terminal domain of major plant light‐harvesting complex LHCII.8 The model is based on seven oligomer restraints from LHCII trimers that were singly labeled at residues 3, 4, 7, 9, 10, 11, and 12,50 seven coarse bilayer immersion depth restraints that were obtained by deuterium electron spin echo envelope modulation spectroscopy for the same residues,51 and six distance distribution restraints within the flexible section (3/34, 3/59, 7/34, 7/59, 11/34, 11/59) that were obtained from heterogeneous trimers where only one of the three protomers is doubly spin‐labeled and the other two are unlabeled.8 The backbone of 25 conformers is visualized by semi‐transparent green coil models and the Cα atom of residue 3 by a semi‐transparent pale green sphere. The view along the bilayer normal [Fig. 5(A)] shows the domain to turn inward from residue 14 that is positioned on the outer rim of the trimer. For the side view in Figure 5(B), the bilayer was visualized by pale pink lipid headgroup planes and a pale green bilayer center plane. The center plane and thickness of the bilayer were fitted by minimzing the free energy contribution for bilayer immersion of the side groups of α‐helical residues,52 whereas the bilayer normal was taken along the C ₃ symmetry axis that can be inferred by symmetry from the crystal structure PDB 2BHW.

Figure 5.

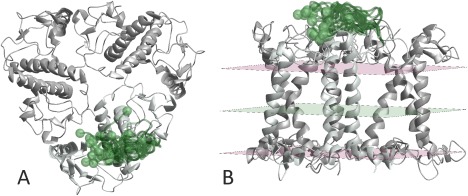
Ensemble model of residues 3–13 (semi‐transparent green coil) of major plant light‐harvesting complex LHCII based on the crystal structure of residues 14–232 (PDB 2BHW), 13 distance restraints, and 7 bilayer immersion depth restraints (see reference8). The ensemble is shown only for one protomer (mintcream). The Cα atoms of residue 3 of all 25 conformers are visualized as semi‐transparent palegreen spheres. (A) View along the membrane normal. (B) Side view with the lipid bilayer visualized by pink headgroup planes and a pale green center plane

RigiFlex Modeling

Large protein complexes are often reasonably approximated as an assembly of a few rigid bodies, which can be protein domains, whole protomers, RNA stem loops etc. The rigid bodies are linked by flexible peptide or nucleic acid sections. Possibly, the arrangement of the rigid bodies may have ensemble character, that is, the relative positions and orientations may be distributed. Such models can be built from structures of the individual rigid bodies by relying on a sufficient number of inter‐rigid‐body restraints. The flexible sections can then be inserted as described earlier.

The arrangement of n rigid bodies has 6(n–1) free translation and rotation parameters. Each chiral rigid body can be uniquely positioned and oriented if the coordinates of three reference points in this body are specified. Up to 9n(n–1)/2 unique distances can then be measured between reference points in different rigid bodies, that is, the arrangement problem can be overdetermined for any number of rigid bodies. It is useful, however, to be able to generate model ensembles already at a stage where the problem is still underdetermined. Hence, the rigid‐body arrangement problem needs to be solved by a mathematical approach that allows for such underdetermination and for fast sampling of a huge parameter space. In MMM, this problem is solved by distance geometry.

The RigiFlex algorithm consists of three steps. First, an ensemble of rigid‐body arrangements is generated by the Rigi module, which relies on distance distribution restraints between reference points, auxiliary distance distribution restraints between other sites in the rigid bodies, linker length restraints (<3.8 Å per amino acid residue, <7 Å per nucleotide), crosslink restraints, and fit quality of small‐angle scattering data. The Rigi module rejects arrangements with clashes. In the second step, the Flex module generates ensembles for all flexible linkers in all rigid‐body arrangements. The same restraints are applicable as in ensemble modeling of flexible domains and conformers are rejected that clash with any rigid body. In the third step, the assembler module tests combinations of flexible domain conformers for clashes and for fit quality of the complete model with respect to small‐angle scattering data. The final ensemble is based on the best‐fitting combinations.

RigiFlex results for the FnIII‐3,4 domains of integrin α6β4 are shown in Figure 6. The 13 distance restraints between the two rigid bodies, among them six between reference points, and two distance restraints from one site in each rigid body to the central residue of the flexible domain as well as the SAXS curve were taken from Reference.³⁷ Ten rigid‐body arrangements were computed and for each of them, up to 4 h computation time was spent to generate an ensemble of up to 10 flexible linkers.

Figure 6.

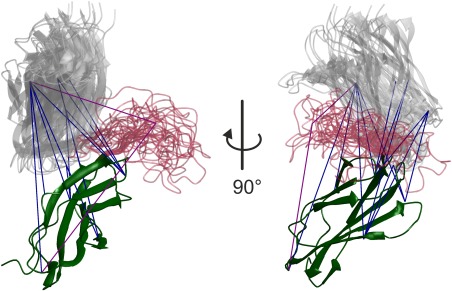
RigiFlex model of the FnIII‐3,4 domains of integrin α6β4 based on crystal structures of the individual domains, on 15 DEER distance distribution restraints between spin labels, and on a SAXS curve (see reference41). The FnIII‐3 domains (darkgreen) are superimposed, the modeled loop is shown in semitransparent crimson, and the FnIII‐4 domain in semitransparent gray color. Blue lines visualize distance restraints between rigid bodies and purple lines restraints between a rigid‐body reference point and the central residue of the flexible linker

Conclusion

MMM offers a range of modeling tools that mostly focus on the use of distance distribution restraints between spin labels in combination with atomic resolution structures. Several of these tools, in particular the RigiFlex tool, can incorporate restraints from other experimental technique for integrative modeling. The underlying set of subroutines for analysing and modifying protein and nucleic acid structure information—not described in detail in this paper, but available in open‐source form—allows for facile extension of existing modeling modules or addition of new ones. Wherever possible, MMM interfaces existing well tested and maintained third‐party software for solving subtasks. Future development of MMM will focus on extending the types of restraints that can be used, for instance, by adding FRET restraints between chromophores and a larger range of NMR restraints to the repertoire.

Supporting information

Supporting Information 1