Ensemblator v3: Robust atom‐level comparative analyses and classification of protein structure ensembles

Abstract

Ensembles of protein structures are increasingly used to represent the conformational variation of a protein as determined by experiment and/or by molecular simulations, as well as uncertainties that may be associated with structure determinations or predictions. Making the best use of such information requires the ability to quantitatively compare entire ensembles. For this reason, we recently introduced the Ensemblator (Clark et al., Protein Sci 2015; 24:1528), a novel approach to compare user‐defined groups of models, in residue level detail. Here we describe Ensemblator v3, an open‐source program that employs the same basic ensemble comparison strategy but includes major advances that make it more robust, powerful, and user‐friendly. Ensemblator v3 carries out multiple sequence alignments to facilitate the generation of ensembles from non‐identical input structures, automatically optimizes the key global overlay parameter, optionally performs “ensemble clustering” to classify the models into subgroups, and calculates a novel “discrimination index” that quantifies similarities and differences, at residue or atom level, between each pair of subgroups. The clustering and automatic options mean that no pre‐knowledge about an ensemble is required for its analysis. After describing the novel features of Ensemblator v3, we demonstrate its utility using three case studies that illustrate the ease with which complex analyses are accomplished, and the kinds of insights derived from clustering into subgroups and from the detailed information that locates significant differences. The Ensemblator v3 enhances the structural biology toolbox by greatly expanding the kinds of problems to which this ensemble comparison strategy can be applied.

Broad Statement

To compare ensembles of protein structures with residue level detail and without losing the ensemble information, we have developed Ensemblator v3. It is a versatile, user‐friendly, and open‐source tool that allows the facile assembly of related protein models to create an ensemble, the automatic clustering of these models into subgroups, and the global and local comparisons of these subgroups, pinpointing areas of significant difference or similarity using a novel “discrimination index”.

Introduction

Proteins are dynamic biological macromolecules that sample many different conformations depending on their intrinsic structural properties and their environment. Even for natively folded proteins, the true native state cannot be perfectly represented by a single model, meaning that an ensemble of structures is needed to capture the breadth of the native state.1, 2, 3 Also, ensembles can be used to capture the uncertainty associated with a structure determination or prediction approach. For both reasons, the use of ensembles to describe protein structure is a critical component of especially NMR, but also cryo‐EM, X‐ray crystallography, molecular dynamics simulations, and structure predictions. In addition, even though protein crystal structures are still typically modeled as a single conformation, the gathering of structures from multiple independent structure determinations into an “X‐ray ensemble” provides a more complete view of the range of conformations associated with the native state, as has been underscored by the creators of the Conformational Diversity of the Native State (CoDNaS) database.4

To make the best use of such information, it is critical to be able to quantitatively compare and analyze ensembles of protein structures without losing the ensemble information; yet few methods exist for direct quantitative comparisons of ensembles. For instance, authors of one recent report concluded that to account for the role of conformational diversity in assessing protein predictions “would necessarily require new improvements and novel methodologies of model evaluation.”5 To address this need, in 2015, we introduced the Ensemblator 1.06 as a conceptually simple tool for global and local comparisons of ensembles of structures that reveals residue‐ (and even atom‐) level details about systematic differences between ensembles. Also in 2015, the ENCORE7 toolkit was released to address the “need for algorithms and software that can be used to compare structural ensembles in the same way as the root‐mean‐square‐deviation is often used to compare static structures.” ENCORE very effectively enables the comparison of large sets (10,000s) of protein structures, however, ENCORE does not provide residue‐level details of where differences occur. As noted by the authors, “it is difficult to provide a simple geometric interpretation of the scores, [and] we suggest they are currently best interpreted in a relative fashion (e.g., ensemble A is more similar to B than to C).”

The power of Ensemblator 1.0 for providing geometrically meaningful details of structural differences was demonstrated in our original paper6 through analyses of an RNAse Sa8 NMR ensemble and its comparison to a two‐member X‐ray ensemble, as well as comparisons for a different protein of an eight‐member X‐ray ensemble to three NMR‐derived ensembles generated by different refinement approaches. In addition to illustrating the value of Ensemblator 1.0 analyses, however, we acknowledged a serious limitation related to the need to have the compared proteins be identical in sequence and have input files contain identical atoms in the same order.

In addressing this limitation, we have developed Ensemblator v3, a substantially more robust, versatile and user‐friendly tool. It has been entirely developed in Python, and extensive new features have been added such as multiple sequence alignments using MUSCLE9 to handle proteins of diverse sequence, “ensemble clustering” of the models into subgroups, and the calculation of a novel “discrimination index” to quantify the levels of similarity/difference between any pair of compared subgroups, per atom or per residue. Recently, we applied the Ensemblator v3 to readily locate subtle differences between an NMR‐based structure of the HIV reverse transcriptase thumb domain and the same domain as seen in the 28 highest resolution reverse transcriptase crystal structures.10 Here, we describe the novel features of Ensemblator v3, along with three case studies which briefly showcase its utility for generating useful information and facilitating insight.

Description of the Ensemblator v3

Strategy

The essential comparison strategies implemented in Ensemblator v3 are identical to those of Ensemblator 1.0 and involve: (1) carrying out a complete set of pair‐wise comparisons to define a set of global core atoms with consistent positions in all structures being compared [see Fig. 2(A) of Clark et al.6] and using those to guide a global overlay from which atom‐level global comparisons can be made, (2) carrying out a complete set of pair‐wise comparisons using the locally overlaid dipeptide residual (LODR) as a measure of residue‐level local backbone similarity (see Fig. 3 of Clark et al.6), and finally (3), for both the global and local comparisons of the two subgroups of structures for which comparison was sought, calculate four quantities: the two intra‐subgroup variations, the inter‐subgroup variation, and the closest approach of any member of subgroup 1 with a member of subgroup 2 [see Fig. 1(A) of Clark et al.6]. However, everything else about Ensemblator v3 is different as a result of the complete recoding from scratch in Python. The Ensemblator v3 has just two stages: “prepare” and “analyze.” In the prepare stage, input structure files are processed to build a single PDB‐formatted “ensemble file” for analysis. In the analyze stage, the comparisons noted above are carried out, and then either user‐defined subgroups are compared as noted in step “(3)” above, or automated clustering is performed and the resulting subgroups are compared with each other. For each pair of sub‐groups compared, the Ensemblator reports three key metrics. A “global” output file gives the RMSDs, global discrimination index (DI), and core‐status for each atom based on a final “best” overlay; a “local” output file, which reports the LODR scores and local DI for each residue; and a discrimination index file which reports for each residue the global, local and unified DI values. The following sections provide a basic description of key steps, and readers are referred to the Ensemblator documentation (on GitHub) for further details12 including a detailed description of these and other output files produced by the Ensemblator.

Figure 2.

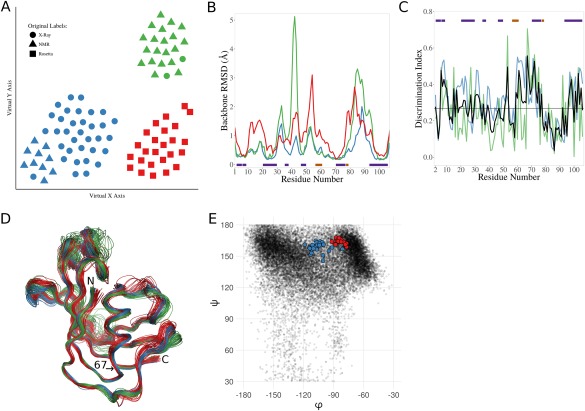
Analysis of a mixed‐source ensemble of the FK506 binding protein (FKBP). (A) t‐SNE dimensionality reduction results showing a 2D visualization of the relationships between the models in the N‐dimensional space used to cluster them. Per the key, the shape of each point represents the original label for a given model, and the clusters are differentiated by color (1—blue, 2—green, 3—red). (B) Backbone RMSDs along the chain for the final set of X‐ray (blue), NMR (green), or Rosetta (red) produced models. The bars indicate positions of β‐strands (purple), and α/3–10 helices (orange). (C) Discrimination Index (DI) plots for the Rosetta models vs. the X‐ray models. Residue‐based global (blue), local (green), and unified (black) DI are shown, along with the median unified DI (horizontal black line). Secondary structure indicated as in (B). (D) Wire‐diagram tracing the backbone for the X‐ray (blue), the NMR (green) and the Rosetta (red) models. The N‐ and C‐terminal are indicated, as well as the position of residue 67, at the base of an α‐helix. (E) The φ,ψ‐angles for serine 67 in the Rosetta (red) and the X‐ray structures (blue) are shown. As context, the φ,ψ‐values of all serine residues in crystal structures at 1.5 Å resolution or better with ≤25% sequence identity to one another are indicated (black dots).

Figure 3.

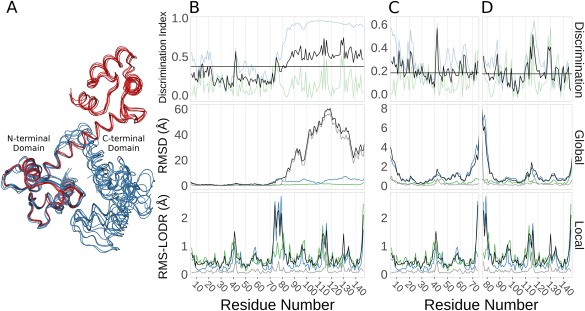
Ensemblator analysis of calmodulin (CaM) crystal structures. (A) Wire‐diagram backbone tracing for the ligand‐bound models (blue), and the ligand‐free models (red), as overlayed by the Ensemblator. (B) Discrimination indices (top panel; global (blue), local (green), unified (black), and median unified (horizontal black line)), and RMSDs from the global (middle panel) and local (bottom panel) comparisons for the entire CaM protein. In the global and local comparisons, the within group variation is shown for the ligand‐bound (green) and ligand‐free (blue) conformations. Also indicated is the inter‐group variation (black) and the closest approach distances (grey). (C) As in (B), except the analysis only included the N‐terminal domain. (D) As in (B), except the analysis only included the C‐terminal domain.

Figure 1.

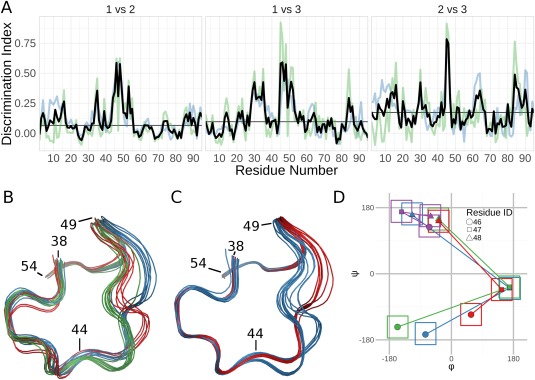
Analysis of the solution structure of RNase Sa. (A) Discrimination Index (DI) plots for the pairwise comparisons of the three groups identified by the Ensemblator. The residue‐based global DI (blue) and the local DI (green) are averaged to create the unified DI (red). The median unified DI is also indicated (black line). (B) Wire‐diagram tracing of the backbone path in the region of largest inter‐group difference (residues 44–49): Group 1 (blue; models 1,2,7,8,10,13–15); Group 2 (green; models 3–6,9,11,12); Group 3 (red; models 16–20). (C) Wire‐diagram as in (B), for groups identified by analysis of only residues 38–58: Group 1 (blue; models 3–7,9,12,16–20); Group 2 (red; models 1,2,8,10,11,13–15). The tighter backbone spread results from the more local overlay. (D) φ,ψ values for residues 46 (circles), 47 (squares), and 48 (triangles) representative of the three groups shown in panel (B) (blue, green, red) and the X‐ray structures (purple). The ±30° boxes indicate the areas used in Protein Geometry Database11 searches for tripeptides present in structures solved at 1.5‐Å resolution or better that have no more than 25% sequence identity to one another. The tripeptide conformation in all the X‐ray models was found 467 times (0.34% of all tripeptides), while zero occurrences were found for the NMR conformations.

Preparation of an “ensemble file”

To prepare an “ensemble file” that contains the atoms common to all input structures, the user must provide a set of input structures in either PDB or mmCIF format. The Ensemblator will first convert each input file into a set of separate files for each chain (or model), and each alternate conformation present. Then either immediately, or after a sequence alignment is done, these files are assembled residue‐by‐residue into a set of models in which any atoms not present in every included structure are removed (e.g., truncating aligned Ser and Tyr sidechains both to Cβ, and for an aligned Lys and Met removing Cδ and Sδ but retaining Cɛ). If atoms in regions of interest are lost in this process, a user can identify and leave the causative input file(s) out of the analysis. To facilitate this, a maximum number of allowed chain breaks per model can be specified. A benefit of this process is that by limiting the residues present in any single input file one can trivially create an ensemble file that only has a specific region of interest.

If all PDB files to be included have the same residue numbering throughout, they can be combined without carrying out a sequence alignment; otherwise, an alignment using MUSCLE9 (which must be installed separately) may be done as part of the preparation. In this case, the sequences in the split files are aligned and the residues are renumbered per the multiple sequence alignment. To filter out nonhomologous chains from the final ensemble, a series of alignments are carried out with increasing stringency on model similarity (using a BLOSUM6213‐based similarity score) until the cutoff reaches a user defined value. In the aligned sequences, the residue numbers in all output files will reflect the multiple sequence alignment numbering rather than the original values.

Determination of the common‐core atoms and global overlay

The global overlay of the structures is the standard least‐squares best overlay calculated using a set of “common‐core” atoms that are selected using the process described by Clark et al.6 In Ensemblator 1.0, the common‐core calculation was carried out for a wide range of prespecified cutoff‐distances (d _cut) and then the user had to decide which result to use. In the Ensemblator v3, the user can define d _cut, but the recommended option is to have it identified automatically by the Ensemblator. What d _cut value is “best” is subjective and will depend on the ensemble and the goal of the analysis, but our experience with a variety of proteins has led us to conclude that a good place to start is with a common core including 20–40% of the atoms. So in the automatic mode, a systematic process is followed to obtain a d _cut value producing a common core in that range.

Clustering of structures using evidence accumulation and ensemble clustering

A completely new feature of the Ensemblator v3 is automatic clustering. In the process of defining the common‐core (above), the program accumulates for every pair of structures the fraction of atoms (p) in the core of that pair (i.e., aligning closer than d _cut) and their RMSD (RMSD_c) as well as the RMSD of the non‐core atoms (RMSD_nc). The distance score used for clustering is defined as: distance score =  ${{\text{RMSD}}_{\mathrm{c}}}^{\mathrm{p}}$ × RMSD_nc 1 ^{– p}, which is essentially a weighted geometric mean14 of the RMSD_c and RMSD_nc. This novel distance metric has a few useful qualities. First, its two extreme values are simply RMSD_c (if all the atoms are in the core) or RMSD_nc (if no atoms are in the core). Second, because RMSD_c will always be smaller than RMSD_nc, it will be more heavily weighted, due to the fact that a geometric mean is always smaller than an arithmetic mean when the terms are not all equal and all the terms are positive.15 This is advantageous as we are more interested in the similarity of the core atoms than we are in the difference in the noncore atoms (but we still want to utilize information present in the non‐core atoms). Third, the favoring of RMSD_c also makes the values more resistant to extreme outliers. Using a more traditional distance metric, such as the arithmetic mean or the total RMSD, outliers would be far away from the other points in the N‐dimensional space (for N‐models), increasing the overall sparsity and worsening the quality of the subsequent clustering experiments.

The clustering is done by “ensemble clustering,” that combines the results from multiple independent clustering approaches and is known to be more robust and insensitive to noise.16 First, affinity propagation17, 18 is carried out, perhaps a few thousand times, varying the “preference” value from a low number that results in a single cluster, increasing by 1% each run until every point is its own cluster. Next, k‐means clustering19 is performed 10 × (N‐2) times, increasing the specified number of clusters, K, from 2 to N‐1, and running ten iterations for each K value with different initial conditions. Each of these independent clustering results are used fill a co‐occurrence matrix, a form of evidence accumulation,20 which records how many times each model is clustered with each other model. Finally, agglomerative hierarchical clustering is performed on this co‐occurrence matrix as a “finishing technique”,16 and provides both the final clusters used for comparisons, and a dendrogram that indicates the relationships between the models and clusters. The final number of clusters, between 2 and a user‐specified maximum number of clusters, will be the solution that provides the highest average silhouette index21 (a metric that captures how far each point is from other members of its own cluster, relative to its distance to members of the nearest other cluster; it ranges from −1 to 1 with higher values indicating a greater distinction between the clusters). Finally, the Ensemblator performs t‐SNE dimensionality reduction18 on the original distance matrix to provide a visual interpretation of the distribution independent of the clustering results. Briefly, t‐SNE works by (1) constructing a probability distribution to describe all pairs of points in the N‐dimensional space, (2) arbitrarily placing N points in a low‐dimensional space (in our case two‐dimensional) and constructing another probability distribution to describe all pairs of these points, and then (3) minimizing the divergence between the two distributions by altering the locations of the points in the low‐dimensional space.22 In our implementation, the Ensemblator uses the same set of default parameters for every dataset, and may not show groupings in two‐dimensional space that are optimally analogous to the results of the clustering experiment; however, as all the distance information that is used in the clustering and dimensionality reduction is output to a file, users may carry out any further analyses of their choice.

The local overlay strategy and LODR score

As described by Clark et al.,6 the locally overlaid dipeptide residual (LODR) is a simple distance‐based quantity that assesses the similarity between any pair of backbone conformations. Briefly, to calculate it, the equivalent dipeptides from two models are overlaid based on the Cα, C, O, N, and Cα atoms of the peptide unit preceding the residue, and then the LODR‐score is defined as the RMSD between the C, O, N, and Cα atoms in the subsequent peptide unit [see Fig. 3(A) of Clarke et al.6]. Given this definition, LODR values cannot be calculated for the first and last residues in a protein or for residues bordering chain‐breaks as there are not complete peptide units on both sides of these residues. LODR values range from 0 Å for identical conformations to ∼5 Å for residues differing by 180° in their phi values [see Fig. 3(B) of Clarke et al.6].

Calculation of the discrimination index (DI)

Our “discrimination index” combines local and global information into a single metric that indicates how similar or different a given residue or atom is between two sets of structures. It is based on the mathematics used for calculating silhouette scores.21 Considering two groups of structures (M and N), a discrimination score assessing the significance of differences can be calculated for each atom in each group, as the mean of the pairwise distances between the groups minus the mean of the pairwise distances within the group, divided by the higher of the two values:

$$\text{discrimination} \text{score} =\frac{\left(\text{mean}\left(d_{\text{inter}}\right) - \text{mean}\left(d_{\text{intra}}\right)\right)}{\text{max}\left(\text{mean}\left(d_{\text{inter}}\right), \text{mean}\left(d_{\text{intra}}\right)\right)}$$

Because this measure differs depending on which group is taken as the reference group, values are calculated for group M and for group N and averaged to create the global discrimination index (DI) for each atom. To create a residue‐level global DI, the global DI values for the N, Cα, C, and O atoms of each residue are averaged. A local DI for the backbone conformation is similarly calculated for each residue based on the LODR values. Each of these scores is saved and output in a table containing all the global or local information about each atom or residue, respectively.

A unified DI for each residue is then defined as the average of the residue‐based global and local DI values. This measure goes from near 0 to near 1 as the groups go from indistinguishable to systematically distinct. Whereas the individual local and global DI values have additional information, the value of the unified DI is that it provides a single plot that allows facile identification of the most significant regions of backbone difference between the two groups being compared.

Program details

The Ensemblator v3 is written in Python, and is currently maintained and distributed from a GitHub repository,12 where the source code is freely available. It exists as three python scripts: a core script which does all the computation, and two handler scripts which use either a command line or graphical user interface (GUI) to pass options and input files to the core script. As output, the Ensemblator provides all the data produced during analysis, as well as automatically generated plots for all the key metrics. The Ensemblator v3 GUI was written using the tkinter Python library, which should ensure compatibility with a wide range of systems. Furthermore, the Ensemblator is capable of running on multiple processors in parallel to speed larger comparisons. Issues and bugs are reported and tracked on GitHub. As they are developed, other useful, related scripts will also available in this repository (e.g., currently available is a script to choose a representative model from each subgroup of a larger ensemble).

Case Studies

Case study 1: Basic tests using the NMR solution structure of RNase Sa

Because Ensemblator v3 was a rewrite from scratch, we sought first to document that the basic algorithms are correctly coded by showing that it delivers the same results for previous test cases. We chose the analysis of an RNase Sa NMR ensemble8 for which we had identified a peptide flip between residues 82 and 83 relative to the crystal structure (PDB code: 1RGG), and also that residues 31–33 adopted a conformation in models 19 and 20 of the NMR ensemble that were unusual enough to be considered implausible.6 The reanalysis of the RNase Sa ensemble with Ensemblator v3 not only reproduced our earlier results (data not shown), but it additionally illustrated the value of automatic clustering to lead to further insight. The 20 RNase Sa NMR models cluster into three subgroups, and consistent with previous results, residues 30–33 are highlighted by their high unified DI as a region of difference between groups [Fig. 1(A)]. Notable is that residues 45–53 have a DI even higher than residues 30–33, and are thus a region of even greater significant difference.

Inspection reveals three distinct conformations for residues 45–53 that mostly but not perfectly match the clusters [Fig. 1(B)]. Such local mismatches can occur if the outlier models are more similar to their respective groups elsewhere, because the clustering is based on global similarity rather than the similarity of this particular region. This illustrates that the DI values, by taking all models into account, is much more useful for discovering significant differences compared with our previously recommended strategy of looking for regions where the closest approach distance is greater than the within group variation; the latter criteria shows nothing abnormal at this region. A quick rerun of the Ensemblator on only residues 38–58 results in a precise separation into two groups [Fig. 1(C)], with one of the groups having two slightly different conformations.

To determine the relative plausibility of the three backbone paths, we looked at the φ and ψ angles of the three‐residue segment with the highest deviations (i.e., residues 46, 47, 48) in the 20 NMR models as well as in a set of RNase SA crystal structures [Fig. 1(D)]. Surprisingly, each of the three NMR paths through φ,ψ space differ substantially from the conformations in all of the crystal structures. Even more notable, Protein Geometry Database11 searches showed that none of the conformations adopted by residues 46–48 in the NMR models has ever been seen in a large set of deposited high resolution crystal structures, whereas the conformation observed in the crystal structures is observed 467 times (∼0.4% of tripeptides) [Fig. 1(D)]. This suggests that just like the conformations seen for residues 31–33 in models 19 and 20,6 all of the conformations of residues 46–48 in all of the NMR models are dubious.

Case study 2: Clustering of a mixed‐source ensemble using the FK506 binding protein (FKBP)

Recently, Tyka et al.23 showed, using a set of FKBP models produced from X‐ray crystallography, NMR, and Rosetta, that the models are all similar, with the Rosetta‐produced template based models (based on an FKBP crystal structure) having less variability than the NMR models, but more than the crystal structures (see Fig. 6 of that paper). We requested these models to test the extent to which the Ensemblator could guide the discovery of systematic differences among them. The ensemble we received included 34, 30, and 25 models designated as “X‐ray,” “NMR” (from two studies), and Rosetta, respectively. Ensemblator analysis with automatic clustering readily divided the set into three subsets that as visualized by the t‐SNE dimensionality reduction plot [Fig. 2(A)] can be seen to largely, but not perfectly, correspond to their original labels. Importantly, the exceptions all identified structures that had misleading designations: the ten models of one NMR ensemble (PDB entry 1F40) that clustered with the X‐ray structures were from a study24 in which the ligand placement into FKBP was based on NMR observations, but the protein coordinates were taken unchanged from a crystal structure (PDB entry 1FKG); and the two models designated as “X‐ray” (entries 1FKS and 1FKT) that grouped with the NMR‐derived models in PDB entry 1FKR,25 were actually not crystal structures, but were a 21st member of the NMR ensemble and an average structure based on the other 21 models. Based on a consultation with the Baker Lab, it seems that the inclusion of these models in the set we received stemmed from a difficulty in retrieving archived data, and as these mislabeled models brought no unique information, we removed them from further analyses.

With the mislabeled models removed, Ensemblator clustering perfectly separated the X‐ray, NMR, and Rosetta models into subgroups, implying that systematic differences do exist between them despite their similar appearances. Consistent with the findings by Tyka et al.,23 the Rosetta models include more overall variation than the X‐ray models, and the NMR models even more so [Fig. 2(B)]. However, the Ensemblator analysis yields the additional information that the higher variation in the NMR models is not at all uniform, but the NMR models have much more variation in two loops, even while they have less variation than Rosetta in two other loops. Examination of the unified DI plots reveals that while the NMR ensemble appears to be roughly equally distinct from the Rosetta and the X‐ray models (Supporting Information Fig. S1), the Rosetta and X‐ray models are rather similar, but have a handful of high DI peaks [Fig. 2(C)]. It is outside the scope of this article to analyze all the differences, but as an example we consider here the highest peak, near residue 67. Inspection of the models reveals that the absolute difference between the Rosetta models and the crystal structures at this position is quite small [Fig. 2(D)], but it is significant because the variation in each subgroup is even smaller. The difference originates in the φ, ψ angles of Ser67, with the Rosetta models having values shifted toward the more densely populated P_II‐region compared to most of the X‐ray structures (including 2PPP, the structure that was used as the template for the Rosetta models) [Fig. 2(E)]. This shift could plausibly be caused by the Rosetta knowledge‐based φ,ψ‐potential,26 which would favor the more populated conformation.

Case study 3: Domain and hinge residue identification using calmodulin (CaM) crystal structures

In Clark et al.,6 it was noted but not demonstrated that the Ensemblator is designed for the analysis of single domains (or multidomain proteins that do not undergo domain movements), but that the local LODR comparisons done by the Ensemblator could be useful for identifying flexible hinge regions. This would in turn allow Ensemblator analysis of the separate domains. To illustrate this application we used calmodulin, which has homologous N‐ and C‐terminal EF‐hand domains, and undergoes a large conformational change upon binding peptide ligands with what has been described as “no significant conformational change within each domain (residues 4–74 and 82–146).”27 Using the CoDNaS database,4 we collected the set of all calmodulin crystal structures solved at 1.8‐Å resolution or better. This X‐ray ensemble contains 16 models from ten crystal structures that all have bound calcium and represent six different crystal forms; the five crystal structures without a peptide ligand are from the same crystal form.

Ensemblator clustering splits these 16 models into two groups, corresponding to the ligand‐free dumbbell conformation and ligand‐bound globular conformation with calmodulin wrapped around the peptide ligand [Fig. 3(A)]. As seen in the global RMSD plot, the first domains overlay well, making the second domains very distant [Fig. 3(B), middle panel]. Based on this plot, it is impossible to learn about intra‐domain global differences in the C‐terminal domains because the domain shift dominates the plot. In contrast to the global analysis, the local analysis [Fig. 3(B), lower panel], shows clearly that within each domain the conformations are highly similar (low LODR scores), and readily identifiable is that residues 74–80 are linker residues that not only change conformation upon peptide‐binding but also are somewhat variable among the ligand‐bound models. With this information in hand, it is trivial to then build separate ensemble files after truncating one PDB input file to either contain only the N‐ or the C‐terminal domain, to be able to perform a separate Ensemblator analysis for each domain. These runs then yield meaningful global results for both domains which combined with the unchanged local results leads to a more informative unified DI [Fig. 3(C,D)].

Interestingly, the DI plots for the separate domains each contain a dominant peak occurring at residues 41 and 114 [Fig. 3(C,D), upper panel]. These residues are at equivalent positions in the two EF‐hand domains, in a loop between the E and F helices. Whereas both have been noted before as residues that commonly interact with the bound peptides,28, 29 we have not found any mention in the extensive calmodulin literature that upon ligand binding these residues tend to undergo a similar conformational change from the beta‐region to the P_II‐region of the φ,ψ‐plot (Supporting Information Fig. S2). This backbone conformational change does not occur in every ligand bound conformation, but may be of interest for further analysis. Additional extensions of this work could involve comparing the X‐ray ensembles of calmodulin with NMR ensembles of the free and peptide‐bound forms that have been used to characterize its motions.30

Discussion

Ensemblator 1.06 introduced a tool that allowed the direct comparisons of ensembles of protein structures, rather than requiring the ensembles to be represented by a single exemplar or average structure. It also provided detailed information, for both global and local comparisons, that allowed an unprecedented residue‐level pinpointing of significant differences between the sets of structures. Our original goal in improving on Ensemblator 1.0 was to make the program much more widely applicable, by making it robust to: differences in the input coordinate files such as missing atoms and changes in residue numbering or atom order, and minor differences in sequence such that point mutants and homologs could be included in comparisons. That we have done this is well documented though Case Study #3 in which a diverse set of PDB entries obtained from the CoDNaS database for calmodulin are quickly combined for analysis, and when a separate analysis of the N‐ and C‐terminal domains is targeted as a follow‐up study, these files are also easily prepared. Three additional minor program enhancements are an algorithm for finding a suitable d _cut value for carrying out the global overlay, a GUI interface, and the ability to run on multiple processors to increase speed and scalability. The most time‐intensive part of the Ensemblator is the pairwise comparisons, and running on eight cores, its runtime is about 2 h for an ensemble of ∼1000 200‐residue structures.

In addition to these important technical improvements, the Ensemblator v3 also includes two innovations that greatly enhance the information it can provide. These are a clustering option that automatically finds conformational subgroups, and the reporting of a novel “discrimination index” as a useful metric for identifying regions of significant difference or similarity. In Ensemblator 1.0, the user had to define which models belong to each group of structures being compared—such as comparing two NMR‐ensembles to each other, an X‐ray ensemble to an NMR ensemble, or a set of liganded structures to unliganded structures—but this user‐driven approach is much less powerful than allowing features common to groups of structures to be automatically recognized through clustering. Whereas there is no universal best‐approach to clustering, we have implemented a type of “ensemble clustering” that has been documented as being broadly effective, especially on biological data.16 Each of the three case studies illustrates utility of the clustering for discovering interesting subgroups among ensembles analyzed. Especially noteworthy in our view is Case Study #2 in which the clustering makes it absolutely clear that FKBP models derived from crystal structures, NMR analyses, or from Rosetta modeling are not simply versions of the same average structures with differing amounts of uncertainty or spread; instead they are readily distinguishable as being different from each other, despite that not being obvious by visual examination. At the suggestion of a reviewer, we tested if Ensemblator clustering was sensitive to subtle differences reported by Monzon et al.31 to be important functional motions of side‐chains that could open up cavities or tunnels in proteins that have “rigid” backbones. The Ensemblator grouped the eight cellulase cel48F structures shown in Figure 5 of Monzon et al.31 into two clusters, with seven chains in one cluster and chain 1F9O_A—the chain identified by those authors as uniquely having a long tunnel—as the sole member of the second cluster, indicating that in at least some cases the Ensemblator is sensitive to these very subtle differences.

Each of the case studies also nicely illustrates the value of the novel discrimination index (DI) as a major improvement over our previous suggestion6 that the most significant differences between subgroups of structures will be the places at which the closest approach of any member of the two subgroups was larger than the spread of the ensembles. The latter metric completely misses cases in which two sets of models are widely different, but happen to have at least one member that is similar. The unified DI, in contrast, takes the full ensemble information into account as well as giving weight to both the global comparison and to the local comparison. For RNase Sa, this DI strongly identifies residues 45–50 as a segment of major difference between subgroups [Fig. 1(A)] even though each subgroup has a member that is like the other subgroup [Fig. 1(B)]. When comparing the X‐ray FKBP structures to the Rosetta produced structures, the top DI peak identified a small but significant difference would otherwise be entirely nonobvious from visual inspection of the ensembles [Fig. 2(D)], but that could be a clue to how to improve the Rosetta force field (e.g., Song et al.32). For calmodulin, in addition to making the hinge region readily identifiable, the discrimination index enabled the identification of a small conformational change within each domain that seems to strongly correlate with ligand‐binding and that, as far as we found, had not been noticed before despite extensive studies that have been done on calmodulin. The DI metric is simple to understand and use in practice, and further examples of its utility can be seen in our recently published identification of regions of significant difference between a solution NMR structure of HIV reverse transcriptase thumb domain and the same domain as seen in crystal structures of reverse transcriptase.10

The effective analysis of ensembles of protein structures requires many tools, and the Ensemblator fills a gap by being able to compare ensembles of on the order of hundreds of structures and provide exquisitely detailed information about atom‐ and residue‐level differences in conformation between groups of models. This purpose is quite different than that of ENCORE which enables the comparison of very large sets (10,000s) of protein structures, but does not provide residue‐level details.7 We suggest that the programs could effectively be used in concert with each other, for instance by using ENCORE to group very large sets of structures and then using the Ensemblator to analyze representatives of each of the ENCORE groups, to identify the nature of the most notable conformational differences between them.

The Ensemblator v3 takes the conceptual advances of the original Ensemblator,6 and makes them easily applicable to a much wider set of protein models. Furthermore, it extends the general methodology such that the only strictly required user‐input is a set of protein structures to analyze; the user no longer needs to have any preconceived knowledge about the structures (e.g., subgroups to compare or the d _cut value that would identify the ideal core). While the Ensemblator provides the greatest amount of information when applied to single domains, its application to multi‐domain proteins allows the identification of domains that have consistent internal folding as well as variable linker regions that may connect them, and as is seen in Case Study #3, it can be serially applied to the whole protein and then to identified domains to maximize the information gained. Also, even for a single domain, as seen in Case Study #1, it can be effectively applied to any substructure of interest to ensure that the global overlay and clustering provide the greatest information about that region [Fig. 1(C)]. The kinds of insights generated here in the three well‐studied proteins used as case studies, along with our recent analysis of an NMR‐derived structure of the HIV thumb domain10 illustrate how Ensemblator comparisons add a unique and useful tool to the structural biology toolbox.

Supporting information

Supporting Information Figures.