Robust intensity‐modulated proton therapy to reduce high linear energy transfer in organs at risk

Abstract

Purpose

We propose a robust treatment planning model that simultaneously considers proton range and patient setup uncertainties and reduces high linear energy transfer (LET) exposure in organs at risk (OARs) to minimize the relative biological effectiveness (RBE) dose in OARs for intensity‐modulated proton therapy (IMPT). Our method could potentially reduce the unwanted damage to OARs.

Methods

We retrospectively generated plans for 10 patients including two prostate, four head and neck, and four lung cancer patients. The “worst‐case robust optimization” model was applied. One additional term as a “biological surrogate (BS)” of OARs due to the high LET‐related biological effects was added in the objective function. The biological surrogate was defined as the sum of the physical dose and extra biological effects caused by the dose‐averaged LET. We generated nine uncertainty scenarios that considered proton range and patient setup uncertainty. Corresponding to each uncertainty scenario, LET was obtained by a fast LET calculation method developed in‐house and based on Monte Carlo simulations. In each optimization iteration, the model used the worst‐case BS among all scenarios and then penalized overly high BS to organs. The model was solved by an efficient algorithm (limited‐memory Broyden–Fletcher–Goldfarb–Shanno) in a parallel computing environment. Our new model was benchmarked with the conventional robust planning model without considering BS. Dose–volume histograms (DVHs) of the dose assuming a fixed RBE of 1.1 and BS for tumor and organs under nominal and uncertainty scenarios were compared to assess the plan quality between the two methods.

Results

For the 10 cases, our model outperformed the conventional robust model in avoidance of high LET in OARs. At the same time, our method could achieve dose distributions and plan robustness of tumors assuming a fixed RBE of 1.1 almost the same as those of the conventional robust model.

Conclusions

Explicitly considering LET in IMPT robust treatment planning can reduce the high LET to OARs and minimize the possible toxicity of high RBE dose to OARs without sacrificing plan quality. We believe this will allow one to design and deliver safer proton therapy.

1. Introduction

Intensity‐modulated proton therapy (IMPT) has the potential to enable the generation of high‐quality treatment plans. By flexibly setting nonuniform intensities for different beamlets, treatment planners can achieve highly conformal dose coverage of the target and superior sparing of adjacent organs.^{1, 2}

Despite its advantages, IMPT has problems arising in the stage of treatment planning and delivery.³ Among them, variable relative biological effectiveness (RBE) and plan robustness are two prominent issues. Because the dose deposition processes of photons and protons are distinct, the biological effectiveness of IMPT may differ from that of photon therapy even for the same physical dose. Consequently, RBE is often applied to calculate the actual biological effect of IMPT, with photon therapy as a reference. Currently dosimetric calculations use a constant RBE of 1.1. Although the use of a constant RBE was judged to be acceptable in passive‐scattering proton therapies, this assumption resulted from the lack of biological input parameters and oversimplified the real situation, especially for IMPT.^{4, 5, 6, 7} The problem of determining RBE values is complex and involves various factors including beam radiation quality (e.g., linear energy transfer [LET]), tissue type, physical dose, and biological endpoint.^{4, 8} According to in vitro experimental results, the RBE value varies markedly (from 1.0 to 1.5 for IMPT) at different regions of a proton beam. Underestimation of RBE resulting from hot spots of the LET distribution, along with the heterogeneous beamlet intensities of proton beams, could lead to unforeseen complications of organs at risk (OARs).^{8, 9}

Furthermore, IMPT is more sensitive to uncertainties including proton beam range and patient setup uncertainty than photon therapy.^{10, 11, 12, 13} Considering only the nominal scenario and neglecting these uncertainties may result in an overshoot or undershoot and may deteriorate the treatment quality. Various robust planning models have been proposed to consider these uncertainties and hedge against their negative influence.^{14, 15, 16, 17, 18, 19, 20, 21, 22} In addition, LET (thus RBE) also changes under different uncertainty scenarios. This poses additional challenges to building an effective model able to avoid high RBE doses in OARs.

In heavy ion therapy, variable RBE and incorporation of variable RBE into treatment planning is the norm in heavy ion therapy for decades.^{23, 24, 25} However, for proton therapy, it is relatively new. From now on, we will only focus on the variable RBE and its application in treatment planning in proton therapy. Previous studies about RBE in proton therapy can be classified into two categories. The first category is the measurement of variable RBE and its clinical impact.^{4, 5, 26, 27} These experimental studies sparked the interest in applying variable RBE to the IMPT planning especially recently. The second category is about mitigating the influence of variable RBE in treatment planning. Tilly et al.²⁶ applied an RBE correction method to account for variable RBE. In their work, Wilkens and Oelfke²⁸ integrated RBE into the inverse treatment planning of IMPT with multiple different scanning techniques.

Several models are available to calculate RBE‐weighted dose.^{27, 29, 30, 31, 32} However, because of the considerable uncertainties in determining the tissue‐related parameters (α and β), these models may lead to inaccuracies in IMPT planning.²⁷ Yet exact LET can be calculated through analytical methods or Monte Carlo simulations.^{33, 34, 35, 36, 37} In proton therapy, RBE values increase monotonically with LET, if the same dose, the same tissue, and the same biological endpoint are given.^{27, 38} Therefore, LET could be used as a good surrogate for indirect RBE optimization to avoid the controversy to calculate RBE from LET in proton therapy.^{8, 39} Several multistage methods have been developed recently to perform the LET‐guided optimization (indirect RBE optimization) in IMPT treatment planning. Giantsoudi et al.³⁹ introduced a multicriteria optimization IMPT treatment planning system. After the initial base plans were obtained, a set of LET‐related parameters were used to evaluate the biological dose distributions and combine the base plans to maximize dose‐averaged LET in tumor targets while simultaneously minimizing dose‐averaged LET in normal tissue structures. Fager et al.⁴⁰ applied split target planning method and multiple radiation fields to achieve higher dose‐averaged LET and smaller physical dose in tumor without changing the biological effectiveness. Recently, Tseung et al.⁴¹ used a GPU‐based simulation method to demonstrate the feasibility of biological planning with variable RBE. In the work of Unkelbach et al.,⁸ prioritized optimization methods were used for LET‐guided optimization in IMPT treatment planning. IMPT plans were optimized first on the basis of physical doses only. In the second step, variable RBE were accounted for and plans were adjusted under certain constraints, thereby ensuring that the physical dose distribution would be minimally compromised.

In the aforementioned works, plan robustness under range and patient setup uncertainties was either neglected or implicitly dealt with by adding margins to targets. The application of margin or “planning target volume” method in proton therapy is still controversial as the dose can be distorted inside the tumor under uncertainties.¹ An ideal robust planning model of IMPT should explicitly consider the LET and the aforementioned uncertainties together.

Therefore, in this paper, we extend the LET‐guided optimization methods developed in different groups^{8, 39, 42} and propose a LET‐guided robust planning model that simultaneously considers proton range and patient setup uncertainties and spares high RBE in the OARs. Our model is an extension of the model in Liu et al.,¹ which has been shown to be effective in dealing with uncertainties. Unlike the multistage optimization models mentioned above,^{8, 39, 42} our model can find an optimal plan in a single stage using the conventional quadratic optimization. Thus, our method can be easily integrated into the current commercial treatment planning system for proton therapy such as Eclipse^TM (Varian Medical Systems, Palo Alta, CA, USA). The model can minimize the high LET in OARs while maintaining almost the same tumor dose coverage and robustness in targets as those of the conventional robust model for IMPT treatment plans.

2. Materials and methods

2.A. Worst‐case robust planning model with linear energy transfer

During IMPT, the patient receives irradiation in multiple proton beams with different incident angles. Each beam can be divided into thousands of beamlets and we used j as the index of beamlet. With k _ij as the physical dose deposited to voxel i by beamlet j with unit intensity (so‐called influence matrix), the physical dose of voxel i D _i is calculated by $D_i={\sum }_j{k}_{ij}{\mathit{\omega }}_j^2$. Of note, to guarantee the non‐negativity, we used ${\mathit{\omega }}_j^2$ to denote the intensity of beamlet j. We denoted the prescription dose of tumor and allowable dose to organ as D _0,CTV and D _0,OAR .

Proton range and patient setup uncertainties can cause k _ij to deviate from its nominal value. To hedge against the negative influence of uncertainties, Liu et al. studied a robust model using the worst‐case dose (i.e., maximum and minimum doses inside the tumor and maximum doses for normal organs assuming a fixed RBE of 1.1) in the objective function and penalized excessively high and low doses of tumors and high doses of organs.^{1, 43, 44} In the present work, we extended the original robust model by adding a term that took into account the “biological surrogate (BS)” for each voxel in the OARs, as well as its robustness under uncertainties.

2.B. Ro(bs)

$$\begin{array}{cc}\hfill min& \sum _{i\in CTV}\left(\right.p_{CTV}^c{(D_i^{min}-D_{0,CTV})}^2\hfill \\ & +p_{CTV}^h{(D_i^{max}-D_{0,CTV})}^2\left)\right.+\sum _{i\in OARs}{p}_{OAR}\left(\right.D_i^{max}\hfill \\ & -D_{0,OAR}{\left)\right.}_{+}^2+\underset{\_}{\sum _{i\in OARs}{p}_{OAR}^{BD}{(B{S}_i^{max}-B{S}_{0,OAR})}_{+}^2}\hfill \end{array}$$ (1)

The Heavyside function ${(B{S}_i^{max}-B{S}_{0,OAR})}_{+}$ takes the value of $(B{S}_i^{max}-B{S}_{0,OAR})$ if $(B{S}_i^{max}-B{S}_{0,OAR})\ge 0$ and 0 otherwise. For targets, we constrained only the hot and cold spots based on physical dose in clinical target volume (CTV). But for OARs, we added a new term (underlined) that aimed to restrict the high BS. Considerable controversy exists about how to calculate RBE from LET.^{8, 9, 40} And it has been reported that the RBE values in proton therapy increases monotonically with LET with a given endpoint, dose, and tissue type.^{27, 38} Therefore, LET could be used as a good surrogate for indirect RBE optimization to avoid the controversy to calculate RBE from LET in proton therapy.^{8, 39} Therefore, here we followed the idea proposed by Unkelbach et al.¹² to use LET as a surrogate of RBE.⁸ The biological surrogate BS _i is defined as ${\sum }_j(1+c{L}_{ij})k_{ij}{\mathit{\omega }}_j^2$, where L _ij is the LET of beamlet j in voxel i and c is a scaling parameter.⁸ c is set to be 0.04 μm/keV following the suggestion from Unkelbach et al.,⁸ which yields an RBE of 1.1 in the center of a spread‐out Bragg peak of 5‐cm modulation and 10‐cm range where the dose‐averaged LET is approximately 2.5 keV/μm. The BS _i can also be expressed as $D_i+c{\sum }_j{L}_{ij}{k}_{ij}{\mathit{\omega }}_j^2$. Therefore, the $c{\sum }_j{L}_{ij}{k}_{ij}{\mathit{\omega }}_j^2$ can be seen as an extra biological effect (xBD) that resulted from the dose‐averaged LET. $p_{CTV}^c$, $p_{CTV}^h$, p _OAR , and $p_{OAR}^{BD}$ are the penalty weights for different terms. Similar to other terms, in the optimization step, the worst (maximum) BS _i among all scenarios is derived. The BS larger than BS _0,OAR is penalized in the model.

By removing the underlined term we obtained a conventional robust model that did not consider biological effect of LET, as proposed in Liu et al.¹ Our new model, denoted by RO(BS), was benchmarked with this conventional model (denoted by RO). To demonstrate the importance of considering different LET in different scenarios, we also compared the new model with a benchmark that considers only nominal LET, denoted by RO(BS₀). RO(BS₀) was obtained by replacing the underlined term with ${\sum }_{i\in OARs}{p}_{OAR}^{BD}{(B{S}_i^0-B{S}_{0,OAR})}_{+}^2$, where $B{S}_i^0$ represents the BS in the nominal scenario.

2.C. Patient data and computation settings

In this exploratory study, we tested the effectiveness of our model on 10 clinical cases: two prostate cancer, four head‐and‐neck cancer, and four lung cancer. For each case, we generated eight representative scenarios in addition to the nominal scenario for the proton range and patient setup uncertainties. The patient setup uncertainties were simulated by shifting the isocenter of the patient in the anteroposterior (A‐P), superior–inferior (S‐I), and right–left (R‐L) directions by 3 mm yielding six scenarios. This distance is disease‐site dependent and it was set as 3 mm in this study for demonstration purposes. Range uncertainties were simulated by scaling the stopping power ratios by ±3.5% to generate two additional scenarios. The influence matrix for nominal or for each of the uncertainty scenario was calculated using a treatment planning system developed in‐house.^{1, 45} The calculation of LET effect (L _ij ) in each scenario was performed with an in‐house fast LET calculation method based on Monte Carlo simulations. Computational settings are listed in Table A1.

2.D. Solution methods and plan evaluation

The new model RO(BS), the conventional robust model RO, and RO(BS₀) are classified as unconstrained convex programming problems. The dose volume constraints can be implemented following the method of Wu and Mohan.⁴⁶ Computation of the cases was completed in a parallel computation environment based on the L‐BFGS (limited‐memory Broyden–Fletcher–Goldfarb–Shanno) algorithm.⁴⁷

To evaluate the quality of tumor dose distribution, we used D_95%, D_5%–95%, and width of the dose–volume histogram (DVH) band, which displayed the envelope of all DVHs of the nine scenarios. These three parameters reflect dose coverage, dose homogeneity, and plan robustness, respectively. To assess the protection of OARs with biological effects due to the high LET considered, we applied the BS‐volume histogram (BSVH) or xBD‐volume histogram (xBDVH) (a cumulative volume histogram showing the relative volume of an organ receiving at least a certain value of BS or xBD). The xBDVH is adopted for the graphical evaluation in Figure A2. For quantitative evaluation in Table 2, we chose the same indices of the BSVH as those of the dose DVH assuming a fixed RBE of 1.1 (e.g., V₂₅ of rectum and D_1% of brain stem) as no standard is widely accepted to evaluate RBE‐weighted dose. Please note that the absolute value of xBD and BS is not important, but rather the relative comparison of xBD and BS matters, which shows the better protection of OARs due to the smaller biological effects caused by high LET between different treatment planning methods.

Figure A2.

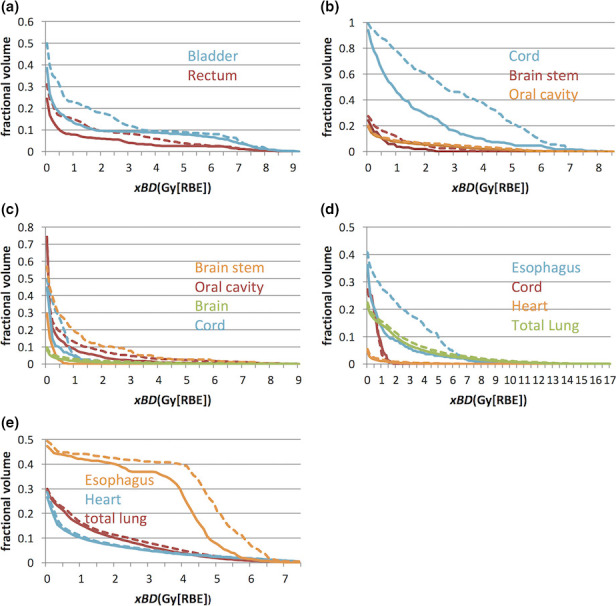
The xBD ‐volume histograms of the cases 1–5 (in the nominal scenario) for RO (dashed Line) and RO(BS) (solid Line), respectively. The curves from our new robust model RO(BS) were drawn as solid lines and ones from the conventional model RO as dashed lines. The RO model can reduce xBD , although the degree of reduction varies from patient to patient and organ to organ. [Color figure can be viewed at wileyonlinelibrary.com]

Table 2.

Comparison of biological surrogate‐volume histogram indices in organs at risk for the 10 cases. Our new model RO(BS) can drastically reduce BS in all organs compared with RO. In comparing the results from RO(BS) and RO(BS₀), consideration of varying linear energy transfer in different uncertainty scenarios can generally further decrease the BS index. The unit of Gy[LET] is used here to emphasize that the values reported here are not RBE doses, but rather biological surrogates, which only have LET information

Case no.	Organ		RO(BS)		RO		RO(BS0)
			Nominal	Maximum	Nominal	Maximum	Nominal	Maximum
1	Rectum	V25, %	6	7	9	13	5	7
	Bladder	V25, %	9	17	15	19	10	16
2	Brain stem	D1%, Gy[LET]	54.2	54.5	55.7	56.2	54.2	56.8
	Cord	D1%, Gy[LET]	11.8	18.1	23	30.9	12.6	24.2
	Oral cavity	Dmean, Gy[LET]	2.5	3.3	2.86	3.61	2.54	3.35
3	Brain stem	D1%, Gy[LET]	2.5	5.2	30.2	38.7	4.5	8.5
	Brain	D1%, Gy[LET]	15.7	20.9	26	30.9	17.6	22.7
	Cord	D1%, Gy[LET]	6.1	7.4	20.1	22.2	7.7	9.2
	Oral cavity	Dmean, Gy[LET]	2.73	3.28	4.13	5.02	2.89	3.53
4	Lung	V20, %	10	11	11	12	10	12
		Dmean, Gy[LET]	5.36	6.05	6	6.72	5.5	6.2
	Heart	D33%, Gy[LET]	0	0	0	0	0	0
	Esophagus	D33%, Gy[LET]	1.2	1.8	3.4	6.5	1.4	2
	Cord	D1%, Gy[LET]	27.1	35.6	37.4	38.2	36.4	37
5	Lung	V20, %	0.11	0.12	0.14	0.15	0.12	0.13
		Dmean, Gy[LET]	5.58	5.88	6.28	6.59	5.62	5.92
	Heart	D33%, Gy[LET]	0.2	0.3	0.3	0.5	0.2	0.3
	Esophagus	D33%, Gy[LET]	38.4	42.1	48.6	49.1	35.8	41.4
6	Rectum	V25,%	16.7	26.7	20.6	31.1	16.3	26.7
	Bladder	V25,%	18.4	25	19.4	26	18.1	24.6
7	Brain Stem	D1%, Gy[RBE]	19.1	24.6	22.2	27.2	19.8	25.3
	Brain	D1%, Gy[RBE]	38.7	51.8	41.5	54.4	39.4	52.8
	Cord	D1%, Gy[RBE]	2.9	6.3	3.1	6.8	2.9	6.5
8	Brain Stem	D1%, Gy[RBE]	3.1	5.9	7.6	15.3	4	7.4
	Brain	D1%, Gy[RBE]	45.2	52.9	71.1	75.7	43.2	53
	Cord	D1%, Gy[RBE]	26.4	38.2	52.4	63.9	32.9	42.8
9	Lung	V20, %	14.5	14.7	14.8	15	14.5	14.8
		Dmean, Gy[RBE]	6.8	7	7	7.1	6.9	7
	Heart	D33%, Gy[RBE]	0	0	0	0	0	0
	Esophagus	D33%, Gy[RBE]	3.2	5.4	7.8	11.7	4.4	8.6
10	Lung	V20, %	0.13	0.17	0.15	0.18	0.14	0.17
		Dmean, Gy[RBE]	7.7	8.8	8.6	9.8	7.8	9
	Heart	D33%, Gy[RBE]	0.1	0.2	0.1	0.2	0.1	0.2
	Esophagus	D33%, Gy[RBE]	4.7	10.7	19.9	26.4	5.5	11.5

3. Results

3.A. Tumor dose distribution assuming a fixed RBE of 1.1

Table 1 lists the results of the 10 cases. Because multiple scenarios were considered, the table shows the nominal value and the maximum and minimum values for D_95% and D_5%–95% among all scenarios. Band widths, which indicate plan robustness, were calculated as the difference between the maximum and the minimum value among all scenarios at D_95%, D_50%, and D_5%. These parameter values of the new model RO(BD) and the conventional robust model RO are similar, and the difference is less than 1.0 Gy[RBE]. Figure A1 further illustrates the DVH curves on the basis of per‐voxel maximum and minimum doses of tumor in case 2. Only a minor difference was found between the two plans, which indicates similar plan robustness of targets between the two methods.

Table 1.

Comparison of tumor dose distribution assuming a fixed RBE value of 1.1. The new model RO(BS) and the conventional model RO are almost the same in quality of tumor dose coverage, homogeneity, and robustness

Index	Scenario	Case 1		Case 2		Case 3		Case 4		Case 5
		RO(BS)	RO	RO(BS)	RO	RO(BS)	RO	RO(BS)	RO	RO(BS)	RO
D95%, Gy[RBE]	Nominal	75.8	75.9	46.5	46.6	59.8	59.8	59.6	59.6	44.5	44.8
	Max	75.8	75.9	46.5	46.6	59.9	59.9	59.6	59.6	44.5	44.8
	Min	75.2	75.6	45.2	45.7	59.4	59.6	58.3	58.2	44.2	44.5
D5%–D95%, Gy[RBE]	Nominal	1.4	1	3.6	3.3	0.9	0.9	3.9	3.8	1.8	1.3
	Max	1.7	1.1	4.6	4	1.2	1.1	4.6	4.5	2	1.5
	Min	1.3	0.8	3.6	3.3	0.9	0.9	3.6	3.6	1.7	1.3
D95% DVH band, Gy[RBE]		0.6	0.3	1.3	0.9	0.5	0.3	1.3	1.4	0.3	0.3
D50% DVH band, Gy[RBE]		0.2	0.2	0.4	0.2	0.4	0.4	0.2	0.2	0.2	0.2
D5% DVH band, Gy[RBE]		0.6	0.4	0.6	0.7	0.5	0.4	1.3	1.5	0.3	0.3
		Case 6		Case 7		Case 8		Case 9		Case 10
		RO(BS)	RO	RO(BS)	RO	RO(BS)	RO	RO(BS)	RO	RO(BS)	RO
D95%, Gy[RBE]	Nominal	76.6	76.8	59.5	59.4	56.7	56.7	44.4	44.5	59.7	59.8
	Max	76.7	76.8	59.5	59.4	57.2	57.2	44.4	44.5	59.7	59.8
	Min	75.2	75.4	53.7	53.7	55.7	55.8	43.2	43.7	58	58.7
D5%–D95%, Gy[RBE]	Nominal	4.3	4.3	7.4	7.6	8.5	8.4	3.3	3.2	2.9	2.6
	Max	8	7.8	12.3	12.3	9.2	9	3.9	3.6	2.5	3.1
	Min	3.8	3.1	7.4	7.6	7.9	7.7	3.3	3.1	2.9	2.4
D95% DVH band, Gy[RBE]		1.5	1.4	5.8	5.7	1.5	1.4	1.2	0.8	1.7	1.1
D50% DVH band, Gy[RBE]		0.3	0.2	1.4	1.4	1.1	1.1	0.9	0.6	0.4	0.3
D5% DVH band, Gy[RBE]		3.7	3.7	1.5	1.5	1.9	1.7	1	0.8	1.5	1.6

DVH, dose–volume histogram.

Figure 3.

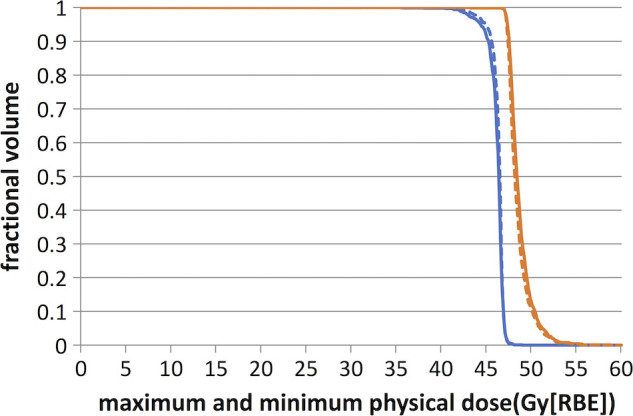
Comparison of DVH curves generated by the per‐voxel maximum (red and dark) and minimum (blue and gray) l doses of tumor assuming a fixed RBE of 1.1 derived from the models with and without BS terms for the head‐and‐neck cancer case. The new model RO(BS) is represented by solid curves and the conventional model RO by dashed curves. The difference between the DVH curves generated by the per‐voxel maximum and minimum doses of tumor indicates plan robustness. The difference of plan quality and plan robustness is only minor between the two models. [Color figure can be viewed at wileyonlinelibrary.com]

3.B. Comparison of biological surrogate in OARs using xBDVHs and BDVHs

We defined a biological surrogate as BS and extra biological effects xBD in Section 2 to represent the biological effects because of the high LET. Figure A2 shows the xBDVHs of OARs for the first five cases. Please note again that the absolute value of xBD and BS is not important, but rather the relative comparison of xBD and BS matters, which shows the better protection of OARs due to the smaller biological effects caused by high LET between different treatment planning methods. Clearly, our new model can reduce the xBD in most OARs for all cases although the degree of reduction varies. Table 2 summarizes the BS of critical organs using the same indices as those of doses assuming a fixed RBE of 1.1 under the uncertainty scenarios and compares results of RO, RO(BD), and RO(BD₀) models. Both tables clearly show that the biological effects due to high LET are considerably reduced from our LET‐guided robust optimization method.

Figure 1 further illustrates the difference of LET distributions of the RO(BS) and the RO for case 2 (one typical head‐and‐neck cancer patient). Figures 1(a) and 1(b) show the dose distribution assuming a fixed RBE of 1.1; Figures 1(c) and 1(d) show the distribution of LET. From Figure 1 (comparing (c) to (d)) we can see that the hot spot area of the LET distribution in spinal cord (with cyan contour line) is considerably reduced (highlighted by red circles in Figures 1(a) and 1(b)), while the dose distribution assuming a fixed RBE of 1.1 in tumors is very similar (comparing (a) to (b)) (highlighted by red circles in Figures 1(a) and 1(b)).

Figure 1.

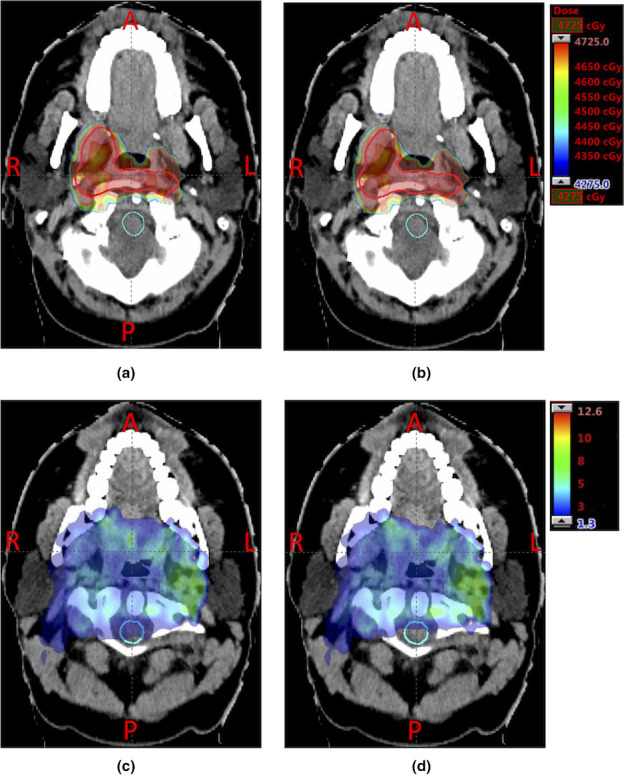
Comparison of dose distribution assuming a fixed RBE of 1.1 (top row) and LET distribution (bottom row) for case 2 in the nominal scenario. (a) and (b):distribution of dose assuming a fixed RBE of 1.1. (c) and (d):distribution of the LET (unit: kev/μm). (a) and (c) are the results from the conventional model RO; (b) and (d) are the results from our new model RO(BS). Clinical target volume (CTV) and spinal cord are contoured by red (top middle enclosed area) and cyan lines (bottom enclosed area), respectively. In RO(BS), the high LET distribution in spinal cord (comparing (c) and (d)) is considerably reduced, while the physical dose distribution of the tumor is very similar. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 2 shows the difference of doses assuming a fixed RBE of 1.1 between the RO(BS) model and the RO model, reporting the results of the plan derived from RO(BS) minus the results of the plan from RO. To avoid high BS in the brainstem (yellow contour), the lower beam confines its high‐intensity beamlets within its distal half and reduces the intensity of the beamlets deposited at the proximal edge of the target (red contour) when the brainstem (yellow contour) is proximal to the target. However, beamlet intensities in the upper beam parallel to the organ will increase to compensate the physical dose in the target, which leads to an increased physical dose in the red area.

Figure 2.

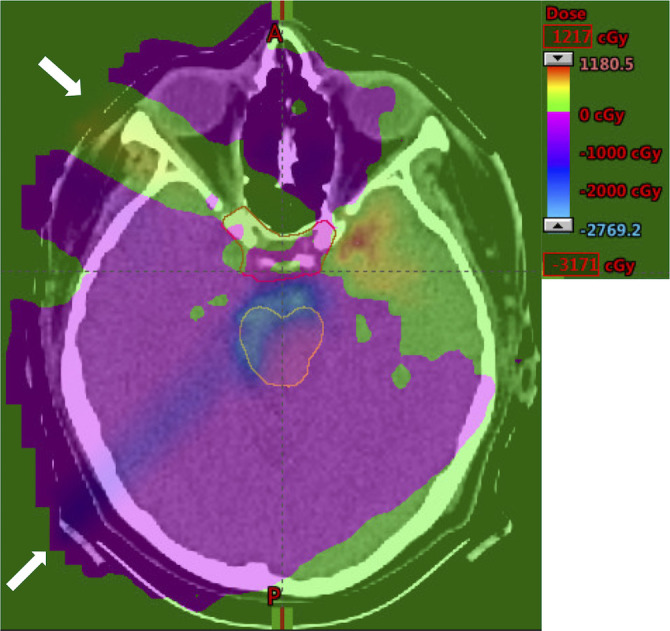
Difference of doses from the results of the plan derived from the RO(BS) model minus the results of the plan derived from the RO model assuming a fixed RBE of 1.1. A representative transverse slice of case 2 under nominal scenario is shown. For two beams with their directions indicated by white arrows, the RO(BS) model clearly will reduce the intensity of beamlets of the lower beam deposited at the proximal edge of the target (red contour and top enclosed area) when brainstem (yellow contour and bottom enclosed area) is proximal to the target. This effect will lead to an decrease of physical dose (blue area and left bottom gray area) from the RO(BS) model compared with the RO model. Correspondingly, the beamlet intensities in the upper beam parallel to the brain stem will increase to compensate the physical dose in the target. This causes an increase of the physical dose in the red area (top right dark area). [Color figure can be viewed at wileyonlinelibrary.com]

3.C. Effect of considering varying LETs in different uncertainty scenarios

To demonstrate the importance of considering LET under different uncertainty scenarios, we include results from the RO(BS₀) model in Table 2. By comparing the results of the three models, we find that both RO(BS) and RO(BS₀) can drastically reduce the BS. Generally, after including varying LETs in different uncertainty scenarios, the BS can be decreased further. Several exceptions exist — nominal V₂₅ of rectum and worst‐case V₂₅ of bladder in case 1 and 6 and nominal and worst‐case D_33% of esophagus in case 5. The decrease is not obvious when the dose value is already small in the conventional RO models.

4. Discussion

As we have emphasized in the Introduction, LET could be used as a good surrogate for indirect RBE optimization to avoid the controversy to calculate RBE from LET in proton therapy.^{8, 39} One may argue that the formula proposed by Unkelbach et al.⁸ and used in this work can also be considered as a RBE model, which only includes LET information. However, the aim of this work was to implement a robust optimization method for IMPT to reduce high LET in OARs at no or littile cost of plan quality and plan robustness of targets. It is certainly not our intention in this work to propose a new RBE model and demonstrate its validity.

The LET is usually ignored in IMPT planning and high LET may lead to high risk of complications in OARs. Our new model simultaneously considers LET and the proton range and patient setup uncertainties so that toxic doses to organs can be minimized and tumors are still adequately covered in the face of uncertainties. On the basis of the dose‐averaged LET, we defined a biological surrogate due to high LET following Unkelbach et al.⁸ and added a term penalizing high BS of each OAR into the IMPT robust planning model of Liu et al.¹ The new model was easy to implement and solve. All cases can be solved efficiently in a parallel computing environment.

The major concern is that introduction of new terms will compromise the tumor physical dose distribution in the original model. We investigated the influence of new terms introduced to control the distribution of LET in OARs on the quality of tumor dose distribution (Table 1 and Figure A1). We found that the tumor physical dose distribution from our new model was almost the same as from the conventional robust model. The robustness of tumor dose distribution was not compromised. Reduction in the BD does little in sacrificing the quality of tumor physical dose distribution. As demonstrated by Table 1, the nominal D_95% change (nominal D_95% of the RO model minus that of the RO(BD) model as shown as (mean [min, max])) were (0.08 [−0.1, 0.3]) Gy[RBE] and the nominal D_5%–D_95% change as shown as (mean [min, max]) were (−0.16[−0.5, 0]) Gy[RBE]. For robustness, the band width changes at D_95% as shown as (mean [min, max]) were −0.21 [−0.6, 0.1]) Gy[RBE].

Our new model drastically reduces the xBD because of the high LET and hence provides better overall protection to normal organs than the conventional model (Figure A2). This result is achieved primarily by reducing the mean value of xBD rather than the maximum xBD. For all cases, the middle part of the curve dropped notably while the maximums of curves varied little. This might be important for the sparing of some important parallel organs such as parotids, oral cavity, total lung, etc. The RO(BS) model and RO(BS₀) models can both greatly reduce the BS (Table 2). This reduction is more obvious in organs receiving a large BS (>1.0 Gy[RBE]) under the RO planning, such as the brain stem of case 3, the cord of case 2, and the brain of case 8. The improved distribution of BS can decrease a patient's potential risk of organ complication.

Our RO(BS) model better protects organs against high BS (Fig. 2). Previous studies found that the LET increased exponentially at the end of range (at and beyond the Bragg peak).⁶ Therefore, among various degenerate robust solutions, our RO(BS) model is able to find the one that reduces the intensities of beamlets deposited at the proximal edge of tumors and confines the high‐intensity beamlets within its distal half. This decreases the high LET exposure in organs proximal to tumors. This observation is consistent with Grasssberger et al.⁶ At the same time, to compensate the physical dose in the tumor, a beam parallel to critical structures will increase intensities of its beamlets in the target. This will further reduce high LET in critical organs as the lateral falloff of a beamlet has much lower LET compared to the distal falloff.

In this study, we explored the effect of different LETs under different uncertainty scenarios. Compared with RO(BS₀) which includes only the LET in nominal scenario, the new model RO(BS) can further reduce the BS in critical organs as it proactively hedges against the influence of varying LET for different uncertainty scenarios at the planning stage. Some exceptions are observed, such as the nominal V₂₅ of rectum in case 1 and 6 and nominal and worst‐case D_33% of esophagus in case 5. These exceptions can be explained by the fact that in particular challenging cases, achievement of a good protection level of one organ is contradictory with that of the other organ; hence, some organs have to be compromised.

The RO(BS) model is less effective in controlling maximum xBD. This problem could be solved by explicitly adding constraints, which can be implemented by following the techniques of Wu and Mohan.⁴⁶ Another alternative method is to modify the beam direction. However, incorporating new constraints or beam angle selection into treatment planning model increases the computational complexity.

5. Conclusion

In this work, we simultaneously included variable LET and the proton range and patient setup uncertainties into the robust IMPT planning. The plans obtained from the model were able to hedge against high LET and maintain adequate tumor coverage in the face of uncertainties. Effectively, our new model could minimize adverse consequences of the high LET exposure in OARs.

Conflicts of interest

The authors declare that they do not have any conflict of interest.

Appendix 1.

Table A1.

Parameter values for the 10 cases

Case	Tumor type	Beam	Voxels
1	Prostate	1: 2,796	CTV: 303
		2: 2,788	Bladder: 651
			Rectum: 1,545
2	Head and neck	1: 5,988	CTV: 991
		2: 6,168	Brain stem: 216
		3: 6,582	Cord: 157
			Oral cavity: 1,608
3	Head and neck	1: 18,478	CTV: 1,087
		2: 14,060	Oral cavity: 1,077
			Cord: 188
			Brain stem: 195
			Brain: 12,364
4	Lung	1: 5,394	GTV: 827
		2: 7,490	Cord: 309
			Esophagus: 388
			Heart: 4,761
			Lung: 20,546
5	Lung	1: 6,780	ITV: 1,155
		2: 6,810	Lung: 26,173
		3: 7,026	Heart: 5,291
			Esophagus: 387
6	Prostate	1: 4,608	CTV: 967
		2: 4,048	Bladder: 2,776
			Rectum: 1,373
7	Head and neck	1: 2,378	CTV: 415
		2: 3,664	Brain stem: 222
		3: 3,748	Brain: 10,751
			Cord: 50
8	Head and neck	1: 11,374	CTV: 3,786
		2: 11,868	Cord: 228
		3: 2,478	Brain stem: 231
		4: 4,616	Brain: 13,066
9	Lung	1: 8,662	ITV: 1,123
		2: 4,952	Esophagus: 379
		3: 5,498	Heart: 7,085
			Lung: 24,394
10	Lung	1: 31,756	CTV: 661
		2: 37,216	Lung: 5,489
			Heart: 695
			Esophagus: 50