Abstract
Purpose
Accurately analyzing the rapid structural evolution of human brain in the first year of life is a key step in early brain development studies, which requires accurate deformable image registration. However, due to (a) dynamic appearance and (b) large anatomical changes, very few methods in the literature can work well for the registration of two infant brain MR images acquired at two arbitrary development phases, such as birth and one‐year‐old.
Methods
To address these challenging issues, we propose a learning‐based registration method, which can handle the anatomical structures and the appearance changes between the two infant brain MR images with possible time gap. Specifically, in the training stage, we employ a multioutput random forest regression and auto‐context model to learn the evolution of anatomical shape and appearance from a training set of longitudinal infant images. To make the learning procedure more robust, we further harness the multimodal MR imaging information. Then, in the testing stage, for registering the two new infant images scanned at two different development phases, the learned model will be used to predict both the deformation field and appearance changes between the images under registration. After that, it becomes much easier to deploy any conventional image registration method to complete the remaining registration since the above‐mentioned challenges for state‐of‐the‐art registration methods have been well addressed.
Results
We have applied our proposed registration method to intersubject registration of infant brain MR images acquired at 2‐week‐old, 3‐month‐old, 6‐month‐old, and 9‐month‐old with the images acquired at 12‐month‐old. Promising registration results have been achieved in terms of registration accuracy, compared with the counterpart nonlearning based registration methods.
Conclusions
The proposed new learning‐based registration method have tackled the challenging issues in registering infant brain images acquired from the first year of life, by leveraging the multioutput random forest regression with auto‐context model, which can learn the evolution of shape and appearance from a training set of longitudinal infant images. Thus, for the new infant image, its deformation field to the template and also its template‐like appearances can be predicted by the learned models. We have extensively compared our method with state‐of‐the‐art deformable registration methods, as well as multiple variants of our method, which show that our method can achieve higher accuracy even for the difficult cases with large appearance and shape changes between subject and template images.
Keywords: auto‐context model, deformable image registration, infant brain MRI , random forest regression
1. Introduction
Deformable registration of infant brain MR images can establish accurate anatomical correspondences for mapping brain structures and functions, which is important for quantifying brain development from a set of individual subjects. Specially, intersubject registration is challenging and quite important for analyzing infant brain images for population study. Note that the goal of intersubject registration here is to reduce anatomical variability across subjects by establishing one‐to‐one correspondences or dense deformation field in the three‐dimensional (3D) brain image space. This enables representing the entire group of subjects in the common space, or comparing brain structures and functions between different groups, e.g., patients vs. normal controls.1, 2 To measure brain development and evolution during the first year of life, accurate deformable image registration for different subjects is of high demand. However, the accurate registration of infant brain images is challenging, since the brain structures develop very fast and also the appearances of gray matter (GM), white matter (WM), and cerebral spinal fluid (CSF) changes dynamically during the early development. Moreover, besides the expansion of whole brain volume, the folding patterns in cortical regions also develop rapidly from birth to 1‐year‐old,3, 4, 5 as shown by the examples of two infant subjects in Fig. 1, each with its respective T1‐weighted MRI, T2‐weighted MRI and tissue segmentation map provided in the top, middle and bottom rows. Hence, it requires a registration algorithm to deal with the complex appearance differences and large anatomical changes, when registering the two infant MR images scanned at two different time‐points with possibly large age gap.
Figure 1.
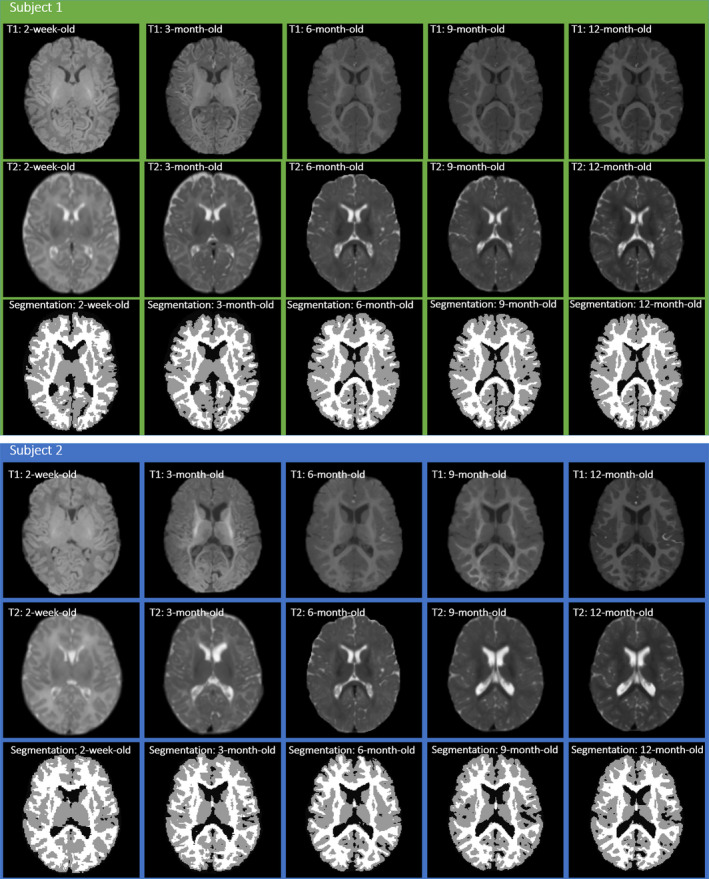
Examples of two infant subjects with images scanned at five time‐points: 2‐week‐old, 3‐month‐old, 6‐month‐old, 9‐month‐old, and 12‐month‐old (from left to right) in each of two subject panels. In each panel, the top, middle and bottom rows show the axial slices of T1‐weighted MRI, T2‐weighted MRI, and the tissue segmentation map, respectively. [Color figure can be viewed at wileyonlinelibrary.com]
Although many registration methods have been proposed for deformable image registration, most of them are developed to align images with similar appearances or structures,6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23 which have limited power to solve the challenging infant brain registration problem. In general, most of the deformable image registration methods fall into the following categories:
Intensity‐based methods. This category of deformable registration methods builds the local image matching based on the image intensities via different similarity measures, e.g., mutual information (MI‐based),13, 14 cross‐correlation (CC‐based),15, 16 and others.17, 24, 25 Large Deformation Diffeomorphic Metric Mapping (LDDMM) algorithm19 uses a steepest gradient descent approach to estimate the velocity field with the time‐dependent diffeomorphic transformation. Demons17 is a popular intensity‐based image registration method, which is widely used in clinical applications. During registration, it performs diffusion process, which iteratively estimates the displacements with the regularization, to obtain the final transformation. However, it cannot be directly applied to infant brain registration, since the intensity relationship between infant brain images scanned at different time‐points are quite variable. Other intensity‐based image registration methods also mainly focus on image intensities or local appearances,13, 14, 15, 16, 17, 18 thus these methods can also hardly handle the deformable registration of infant brain images with such dynamic appearance changes over time.
Feature‐based methods. For feature‐based registration methods, the estimation of deformation field is driven by robust feature matching, instead of simple comparison of image intensities. HAMMER26 is a typical feature‐based registration method, which uses geometric moments for all tissue types as the morphological signature to represent each voxel. Xue et al.27 propose a longitudinal feature‐based registration method by establishing longitudinal spatial correspondences of cerebral cortices for the developing infant brain images. Shi et al.28 further take the advantage of high tissue contrast at later ages for obtaining a subject‐specific tissue probability atlas to guide tissue segmentation at earlier ages, along with iterative bias correction for registration. However, to obtain accurate registration results, the accurate tissue segmentation is necessary for these methods, which is actually also a challenging task for the infant brain MR images.
Learning‐based methods. Csapo et al.29 propose a model‐based image similarity measurement to learn the intensity changes for longitudinal image registration, and obtain better results than the MI‐based registration method. Wang et al.30 propose a sparsity‐learning‐based strategy to tackle the longitudinal registration of infant brain images, by utilizing a sparse learning technique to identify correspondences in the intermediate images at the same age. Wu et al.31 also propose a sparse‐representation‐based image registration method for infant brain images, by learning the growth trajectory from a set of training longitudinal images to guide the registration of two different time‐point images with significant image appearance differences. Kim et al.32 use the spatial intensity growth maps (IGM) to compensate the local appearance inhomogeneity for capturing the expected intensity changes. Cao et al.33, 34 propose to use random forest to eliminate the appearance difference in order to facilitate accurate and effective multimodal image registration. Most of these previous methods rely on the learning of appearance changes, without jointly considering the possible anatomical changes as shown in Fig. 1.
We also develop a learning‐based image registration method35 by employing random forest regression to learn both appearance and shape evolution for the infant brain images, and obtain reasonable deformable registration results. In particular, two random forest regression models are learned separately: (a) appearance–displacement model (AD‐Model), to learn the relationship between local image appearance and its displacement toward the template, (b) appearance–appearance model (AA‐Model), to learn the local appearance changes between any two arbitrary time‐points. However, there are still some limitations of this method: (a) only one imaging modality is used, thus insufficient to steer the complex learning procedure for the cases of large shape and dynamic appearance changes. (b) the displacement vector is independently predicted based on the local patch, while the crucial spatial constraint is ignored, which may lead to geometric issues in the estimated deformation field.
To address two above issues and further improve the accuracy of the learned mapping models, in this paper, we further exploit the learning‐based registration method by proposing the following three novel strategies. (a) We use multimodal MRI, i.e., TI‐weighted and T2‐weighted MRI (with enhanced anatomical details), to learn the AD‐model and AA‐model respectively. (b) We leverage the high‐level context features (i.e., the relative location information) to further improve the prediction of displacements and patch‐wise appearances. (c) We use a multioutput learning strategy to jointly learn both the AD‐model and AA‐model. We validate our method against: (a) MI‐based deformable registration, (b) CC‐based deformable registration, (c) 3D‐HAMMER, and (d) our previous work for infant brain registration. The experimental results demonstrate that our proposed method can obtain higher performance, compared with the state‐of‐the‐art registration methods.
2. Methods
2.A. Overview
Our goal here is to improve the learning‐based registration method35 for registering any infant image S in the first year of life (with possible large age gap) to a predefined template image T, for the cases of either same subject (intrasubject) or different subjects (intersubject). In our proposed method, image registration will be performed in two steps. The first step is the learning of both appearance and displacement models with respective regression forests, for alleviating the shape and appearance variations between infant brain images acquired at different development stages which facilitates the subsequent deformable registration. The second step is using a conventional deformable registration method, e.g., HAMMER, Demons, or other methods, to further estimate the remaining deformations in an effective manner. In the following subsections, we will first briefly describe our previous work of the learning‐based registration method,35 and then introduce our new proposed learning method, i.e., multioutput random forest regression with auto‐context model.
Since there are significant shape and appearance changes for the infant MR images under registration, we leverage the regression forest36, 37, 38 to learn two complex mappings in a patch‐wise manner: (a) Patch‐wise appearance–displacement model. This model characterizes the mapping from the patch‐wise image appearance to the displacement vector of the center voxel of the input image patch; (b) Patch‐wise appearance–appearance model. This model will eventually encode the appearance evolution during early brain development, by learning a complex appearance mapping from the patch‐wise appearance of one brain development stage to the patch‐wise appearance of the template image (i.e., from another early brain development stage). In the application stage, before registering the new infant image to the template, for each voxel in the new infant image, we will first predict its initial displacement to the template by using the learned patch‐wise appearance–displacement model. Then, a dense deformation field will be obtained to initialize the registration of the new infant image to the template. Next, we will further apply the learned patch‐wise appearance–appearance model to predict the template‐like appearance for the new infant image. After that, the appearance difference can be eliminated, and also the large shape variations have been partially handled with the estimated initial deformation field. In this way, many conventional registration methods can be used to refine the final deformation field between the warped new infant image and the template, and eventually obtain accurate registration results.
2.B. Training stage: integration of multioutput random forest regression and auto‐context model
The training dataset includes N groups of infant MR image sequences , which were scanned at 2‐week‐old, 3‐month‐old, 6‐month‐old, 9‐month‐old, and 12‐month‐old (M = 5). Each training group includes both T1‐weighted and T2‐weighted MR images. We obtain the deformation field from each training image to the template by using their tissue segmentation images39 for guiding accurate registration. Since each subject in the training dataset has both structural MRI and DTI scans at 2‐week‐old, 3‐month‐old, 6‐month‐old, and 9‐month‐old and 12‐month‐old, we can obtain its deformation fields by (a) using multimodal longitudinal segmentation method39 to segment images at all time points simultaneously into WM, GM, and CSF and (b) using 4D‐HAMMER registration method40 to estimate temporal deformation fields via segmentation images. In this way, we can regard those estimated deformation fields as the ground truth to evaluate deformation prediction for training the appearance–displacement model. Besides, for each voxel u in the training image , we know its corresponding location in the template image. In this way, the corresponding appearances in each training image and the template image can be used to train the patch‐wise appearance–appearance model. In the following, we will introduce the details of how to train both the patch‐wise appearance–displacement and appearance–appearance regression models, from any time‐point t to the template time‐point t ′(t ≠ t ′).
2.B.1. Patch‐wise appearance–displacement model
(1) Random forest regression (RFR) for appearance–displacement model
The training data are structured by pairs of the randomly sampled local image patch extracted at the location u of the training image and the corresponding image patch extracted at the location of the template T. The local image patch extracted at voxel u of the training image and its displacement vector are used for training the patch‐wise appearance–displacement model. In this paper, random forest regression36, 37 is used to learn the relationship between local image patch and its corresponding displacement vector . Specifically, we calculate two kinds of patch‐wise image features from , including (a) the intensity features, and (b) the 3‐D Haar‐like features. Here, the intensity features include the original intensity values of the image patch, along with the coordinates of the patch center location for providing more spatial information. The 3‐D Haar‐like features are kinds of one‐ and two‐block Haar‐like features, which are obtained by calculating the average intensity at a location of the local patch or the average intensity difference between two locations within the local patch respectively. The mathematical definition of Haar‐like features can be formulated as:41, 42
| (1) |
where is a Haar‐like feature with parameters c 1, s 1, c 2, s 2. c 1 and s 1 are the center and size of the positive block respectively. c 2 and s 2 are the center and size of the negative block respectively. λ ∈ (0, 1) is the controller for one‐ and two‐block Haar‐like features. Particularly, λ = 0 indicates one‐block Haar‐like features, and λ = 1 indicates two‐block Haar‐like features. In addition, these features are extracted in a multiresolution manner. That is, each original image is down‐sampled to cover a wider neighborhood, thus both the global and local information can be included for each sampled voxel.
To learn the appearance–displacement model, multiple regression trees are trained independently using the concept of bagging. In terms of the tree structure, a regression tree comprises of two types of nodes, i.e., split node and leaf nodes. During the tree growth, the split node (including a set of samples) can be split to the left and right subnodes by selecting a feature element f and optimizing its threshold th. Let Θ denotes the split node in a random regression tree, and thus the f and th can be determined by maximizing the information gain (G), as defined below:
| (2) |
where Θ i () denotes the left/right (L/R) subnode of the split node Θ. C i and C denote the number of training samples at the left/right subnode and the number of training samples at the node Θ respectively.
Recent works on both multitask learning43 and multioutput random forest42, 44 show that, using a shared representation simultaneously learn the related tasks could improve the generalization of the learned model. Inspired by these, we incorporate the Jacobian determinant J of the deformation field into the regression output, to constrain the volumetric changes for the learned deformation field. The Jacobian determinant J of the deformation field can be defined as:
| (3) |
where h is the displacement vector at voxel u. Then, Eq. (2) can be calculated for the two targets. σ(Θ) is the variance calculated from all training samples at the node Θ, which can be defined as:
| (4) |
| (5) |
where Z (Θ) is the training set at the node Θ, and is the mean of all training displacement vector samples at the node Θ for displacement vector target as well as the mean of all training Jacobian determinant samples at the node Θ for Jacobian determinant target. By maximizing Eq. (2), all training samples are split into the left and right subnodes with the determined features and threshold. The same splitting process is recursively conducted on the left and right subnodes until the maximal tree depth is reached or the number of training samples falling into one node is less than a predefined number. The node, which is no longer splitting, is regarded as the leaf node. It stores both the mean displacement and the mean Jacobian determinant, which can be used for prediction during the testing stage.
Specifically, both the original deformation field and its Jacobian determinant J will be used as two tasks to help learn the same appearance–displacement model, for better predicting the deformation field.
The respective objective function of multioutput random forest can be formulated as follows:
| (6) |
where f, th are the optimized feature and threshold of current node, w i and is the weight for each task. G i is the information gain of each task by using . For our case of two tasks, G 1 is the information gain obtained by the displacement regression, and G 2 is the information gain obtained by the Jacobian determinant regression. In this paper, we use the same weight for each task (i.e., w 1 = w 2 = 0.5).
(2) Auto‐context model (ACM) for appearance–displacement model
It is obvious that the above‐proposed RFR model learning only uses the low‐level image appearance features. Since the image contrast in the infant brain images is relatively low, some high‐level feature representations are of high necessity to further improve the prediction accuracy of the deformation field. Specifically, we employ the context features that describe the spatial relationship of displacement vectors in the local brain regions. These context features can be extracted from both the prediction displacement vector map and the Jacobian determinant map by using the same manner as extracting features from the intensity image (as shown in Fig. 2, where the intensity features and 3‐D Haar‐like features are extracted from the x, y, z displacement maps and the Jacobian determinant map respectively). Then, we can use these context features as additional features, along with the original appearance features, to train the next layer of RFR for further refining the appearance–displacement model.
Figure 2.
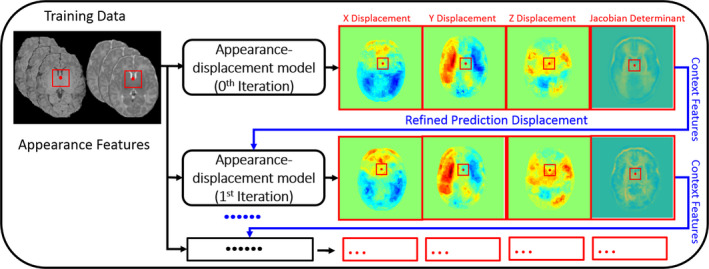
The schematic illustration of using auto‐context model (ACM) in the appearance–displacement model. [Color figure can be viewed at wileyonlinelibrary.com]
Since these high‐level context features are used to refine the RFR, the predicted displacement can be updated (along with the updated context features), as shown in the red box in Fig. 2. By repeating these steps (i.e., re‐calculating the context features and training the new random forest) until convergence, the prediction accuracy can be improved iteratively.
(3) Topology preservation on estimated deformation fields
Since the initial deformation field estimated by the above proposed method is obtained independently for each voxel without regularization, it may contain the regions with violated topology. To address this issue, we enforce topology preservation on the estimated deformation fields when estimating the initial deformation field. Considering the Jacobian constraint can enforce the topology preservation and also smooth a given deformation field, we employ Jacobian constraint to preserve the topology of the deformation field, without removing any important morphologic characteristics.9, 45, 46 The effect of this method is demonstrated in Fig. 3, which shows the histograms of Jacobian determinants of different deformation fields, i.e., (a) the ground‐truth deformation field, (b) the learned deformation field, and (c) the learned deformation field after smoothing with Jacobian constraints. It is apparent to see the effectiveness of the method for topology preservation on estimated deformation fields.
Figure 3.
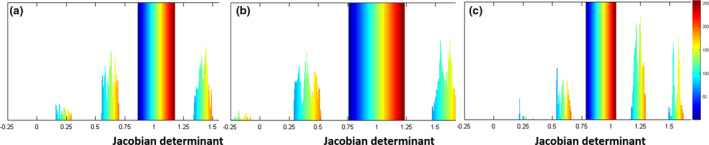
Comparison of histograms of Jacobian determinants from three different deformation fields: (a) the target (ground‐truth) deformation field, (b) the learned deformation field, and (c) the learned deformation field after smoothing under Jacobian constraints. [Color figure can be viewed at wileyonlinelibrary.com]
2.B.2. Patch‐wise appearance–appearance model
(1) Random forest regression (RFR) for appearance–appearance model
Again, similar as the above, the training data are structured by pairs of the randomly sampled local image patch at voxel u of the training image and the corresponding image patch extracted at the corresponding location of the template T. The learning procedure of the patch‐wise appearance–appearance model is the same as the procedure in Section 2.B.1 proposed for learning the patch‐wise appearance–displacement model. It is worth noting that, different from the appearance–displacement model that utilizes the displacement vector and its Jacobian determinant as the regression targets, the regression targets of this appearance–appearance model are the template‐like image patch and its gradient map, where the mean patch intensity and the gradient value will be stored in the leaf nodes of the trained random forest for final prediction, respectively.
(2) Auto‐context model (ACM) for appearance–appearance model
For the appearance–appearance model, it is straightforward to apply the same ACM strategy to enhance the accuracy of the predicted results, by integrating the context features as additional features for refining the patch‐wise appearance–appearance model. Besides using just the template image as a regression task, we further use its gradient map as a second task to jointly learn the appearance–appearance model with the multioutput random forest as also used in Section 2.B.1. Figure 4 shows the use of ACM for learning the appearance–appearance model.
Figure 4.
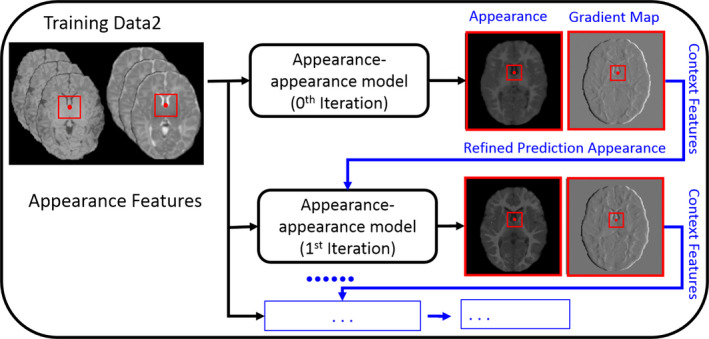
The schematic illustration of using auto‐context model in the appearance–appearance model. [Color figure can be viewed at wileyonlinelibrary.com]
2.C. Application stage
In the application stage, the trained patch‐wise appearance–displacement model will be used to predict the displacement vector for each voxel of a new infant image, while the trained patch‐wise appearance–appearance model will be used to predict the intensity/appearance for each voxel of a new infant image, in order to make its appearances similar to the template image.
Three steps for registering a new infant subject S with the predefined template T, which can be summarized below and also illustrated in Fig. 5.
Figure 5.
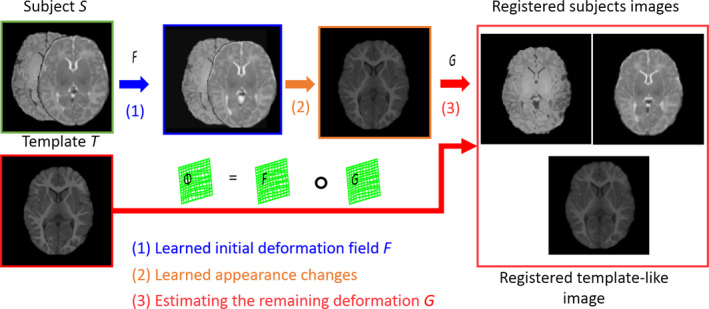
The schematic illustration of the proposed registration process with three steps: (1) Estimating the initial deformation field; (2) Producing the template‐like image and also obtaining the remaining deformation field; (3) Composing the initial deformation field and the estimated remaining deformation field as the final deformation field. [Color figure can be viewed at wileyonlinelibrary.com]
(1) First, we visit each voxel u of a given new infant subject S (u ∈ Ω s ), with S 1 (T1‐weighted) and S 2 (T2‐weighted) images, which have been affine aligned to the template image in the preprocessing stage, and use the learned patch‐wise appearance–displacement model to predict the displacement at the voxel u for generating the dense deformation field defined in the template image space.
(2) Then, the patch‐wise appearance–appearance model is used to predicate a template‐like appearance image after deforming the subject images S 1 and S 2.
(3) Finally, the conventional deformable registration method, i.e., diffeomorphic Demons17 or HAMMER,26 is employed to estimate the remaining deformation G for refining the final deformation filed Φ from the subject image S to the template image T , i.e., by Φ = F ∘ G , where ‘∘’ stands for the deformation composition.47
2.D. Performance evaluation
(1) Dice Similarity Coefficient (DSC). DSC is used to evaluate the registration accuracy, which can be defined as:
| (7) |
For the case of measuring the DSC for the combined WM and GM regions, A and B in Eq. (7) are the voxel sets of the template image and the registered subject images respectively. Besides, we also calculate DSC for the hippocampus after registration. In this case, A and B in Eq. (7) are the hippocampus voxel sets of the template image and the registered subject images respectively.
(2) Peak Signal to Noise Ratio (PSNR). PSNR is also used to quantitatively characterize the predicted displacement and appearance performance, which can be defined as:
| (8) |
where T is the template image, is the registered image, V is the maximal intensity value of the images and , and N v is the number of voxels in each image. The better prediction result should have higher PSNR.
(3) Normalized Mutual Information (NMI). NMI is further used to quantitatively characterize the performance of the displacement and appearance prediction, and can also be used to measure the registration results, which can be defined as:
| (9) |
Where is the learned image, is the mutual information between and T, and is the information entropy. The better prediction and registration results should have higher NMI.
3. Experiments and discussion
3.A. Dataset description and data preprocessing
The experimental dataset consists of totally 24 infant subjects, each of which includes T1‐weighted and T2‐weighted MR images at five time points (i.e., 2‐week‐old, 3‐, 6‐, 9‐ and 12‐month‐old). The size of T1‐weighted images is 256 ×256 × 198 with the resolution of 1 × 1 × 1 mm3 and the size of T2‐weighted images is 256 × 256 × 198 with the resolution of 1.25 × 1.25 × 1.95 mm3. For each subject, the T2‐weighted MR image was linearly aligned to the T1‐weighted MR image at the same acquisition time‐point using FSL's linear registration tool (FLIRT).48 Hippocampal regions were manually segmented for the images of all time‐points of 10 infant subjects.
Since our work mainly focuses on the more challenging intersubject registration with large age gap, for the total 24 subjects, we select one subject as the template. For the remaining 23 subjects, the leave‐one‐out cross‐validation is performed to train the appearance–displacement and appearance–appearance models. Then, the 2‐week‐old, 3‐month‐old, 6‐month‐old and 9‐month‐old of each testing subject are registered to the 12‐month‐old template image.
Each subject in the training dataset has structural MRI as well as DTI (diffusion tensor imaging, which will be used for guiding the tissue segmentation for the training subjects) at the 2‐week‐old, 3‐month‐old, 6‐month‐old, 9‐month‐old, and 12‐month‐old. The image preprocessing includes three steps. (a) Skull‐stripping and bias correction. Skull stripping is performed to remove nonbrain tissues,49 while bias correction50 is performed by a nonparametric nonuniform intensity normalization method to reduce the intensity nonuniformity in the MR images. (b) Affine image registration. Since the brain size increases significantly due to fast brain development in the first year of life, the global affine transformation is performed to handle the global changes, i.e., registering all other time‐point images to the 12‐month‐old image of the same subject. Furthermore, all subjects are affine aligned to the selected template image space by FLIRT in FSL package (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/).51 Since there are dynamic appearance changes in the first year of life, we use mutual information as the similarity metric for affine registration. (c) Image segmentation. Since it is very difficult to segment infant images accurately, especially for the 6‐month‐old images, in the preprocessing stage, we use multimodal MR images (including T1‐weighted MRI, T2‐weighted MRI, and DTI) and longitudinal images for multimodal longitudinal infant image segmentation,39, 52 thus obtaining reasonable tissue segmentation maps of each time‐point for WM, GM, and CSF. Since these segmentation images are without appearance changes, we can estimate the accurate deformation fields by the longitudinal image registration method40 for each training image at every time‐point to the predefined template image T. These estimated deformation fields (based on the segmentation images) are used as the ground truth for both training and validation in our experiments.
3.B. Parameter setting
The input patch size is 7*7*7, where 300 Haar‐like features are extracted. The number of candidate thresholds is 100. Totally, 50 trees are trained for each model, with the tree depth setting to 30. The minimum number of samples in each leaf node is 8 for both appearance–displacement model and appearance–appearance model. In ACM, two iterations are used for each model.
3.C. Comparing the visual registration results
We can visually check the registration results in Fig. 6. The first row shows the same template at different columns. The second row shows the 2‐week‐old, 3‐month‐old, 6‐month‐old, and 9‐month‐old T1‐weight MR images of one subject after preprocessing. Since the T1 MR image has better tissue contrast for 12‐month‐old, we need to estimate the new T1 MR images from the 2‐week‐old, 3‐month‐old, 6‐month‐old, and 9‐month‐old, using their respective T1 and T2 images, and then register all these estimated new T1 MR images to the 12‐month‐old T1 MR image of the template. The 3rd–8th rows show the registration results by SyN (using MI on original images), SyN (using CC on original images), 3D‐HAMMER, our method with no ACM and single output, our method with ACM and single output), and our method with ACM and multioutput respectively. It is apparent that (a) our learning‐based registration method achieves much better registration results than directly using conventional registration method (SyN), (b) the registration performance is further improved by our new proposed learning‐based method, (c) the registration results from 2‐week‐old and 3‐month‐old to 12‐month‐old are not satisfactory, indicating the necessity of further improving the intersubject registration.
Figure 6.
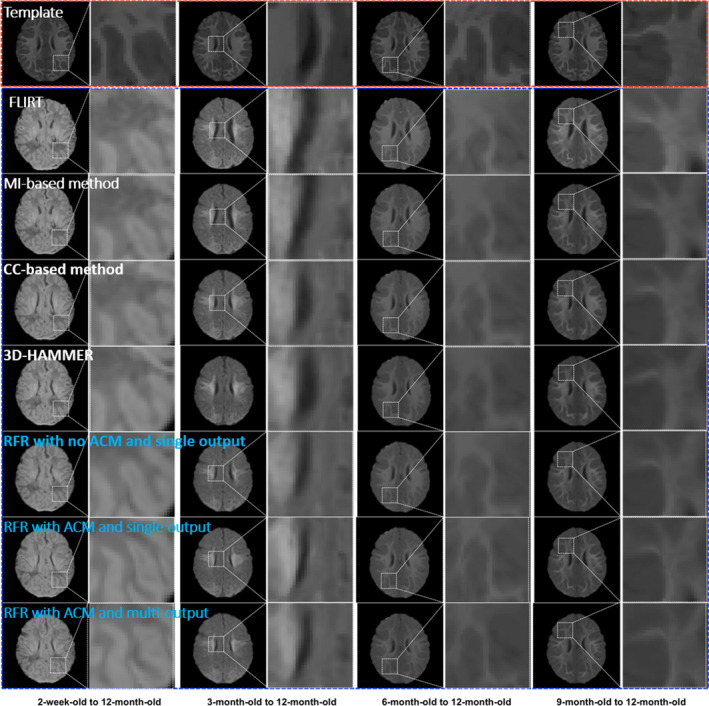
Intersubject registration results on infant brain images. The first row shows the template. The registration results are obtained by directly using FLIRT (2nd row), MI (3rd row), CC (4th row), 3D‐HAMMER (5th row), RFR with no ACM and single output (6th row), RFR with ACM and single output (7th row), and RFR with ACM and multioutput (8th row) respectively. [Color figure can be viewed at wileyonlinelibrary.com]
3.D. Comparing the DSC of combined WM/GM and hippocampus
We compare the registration accuracy of different procedures in our method with several state‐of‐the‐art deformable registration methods. (a) Intensity‐based image registration methods such as SyN, which uses MI14 and CC16 as the similarity measurement. (b) Feature‐based image registration method such as HAMMER.26 (c) Our previous proposed learning‐based image registration method.35, 53 We use DSC as the measurement to evaluate the overlap degree between the registered infant image and the template image. Actually, when we evaluate the registration performance based on tissue segmentation maps, the DSC value of infant brain is always lower than that of adult brain due to the following two reasons. (a) For the infant brain images, the ground truth of gray matter and white matter is often very difficult to obtain accurately, and often has some errors because of fast growth of infant brain in the first year of life. (b) The local shapes of infant brain are also quite variable across different ages of even the same subject. In this way, compared with the registration performance on adult brain images as reported in the literature,20 the absolute DSC value reported here is still acceptable, although it is a little bit lower.
Table 1 shows the mean DSC (with standard deviation) of the combined GM and WM. To further evaluate the registration performance on small brain region, the mean DSC values (with standard deviation) of hippocampus are also provided in Table 2. From these results, we can observe: (a) our proposed learning‐based registration method achieves much better results than directly using either intensity‐based or feature‐based registration method; (b) the registration results are further improved by our extended learning‐based methods. This also demonstrates that the proposed multioutput random forest with ACM‐based refinement can build more accurate and robust appearance–displacement model and appearance–appearance model, which eventually lead to higher registration performance. It is also apparent that our proposed method achieves better overlap ratio, where ‘*’ indicates the statistically significant improvement of our method over the counterpart methods based on the paired t‐test (P < 0.05, two‐tailed).
Table 1.
The mean DSC with standard deviation on the combined WM and GM after intersubject image registration by MI, CC, and 3D‐HAMMER, and three variants of our learning‐based method such as (a) RFR with no ACM and single output, (b) RFR with ACM and single output, and (c) RFR with ACM and multi‐output from the 2‐week‐old, 3‐, 6‐, 9‐month‐old images to the 12‐month‐old image. The best result for each column is shown in bold
| Method | 2‐week‐old to 12‐month‐old | 3‐month‐old to 12‐month‐old | 6‐month‐old to 12‐month‐old | 9‐month‐old to 12‐month‐old |
|---|---|---|---|---|
| MI | 0.614 ± 0.025* | 0.602 ± 0.022* | 0.675 ± 0.030* | 0.717 ± 0.022* |
| CC | 0.643 ± 0.030* | 0.618 ± 0.025* | 0.684 ± 0.024* | 0.722 ± 0.020* |
| 3D‐HAMMER | 0.662 ± 0.023* | 0.642 ± 0.026* | 0.688 ± 0.025* | 0.715 ± 0.023* |
| RFR with no ACM and single output | 0.692 ± 0.035* | 0.684 ± 0.037* | 0.726 ± 0.067* | 0.766 ± 0.033* |
| RFR with ACM and single output | 0.707 ± 0.013* | 0.703 ± 0.018 | 0.731 ± 0.015* | 0.776 ± 0.012* |
| RFR with ACM and multi‐output | 0.710 ± 0.012 | 0.701 ± 0.024 | 0.735 ± 0.026 | 0.780 ± 0.006 |
Table 2.
The mean DSC with standard deviation on the hippocampus after intersubject image registration by MI, CC, 3D‐HAMMER, and three variants of our learning‐based method such as (a) RFR with no ACM and single output, (b) RFR with ACM and single output, and (c) RFR with ACM and multi‐output. The best result for each column is shown in bold
| Method | 2‐week‐old to 12‐month‐old | 3‐month‐old to 12‐month‐old | 6‐month‐old to 12‐month‐old | 9‐month‐old to 12‐month‐old |
|---|---|---|---|---|
| MI | 0.437 ± 0.073* | 0.465 ± 0.072* | 0.569 ± 0.058* | 0.631 ± 0.061* |
| CC | 0.442 ± 0.081* | 0.471 ± 0.078* | 0.573 ± 0.053* | 0.627 ± 0.053* |
| 3D‐HAMMER | 0.461 ± 0.071* | 0.512 ± 0.069* | 0.568 ± 0.062* | 0.621 ± 0.050* |
| RFR with no ACM and single output | 0.480 ± 0.078* | 0.537 ± 0.059* | 0.590 ± 0.050* | 0.628 ± 0.079* |
| RFR with ACM and single output | 0.485 ± 0.086* | 0.543 ± 0.046* | 0.593 ± 0.060* | 0.630 ± 0.071* |
| RFR with ACM and multioutput | 0.488 ± 0.064 | 0.560 ± 0.060 | 0.598 ± 0.063 | 0.633 ± 0.067 |
3.E. Evaluating the contribution of ACM and multioutput regression forest
We further evaluate the contribution of ACM‐based refinement on both appearance–displacement and appearance–appearance models. Figure 7 shows the learned deformation fields by different learning‐based procedures, compared with the ground‐truth deformation field (in the last rectangle), by using different number of iterations (from 0 to 2 iterations in the orange rectangle) for the ACM. It can be observed that, the quality of the learned deformation field is gradually improved as more layers of random forest are trained with additional context features. Note that the final deformation field is obtained by composing the predicted deformation field with the estimated remaining deformation field.
Figure 7.

Demonstration of the contribution of auto‐context model (ACM) in predicting the deformation field. Subject S are the 2‐week‐old with T1‐weighted and T2‐weighted MR images. Template T is the 1‐year‐old with T1‐weighted image. The deformation field in the first three rectangles shows the progress of the predicted deformation field with iteration in ACM. The deformation field in the fourth rectangle shows the composed deformation field by integrating the predicted deformation field with the estimated remaining deformation field. The deformation field in last rectangle shows the ground‐truth deformation field. [Color figure can be viewed at wileyonlinelibrary.com]
The contribution of ACM in predicting appearance changes is demonstrated in Fig. 8. The image in the last rectangle shows the 12‐month‐old template T1‐weighted MR image T. Images in the orange rectangles show the predicted appearance changes using 0 to 2 iterations in ACM, for the 2‐week‐old, 3‐month‐old, 6‐month‐old, and 9‐month‐old images respectively. The learned appearances become more and more similar to the template image (in the right end), as more layers of random forest are trained with additional context features.
Figure 8.
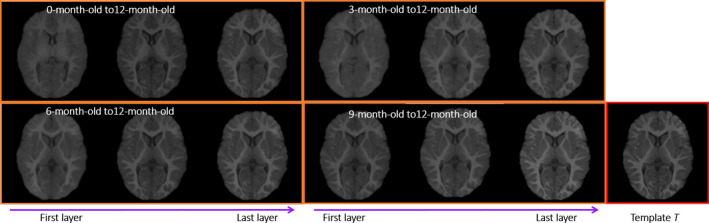
Demonstration of the contribution of ACM in predicting the appearance changes. Subject S is the 2‐week‐old with T1‐weighted and T2‐weighted MR images. Template T is the 1‐year‐old with T1‐weighted MR image. The images in each rectangles show the predicted appearance changes from 0 to 2 iterations in the ACM. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 9 shows both PSNR and NMI values after registration from the 2‐week‐old, 3‐month‐old, 6‐month‐old, and 9‐month‐old images to the 12‐month‐old template, where ‘*’ indicates the statistically significant improvement based on the paired t‐test (P < 0.05, two‐tailed). These results also show the contribution of ACM in our proposed learning models.
Figure 9.
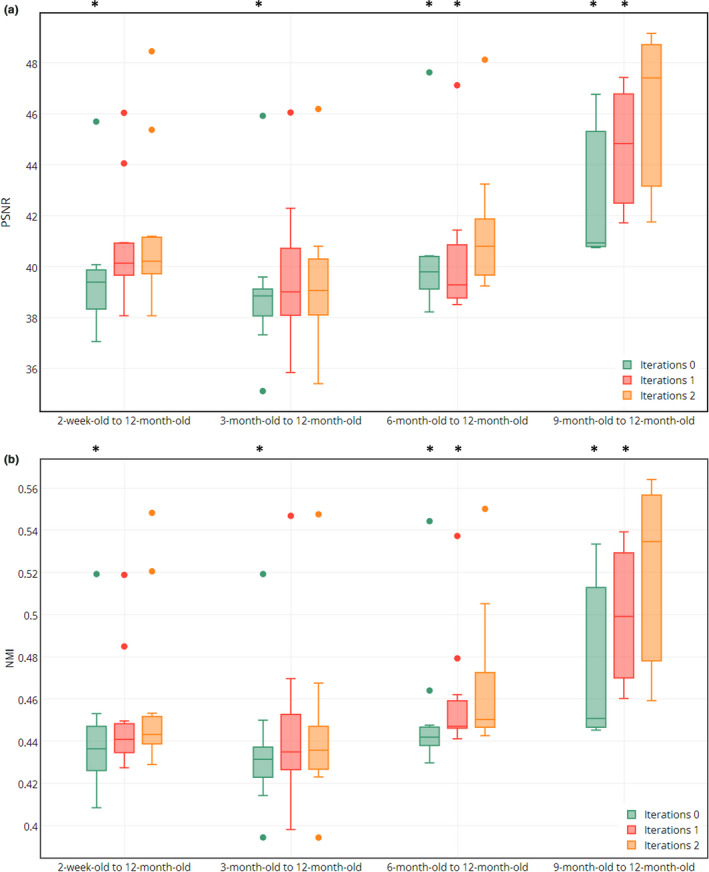
Demonstration of contribution of ACM in our proposed learning models. (a) and (b) show PSNR and NMI values for the results of registering the 2‐week‐old, 3‐month‐old, 6‐month‐old, and 9‐month‐old images to the template, using 0 to 2 iterations in ACM. [Color figure can be viewed at wileyonlinelibrary.com]
All the above experimental results show that the ACM is very useful in building accurate and robust appearance–displacement and appearance–appearance models for guiding accurate registration.
We further evaluate our method by comparing it with other three variants of our method, such as (a) our method without ACM, (b) our method with ACM, and (c) our method with ACM and multioutput, to demonstrate the importance of two proposed strategies, i.e., ACM and multioutput random forest. Figure 10 shows the NMI between the registered images and the template image after registration from the 2‐week‐old, 3‐month‐old, 6‐month‐old, and 9‐month‐old to the template,where ‘*’ indicates the statistically significant improvement based on the paired t‐test (P < 0.05, two‐tailed). Apparently, both ACM and multioutput random forest can further refine the prediction results, reflected by the improved registration accuracy.
Figure 10.
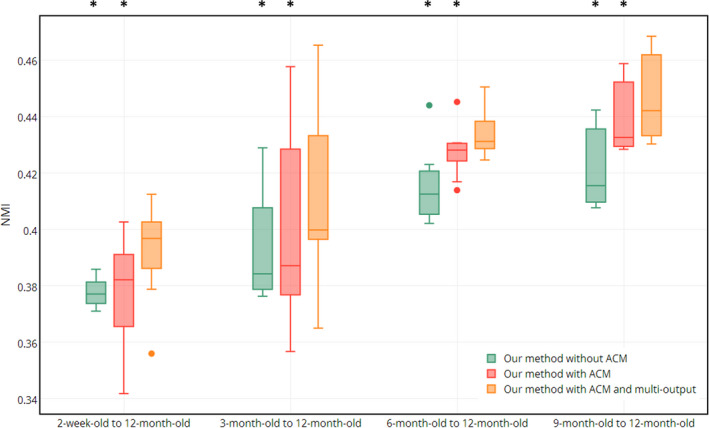
Evaluation of two proposed strategies: ACM and multioutput random forest. Plots of NMI value between the registered images (of 2‐week‐old, 3‐month‐old, 6‐month‐old, and 9‐month‐old) and the template image are provided. [Color figure can be viewed at wileyonlinelibrary.com]
4. Conclusion
We have proposed a new learning‐based registration method to tackle the challenging issues in registering infant brain images acquired from the first year of life, by leveraging the multioutput random forest regression with auto‐context model to learn the evolution of shape and appearance from a training set of longitudinal infant images. Thus, for the new infant image, its deformation field to the template and also its template‐like appearances can be predicted by the learned models. We have extensively compared our method with MI‐based, CC‐based, and 3D‐HAMMER deformable registration methods, as well as multiple variants of our method. Experimental results have shown that our method can achieve higher accuracy even for the difficult cases with large appearance and shape changes between the subject and template images.
In this paper, we utilize random forest regression to train the appearance–displacement and appearance–appearance models for guiding infant MR image registration. This formulation is general and can be implemented with other learning models. In recent years, deep learning algorithms, particularly the Convolutional Neural Network (CNN), have been proven effective in medical images analysis.54 In the future work, we will investigate how the CNN can be used to replace the random forest for training more effective appearance–displacement and appearance–appearance models to guide better registration.
Conflict of interest
The authors have no relevant conflicts of interest to disclose.
Acknowledgments
This research was supported by the grants from China Scholarship Council, National Natural Science Foundation of China (Grant No. 61501120, 61701117), Natural Science Foundation of Fujian Province (Grant No. 2017J01736), and National Institutes of Health (NIH) (MH100217, AG042599, MH070890, EB006733, EB008374, EB009634, NS055754, MH064065, and HD053000).
Co‐first authors.
References
- 1. Ardekani BA, Guckemus S, Bachman A, Hoptman MJ, Wojtaszek M, Nierenberg J. Quantitative comparison of algorithms for inter‐subject registration of 3D volumetric brain MRI scans. J Neurosci Methods. 2005;142:67–76. [DOI] [PubMed] [Google Scholar]
- 2. Feng S, Yap PT, Wei G, Lin W, Gilmore JH, Shen D. Altered structural connectivity in neonates at genetic risk for schizophrenia: a combined study using morphological and white matter networks. NeuroImage. 2012;62:1622–1633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Choe MS, Ortiz‐Mantilla S, Makris N, et al. Regional infant brain development: an MRI‐based morphometric analysis in 3 to 13 month olds. Cereb Cortex. 2013;23:2100–2117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Knickmeyer RC, Gouttard S, Kang CY, et al. A structural MRI study of human brain development from birth to 2 years. J Neurosci. 2008;28:12176–12182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Kapellou O, Counsell SJ, Kennea N, et al. Abnormal cortical development after premature birth shown by altered allometric scaling of brain growth. PLoS Med. 2006;3:e265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Sotiras A, Davatzikos C, Paragios N. Deformable medical image registration: a survey. IEEE Trans Med Imaging. 2013;32:1153–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Klein S, Staring M, Murphy K, Viergever MA, Pluim JP. Elastix: a toolbox for intensity‐based medical image registration. IEEE Trans Med Imaging. 2010;29:196–205. [DOI] [PubMed] [Google Scholar]
- 8. Yang JZ, Shen DG, Davatzikos C, Verma R. Diffusion tensor image registration using tensor geometry and orientation features. Med Image Comput Comput Assist Interv. 2008;5242:905–913. [DOI] [PubMed] [Google Scholar]
- 9. Xue Z, Shen DG, Davatzikos C. Statistical representation of high‐dimensional deformation fields with application to statistically constrained 3D warping. Med Image Anal. 2006;10:740–751. [DOI] [PubMed] [Google Scholar]
- 10. Tang SY, Fan Y, Wu GR, Kim M, Shen DG. RABBIT: rapid alignment of brains by building intermediate templates. NeuroImage. 2009;47:1277–1287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Yap PT, Wu GR, Zhu HT, Lin WL, Shen DG. TIMER: tensor image morphing for elastic registration. NeuroImage. 2009;47:549–563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Klein A, Andersson J, Ardekani BA, et al. Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. NeuroImage. 2009;46:786–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Maes F, Collignon A, Vandermeulen D, Marchal G, Suetens P. Multimodality image registration by maximization of mutual information. IEEE Trans Med Imaging. 1997;16:187–198. [DOI] [PubMed] [Google Scholar]
- 14. Wells WM 3rd, Viola P, Atsumi H, Nakajima S, Kikinis R. Multi‐modal volume registration by maximization of mutual information. Med Image Anal. 1996;1:35–51. [DOI] [PubMed] [Google Scholar]
- 15. Pratt WK. Correlation techniques of image registration. IEEE Trans Aerosp Electron Syst. 1974;Ae10:353–358. [Google Scholar]
- 16. Roche A, Malandain G, Pennec X, Ayache N. The correlation ratio as a new similarity measure for multimodal image registration. Lect Notes Comput Sci. 1998;1496:1115–1124. [Google Scholar]
- 17. Vercauteren T, Pennec X, Perchant A, Ayache N. Diffeomorphic demons: efficient non‐parametric image registration. NeuroImage. 2009;45:S61–S72. [DOI] [PubMed] [Google Scholar]
- 18. Vereauteren T, Pennec X, Perchant A, Ayache N. Non‐parametric diffeomorphic image registration with the demons algorithm. Med Image Comp Comput Assist Interv. 2007;4792:319–326. [DOI] [PubMed] [Google Scholar]
- 19. Beg MF, Miller MI, Trouve A, Younes L. Computing large deformation metric mappings via geodesic flows of diffeomorphisms. Int J Comput Vision. 2005;61:139–157. [Google Scholar]
- 20. Wu G, Jia H, Wang Q, Shen D. SharpMean: groupwise registration guided by sharp mean image and tree‐based registration. NeuroImage. 2011;56:1968–1981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Yang J, Shen D, Davatzikos C, Verma R. Diffusion tensor image registration using tensor geometry and orientation features. Med Image Comput Comput Assist Interv. 2008;11:905–913. [DOI] [PubMed] [Google Scholar]
- 22. Xue Z, Shen D, Davatzikos C. CLASSIC: consistent longitudinal alignment and segmentation for serial image computing. NeuroImage. 2006;30:388–399. [DOI] [PubMed] [Google Scholar]
- 23. Jia H, Yap PT, Shen D. Iterative multi‐atlas‐based multi‐image segmentation with tree‐based registration. NeuroImage. 2012;59:422–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Andersson JLR, Jenkinson M, Smith S. Non‐linear registration, aka spatial normalization. FMRIB Analysis Group of the University of Oxford, FMRIB Technical Report TR07JA2; 2010.
- 25. Flandin G, Friston KJ. Statistical Parametric Mapping. Scholarpedia. 2008;3:6232. [Google Scholar]
- 26. Shen DG, Davatzikos C. HAMMER: hierarchical attribute matching mechanism for elastic registration. IEEE Trans Med Imaging. 2002;21:1421–1439. [DOI] [PubMed] [Google Scholar]
- 27. Xue H, Srinivasan L, Jiang S, et al. Longitudinal cortical registration for developing neonates. Med Image Comput Comput Assist Interv. 2007;10:127–135. [DOI] [PubMed] [Google Scholar]
- 28. Shi F, Fan Y, Tang S, Gilmore JH, Lin W, Shen D. Neonatal brain image segmentation in longitudinal MRI studies. NeuroImage. 2010;49:391–400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Csapo I, Davis B, Shi Y, Sanchez M, Styner M, Niethammer M. Longitudinal image registration with temporally‐dependent image similarity measure. IEEE Trans Med Imaging. 2013;32:1939–1951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Wang Q, Wu GR, Wang L, Shi PF, Lin WL, Shen DG. Sparsity‐learning‐based longitudinal MR image registration for early brain development. Mach Learn Med Imaging. 2014;8679:1–8. [Google Scholar]
- 31. Wu Y, Wu GR, Wang L, et al. Hierarchical and symmetric infant image registration by robust longitudinal‐example‐guided correspondence detection. Med Phys. 2015;42:4174–4189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Kim SH, Fonov VS, Dietrich C, et al. Adaptive prior probability and spatial temporal intensity change estimation for segmentation of the one‐year‐old human brain. J Neurosci Methods. 2013;212:43–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Cao X, Yang J, Gao Y, Guo Y, Wu G, Shen D. Dual‐core steered non‐rigid registration for multi‐modal images via bi‐directional image synthesis. Med Image Anal. 2017;41:18–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Cao X, Gao Y, Yang J, Wu G, Shen D. Learning‐based multimodal image registration for prostate cancer radiation therapy. In: International Conference on Medical Image Computing and Computer‐Assisted Intervention. Springer International Publishing; 2016:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Hu S, Wei L, Gao Y, Guo Y, Wu G, Shen D. Learning‐based deformable image registration for infant MR images in the first year of life. Med Phys. 2017;44:158–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Breiman L. Random forests. Mach Learn. 2001;45:5–32. [Google Scholar]
- 37. Criminisi A, Robertson D, Konukoglu E, et al. Regression forests for efficient anatomy detection and localization in computed tomography scans. Med Image Anal. 2013;17:1293–1303. [DOI] [PubMed] [Google Scholar]
- 38. Criminisi A, Shotton J, Robertson D, Konukoglu E. Regression forests for efficient anatomy detection and localization in CT studies. Med Comput Vis. 2011;6533:106–117. [DOI] [PubMed] [Google Scholar]
- 39. Wang L, Gao Y, Shi F, et al. LINKS: learning‐based multi‐source IntegratioN frameworK for Segmentation of infant brain images. NeuroImage. 2015;108:160–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Shen DG, Davatzikos C. Measuring temporal morphological changes robustly in brain MR images via 4‐dimensional template warping. NeuroImage. 2004;21:1508–1517. [DOI] [PubMed] [Google Scholar]
- 41. Viola P, Jones MJ. Robust real‐time face detection. Int J Comput Vision. 2004;57:137–154. [Google Scholar]
- 42. Gao Y, Shao Y, Lian J, Wang AZ, Chen RC, Shen D. Accurate segmentation of CT male pelvic organs via regression‐based deformable models and multi‐task random forests. IEEE Trans Med Imaging. 2016;35:1532–1543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Caruana R. Multitask learning. Mach Learn. 1997;28:41–75. [Google Scholar]
- 44. Zhao XW, Kim TK, Luo WH. Unified face analysis by iterative multi‐output random forests. 2014 IEEE Conference on Computer Vision and Pattern Recognition (Cvpr); 2014. 10.1109/cvpr.2014.228:1765-1772. [DOI]
- 45. Karacali B, Davatzikos C. Estimating topology preserving and smooth displacement fields. IEEE Trans Med Imaging. 2004;23:868–880. [DOI] [PubMed] [Google Scholar]
- 46. Xue Z, Shen D, Karacali B, Stern J, Rottenberg D, Davatzikos C. Simulating deformations of MR brain images for validation of atlas‐based segmentation and registration algorithms. NeuroImage. 2006;33:855–866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Ashburner J. A fast diffeomorphic image registration algorithm. NeuroImage. 2007;38:95–113. [DOI] [PubMed] [Google Scholar]
- 48. Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM. Fsl. Neuroimage. 2012;62:782–790. [DOI] [PubMed] [Google Scholar]
- 49. Sled JG, Zijdenbos AP, Evans AC. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans Med Imaging. 1998;17:87–97. [DOI] [PubMed] [Google Scholar]
- 50. Shi F, Wang L, Gilmore JH, Lin WL, Shen DG. Learning‐based meta‐algorithm for MRI brain extraction. Med Image Comput Comput Assist Interv. 2011;6893:313–321. [DOI] [PubMed] [Google Scholar]
- 51. Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med Image Anal. 2001;5:143–156. [DOI] [PubMed] [Google Scholar]
- 52. Dai YK, Shi F, Wang L, Wu GR, Shen DG. iBEAT: a toolbox for infant brain magnetic resonance image processing. Neuroinformatics. 2013;11:211–225. [DOI] [PubMed] [Google Scholar]
- 53. Wei L, Hu S, Gao Y, Cao X, Wu G, Shen D. Learning appearance and shape evolution for infant image registration in the first year of life. Machine learning in medical imaging‐Workshop, MLMI with MICCAI; 2016. 36–44. 10.1007/978-3-319-47157-0_5. [DOI]
- 54. Litjens G, Kooi T, Bejnordi BE, et al. A Survey on Deep Learning in Medical Image Analysis; 2017. arXiv:1702.05747. [DOI] [PubMed]


