A state transition framework for patient-level modeling of engagement and retention in HIV care using longitudinal cohort data

Abstract

The HIV care cascade is a conceptual model used to outline the benchmarks that reflects effectiveness of HIV care in the whole HIV care continuum. The models can be used to identify barriers contributing to poor outcomes along each benchmark in the cascade such as disengagement from care or death. Recently the HIV care cascade has been widely applied to monitor progress towards HIV prevention and care goals in an attempt to develop strategies to improve health outcomes along the care continuum. Yet there are challenges in quantifying successes and gaps in HIV care using the cascade models that are partly due to the lack of analytic approaches. The availability of large cohort data presents an opportunity to develop a coherent statistical framework for analysis of the HIV care cascade. Motivated by data from the Academic Model Providing Access to Healthcare (AMPATH), which has provided HIV care to nearly 200,000 individuals in western Kenya since 2001, we developed a state transition framework that can characterize patient-level movements through the multiple stages of the HIV care cascade. We describe how to transform large observational data into an analyzable format. We then illustrate the state transition framework via multistate modeling to quantify dynamics in retention aspects of care. The proposed modeling approach identifies the transition probabilities of moving through each stage in the care cascade. In addition this approach allows regression-based estimation to characterize effects of (time-varying) predictors of within and between state transitions such as retention, disengagement, re-entry into care, transfer-out, and mortality.

1. Introduction

The HIV care cascade (or continuum) is a conceptual model describing key benchmarks that people living with HIV (PLWH) must pass through to maximize benefits of antiviral therapy (ART). In most formulations, the optimal pathway consists of (1) HIV diagnosis through testing, (2) linkage to care, (3) engagement and retention in care, (4) initiation of ART through retention, and (5) sustained suppression of viral load. The conceptual model provides a useful framework for defining and evaluating the benchmarks that measure the effectiveness of HIV care, and for developing strategies to improve HIV outcomes for PLWH [1–4]. The HIV care cascade has become a framework for monitoring progress and identifying HIV care needs in the US since the release of the National HIV/AIDS Strategy in 2010. Furthermore, the HIV care cascade is used globally as a monitoring rubric to evaluate the performance of HIV/AIDS health system management; the World Health Organization (WHO) has emphasized the cascade model as the central assessment metric for HIV care programs [5]. The UNAIDS recently announced a new global target based on steps (1), (4), and (5) in the cascade: by the year 2020, 90 percent of PLWH should be diagnosed and know their status, 90 percent of those diagnosed on antiviral therapy, and 90 percent of those on therapy have viral suppression

Quantitative analyses such as macro level summaries of proportion meeting specific benchmarks, models that examine predictors of engagement in each stage or progression through cascade stages, can provide important information needed to intervene to minimize the negative outcomes and optimize HIV care and treatment efforts to break the cycle of HIV transmission and morbidity. Despite the global acceptance and utility of the HIV care cascade as a conceptual model, our empirical understanding about patient flow through the continuum is still limited, in part because the statistical methods for analyzing cascade data do not have a unified framework. Broadly speaking, there are three main modes of summarizing data related to the care cascade. Macro-level analyses rely on characterizing targeted aspects of the cascade by presenting aggregated data summaries (e.g., number and/or proportion of patients) in each stage of the cascade at certain time points or across time periods [2, 6, 7]. By looking at numbers or proportions of PLWH at each stage, one can readily identify ‘leaks’ or stages where improvements are needed. Risk-factor and regression analyses use individual-level data to identify or evaluate the effect of patient- or program-level factors associated with reaching specific benchmarks such as linkage, retention, and ART initiation [1, 8–11]. For this type of analysis, data are sometimes aggregated across time period to define outcome, or time to event outcomes are considered. A third mode of analysis uses simulation techniques based on an underlying model of progression through the cascade. The mathematical model is specified in advance, and uses inputs from multiple data sources to inform values or ranges of values for the parameters. Parameter values are calibrated using extant data on outcomes of interest, and simulation from the calibrated model are used to obtain predictions of outcomes of interest under different scenarios. This approach has been used to represent complex versions of the cascade and to evaluate impact of different intervention strategies or policies [12–16].

The increasing availability of large-scale patient level cohort data is providing new opportunities for data-driven analyses of the care cascade. For example, the Academic Model Providing Access to Healthcare (AMPATH), based in Eldoret, Kenya, provides HIV and primary care to nearly 200,000 individuals in western Kenya and maintains an electronic health record (EHR) known as the AMPATH Medical Record System (AMRS) [17]. Twice each year, raw data from the AMRS are formatted into a research-grade database that can be used to investigate various clinical and epidemiologic questions related to patient care. Data from the AMRS form a significant component of the NIH-funded International Epidemiology Databases to Evaluate AIDS (IeDEA) for the East African region. The IeDEA consortium, which aggregates patient-level data in multiple regions around the world, contains patient-level data for 1.7 million PLWH globally (iedea.org). Other large-scale cohorts include the CFAR Network of Integrated Clinical Systems (CNICS) [18], EuroCoord [19], Veterans Aging Cohort Study (VACS) [20], to name just a few.

Although the approaches described above are commonly used to analyze cascade data, they do not always take full advantage of the information available in longitudinal patient-level data. Macro-level summaries provide a useful program- or community-level snapshot, but frequently aggregate data over multiple time periods or collapse patient-level longitudinal data into single summaries (such as ‘engaged in care’). This approach can overlook phenomena such as cyclic patient behavior such as coming in and out of care over time [12]. Some regression approaches use only partial longitudinal information, or collapse longitudinal patient data, which precludes examination of or adjustment for important temporal trends such as time, period or cohort effects. Consequently, many analyses reported in the literature tend to capture cross-sectional snapshots of patient behavior [21–26]. Mathematical models, which are more complex, rely on data summaries from different sources of inputs in order to generate simulated outcomes. This raises the question of whether the models represent a specific population of interest. Although mathematical models can handle complexity that cannot be modeled with sparse, micro-level cohort data, the availability of large cohorts of patients with substantial longitudinal information on clinical outcomes presents an opportunity to develop a coherent and portable statistical framework for modeling progression through the care cascade, and for characterizing the role of individual-level factors associated with meeting (or not meeting) key milestones.

However, this ‘big data’ opportunity presents specific challenges: Patient-level cohort data are observational in nature. Data are recorded at irregular time points. Some covariates may be sparsely measured over time, and are often not available from all cohort members. Defining state of care based on raw patient data may not be straightforward, especially for those who have incomplete follow-up or long gaps between clinic visits. These features can make it difficult to even capture a cross-sectional snapshot of the cohort behavior as well as to estimate a temporal trend. These challenges require us to address operationalization of the cascade, data preparation, and specification of the model that can capture the cyclic patient behavior in longitudinal data.

To address some of these challenges, we propose using multistate transition models. We illustrate our approach through analysis of data from 92,215 individuals enrolled in HIV care in AMPATH, the largest HIV care program in Kenya and one of the largest in sub-Saharan Africa. We develop a model for engagement and retention in care, which illustrates many of the key advantages of the multistate modeling approach, such as handling cyclic behavior, modeling time and period effects, and handling competing risks such as death, disengagement, and transfer out of care. The multistate model provides a natural way to incorporate both patient- and program-level covariates and provides a natural framework for extensions that accommodate more states.

The rest of the paper is organized as follows: Section 2 provides details about the AMPATH cohort and provides motivation for adopting the state transition framework. In Section 3, we provide a review of multistate models and make connections to our current application. Section 4 provides details of the model specification for the AMPATH cohort, including how the raw data on engagement in care are translated into discrete states at each time point. Our data analysis appears in Section 5, and a discussion of future directions and potential extensions of the model in Section 6.

2. Data Source and Analysis Goals

AMPATH is a partnership between Moi University College of Health Sciences, Moi Teaching and Referral Hospital in Kenya and a consortium of North American institutions, and has provided HIV care to nearly 200,000 individuals in western Kenya since 2001. Including over 60 HIV/AIDS clinics, AMPATH is one of the largest HIV/AIDS care programs in sub-Saharan Africa. Clinical visit information from individuals who are engaged in medical care within AMPATH is recorded through an electronic medical records database, the AMPATH Medical Record System (AMRS). The AMRS uses an implementation of OpenMRS (wws.openmrs.org), a web-based open source electronic medical record platform that aims to build and manage health systems in the developing countries. Information from AMRS has been used to monitor and evaluate comprehensive intervention and treatment programs in western Kenya [13, 17, 27, 28]

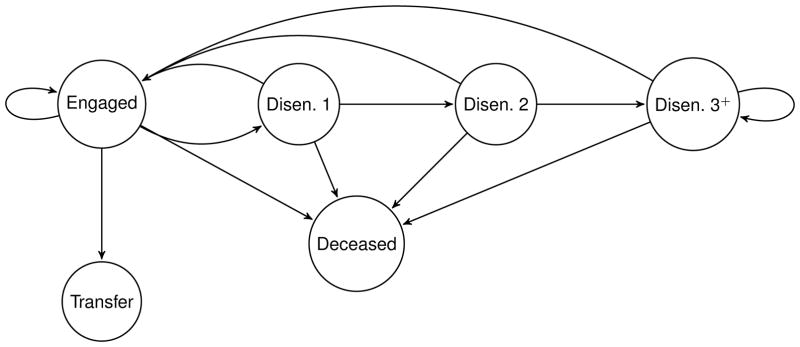
The overall goal of our analysis is to use patient level data to model the part of the HIV care cascade in AMPATH that relates to engagement and retention in care. We utilize a multistate transition model that characterizes individual-level membership in these discrete states as a function of time: engaged in care, disengaged from care, transferred out of care, or deceased. Individuals may pass back and forth between engaged and disengaged, while transferred out and deceased are absorbing states. Duration of disengagement is classified as short, medium or long term, as described below. Figure 1 is a graphical representation of the states and possible transitions.

Figure 1.

The HIV care cascade using AMRS reflecting retention aspect of the cascade in care of AMPATH. At each state, patients are in the following states: Engaged: engaged in care, Disen. 1: disengaged from care for one interval (i.e., disengaged for a short-term), Disen. 2: disengaged from care for two consecutive intervals (i.e., disengaged for a moderate-term), Disen. 3⁺: disengaged from care for more than two consecutive intervals (i.e., disengaged for a long-term), Xfer: transferred-out, and Death: deceased

Given a specific operationalization of the care cascade – or in our case, the process of engagement in care – a key challenge is translation of patient-level data into well-defined stages in the cascade. In the AMPATH data, as with all electronic health records, frequency of observation times are heterogeneous within and between individuals, and key clinical information (e.g., CD4 counts) can be measured sporadically and at irregular times. We use AMPATH patient monitoring guidelines to set equally spaced time intervals to align patient-level data and ascertain membership in each phase over time. In general, AMPATH patients are monitored every 3 months when on ART, and every 6 months if not on ART, so that all patients are expected to re-visit a clinic at six-month intervals regardless of their ART status. We therefore construct a dataset whereby state membership is ascertained and recorded at 200-day intervals following enrollment (every 6 months plus a grace period). Information on time-varying covariates such as CD4 count and treatment status are treated in a similar way. The algorithm used to convert individual patient records into state membership outcomes is described in more detail in Section 4.1.

The multistate model enables several types of summaries and analyses. We can generate summaries of the proportion in each state and rates of transition between states as a function of time for examining temporal trends. The model naturally incorporates the commonly-observed cyclic pattern of temporary disengagement followed by re-engagement in care [29]. State transitions can be modeled as a function of covariates using multinomial regression for repeated measures, enabling examination of the effects of individual- and program-level factors for evaluation and prediction. Treating state membership using multinomial regression has the added advantage of handling competing risks for terminal events such as death and transfer out of care.

Given the focus on engagement and retention, we use ART initiation as a covariate rather than a state to examine its effect on outcomes over time. More broadly, we examine individual-level characteristics such as age, gender, CD4 counts, and calendar year that predict passage from one stage of the cascade to another, illustrating how the model can be used to identify potential factors associated with negative outcomes such as disengagement and death.

3. Multistate process and Markov models

A multistate process is a stochastic process that represents movement through a series of discrete states over time. Let {S(t) : t ≥ 0} be a multistate process with a finite state space 𝒮 = {1, 2, … , L}. Multistate processes can be characterized in terms of probability of transition from state k at time t to state l at time t + u, for u > 0, given by

$$p_{kl}(t,t+u)=\text{pr}\{S(t+u)=l\mid S(t)=k\},k,l\in \mathcal{S},t\ge 0,u>0.$$ (1)

For continuous-time processes, a transition intensity function

$$q_{kl}(t)=\underset{\mathrm{\Delta }t\to 0}{lim}\frac{p_{kl}(t,t+\mathrm{\Delta }t)}{\mathrm{\Delta }t},$$ (2)

describes instantaneous risk of transitioning from state k to l at time t, and can be elaborated by including dependence on covariates or on prior states. For discrete-time processes where the time increment u is a fixed constant, S(t) is observed at times t₀, t₁, t₂, …, where t₀ = 0 and t_j = uj for j = 1, 2, …. We can rewrite (1) in terms of transition probabilities

$$p_{kl}(t_{j^{\prime }},t_j)=\text{pr}(S_j=l\mid S_{j^{\prime }}=k),k,l\in \mathcal{S},t_{j^{\prime }}<t_j,$$

where S_j = S(t_j). Let {X(t) : t ≥ 0} denote a (possibly multivariate) covariate process, and let ℱ_t⁻ denote the accumulated history of S(t) and X(t) up to but not including time t. Some components of X(t) may be time invariant (e.g., baseline covariates and attributes such as gender and age at enrollment). In this article, we will model one-step transitions between states using a discrete-time model having a first-order dependence structure such that

$$\begin{gathered} p_{kl}(t_j,t_{j-1}\mid {\mathcal{F}}_{t^{-}})=\text{pr}(S_j=l\mid S_{j-1}=k,{\mathcal{F}}_{t_j}) \\ =\text{pr}(S_j=l\mid S_{j-1}=k,{\mathbf{X}}_j), \end{gathered}$$ (3)

where, using a slight abuse of notation, ${\mathbf{X}}_j=\mathbf{X}(t_j^{-})$ is the information in X(t) available up to but not including t_j. In words, this assumption implies first-order dependence in state transitions conditionally on covariate information X_j.

An early accounting of large sample theory and inference procedures for multistate models can be found in Albert [30]. Continuous time formulations can also be represented in terms of counting processes; see Kalbfleisch and Lawless [31] and Andersen et al. [32] for a comprehensive treatment. A variety of applications are described in Putter et al. [33] and Therneau and Grambsch [34]. Discrete-time models can be formulated in terms of log-linear models [35], which is closer to the approach we take here.

Multistate transition models have broad application and have been widely applied in biomedical research, particularly for describing disease progression [36–39] and evolution [40]. In HIV/AIDS, they have been used to model disease progression [41–44] and to characterize trajectories of associated markers of progression [45, 46]. Another important application concerns the evolution of antiretroviral drug resistance [47, 48]. Discrete time models also have been used to characterize and predict HIV/AIDS epidemics [49, 50].

Applications of multistate modeling to the HIV care cascade are relatively new but can be expected to increase. For example, Yehia et al. [51] used multinomial models to characterize transitions between states defined in terms of retention in care and viral suppression; however, their analysis considered only one-year transitions during a brief time period. Nosyk et al. [29] use a recurrent event model to characterize retention on antiviral therapy. The emerging importance of the HIV care cascade as a framework for monitoring patient- and program-level outcomes, combined with the increasing availability of large-scale cohort data and data from electronic health records, provides a natural and important opportunity for new applications of multistate modeling. The model presented here is intended to describe a basic framework and to provide a basis for formulating more elaborate and complex statistical approaches to representing the full care cascade.

4. Multistate model for engagement in care

4.1. Defining states

Let i = 1, … , n index individuals in a cohort enrolled at time t = 0 and followed until a fixed date on which the database is closed. Because of staggered enrollment times, the maximum possible follow up time for individual i is $t_i^{\ast }$. Following Figure 2, we discretize the time axis into intervals [0, t₁], (t₁, t₂], (t₂, t₃], … having equal length u = t_j − t_j−1, where t₀ = 0 is enrollment time.

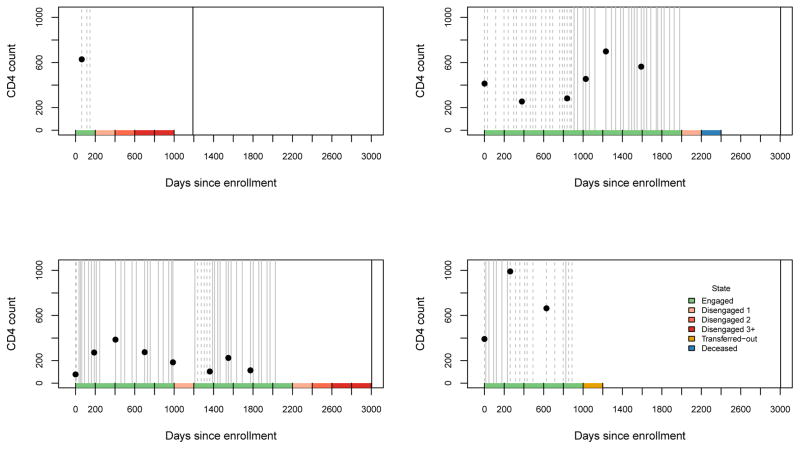
Figure 2.

Example of state ascertainment using data from four individuals in the AMPATH dataset. Grey vertical lines represent patient visits (solid if on treatment, dashed if not). The solid black vertical line is database closure date. CD4 counts are plotted as a function of time (black dot). Color-coded state membership depicted along the bottom of the graph.

Patient-level data related to engagement in care can be represented in terms of three distinct counting processes. For individual i and for t ≥ 0, let $N_i^V(t)$ denote number of visits, and let $N_i^D(t)$ and $N_i^T(t)$ denote zero-one counting processes for death and transfer out of care, respectively. Let $Y_i(t)=I\{t\le t_i^{\ast },N_i^T(t)=N_i^D(t)=0\}$ denote an ‘at-risk’ variable that indicates whether an individual is eligible to return for clinic visits. Information in the counting processes is used to generate a discrete-time multistate process {S_i(t) : t = 0, t₁, t₂, … , t_Ji}, where S_i(t) ∈ {1, 2, … , L} is state membership at time t and $J_i={max}_j\{t_j\le t_i^{\ast }\}$ is the number of intervals (t_j−1, t_j ] such that $t_j\le t_i^{\ast }$. Alternatively we can write {S_ij : j = 0, 1, 2, … , J_i}, where S_ij = S_i(t_j).

For the AMPATH data, counting process information is converted into the discrete-time process as follows:

$$S_{ij}=\{\begin{array}{llll}1\hfill & \text{if}\hfill & Y_i(t_j){\int }_{(t_{j-1},t_j]}d{N}_i^V(u)>0\hfill & (\text{engaged})\hfill \\ 2\hfill & \text{if}\hfill & Y_i(t_j){\int }_{(t_{j-1},t_j]}d{N}_i^V(u)=0\text{and}{S}_{i,j-1}=1\hfill & (\text{disengaged}\text{for}1\text{period})\hfill \\ 3\hfill & \text{if}\hfill & Y_i(t_j){\int }_{(t_{j-1},t_j]}d{N}_i^V(u)=0\text{and}{S}_{i,j-1}=2\hfill & (\text{disengaged}\text{for}2\text{periods})\hfill \\ 4\hfill & \text{if}\hfill & Y_i(t_j){\int }_{(t_{j-1},t_j]}d{N}_i^V(u)=0\text{and}{S}_{i,j-1}\in \{3,4\}\hfill & (\text{disengaged}\text{for}3+\text{periods})\hfill \\ 5\hfill & \text{if}\hfill & N_i^T(t_j)=1\hfill & (\text{transferred}\text{out})\hfill \\ 6\hfill & \text{if}\hfill & N_i^D(t_j)=1\hfill & (\text{deceased})\hfill \end{array}$$ (4)

Put simply, S_ij denotes state membership at the end of interval (t_j−1, t_j ]. All cohort members are engaged at enrollment to care so that S_i0 = 1 for all i. For those with Y_i(t_j) = 1 (not dead or transferred out), S_ij = 1 (engaged) if one or more visits occur within the interval and S_ij = 2, 3, or 4 (disengaged) if not. States 2, 3 and 4 represent durations of disengagement from care, measured in intervals. In principle the number of ‘disengaged’ states can be increased. Preliminary analyses of the AMPATH cohort indicates that the probability of returning to care after 3 or more intervals without a visit is less than .02, motivating our choice to use only 3 categories; in principle, the number of categories can be greater. Note that S_ij = 4 is not an absorbing state: individuals can return to care even after being disengaged for 3 or more intervals.

States 5 (transfer out) and 6 (death) are absorbing states. In the AMPATH EMR, a transfer indicator (yes/no) is available but transfer date is not. Therefore transfer is assumed to occur in the first interval following the most recent engagement in care. For those who died, state membership becomes deceased from the date of death.

Translation of counting processes into discrete-time states is illustrated in Figure 2. Each panel depicts data from a single patient starting from enrollment at t = 0 and extending through database closure (August 24, 2016). Grey vertical lines represent patient visits; at each visit, $d{N}_i^V(t)=1$. State membership is represented along the bottom of Figure 2. Database closure can induce right censoring of the last time interval. In our analysis we assume this administrative censoring is non-informative; hence we do not include information from these incompletely observed intervals.

In addition to information about state of engagement, we assume there is information available on an r-dimensional covariate process {X_ij : j = 0, 1, 2, … , J_i}, where ${\mathbf{X}}_{ij}={\mathbf{X}}_i(t_j^{-})$ is the most recently observed value of X_i(t) at the instant prior to t_j. Referring again to Figure 2, observed CD4 counts are plotted as a function of time, and treatment status is represented using solid or dashed vertical line for each visit. Some of the covariates, such as gender and age at enrollment, are time-independent.

4.2. State transitions

An important quantity describing change over time is the state transition probability p_jkl = pr(S_j = l | S_j−1 = k), which forms the basis of several types of analyses. In the absence of covariates, the collection of transition probabilities can be used to form the L × L transition matrix P_j, where element (k, l) is p_jkl. An annotated version of P_j corresponding to the AMPATH engagement states in (4) is given in Table 2. Note that the sum of each row of P_j is 1.

Table 2.

Annotated transition matrix P_j corresponding to state definitions given in equation (4).

State at tj−1	State at tj
	Engaged	Diseng 1	Diseng 2	Diseng 3+	Transfer-out	Death
Engaged	pj11	pj12	0	0	pj15	pj16
Diseng 1	pj21	0	pj23	0	0	pj26
Diseng 2	pj31	0	0	pj34	0	pj36
Diseng 3+	pj41	0	0	pj44	0	pj46
Transfer-out	0	0	0	0	1	0
Death	0	0	0	0	0	1

From a programmatic point of view, time-specific or aggregated summaries of P_j can be useful in identifying ‘leaks’ in the process of retention in care. Specific elements of the transition matrix can be plotted as a function of time, providing visual representation to identify periods of high risk where unfavorable outcomes such as patient disengagement from care or death are more pronounced. Moreover, under certain assumptions, the transition matrix can be used to estimate marginal probability of state membership as a function of time. To illustrate, let π_jl = pr(S_j = l) and let π_j = (π_j1, π_j2, … , π_jL)^T denote the vector of state membership probabilities at time j. Under the assumption of first-order Markov dependence, and in the absence of covariates, marginal state membership probabilities are calculated as ${\mathit{\pi }}_j={\mathit{\pi }}_1^{\mathrm{T}}{\prod }_{m=2}^j{\mathbf{P}}_m$.

4.3. Regression models for state transitions

In the discrete time domain, state membership S_ij at each time point t_j follows multinomial distribution. Recall that S_ij ∈ {1, … , L}. The general multinomial model can be elaborated as follows to incorporate the effect of covariates on transition dynamics:

$$S_{ij}\mid S_{i,j-1}=k,{\mathbf{X}}_{ij}=\mathbf{x},Y_i(t_{j-1})=1~\text{Mult}\{{\mathbf{p}}_{\mathit{ijk}}(\mathbf{x})\},j=1,\dots ,J_i;k=1,\dots ,L,$$ (5)

where p_ijk(x) = (p_ijk1(x), … , p_ijkL(x))^T is an L-vector having elements p_ijkl(x) = pr(S_ij = l | S_i,j−1 = k, X_ij = x), with ${\sum }_{l=1}^L{p}_{\mathit{ijkl}}(\mathbf{x})=1$. Having absorbing states or order restrictions, as in Table 2, constrains a subset of the transition probabilities to be zero. In practice the domain of k in model (5) is limited to non-absorbing states, a constraint that is easily imposed in practice by conditioning on Y_i(t_j−1) = 1 and restricting sample at t_j to those still in the risk set. Although this model assumes first-order dependence as in (3), more general dependence structures are possible and are discussed further in our data analysis in Section 5.

The specification in (5) lends itself directly to formulation of regression models for longitudinal multinomial data [35, 52]. We adopt the commonly-used loglinear specification that models rate of transition from one state to another relative to a reference state, and captures covariate effects in terms of log relative rate ratios (RRR). Suppressing subscript i, a fully general specification is

$$log\left\{\frac{p_{\mathit{jkl}}({\mathbf{x}}_j)}{p_{jk1}({\mathbf{x}}_j)}\right\}=g_{\mathit{jkl}}({\mathbf{x}}_j)$$ (6)

where, for j = 1, … , max_i{J_i}, k = 1, … , L and l = 2, … , L, the coefficient g_jkl(x) is a function that represents the effect of x_j on log rate of the transition from state k → l relative to k → 1. In practice it will typically be necessary to impose structure on g in order to fit the model, such as assuming g has a known functional form, that the form of g is constant over time, or that g is indexed by a finite-dimensional parameter vector.

Subscripting g_jkl by k implicitly indicates that prior state S_j−1 is part of the regression function, and that regression effects are state-specific. For example, looking at transitions from k = 1 (engaged) at t_j−1 to l = 2 (disengaged) at t_j as a function of a scalar, time invariant covariate x, we can write

$$log\left\{\frac{p_{j12}(x)}{p_{j11}(x)}\right\}=I(S_{j-1}=1)({\alpha }_{j12}+{\beta }_{j12}x),$$

where α_j12 is an intercept term and β_j12 is the log RRR characterizing the effect of x on transition rate p_j12(x) (from engaged to disengaged) relative to rate p_j11(x) (from engaged to engaged). When g is linear in a regression coefficient β, as in this example, the relative risk ratio exp(β) may provide more natural interpretation about the effect of the covariate.

In addition to the effect of clinical or socio-economic covariates on the relative transitions, we can also estimate various types of temporal variations such as time, period, or cohort effects that are often of interest in epidemiologic studies. Briefly, the time effect refers to the effect of follow-up time, the period effect is the effect of calendar time, and the cohort effect represents the effect of enrollment time/date. It is known that these three effects cannot be evaluated simultaneously, even with longitudinal data. However, any two of them can be captured within the regression function by appropriately parameterizing the design matrix. In Section 5, we estimate period effects using a regression spline and time effects using indicator variables for interval number j.

4.4. State membership prediction

Recall that in the absence of covariates, the matrix P_j contains the one-step transition probabilities {p_jkl} as listed in Table 2. Elements of a matrix P_j(x) having covariate-dependent transition probabilities {p_jkl(x)} are calculated via

$$\begin{gathered} p_{jk1}(\mathbf{x})=\frac{1}{1+{\sum }_{m=2}^{L}exp\{g_{\mathit{jkm}}(\mathbf{x})\}},l=1; \\ {p}_{\mathit{jkl}}(\mathbf{x})=\frac{exp\{g_{\mathit{jkl}}(\mathbf{x})\}}{1+{\sum }_{m=2}^{L}exp\{g_{\mathit{jkm}}(\mathbf{x})\}},l=2,\dots ,L. \end{gathered}$$

For settings where covariates are exogenous, marginal state membership probabilities as a function of x_j can be calculated as described in Section 4.2. Specifically, let x̄_j = (x₁, … , x_j) denote the longitudinal history of {x_j}, and let π_j(x̄_j) represent the L × 1 vector of (covariate-specific) marginal state probabilities π_jl(x̄_j) = pr(S_j = l | x̄_j). Then ${\mathit{\pi }}_j({\overline{\mathbf{x}}}_j)={\mathit{\pi }}_1^{\mathrm{T}}({\mathbf{x}}_1){\prod }_{m=2}^j{\mathbf{P}}_m({\mathbf{x}}_m)$. Averaging over the distribution of x̄_j yields predicted distribution across states for the population. When covariates are endogenous, as is the case with CD4 count and similar disease markers, predicting state membership probabilities requires a model for the joint distribution of the covariate and state transition processes.

4.5. Estimation and model diagnostics

The time-specific transition probabilities listed in Table 2 can be estimated using those in the risk set at each time t_j,

$${\widehat{p}}_{\mathit{jkl}}=\frac{{\sum }_i{Y}_i(t_{j-1})I\{S_{ij}=l,S_{ij-1}=k\}}{{\sum }_i{Y}_i(t_{j-1})I\{S_{ij-1}=k\}}$$

Under the assumption of first-order dependence, these can subsequently be used to estimate state membership probabilities as described in Section 4.2.

Estimation and inference about covariate effects requires simplifications of the regression functions g_jkl(x). A natural simplification, which we adopt in our example, is to assume the functional form of g is known, is constant over time, and is indexed by an unknown vector of regression parameters. Specifically, we consider versions of model (6) that can be written as

$$log\left\{\frac{p_{\mathit{jkl}}({\mathbf{x}}_j)}{p_{jk1}({\mathbf{x}}_j)}\right\}={\alpha }_{\mathit{jkl}}+{\mathbf{x}}_j{\mathit{\beta }}_{kl}+h_{kl}(d_j;{\mathit{\gamma }}_{kl})$$ (7)

where, for k → l transitions, α_jkl is a time-specific intercept and β_kl is a vector of regression coefficients having the same dimension as x_j. The term h_kl(d_j ; γ_kl) captures a transition-specific period effect: d_j is calendar date corresponding to interval endpoint t_j (which varies by individual) and each h_kl(·; γ_kl) is a smooth function parameterized by a finite-dimensional parameter γ_kl. In practice h can specified using regression splines or other low-rank smoothing techniques. In our application we specify h using thin plate regression splines [53] and implement estimation using the mgcv package in R. In principle, estimation and inference can be carried out using any statistical software package that fits multinomial regression models.

Consistent estimates of model parameters in (7) can be obtained by using maximum likelihood to fit a multinomial regression to the longitudinal observations, treating them as if they are independent. Consistency in this case requires (i) length of follow up is non-informative in the sense that it is unrelated to state transition rate at each time t_j, conditionally on x_j ; and (ii) the number of individuals increases in such a way that the ratio of individuals to intervals is a constant. This second condition permits estimation of time-specific intercepts even though the number of time points may increase with the number of individuals. Asymptotic normality of the parameter estimates relies on mild regularity conditions in [54] along with some conditions on working covariance structure described in [55]. Estimation of standard errors must acknowledge within-subject correlation. Either robust standard errors [56] or bootstrap resampling (within individuals as the sampling unit) can then be used.

Model fit can be assessed by comparing, at each time j and for those with Y_i(t_j−1) = 1, the observed and predicted proportion in each state (i.e., marginal state membership probability). Chi-square type goodness-of-fit tests applied to large datasets may be prone to generating statistically significant discrepancies; visual comparisons may be more useful for identifying meaningful differences between observed and fitted values. Examples are provided in our analysis of AMPATH data.

Finally, the assumption of first-order Markov dependence is a strong one. As a practical matter, it is may not be feasible to test all possible violations of first-order dependence. However, one straightforward approach — used in our analysis — is to fit model (6) with S_j−2 as a covariate, possibly interacted with elements of X_j, and test for violations of first-order Markov dependence using a Wald test for the added covariates (with standard errors calculated as indicated above).

5. Application to AMPATH Data

5.1. Overview

We illustrate application of the multistate modeling approach using data from AMPATH as described in Section 2. Our analysis uses data on 92,215 HIV infected adults aged 18 years or greater who enrolled in AMPATH supported clinics between June 2008 and August 2016. The time axis originates at enrollment in care (t₀ = 0; baseline). Characteristics at enrollment and data on follow-up information are shown in Table 1. The database closure date is August 24th, 2016, which yields a maximum of max_i{J_i} = 15 intervals for ascertaining state membership.

Table 1.

Baseline (i.e., at enrollment) characteristics of 92,215 HIV infected adults who enrolled in AMPATH between June 2008 and August 2016.

Variable	Number (%)	Median (IQR)
Male	30,900 (33.5)
Age		35 (28, 43)
CD4*		247 (101, 439)
Taking ART	11,791 (12.8%)
Year of enrollment
2008	8,475 (9.2)
2009	16,016 (17.4)
2010	14,922 (16.2)
2011	13,988 (15.2)
2012	11,235 (12.2)
2013	9,177 (10.0)
2014	9,411 (10.2)
2015	8,244 (8.9)
2016	747 (0.8)

^*CD4 was measured and available for 31,535 (34%) patients at the time of enrollment to AMPATH care.

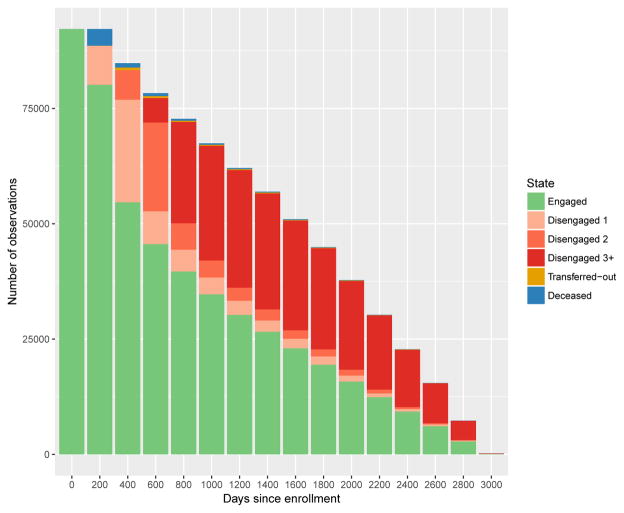
We operationalized the 6-state engagement process as described in Section 2 using intervals of length u = 200 days. We used the mapping in (4) to define, for each individual, state membership S_ij at times {t₀, t₁, t₂, …} = {0, 200, 400, …}. We also incorporated covariate information on age and gender at enrollment, and on CD4 count and treatment status, both of which vary over time. Figure 2 depicts raw data on visit times, treatment status and CD4 count for four different patients, and illustrates how information on visit times (vertical lines) is converted into state membership (color-coded bars along horizontal axis). Figure 3 shows the number of individuals with available data as a function of potential length of follow-up time.

Figure 3.

Number of subjects in each state over time. At baseline, 92,215 unique individual records are available from AMPATH data. Six states are considered: engaged in care, disengaged from care for one interval ( Disengaged 1), 3 = disengaged for two consecutive intervals ( Disengaged 2), 4 = disengaged for more than two consecutive intervals ( Disengaged 3⁺), and 5 = transferred-out, 6=deceased. By definition, all individuals are engaged in care at baseline (day 0).

Our analysis is designed to characterize state transitions appearing in Table 2, and has several components. First, we summarize state transition rates in P_j as a function of time since enrollment and overall (aggregating over time). Next, we use multinomial regression to estimate the effects of age, gender, time-varying CD4 count and time-varying treatment status on state transitions over time. We also use the model to characterize period effects (calendar time) and effect of time since enrollment. Finally, we apply goodness of fit tests and investigate possible violations of the first-order Markov assumption.

5.2. Summarizing state transition rates and temporal trends

Table 3 provides a summary of state transition rates using all data aggregated over time. Entries in the upper left indicate the cyclic nature of engagement in care: among those engaged at a specific time, rate of continued engagement is .85 and rate of disengagement is .13. Among those disengaged for one period of time, about 11 percent return to care.

Table 3.

Mean state probabilities and state transition rates over follow-up period in the transition matrix format. Diseng. 1, Diseng. 2, and Diseng. 3⁺ represents disengaged for a short-term, disengaged for a moderate-term, and disengaged for a long-term state, respectively.

State at tj−1	State at tj
	Engaged	Diseng. 1	Diseng. 2	Diseng. 3+	Transfer-out	Death
Engaged	.85	.13	0	0	.01	.01
Diseng. 1	.11	0	.88	0	0	.01
Diseng. 2	.05	0	0	.94	0	<.01
Diseng. 3+	.02	0	0	.98	0	<.01
Transfer-out	0	0	0	0	1	0
Death	0	0	0	0	0	1

Transitions related to the disengaged states illustrate the deleterious effects of being disengaged in care for more than 200 days. Among those disengaged for a single interval (Disengaged 1), 88 percent will remain disengaged for a second interval (Disengaged 2); subsequent to that, 94 percent will become disengaged for 3 or more intervals (Disengaged 3⁺). Hence, among those who become disengaged for one interval, the probability of remaining disengaged for 3 or more intervals is (.94)(.88) ≈ .83.

Table 3 also indicates that the per-interval mortality rate is slightly over .02 (aggregating values in the last column). It must be noted that mortality estimates are based only on deaths that are confirmed and recorded in the AMRS, and that these estimates have a potentially substantial downward bias [57–59]. Another potential source of mortality rate under-estimation is reporting lag because death registration data is not linked directly to AMRS.

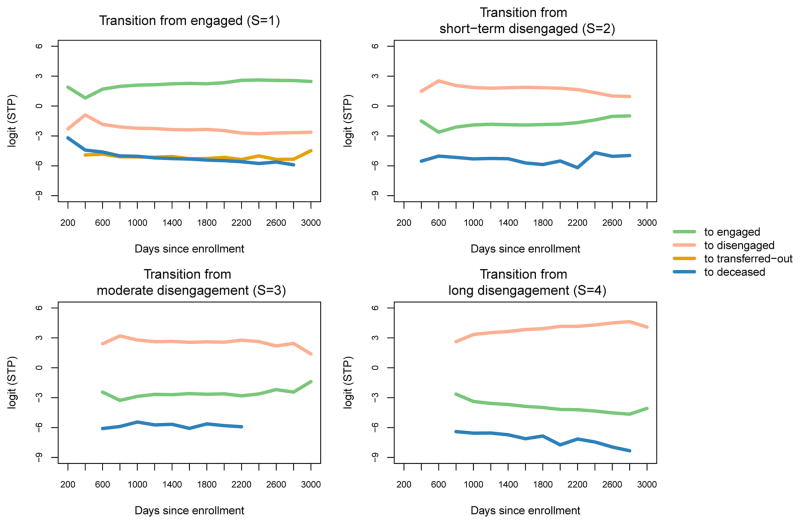
Figure 4 shows temporal trends in the state transition rates, and can be viewed as a visualization of the entries of the transition matrix P_j as a function of interval endpoint times t_j. The plot is rendered in the logit scale to make temporal trends and fluctuations more apparent. The plot of transitions from the engaged state (S = 1) suggest that the most critical period for retention in care is the first interval after enrollment, where we see a sharp decrease in re-engagement following enrollment. Referring to transitions from ‘disengaged 1’ (S = 2, upper right panel), we see that those who are disengaged in this first interval are additionally at higher risk for remaining disengaged in the second interval. Thereafter, retention and re-engagement rates (green lines) tend to remain steady or even increase slightly, except for those who have been disengaged for more than 3 intervals (S = 4, lower right panel). Rates for mortality and transfer-out are relatively low and remain roughly constant over time.

Figure 4.

Temporal trends in (unadjusted) state transition probabilities (STP) calculated at every 200 days. STP are presented in the logit scale to make temporal trends and fluctuations more apparent. All patients started from engagement in care at day 0, and thus no transitions from state 2 to other states were made at day 0. In each title, S=s (s=1,2,3,4) represents prior state membership. Transition to transfer-out was not allowed from state 2,3, and 4.

Overall, plots for transitions from various disengagement status imply that disengaged patients who did not come back in the first to the second follow up years are at high risk of having a long gap to come back for care and ultimately become lost. These plots simultaneously identify when and where the greatest gaps in AMPATH care exist. The gaps are attributable to high continued disengagement rate in the early follow up period, which further leads to a high chance of having a long gap and becoming lost-to-follow-up in the following years.

5.3. Regression modeling

We use a version of the regression model given in (7) for our analysis in this section. Specifically, our model has the form

$$log\left\{\frac{p_{\mathit{jkl}}({\mathbf{x}}_{ij},d_{ij})}{p_{jk1}({\mathbf{x}}_{ij},d_{ij})}\right\}={\alpha }_{\mathit{jkl}}+{\mathbf{x}}_j{\mathit{\beta }}_{kl}+h_{kl}(d_{ij};{\mathit{\gamma }}_{kl}),k=1,\dots ,4;l=2,\dots ,6.$$

The domain of k indicates that only those transitions k → l from states k = 1, … , 4 are being modeled. Further restrictions apply as they relate to modeling transitions from the disengaged state (Table 2); in particular the model only applies to transition rates that are not deterministically 0 or 1. The variable d_ij captures period effect, and represents the number of days elapsed from January 1, 2008 until the (individual-specific) date associated with time t_j. The period effect is captured by the smooth function h_kl, which is specific to each k → l transition but does not vary with enrollment time. As indicated previously, we use thin plate regression splines to specify h_kl.

The covariate matrix X_ij is set up as follows. Let X_i0 = (I{Age_i ≥ 35}, Male_i) denote the 1 × 2 indicator vector for age and gender at baseline (Male_i = 1 if male, 0 if female). We define a 3-level nominal variable for time-varying CD4 count based on the most recently observed value of CD4 as of t_j, and a two-level variable for treatment based on whether or not an individual is on antiretroviral therapy at t_j (1 if yes, 0 if no). The CD4 variable takes value 1 if the most recently observed CD4 count is less than or equal to 350; value 2 if over 350, and value 0 if CD4 has not been measured between t₀ and t_j. We then create a 1 × 5 vector of indicators to reflect the full interaction between these two, using {CD4 < 350,ARV⁻} as the reference category. Appended to X_i0, this generates a 1 × 7 covariate vector X_ij for the risk set {i : Y_i(t_j) = 1} at each time t_j, so that the coefficient vector β_kl has dimension 7 × 1. Table 4 and 5 show the effect of covariates in X_j on state transition probabilities in terms of relative rate ratios (RRR).

Table 4.

Relative risk ratios (RRR) and 95% bootstrapped confidence intervals for effect of covariates on transitions from engaged in care (S_j−1 = 1) to disengaged (S_j = 2), transfer-out (S_j = 5) or death (S_j = 6), relative to remaining engaged in care (S_j = 1); i.e., remaining engaged in care is the reference state.

State at tj−1	Engaged
State at tj	Disengaged	Transfer	Death
Age ≥ 35	.64 (.63, .65)	.57 (.52, .62)	1.14 (1.08, 1.20)
Male	1.09 (1.07, 1.12)	.87 (.79, .95)	1.72 (1.63, 1.81)
CD4 < 350, ARV−	Reference
CD4 < 350, ARV+	.16 (.16, .17)	.29 (.24, .34)	.47 (.44, .51)
CD4 ≥ 350, ARV−	.31 (.30, .32)	.24 (.20, .30)	.11 (.10, .12)
CD4 ≥ 350, ARV+	.12 (.11, .12)	.19 (.16, .23)	.13 (.12, .15)
No CD4, ARV−	1.70 (1.62, 1.77)	1.18 (.90, 1.54)	.90 (.81, 1.00)
No CD4, ARV+	.44 (.42, .46)	.55 (.45, .68)	.53 (.48, .59)

Table 5.

Relative risk ratios (RRR) and 95% bootstrapped confidence intervals for effect of covariates on transitions from disengaged states to continued disengagement or death, relative to remaining engaged in care.

State at tj−1	Disengaged 1		Disengaged 2		Disengaged 3+
State at t	Disengaged 2	Death	Disengaged 3+	Death	Disengaged 3+	Death
Age≥35	.88 (.83, .93)	1.32 (1.01, 1.72)	.95 (.87, 1.04)	1.42 (.95, 2.12)	.96 (.90, 1.03)	1.06 (.75, 1.49)
Male	.93 (.88, .99)	1.30 (1.02, 1.67)	.91 (.83, 1.01)	.96 (.66, 1.41)	.82 (.77, .88)	1.28 (.93, 1.77)
CD4<350, ARV−	Reference		Reference		Reference
CD4<350, ARV+	.27 (.24, .30)	.71 (.49, 1.03)	.31 (.27, .37)	.77 (.44, 1.34)	.24 (.21, .27)	.50 (.33, .75)
CD4≥ 350, ARV−	.54 (.47, .60)	.31 (.18, .52)	.74 (.62, .89)	.27 (.12, .63)	.69 (.60, .79)	.40 (.23, .70)
CD4≥ 350, ARV+	.26 (.23, .29)	.29 (.17, .48)	.30 (.25, .36)	.14 (.06, .35)	.16 (.14, .19)	.10 (.05, .21)
No CD4, ARV−	2.06 (1.74, 2.45)	1.45 (.83, 2.53)	2.05 (1.57, 2.66)	1.40 (.59, 3.35)	1.58 (1.30, 1.93)	.93 (.48, 1.80)
No CD4, ARV+	.40 (.35, .45)	.42 (.24, .71)	.34 (.29, .41)	.42 (.19, .93)	.15 (.13, .17)	.16 (.08, .31)

Table 4 shows covariate effects for transitions from the engaged state (S = 1). To illustrate interpretations, consider the effect of age on transition from engaged to disengaged, for which RRR = .64. The RRR represents a comparison, between those with Age ≥ 35 and Age < 35, of the rate ratio p₁₂/p₁₁, where the transition rate engaged → disengaged is in the numerator and engaged → engaged in the denominator (i.e., transition to engaged is the reference transition). Using a slight abuse of notation, we can see that the RRR is actually a ratio of ratios by writing

$$\text{RRR}(\text{Age}\ge 35:\text{Age}<35)=\frac{p_{12}(\text{Age}\ge 35)/p_{11}(\text{Age}\ge 35)}{p_{12}(\text{Age}<35)/p_{11}(\text{Age}<35)}=\mathrm{.64.}$$

In short, the RRR here indicates that older individuals are less likely to disengage in care, once engaged. Reading across the first row, we see that older individuals also are less likely to transfer from care (RRR = .57) and are at higher risk for mortality (RRR = 1.14), once engaged in care. The gender effect indicates that men are at higher risk for becoming disengaged and for mortality. Note that the RRR for any individual covariate is conditional on other covariates included in the model. Hence the RRR shown in Tables 4 and 5 are conditional on the other covariates listed as well as calendar time.

An examination of the time-varying covariates in Table 4 allows comparison of groups defined by their CD4-treatment profile. Looking first at those with CD4 < 350, we see those on ARV have lower rates of disengagement, transfer and mortality, compared to those not on ARV (the reference group). The effect of treatment within the other CD4 categories can be seen by comparing RRR within category. For example, among those with CD4 ≥ 350, the RRR for becoming disengaged is .12 while on ARV and .31 if not, suggesting lower overall risk of disengagement while on ARV. The effect of ARV is more pronounced if information on CD4 is absent. Though not shown here, confidence intervals for these within-category comparisons can be obtained by changing the reference category or by direct computation from the estimated variance-covariance matrix of the model parameters.

Table 5 summarizes covariate effects for transitions from disengaged states. Among the key findings: (i) once disengaged from care for one interval, men and those over 35 are less likely to remain disengaged (or, more likely to return to care), but the effect dissipates once disengagement lasts for two or more intervals; (ii) within each CD4 category, those on treatment are less likely to remain disengaged and tend to have lower rates of mortality.

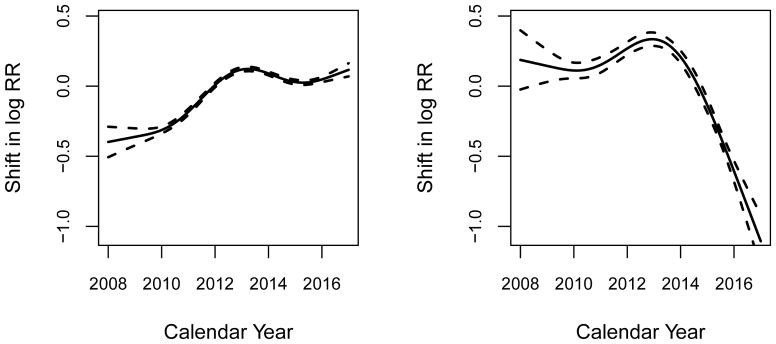
Figure 5 shows estimated calendar-year effects in terms of shifts in log relative risk of disengagement and death among those who are engaged in care. The left panel indicates that rate of disengagement from care increased between 2008 and 2014, but leveled out thereafter; the right panel indicates a substantial reduction in observed mortality starting around 2013. It is possible that these trends are tied to programmatic changes such as the introduction of viral load monitoring in 2014. However attributing the trends to specific causes requires a more comprehensive analysis and the curves should not be over-interpreted. It is likely that the sharp decrease in observed mortality among those engaged in care is at least partially attributable to reporting lags. Similar trends are seen in the period effect for transitions from disengaged state to mortality (not shown). For those effects, incorporating information from contact tracing and double sampling could be used to partially correct this potential bias, as indicated above [57–59].

Figure 5.

Calendar year effects (i.e., period effects) on transition from engaged to disengaged (left panel) and transition from engaged to death (right panel). Splines were used to estimate the smoothed effect of calendar years.

5.4. Model assessment

To assess potential lack of fit, we constructed plots of observed and fitted state membership probabilities for each interval with follow-up data available. Results are presented in Figure 1 in Appendix. With small exceptions, the model shows good agreement with the observed data.

A key assumption in our model is first-order Markov assumption. In our implementation, we assume state membership at t_j depends only on state and covariate information at t_j−1, and conditionally on that information, is independent of observed-data history at or before t_j−2. To assess the effects of potential violations of this assumption, we re-fit the model of transitions from engaged, adding information about S_j−2 as a categorical covariate. We examined a second order dependence for the engagement model only, because disengagement state at t_j is always determined by second order state membership S_j−2. Results shown in Table 1 in Appendix indicate that there is evidence of second order dependence in transitions from engaged to other states. The results imply that those who engaged in two consecutive intervals are less likely to disengage from care, transfer-out, and die, compared to those who missed visits and return to care. However, second order dependence did not change the substance of our findings and the estimated effect of covariates on transition rates are very robust between two multistate models with and without adjusting for S_j−2.

Using second order dependence model, we re-generated the plots of observed and fitted state membership probabilities. Figure 2 in Appendix shows that inclusion of second-order term seems to improve the model fit for early disengagement (day 200 in short disengagement) and transfer-out. Although the impact of second-order term does not seem substantial, it would be important to account for higher order dependence in model for predictive inference about state membership.

6. Discussion

This paper describes the use of a multistate modeling framework for the HIV care cascade. With the growing and widespread availability of large-scale individual-level cohort data, our work addresses the need for statistical modeling approaches that can be used to take full advantage of the rich information about longitudinal individual-level outcomes in these on these large datasets for both programmatic and research purposes [21].

We focus here on the process of engagement and retention in care, and use a discrete-time multistate model of longitudinal transitions between states that characterize engagement, duration of disengagement, transfer out of care, and mortality. State membership is defined at pre-specified interval endpoints that correspond to a maximum expected lag time between visits for individuals engaged in HIV care, where the lag time is set by the user.

The model works on the assumption that care engagement status will be ascertained at discrete points in time, starting from enrollment in care. This confers some advantages: it enables transparent translation of irregular data from electronic health records into an analyzable format; it allows users to apply, with some specialization, statistical software for fitting multinomial models for longitudinal data; it enables prediction, evaluation of covariate effects, and estimation of state membership probabilities at fixed points in time. We have given suggestions on how to translate data on multiple counting processes into a discrete-time state transition process, and illustrated how to use the model by analyzing data from over 90,000 individuals from AMPATH. We have also shown how to use the model to deal with cyclic engagement in care, long-term disengagement, and competing risks of terminal events such as transfer from care and death. With some modification, the model can be extended to handle other categories that are important in the care cascade.

The model does rely on some key assumptions. A basic assumption is first-order Markov dependence. We used it in our example, but we also showed how it can be relaxed. A second assumption is that the expected visit frequency in our definition of ‘engaged in care’ applies to all individuals at all time points, when in reality visit frequencies can be dependent on clinical characteristics and treatment status.

The existing limitations of our model, combined with the broader scope of analytic needs related to the HIV care cascade, point to several potential avenues of further development. First, the definition of ‘engaged in care’ can be elaborated to accommodate expected time of return visit; more generally, a model structure that accommodates patient visits as a continuous-time process can be considered. Both of these extensions would trade simplicity for complexity, and it will be important to understand the potential benefits of increasing model complexity as it pertains to fulfilling the larger analytic goals related to summarizing the cascade.

Second, we are working on models that increase the number of states needs to be expanded to accommodate the important benchmarks related to initiating antiviral treatment and having viral load suppression. AMPATH has recently instituted annual viral load monitoring for most of its clients, which makes this extension more practically feasible. Third, as most data on the care cascade is observational, there is a need to develop a framework for causal inference or, more generally, handling exogenous covariates. We are currently working on using inverse probability weighting and g estimation, which build naturally on the longitudinal regression framework, to assess causal effects for key cascade-related outcomes. In addition, we are working on incorporating variable selection tools.

Fourth, variable selection and the ability to handle more covariates is clearly important. Data from cohort studies typically collect comprehensive information about risk factors, diagnosis, and lab test results. We are working to incorporate formal approaches to variable selection to allow users to identify specific determinants of transition dynamics along the care cascade, and thereby make better use of existing resources for interventions.

Finally, misclassification of deaths and other outcomes is a common problem in state membership ascertainment. Incorporation of data from contact tracing and double sampling can lead to significant improvements in estimation. A major priority in the next step of model development is incorporation of external information derived by tracing those who are disengaged for an extended period of time.

7. Appendix

Appendix contains supplementary figures for Section 4 of the main text.