Computational Insights into an Enzyme-Catalyzed [4+2] Cycloaddition

Abstract

The enzyme SpnF, involved in the biosynthesis of spinosyn A, catalyzes a formal [4+2] cycloaddition of a 22-membered macrolactone, which may proceed as a concerted [4+2] Diels–Alder reaction or a stepwise [6+4] cycloaddition followed by a Cope rearrangement. Quantum mechanics/molecular mechanics (QM/MM) calculations combined with free energy simulations show that the Diels–Alder pathway is favored in the enzyme environment. OM2/CHARMM free energy simulations for the SpnF-catalyzed reaction predict a free energy barrier of 22 kcal/mol for the concerted Diels–Alder process and provide no evidence of a competitive stepwise pathway. Compared with the gas phase, the enzyme lowers the Diels–Alder barrier significantly, consistent with experimental observations. Inspection of the optimized geometries indicates that the enzyme may prearrange the substrate within the active site to accelerate the [4+2] cycloaddition and impede the [6+4] cycloaddition through interactions with active-site residues. Judging from partial charge analysis, we find that the hydrogen bond between the Thr196 residue of SpnF and the substrate C15 carbonyl group contributes to the enhancement of the rate of the Diels–Alder reaction. QM/MM simulations show that the substrate can easily adopt a reactive conformation in the active site of SpnF because interconversion between the C5–C6 s-trans and s-cis conformers is facile. Our QM/MM study suggests that the enzyme SpnF does behave as a Diels-Alderase.

Introduction

The Diels–Alder reaction between a 1,3-diene and alkene is a [4+2] cycloaddition reaction, in which a cyclohexene ring is formed in a concerted manner.¹ This reaction is particularly useful for the construction of cyclic products with good control over regio- and stereoselectivity, and it has thus been considered as one of the most important reactions in organic synthesis.² It has been applied extensively to the synthesis of complex pharmaceutical and biologically active compounds.^3,4 Despite the prominence of the Diels–Alder reaction in modern synthetic chemistry, the question of whether biosynthetic enzymes have evolved to catalyze this reaction is still open.

Research on secondary metabolism has led to the discovery of numerous natural products that contain one or more cyclohexene rings that are commonly generated via a Diels–Alder reaction in organic synthesis.³ However, the presence of a cyclohexene moiety with a defined stereochemical configuration in natural products is no unambiguous proof of biocatalysis by a Diels-Alderase, because [4+2] cycloadditions may also occur in the absence of a catalyst or may even proceed stepwise via dipolar or diradical intermediates.⁵ While it has not yet been unequivocally established whether true Diels-Alderases exist in nature, there are several enzymes that catalyze biotransformations that may involve a Diels–Alder process. We briefly summarize the available evidence.

Solanapyrone synthase of the fungus Alternaria solani was found to show activity for the formation of (−)-solanapyrone A from achiral prosolanapyrone II, which led to the claim that it is the first example of a natural Diels-Alderase.⁶⁻⁹ Lovastatin nonaketide synthase was reported to catalyze a Diels–Alder cycloaddition at the hexaketide stage to form the fused rings of the decalin system of dihydromonation L during polyketide chain elongation.^10,11 Riboflavin synthase mediates the final step in the biosynthesis of riboflavin, which involves the transfer of a four-carbon fragment between two molecules of the substrate 6,7-dimethyl-8-ribityllumazine, leading to the formation of riboflavin and 5-amino-6-ribitylamino-2,4(1H,3H)-pyrimidinedione.^12,13

Macrophomate synthase (MPS) catalyzes an unusual multistep reaction cascade involving a cyclization between 2-pyrone and oxaloacetate to form macrophomic acid in the fungus Macrophoma commelinae.¹⁴⁻¹⁷ The protein X-ray structure of MPS¹⁵ enabled theoretical research on the detailed mechanism of MPS catalysis, which indicated that the alternate route of a stepwise Michael aldol reaction is preferred over the Diels–Alder cyclization because it is energetically more favorable in the MPS active site.¹⁶ Later, there was additional experimental support for the second half of the proposed stepwise Michael–aldol mechanism.¹⁷ The biosynthesis of pyrroindomycins, pentacyclic spirotetramate natural products first isolated from Streptomyces rugosporus,¹⁸ was found to involve an enzymatic [4+2] cyclization cascade that forms the rigid pentacyclic core in a regio- and stereoselective manner;¹⁹ the crystal structure of the PyrI4 enzyme involved in this cascade was recently determined.²⁰ The key enantiodivergent step in the biosynthesis of stephacidin and notoamide natural products is believed to be an intermolecular Diels–Alder cycloaddition of an achiral azadiene.²¹ In the final step of thiazolyl peptide biosynthesis, a single enzyme (TclM) was found to catalyze the formation of the trisubstituted pyridine core, through a formal [4+2] cycloaddition between dihydroalanine residues.²² The biosynthesis of versipelostatin (VST) was shown to involve an enzyme-catalyzed stereoselective [4+2] cycloaddition that generates the spirotetronate skeleton of VST.²³ A recent experimental and theoretical study using enzyme assays, X-ray crystal structures, and simulations provided strong evidence that the spirotetronate cyclase AbyU catalyzes a transannular Diels–Alder reaction on the abyssomicin C biosynthetic pathway.²⁴

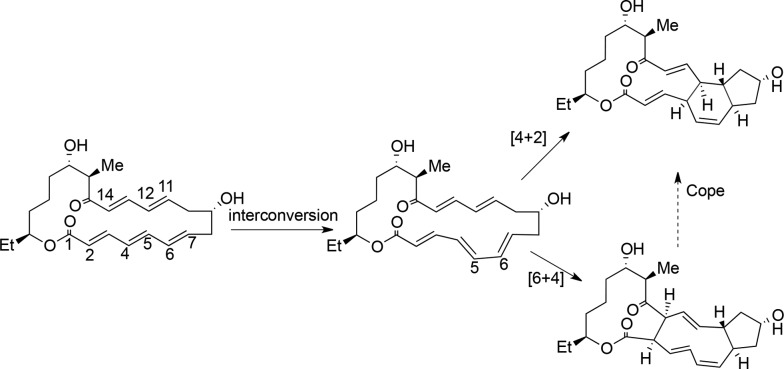
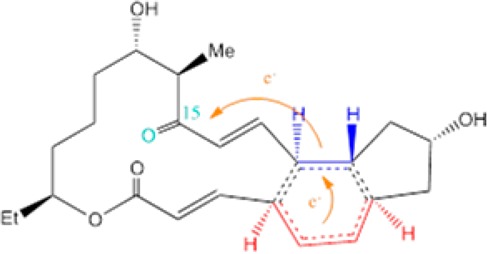
Another recent example of a natural Diels-Alderase was reported in the biosynthesis of spinosyn A by the actinomycete bacterium Saccharopolyspora spinosa.^25,26 This work identified a cyclase, SpnF, which catalyzes a transannular [4+2] cycloaddition on a 22-membered macrolactone to forge an embedded cyclohexene ring.²⁵ Kinetic analysis yielded an estimated 500-fold rate enhancement (k_cat/k_non) in the SpnF-catalyzed cycloaddition. As SpnF acts as a stand-alone enzyme, its monofunctionality and specificity for catalyzing the cycloaddition make it a particularly relevant case among the reported putative Diels-Alderases. Density functional theory (DFT) studies of model substrates related to spinosyn A suggest a concerted, highly asynchronous Diels–Alder mechanism for the chosen lactone.²⁷ However, molecular dynamics (MD) investigations at the DFT level indicate that the transition state of the model substrate for the reaction is ambimodal and may lead directly to both the observed Diels–Alder adduct and an unobserved [6+4] cycloadduct, which can be converted into the observed [4+2] adduct through a rapid Cope rearrangement; the latter mechanism is called bis-pericyclic (Scheme 1).²⁸ A very recent detailed DFT study concludes that both routes may coexist in water, with the bis-pericyclic one being dominant (83% vs 17% via Diels–Alder).²⁹ On the experimental side, Liu and co-workers recently determined the 1.50 Å resolution crystal structure [Protein Data Bank (PDB) entry 4PNE] of SpnF bound to S-adenosylhomocysteine (SAH) and a molecule of malonate;²⁶ this sets the stage for computational studies of the entire enzyme that aim to verify SpnF as a bona fide Diels-Alderase.

Scheme 1. Proposed Cycloaddition Mechanism in the Biosynthesis of Spinosyn A.

If it is confirmed to be a Diels-Alderase, SpnF can be used to gain insight into the biocatalysis of Diels–Alder reactions. A rate enhancement by an enzyme may be achieved through electrostatic effects³⁰ or substrate geometry “prearrangement” within the active site through hydrophobic and hydrophilic interactions^4,31 or a combination of both factors. Frontier molecular orbital theory has commonly been used to describe and understand Diels–Alder reactions in qualitative terms. The highest occupied molecular orbital (HOMO) of the diene interacts with the lowest occupied molecular orbital (LUMO) of the dienophile to form two new bonds. The reaction is facilitated by increasing the nucleophility of the diene and/or the electrophilicity of the dienophile, which decreases the HOMO–LUMO gap. Hydrogen bonding between substrate and enzyme residues may also modulate the HOMO and LUMO energies.³² In SpnF, Thr196 may form a hydrogen bond to the C15 ketone, which could render the reacting double bond more electron deficient and thus accelerate the cycloaddition.^26,31 A detailed understanding of how SpnF catalyzes the reaction may enhance biosynthetic strategies and guide the production of designer metabolites.

In this work, we combine quantum mechanics/molecular mechanics (QM/MM)^33,34 computations with MD simulations and free energy calculations³⁵⁻³⁷ to study the cycloaddition in the active site of SpnF. The aims are to determine the preferred mechanism for this enzyme-catalyzed cycloaddition and to analyze the role of the enzyme SpnF in this reaction.

Computational Details

System Setup

Initial coordinates were taken from the 1.50 Å resolution crystal structure of SpnF from Saccharopolyspora spinosa (PDB entry 4PNE),²⁶ which contains two monomers in the asymmetric unit within space group P2₁. Monomer B was selected for our computational study, because there are fewer residues missing than in monomer A. The slight difference in the pitch of helix αG of the two monomers is expected to be irrelevant. The malonate in the crystal structure was replaced by the substrate because both are anticipated to bind in the same cavity.²⁶ The substrate structure was extracted from the crystal structure of spinosyn A³⁸ and fully optimized at the DFT level. We considered four possible conformers SUB-x (x = a1, a2, b1, and b2) for the substrate (see Figure 1), which differ in the conformations at C5–C6/C1–O22: s-trans/s-trans for SUB-a1, s-cis/s-trans for SUB-a2, s-trans/s-cis for SUB-b1, and s-cis/s-cis for SUB-b2. SpnF adopts the fold of S-adenosylmethionine-dependent methyltransferases (MTs). Substrate docking via AutoDock Vina³⁹ (see the Supporting Information for details) indicates that SAH does not make any direct contact with any of the substrate conformers or products. For the docking of substrate conformers SUB-x (x = a1, a2, b1, and b2) into the active site of SpnF, at least 10 poses of the substrate were scored and ranked by the program according to the calculated interaction affinity. The orientation shown in Figure S1 was favored for all four substrates after docking and minimization with the CHARMM force field. This is chemically reasonable and consistent with the docking modes obtained previously.²⁶

Figure 1.

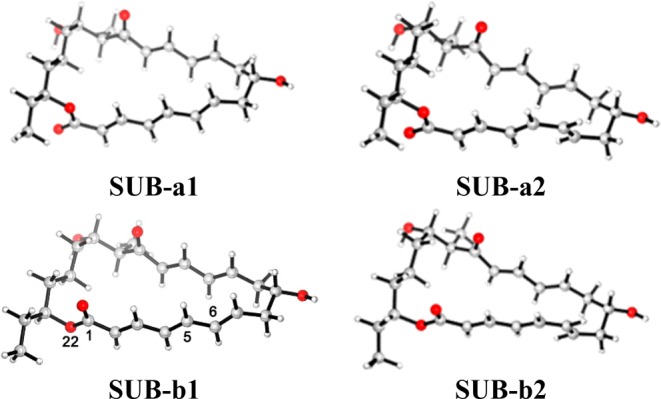
Four substrate conformers considered in this work, with definition of the atom labels used in the text.

The protonation states of the titratable residues in the enzyme (such as His, Glu, and Asp) were determined at pH 8 by the PROPKA procedure⁴⁰ and then verified by visual inspection. Thereafter, the whole enzyme was solvated in a water ball with a 50 Å radius centered at the SpnF center of mass. The total charge of the resulting system was −13 e. To neutralize the negative charge and to establish a proper salt concentration (50 mM), Na⁺ and Cl^– ions were added by random substitution of solvent water molecules lying at least 5.5 Å from any protein atom. The resulting system contained 20598 atoms.

In the next step, this system was relaxed via energy minimization and MD simulations at the MM level using the CHARMM22 force field⁴¹ as implemented within the CHARMM program.⁴² During MD simulations, the NVT ensemble was employed and a potential was imposed on the water sphere to prevent the outside solvent water molecules from drifting away into the vacuum, and the whole system was allowed to move freely except for the substrate, which was kept fixed after docking.

QM/MM Model

A snapshot from the classical MD trajectory was used as the starting point for further QM/MM calculations. The QM part was treated by the semiempirical method OM2⁴³⁻⁴⁵ and the DFT(B3LYP) approach, while the MM part was described by the CHARMM22 force field. Empirical dispersion corrections⁴⁶ were applied for the B3LYP method (B3LYP-D3) to improve the description of weak interactions. The covalent bonds cut at the QM/MM border were saturated by hydrogen link atoms, and the coupling between the QM and MM regions was handled by the electrostatic embedding model⁴⁷ using the charge shift scheme.⁴⁸ The QM/MM calculations were performed with the ChemShell package.^49,50 The energy and gradient for the QM part were obtained from the Gaussian program,⁵¹ and those for the MM part were computed by the DL_POLY program.⁵² The chosen QM/MM methodology is analogous to that used in previous studies by our group.³⁴ QM/MM dynamics runs were performed with the dynamics module of ChemShell. The MD simulations employed the NVT ensemble with a Nosé-Hoover thermostat.^53,54 The SHAKE procedure⁵⁵ was applied for the O–H bonds in water molecules.

In the QM(B3LYP-D3/TZVP)/CHARMM geometry optimizations, the QM region consisted of the substrate and the hydrogen-bonded residues Met22, Hsd42, Gln148, Thr196, and Trp256. The optimized QM region in the reactant complex is shown in Figure 2, featuring hydrogen bonds between the C1=O group and Trp256, the C9–OH group and Met22, the C15=O group and Thr196, and the C17–OH group and Hsd42 and Gln148. In the optimizations, the active region included all the QM atoms and all residues and water molecules of the MM region within 10 Å of the C15 atom of the substrate (Figure 3), which covers all enzyme residues around the binding pocket; all other atomic coordinates were frozen.

Figure 2.

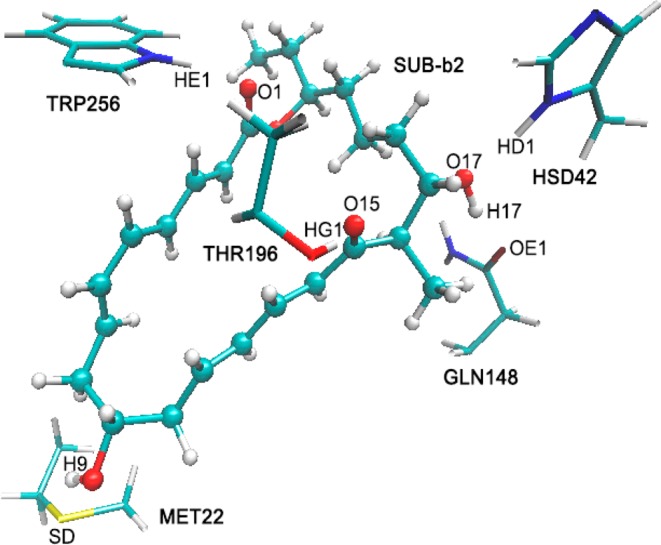
Enzyme–reactant complex (QM region only) optimized at the QM(B3LYP-D3/TZVP)/CHARMM level with residue names.

Figure 3.

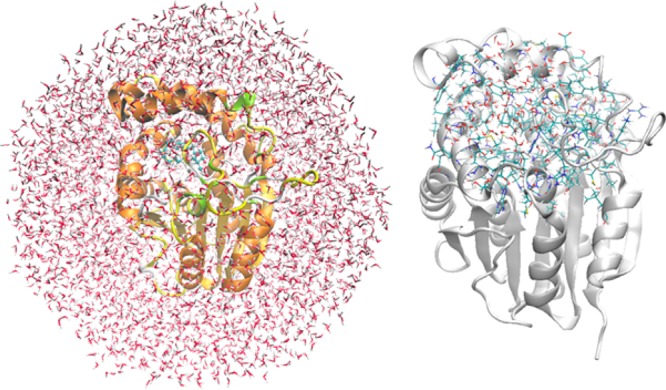
System for QM/MM calculations (left) and optimized active region (right) (the frozen part of the enzyme is shown as a “cartoon” view with a gray background).

Free Energy Calculations

To determine the minimum free energy path, we employed umbrella sampling simulations and the finite-temperature string method.⁵⁶ The initial string connecting reactant and product states is defined as an M-dimensional curve [s₀(ξ) = f₀¹(ξ), ..., f₀(ξ)]. The string is parametrized by its reduced length ξ (0 ≤ ξ ≤ 1), with distances defined by the arc length using a Euclidian metric in the space of the collective coordinates. The function f₀ⁱ(ξ) represents the value of the ith collective coordinate, with f₀(0) and f₀ⁱ(1) corresponding to the reactant and product states, respectively. Umbrella sampling was performed for each image, with harmonic restraints centered at s₀(ξ_i) for each of the M reaction coordinates. Restraining potentials with force constants of 100 kcal mol^–1 Å^–2 were applied during the umbrella sampling simulations. For both mechanisms considered, 30 images along the reaction pathway were chosen, and 1 ps OM2/CHARMM MD simulations were run with the standard QM region (see above). Thereafter, the string was updated by fitting high-order polynomials to the average collective coordinates of each image and then divided again into N segments of equal arc length to obtain new centers of the restraining potentials for the next round of umbrella sampling simulations. The string was considered to be converged when the root-mean-square deviation (RMSD) between all coordinates of the latest string and their mean values of the previous 10 interactions fell below a threshold of 0.1 Å. The total simulation time for the [4+2] cycloaddition was 21 ps. Finally, the results were unbiased using the multidimensional weighted histogram analysis method (WHAM)⁵⁷ with a convergence threshold of 0.001 kcal/mol.

Results and Discussion

Substrate Conformations

The C5–C6 s-trans conformation of the substrate is known to be most stable in the gas phase,⁵⁸ whereas the C5–C6 s-cis conformation is required for the cycloaddition. In addition, the energy of the enzyme–substrate complex is found to be strongly dependent on the conformation around the C1–O22 bond. Therefore, we decided to study the stability of the four corresponding substrate conformers (see Figure 1) in the active site of SpnF. The computed relative energies are listed in Table 1. In the gas phase, the conformers with a C1–O22 s-cis orientation are less stable than their s-trans counterparts (see SUB-a1 vs SUB-b1 and SUB-a2 vs SUB-b2). The opposite is true when the substrate is placed in the active site of the SpnF enzyme (Table 1). This may be traced back to stronger hydrogen bonding: for example, the hydrogen bond of the C1=O group with Trp256 in SUB-b2 (1.81 Å) is much shorter than that of the C1–O22 group in SUB-a2 [2.39 Å (see Figure S3)]. Hence, the C1–O22 s-cis conformation is favored in the pocket of SpnF.

Table 1. Relative Energies (kilocalories per mole) at Optimized QM or QM/MM Geometries.

	SUB-a1	SUB-a2	SUB-b1	SUB-b2
C5–C6/C1–O22 conformation	trans/trans	cis/trans	trans/cis	cis/cis
Gas Phase, QM Energy
B3LYP-D3/TZVP	0.0	4.2	3.8	6.8
Enzyme, QM/MM Energy
OM2/CHARMM	0.0	3.7	–13.0	–14.0
DFT(B3LYP-D3/SVP)/CHARMM	0.0	10.3	–10.2	–10.4
DFT(B3LYP-D3/TZVP)/CHARMM	0.0	11.8	–8.4	–8.2

With regard to the C5–C6 conformation, the s-trans form is confirmed to be more stable than the s-cis form in the gas phase. This remains true when the substrate is bound in the active site of SpnF with the C1–O22 s-trans conformation (see SUB-a1 vs SUB-a2). However, both C5–C6 conformers are close in energy in the enzyme when the substrate adopts the more stable C1–O22 s-cis conformation (see SUB-b1 vs SUB-b2), within 0.2 kcal/mol at the DFT(B3LYP-D3)/CHARMM level and within 1.0 kcal/mol at the OM2/CHARMM level. This may reflect minor differences in weak hydrogen bonds, for example, between O9H on the substrate and Met22 (Figure S3).

Overall, the OM2/CHARMM and DFT(B3LYP-D3)/CHARMM methods give similar trends in the computed relative energies for the different substrate conformers in the enzyme, particularly with regard to the preference for the C1–O22 s-cis conformation. Likewise, both methods give very similar optimized QM regions for the substrate–enzyme complexes (Figure S4). This supports the use of OM2/CHARMM in QM/MM MD simulations of the substrate–enzyme complexes.

MD Simulations of Conformational Change

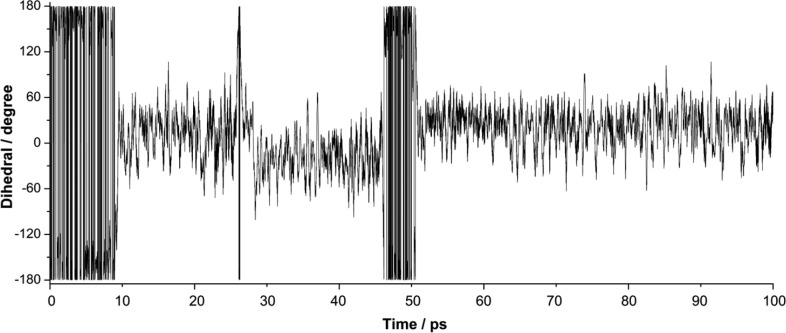
In an attempt to study the conformational changes of the substrate in the enzyme before cycloaddition, a 100 ps OM2/CHARMM MD simulation was performed, with only the substrate in the QM region and SUB-b1 as the starting conformation. Figure 4 shows the variation of the key H–C5–C6–H dihedral angle during the MD simulation. This H–C5–C6–H dihedral angle is 180° and 0° in the s-trans and s-cis conformations, respectively. After the system had been heated to 300 K, the substrate remained in the SUB-b1 conformation for ∼10 ps before it converted to SUB-b2 (C5–C6 s-cis conformation). For the following 90 ps, SUB-b2 remained the dominant conformer, even though SUB-b1 was visited again after 27 ps (for ∼1 ps) and after 46 ps (for ∼5 ps). Thus, the dynamics results indicate that the interconversion of the C5–C6 s-trans and s-cis conformations is feasible in the enzyme (between SUB-b1 and SUB-b2).

Figure 4.

Evolution of the H–C5–C6–H dihedral angle during a 100 ps OM2/CHARMM MD simulation of the substrate in the active site of SpnF (starting from SUB-b1).

An analogous 100 ps OM2/CHARMM MD simulation was performed with SUB-a1 as the starting conformation (data not shown). The SUB-a1 conformer converts to SUB-b1 after ∼50 ps, which remains the dominant conformer during the following 50 ps. Hence, even if the most stable gas-phase conformer SUB-a1 is initially bound by the enzyme, conformers SUB-b1 and SUB-b2 are easily dynamically accessible in the enzyme, where they are more stable than SUB-a1 (see Table 1).

Snapshot Selection

To choose a suitable snapshot as a starting point for the following QM/MM computations, a 500 ps classical MD simulation was performed. The RMSD data for the whole protein in Figure 5 show that the system tends to equilibrium after ∼100 ps.

Figure 5.

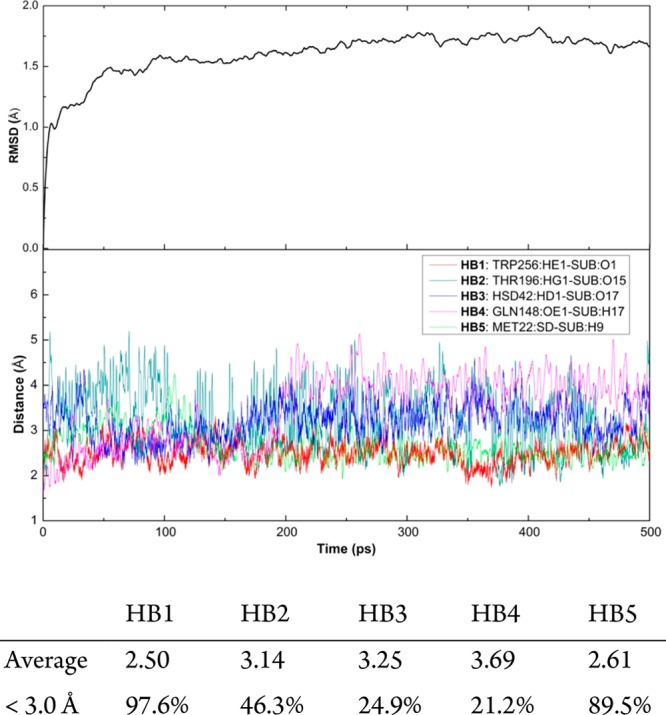
RMSD for the whole system (top) and five selected hydrogen bond distances between SpnF and substrate (bottom) during a 500 ps classical MD simulation. Listed below the figure are the average hydrogen bond distances and the percentages of hydrogen bonds shorter than 3.0 Å after 100 ps.

Because hydrogen bonds (HBs) may affect the Diels–Alder reaction, we show the variation of five possible HB distances during the 500 ps classical MD run in Figure 5. The Trp256 HE1–substrate O1 and Met22 SD–substrate H9 HBs are very stable, with 97.6 and 89.5% of the distances being shorter than 3.0 Å after 100 ps, respectively. This may help stabilize the reaction pocket and thereby improve substrate binding. Residues Hsd42 and Gln148 form competing HBs with the substrate O17–H17 bond, which are rather weak (<25% of the distances shorter than 3.0 Å). We selected a snapshot that features all five hydrogen bonds with active-site residues for the following QM/MM calculations.

In a recent DFT model study,²⁸ the most stable form of the substrate was found to contain an intramolecular HB (involving substrate O15 and substrate O17 in the notation of Figure 5). We confirm that this is the most stable substrate conformer in the gas phase (by 3.9 kcal/mol at the B3LYP-D3/TZVP level). This is not true in the enzyme, where the reactive conformer SUB-b2+enzyme is 4.6 kcal/mol lower in energy than the corresponding species SUB-b2-HB+enzyme with an intramolecular HB, at the QM(B3LYP-D3/TZVP)/CHARMM level. In the enzyme environment, there is competition between the intramolecular HB and the substrate–residue HBs (HB2 and HB3 in the notation of Figure 5), with the latter prevailing in the case of reactive conformer SUB-b2.

Mechanistic Investigation

We chose SUB-b2 as the starting reactant conformer to study the mechanism of cycloaddition at the QM(B3LYP-D3/TZVP)/CHARMM level. Key interatomic distances are listed in Table 2, which also depicts the optimized geometries at the QM/MM (cyan) and QM (gray) levels. For SUB-b2 in SpnF, the C7–C11, C4–C12, and C2–C14 distances are 0.04, 0.26, and 0.13 Å shorter than the corresponding distances in the gas phase, respectively.

Table 2. Optimized B3LYP/TZVP (gray) and QM(B3LYP-D3/TZVP)/CHARMM (cyan) Geometries^a.

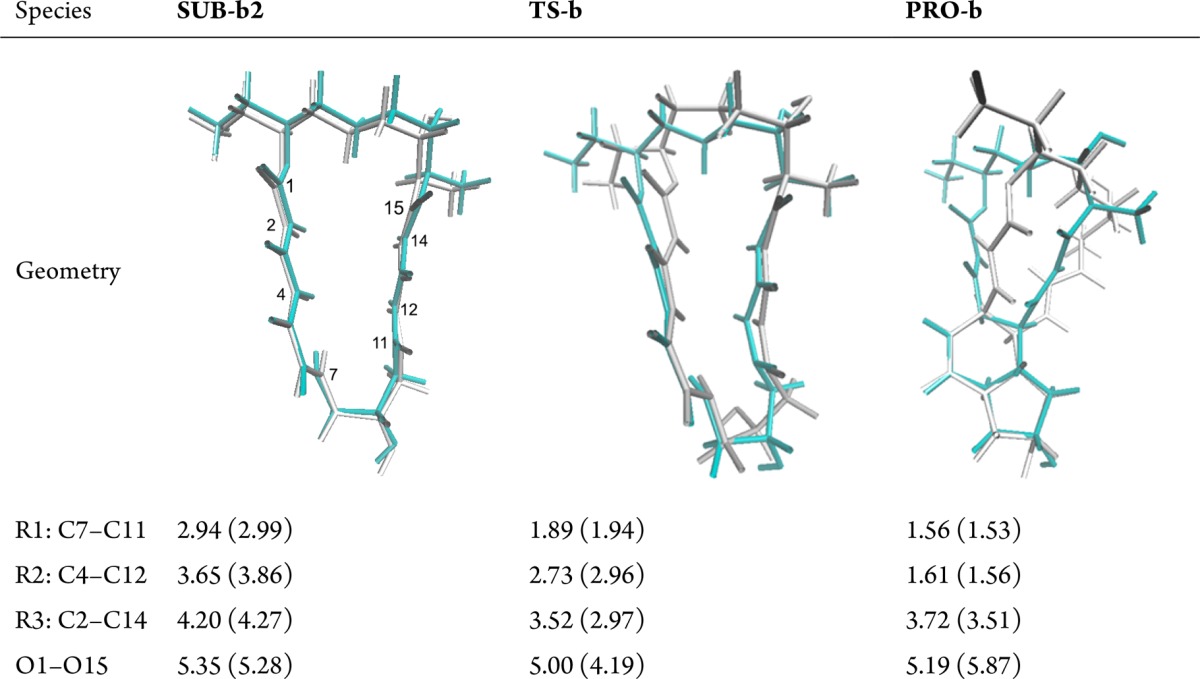
^aAlso given are key distances from the QM/MM (QM) optimizations (in angstroms).

For transition state TS-b in SpnF, both the C7–C11 and C4–C12 distances are slightly shorter than their gas-phase counterparts, indicating a slightly “later” transition state for cycloaddition in SpnF. Importantly, the C2–C14 distance in TS-b is much longer in SpnF (3.52 Å) than in the gas phase (2.97 Å). It was previously shown²⁸ that the gas-phase transition state is ambimodal and leads directly to the [4+2] and [6+4] cycloadducts, having similar C4–C12 and C2–C14 distances (2.96 and 2.97 Å, respectively). In SpnF, these distances differ much more in TS-b (2.73 and 3.52 Å, respectively), which suggests that the enzyme environment in SpnF may facilitate the [4+2] cycloaddition and impede the [6+4] cycloaddition. The long C2–C14 distance of TS-b in SpnF (3.52 Å) may well be related to the hydrogen bonds of the neighboring O1 and O15 atoms to active-site residues Trp256 and Thr196, respectively, which exert a pulling effect that increases the O1–O15 distance in the transition state from 4.19 Å in the gas phase to 5.00 Å in the enzyme (Table 2); this will tend to increase the neighboring C2–C14 distance in SpnF. On the other hand, when going from the reactant to TS-b in SpnF, the C7–C11 distance decreases strongly, more so than C4–C12, indicating that the cycloaddition may proceed via a concerted but highly asynchronous process.

For product PRO-b in SpnF, the C7–C11, C4–C12, and C2–C14 distances are all somewhat longer than those in the gas phase. Likewise, the hydrogen bonds between the substrate and the surrounding residues of the enzyme are generally longer for PRO-b than for SUB-b2 and TS-b+enzyme (see Figure S5). These observations suggest that the product may not be bound particularly well in SpnF, which may facilitate the release of the product from the active site.

The energy profile for the cycloaddition computed at the B3LYP-D3/TZVP level in the gas phase is presented in Figure 6. The most stable substrate SUB-a1 first undergoes a conformational change around C5–C6 from s-trans to s-cis to generate the reactive substrate SUB-a2; the energy barrier of 10.5 kcal/mol is readily traversed at room temperature. Thereafter, SUB-a2 goes through transition state TS2-a, which may lead to product PRO-a directly via a [4+2] cycloaddition or to an intermediate INT-a via a [6+4] cycloaddition. INT-a is converted to the final product PRO-a through a Cope rearrangement via TS3-a, which has a relative energy (19.7 kcal/mol) that is lower than that of TS2-a (23.0 kcal/mol). The overall energy and free energy barriers are 23.0 and 25.4 kcal/mol, respectively, with the cycloaddition step being rate-limiting. This energy profile is similar to that reported previously.²⁸

Figure 6.

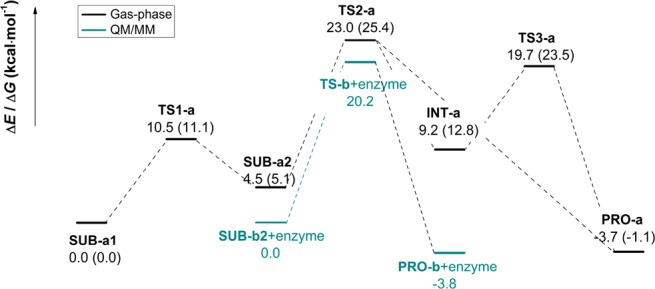
Calculated energy profile at the B3LYP-D3/TZVP level in the gas phase and at the QM(B3LYP-D3/TZVP)/CHARMM level (cyan) inside the active site of SpnF. The energies (kilocalories per mole) for the stationary points along the reaction profile are given relative to the reactant (SUB-a1 or SUB-b2+enzyme). In the gas phase, they include zero-point energy corrections. The computed free energies in the gas phase are given in parentheses.

Also shown in Figure 6 is the QM/MM energy profile for the reaction in the enzyme. Using geometry optimizations at the QM(B3LYP-D3/TZVP)/CHARMM level, we found a one-step [4+2] cycloaddition pathway with a barrier of 20.2 kcal/mol. Transition state TS-b+enzyme is fully characterized in the Supporting Information (section S-IV). Briefly, it has one imaginary frequency (i325 cm^–1), with a transition vector that mainly involves C7–C11 motion (bond formation). Geometry optimizations starting from distorted transition state structures and intrinsic reaction coordinate (IRC) calculations in backward and forward reactions invariably led to the substrate–enzyme complex (SUB-b2+enzyme) or to the product–enzyme complex (PRO-b+enzyme). We did not detect a [6+4] cycloaddition pathway during these runs. In separate DFT/CHARMM optimizations, we found the minimum for the intermediate (INT-b+enzyme) formally arising from a [6+4] cycloaddition in SpnF but could not locate the associated transition states in the enzyme.

In summary, our mechanistic investigations at the QM(B3LYP-D3/TZVP)/CHARMM level establish the feasibility of the direct [4+2] cycloaddition in SpnF and provide evidence that it should be favored over the [6+4] cycloaddition (more so than in the gas phase, because of the influence of the protein environment). While we find no computational evidence of the [6+4] cycloaddition, we do not claim that there is no such pathway in the enzyme, simply because we have not explored the DFT/CHARMM potential energy surface in an exhaustive manner, which would require extensive DFT/MM dynamics runs (e.g., as performed in ref (28) at the DFT level for a model system).

NPA Charge Analysis

It is known from both experimental and theoretical investigations that hydrogen bonding by water or polar solvents tends to accelerate cycloaddition reactions, through modulation of the HOMO and LUMO energies.^59,60 Positioning a hydrogen bond donor next to the alkene moiety or a hydrogen bond acceptor next to the diene moiety may thus narrow the HOMO–LUMO energy gap and lower the activation barrier. In the QM region (Figure 2), Thr196 and Hsd42 are possible hydrogen bond donors close to the alkene moiety, while Met22 may act as a hydrogen bond acceptor close to the diene moiety. We employed natural population analysis (NPA)⁶¹ to calculate the natural atomic charges of the relevant optimized species (Table 3). The NPA charge on the diene moiety is larger in the enzyme than in the gas phase, both for the reactant (0.099 e vs 0.058 e) and for the transition state (0.117 e vs 0.082 e), while the NPA charge on the alkene moiety remains similar in both cases (0.061 e vs 0.050 e for the reactant and 0.065 e vs 0.065 e for the transition state). The diene moiety thus appears to be precharged positively in the enzyme, favoring electron transfer from the alkene to the diene during the cycloaddition. The O15 atom of the substrate is engaged in a hydrogen bond with the Thr196 residue of SpnF, and therefore, its NPA charge is significantly more negative in the enzyme than in the gas phase, both for the reactant (−0.611 e vs −0.563 e) and for the transition state (−0.633 e vs −0.583 e). The increased negative charge on O15 in SpnF will in turn facilitate withdrawal of electron density from the diene moiety through the C11–C15 conjugated π-system. Hence, residue Thr196 may play an important role in accelerating the [4+2] cycloaddition in the active site of SpnF.

Table 3. Computed NPA Charges of Selected Portions of the Relevant Species at the B3LYP-D3/TZVP level^a.

species	SUB-a2	TS2-a
diene moiety	0.058	0.082
alkene moiety	0.050	0.065
O15 atom	–0.563	–0.583

species	SUB-b2+enzyme	TS-b+enzyme
diene moiety	0.099	0.117
alkene moiety	0.061	0.065
O15 atom	–0.611	–0.633

^aThe diene (red) and alkene (blue) moieties are color-coded.

Free Energy Simulations

To determine the minimum free energy paths for the [4+2] and [6+4] cycloadditions and to compare the free energy barriers for these two possible pathways in SpnF, we decided to perform free energy simulations. For practical reasons, this was affordable only at the OM2/CHARMM level. For the purpose of validation, we recomputed all relevant stationary points and the energy profile in the gas phase at the OM2 level (see the Supporting Information, section S-II, for details) and compared them with the corresponding B3LYP-D3/TZVP results (see Figure 6). The two methods give qualitatively similar geometries and energy profiles, and we consider the agreement in the numerical results sufficient to justify the use of OM2/CHARMM in the free energy simulations (see the Supporting Information, section S-II).

For further validation, we computed the energy profile for the [4+2] cycloaddition in the enzyme at the OM2/CHARMM level (see the Supporting Information, section S-V). Compared with the B3LYP-D3/TZVP results (see Figure 6), the structures of the stationary points (SUB-b2+enzyme, TS-b+enzyme, and Pro-b+enzyme) are qualitatively similar. The OM2-based barriers in the enzyme (gas phase) of 25.2 (27.8) kcal/mol are higher than the corresponding DFT-based values of 20.2 (23.0) kcal/mol; the barrier is lower in the enzyme by almost 3 kcal/mol at both levels (for further details, see the Supporting Information, section S-V).

Figure 7 shows the one-dimensional (1D) and two-dimensional (2D) free energy profiles for the [4+2] cycloaddition pathway (OM2/CHARMM). The C7–C11, C4–C12, and C2–C14 distances are defined as R₁, R₂, and R₃, respectively. Figure 7 (bottom) includes the initial (dotted) and final (solid) strings for the [4+2] pathway, with the strings being projected into the 2D space of collective reaction coordinates R₁ and R₂.

Figure 7.

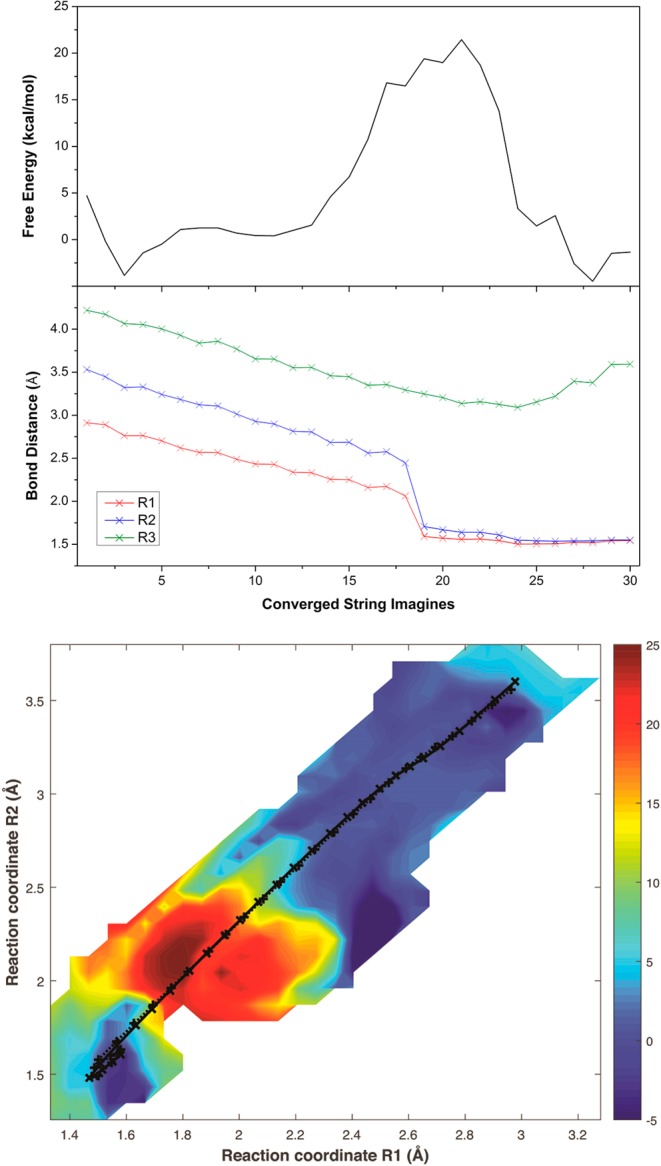
1D free energy profiles (top) and 2D free energy surface (bottom) obtained from OM2/CHARMM simulations of the [4+2] cycloaddition, as well as the changes in reaction coordinates (middle) along the converged string images. For the 2D free energy surface, the initial (dotted lines) and final (solid lines) strings are projected into the space of collective coordinates R₁ and R₂, and the color scale denotes the free energy in units of kilocalories per mole.

Figure 7 (top) shows the 1D free energy profile along the converged strings, which corresponds to the minimum free energy path (MFEP). The predicted free energy barrier for the [4+2] cycloaddition is around 22 kcal/mol. In the gas phase, OM2 overestimates the barrier compared with DFT by ∼5 kcal/mol (OM2, 27.8 kcal/mol; B3LYP-D3/TZVP, 23.0 kcal/mol). Taking this into account, we expect the free energy barrier in the enzyme to be around 17 kcal/mol at the DFT(B3LYP-D3/TZVP)/CHARMM level, close to the value of 18.4 ± 0.1 kcal/mol derived from the experimentally observed turnover of 14 ± 1.6 min^–1 in SpnF^25,26 by using the Eyring equation. The calculated free energy barrier in the enzyme is considerably lower than the computed barriers in the gas phase, implying a significant acceleration of the [4+2] cycloaddition in SpnF. This is consistent with the experimental observation that the rate enhancement in SpnF is approximately 500-fold, which corresponds to a decrease in the free energy barrier by 3.7 kcal/mol.

Figure 7 (middle) displays the average values for reaction coordinates R₁, R₂, and R₃ of each image from the last converged string along the MFEP. In the transition state region of the [4+2] cycloaddition pathway, distances R₁ and R₂ of the forming C7–C11 and C4–C12 bonds change drastically and almost simultaneously from 2.06 and 2.44 Å to 1.59 and 1.70 Å, respectively. This indicates that the [4+2] reaction takes place in an essentially concerted manner. Therefore, the free energy simulations at the OM2/CHARMM level support the notion that the [4+2] cycloaddition in SpnF can be considered as a Diels–Alder reaction.

Analogous simulations for the [6+4] cycloaddition were attempted as documented in the Supporting Information (section S-VI). However, the initial string chosen for this pathway is quite approximate, because we could locate only intermediate INT-b+enzyme at the OM2/CHARMM level but not the transition state for a subsequent Cope rearrangement in SpnF. A downhill path to product PRO-b+enzyme was found in these free energy simulations, as well as in straightforward OM2/CHARMM MD simulations (NVT ensemble) starting from INT-b+enzyme (see the Supporting Information, section S-VI). This implies that INT-b+enzyme can be only a very shallow minimum on the OM2/CHARMM surface that relaxes directly to the Diels–Alder product. As a caveat, we emphasize that the situation may be different at the DFT/CHARMM level, which may support dynamically competing pathways [in analogy to the gas-phase dynamics results (see ref (28))].

Limitations

While the computational study presented here provides evidence in favor of the Diels–Alder pathway in the SpnF enzyme, it cannot be regarded as being definitive in this regard, for several reasons. First, in general terms, the chosen methods (DFT/CHARMM for geometry optimization and OM2/CHARMM for free energy simulation) are the state of the art for studies of enzymatic reactivity but still of limited accuracy. Second, and more importantly, we have investigated only one particular snapshot and four substrate conformers within this snapshot. By contrast, a recent DFT model study²⁹ of the macrocyclic substrate in water (PCM) reported 560 unique conformers and 376 unique transition states with energies within 30 kcal/mol of the lowest one. In static DFT computations and DFT MD simulations of the substrate in water (SMD),²⁸ the relevant transition states were found to contain an intramolecular hydrogen bond (see Figures 1 and 4 of ref (28)). As described above (see Snapshot Selection), we chose an MD snapshot as a starting point for our QM/MM calculations that featured the maximum number of intermolecular hydrogen bonds between the substrate and the active-site residues, thus assuming implicitly that this would be the favored arrangement in the enzyme; this has been confirmed by DFT/CHARMM calculations for reactive conformer SUB-b2+enzyme and is consistent with our classical MD simulations, in which these intermolecular hydrogen bonds are frequently present (Figure 5). Our QM/MM calculations explored the potential energy and free energy surfaces of the enzyme–substrate system starting from this particular snapshot and thus covered only part of the conformational space. It may well be that snapshots with different features (e.g., with an intramolecular hydrogen bond²⁸) could give rise to different reactivity patterns. For a more definitive assessment, the present QM/MM study would thus need to be extended by investigating further representative snapshots.

On the other hand, we expect that many of the qualitative insights gained from our present QM/MM work will remain valid upon such an extension, for example, with regard to the influence of the active state environment on the stability of the substrate conformers, on the geometry and charge distribution in the transition states, and on the reaction barriers (see also Conclusions).

Conclusions

We have investigated the mechanism of cycloaddition in the enzyme SpnF at the DFT/CHARMM (DFT = B3LYP-D3/TZVP) and OM2/CHARMM levels. The QM/MM simulations show that the interconversion of s-trans and s-cis conformations around the C5–C6 bond is easily feasible in SpnF. The QM/MM calculations and free energy simulations indicate that the cycloaddition in the enzyme proceeds through a concerted [4+2] Diels–Alder reaction. OM2/CHARMM free energy simulations yield a free energy barrier of 22 kcal/mol, which agrees reasonably well with the value (18.4 ± 0.1 kcal/mol) derived from the experimentally observed turnover. Compared with the gas phase, the enzyme lowers the Diels–Alder barrier by almost 3 kcal/mol (both at the DFT and OM2 levels), consistent with experimental observations. NPA charge analysis at the DFT level indicates that the hydrogen bond between the Thr196 residue of SpnF and the C15 carbonyl group facilitates withdrawal of electron density from the C11–C15 extended conjugated π-system and thus makes the diene moiety more positive and thus more reactive.

In summary, these QM/MM computations provide evidence that the Diels–Alder pathway is favored in the SpnF enzyme to catalyze cyclohexene ring formation in the 22-membered macrolactone. The Diels–Alder reaction in SpnF benefits from substrate prearrangement within the active site and from electrostatic effects arising from hydrogen bonding with residue Thr196.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.joc.7b02794.

• Results from docking different substrate conformers into the SpnF enzyme, OM2 optimization of pathways in the gas phase, graphical representations of optimized QM regions, QM/MM characterization of TS-b+enzyme, free energy simulations of the [6+4] cycloaddition, and Cartesian coordinates of the optimized QM regions in the gas phase and in the enzyme (PDF)

The authors declare no competing financial interest.