Abstract
Expert performance is often evaluated assuming that good experts have good outcomes. We examine expertise in medicine and develop a model that allows for two dimensions of physician performance: decision making and procedural skill. Better procedural skill increases the use of intensive procedures for everyone, while better decision making results in a reallocation of procedures from fewer low-risk to high-risk cases. We show that poor diagnosticians can be identified using administrative data and that improving decision making improves birth outcomes by reducing C-section rates at the bottom of the risk distribution and increasing them at the top of the distribution.
I. Introduction
Many important jobs are held by experts, such as teachers, judges, or doctors. Yet despite the importance of their activities, the quality of an expert’s performance is difficult to evaluate. We often end up looking at outcomes and assuming that good experts have good outcomes, despite the fact that such inferences are clouded by selection and measurement issues. That is, performance is often summarized using an expert-specific “fixed effect.” Medicine is something of an exception in that metrics have been developed to judge the actions taken by doctors as well as the realized outcomes. However, these metrics often take the form of simple directives that do not fully account for the complexity of patients’ conditions.
In the case of child birth, it is widely believed that there are too many Cesarean sections (C-sections) in the United States. The large rise in C-section rates from 20.7% in 1996 to a peak of 32.9% in 2009 (http://www.cdc.gov/nchs/data/databriefs/db124.htm) has led to many proposals to reduce these rates. For example, on January 1, 2014, the Joint Commission that provides hospital accreditation and allows hospitals to participate in the Medicaid and Medicare programs implemented a measure aimed at encouraging hospitals to reduce C-section rates among first-time mothers with head-down single fetuses. The Commission will publish a target rate based on a national sample of hospitals every quarter and will require hospitals to publish and track their own rates in order to create pressure on them to lower rates (Joint Commission 2014; see measure PC-02). Similarly, Consumer Reports (2015) created rankings for hospitals on the basis of C-section rates for women without previous C-sections who were delivering full-term single fetuses. Yet clearly something could go wrong in these deliveries and necessitate a C-section. Creating incentives for hospitals to lower rates across the board could have negative consequences if it makes women less likely to receive what can be a life-saving procedure for mothers and babies. It would be preferable to reduce the use of unnecessary procedures while actually increasing procedure use among the highest-risk mothers. However, meeting this goal requires improvements in how doctors allocate procedures across patients.
In this paper, we develop a model that highlights two dimensions of a doctor’s performance: whether the doctor makes the right decision regarding procedure choice and whether the doctor subsequently executes that decision well. We then demonstrate that the model can be used to interpret data from C-section deliveries. Our work makes several contributions. First, we show that standard administrative data that are already collected by every state can be used to identify doctors whose decision making is significantly worse than the norm. Second, we show that poor decisions are associated with bad health outcomes. These are surprising and important findings given that doctors undoubtedly have much more information about each individual case than we can observe in our data. Nevertheless, doctors have only their individual training and experience to rely on, whereas the “big data” available to state administrators can be mined for much additional information that is potentially relevant to procedure choice.
Studying expertise in the context of C-sections is interesting for a number of reasons. First, there is widespread recognition that C-section rates vary across hospitals in ways that cannot be explained either by the condition of the patients or by their preferences (Kozhimannil, Law, and Virnig 2013). Second, as discussed above, there is pressure to reduce C-section rates. Third, the C-section is the most common surgical procedure in the United States, so the caseload as a whole provides a wealth of information. Fourth, birth records contain detailed information about the mother’s and child’s condition that can be used to develop a model of procedure choice.
Applying our model to data on all deliveries in New Jersey from 1997 to 2006, we find that when decision making increases by one standard deviation, C-section rates fall 15.5% for women in the bottom half of the risk distribution, but they rise 5.5% among women in the high-risk half of the distribution. Given that there are many more C-sections among the high-risk to begin with, we estimate that improved decision making would have resulted in 7,490 fewer C-sections in the bottom half of the distribution but 14,975 more C-sections in the top half of the distribution, for a net increase of 7,485 C-sections. These extra C-sections among those at high risk would have generated $35 million (2006 dollars) in additional costs, and they might have averted about a third of the 2,997 deaths that occurred in this high-risk group over this 10-year period, for a cost per life saved of about $35,000. Among those at low risk, the C-sections averted would have saved about $35 million and would have prevented about 2,346 cases of maternal complications. Of course, neonatal death is a rare outcome, and our estimates are subject to error, but taken at face value, they imply that better decision making could have improved outcomes for both infants and their mothers at a very modest cost.
Thus, a surprising implication of our analysis is that not only are there too many C-sections being performed on low-risk women but there are too few C-sections being performed on high-risk women. A one standard deviation improvement in decision making leads to reductions in the probability of a negative health outcome: there is a reduction of 15.3% among the low-risk and of 9.1% among the high-risk. When we further divide bad health outcomes into those that are bad for the mother and those that are bad for the infant, we find that reductions in bad outcomes among mothers are concentrated in the low-risk (who become less likely to suffer the consequences of unnecessary surgeries), while bad outcomes for infants are reduced across the board. The one exception is neonatal death, which declines with better diagnosis only among those at high risk (suggesting that C-sections are indeed life-saving among infants born to the highest-risk mothers).
Contrasting the effects of decision making and surgical skill, we find that a one standard deviation improvement in surgical skill would increase the incidence of C-section 16.5% among patients in the lower half of the risk distribution and by 8.7% among patients in the upper half. The same change is estimated to reduce the incidence of any bad health outcome by 55.3% among the low-risk and by 50.4% among the high-risk.
One might conclude that it is more important to improve surgical skill than to improve decision making. But it may be considerably easier to improve decision making than to make bad surgeons into good ones. Indeed, policies such as checklists, computer-aided diagnosis, or administrative structures that require physicians to seek approval before scheduling C-sections in women without risk factors could perhaps be used as methods of improving decision making (Doi 2007; Baker et al. 2008; Gawande 2009). Our results suggest that with common procedures like C-section, it may well be possible to use existing administrative health databases to identify doctors who are making poor decisions and to make changes that will improve patient health outcomes.
The rest of the paper is laid out as follows. Section II briefly reviews some of the relevant literature. We develop a model in Section III, which assists us in interpreting the two dimensions of performance. Briefly, we first use the observable data to construct a measure of each patient’s appropriateness for having a C-section. We then estimate doctor-specific regressions of the propensity to perform a C-section on this measure of appropriateness. This procedure yields an intercept and a slope term for each doctor, and the model explains the circumstances in which the estimated slope can be interpreted as a measure of the doctor’s decision making. We also propose a proxy for the doctor’s surgical skill. Section IV explores the relationship between these measures and outcomes, and this is followed by a discussion and conclusions in Section VI.
II. Background
Health care is an important area in which we all rely on experts to choose procedures and then to carry out the chosen procedures. Hence, it is not surprising that many studies of expertise have focused on physicians. Meehl (1954) reviews a number of studies, mainly of clinical psychologists, and compares their forecasts to those generated by simple statistical models, including optimal linear combinations of variables that the experts also observed. He argues that predictions based on these simple models were generally more accurate than those of the experts. A more recent meta-analysis of 136 studies in clinical psychology and medicine also finds that algorithms tend to either outperform or to match the experts (Grove et al. 2000).
Kahneman and Klein (2009) argue that algorithms are most useful when we have confidence in the list of variables to be used for prediction, when we have a reliable and measurable outcome, when there is a large body of similar cases, when the cost/benefit ratio warrants the investment in developing an algorithm, and when the situation is sufficiently stable that the algorithm will not immediately become obsolete. Our study of C-sections appears to satisfy all of these criteria, as we will argue further in the data section below. In the psychological studies discussed above, the experts and the statisticians generally had access to the same data. The advantage of the algorithms arises mainly because the algorithms are more consistent than the experts. An additional advantage in our application is that in our administrative birth records, we observe the universe of cases over a given time period, whereas each doctor observes only their own cases. A possible disadvantage is that the doctor may have private information that is not in the health record and that therefore we do not observe. We will argue below that it is an empirical matter whether the advantage due to “big data” outweighs the limitation of unobservable factors that influence the decision making of physicians when using the observable data to assess the quality of physician decision making.
Another difference between our study and many of those in psychology is that we are agnostic about the source of the “errors” in decision making. The psychology literature is concerned with whether the errors arise from factors such as overconfidence or other heuristic biases. We are concerned with doctors who, for a variety of possible reasons, do not make the best use of the publicly observable information at their disposal to make good decisions. The literature in health economics offers many possible reasons for these “mistakes.”
One common explanation for faulty decision making is “defensive medicine,” the idea that doctors perform unnecessary procedures in order to protect themselves from lawsuits. However, Baicker, Fisher, and Chandra (2007) argue that there is little connection between malpractice liability costs and physician treatment of Medicare patients, while Dubay, Kaestner, and Waidmann (1999) and Currie and MacLeod (2008) cast doubt on the idea that physicians perform unnecessary C-sections primarily due to fear of lawsuits.
There is more evidence that physician decision making is swayed by financial incentives. The fee for performing C-sections exceeds the fee for performing vaginal deliveries. Gruber and Owings (1996) and Gruber, Kim, and Mayzlin (1999) show that the incidence of C-sections increases with the wedge between the two fees. Johnson and Rehavi (2016) add to this literature by showing that financial incentives affect the treatment of non-physicians but have no impact on the treatment of physician-patients, who are presumably better informed and therefore less likely to meekly tolerate unnecessary procedures. Thus, excessive use of C-sections could be a case of “induced demand” motivated by financial gain (Dranove 1988).
A third explanation of faulty decision making is that doctors are influenced by the decisions of those around them. Chandra and Staiger (2007) study the choice of surgery versus medical management of cardiac patients. Knowledge spillovers are the main theoretical driver of small-area variation in procedure use in their model. Physicians in areas that specialize in surgery are assumed to become better at surgery and worse at medical management and vice versa. Their model raises the possibility of mismatch between patients and physicians. All patients in high-surgery areas will be more likely to have surgery even if medical management would be more appropriate for some of them.
Both Epstein and Nicholson (2009) and Dranove, Ramanarayanan, and Sfekas (2011) investigate the prevalence of spillovers in the case of C-sections, and neither find much evidence for them: there is no convergence in practice styles among physicians in the same hospitals over time. Similarly, Chan (2015) looks at how doctors’ practice style develops early in their careers and finds that the practice styles of attending physicians have little impact on those junior to them. Since the C-section is often considered a rather simple surgery, the benefits from specialization may also be muted. Still, the model we discuss below is not inconsistent with the potential existence of either specialization or spillovers, as practice presumably does help and doctors could learn both to be better diagnosticians and better surgeons from observing their colleagues.
The most important insight from the Chandra and Staiger (2007) model may be that a reduction in the use of surgery in high-use areas cannot be Pareto-improving because patients who are good candidates for surgery will be harmed by a decline in the skill level of the physicians serving them. This is also a feature of the model developed by Chandra and Staiger (2011), which more explicitly considers the overuse and underuse of invasive procedures (in their case coronary procedures for AMI patients) across hospitals. We will also argue that an across-the-board cut in C-section rates cannot be optimal because such a reduction will reduce the probability that high-need mothers will receive the procedure. What is desirable instead is a reallocation of C-sections from low-need to high-need mothers.
Patient preferences are often cited as a fourth potential reason for medically unnecessary procedure use. In an innovative study using vignettes from patient and physician surveys, Cutler et al. (2013) assess the hypothesis that regional variations in procedure use are driven by differences in patient demand across areas. They conclude that patient demand is a relatively unimportant determinant of regional variations and that the main driver is physician beliefs about appropriate treatment that are often unsupported by clinical evidence. Similarly, previous studies have found little evidence that patient demand is driving the large differences in C-section rates across providers (McCourt et al. 2007).
Finkelstein, Gentzkow, and Williams (2014) address the same question using longitudinal Medicare claims data that allow them to track the same patients as they move through different healthcare markets. They suggest that about half of the observed variation in procedure use is due to supply-side factors, while half is due to patient-level, or demand-side, factors. However, they conclude that much of the variation in patient demand is driven by exogenous patient health, so that probably it does not primarily reflect patient tastes for procedures. These findings agree with those of Cutler et al. (2013) in suggesting that patient preferences play a relatively small role in explaining variations in care.
Finally, there is literature looking at more explicit ways to incentivize doctors to “do the right thing.” Abaluck et al. (2014) consider the case of negative test results. The idea is that if a doctor screens a lot of people for a condition and all the tests come back negative, then this is a good indication that the doctor is overscreening. Screening tests are an important but rather special case. With most medical interventions, we observe procedures that were chosen and a health outcome, but it is often impossible to tell if any specific intervention led directly to a specific outcome.
Many authors have considered incentives based on risk-adjusted patient outcomes (see Newhouse 1994; Dranove et al. 2003; Dranove and Jin 2010; Song et al. 2010; Newhouse et al. 2013), where the ultimate goal is to be able to align payments with appropriate decision making (Frank and McGuire 2000). A persistent problem highlighted by this literature is that doctors can be expected to have more information than regulators, and if they are penalized for bad outcomes conditional on patient characteristics that the regulators can observe, then they will have strong incentives to avoid patients their private information suggests are bad risks. Our approach is different in that we propose to evaluate physician decision making simply on the basis of whether doctors tailor their decisions to the observable characteristics of patients in the same way as a reference or standard physician. The standard we use in what follows is the average New Jersey obstetrician. However, in principle, one could use any set of highly regarded physicians to set the standard. Rather than simply assuming that physicians who have bad outcomes made bad decisions, we then show that doctors who are less responsive than the standard physician to the observable information about the patient tend to have worse patient outcomes. In this way, we are able to focus on characteristics of the decisions themselves and to validate the idea that responsiveness to observable patient characteristics is an important dimension of decision quality. Of course, unobservable patient characteristics are also likely to be important to decision making, but as long as these are correlated in a systematic way with the observables in the population, then their influence will be at least partially captured in the formation of the standard.
III. Framework
This section lays out the empirical and theoretical framework of our model. Empirically, we first use all of the available data for New Jersey to uncover how the standard physician responds to all of the observable characteristics of the patient. We do this by following a standard machine learning approach (Hastie, Tibshirani, and Friedman 2009), in which the function that describes the decision making is “trained” on data from actual decisions. The goal is to provide an accurate representation of how doctors map observable patient characteristics into decisions about behavior. Given this representation, we can then identify doctors who seem to deviate systematically from the standard and ask whether this deviation has consequences for patient outcomes. It is possible for doctors who deviate to have systematically better outcomes. For instance, if there is important unobserved information that is uncorrelated with the observables, and if good doctors make better use of this information, then we might expect doctors who put less weight than the standard on the observables to achieve better patient outcomes. In fact, we will show that the opposite is true: doctors who appear to disregard patient observables in their decision making have worse patient outcomes.
We then interpret these results through the lens of a model of Bayesian decision making in which decisions reflect information processing, prior beliefs about the correct procedures, and surgical skill. Section III.A describes the model of patient condition, Section III.B introduces the model of Bayesian decision making, and Section III.C connects the empirical model to the theory.
A. Modeling Patient Condition
We begin by estimating a qualitative choice model using all of the data for the state of New Jersey between 1997 and 2006, following Smith et al. (2004), who show that a logistic model provides a clinically useful summary of factors related to C-section risk:
| (1) |
Given the large number of physicians in the sample, the predicted probability is insensitive to the decisions of any one of them. We use the model to construct a measure of the patient’s appropriateness for C-section:
| (2) |
This constructed measure captures the standard of practice in New Jersey. Note that although it only contains observable X’s, the influence of un-observables will also be reflected in the estimated coefficients to the extent that unobservables are systematically correlated with observables in the population. Ideally, one might choose to construct using only a set of “good doctors” to form the standard, but as we will show below, there seems to be a good deal of consensus on the ranking of different patients by appropriateness for C-section in our data.
For each doctor j ∈ J, we estimate a model of the form:
That is, each doctor has an intercept that captures that doctor’s mean likelihood of performing a C-section, as well as a slope term θj. We then investigate the extent to which these physician-specific parameters are related to outcomes.
We let hi represent the true underlying condition of the patient and suppose that our estimate (from eq. [2]) satisfies
| (3) |
where the error term has variance . The physician also has a signal of patient condition hi, and the precision of this signal is what we use as a measure of decision making. We will show that this measure of decision making is positively related to the slope term θj, whereas surgical skill affects the intercept term, γj but not θj.
B. Modeling Physician Decision Making
We assume that physicians maximize their utility but that they care about patient outcomes (Gaynor, Rebitzer, and Taylor 2004; Arlen and MacLeod 2005; Currie and MacLeod 2008; Chandra, Cutler, and Song 2012). The physician chooses between two procedures, T ∈ {N, C}, which generate the following physician payoffs:
The first term is an index of the health status of the patient when procedure T is chosen and the physician is of average procedural skill, sj is the procedural skill of the physician performing procedure T, and PT is the cost of the procedure.1
The term represents a patient preference for procedure C (if it is negative, then she prefers procedure N).2 The extent to which the physician responds to the preferences of the mother is denoted by .3 In what follows, we do not observe , and this term can thus also be thought of as incorporating any other variables that are observed by the physician but that are unrecorded in the data.
Given information Iij, the physician chooses C if and only if
| (4) |
Normalizing E{εijC − εijN} = 0, we can restate the physician decision rule (4) as: The physician chooses the intensive procedure (T = C) if and only if
| (5) |
where , mj = mj(PC) − mj(PN), and . For simplicity, normalize , so that . The term for technical skill (sj) increases with skill at C and decreases with skill at N. The term mj represents the relative cost of procedures C and N. Increases in the price of procedure C are expected to increase mj, while an increase in the price of procedure N would decrease this term.
Suppose that the physician has prior beliefs regarding the patient’s true condition hi such that . If , then the physician believes that most women in the physician’s practice should be getting a C-section. The variance of prior beliefs, , represents uncertainty about the appropriate choice. Define
When Bj is large ( is small), then the physician has strong prior beliefs that make the physician less sensitive to the new information in Xi.
Given these beliefs, the physician observes the patient’s condition and makes an assessment of her health status:
| (6) |
where εji is normally distributed with mean zero and variance . We define the precision of the health assessment of as
When Dj is higher, the physician makes a more accurate estimate of the patient’s condition hi and therefore is more likely to choose the correct procedure. Given these definitions we have:
Proposition 1
Given a doctor’s prior beliefs about the patient’s condition , the strength of the physician’s prior beliefs, Bj, the precision of the physician’s health assessment Dj, and the physician’s information about the patient’s condition, hij, then the physician’s medical assessment of a patient’s condition is given by
where π0 = Bj/(Bj + Dj) and πh = 1 − π0 = Dj/(Bj + Dj).
The proof of this and subsequent propositions is in the appendix (and follows DeGroot 1972). Physicians with higher-quality decision making are more responsive to new information and less dependent on prior beliefs.
The final piece of data used by the physician is the patient’s preference for a C-section, given by . Suppose that patient preferences follow an arbitrary distribution , where and are practice-specific parameters that can also affect the observed decision.
This decision model illustrates that there are at least five physician characteristics that affect decision making, which can be summarized by , physician surgical skill, prior beliefs about patient condition, the strength of these prior beliefs, the precision of the health assessment, and the parameter from the doctor’s utility function describing how sensitive the physician is to patient preferences. Unobserved practice characteristics are given by . Let ωj = {ωDj, ωPj} denote the full set of physician and practice level characteristics.
Substituting these expressions into equation (5), it can be shown that procedure T = C is chosen by physician j for patient i if and only if
| (7) |
We can now derive the probability that a patient will receive procedure C as a function of her underlying condition hi. Procedure C is chosen if and only if
| (8) |
where is defined as the variation from the mean of patient preferences, . We can rewrite the second term of this equation as
where are physician-specific characteristics that are not part of physician expectations. Let us define
which is a normally distributed random variable with mean zero and variance
Then the probability of a C-section conditional on a patient’s true medical condition hi is given by
| (9) |
where . This equation suggests that physician behavior can be characterized by an intercept and a slope. Notice that the slope term increases with the precision of the health assessment made by the physician. In the special case where there are no unobserved preferences for C-section (or other relevant unobserved medical information), then . In the special case where physicians disregard patient preferences (or unobserved medical information), then . In either special case, the slope is completely determined by the precision term, Dj. However, even in the special case where , the intercept term γj, is affected by a mix of physician beliefs, surgical skill, and prices, as well as being negatively related to Dj. A possible interpretation of the latter is that as the health assessment becomes more diffuse and less informative, the observable features of the patient’s condition have less impact on treatment decisions. As discussed above, Cutler et al. (2013) and Finkelstein et al. (2014) suggest that procedure choice is not generally driven by patient preferences, and hence in what follows we identify variations in the slope term as primarily reflecting the quality of decision making.
C. Measuring Physician Behavior
We now have a model that connects observed patient conditions to physician decision making. The final step is to link this behavior to observables. We cannot directly observe patient condition hi, but we can derive the probability of observing a C-section conditional on the constructed measure, .
Proposition 2
The probability that physician j chooses T = C when patient condition is observed to be is given by
| (10) |
where γj can be characterized as treatment style, and the slope term, θj, reflects the sensitivity of the doctor to the patient’s condition and is given by
| (11) |
where is the variance of the doctor’s information conditional upon patient health and is the variance of the measure of patient health given the observed birth record.
This proposition summarizes the effects of physician characteristics on procedure choice as a function of the information that we can observe. We can directly estimate both the slope parameter, θj, and the doctor-specific intercept, γj, which together characterize a doctor’s decision making.
Since we are measuring patient condition with error, the slope term we measure is less steep than the slope with respect to true underlying condition . Despite this issue, as long as our proxy for patient condition, , is correlated with true patient condition ( is finite), then variations in physician characteristics will lead to variations in both the intercept, γj, and the slope, θj. We now detail these effects.
1. Determinants of the Intercept Term
Equation (10) shows that any increase in γj leads to an increase in the incidence of procedure C. This intercept is affected by several attributes of physicians and their practices, as summarized in a corollary to proposition 2:
Corollary 1
The incidence of procedure C is increasing in physician beliefs , relative surgical skill for procedure , and the relative pecuniary returns to procedure . It may also be affected by both patient preferences and physician sensitivity to preferences, the term.
2. Determinants of the Slope Term
The following corollary summarizes the effects of physician characteristics on the slope term.
Corollary 2
The slope, θj, is increasing with the quality of physician decision making (∂θj/∂Dj > 0), decreasing with physician sensitivity , the strength of physician prior beliefs (∂θj/∂Bj < 0), and with the variance of patient preferences . It is unaffected by physician surgical skill, physician expectations, and treatment costs.
This result follows immediately from an inspection of the formula for the slope in proposition 2.
Consider now the relationship between decision making and the slope term, θj. Define the elasticity of decision making with respect to θj as
Using this definition and proposition 2 we have:
Corollary 3
An increase in decision-making quality increases incidence of treatment C if and only if
For patients at high risk for procedure , an increase in decision making increases the incidence of procedure C, while the reverse occurs for low-risk patients . This result is in sharp contrast to the effect of surgical skill. If a physician is better at performing a C-section, then this increases the incidence of C-sections for all patients.
The contrasting effects of the quality of decision making and surgical skill are illustrated in figures 1 and 2. In each figure, patients are arrayed along the X-axis from those with the lowest values of to those with the highest values. The lower line in figure 1 illustrates the initial relationship between the observed patient condition and the probability that the intensive procedure is performed. The upper line in figure 1 shows how this relationship would be expected to change with increases in surgical skill. The main takeaway is that one would expect an increase in the use of intensive procedures for both high- and low-risk patients.
Fig. 1.
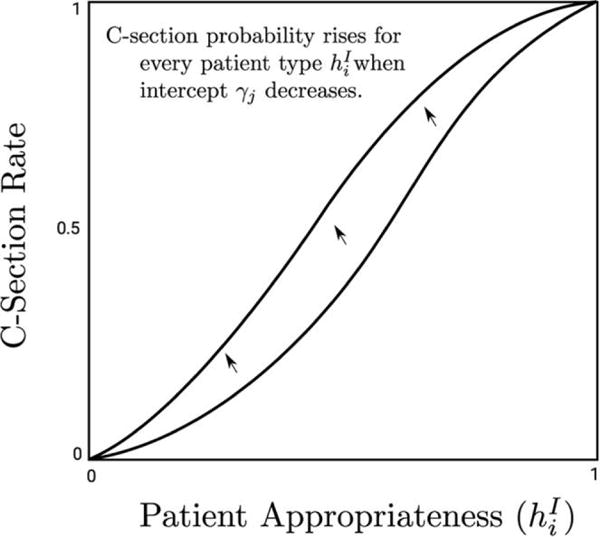
Effect of intercept upon procedure use
Fig. 2.
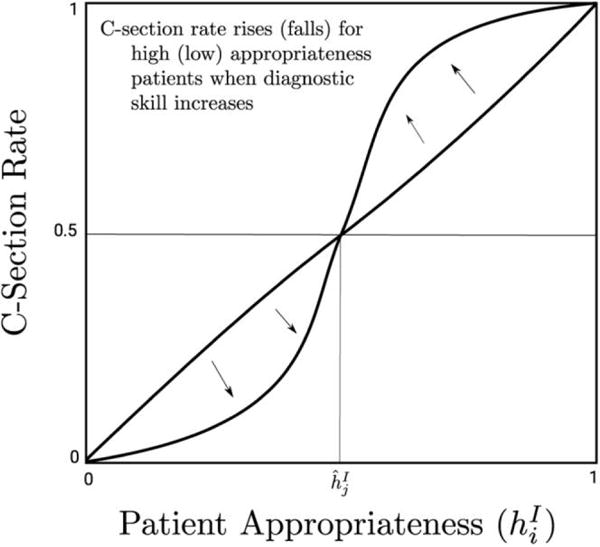
The effect of decision making on procedure choice
Figure 2 illustrates the effect of improving decision making. From corollary 1 we have that patients with observed condition greater than have higher C-section rates when decision making increases and lower rates when is less than the threshold . This is illustrated in figure 2 by the move from the dark line to the light line. Thus, as decision making improves, the use of the intensive procedure falls among those with low and increases among those with high . Other things being equal, we expect that reallocating procedures from those who do not need them to those who do need them will improve outcomes. The appendix shows more formally that this is the case; see propositions A1 and A2.
IV. Data and Method
C-section is the most common surgical procedure in the United States. The technology has been stable for a long time, and there are detailed records on millions of births, meaning that it should be possible to use the available data to rank pregnant women in terms of their a priori risk of C-section with a fair degree of accuracy. Moreover, we can investigate a variety of health outcomes, including both poor outcomes for the mother and poor outcomes for the child and thus directly relate decision making to outcomes.
The data for this project come from approximately a million New Jersey Electronic Birth Certificates (EBC) spanning from 1997 to 2006. In addition to information about the method of delivery, they include detailed information about the medical condition of the mother, including the mother’s age, whether it is a multiple birth, whether the mother had a previous C-section, whether the baby is breech, whether there is a medical emergency such as placenta previa or eclampsia that calls for C-section delivery, and whether the mother had a variety of other risk factors for the pregnancy such as hypertension or diabetes.
Birth records include detailed information about health outcomes for both the mother and the child, including complications that occur during the delivery (maternal bleeding, fever, or seizures), maternal complications that occur after the delivery, fetal distress (measured by the presence of meconium), birth injuries (fracture, dislocated shoulder, and other injuries), and neonatal death (death in the first 30 days of life). We also combine all of these measures into an indicator equal to one if there was “any bad outcome.”4
Finally, the data have information about the latitude and longitude of each woman’s residence, as well as codes for doctors and hospitals.5 The data include demographic information about the mother, such as race, education, marital status, and whether the birth was covered by Medicaid, all of which have been shown to be related both to the probability of C-section and to birth outcomes.
These data are used to construct analogs of the key model concepts. Variable , the mother’s risk of C-section, is estimated using a logit model of the probability of C-section given all of the purely medical risks recorded in the birth data, as in equation (1). Given that we are trying to define medical risk, variables such as the type of insurance and race are not included in the logit models, and this model is estimated using all New Jersey births over the sample period. The estimates are shown in column 1 of table 1. The model predicts well, with a pseudo R-squared of almost .32.
Table 1.
Logistic Regression Model of C-Section Risk (ρ): All Doctors
| Coefficient | SE | Marginal Effect | |
|---|---|---|---|
| Age < 20 | −.337 | .013 | −.075 |
| Age ≥ 25 and < 30 | .262 | .008 | .058 |
| Age ≥ 30 and < 35 | .434 | .008 | .096 |
| Age ≥ 35 | .739 | .009 | .164 |
| 2nd birth | −1.347 | .007 | −.298 |
| 3rd birth | −1.645 | .009 | −.364 |
| 4th or higher birth | −2.140 | .012 | −.474 |
| Previous C-section | 3.660 | .008 | .810 |
| Previous large infant | .139 | .029 | .031 |
| Previous preterm | −.293 | .025 | −.065 |
| Multiple birth | 2.879 | .014 | .638 |
| Breech | 3.353 | .016 | .742 |
| Placenta previa | 3.811 | .054 | .844 |
| Abruptio placenta | 2.048 | .030 | .454 |
| Cord prolapse | 1.761 | .047 | .390 |
| Uterine bleeding | .026 | .035 | .006 |
| Eclampsia | 1.486 | .096 | .329 |
| Chronic hypertension | .745 | .025 | .165 |
| Pregnancy hypertension | .639 | .013 | .142 |
| Chronic lung condition | .064 | .014 | .014 |
| Cardiac condition | −.121 | .020 | −.027 |
| Diabetes | .558 | .011 | .124 |
| Anemia | .131 | .018 | .029 |
| Hemoglobinopathy | .116 | .047 | .026 |
| Herpes | .461 | .024 | .102 |
| Other STD | .052 | .017 | .012 |
| Hydramnios | .616 | .018 | .136 |
| Incompetent cervix | .043 | .035 | .010 |
| Renal disease | −.024 | .031 | −.005 |
| Rh sensitivity | −.045 | .040 | −.010 |
| Other risk factor | .276 | .006 | .061 |
| Constant | −1.414 | .007 | −.313 |
| Pseudo R2 | .32 |
Note.—Number of observations = 1,169,654.
This model reflects actual practice but not necessarily best practice. One might wish to estimate the model of medical risk using only the best doctors or perhaps only the beginning of the time period when C-section rates were much lower. We have experimented with several alternative models and have found that the correlation between the ranking of C-section risk produced by our model and the ranking produced by the alternatives is above .95. These alternatives included a model with fewer risk factors, a model using births from 1997 to 1999 only, and a model using only doctors who were below the 25th percentile in terms of the fraction of births with negative outcomes in their practices. The estimated coefficients were similar in all of these models, suggesting that there is not a lot of controversy about the ranking of which women are the best candidates for C-section, even if (as we shall see) different doctors have much flatter need-C-section profiles than others.
Corollary 2 showed that the slope term in the model, θj, is affected by decision making (Dj). The empirical analog can be obtained for each doctor by using the estimated β’s from (1) to create the index of maternal condition (this is simply βXi) and then estimating a regression model for each doctor’s propensity to perform C-sections as a function of . The estimated coefficient on , denoted by Decisionj, is an indicator of how sensitive the doctor is to this index of observable indicators of patient risk and varies with decision making, as we discussed above. The distribution of slope coefficients has a mean of 1.033 and a standard deviation of 0.183. The first percentile is 0.576, while the 99th percentile is 1.491, suggesting that doctors range from being quite insensitive to quite sensitive to maternal conditions. We normalize this measure by calculating a Z-score, for ease of interpretation.
Figure 3 plots the distribution of estimated propensity scores for those who did not get a C-section and for those who did get a C-section. The figure shows that most of the mass among those who did not get a C-section is concentrated among those with propensity scores less than 0.35, while among those who did get a C-section, there is a lot of mass concentrated above 0.7 but also quite a bit of mass in the 0.1 to 0.4 range. These distributions indicate that there are individuals with no apparent observable risk factors who nevertheless have C-sections, and perhaps more disturbingly, there are women with many risk factors for C-section who do not receive the procedure. For a given level of medical risk, the probability of a C-section increased over our sample period at all but the highest risk levels, as shown in appendix figure A1. In fact, at the start of our sample period, New Jersey, with a rate of 24%, had a lower C-section rate than several other states, including Arkansas, Louisiana, and Mississippi, while by the end of our sample period, New Jersey had pulled ahead to have the highest C-section rate of any state, at almost 40%. Appendix figure A2 shows that this increase was not due to a change in the underlying distribution of medical risks. The figure shows only a slight increase in the number of high-risk cases, which is attributable to an increase in the number of older mothers, mothers with multiple births, and women with previous C-sections (itself driven by the increasing C-section rate).
Fig. 3.
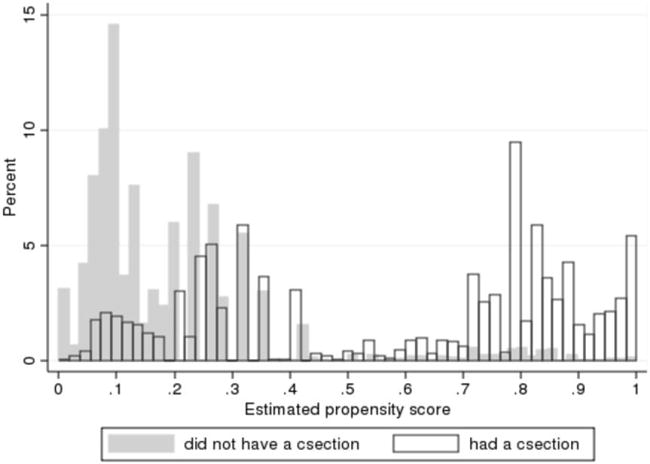
The distribution of estimated propensity scores for those with and without C-section.
Figure 3 also shows that those who had values of less than 0.06 (a group we designate the very-low-risk) were very unlikely to have C-sections, while those with greater than 0.8 (a group we designate as the very-high-risk) were highly likely to have C-sections. Of the women deemed very-high-risk, 89% received a C-section, while among the women deemed very-low-risk, only 6% received a C-section. We measure procedural skill by calculating the rate of any bad outcomes among very-low-risk birth and the rate of bad outcomes among high-risk births for each doctor and then taking the difference between them. Taking the difference in the incidence of bad outcomes between these two groups is suggested by the model, in which it is the difference in skill in procedure C and in procedure N that affects the physician’s choice. The rate of bad outcomes in each group proxies for surgical skill because, as noted above, the vast majority of high-risk women get C-sections and most very-low-risk women do not. At the same time, because the very-high-risk and very-low-risk groups are defined only in terms of underlying medical risk factors, the measure is not contaminated by the endogeneity of the actual choice of C-section within these risk categories. This measure also exhibits considerable variation between doctors, with a mean of −0.0493 (given that bad outcomes are more frequent in high-risk cases than in low-risk cases) and a standard deviation of 0.0646. The first percentile of this variable is −0.25, while the 99th percentile is 0.079. Again, we normalize this measure by calculating a Z-score, for ease of interpretation.
Although relative prices for C-sections and normal deliveries have been shown to be an important determinant of C-section rates, they are not the main focus of our analysis and are not well measured in our data. We use data from the Health Care Utilization Project (HCUP), which includes hospital list charges for every discharge. For each market and year, we take the mean price of all C-section deliveries that did not involve any other procedures less the mean price of normal deliveries without other procedures. The mean differential was $4,711 real 2006 dollars.6
Having constructed these measures, we estimate models of the following form:
| (12) |
where Outcomeijt ∈ {0, 1}, where 0 is a vaginal delivery (or good birth outcome) and 1 is a C-section (or bad birth outcome), i indexes the patient, j indexes the doctor, and t indexes the year. The vector Zit includes maternal age (missing, less than 20, 25–34, 35 and over), education (missing, less than 12, 12, 13–15), marital status, race/ethnicity (African American, Hispanic), and whether the birth was covered by Medicaid, as well as the child’s gender and indicators for birth order. We include month and year effects in order to control for seasonal differences in outcomes and for longer term trends affecting all births in the state (e.g., due to other improvements in medical care), zip code fixed effects (3 digit) in order to control for characteristics of the location that may be associated with both medical care and outcomes, and we also include indicators for missing marital status, smoking, birth order, and whether the birth occurred on a weekday. The standard errors are clustered at the level of the zip code in order to allow for unobserved correlations across a physician’s cases.
Sample means are shown in table 2. The estimation sample is smaller than in table 1 because, while we used all births to calculate the probability of C-section, in the rest of the paper we exclude births that were not attended by a doctor, as well as those for whom we cannot calculate our measure of decision making (because there are too few births per provider, defined as 25 or less).7 These exclusions leave us with approximately 1,000 providers, who together deliver the vast majority of the babies in New Jersey over the sample period. We show sample means for all women and for those with (low C-section risk) and those with (high C-section risk). This cutoff is chosen because figure 3 suggests a gap in C-section propensities at that value and because it divides the sample approximately in half. The first panel shows how the outcome variables vary with risk. As expected, higher-risk women have more C-sections and a higher risk of a bad outcome. Examining the type of bad outcome more narrowly suggests that women at high risk of C-section are more likely to experience complications of labor and delivery, as well as late maternal complications, and that their infants are at a higher risk of neonatal death.
Table 2.
Means for Full Sample and by Probability of C-Section
| C-Section Risk | Full Sample | Low Risk of C-Section | High Risk of C-Section |
|---|---|---|---|
| Outcomes: | |||
| C-section rate | .331 | .103 | .545 |
| Any bad outcome | .127 | .111 | .143 |
| Bad maternal outcome | .055 | .037 | .073 |
| Bleeding, fever, seizures at delivery | .039 | .024 | .053 |
| Late maternal complications | .019 | .014 | .024 |
| Bad child outcome | .080 | .080 | .081 |
| Fetal distress | .071 | .073 | .069 |
| Birth injury | .003 | .003 | .003 |
| Neonatal death | .004 | .003 | .006 |
| Doctor characteristics: | |||
| No. of deliveries per doctor | 1,019.45 (650.15) | 1,030.34 (674.73) | 1,009.22 (626.00) |
| Decision making | .000 (1.000) | −.032 (1.013) | .030 (.987) |
| Procedural skill differential | .000 (1.000) | −.016 (1.026) | .014 (.974) |
| Market price differential ($1,000) | 4.711 (1.606) | 4.687 (1.590) | 4.734 (1.621) |
| Share high risk | .122 | .116 | .127 |
| Mother and child characteristics: | |||
| African American | .158 | .185 | .132 |
| Hispanic | .210 | .244 | .179 |
| Married | .713 | .645 | .776 |
| High school dropout | .128 | .177 | .082 |
| Teen mom | .030 | .052 | .009 |
| Mom age 35 or more | .238 | .221 | .254 |
| Smoked | .081 | .090 | .073 |
| Child male | .513 | .514 | .513 |
| Child first born | .398 | .200 | .584 |
| Medicaid | .206 | .260 | .155 |
| Observations | 968,748 | 469,170 | 499,578 |
Note.—The analysis sample excludes birth attendants who were not physicians and birth attendants who had too few deliveries for a measure of diagnositic skill to be computed. Standard deviations are in parentheses.
The second panel explores the characteristics of doctors and provides some initial evidence with regard to an important question—the extent to which higher-risk patients see doctors with particular characteristics. Table 2 suggests that the doctors who treat low-risk patients do vary systematically from those that treat higher-risk patients. As discussed above, our measures of decision making and procedural skill have been transformed into Z-scores, so in the full sample, they have a mean of zero and a standard deviation of one. Table 2 shows that, on average, high-risk patients see doctors with slightly better decision making (0.03 standard deviations) and slightly better surgical skills (0.014 standard deviations). Conversely, low-risk patients see doctors with slightly lower decision making (−0.032 standard deviations) and procedural skill (−0.016 standard deviations). Thus, while there is some evidence of sorting, the extent of sorting appears to be quite small. There is also some evidence that high-risk patients see doctors with slightly fewer deliveries and higher shares of high-risk patients in their practices. Again, however, these differences are quite small.
The third panel of the table provides an overview of selected maternal and child characteristics, including race and ethnicity, maternal education, marital status, and whether the birth is covered by Medicaid. The table suggests that women at higher risk of C-section tend to be older, married, and more likely to have private insurance rather than Medicaid. They are also more likely to be delivering a first child, and they are less likely to be African American or Hispanic.
One empirical difficulty involved in estimating (12) is the possibility that women choose their doctors on the basis of the doctor’s skill. If women with high-risk pregnancies choose better doctors, then the estimated effect of doctor skill on birth outcomes will be biased toward zero. Table 2 suggests that there is some evidence of this type of selection, although it appears to be quite small. A second empirical problem is that we are using estimated values of diagnostic and surgical skill, which are inevitably measured with some error.
One way to address these issues is to estimate models using market-level measures of skill as instruments for individual doctor’s skill levels. Following Kessler and McClellan (1996), our definition of a hospital market is all of the providers actually selected by women in a particular zip code in a particular year. Specifically, we include all hospitals within 10 miles of the woman’s residence plus any hospital used by more than three women from her zip code of residence in the birth year, and we consider all of the providers who practiced in those hospitals in that year as part of the relevant market. Figure 4 shows the distribution of hospitals and illustrates this way of defining markets. The figure shows that most women choose nearby hospitals but that some women bypass nearby hospitals in favor of hospitals further away. In some cases, these are regional perinatal centers that are better equipped to deal with high-risk cases. For example, women from Princeton, New Jersey, could give birth in the hospital in town, but many travel as far away as Morristown (two counties to the north) to deliver in other hospitals.8 Thus, there is a distinct market, or set of provider choices, facing each woman at the time of each birth.
Fig. 4.
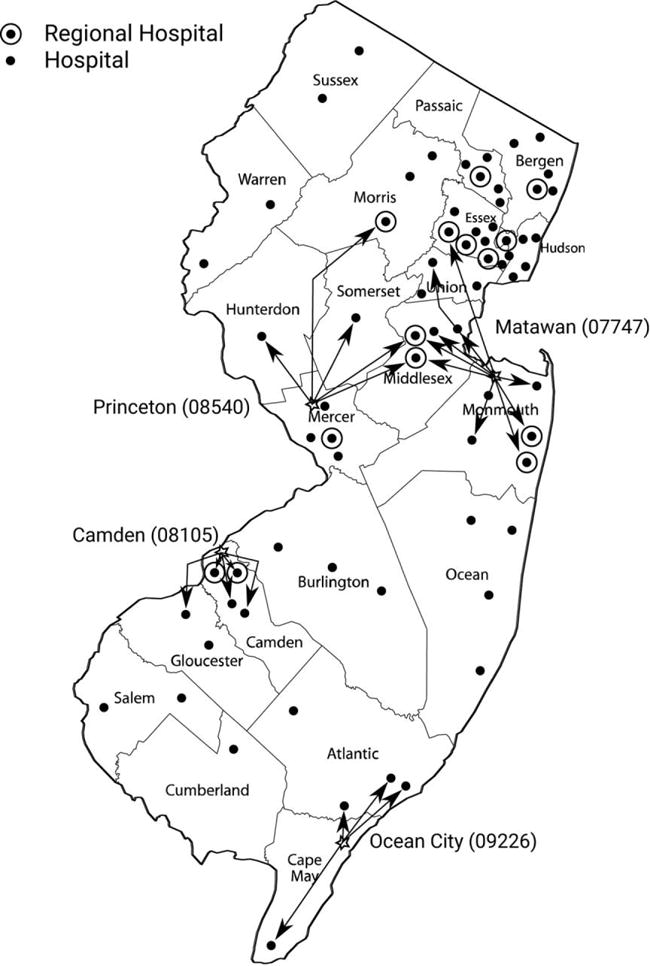
Illustrating the definition of a market
Given this definition of a market, we construct instruments by taking the weighted mean of the decision-making and surgical skill measures for all physicians in the market in the birth year, where the weights are given by the number of deliveries by each physician.9 We interpret this instrument as a summary measure of the choices available to a woman in a particular market.10 By definition, these choices are affected by where women live, but recall that we control for zip code fixed effects in all our models. Therefore, variation in the set of providers facing each woman at a point in time comes mainly from entry and exit of providers into the various markets rather than from any fixed long-term differences in the availability of services. So as long as women are not moving in order to take advantage of year-to-year fluctuations in the skill set of local physicians, our instruments will be valid. Using instrumental variables is also a valid approach to producing standard errors that account for the fact that the health index is estimated in the first step of our procedures. Our standard errors are clustered at the zip code level to allow for possible within-zip correlation in the errors. Table 3, which shows the first-stage regressions, shows that these instruments are highly predictive.11 Note that it is important to include the provider actually chosen in the possible choice set. Otherwise, people living in an area with only one provider (for whom endogeniety of provider choice is not an issue since they only have one choice) would have to be excluded from the model. Our argument is similar to that of Angrist, Imbens, and Rubin (1996) in that we assume that if the mean surgical skill of doctors in an area increases, then a woman will be more likely to end up with a highly skilled doctor.
Table 3.
First-Stage Regressions of Doctor-Level Measures on Market Skill Measures
| Doctor Decision Making
|
Doctor Surgical Skill
|
|||||
|---|---|---|---|---|---|---|
| All | Low | High | All | Low | High | |
| Market decision making | .353 (.002) |
.356 (.002) |
.347 (.002) |
−.026 (.002) |
−.024 (.002) |
−.028 (.002) |
| Market surgical | −.014 (.001) |
−.009 (.002) |
−.019 (.002) |
.284 (.002) |
.290 (.003) |
.276 (.003) |
| R2 | .165 | .179 | .152 | .098 | .105 | .090 |
Note.—Standard errors (in parentheses) are clustered at the 3-digit zip code level. Regressions also include market price, estimated C-section risk, indicators for African American, Hispanics, race missing, education (less than high school, high school, some college, missing), married, married missing, Medicaid, Medicaid missing, teen mom, 25–34, 35 plus, smoking, smoking missing, male child, parity 2, parity 3, parity 4 plus, parity missing, month and year of birth indicators, indicators for 3-digit zip code, and an indicator for whether the birth was on a week day.
A third issue is that, by construction, good decision makers should be less likely to perform C-sections on low-risk women and more likely to perform C-sections on high-risk women. Similarly, physicians with good procedural skills should have better outcomes for the high-risk relative to the low-risk. However, it is important to note that there is no mechanical reason for our measure of decision making to affect health outcomes, and similarly there is no mechanical reason for our measure of procedural skill to affect C-section rates. Thus, estimates of these two relationships form the true test of our model.
V. Results
Table 4 shows both ordinary least squares (OLS) and two-stage least squares (2SLS) estimates of equation (12), where the dependent variable is whether there was a C-section. These models include all of the control variables discussed above. The full OLS models for the probability of C-section are shown in appendix table A1. Conditional on C-section risk, African American and Hispanic women are more likely to have C-sections, as are less educated women, single women, older mothers, and mothers of first-born children. These estimates suggest that the stereotype that it is primarily older, better-educated white women who are “too posh to push” may be incorrect. The estimated effect of market prices is positive, but it is not precisely estimated.
Table 4.
Effect of Doctor Decision Making and Surgical Skill on P(C-Section) and Health Outcomes
| C-Section Risk (Ordinary Least Squares)
|
C-Section Risk (Two-Stage Least Squares)
|
|||||
|---|---|---|---|---|---|---|
| All | Low | High | All | Low | High | |
| Dependent variable = C-section: | ||||||
| Decision making | .004 (.002) |
−.011 (.002) |
.018 (.002) |
.000 (.006) |
−.016 (.005) |
.019 (.008) |
| Procedural skill difference | .003 (.002) |
.003 (.001) |
.003 (.002) |
.020 (.010) |
.017 (.008) |
.030 (.011) |
| R2/x2 | .410 | .044 | .321 | 710,797 | 15,293 | 62,526 |
| Dependent variable = any bad outcome: | ||||||
| Decision making | −.008 (.002) |
−.007 (.001) |
−.009 (.002) |
−.013 (.006) |
−.013 (.007) |
−.013 (.006) |
| Procedural skill difference | −.017 (.002) |
−.008 (.002) |
−.027 (.002) |
−.058 (.006) |
−.047 (.007) |
−.072 (.006) |
| R2/x2 | .020 | .016 | .023 | 6,750 | 13,635 | 1,695 |
| Observations | 968,748 | 469,170 | 499,578 | 968,748 | 469,170 | 499,578 |
Note.—Standard errors (in parentheses) are clustered at the 3-digit zip code level. Regressions also include market price, estimated C-section risk, indicators for African American, Hispanics, race missing, education (less than high school, high school, some college, missing), married, married missing, Medicaid, Medicaid missing, teen mom, 25–34, 35 plus, smoking, smoking missing, male child, parity 2, parity 3, parity 4 plus, parity missing, month and year of birth indicators, indicators for 3-digit zip code, and an indicator for whether the birth was on a week day. R-squared is shown for ordinary least squares and chi-squared is shown for two-stage least squares.
As discussed above, the OLS coefficients on the measures of physician skill may be biased by selection and by measurement error. For example, a woman who desires a C-section regardless of her medical condition will be likely to seek a physician who does not insist on using her medical condition to determine treatment. In our taxonomy, this will be a physician with a low slope term, which we are identifying with poor decision making. In this case, OLS estimates of the coefficients on decision making will be biased toward zero. It is less clear how the coefficient on surgical skill will be affected. Other things being equal, a woman bent on surgery might prefer a better surgeon. However, decision making and surgical skill tend to be positively correlated in our data (the correlation in the raw measures is 0.259), so in choosing someone willing to disregard her medical condition, she may also be choosing a relatively poor surgeon, in which case the coefficient on surgical skill will also be biased downward.
Table 4 suggests that the coefficients on both skill measures are biased toward zero in the OLS, although we do not have the precision to reject the null hypothesis that the OLS and 2SLS estimates of the effects of decision making are the same. The 2SLS estimates indicate that a one standard deviation increase in decision making would reduce the risk of C-section by 1.6 percentage points among women in the lower half of the risk distribution (a 15.5% reduction in the probability of C-section for these women) but would increase the probability of C-section by 1.9 percentage points (a 3.5% increase in the probability of C-section) in the upper half of the distribution. Overall, our measure of decision making has little effect, but this overall result masks the type of heterogeneity in the effects of decision making on low-risk and high-risk women that is predicted by our model.
An increase in surgical skill is estimated to increase the risk of C-section for everyone. For women in the lower half of the risk distribution, the 2SLS estimate is 1.7 percentage points, indicating that a one standard deviation increase in surgical skill would increase the risk of C-section by 16.5%. Among women in the top half of the risk distribution, the increase is 3 percentage points, or 5.5%. In the case of surgical skill, the 2SLS estimates are considerably larger than the OLS estimates. Table 2 does not suggest a huge amount of selection in terms of surgical skill. However, given that each surgeon has a relatively small number of very-high-risk and very-low-risk cases and that bad outcomes are thankfully relatively rare, our measure of surgical skill is likely to be quite noisy. Thus, measurement error may account for the increase in the absolute value of the estimated coefficients when we move to 2SLS.
The second panel of table 4 shows the estimated effect of the two types of skill on the probability of any bad outcome. Once again, the OLS coefficients are smaller than the 2SLS coefficients, and this is especially pronounced for the measures of surgical skill. The 2SLS estimates suggest that a one standard deviation increase in decision making is associated with a 1.3 percentage point decrease in the probability of any bad outcome among both low-risk and high-risk women. This translates into a 15.3% decline among the low risk and a 9.1% decline among the high risk. Similarly, a one standard deviation increase in surgical skill reduces the probability of any bad outcome by 42.3% among the low risk and by 50.3% among the high risk.
Tables 5 and 6 delve more deeply into the types of bad outcomes experienced by mothers and children, respectively. Table 5 shows the effects of skill on any bad maternal outcome and then divides these outcomes temporally into bleeding, fever, and seizures that take place during the labor and delivery and complications that take place after the delivery (e.g., infection or bleeding following surgery). Once again, we focus on the 2SLS results, which tend to be larger than the OLS estimates, especially for the surgical skill measures. Better decision making is estimated to reduce the incidence of bad maternal outcomes, especially for those at low risk. Among the low-risk group, decision making significantly reduces the incidence of bleeding, fever, or seizures during delivery, perhaps by discouraging unnecessary surgery. Among the high-risk group, there is no overall effect since better diagnosis reduces the incidence of bad outcomes during delivery but increases late maternal complications. A possible interpretation is that these women are more likely to need C-section deliveries so that providing C-section reduces the incidence of poor outcomes during delivery. However, major abdominal surgery is not without risk, and it increases the probability of complications after the delivery. Better surgical skills also reduce the incidence of maternal bad outcomes, but they have a greater percentage point impact among those at high risk than among those at low risk, which is to be expected given that the later are more likely to have surgery.
Table 5.
Effect of Doctor Decision Making and Surgical Skill on Maternal Health Outcomes
| C-Section Risk (Ordinary Least Squares)
|
C-Section Risk (Two-Stage Least Squares)
|
|||||
|---|---|---|---|---|---|---|
| All | Low | High | All | Low | High | |
| Dependent variable = any bad maternal outcome | ||||||
| Decision making | −.005 (.001) |
−.004 (.001) |
−.005 (.001) |
−.004 (.003) |
−.005 (.002) |
−.003 (.003) |
| Procedural skill difference | −.013 (.002) |
−.005 (.001) |
−.022 (.002) |
−.035 (.007) |
−.023 (.007) |
−.049 (.008) |
| R2/x2 | .018 | .013 | .016 | 4,342 | 15,389 | 1,993 |
| Dependent variable = bleeding, fever, seizures during delivery: | ||||||
| Decision making | −.006 (.000) |
−.004 (.000) |
−.008 (.001) |
−.012 (.002) |
−.008 (.001) |
−.016 (.003) |
| Procedural skill difference | −.007 (.001) |
−.001 (.000) |
−.013 (.001) |
−.009 (.003) |
−.004 (.002) |
−.018 (.004) |
| R2/x2 | .013 | .009 | .011 | 13,222 | 3,679 | 2,374 |
| Dependent variable = maternal complications after delivery: | ||||||
| Decision making | .001 (.001) |
−.0001 (.001) |
.002 (.001) |
.008 (.002) |
.003 (.002) |
.013 (.003) |
| Procedural skill difference | −.007 (.002) |
−.004 (.001) |
−.011 (.002) |
−.028 (.006) |
−.021 (.006) |
−.036 (.007) |
| R2/x2 | .017 | .013 | .020 | 5,822 | 1,002 | 648 |
| Observations | 968,748 | 469,170 | 499,578 | 968,748 | 469,170 | 499,578 |
Note.—Standard errors (in parentheses) are clustered at the 3-digit zip code level. Regressions also include market price, estimated C-section risk, indicators for African American, Hispanics, race missing, education (less than high school, high school, some college, missing), married, married missing, Medicaid, Medicaid missing, teen mom, 25–34, 35 plus, smoking, smoking missing, male child, parity 2, parity 3, parity 4 plus, parity missing, month and year of birth indicators, indicators for 3-digit zip code, and an indicator for whether the birth was on a week day. R-squared is shown for ordinary least squares and chi-squared is shown for two-stage least squares.
Table 6.
Effect of Decision Making and Surgical Skill on Child Health Outcomes
| C-Section Risk (Ordinary Least Squares)
|
C-Section Risk (Two-Stage Least Squares)
|
|||||
|---|---|---|---|---|---|---|
| All | Low | High | All | Low | High | |
| Dependent variable = any bad infant outcome: | ||||||
| Decision making | −.005 (.001) |
−.005 (.001) |
−.006 (.001) |
−.010 (.007) |
−.009 (.007) |
−.010 (.007) |
| Procedural skill difference | −.006 (.001) |
−.004 (.001) |
−.008 (.002) |
−.031 (.009) |
−.029 (.009) |
−.032 (.009) |
| R2/x2 | .013 | .010 | .017 | 17,881 | 1,126 | 2,044 |
| Dependent variable = fetal distress: | ||||||
| Decision making | −.003 (.001) |
−.004 (.001) |
−.003 (.001) |
−.012 (.006) |
−.012 (.006) |
−.012 (.006) |
| Procedural skill difference | −.003 (.001) |
−.003 (.000) |
−.004 (.001) |
−.024 (.006) |
−.025 (.006) |
−.023 (.006) |
| R2/x2 | .013 | .009 | .011 | 3,964 | 3,997 | 2,338 |
| Dependent variable = birth injury: | ||||||
| Decision making | .0001 (.000) |
.0001 (.000) |
.0001 (.000) |
.004 (.003) |
.003 (.002) |
.005 (.004) |
| Procedural skill difference | −.001 (.001) |
−.001 (.001) |
−.002 (.001) |
−.009 (.004) |
−.006 (.003) |
−.011 (.006) |
| R2/x2 | .003 | .002 | .004 | 1,023 | 380 | 603 |
| Dependent variable = neonatal death: | ||||||
| Decision making | −.002 (.000) |
−.001 (.000) |
−.002 (.000) |
−.001 (.001) |
−.0003 (.000) |
−.002 (.001) |
| Procedural skill difference | −.001 (.000) |
−.0003 (.000) |
−.002 (.000) |
.001 (.001) |
.001 (.000) |
.001 (.001) |
| R2/x2 | .007 | .004 | .010 | 2,231 | 1,438 | 2,015 |
| Observations | 968,748 | 469,170 | 499,578 | 968,748 | 469,170 | 499,578 |
Note.—Standard errors (in parentheses) are clustered at the 3-digit zip code level. Regressions also include market price, estimated C-section risk, indicators for African American, Hispanics, race missing, education (less than high school, high school, some college, missing), married, married missing, Medicaid, Medicaid missing, teen mom, 25–34, 35 plus, smoking, smoking missing, male child, parity 2, parity 3, parity 4 plus, parity missing, month and year of birth indicators, indicators for 3-digit zip code, and an indicator for whether the birth was on a week day. R-squared is shown for ordinary least squares and chi-squared is shown for two-stage least squares.
Table 6 breaks down the infant health outcomes. The first panel suggests that improvements in decision making reduce poor child health outcomes, though the 2SLS estimates are not very precise. The second panel indicates that there is a significant negative effect of poor decision making on the probability of fetal distress. This is slightly offset by a positive, though not statistically significant, effect on the probability of birth injury. A possible interpretation is that infants are more likely to sustain an injury such as a dislocated shoulder if a vaginal delivery is attempted. The last panel indicates that decision making has a significant negative effect on the probability of neonatal death, but only among the high-risk. This result suggests that C-sections can be life-saving for infants of mothers who really require a C-section but that unnecessary surgery does not pose a threat to the life of the infant among the low-risk.
A. Robustness
Given that the breakdown into high- and low-risk categories is arbitrary, one obvious way to explore the robustness of our results is by dividing mothers differently. Moreover, because, as we showed above, there is considerable consensus about the ranking of patients by appropriateness for C-section, we can assume that there is consensus about the high-risk and the low-risk but perhaps controversy about the people in the middle. Table 7 shows estimates based on three risk categories, where now low-risk is defined as the lowest quartile of , high-risk is defined as the highest quartile, and medium-risk is defined as the two quartiles in the middle. The first row of table 7 suggests that better decision making significantly reduces C-sections among the lowest-risk group but that it has a large positive effect on the highest-risk group. Better procedural skill increases C-section rates across the board. In keeping with the previous tables, the rest of table 7 suggests that better decision making and better procedural skill are broadly beneficial, even though for the low-risk these characteristics lead to fewer C-sections, while for the high-risk they lead to more.
Table 7.
Two-Stage Least Squares Estimates of Effect Decision Making and Surgical Skill, Three Risk Categories
| C-Section Risk
|
|||
|---|---|---|---|
| Low (p(csect) < .084) and | Medium (p(csect) ≥ .084 p(csect) ≤ .439) | High (p(csect) > .439) | |
| Dependent variable = C-section: | |||
| Decision making | −.015 (.004) |
−.013 (.009) |
.043 (.006) |
| Procedural skill difference | .014 (.007) |
.022 (.012) |
.034 (.012) |
| x2 | 5,100 | 24,066 | 11,817 |
| Dependent variable = any bad outcome: | |||
| Decision making | −.009 (.007) |
−.018 (.008) |
−.010 (.003) |
| Procedural skill difference | −.043 (.006) |
−.058 (.008) |
−.078 (.005) |
| x2 | 4,709 | 9,404 | 5,726 |
| Dependent variable = bad maternal outcome: | |||
| Decision making | −.004 (.002) |
−.008 (.004) |
.003 (.004) |
| Procedural skill difference | −.017 (.006) |
−.033 (.009) |
−.060 (.008) |
| x2 | 6,11 | 2,238 | 3,778 |
| Dependent variable: bad infant outcome: | |||
| Decision making | −.006 (.006) |
−.011 (.010) |
−.013 (.004) |
| Procedural skill difference | −.029 (.007) |
−.034 (.011) |
−.025 (.007) |
| x2 | 20,201 | 3,886 | 4,540 |
| Observations | 251,948 | 472,955 | 243,845 |
Note.—Standard errors (in parentheses) are clustered at the 3-digit zip code level. Regressions also include market price, estimated C-section risk, indicators for African American, Hispanics, race missing, education (less than high school, high school, some college, missing), married, married missing, Medicaid, Medicaid missing, teen mom, 25–34, 35 plus, smoking, smoking missing, male child, parity 2, parity 3, parity 4 plus, parity missing, month and year of birth indicators, indicators for 3-digit zip code, and an indicator for whether the birth was on a week day.
Table 8 considers only first-born children. The reason for this restriction is that the C-section rate is very high among mothers who have already had a C-section, and doctors may have more uncertainty about likely pregnancy outcomes in first births (because they do not have the birth history to rely on). In this sample, procedural skill has much the same effect as in table 7. Poor decision making also appears to have negative effects among the low-risk group, though there is less evidence of a significant effect among high-risk first births.
Table 8.
Two-Stage Least Squares Estimates of Effects of Decision Making and Surgical Skill, Three Risk Categories, First Births Only
| C-Section Risk
|
|||
|---|---|---|---|
| Low (p(csect) < .217) and | Medium (p(csect) ≥ .217 p(csect) ≤ .309) | High (p(csect) > .309) | |
| Dependent variable = C-section: | |||
| Decision making | −.018 (.007) |
−.015 (.010) |
.003 (.014) |
| Procedural skill difference | .021 (.013) |
.022 (.012) |
.028 (.017) |
| x2 | 3,619 | 14,647 | 73,872 |
| Dependent variable = any bad outcome: | |||
| Decision making | −.025 (.007) |
−.020 (.011) |
.000 (.008) |
| Procedural skill difference | −.066 (.011) |
−.067 (.010) |
−.084 (.009) |
| x2 | 4,725 | 17,470 | 131 |
| Dependent variable = bad maternal outcome: | |||
| Decision making | −.005 (.005) |
−.011 (.004) |
.001 (.004) |
| Procedural skill difference | −.043 (.015) |
−.039 (.009) |
−.054 (.010) |
| x2 | 1,179 | 6,085 | 303 |
| Dependent variable = bad infant outcome: | |||
| Decision making | −.022 (.006) |
−.009 (.013) |
.0004 (.009) |
| Procedural skill difference | −.032 (.009) |
−.04 (.013) |
−.045 (.010) |
| x2 | 1,840 | 1,359 | 690 |
| Observations | 95,118 | 184,210 | 105,739 |
Note.—Standard errors (in parentheses) are clustered at the 3-digit zip code level. Regressions also include market price, estimated C-section risk, indicators for African American, Hispanics, race missing, education (less than high school, high school, some college, missing), married, married missing, Medicaid, Medicaid missing, teen mom, 25–34, 35 plus, smoking, smoking missing, male child, parity 2, parity 3, parity 4 plus, parity missing, month and year of birth indicators, indicators for 3-digit zip code, and an indicator for whether the birth was on a week day.
VI. Discussion and Conclusions
The previous literature on treatment choice emphasizes that it is affected by physician skill but only allows physician skill to vary along a single dimension that can be thought of as technical skill in executing procedures, or surgical skill. Taking a cue from the literature on expert decision making, we develop a model that includes an additional dimension of skill: diagnostic decision making. In our model, a good doctor is one who not only is technically skilled but also able to draw the correct inferences from the available data in order to match patients correctly to the procedures that are most likely to benefit them. Suppose for example, that a policy is set so that a C-section rate of one-sixth is desired. One way to obtain a perfect rate would be to simply roll a die and give each woman with a six a C-section. And yet we do not think this would maximize health outcomes. Physicians in the data with flat “slopes” have both too low a C-section rate for high-risk cases and too high a C-section rate for low-risk patients. Effective policies to address procedure use should consider the possibility of variation in decision making and focus on assisting physicians in making the right decisions on an individual basis. Moreover, the right decision depends on the mother-physician pair, since physicians who are more skilled at performing surgery should have higher C-section rates, all other things being equal. In other words, the optimal policy is a function of both the condition of the patient and the quality of the physician’s human capital.
This simple framework yields rich predictions and allows us to distinguish between the two factors that we identify with the quality of decision making and procedural skill. The Bayesian learning model implies that better procedural skill leads to higher use of intensive procedures across the board for both high- and low-risk patients. In contrast, better decision making results in fewer procedures for those at low risk but more procedures for those at high risk. That is, better decision making improves the matching between patients and procedures and thus leads to better health outcomes in both groups.
We estimate the model parameters using data on C-sections, the most common surgical procedure performed in the United States. We find that improving decision making by one standard deviation would reduce C-section rates by 15.5% in the lower half of the distribution of C-section risk but would actually increase C-sections by 5.5% in the top half of the distribution. This finding suggests that not only are there too many C-sections among women without risk factors but there are too few C-sections in the group that really needs them. In fact, given the base rates shown in table 2, we estimate that improved decision making would have resulted in 7,490 fewer C-sections in the bottom half of the distribution but 14,975 more C-sections in the top half of the distribution, for a net increase of 7,485 C-sections. These extra C-sections among the high risk would have generated $35 million (2006 dollars) in additional costs and might have averted about a third of the 2,997 deaths that occurred in this high risk group over this 10-year period, for a cost per life saved of about $35,000. Among the low risk, the C-sections averted would have prevented about 2,346 cases of maternal complications. Of course, neonatal death is a rare outcome, and our estimates are subject to error, but taken at face value, they imply that with only modest increases in overall costs, better decision making could have improved outcomes for both infants and their mothers.
Our work highlights the importance of diagnostic decision making in medicine and suggests an empirical approach to measuring it: given a prediction of a patient’s medical appropriateness for a procedure, a doctor’s decision making can be evaluated by looking at whether he or she is responsive to this information. Note that if doctors did not respond to publicly observable information because they were basing their decisions on superior private information, then we would see that doctors who did not respond to public information had better outcomes. We show instead that doctors who are not responsive to the publicly observed patient medical information typically achieve worse health outcomes.
This finding suggests then that the medical information contained in sources such as electronic patient records could be used to improve medical decision making. We are not suggesting that doctors be replaced by machines but that a doctor’s individual expertise, which perforce depends on his or her individual experience, could be enhanced by applying simple algorithms to the “big data” contained in millions of administrative medical records. Another idea that follows from these results is that if we can distinguish between various forms of skill, then we might be able to improve outcomes by having teams deliver care. In our example, one doctor might make the decision regarding C-section, while another doctor executed it.
Finally, it is worth considering whether our example sheds light on how we might evaluate other types of experts. As we highlighted in the introduction, protocols and checklists have already been introduced in medicine. While we argue that these protocols could be improved, they do highlight the actions of doctors as well as the outcomes of patients. In contrast, there are many markets (such as teaching) where we seek to evaluate the quality of experts but focus almost exclusively on outcomes (e.g., student test scores) with little attention paid to either collecting or analyzing data about the expert’s actions. This is despite a long history in labor economics of understanding that sometimes it is better to base compensation on inputs rather than outputs (Lazear 1986). Viewed in this light, our results suggest that research on evaluating (e.g., Rockoff et al. 2010) and characterizing the actions of successful experts (e.g., Dobbie and Fryer 2013) represents an important first step in the assessment of their quality.
Acknowledgments
We thank Samantha Heep, Dawn Koffman, Jessica Van Parys, and Geng Tong for excellent research assistance, and Amitabh Chandra, Jonathan Gruber, Amy Finkelstein, Kate Ho, Robin Lee, Jonathan Skinner, and seminar participants at Princeton, Georgetown University, Havard Medical School, Kyoto University, New York University, the Japanese National Institute of Population and Social Security Research, Warwick University, University College London, the London School of Economics, the Paris School of Economics, the NBER Summer Institute, and the University of Michigan for helpful comments. This research was supported by a grant from the Program on US Health Policy of the Center for Health and Wellbeing.
Appendix
Proofs
Proof of Proposition 1
If x ∼ N(m, σ2) has a normal prior distribution, and one has an observation y = x + ε, where is normally distributed and independent of x, then from theorem 1 of DeGroot (1972, section 9.5), the posterior distribution of x ∼ N(πm + (1 − π)y, ρx + ρy), where ρx = 1=σ2 and are the precisions of x and y, while π = ρx=(ρx + ρy) is the weight on prior mean.
The normal distribution is called a conjugate family because when the prior and signals are normally distributed, then so is the posterior. This allows for very simple linear learning rules. We can use other distributions, but it would greatly complicate the analysis while providing few benefits in terms of new insights. QED
Proof of Proposition 2
From (8) we have T = C if and only if
| (A1) |
The right-hand side is a normal distribution with zero mean and variance
| (A2) |
Hence, we can write (A1) as
where ε ∼ N(0, 1). Hence, we have
from which we obtain the result. QED
The Effect of Diagnostic and Surgical Skill on Outcomes
Let IC(hi, ωj) = 1 if and only if physician j chooses procedure C for patient i with condition hi, and equal zero otherwise. Given this indicator for procedure choice, the expected medical outcome of a patient with condition hi being treated by physician j is given by
However, since physicians take into account both costs, mj, and patient preferences, , their decisions do not maximize observed medical benefit, which complicates the computation of the effect of exogenous parameters on measured medical outcomes.
In this section, we derive the effect of physician characteristics on observed medical outcome by measured risk . Formally we wish to compute
Since we have assumed that information about health is normally distributed, we can use results about the expectation of normally distributed random variables conditional on a truncated distribution to obtain a closed form solution for patient welfare. See Birnbaum (1950).
Proposition A1
The expected medical benefit from treatment satisfies
This is an exact formula that essentially replaces hi with plus an adjustment term to control for the fact that we do not observe hi but only an indicator, . If we assume that the effect of physician characteristics on the final term in welfare, , is small, then we can derive an intuitive expression for the effects of physician characteristics on outcomes.
Consider first the effect of surgical skill:
This formula shows that the effect of skill on patient welfare can be broken into two parts. The first term is always positive, indicating that for a woman who is having the intensive procedure, more skill is always better. However, the second term is ambiguous in sign. We know that , so that other things being equal, greater doctor skill increases the probability that an intensive procedure will be performed. If , then the second term is positive and greater doctor skill enhances patient welfare. However, for a low enough value of , it is possible that (health status is in log terms, and hence is negative for low values). If is large enough, then increases in doctor skill could make patients who do not need a C-section worse off by increasing the probability that they will receive an unnecessary procedure.
Next, consider the effect of physician sensitivity to patient condition, θj. The variable is a combination of various aspects of physician characteristics, but we cannot separately observe these aspects. We do observe θj and γj for each physician in our data, and hence we can ask how outcomes would vary if we were to hold γj fixed but allow θj to vary. Since θj has a first-order effect on our last term, we include it, and leave out the f′′ term. In that case, we get
This result illustrates the fact that the preferences of the physician take into account their prior beliefs, costs, and patient preferences. Hence, in general, γj ≠ sj. Whenever then it is possible to have sign(∂W=∂θj) < 0, but in all other cases we have a positive effect.
Proof
We can write welfare as
Next we condition on and observe that , since this is strictly less information. First, we already have from equation (10):
Next we have from equation (8):
From Birnbaum (1950), we have that if X and Z are two normally distributed random variables with variances and , then
where R(x) = f(x)/(1 − F x)) is the Mills ratio for the normal distribution. Applying this formula with , , and we get
where σj is defined in (A2). Notice that θj = 1=σj and . Thus, we get
Now
and therefore we may write
Proposition A2
Suppose , then increasing decision making improves medical outcomes.
Table A1.
Effect of Decision Making and Surgical Skill on Probability of C-Section (Ordinary Least Squares)
| All | Low Risk | High Risk | |
|---|---|---|---|
| Decision making | .004 (.002) |
−.011 (.002) |
.019 (.002) |
| Procedural skill difference | .003 (.002) |
.003 (.001) |
.003 (.002) |
| Market price (coefficient 100) | .276 (.226) |
.291 (.249) |
.285 (.221) |
| C-section risk | 1.002 (.007) |
.902 (.069) |
.906 (.009) |
| African American | .050 (.004) |
.047 (.003) |
.050 (.005) |
| Hispanic | .036 (.003) |
.024 (.002) |
.051 (.005) |
| Less than high school | .022 (.003) |
.019 (.002) |
.026 (.005) |
| High school | .026 (.001) |
.022 (.002) |
.032 (.003) |
| Some college | .012 (.001) |
.011 (.002) |
.013 (.002) |
| Married | −.007 (.002) |
−.009 (.003) |
−.006 (.003) |
| Medicaid | .005 (.004) |
.007 (.004) |
.001 (.006) |
| Teen mom | −.013 (.004) |
−.023 (.005) |
.012 (.009) |
| Mother age 25–34 | .019 (.003) |
.028 (.002) |
.005 (.004) |
| Mother age 35+ | .025 (.003) |
.041 (.003) |
.013 (.005) |
| Mother smoked | .007 (.004) |
.010 (.003) |
.004 (.006) |
| Child male | .023 (.001) |
.018 (.001) |
.027 (.002) |
| Child 2nd born | −.013 (.003) |
−.040 (.008) |
.051 (.004) |
| Child 3rd born | −.018 (.003) |
−.043 (.009) |
.032 (.006) |
| Child 4th born or higher | −.022 (.006) |
−.034 (.010) |
.001 (.010) |
| R2 | .410 | .044 | .319 |
| Observations | 968,748 | 469,170 | 499,578 |
Note.—Standard errors (in parentheses) are clustered by 3-digit zip code. Regressions also include indicators for month and year of birth and 3-digit zip code, as well as indicators for missing education, marital status, Medicaid coverage, smoking, parity, and an indicator for birth on a weekday.
Fig. A1.
Shift in probability of C-section given medical risk over time
Fig. A2.
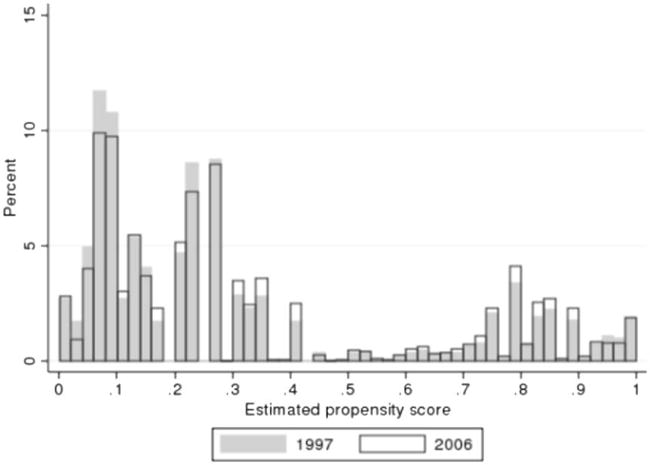
Shift in medical risks over time
Footnotes
This paper was presented as part of the Presidential Address of the SOLE/EALE meeting in Montreal, in June 2015.
It is assumed that we have taken logs of level variables, and hence utility is any real number (positive or negative), and the units have been defined appropriately.
We could put these preference terms into both equations, but ultimately we are concerned about the relative preference of procedure C to N, and so we need only place this term into one equation.
We do not include low birth weight and short gestation in this index, because they can be the direct consequence of the decision to do a C-section in an otherwise normal pregnancy. This is why organizations such as the March of Dimes specifically targeted the elimination of non-medically-indicated (elective) deliveries before 39 weeks gestational age as a strategy to reduce prematurity.
These codes do not identify the physician but allow us to identify all births delivered by the same physician. We found, as a practical matter, that very few doctors practiced in more than one hospital in a single year; hence, the choice of doctor also defines the choice of hospital.
It is important to note that physician charges are generally separate from hospital charges and are not included in HCUP. Also, while Medicaid generally reimburses less than private insurance for deliveries, we do not find a significant effect of Medicaid coverage on C-section delivery, as shown in table A1.
We also exclude a very small number of doctors who did not have at least one high-risk patient and at least one low-risk patient.
The figure also illustrates that the common practice of drawing a circle around a location in order to define a market is likely to be seriously misleading: a circle wide enough to include all the hospitals actually chosen would include hospitals that were never chosen, and a circle wide enough to include most hospitals could miss specialty hospitals that were further away and yet within the choice set.
In the crowded northern New Jersey hospital market, we included only hospitals within 5 miles of the zip code centroid.
Note that the rationale for this instrument has nothing to do with the presence or absence of provider spillovers. Rather, market-level measures reflect what is available to the patient and therefore will affect the type of physician chosen. Consider two markets: in A, all of the physicians are very responsive, and in B, physicians flip coins in order to determine whether to do C-sections. In this scenario, patients living in market A would be more likely to have responsive physicians, while for those living in market B, the probability of C-section would be independent of patient condition. The main threat to identification in this scenario would be that patients in markets A or B might just have very different unobservables. This is why we include market-specific fixed effects. With the inclusion of these effects, we are identified using year-to-year fluctuations in the types of physicians who are available. Stable long-term differences in the populations of physicians will be controlled by the fixed effects. Hence, our identification is only threatened if mothers systematically change residences with the short-run fluctuations in available physician types.
The IV estimate assumes that the instrument affects outcomes only through the quality of the doctor. Yet it is conceivable that the quality of the hospital in terms of nursing staff, for example, also matters. In this case, the IV estimate is going to pick up the “true” effect of the physician skill level plus the nearby-hospital-specific effects. If better doctors practice in higher-quality hospitals, then the 2SLS estimates could be biased upward. In this case, the true estimate would be bounded by the OLS and IV. However, in practice, we found that there was as much variation in doctor quality within hospitals as between hospitals, leading us to believe that doctors are not strongly sorted into particular hospitals.
Contributor Information
Janet Currie, Princeton University and National Bureau of Economic Research.
W. Bentley MacLeod, Columbia University and National Bureau of Economic Research.
References
- Abaluck Jason, Agha Leila, Kabrhel Christopher, Raja Ali, Venkatesh Arjun. Negative tests and the efficiency of medical care: What determines heterogeneity in imaging behavior? National Bureau of Economic Research; Cambridge, MA: 2014. (NBER Working Paper no. 19956). [Google Scholar]
- Angrist Joshua D, Imbens Guido, Rubin Donald B. Identification of causal effects using instrumental variables. Journal of the American Statistical Association. 1996;91(434):444–55. [Google Scholar]
- Arlen Jennifer, MacLeod W Bentley. Torts, expertise, and authority: Liability of physicians and managed care organizations. Rand Journal of Economics. 2005;36(3):494–519. [PubMed] [Google Scholar]
- Baicker Katherine, Fisher Elliott S, Chandra Amitabh. Malpractice liability costs and the practice of medicine in the medicare program. Health Affairs. 2007;26(3):841–52. doi: 10.1377/hlthaff.26.3.841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ross Baker G, MacIntosh-Murray Anu, Porcellato Christina, Dionne Lynn, Stelmacovich Kim, Born Karen., editors. High performing health-care systems: Delivering quality by design. Toronto: Longwoods; 2008. [Google Scholar]
- Birnbaum ZW. Effect of linear truncation on a multinormal population. Annals of Mathematical Statistics. 1950;21(2):272–79. [Google Scholar]
- Chan David C. Tacit learning and influence behind practice variation: Evidence from physicians in training. University of Maryland; College Park: 2015. Unpublished manuscript. [Google Scholar]
- Chandra Amitabh, Cutler David, Song Zirui. Who ordered that? The economics of treatment choices in medical care. In: Mcguire Thomas G, Pauly Mark V, Barros Pedro P., editors. Handbook of health economics. Vol. 2. Amsterdam: Elsevier; 2012. pp. 397–432. [Google Scholar]
- Chandra Amitabh, Staiger Douglas O. Productivity spillovers in health care: Evidence from the treatment of heart attacks. Journal of Political Economy. 2007;115(1):103–40. doi: 10.1086/512249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chandra Amitabh, Staiger Douglas O. Expertise, underuse, and overuse in healthcare. 2011 Unpublished manuscript. [Google Scholar]
- Consumer Reports. Risks of C-sections. Consumer Reports. 2015 http://www.consumerreports.org/doctors-hospital/your-biggest-c-section-risk-may-be-your-hospital/
- Currie Janet, MacLeod W Bentley. First do no harm? Tort reform and birth outcomes. Quarterly Journal of Economics. 2008;123(2):795–830. [Google Scholar]
- Cutler David, Skinner Jonathan, Stern Ariel Dora, Wennberg David. Physician beliefs and patient preferences: A new look at regional variation in health care spending. National Bureau of Economic Research; Cambridge, MA: 2013. (NBER Working Paper no. 19320). [Google Scholar]
- DeGroot Morris H. Optimal statistical decisions. New York: McGraw-Hill; 1972. [Google Scholar]
- Dobbie Will, Fryer Roland G. Getting beneath the veil of effective schools: Evidence from New York City. American Economic Journal: Applied Economics. 2013;5(4):28–60. [Google Scholar]
- Doi Kunio. Computer-aided diagnosis in medical imaging: Historical review, current status and future potential. Computerized Medical Imaging Graphics. 2007;31(4):198–211. doi: 10.1016/j.compmedimag.2007.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dranove David. Demand inducement and the physician/patient relationship. Economic Inquiry. 1988;26(2):281–98. doi: 10.1111/j.1465-7295.1988.tb01494.x. [DOI] [PubMed] [Google Scholar]
- Dranove David, Jin Ginger Zhe. Quality disclosure and certification:Theoryandpractice. Journal of Economic Literature. 2010;48(4):935–63. [Google Scholar]
- Dranove David, Kessler Daniel, McClellan Mark, Satterthwaite Mark A. Is more information better? The effects of “report cards” on health care providers. Journal of Political Economy. 2003;111(3):555–87. [Google Scholar]
- Dranove David, Ramanarayanan Subramaniam, Sfekas Andrew. Does the market punish aggressive experts? Evidence from Cesarean sections. BE Journal of Economic Analysis and Policy. 2011;11(2):1–33. [Google Scholar]
- Dubay Lisa, Kaestner Robert, Waidmann Timothy. The impact of malpractice fears on Cesarean section rates. Journal of Health Economics. 1999;18(4):491–522. doi: 10.1016/s0167-6296(99)00004-1. [DOI] [PubMed] [Google Scholar]
- Epstein Andrew J, Nicholson Sean. The formation and evolution of physician treatment syltes: An application to Cesarean sections. Journal of Health Economics. 2009;28(6):1126–40. doi: 10.1016/j.jhealeco.2009.08.003. [DOI] [PubMed] [Google Scholar]
- Finkelstein Amy, Gentzkow Matthew, Williams Heidi. Sources of geographic variation in health care: Evidence from patient migration. National Bureau of Economic Research; Cambridge, MA: 2014. (NBER Working Paper no. 20789). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank Richard G, McGuire Thomas G. Economics and mental health. In: Culyer Anthony J, Newhouse Joseph P., editors. Handbook of health economics. pt. B. Vol. 1. Amsterdam: Elsevier; 2000. pp. 893–954. [Google Scholar]
- Gawande Atul. The checklist manifesto: Getting things right. New York: Picador; 2009. [Google Scholar]
- Gaynor Martin, Rebitzer James B, Taylor Lowell J. Physician incentives in health maintenance organizations. Journal of Political Economy. 2004;112(4):915–31. [Google Scholar]
- Grove William M, Zald David H, Lebow Boyd S, Snitz Beth E, Nelson Chad. Clinical versus mechanical prediction: A meta-analysis. Psychological Assessment. 2000;12(1):19–30. [PubMed] [Google Scholar]
- Gruber Jonathan, Kim John, Mayzlin Dina. Physician fees and procedure intensity: The case of Cesarean delivery. Journal of Health Economics. 1999;18(4):473–90. doi: 10.1016/s0167-6296(99)00009-0. [DOI] [PubMed] [Google Scholar]
- Gruber Jonathan, Owings Maria. Physician financial incentives and Cesarean section delivery. RAND Journal of Economics. 1996;27(1):99–123. [PubMed] [Google Scholar]
- Hastie Trevor, Tibshirani Robert, Friedman Jerome. The elements of statistical learning: Data mining, inference, and prediction. 2nd. New York: Springer; 2009. [Google Scholar]
- Johnson Erin M, Rehavi M Marit. Physicians treating physicians: Information and incentives in childbirth. American Economic Journal: Economic Policy. 2016;8(1):115–41. [Google Scholar]
- Joint Commission. Specification manual for Joint Commission National Quality Core Measures. Joint Commission; 2014. Version 2014A1 https://manual.jointcommission.org/releases/TJC2014A1/ [Google Scholar]
- Kahneman Daniel, Klein Gary. Conditions for intuitive expertise: A failure to disagree. American Psychologist. 2009;64(6):515–26. doi: 10.1037/a0016755. [DOI] [PubMed] [Google Scholar]
- Kessler Daniel, McClellan Mark. Do doctors practice defensive medicine? Quarterly Journal of Economics. 1996;111(2):353–90. [Google Scholar]
- Kozhimannil Katy Backes, Law Michael R, Virnig Beth A. Cesarean delivery rates vary tenfold among US hospitals: Reducing variation may address quality and cost issues. Health Affairs. 2013;32(3):527–35. doi: 10.1377/hlthaff.2012.1030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazear Edward P. Salaries and piece rates. Journal of Business. 1986;59(3):405–31. [Google Scholar]
- McCourt Chris, Weaver Jane, Statham Helen, Beake Sarah, Gamble Jenny, Creedy Debra K. Elective Cesarean section and decision making: A critical review of the literature. Birth. 2007;34(1):65–79. doi: 10.1111/j.1523-536X.2006.00147.x. [DOI] [PubMed] [Google Scholar]
- Meehl Paul E. Clinical versus statistical prediction: A theoretical analysis and a review of the evidence. Minneapolis: University of Minnesota Press; 1954. [Google Scholar]
- Newhouse Joseph P. Patients at risk: Health reform and risk adjustment. Health Affairs. 1994;13(1):132–46. doi: 10.1377/hlthaff.13.1.132. [DOI] [PubMed] [Google Scholar]
- Newhouse Joseph P, McWilliams J Michael, Price Mary, Huang Jie, Fireman Bruce, Hsu John. Do Medicare Advantage plans select enrollees in higher margin clinical categories? Journal of Health Economics. 2013;32(6):1278–88. doi: 10.1016/j.jhealeco.2013.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rockoff Jonah E, Staiger Douglas O, Kane Thomas J, Taylor Eric S. NBER Working Paper. 16240. National Bureau of Economic Research; Cambridge, MA: 2010. Information and employee evaluation: Evidence from a randomized intervention in public schools. [Google Scholar]
- Smith Gordon CS, Dellens Michael, White Ian R, Pell Jill P. Combined logistic and Bayesian modeling of Cesarean section risk. American Journal of Obstetrics and Gynecology. 2004;191(6):2029–34. doi: 10.1016/j.ajog.2004.04.027. [DOI] [PubMed] [Google Scholar]
- Song Yunjie, Skinner Jonathan, Bynum Julie, Sutherland Jason, Wennberg John E, Fisher Elliott S. Regional variations in diagnostic practices. New England Journal of Medicine. 2010;363(1):45–53. doi: 10.1056/NEJMsa0910881. [DOI] [PMC free article] [PubMed] [Google Scholar]


