Abstract
The dual-energy CT-based (DECT) approach holds promise in reducing the overall uncertainty in proton stopping-power-ratio (SPR) estimation as compared to the conventional stoichiometric calibration approach. The objective of this study was to analyze the factors contributing to uncertainty in SPR estimation using the DECT-based approach and to derive a comprehensive estimate of the range uncertainty associated with SPR estimation in treatment planning. Two state-of-the-art DECT-based methods, the Hünemohr-Saito method (2014, 2012) and the Bourque method (2014), were selected and implemented on a Siemens SOMATOM Force DECT scanner. The uncertainties were first divided into five independent categories. The uncertainty associated with each category was estimated for lung, soft and bone tissues separately. A single composite uncertainty estimate was eventually determined for three tumor sites (lung, prostate and head-and-neck) by weighting the relative proportion of each tissue group for that specific site. The uncertainties associated with the two selected DECT methods were found to be similar, therefore the following results applied to both methods. The overall uncertainty (1σ) in SPR estimation with the DECT-based approach was estimated to be 3.8%, 1.2% and 2.0% for lung, soft and bone tissues, respectively. The dominant factor contributing to uncertainty in the DECT approach was the imaging uncertainties, followed by the DECT modeling uncertainties. Our study showed that the DECT approach can reduce the overall range uncertainty to approximately 2.2% (2σ) in clinical scenarios, in contrast to the previously reported 1%.
1. Introduction
The rapid increase in the number of proton radiotherapy centers worldwide can be largely attributed to the unique characteristics of proton dose distribution (i.e., high dose-gradient at the distal end of the Bragg peak). The high dose-gradient enables the delivery of high doses to the tumor while sparing critical organs distal to the target (Mitin and Zietman, 2014; Loeffler and Durante, 2013; Karger et al., 2010; Smith, 2009; Schardt et al., 2010). However, a small shift of the highly conformal high-dose area can cause the target tumor to be substantially under-dosed or the critical organs to be substantially over-dosed (McGowan et al., 2013; Engelsman et al., 2013; Kang et al., 2007; Mirkovic et al., 2007). To solve this problem, treatment planning requires large margins to ensure adequate dose coverage of the target (Moyers et al., 2001), preventing us from fully exploiting the potential of proton beams. Moreover, range uncertainty undermines the physician’s confidence to select the beam angles that take full advantage of the proton beams (i.e., the beam angle with critical structures located right behind the target). This may account for the relative lack of prospective data from clinical trials that shows a clinical benefit for proton radiotherapy despite its theoretical advantages (Miller et al., 2013; Ju et al., 2014).
A major contributing factor to range uncertainty is the uncertainty related to the estimation of proton stopping-power-ratio (SPR) distribution inside a patient, required to account for tissue heterogeneities upon calculation of the dose distribution. The standard method to determine proton SPR within a patient is the stoichiometric calibration, which derives SPR from the patient’s CT images based on a pre-determined Hounsfield unit (HU)-to-SPR calibration curve (Schaffner and Pedroni, 1998; Schneider et al., 1996). We previously showed that this method is susceptible to tissue composition variations between patients because of the degeneracy between HU and SPR (Yang et al., 2010; Yang et al., 2012). The SPR estimated using the stoichiometric method was estimated to carry approximately 3.5% uncertainty (Moyers et al., 2001; Moyers et al., 2010; Yang et al., 2012; Paganetti, 2012), although the results from the latest multi-institutional study indicated that this percentage may be larger (Moyers, 2014).
An alternative approach is to scan patients using dual energy CT (DECT) (Yang et al., 2010, 2011; Hünemohr et al., 2014; Bourque et al., 2014), through which both electron density ratio (EDR, ρe) and effective atomic number (EAN, Z) can be determined simultaneously. The idea of using DECT for proton SPR estimation was first proposed by Yang et al (2010). Their study discovered a unique relationship between Z and the mean excitation energy (MEE, I) of human body tissues, allowing the calculation of proton SPR from Z and ρe. The investigators also showed that the DECT approach is substantially more robust than the standard stoichiometric calibration approach in the presence of tissue composition variations.
Other groups have experimentally evaluated the DECT approach on tissue equivalent materials (Hünemohr et al., 2014; Bourque et al., 2014; Hansen et al., 2015; Han et al., 2016; Taasti et al., 2016). These studies reported that the DECT approach can predict proton SPR values within 1% error for tissue equivalent materials. However, in our opinion, these studies did not include all major uncertainty contributing factors. For example, the beam hardening artefact was not accounted for by using exactly the same scanning condition between the calibration and the testing (e.g., the same phantom size and the same location of the insert within the phantom). In reality, the size of the calibration phantom will not always be the same as that of the patient, and there exists same tissue types located at different body sites. Our prior studies showed that the beam hardening effect together with the beam hardening correction algorithm employed in the CT reconstruction process can cause substantial variation in the measured CT number and that the DECT approach is generally very sensitive to CT number variation (Yang et al., 2011; Yang et al., 2012). Another factor contributing to uncertainty that has not been considered is the uncertainty due to tissue composition variation between different patients. The uncertainty in SPR estimation will be underestimated when these factors are not considered. Consequently, treatment planning with the added margin based on those estimates may be less robust. These findings motivated us to comprehensively study the uncertainty in proton SPR estimation by using the DECT approach in a clinical setting. Our additional goal was to identify the bottle neck in the current DECT approach to further address it in future studies.
2. Materials and methods
2.1. The DECT-based approach
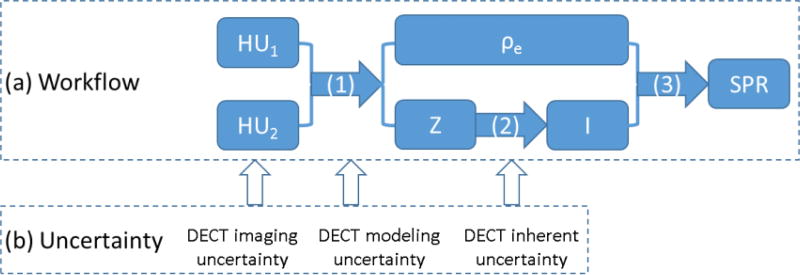
The DECT approach to estimating SPR typically includes three steps (figure 1(a)): 1) calculation of the EDR (ρe) and EAN (Z) from two HU values of the same CT voxel, acquired through two CT scans with different energy; 2) conversion of Z to MEE (I), based on an empirical relationship between these two quantities, as observed in human tissues (figure 2); 3) calculation of SPR from ρe and I, using the Bethe-Bloch equation, written as
| (1) |
where me c2 is the rest mass energy of the electron, β denotes the proton velocity relative to light speed, and Iw is the mean excitation energy of water.
Figure 1.
(a) Workflow of the DECT-based approach to predict proton SPR in human tissues and (b) corresponding uncertainties related to the DECT method. (1) Calculation of ρe and Z using the DECT HU values; (2) derivation of I from Z through their empirical relationship (shown in figure 2); (3) SPR calculation based on the Bethe-Bloch equation. The uncertainties categorization is discussed in detail in Section 2.2.
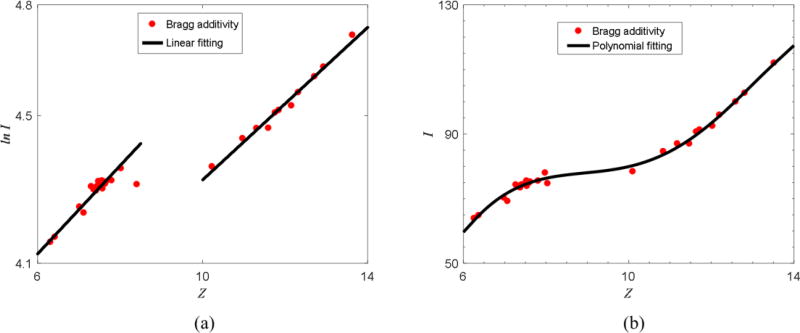
Figure 2.
(a) Empirical linear relationship between Z and ln I observed in human tissues. The dots represent human tissues. The two black lines indicate the linear fitting based on human tissue data points. (b) Polynomial fitting of Z and I proposed by Bourque et al. (2014). Note that the definition of Z is different from Mayneord’s equation.
A few DECT-based methods have been reported, which mainly differ in the first ρe and Z calculation step. In this study, we chose two methods that could potentially improve SPR accuracy in the clinical setting: the Hünemohr method and the Bourque method (Hünemohr et al., 2014; Bourque et al., 2014). The DECT method used in our previous study (Yang et al., 2010) was not included because it was found substantially more sensitive to CT number variation than the selected methods. The two selected DECT-based methods were briefly reviewed here, but readers can refer to the original manuscript for more details.
To validate our implementation, we tested the selected methods on two sets of experimental data. One data set was adopted from table 2 in the study by Hünemohr et al. (2014) for direct comparison. The other was our own dataset acquired on a Siemens SOMATOM Force DECT scanner (Munich, Germany).
2.1.1. The Hünemohr-Saito method
The method proposed by Hünemohr et al. (2014) assumes that the x-ray attenuation coefficient (μx) can be decomposed into photoelectric absorption and Compton scattering effect contributions, written as
| (2) |
where fKN is the Klein-Nishina formula, and E denotes the photon energy. The values of α, β, m and n depend on the energy spectra and materials used in the CT scan. Through a theoretical derivation, the investigators established two equations to determine ρe and Z from two HU values, expressed by
| (3) |
| (4) |
where μ1, μ2 are shifted HUs defined by , Zw is the effective atomic number of water. n was determined as 3.3, which gave the best fit between the EANs calculated using Mayneord’s equation (Mayneord, 1937) and the EANs calculated from CT numbers of 80 kVp and 150 kVp/Sn for standard human biological tissues (Yang et al. (2010)). Of note, ce, de can be calibrated by a single material other than water, but different calibration materials may yield inconsistent values.
Once Z is calculated, it can be parameterized to the logarithm of I (ln I), as demonstrated in figure 2(a). Having calculated ρe and ln I, the proton SPR of the materials can be estimated through the Bethe-Bloch equation.
Although this method needs only one calibration material, we found that the material selection has a substantial impact on the accuracy of SPR estimation. To address this issue, we adopted the method proposed by Saito (2012) to determine ρe, which was expected to be more robust because multiple materials could be used for calibration. A comparison between the Hünemohr and the Saito method can be found in Section 3.1.
The Saito method can be written as follows:
| (5) |
| (6) |
where α is the weighting factor of the subtracted CT number ΔαHU, and a and b are the linear fitting parameters. The value of α was determined by optimizing the fitting between ρe and ΔαHU. One interesting finding was that the calculation of ρe in the Hünemohr method is an ideal case for the Saito method (Farace, 2014). In the Hünemohr method, the CT number of water should consistently be zero at different energy levels. However, this constraint is relaxed in the Saito method because of the imperfections in the realistic CT system.
Inspired by the Saito method, we generalized the calculation of Z used in the Hünemohr method. Z can be parameterized as
| (7) |
| (8) |
where β is the weighting factor of the subtracted CT number ΔβHU, and c and d are the linear fitting parameters. The value of β was determined by optimizing the fitting between Z and ΔβHU, which may yield a different value from that of α. The combination of the Saito method and the Hünemohr method to calculate ρe and Z is referred to as the Hünemohr-Saito (HS) method in this study. The justification of the HS method is discussed in Section 3.1.
2.1.2. The Bourque method
Bourque et al. (2014) adapted a dual energy index that only depends on Z. The dual energy index can be expressed as
| (9) |
with K as a parameter that controls the level of accuracy. In our study, the K value was preset to 6, as in the original paper. After rewriting the above equation as a matrix form Z = Γc, ck can be determined by the least square method based on the known Z of the calibration materials and the preset K. The Z of the unknown materials can be calculated through the above equation, using DECT HUs.
A rigorous formalism was developed for the DECT-based stoichiometric calibration method as follows:
| (10) |
The above equation can be re-written as U = Fb :
where N is the number of materials, and M is the level of accuracy preset to 6. bm can be calculated by the least square method based on ρe and Z of the calibration materials. Using the relationship defined in Eq. (10), ρe can be calculated by and .
Once Z is determined, I can be estimated based on figure 2(b). With the calculated ρe and I, the Bethe-Bloch equation can be used to estimate SPR.
2.1.3. Theoretical calculation of μx, ρe, Z, I
The linear attenuation coefficient of a material can be calculated theoretically by
| (11) |
where ρx denotes the mass density, wi is the weight of energy Ei in the beam spectra, and ωj, Zj, Aj and (μ/ρ)j denote mass weight, atomic number, mass number and mass attenuation coefficient of the j-th element, respectively. The corresponding CT number can be calculated as
| (12) |
in which μw is the linear attenuation coefficient of water. The reference ρe, Z and I can be calculated with a known element composition and mass density, by following the formula:
| (13) |
| (14) |
| (15) |
where ρe, w is the ρe of water, and Ij is the I of the j-th element. Note that the definition of Z in the Bourque method is based on the bijective relationship with electronic cross section, which is different from the above Mayneord’s equation (14).
2.2. Uncertainty categorization
The uncertainties in the DECT calculation of SPRs were divided into three major independent categories based on the workflow shown in figure 1: 1) DECT imaging uncertainty, 2) DECT modeling uncertainty, and 3) DECT inherent uncertainty. The DECT imaging uncertainty captures the uncertainty in the input HU values caused by HU variation with varying scanning conditions (ΔHU1, ΔHU2). In contrast, the DECT modeling uncertainty captures the uncertainty in the ρe and Z calculation when HUs are acquired under the calibration scanning condition. The DECT inherent uncertainty refers to the uncertainty in the derivation of lnI from Z, which is inherent to all DECT methods. Two additional uncertainty categories, related to SPR calculation but not directly dependent on a particular DECT algorithm, were also included: 1) uncertainties in the mean excitation energy and 2) ignorance of SPR change with proton energy in current commercial treatment planning systems. All five uncertainty categories are described in detail in the following sections.
2.2.1. DECT imaging uncertainty
In the DECT-based approach, SPR is essentially a function of two variables, HU1 and HU2, CT voxel values acquired with two different X-ray spectra. Any scanning conditions differing from the calibration condition will cause the HU values to deviate from their true values (i.e., the values expected by the DECT model). The calibration condition refers to the scanning condition used in the calibration process. This causes uncertainties in the calculation of ρe and Z (Δρe and ΔZ), and eventually propagates to that of SPR (ΔSPR).
The uncertainties in the measured HU values are mainly caused by the so-called beam-hardening effect, which manifests itself as a HU variation of the same material with different scanning conditions (i.e., patient/phantom size, location within the scan [center vs. peripheral]). In this study, we considered three major factors: patient size, location within the scan and random HU variation scanned at different times.
The RMI 467 tissue characterization phantom (Gammex, Middleton, WI) with 16 tissue substitutes inserts is illustrated in figure 3(a). The tissues were classified into three groups: lung tissues, soft tissues and bone tissues. The lung tissue group included LN300 and LN450. The soft tissue group consisted of 6 tissues that contained a negligible amount of calcium (< 1%) and the bone tissue group consisted of 5 tissues that contained a substantial amount of calcium (> 7%). Results are presented separately for each group.
Figure 3.
Images of phantoms used in this study: (a) RMI 467 tissue characterization phantom and (b) head- and body-size customized phantoms. The head-size phantom is circular with a diameter of 16 cm, while the body-size phantom has an elliptical shape with major and minor semi-axes of 40 cm and 28 cm, respectively.
All materials were scanned on a Siemens SOMATOM Force DECT scanner with an 80/150 kVp energy pair with additional tin filtration on 150 kVp beam. The CT number was determined by the mean value of the region of interest (ROI) within each insert.
To estimate CT number variation with patient size, we compared the mean CT number of each material insert acquired in a head-size phantom with that of a body-size phantom [figure 3(b)]. Inserts were scanned one at a time and were always plugged into the center of the phantom. To estimate the impact from different locations, additional DECT scans were taken with each insert placed at the periphery of the body phantom, and the CT number was compared with that in the center. A body phantom was used because of a larger location difference than that of the head phantom. The RMI phantom with all the material inserts was scanned 5 times to estimate CT number variation over time. CT images representing the three measurement categorizations described above are shown in figure 4. Total CT imaging variation was calculated as the root-sum-square (RSS) of these three variations.
Figure 4.
Axial CT images of the same insert scanned under different conditions: (a) insert at the center of the head phantom; (b) insert at the center of the body phantom; (c) insert at the periphery of the body phantom. (a) and (b) were compared to determine CT number variation with size, while (b) and (c) were compared to determine CT number variation with position.
CT number variation will propagate through the DECT calculation and cause variation in the calculated SPR. The relative uncertainty in the estimated SPR can be related to the uncertainty in CT numbers by
| (16) |
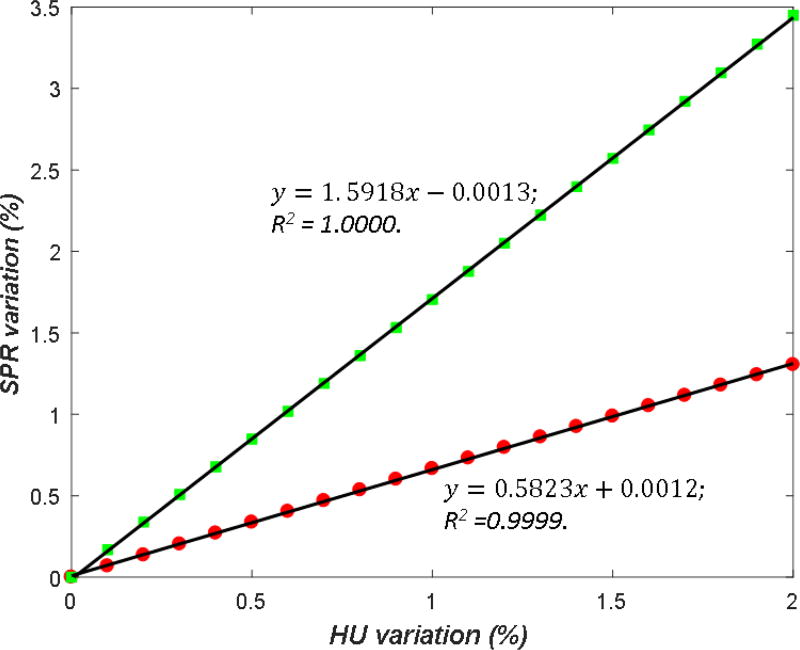
where and are the relative variations in the dual-energy CT numbers. RL and RH are the ratio between the SPR variation and the CT number variation, referred to as the uncertainty propagation ratio (UPR) in this study. The values of RL and RH for each tissue type were determined through a simulation study. A series of known variations were introduced into the measured CT number of each material, and the varied CT numbers were then fed to the DECT calculation. The values of RL and RH were determined by a linear regression fitting between the variation in SPR and the variation in HU (figure 5).
Figure 5.
Simulation of error propagation for the calculation of the uncertainty propagation ratio (UPR). The squares and dots illustrate SPR estimation variation of the HS method caused by high-energy and low-energy CT number (HU) variations, respectively. The black lines illustrate the linear relationship between the two variations. The selected material was CB2-50% (Gammex).
2.2.2. DECT modeling uncertainty
In addition to the DECT imaging uncertainty, ρe and Z calculated based on the HUs acquired under the calibration condition (HU1,ref and HU2,ref) can be different from their ground truth (the values determined experimentally or calculated directly based on the elemental composition), because of the ‘imperfect’ modeling of the CT scanner. This uncertainty is referred to as DECT modeling uncertainty in this study.
The ideal way to estimate the modeling uncertainty is to compare ρe and Z estimated through the DECT approach with the ρe and Z measured experimentally for various human tissue samples. However, this may not be feasible for a large number of body tissues. Instead, this uncertainty was estimated based on the tissue equivalent material inserts used in the calibration process. Because the elemental composition was known for each insert, the ground truth values of ρe and Z (ρe,true and Ztrue) were calculated and compared with ρe and Z calculated from the HU values acquired in the calibration process. We mainly employed the leave-one-out cross-validation strategy here: each time, one material was selected for testing, while the others were used for calibration. The reason we used the leave-one-out strategy was to mimic a realistic situation in which the human tissue of interest is not used as part of the calibration material. With the leave-one-out strategy, however, we observed that calibrating without substitutes with the lowest and the highest HUs (i.e., LN300 and cortical bone) results in a bad calibration putatively due to extrapolation. To prevent this issue but to still imitate a clinical scenario, we used all materials for calibration for these two substitutes but retained the leave-one-out strategy for the other substitutes. This approach greatly improved the inconsistency within the lung and bone tissue groups.
An error propagation analysis was performed to determine the impact ratio between ρe, Z variations and SPR variation. By setting the proton kinetic energy to 200 MeV, the Bethe-Block equation (Eq. (1)) was simplified as
| (17) |
where m and n represent the linear relationship between Z and lnI (figure 2(a)). Here we evaluated based on the Z-ln(I) curve proposed by Yang et al. (2010), while the Zmed-I proposed by Bourque et al. (2014) gave similar result. Assuming ρe and Z are independent variables, the relative uncertainty of is written as
| (18) |
in which and are the relative uncertainties of ρe and Z, respectively. By taking the derivative of Eq. (17), we could simplify Eq. (18) as
| (19) |
Knowing the values of and , the DECT modeling uncertainty was estimated using Eq. (19).
2.2.3. DECT inherent uncertainty
No true one-to-one correspondence exists between Z and lnI because of their different physical characteristics (figure 2). For this reason, even lnI derived from Ztrue can deviate from its ground truth (lnI is calculated directly based on the elemental composition). This uncertainty is the fundamental limitation of the DECT-based approach and inherent to all existing DECT methods. Thus, it was referred to as DECT inherent uncertainty.
This uncertainty was estimated by comparing lnI calculated directly from the elemental composition with lnI derived from Ztrue for various human body tissues, which included both ‘reference’ human tissues and ‘individualized’ human tissues. ‘Reference’ human tissues are those with standard values of density and elemental composition reported in the literature (White et al., 1987; White et al., 1989). ‘Individualized’ human tissues were generated by introducing changes into the densities and elemental compositions of ‘reference’ human tissues to account for potential density and composition variation between different patients. ‘Individualized’ human tissues were mainly varied in the key factors from ‘reference’ human tissues. Key factors include hydrogen percentage for lung and soft tissues, calcium percentage for bone tissues, and mass density. We used the same scheme by introducing variations into these key factors as described in (Yang et al., 2012). In this study, 34 human biological tissues were included, and 2000 ‘individualized’ human tissues were generated for each tissue type.
2.2.4. Uncertainties unrelated to the DECT approach
Two additional uncertainty categories, related to SPR calculation but not directly related to the DECT-based approach, were identified: 1) uncertainties in the mean excitation energy, 2) ignorance of SPR change with proton energy in current commercial treatment planning systems. Because these two uncertainties are not directly related to the approach used to estimate SPR, their estimated values should not vary between the DECT approach and the standard stoichiometric calibration approach, as previously reported (Yang et al., 2012). Therefore, these uncertainties were not estimated in this work, and the values from our previous study were used here.
2.3. Composite range uncertainty
The substantial difference between the SPR uncertainties associated with each tissue group led us to derive a single composite margin value for each treatment site, for convenience in routine clinical operations. The total range (R) can be expressed as follows:
| (20) |
where i denotes the i-th tissue group of the three tissue groups, and Ri is the total water-equivalent path length of i-th tissue group. Assuming that the uncertainties of each tissue group are independent from each other, the relative uncertainty of the total range could be calculated as
| (21) |
where wi indicates the relative weight of each tissue group along the beam path from the skin to the proximal or distal end of the target volume. Because all the voxels belonging to the same tissue group share the same relative uncertainty, for each tissue group, . Thus, the relative range uncertainty could be calculated as
| (22) |
The relative weight wi associated with each tissue group was adopted from our previous work (Yang, 2011). These values were determined using a ray-tracing technique based on the treatment plans of 15 proton patients treated at the UT MD Anderson Cancer Proton Center. The 15-patient cohort consisted of five prostate, five lung and five head-and-neck cancer patients.
3. Results
3.1. Validation of our implementation
The HU values from the original study by Hünemohr et al. (2014) were used to test the implementation of the two selected DECT-based methods (Table 2 in Hünemohr et al. 2014.). Our implementation of the Hünemohr and Bourque methods yielded mean SPR estimation errors of 0.7% and 0.6%, respectively, similar to the reported 0.6% and 0.5% (table 1). Our results validated the implementation of these two methods and justified the conclusions presented in the following sessions.
Table 1.
Comparison between our implementation and the reported results from the Hünemohr and Bourque methods.
| Method | Mean estimation error (%) | ||||
|---|---|---|---|---|---|
|
| |||||
| ρe | Z | I | SPR | ||
| Hünemohr | Reported | 0.4 | 1.7 | 3.9 | 0.6 |
| Our implementation a | 0.4 | 1.4 | 3.5 | 0.7 | |
| Bourque | Reported | 0.3 | 1.6 | 4.1 | 0.5 |
| Our implementation b | 0.3 | 0.8 | 3.5 | 0.6 | |
The calibration material was CB2-50%.
The calibration materials included all 13 materials listed in table A1.
As discussed in Section 2.1.1, we also compared the Hünemohr and HS methods to justify the need for modification. We found that the selection of different calibration materials yielded substantially different results for the original Hünemohr method (table 2). Specifically, the root-mean-square (RMS) error in ρe estimation for bone tissues increased from 0.4% to 5.4% when using adipose instead of cortical bone for calibration. In contrast, for the HS method, ρe estimation errors remained below 0.5% for different calibration material combinations. For soft and bone tissues, the Z estimation error difference between different calibration materials was up to 2.3% when using the original Hünemohr method, while it was below 0.5% when using the HS method. These observations provided a justification for our modification. In the following SPR uncertainty evaluation, the HS method was implemented instead of the original Hünemohr method.
Table 2.
Comparison of the Hünemohr method and the Saito method to estimate ρe and Z.
| Method | Calibration materials |
RMS error (%) on ρe estimation | RMS error (%) on Z estimation | ||||
|---|---|---|---|---|---|---|---|
|
| |||||||
| Lung | Soft | Bone | Lung | Soft | Bone | ||
| Hünemohr | Adipose | 0.85 | 0.55 | 5.44 | 2.05 | 1.95 | 2.04 |
| Brain | 0.95 | 0.51 | 1.27 | 2.46 | 2.30 | 4.31 | |
| Cortical bone | 0.98 | 0.54 | 0.42 | 2.21 | 1.70 | 2.34 | |
|
| |||||||
| HS | 3 materials c | 0.01 | 0.33 | 0.49 | 0.03 | 1.94 | 1.27 |
| 7 materials d | 0.11 | 0.33 | 0.42 | 0.25 | 1.43 | 1.30 | |
| 13 materials | 0.17 | 0.32 | 0.41 | 1.02 | 1.47 | 1.34 | |
The calibration material combinations were c[lung (LN450), solid water, CB2-50%] and d[lung (LN450), adipose, breast, solid water, brain, B200, CB2-50%].
3.2. DECT imaging uncertainty
CT number variation with varying phantom sizes, insert position within field-of-view (FOV), and time (repeatability) were measured as described in Section 2.2.1 (table 3). In agreement with our previous study (Yang et al., 2012), smaller CT number variations were observed for the soft tissue group than for the lung and bone tissue groups. For soft tissues, CT number variation was dominated by the position in the FOV, and for lung and bony tissues, it was dominated by the phantom size. Size and location were found to have similar impact for bone tissues using 150 kVp/Sn. Minimal CT number variations were observed between the scans performed at different times, demonstrating the stability of modern DECT scanners. CT number variations associated with each contributing factor were added in quadrature [root-sum-square (RSS)] to determine the total variation for each tissue group and for the scanning energy pair. CT number variations were smaller when using higher scanning energy for soft and bone tissues, which could be explained by a reduced beam hardening effect using higher energy x-rays. A different trend was observed for lung tissues. One possible reason might be the relatively non-uniform nature of the lung inserts due to random distribution of air holes within the inserts, as previously reported by Hudobivnik et al. (2016). The total variation (1σ) results were 1.2%, 0.8% and 1.3% for lung, soft tissue and bone tissue, respectively, when using 80 kVp, and 2.1%, 0.4% and 1.0%, respectively, when using 150kVp/Sn.
Table 3.
CT imaging uncertainties (1σ) caused by different factors for three tissue groups and total uncertainty calculated by root-sum-square (RSS).
| Energy | Factors | CT imaging uncertainties (1σ) | ||
|---|---|---|---|---|
|
| ||||
| Lung (%) | Soft (%) | Bone (%) | ||
| 80 kVp | Size | 1.00 | 0.34 | 1.25 |
| Position | 0.53 | 0.70 | 0.31 | |
| Time | 0.18 | 0.06 | 0.09 | |
| Total (RSS) | 1.16 | 0.78 | 1.30 | |
| 150 kVp/Sn | Size | 2.02 | 0.16 | 0.69 |
| Position | 0.26 | 0.32 | 0.77 | |
| Time | 0.07 | 0.07 | 0.03 | |
| Total (RSS) | 2.06 | 0.37 | 1.04 | |
Through an error propagation simulation, CT number variation and its induced variation in SPR estimation presented a clear linear relationship (figure 5). R80 and R150 denote the ratio between SPR and CT number variation (i.e., UPR) for 80 kVp and 150 kVp/Sn, respectively (table 4). R150 was consistently larger than R80 by approximately one for all tissue groups and both methods, indicating that the variation of the higher-energy CT number has a larger impact on SPR prediction than lower-energy CT. The HS and Bourque methods yielded similar R80 and R150 values, suggesting similar robustness to CT number variation.
Table 4.
The uncertainty propagation ratio (UPR) of SPR variation over HU variation for different tissue groups and DECT-based methods.
| Method | UPR | Lung | Soft | Bone |
|---|---|---|---|---|
| HS | R80 | 0.63 | 0.72 | 0.56 |
| R150 | 1.71 | 1.87 | 1.57 | |
| Bourque | R80 | 0.69 | 0.68 | 0.66 |
| R150 | 1.74 | 1.76 | 1.59 |
The overall uncertainty caused by CT number variation was determined for each tissue group, as defined in Eq. (16). The HS and Bourque methods yielded similar results of 3.6%, 0.9% and 1.8% for lung, soft tissues and bone tissues, respectively (table 5). These results illustrated that the SPR estimation uncertainties caused by CT imaging variation are more substantial in lung and bone tissues than those in soft tissues.
Table 5.
The uncertainties in SPR estimation (1σ) caused by the DECT imaging uncertainty.
| Method | SPR estimation uncertainty (1σ) | ||
|---|---|---|---|
|
| |||
| Lung (%) | Soft (%) | Bone (%) | |
| HS | 3.59 | 0.89 | 1.79 |
| Bourque | 3.67 | 0.84 | 1.87 |
3.3. DECT modeling uncertainty
We estimated the DECT modeling uncertainty based on the tissue equivalent material inserts scanned under the calibration condition. Half of the maximum variation in each tissue group was taken as the uncertainty (1σ) for that tissue group. For both the HS and Bourque methods, the uncertainty estimates (1σ) of the ρe calculation were all under 0.8% except lung tissues with approximately 1.3%, and the uncertainty estimates of the Z calculation were under 5.0% and 2.0% for soft and bone tissues (table 6).
Table 6.
Uncertainties in ρe and Z estimation (1σ) caused by the DECT modeling uncertainty.
| Method | ρe estimation uncertainty (1σ) | Z estimation uncertainty (1σ) | ||||
|---|---|---|---|---|---|---|
|
| ||||||
| Lung (%) | Soft (%) | Bone (%) | Lung (%) | Soft (%) | Bone (%) | |
| HS | 1.26 | 0.43 | 0.37 | 0.55 | 4.74 | 1.43 |
| Bourque | 1.46 | 0.70 | 0.44 | 4.81 | 4.33 | 0.70 |
By using Eq. (19), the impact ratio of SPR variation over ρe variation was calculated as 1.0 consistently, while the value of was approximately 0.1 for all tissue groups. This illustrated that the SPR calculation is more sensitive to the uncertainty in ρe than in Z. For both selected DECT-based methods, the uncertainties in the calculated SPR caused by the DECT modeling uncertainty (1σ) were approximately 1.3%, 0.7% and 0.8% for lung, soft and bone tissues, respectively (table 7).
Table 7.
Uncertainties in SPR estimation (1σ) caused by the DECT modeling uncertainty.
| Method | SPR estimation uncertainty (1σ) | ||
|---|---|---|---|
|
| |||
| Lung (%) | Soft (%) | Bone (%) | |
| HS | 1.26 | 0.64 | 0.42 |
| Bourque | 1.46 | 0.82 | 0.45 |
3.4. DECT inherent uncertainty
We estimated the uncertainty in the calculated SPRs caused by the DECT inherent uncertainty for both ‘reference’ and ‘individualized’ human tissues. The uncertainty estimate (1σ) was determined for each tissue group by the root-mean-square (RMS) of the uncertainties (1σ) of all tissue types within the same tissue group. For ‘individualized’ human tissues, the uncertainty estimate (1σ) of each tissue type was determined based on the 68th percentile value of all 2000 ‘individualized’ tissues generated for that tissue type. The uncertainty in SPR estimation caused by the DECT inherent uncertainty increased slightly after considering tissue composition variation (table 8), demonstrating the robustness of the DECT method against tissue composition variation.
Table 8.
Uncertainties in SPR estimation (1σ) caused by the DECT inherent uncertainty.
| Tissue groups | SPR estimation uncertainties (1σ) | ||
|---|---|---|---|
|
| |||
| Lung (%) | Soft (%) | Bone (%) | |
| ‘Reference’ human tissues | 0.01 | 0.29 | 0.16 |
| ‘Individualized’ human tissues | 0.14 | 0.32 | 0.19 |
3.5. Composite uncertainty in proton SPR estimation
The evaluation of uncertainties in proton SPR estimation by the HS method is summarized in table 8. Because the Bourque method yielded a similar SPR estimation uncertainty, the values adopted here can represent both methods. For lung, soft and bone tissues, the composite uncertainties (1σ) were 3.8%, 1.2% and 2.0%, respectively. The dominant contributing factor was the DECT imaging uncertainty for all three tissue groups.
3.6. Composite range uncertainties
By taking into account the relative weights of different patient tissues, composite range uncertainties were estimated for prostate, lung and head-and-neck tumor sites (table 9). SPR estimation uncertainties were translated into range uncertainties based on Eq. (17). As we calculated the uncertainties for both proximal and distal ends, the maximum value was taken as the composite uncertainty of each tumor site. For all three tumor sites, the range uncertainties were similar, around 1.8% and 2.2%, covering 90% and 95% of all cases. Similar results for different tumor sites were largely due to the dominant percentage of soft tissues in the human body. We also provided the absolute range uncertainty values for these three typical tumor sites. The range values were adopted from previous study by Schuemann et al. (2014). As shown in Table 10, the range uncertainties of the three tumor sites were 0.5–0.6, 0.2–0.4 and 0.1–0.4 g/cm2 covering 95% of all cases, respectively.
Table 9.
Uncertainties (1σ) in SPR estimation caused by different uncertainty sources.
| Uncertainty source | SPR estimation uncertainties (1σ) | ||
|---|---|---|---|
|
| |||
| Lung (%) | Soft (%) | Bone (%) | |
| DECT imaging uncertainty | 3.6 | 0.9 | 1.8 |
| DECT modeling uncertainty | 1.3 | 0.6 | 0.4 |
| DECT inherent uncertainty | 0.1 | 0.3 | 0.2 |
| Uncertainty in the determination of I | 0.2 | 0.2 | 0.6 |
| Uncertainty due to ignorance of SPR change with proton energy by current commercial treatment planning systems | 0.2 | 0.2 | 0.4 |
| Total (RSS) | 3.8 | 1.2 | 2.0 |
Table 10.
Percentile (90th and 95th) of composite range uncertainties estimated for prostate, lung and head-and-neck tumor sites, respectively.
| Tumor site | Range uncertainty | |||
|---|---|---|---|---|
|
| ||||
| 90th percentile | 95th percentile | |||
| % | g/cm2 | % | g/cm2 | |
| Prostate | 1.7 | 0.4–0.5 | 2.1 | 0.5–0.6 |
| Lung | 1.8 | 0.1–0.3 | 2.2 | 0.2–0.4 |
| Head and neck | 1.8 | 0.1–0.4 | 2.1 | 0.1–0.4 |
4. Discussion
4.1. Comparison of our study with previous studies
We performed a comprehensive study that provides a detailed estimate about the range uncertainty related to SPR estimation, using the state-of-the-art DECT-based approach. The estimated range uncertainty (2σ) was approximately 2.2% for three tumor sites, as compared with the 1% uncertainty reported in previous studies (Hünemohr et al., 2014; Bourque et al., 2014; Hansen et al., 2015). The major difference between our study and others is that CT number variation due to the beam hardening effect was previously avoided by using the same scanning condition, upon calibration and real measurements. As shown in our study, the CT number varies substantially with scanning conditions (e.g. size of phantom or location within the phantom). The variation in CT number is further amplified in the DECT calculation process. Our study demonstrated that the DECT-based method can achieve smaller uncertainty than the SECT-based stoichiometric method (Yang et al., 2012), although the difference (1.3%) is smaller than that reported by previous studies (2.5%).
4.2. Additional uncertainty contributing factors not considered in this study
Uncertainty factors that were not considered in this study include random noise in CT imaging, metal streak artefacts, and objects outside the scan field-of-view (FOV). Based on previous studies (Chvetsov and Paige, 2010; Yang et al., 2011) we expected that addition of Gaussian random noise would only have a small impact on the ion range error due to the averaging effect along the beam path. However, Bär et al. (2017) recently showed that a high amplitude random noise may introduce a systematic error in the range estimation when using the DECT approach, which would not be averaged out and thus have a large impact on the range estimation uncertainty. The systematic error is dependent on many factors including the modeling method and the tissue type, but it suggests that DECT may lose its merit over SECT in the presence of high random noise. Although noise can be easily suppressed at the expense of imaging dose, a comprehensive study is worth conducting to identify the impact of random noise in various clinical scenarios.
Metal artefacts were not considered because they are only observed in patients with metallic implants. These cases need to be handled with special care by avoiding the region with the artefact or by applying a larger margin. Because the DECT-based method is especially sensitive to imaging uncertainties, it is unclear whether it is still better than the SECT-based method; further studies are needed to elucidate these differences. The objects outside the scan FOV are additional uncertainty contributing factors that were not considered. This situation may occur in larger patients, or when a special setup requires the patient to be off-centered. Because the object is not fully considered in the reconstruction, the CT number of objects inside the FOV will deviate from the expected values. The results of our intentional phantom offset showed a large deviation of the material insert CT number in the FOV, with HU variations of about 10% and 5% for lung and soft tissues, respectively. Because this can be easily missed, special attention is needed to ensure that all regions of interest are within the FOV. When this cannot be achieved, a larger margin should be applied.
4.3. Optimal energy pair selection for the DECT-based approach
The selection of an optimal energy pair is an essential practical aspect in the implementation of the DECT-based approach and an important question to be addressed early in this study. The three energy pairs available on the Siemens SOMATOM Force DECT scanner were 80 kVp/150 kVp, 90 kVp/150 kVp and 100 kVp /150 kVp. As shown by our previous theoretical study (Yang et al., 2011), the larger the energy spectra difference, the less the uncertainty is amplified through the DECT calculation (i.e., the smaller the UPR values shown in this study). Thus, the energy of the higher energy x-ray component was an easy choice, which should always be the highest energy available, i.e., 150 kVp in this case. The real question was the selection of a lower energy to be coupled with 150 kVp. There were two competing factors here: UPR values and CT number variation. As the energy of the lower energy x-ray component decreases, the UPR values decrease while CT number variation may increase because of a more potent beam-hardening effect. Because of that, we conducted a series of DECT scans with the 90 kVp/150 kVp and 100 kVp/150 kVp pairs in addition to the 80 kVp/150 kVp pair used in this study. We soon discovered that the 80/150 kVp pair was the optimal pair, because the increase in UPR values dominated in these two competing factors for two reasons. First, the UPR increased substantially while CT number variation remained relatively constant as the energy increased. UPR values increased approximately by 20% and 60% for the dominant soft tissue group, when 80 kVp was replaced with 90 kVp and 100 kVp, respectively. Second, an increase in UPRs affected both lower and higher energy components while an increase in CT number variation only affected the lower energy component. Another potential competing factor is the worsening of the accuracy of Z calculation due to the spectral difference within the energy pair. The effective Z depends on the spectrum and the difference in Z between two energies increases with the increase in their spectral difference. A possible solution to get around this issue is to decompose the material based on HU values and calculate the mean excitation energy from the elemental composition directly (Hünemohr et al., 2014b; Lalonde and Bouchard, 2016). In this study, however, this potential difference is incorporated in the modeling uncertainty, and we found that the effective Z remains relatively constant among all three energy pairs used in this study. As a conclusion, it seems reasonable to expect the optimal pair to always be the one with the largest spectra separation available on the DECT scanner, unless the size of the general patient population treated at a specific center is especially large. In that case, further comparison between different energy pairs is warranted.
4.4. Future work
Our study showed that the DECT-based method can reduce uncertainty in proton SPR estimation as compared with the SECT-based approach, although the improvement is limited with the use of current algorithms. The main limitation is the amplification of the uncertainties in CT measurement through the DECT calculation. Therefore, this uncertainty should be reduced to lessen the overall uncertainty in SPR estimation. This uncertainty includes two components: 1) uncertainty in the CT number; 2) amplification of the uncertainty. The uncertainty in the CT number can be reduced by developing an improved beam-hardening correction algorithm in CT reconstruction (e.g., iterative projection-based decomposition, which can, in theory, remove the beam-hardening artefact). Uncertainty amplification can be reduced by increasing the separation of the energy spectra between two CT scanning beams, and for this reason the 80 kVp and the 150 kVp/Sn pair was chosen for our study. Because the spectra separation achieved in our study is currently the largest among commercial DECT scanners, we may not see further improvement with the existing commercial DECT scanners. Better algorithms with a smaller UPR value may be developed for further improvement. The algorithm used in our previous studies (Yang et al., 2010, 2011) yielded UPR values in the range of 6, which are substantially larger than those in the two selected methods. This result indicated that the calculation algorithm can be designed more robustly against CT number variation. New algorithms have recently been proposed (Hansen et al., 2015; Han et al., 2016; Taasti et al., 2016) and will be included for comparison purposes in our future work. Note that these findings might not be directly transferrable to real human tissues, due to the study being based on tissue surrogate phantoms and theoretical human tissues. However, our method can serve as a general guideline for estimating the major uncertainty contributing factors related to the SPR estimation using DECT.
5. Conclusion
We report a comprehensive study on SPR estimation uncertainties using the DECT-based approach. Our study showed that the DECT-based approach can reduce uncertainty to 2.2% in clinical scenarios, in contrast to the previously reported 1%. Our study showed that the SPR uncertainty caused by CT number variation is dominant and needs to be minimized to further reduce the overall uncertainty. Solutions include the development of a better beam-hardening correction algorithm and a DECT calculation algorithm more robust against CT number variation.
Although our analysis of the overall uncertainty in SPR estimation using the DECT approach may serve as a general guideline, we recommend that other centers estimate the uncertainty in their own systems. It is especially important to estimate the uncertainty caused by CT number variation considering its dominance and sensitivity to scanning conditions.
Acknowledgments
We thank Parkland Hospital for granting access to the Siemens SOMATOM Force DECT scanner. We thank Dr. Damiana Chiavolini for editing this manuscript. This work was partially supported by the Cancer Prevention and Research Institute of Texas grant RP160661, NIH grant (P20CA183639-01A1), National Natural Science Foundation of China (No. 81571771), and Ministry of Science and Technology of China (No. 2015BAI01B10).
References
- Bourque AE, Carrier J-F, Bouchard H. A stoichiometric calibration method for dual energy computed tomography. Physics in medicine and biology. 2014;59:2059. doi: 10.1088/0031-9155/59/8/2059. [DOI] [PubMed] [Google Scholar]
- Engelsman M, Schwarz M, Dong L. Physics Controversies in Proton Therapy. Semin. Radiat. Oncol. 2013;23:88–96. doi: 10.1016/j.semradonc.2012.11.003. [DOI] [PubMed] [Google Scholar]
- Farace P. Experimental verification of ion stopping power prediction from dual energy CT data in tissue surrogates. Phys Med Biol. 2014;59:7081–4. doi: 10.1088/0031-9155/59/22/7081. [DOI] [PubMed] [Google Scholar]
- Han D, Siebers JV, Williamson JF. A linear, separable two-parameter model for dual energy CT imaging of proton stopping power computation. Medical Physics. 2016;43:600–12. doi: 10.1118/1.4939082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen DC, Seco J, Sorensen TS, Petersen JBB, Wildberger JE, Verhaegen F, Landry G. A simulation study on proton computed tomography (CT) stopping power accuracy using dual energy CT scans as benchmark. Acta Oncol. 2015;54:1638–42. doi: 10.3109/0284186X.2015.1061212. [DOI] [PubMed] [Google Scholar]
- Hudobivnik N, Schwarz F, Johnson T, Agolli L, Dedes G, Tessonnier T, Verhaegen F, Thieke C, Belka C, Sommer WH, Parodi K, Landry G. Comparison of proton therapy treatment planning for head tumors with a pencil beam algorithm on dual and single energy CT images. Medical Physics. 2016;43:495–504. doi: 10.1118/1.4939106. [DOI] [PubMed] [Google Scholar]
- Hünemohr N, Krauss B, Tremmel C, Ackermann B, Jäkel O, Greilich S. Experimental verification of ion stopping power prediction from dual energy CT data in tissue surrogates. Physics in Medicine and Biology. 2014;59:83–96. doi: 10.1088/0031-9155/59/1/83. [DOI] [PubMed] [Google Scholar]
- Ju M, Berman AT, Vapiwala N. The evolution of proton beam therapy: Insights from early trials and tribulations. Int. J. Radiat. Oncol. Biol. Phys. 2014;90:733–5. doi: 10.1016/j.ijrobp.2014.07.035. [DOI] [PubMed] [Google Scholar]
- Kang Y, Mirkovic D, Mohan R, Dong L. Particle Therapy Co-Operative Group (PTCOG) 46th Annual Meeting. Zibo, China: 2007. Impact of anatomical changes to proton and photon dose distributions. [Google Scholar]
- Karger CP, Jäkel O, Palmans H, Kanai T. Dosimetry for ion beam radiotherapy. Phys. Med. Biol. 2010;55:R193–R234. doi: 10.1088/0031-9155/55/21/R01. [DOI] [PubMed] [Google Scholar]
- Loeffler JS, Durante M. Charged particle therapy-optimization, challenges and future directions. Nat. Rev. Clin. Oncol. 2013;10:411–24. doi: 10.1038/nrclinonc.2013.79. [DOI] [PubMed] [Google Scholar]
- Mayneord W. The significance of the roentgen. Acta of the International Union Against Cancer. 1937;2:271. [Google Scholar]
- McGowan SE, Burnet NG, Lomax AJ. Treatment planning optimisation in proton therapy BR. J. RADIOL. 2013;86 doi: 10.1259/bjr.20120288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller RC, Lodge M, Murad MH, Jones B. Controversies in clinical trials in proton radiotherapy: The present and the future. Semin. Radiat. Oncol. 2013;23:127–33. doi: 10.1016/j.semradonc.2012.11.004. [DOI] [PubMed] [Google Scholar]
- Mirkovic D, Kang Y, Dong L. Sensitivity of Proton and Photon Plans to the Intra- and Inter-Fractional Changes in Patient's Anatomy. Med. Phys. 2007;34:2390-. [Google Scholar]
- Mitin T, Zietman AL. Promise and pitfalls of heavy-particles therapy. J. Clin. Oncol. 2014:2855–63. doi: 10.1200/JCO.2014.55.1945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moyers MF. Comparison of x ray computed tomography number to proton relative linear stopping power conversion functions using a standard phantom. Med. Phys. 2014;41 doi: 10.1118/1.4870956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moyers MF, Miller DW, Bush DA, Slater JD. Methodologies and tools for proton beam design for lung tumors. Int J Radiat Oncol Biol Phys. 2001;49:1429–38. doi: 10.1016/s0360-3016(00)01555-8. [DOI] [PubMed] [Google Scholar]
- Moyers MF, Sardesai M, Sun S, Miller DW. Ion Stopping Powers and CT Numbers. Med. Dosim. 2010;35:179–94. doi: 10.1016/j.meddos.2009.05.004. [DOI] [PubMed] [Google Scholar]
- Paganetti H. Range uncertainties in proton therapy and the role of Monte Carlo simulations. Physics in medicine and biology. 2012;57:R99. doi: 10.1088/0031-9155/57/11/R99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaffner B, Pedroni E. The precision of proton range calculations in proton radiotherapy treatment planning: Experimental verification of the relation between CT-HU and proton stopping power. Phys. Med. Biol. 1998;43:1579–92. doi: 10.1088/0031-9155/43/6/016. [DOI] [PubMed] [Google Scholar]
- Schardt D, Elsässer T, Schulz-Ertner D. Heavy-ion tumor therapy: Physical and radiobiological benefits. Rev. Mod. Phys. 2010;82:383–425. [Google Scholar]
- Schneider U, Pedroni E, Lomax A. The calibration of CT Hounsfield units for radiotherapy treatment planning. Phys Med Biol. 1996;41:111–24. doi: 10.1088/0031-9155/41/1/009. [DOI] [PubMed] [Google Scholar]
- Schuemann J, Dowdell S, Grassberger C, Min C, Paganetti H. Site-specific range uncertainties caused by dose calculation algorithms for proton therapy. Physics in medicine and biology. 2014;59:4007. doi: 10.1088/0031-9155/59/15/4007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith AR. Vision 2020: Proton therapy. Med. Phys. 2009;36:556–68. doi: 10.1118/1.3058485. [DOI] [PubMed] [Google Scholar]
- Taasti VT, Petersen JBB, Muren LP, Thygesen J, Hansen DC. A robust empirical parametrization of proton stopping power using dual energy CT. Medical Physics. 2016;43:5547–60. doi: 10.1118/1.4962934. [DOI] [PubMed] [Google Scholar]
- White D, Booz J, Griffith R, Spokas J, Wilson I. Tissue substitutes in radiation dosimetry and measurement. ICRU Report. 1989;44 [Google Scholar]
- White D, Woodard H, Hammond S. Average soft-tissue and bone models for use in radiation dosimetry. The British journal of radiology. 1987;60:907–13. doi: 10.1259/0007-1285-60-717-907. [DOI] [PubMed] [Google Scholar]
- Yang M. Dual energy computed tomography for proton therapy treatment planning 2011 [Google Scholar]
- Yang M, Virshup G, Clayton J, Zhu XR, Mohan R, Dong L. Theoretical variance analysis of single- and dual-energy computed tomography methods for calculating proton stopping power ratios of biological tissues. Physics in Medicine and Biology. 2010;55:1343–62. doi: 10.1088/0031-9155/55/5/006. [DOI] [PubMed] [Google Scholar]
- Yang M, Virshup G, Clayton J, Zhu XR, Mohan R, Dong L. Does kV-MV dual-energy computed tomography have an advantage in determining proton stopping power ratios in patients? Physics in Medicine and Biology. 2011;56:4499–515. doi: 10.1088/0031-9155/56/14/017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang M, Zhu XR, Park PC, Titt U, Mohan R, Virshup G, Clayton JE, Dong L. Comprehensive analysis of proton range uncertainties related to patient stopping-power-ratio estimation using the stoichiometric calibration. Phys Med Biol. 2012;57:4095–115. doi: 10.1088/0031-9155/57/13/4095. [DOI] [PMC free article] [PubMed] [Google Scholar]