Quantitative Gd-DOTA uptake from cerebrospinal fluid into rat brain using 3D VFA-SPGR at 9.4T

Abstract

Purpose

This study introduces a quantitative technique to assess solute uptake into the brain parenchyma based on dynamic contrast enhanced magnetic resonance imaging (DCE-MRI). With this approach, a small molecular weight paramagnetic contrast agent (Gd-DOTA) is infused in the cerebral spinal fluid (CSF) and whole brain gadolinium concentration maps are derived.

Methods

A 3D variable flip angle spoiled gradient echo (VFA-SPGR) longitudinal relaxation time (T1) technique was implemented and the accuracy was cross validated using an inversion recovery sequence (IR-RARE) using phantoms. Normal Wistar rats underwent Gd-DOTA infusion into CSF via the cisterna magna and continuous MRI for ~130 min using the T1 weighted imaging. Dynamic Gd-DOTA concentration maps were calculated and parenchymal uptake was estimated.

Results

In the phantom study, T1 discrepancies between the VFA-SPGR and IR-RARE sequences were ~6% with a transmit coil inhomogeneity correction. In the in vivo study, contrast transport profiles indicated maximal parenchymal retention of ~19% relative to the total amount delivered into the cisterna magna.

Conclusion

Imaging strategies for accurate 3D contrast concentration mapping at 9.4T were developed and whole brain dynamic concentration maps were derived to study solute transport via the glymphatic system. The newly developed approach will enable future quantitative studies of the glymphatic system in health and disease states.

Introduction

The brain has a high metabolic activity and the parenchyma is devoid of lymph vessels seen in other tissues. The glymphatic system was recently proposed as a substitute for lymphatics to remove the brain’s metabolic waste (1). The glymphatic system is defined anatomically by the peri-vascular compartment and functionally by the aquaporin-4 (AQP4) water channels of glial end-feet that ensheathe the vasculature of the central nervous system. The AQP4 water channels play a pivotal role in regulating cerebrospinal fluid (CSF) flux from the peri-vascular space into the interstitial fluid (ISF) space (1–3). The glymphatic pathway is engaged in the removal of metabolic waste including soluble Aβ and tau proteins (1,4) and is potentially a novel therapeutic target for preventing Alzheimer’s disease and other diseases characterized by protein aggregations. Glymphatic transport of waste solutes is a complex process involving peri-arterial CSF influx, CSF-ISF exchange and peri-vascular CSF-ISF waste efflux via peri-venous conduits with ultimate drainage to lymphatic vessels including the recently discovered meningeal lymphatic vessel (5). Glymphatic transport is controlled by a wide variety of physical forces such as intracranial pressure gradients (e.g. body posture (6)), respiration (7), cardiac pulsation (8) and most intriguingly by the sleep/wake state transition (9).

The discovery and functional characterization of the glymphatic system emanated from studies using in vivo optical imaging techniques. We previously introduced the dynamic contrast enhanced (DCE) magnetic resonance imaging (MRI) in combination with the delivery of a small molecular weight paramagnetic contrast agent into the CSF to capture temporal and spatial characteristics of solute transport via the glymphatic pathway (1,6). Key assumptions for characterizing the glymphatic transport employing DCE-MRI were 1) that the paramagnetic contrast was treated by the brain as a surrogate extracellular ‘waste’ solute in CSF and ISF and 2) that it was inert with respect to normal brain physiology. Briefly, with DCE-MRI, the transport of paramagnetic contrast was tracked in the CSF and brain parenchyma over time through a time series of post-contrast enhanced images (10). There are several advantages of the DCE-MRI approach for studying the glymphatic system compared with other known methods. First, DCE-MRI allows 3D visualization of solute transport in vivo, and therefore provides dynamic visualization of whole brain glymphatic transport, which is not possible with 2-photon optical imaging. Second, other endogenous MR contrast modalities used in conjunction with DCE-MRI revealed key anatomical landmarks such as cerebral vasculature, cranial nerves, and sensory organs, which led to the discovery of additional CSF efflux pathways (6). Third, since the DCE-MRI data delivers spatial and temporal information concurrently it allows more accurate interpretation of the dynamic glymphatic transport process. This is important because multiple coexisting processes are active during the transport and clearance of parenchymal brain waste. Finally, paramagnetic contrast agents are clinically relevant for translational studies of glymphatic transport (11).

The time series of 3D T1 weighted (T1W) spoiled gradient echo (SPGR) brain images acquired during and after paramagnetic contrast delivery into the CSF space were previously used to quantify the contrast-induced ‘enhancement ratio’ (defined by % signal change from the baseline) as a proxy of the contrast concentration. With this semi-quantitative approach, the spatial and temporal characteristics of glymphatic transport revealed influx of CSF along major arteries and parenchymal uptake (10), allowing characterization of changes in glymphatic transport that might occur in a disease (12) or with altered physiological state (6). Previous studies using other techniques were not deriving actual parenchymal or CSF solute fluxes and are remained therefore semi-quantitative. For example, ex vivo optical or electron-microscopy techniques cannot distinguish between slow CSF-ISF exchange and more rapid clearance rates because they are inherently qualitative and temporally static. Ultimately, solute flux quantification is also needed for human studies (11) because parenchymal uptake and clearance of contrast requires prohibitively long time (hours) and is impractical for dynamic studies in the clinic. Thus, a quantitative DCE-MRI approach is needed to characterize transport via the brain’s glymphatic system. The present paper describes an imaging strategy for determining 3D whole brain contrast flux and concentrations at high field by implementing a variable flip angle spoiled gradient echo (VFA-SPGR) T1 mapping technique to quantify longitudinal relaxation time measurements both pre- and post-contrast enhancement.

Methods

Phantom preparation

A total of six phantoms containing various concentrations of commercially available paramagnetic Gd-DOTA (Dotarem, Guerbet USA) contrast were prepared in 1.5 cc micro centrifuge tubes. The original Gd-DOTA concentration of 500 mM was first diluted to 1:37 with sterile water (13.5 mM) and further diluted to a series of Gd-DOTA concentrations of 0.270 mM, 0.180 mM, 0.135 mM, 0.068 mM, 0.045 mM, and 0.022 mM. A custom-made phantom holder arranged in a 3×2 matrix was 3D printed to hold the phantoms securely in the scanner. Because T1 varies 2~3% per °C (13), the ambient temperature in the magnet bore was continuously monitored and maintained between 37°C~37.5°C by delivering and controlling the temperature of heated air into the magnet.

MR imaging

All MRI acquisitions were performed on a Bruker 9.4T/30 magnet (Bruker BioSpin, Billerica MA) with a BGA-12SHP imaging gradient system interfaced to Avance III console controlled by Paravision 5.1 software. For the phantom study a 11.2 cm diameter volumes transmit/receive radio frequency (RF) coil was used while a 4-channel phase array RF receiver head coil and volume RF transmit coil were used for the in vivo rat brain study.

In vivo rat studies

For the animal study, a small catheter attached to a glass cannula tip was surgically implanted into the cisterna magna (CM) for infusion of Gd-DOTA. A total of five Wistar rats (body weight: 291 ± 34 g; 8~10 weeks old males) were anesthetized with dexmedetomidine (0.015–0.020 mg/kg/hr) supplemented with 0.5~0.8 % isoflurane delivered in a 1:1 Air:O₂ mixture breathing spontaneously during the MR scans. All animals were positioned supine and physiological parameters including respiratory rate, oxygen saturation, body temperature, and heart rate were continuously monitored using MRI compatible optical monitors (SA Instruments, Inc., Stony Brook, NY) and maintained within normal physiological range during the scans.

Following an anatomical localizer along three orthogonal planes, a spatial inhomogeneity profile of the RF transmit (B1+) was acquired using a double angle method (14). Specifically, we used a rapid acquisition with relaxation enhancement (RARE) sequence (TR = 10000 ms, TE = 22 ms, Average = 1, RARE factor =4, number of slices =50, in plane resolution = 0.24 mm/pixel, slice-thickness =0.4 mm, slice gap =0.2 mm Flip angles=70° and 140°). Subsequently, acquisition of 3D T1 mapping was performed using a VFA-SPGR method (TR=15 ms, TE=4 ms, Average=1, scanning time=4 min, matrix=128×128×128 reconstructed at 0.24×0.24×0.26 mm). A set of six flip angles (2°, 5°, 10°, 15°, 20°, 30°) were acquired for pre-contrast T1 maps. Following the pre-contrast T1 mapping, the imaging strategy remained the same as previously described (6,10) by taking a series of spoiled gradient echo images using a flip angle of 15° until the end of the experiment (~130min). The time series comprised three baseline scans followed by an infusion of 13.5 mM Gd-DOTA at a constant rate of 1.5 μl/min for 13 min. Considering the dead space within the catheter, the actual infused volume of the contrast was 19 μl, which equates a total Gd-DOTA mass of 0.25 μmol. Additionally, in the phantom scans a 2D single slice inversion recovery sequence (IR-RARE) was taken with a non-selective hyperbolic secant inversion pulse (TR = 18000 ms, TE =46 ms, Average = 1, number of slices =1, in plane resolution = 0.39 mm/pixel, slice-thickness =2 mm TI=100~9000 ms).

Data analyses

T1 maps calculated using the IR-RARE sequence

Voxel-wise T1 calculation was performed by fitting image intensities as a function of inversion times with three unknown variables expressed as

$$S=S_0\left[1-\left(1-cos\theta \right)e^{-TI/T1}-cos\theta e^{-TR/T1}\right],$$ [1]

where S, S₀, θ, and T1 represent image intensity, proton-density weighted signal, flip angle and longitudinal relaxation time, respectively. The three unknown variables (S₀, θ and T1) were calculated by the Nelder-Mead Simplex non-linear least square fit algorithm (15). Note that the expression above makes no assumption in regards to the flip angle being 180° but the initial value of iterative search was set to 180°. Following voxel-wise T1 calculation the relaxivity constant, C_Gd, was estimated.

B1+ mapping

Spatially varying B1+ was characterized by a scaling relationship between an effective flip angle (θ_e = αθ_n) and a nominal flip angle (θ_n) (14). A scaling factor, α, was calculated as

$$\alpha =\frac{1}{{\theta }_1}{cos}^{-1}\left(\frac{I_{\theta =140}}{2I_{\theta =70}}\right)\frac{180°}{\pi },$$ [2]

where, θ₁, I_θ=140, and I_θ=70 represent an excitation flip angle in the double angle method (70°), and image intensities of the two excitation flip angles (70° and 140°), respectively. Images acquired from the double angle method were reformatted to match the spatial resolution of 3D VFA-SPGR image using tri-linear interpolation and the calculated 3D α maps were smoothed using a Gaussian smoothing kernel with a full width half maximum of 0.7mm in reducing high frequency background noise.

3D pre-contrast tissue T1 map

In an ideal condition where a transverse relaxation is completely spoiled after each RF excitation and the T2* effect is negligibly small (TE≪T2*), the image intensity of VFA-SPGR, S, is expressed as

$$S=\frac{S_{0}sin{\theta }_e\left(1-e^{-TR/T1}\right)}{1-cos{\theta }_e{e}^{-TR/T1}},$$ [3]

where, TR and S₀ represent the repetition time and the water proton density weighted signal, respectively. Linearization of Eq.3 as expressed in Eq.4 was then solved by an unweighted linear least square fit algorithm to calculate T1 from the slope of the linearized equation (16) expressed as

$$\frac{S}{sin{\theta }_e}=\frac{S}{tan{\theta }_e}{e}^{-TR/T1}+S_0\left(1-e^{-TR/T1}\right).$$ [4]

3D pre-contrast tissue T1 map was calculated by using the set of six flip angles in VFA-SPGR with a correction factor α to calculate the effective flip angle.

3D post-contrast tissue T1 map

Assuming bulk magnetic susceptibility shift is negligible (17), T1 shortening in the presence of the contrast agent, T1_post, is directly proportional to the concentration of contrast agent, n_Gd, derived by Solomon-Bloembergen equation (18) as

$$\frac{1}{T{1}_{\mathit{post}}}=\frac{1}{T1t}+n_{Gd}{C}_{Gd},$$ [5]

where T1t is the pre-contrast T1 and a general expression for contrast enhanced image intensity is derived by substituting Eq.5 into Eq.3

$$S=\frac{S_{0}sin{\theta }_e\left(1-e^{-TR(1/T1t+n_{Gd}{C}_{Gd})}\right)}{1-cos{\theta }_e{e}^{-TR(1/T1t+n_{Gd}{C}_{Gd})}}$$ [6]

$$R=\frac{S_{\mathit{post}-\mathit{contrast}}}{S_{\mathit{pre}-\mathit{contrast}}}=\frac{S(n_{Gd}>0)}{S(n_{Gd}=0)}$$ [7]

$$ER=(R-1)\ast 100\%,$$ [8]

where R and ER represent a ratio between pre- and post-contrast image intensities and enhancement ratio, respectively. Enhancement ratio can be interpreted as “% signal change from the baseline”. Substitution of Eq.6 into Eq.7 and algebraic re-arrangement yields an analytical expression relating contrast concentration, n_Gd, and three variables, R, θ_e, T1t (see supporting material S1) expressed as

$$n_{Gd}=\frac{-1}{C_{Gd}TR}ln\left[\frac{{Re}^{TR/T1t}(e^{TR/T1t}-1)-e^{TR/T1t}(e^{TR/T1t}-cos{\theta }_e)}{Rcos{\theta }_e(e^{TR/T1t}-1)-(e^{TR/T1t}-cos{\theta }_e)}\right],$$ [9]

which is a single algebraic expression in converting dynamic enhancement ratios into contrast concentrations if the proton density weighted, S₀, signal remains constant during the experiment. Therefore, dynamic 3D concentration maps were constructed by using the pre-contrast T1 calculated from the VFA-SPGR and the enhancement ratio calculated from the successive acquisition of SPGR at the single flip angle.

Numerical simulations

To study how the B1+ inhomogeneity leads to errors in calculating enhancement ratios and contrast concentrations, simulations were performed in the presence (α ≠ 1) and in the absence (α = 1) of B1+ inhomogeneity at three Gd-DOTA contrast concentrations (0.01 mM, 0.10 mM, and 0.50 mM) using the same imaging parameters as the SPGR protocol in this study. Discrepancies between simulated and true values were quantified and expressed as

$$\mathit{discrepency}=\left(\frac{V_1-V_0}{V_0}\right)100\%,$$ [10]

where, V₁ and V₀ represent the simulated values at α ≠ 1 and α = 1, respectively. Pre-contrast T1 (T1t) was set to a typical grey matter tissue T1 of 2000ms and C_Gd was set to 2.69 mM⁻¹s⁻¹.

T1 map spatial normalization and segmentation

Individual T1 maps were segmented into grey matter (GM), white matter (WM) and CSF probability maps using an unified segmentation algorithm in SPM12 (http://www.fil.ion.ucl.ac.uk/spm/) (19) using the in-vivo rat tissue probability maps (20) as spatially resolved tissue priors. Segmented GM and WM tissue probability maps in native space were then summed and thresholded to create a brain mask. Total Gd-DOTA uptake in the brain was calculated at each time point by taking the sum of all concentrations within the brain mask multiplied by the voxel volume deriving the total contrast mass (μmol) retained in the brain. By using the same mask, time resolved whole brain T1s and enhancement ratios were also calculated. For visualization purposes, population averaged T1 map, concentration map and anatomical map were constructed by spatially normalizing individual concentration and anatomical maps onto a representative scan using affine transform, and summed to construct population averaged maps highlighting common features, while reducing variability between animals. SPM12 was used for the spatial normalization.

Results

Phantom study

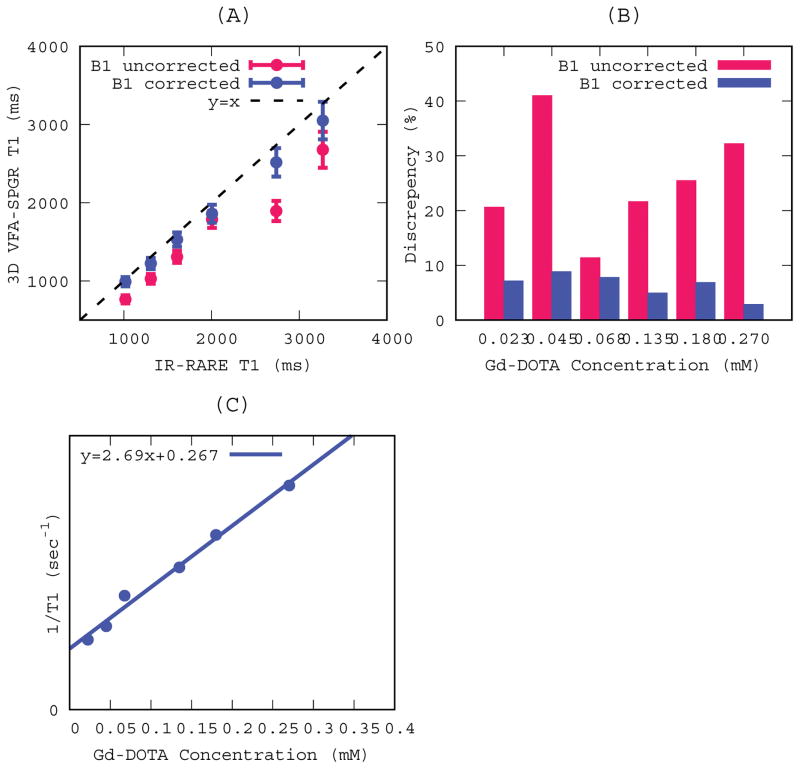
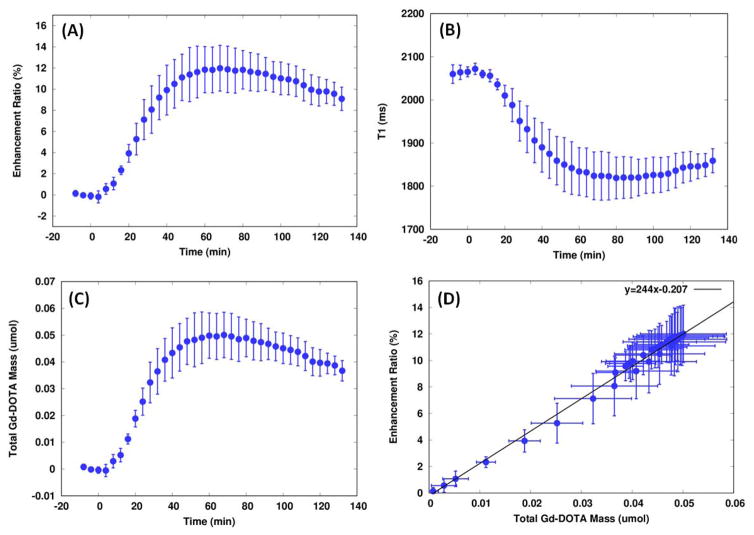
Accuracy and reliability of T1s measured by the VFA-SPGR was cross-validated against those derived from the IR-RARE sequence. Mean and standard deviations were calculated for the regions of interest (ROIs) at each contrast concentration and the T1s measured in the VFA-SPGR were plotted against T1s measured in the IR-RARE as shown in Figure 1A. Contrast concentrations ranging from 0.023 mM to 0.27 mM yielded T1s ranging from 1000msec to 3300msec, which is a reasonable range to implement for the DCE-MR study considering that the T1 of GM at 9.4T is 2000 ms. Error bars in Figure 1A represent standard deviations (SD) of the measured T1s and are indiscernible for IR-RARE because they are too small relative to the scale. The coefficient of variance (COV) of the T1s was likewise much smaller for the IR-RARE (< 0.01%) when compared to the VFA-SPGR (between 12% and 17%). Bar graphs in Figure 1B represent discrepancies between the B1+ corrected and uncorrected T1s as expressed in Eq.10. As can be observed, B1+ uncorrected T1s resulted in substantial discrepancies (25 ± 10 %), while with the B1+ correction agreement between the two methods improved considerably (6 ± 2 %). Longitudinal relaxivity of Gd-DOTA at 9.4T was calculated to be C_Gd =2.69 mM⁻¹sec⁻¹ as shown in Figure 1C and the y-intercept representative T1 of pure solvent, i.e. water, was ~3700msec.

Figure. 1.

T1s measured in 3D VFA-SPGR and IR-RARE at six different Gd-DOTA concentrations. Red and blue lines represent B1 uncorrected and corrected T1s in 3D VFA-SPGR, respectively. (A) T1s measured in 3D VFA-SPGR were plotted as a function of T1s measured in IR-RARE. Dots and error bars represent mean and standard deviations within the regions of interest, respectively. A dotted line represents a line of identity. (B) Discrepancies (see Eq. 8) between IR-RARE and VFA-SPGR in measured T1s at each concentration. (C) 1/T1s measured in IR-RARE plotted as function of Gd-DOTA concentrations in deriving relaxivity constant and a solid line represents a linear regression line.

Numerical simulations

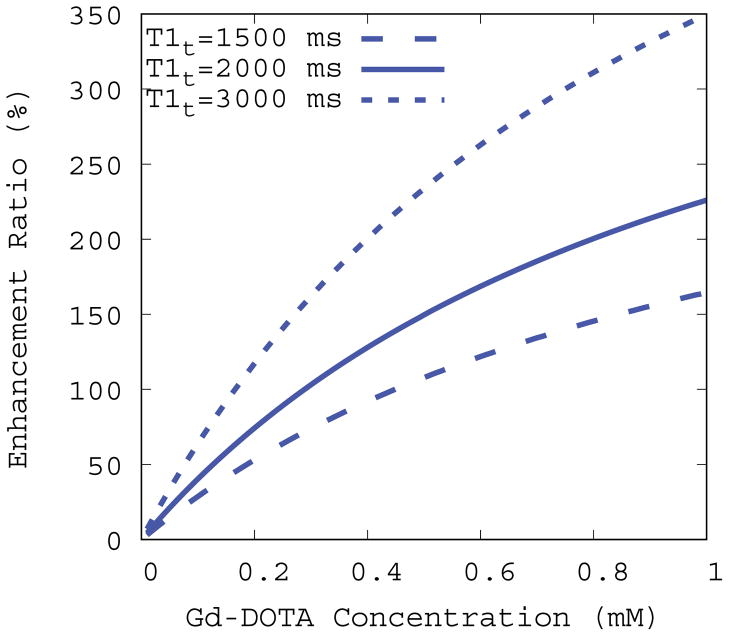
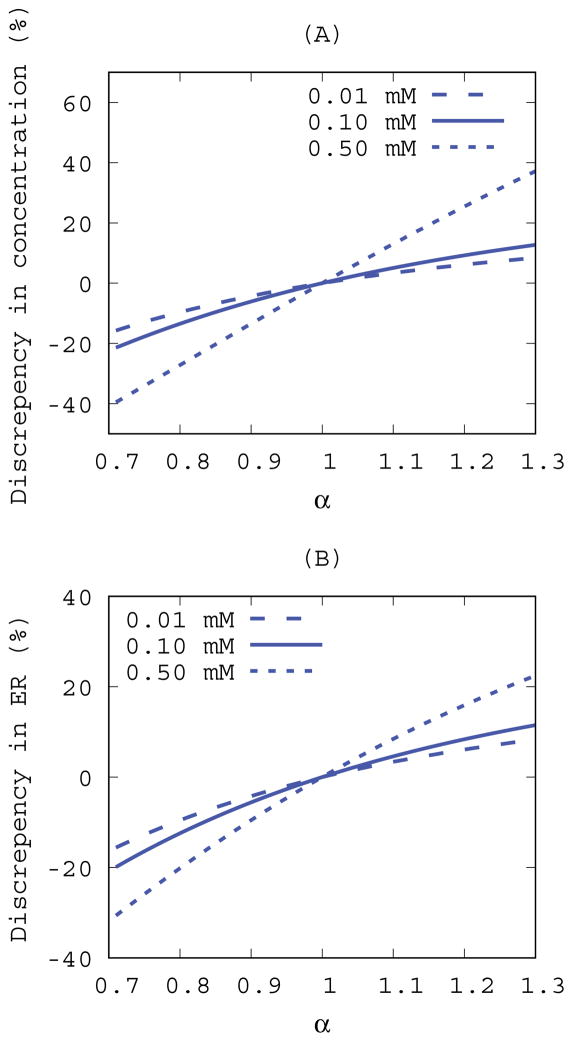
MR signals were simulated under different conditions for evaluating calculated variables including the enhancement ratio and contrast concentrations assuming an ideal noise-less condition as expressed in Eq.5~Eq.8. In the absence of B1+ inhomogeneity (α = 1) the enhancement ratio was uniquely defined at a given set of contrast concentration and pre-contrast T1 and it monotonically increases with increasing contrast concentrations as shown in Figure 2. However, the rate of increase varies depending on the pre-contrast T1 and therefore the enhancement ratio alone does not uniquely define contrast concentration. In the presence of B1+ inhomogeneity (α = 1) the above-mentioned observations were further complicated because the enhancement ratio expressed as Eq.8 would be biased by α as well. Under the set of known contrast concentrations (0.01~0.1 mM), discrepancies between apparent (α ≠ 1) and true (α = 1) enhancement ratios and concentration were quantified using Eq.10 and the results were plotted as a function of α as shown in Figure 3. Deviations from the true values monotonically increased with increasing α but the rate of change in the discrepancy was also asymmetric around α = 1 because VFA-SPGR signals as expressed in Eq.11 is an asymmetric function around the flip angle of 15°. Furthermore, the discrepancies grew proportionally with increasing contrast concentrations for both variables, signifying that the discrepancies depend on the magnitude of α and the contrast concentration.

Figure. 2.

Simulated enhancement ratios plotted as a function of Gd-DOTA concentrations at three different pre-contrast baseline T1s (T1t). Imaging parameters were set to the 3D VFA-SPGR protocol (TR=15ms and θ_n=15°) and the Gd-DOTA relaxivity constant (C_Gd =2.69 mM⁻¹s⁻¹) was derived in this study.

Figure. 3.

Discrepancies between B1+ corrected and uncorrected (A) concentrations and (B) enhancement ratios as a function of B1+ inhomogeneity (α) in ideal noise-less conditions. A pre-contrast baseline was set to T1t=2000 ms and three different Gd-DOTA concentrations were evaluated. Imaging parameters were set to the 3D VFA-SPGR protocol (TR=15ms and θ_n=15°) and the Gd-DOTA relaxivity constant (C_Gd=2.69 mM⁻¹s⁻¹) was derived in this study.

Pre-contrast 3D T1 map

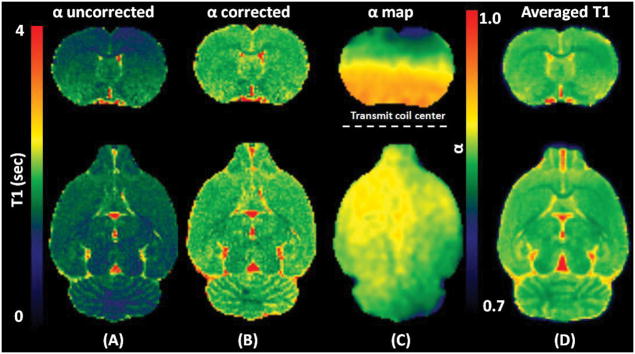
Pre-contrast 3D T1 maps were calculated using the VFA-SPGR taken at six flip angles with B1+ correction as expressed in Eq.4. A representative T1 map with and without B1+ correction, a corresponding α map, and a population averaged T1 map are shown in Figure 4. As seen from Figure 4C, in a spatially dependent manner, α progressively deviates from the nominal flip angle when a voxel position is further away from the center of the RF transmit coil, where the automatic pre-scan was set for calibrating the RF transmission gain, affecting the accuracy of T1 proportionally. Since all rat brain scans were taken in supine position, B1+ inhomogeneity worsens with distance to the coil (i.e. toward the cortex ) while RF receive sensitivity (B1-) enhances as voxels get closer to the coil. With B1+ correction, a more homogeneous T1 profile is clearly discernible. When all T1 maps were spatially normalized and summed together to construct a population averaged T1 map (N=5), the contrast to noise ratio and delineation of anatomical landmarks improved substantially as shown in Figure 4D. By using the rat atlas (20), individual T1 maps were segmented and thresholded to create tissue specific binary masks for calculating T1 in each tissue compartment. From this analysis the T1s of GM, WM, and CSF were 2001 ± 17 ms, 1705 ± 29 ms, and 2822 ± 29 ms, respectively while the brain volumes (sum of GM and WM) were 1695 ± 48 mm³.

Figure. 4.

Images are showing two orthogonal planes of a representative (A) α uncorrected T1 map, (B) α corrected T1 map, and (C) corresponding B1+ correction map (α), and (D) Population averaged α corrected T1 map (N=5) after the spatial normalization. A dotted line was drawn as a reference to the center of the RF transmit coil in an axial plane.

Dynamic Gd-DOTA concentration maps

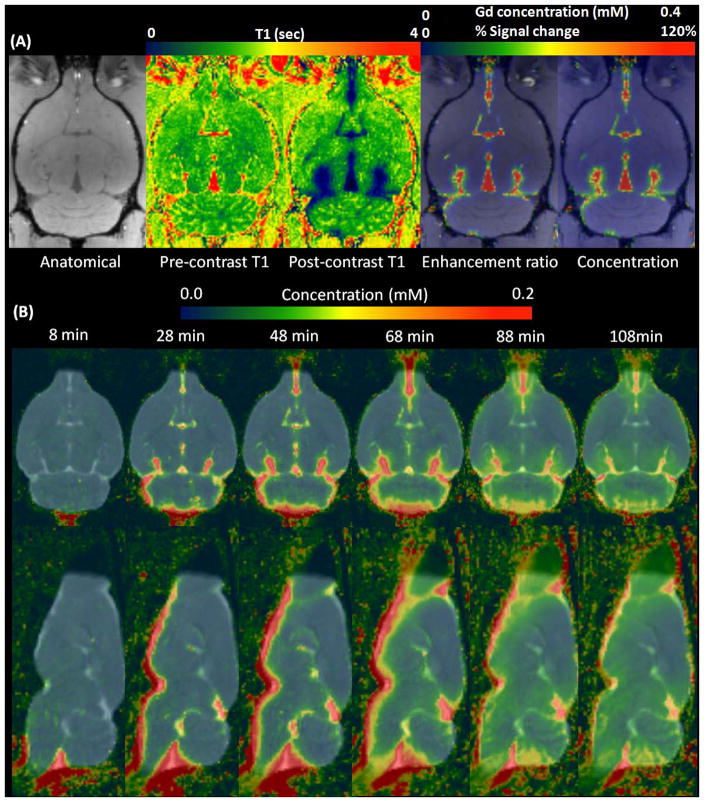
Dynamic enhancement ratio maps were converted into dynamic concentration maps using Eq.9. In Figure 5A, a representative SPGR anatomical scan at the level of the ventral hippocampus is shown with the following corresponding maps: a pre- and post-contrast T1 map, the enhancement ratio at 16 min from the onset of infusion and actual contrast concentration maps. As seen from Figure 5A, the general contrast distribution pattern was identical between the enhancement ratio and the corresponding contrast concentration maps as expected from the simulations. In Figure 5D, the population averaged dynamic concentration maps are shown demonstrating that the group averaged glymphatic transport pattern was consistent with previous studies (10,21). The dynamic concentration maps show that the contrast slowly permeates from the CSF spaces into the brain parenchyma; for example, at approximately 1 hr, a concentration gradient gradually builds up from the site of CSF influx into the cortical and subcortical regions over time.

Figure. 5.

(A) Representative scans showing different modalities at 16min from the onset of Gd-DOTA infusion. (B) Population averaged Gd-DOTA concentration maps (N=5) were overlaid onto the population averaged T1 map over different times from the onset of the infusion.

Concentration maps masked by the tissue probability maps enabled calculation of total Gd-DOTA mass uptake in the brain at any given time during the experiment. Whole brain time activity curves of the enhancement ratio (% signal change), the total contrast mass (μM), and T1s (ms) are shown in Figure 6. As seen from the profiles, contrast solute transport from the cisterna magna into parenchyma occurred relatively rapidly, within the first 10 min from the onset of CSF infusion suggesting a bulk flow driven process. Subsequently, parenchymal uptake raises sharply until ~32 min where it gradually slows down reaching a unimodal peak ~60 min post-infusion. The maximal parenchymal uptake was ~0.05 μmol, which translates into ~19 % of the total Gd-DOTA (0.27 μmol) delivered into the CM. The contrast was then gradually redistributed and cleared from the brain, and the clearance rate of Gd content, defined by the rate of decrease from the peak to the end of experiment, was far less than the rate of its uptake. Accumulation and clearance rates were estimated by fitting the rising and descending trends by two separate lines and the slopes were found to be 0.0016 and 0.00021 μmol/min in the rising and descending components, respectively. Total mass retention and enhancement ratio were plotted as a function of time and the linear regression yielded the slope and y-intercept to be 244 and −0.2, respectively.

Figure. 6.

Whole brain (GM+WM) time activity curves of enhancement ratio, T1, and the total mass of Gd-DOTA retained in the brain were plotted. Dots and bars represent mean and SD, respectively. The onset of infusion was set to zero in the time axis and the pump stopped at 18 min from the onset. (D) Enhancement ratios, as shown in (A), were plotted as a function of the total mass retained in the brain, as shown in (C). A solid line represents a linear regression between the two variables.

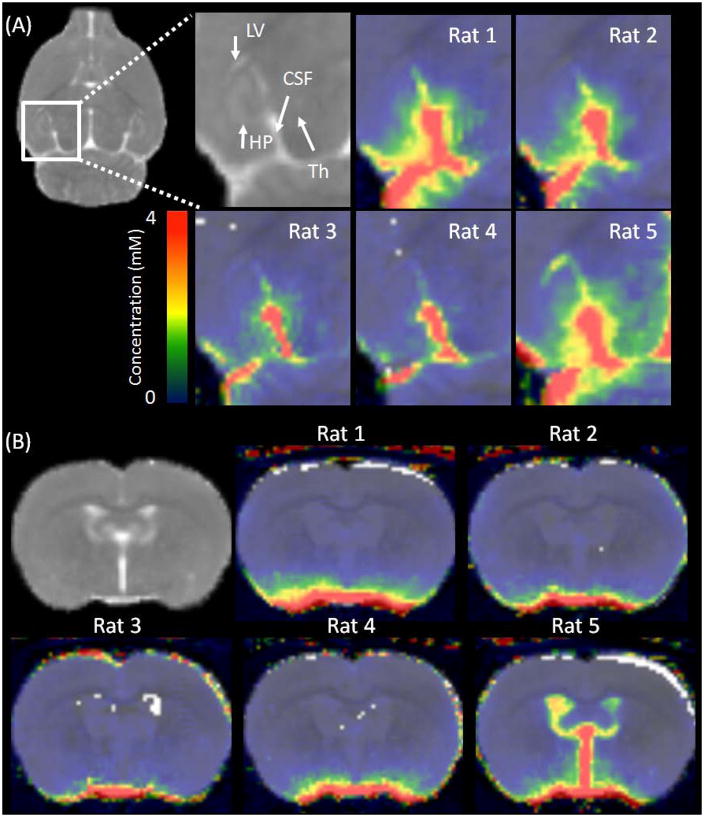
A study using confocal fluorescent imaging techniques recently reported traces of fluorescent tracer depositing from the interpeduncular cistern (21) into the lateral ventricles, suggestive of a continuous CSF pathway from the cisterna magna through the subarachnoid spaces and into the ventricular system. However, possibly due to a technical limitation, the study could not conclude whether the pathway played a significant role in CSF transport. To explore this possibility we time integrated all the dynamic concentration maps thereby creating a single concentration weighted map, thus enhancing the sensitivity for detecting traces of contrast during the experiment. Figure 7 shows the time integrated concentration maps of the five animals at the level of the regions of interest where the continuous passage from the subarachnoid space into lateral ventricles was previously reported (21). As observed in Figure 7, a cleft can be seen between the hippocampus and thalamus. In four out of five rats with normal sized ventricles, there was no indication of the contrast entering into the lateral ventricles through the narrow pathway because signals in the ventricles remained at the background noise level. However, in one rat with marginally enlarged ventricles contrast movement could be appreciated in the lateral ventricles but the ventricular uptake was predominantly through the accumulation of contrast in the enlarged dorsal 3^rd ventricle from where it likely leaked into the cleft as shown in Figure 7.

Figure. 7.

Time integrated concentration maps of each animal are overlaid onto the population averaged T1 map (shown in the background). (A) Coronal views highlighting the area of interpeduncular cistern (marked as CSF) running between the hippocampus (HP) and the thalamus (TH) for evaluation of continuous passage from the subarachnoid space into the lateral ventricle (LV). (B) Axial view showing 3^rd and lateral ventricles of each animal. Marginally enlarged ventricles were observed in one of the five rats in this study.

Discussion

In this study we present a methodological advance for calculating dynamic 3D whole brain contrast concentration maps, allowing quantification of Gd-DOTA uptake from CSF into brain parenchyma. From our previous studies using fluorescent tracers, we documented that the underlying system responsible for the transport of paramagnetic contrast from CSF into parenchyma is indeed the glymphatic pathway (10). However, our previous MRI platform for measuring glymphatic transport was semi-quantitative, limiting the accurate estimation of CSF (and solute) transport from the cisterna magna to the parenchyma in exchange for ISF and also interfering with kinetic analysis strategies (6). Previous studies using similar approaches of CSF infusions of MR or CT compatible contrast agents into the cisterna magna were also semi-quantitative (22–24).

Here we derived an analytical expression relating the brain contrast concentration map with two unknown variables: the pre-contrast T1 and the enhancement ratio. Our initial motivation for using the enhancement ratio as a glymphatic transport measure was to reduce the effect of the spatially inhomogeneous surface radio frequency receive coil (B1-) on the measurements (10). The choice of an optimal T1 quantification method depends on spatial and temporal resolution required to measure T1 as accurately and reliably as possible and many imaging strategies for this purpose were previously developed for intravenously (IV) injected contrast in studies of tumors and stroke (25,26). Some of these methods including the windows method (27), two flip angle method (28,29) and 3D EPI look-locker method (30) were developed specifically for DCE-MRI applications with IV injection of contrast. In the case of the glymphatic system, CSF solute (contrast) transport is much slower (min) compared to IV contrast injection studies (sec) and therefore a 3D VFA-SPGR approach is suitable.

The accuracy of 3D VFA-SPGR was evaluated using phantoms and the measured T1s were cross-validated with a single slice inversion recovery sequence over a reasonable of range of T1s mimicking pre- and post-contrast brain tissue enhancement. Agreement between the two techniques improved substantially when a correction factor, α, for nominal flip angles accounting for the spatially dependent B1+ profile was incorporated, thus reducing the discrepancies between the two methods from ~25% to ~6%. With implementation of the correction factor, whole brain GM, WM, and CSF T1s were also comparable to T1s reported in previous studies (31,32). For accurate and reliable T1 measurements a considerable body of literature exists and some of the known technical issues relevant to our technique will be discussed (33). First, accuracy of α map directly affects the calculated T1s and there are many B1+ mapping techniques available, each of which characterized by unique advantages/disadvantages. The double-angle method was implemented in this study because it is technically straightforward, however it is inherently 2D and a non-linear slice profile may introduce a systematic bias in the calculated B1+ (34). The 3D B1+ mapping technique using a slice non-selective pulse such as an actual flip angle technique (35) or zero-crossing technique (36) should be considered when those pulse sequences become available for pre-clinical systems. Second, the validity of the equations for VFA-SPGR depends on complete dephasing of the transverse relaxation after the readout. In this study, we only applied a gradient spoiler and RF spoiling can be added to further spoil the residual transverse magnetization (37) which may improve the accuracy. Third, a choice of flip angles in search for optimizing T1 accuracy while minimizing scanning time has been a goal for clinical studies for years and a pair of optimal flip angles exists for optimizing the accuracy for a single T1 (38) but applying this to optimize a range of T1s is controversial (39). Our choice of using equally spaced flip angles was to cover the Ernst angle for both tissue and CSF. Some of the aforementioned techniques should certainly be considered for further improvement in the accuracy and reliability of T1 mapping.

This study found that B1+ alone can cause substantial errors in the T1 calculation. When nominal flip angles are uncorrected simulation results showed that deviation from the true values including the enhancement ratio and derived concentrations were directly proportional to α and it progressively worsened with increasing contrast concentration. This is to be expected because the VFA-SPGR signal is proportional to the product of the flip angle and contrast concentration and they are not distinguishable from the signal alone, hence an erroneous flip angle results in an erroneous concentration calculation. Characteristics of the spatially varying B1+ inhomogeneity depends on the RF transmit coil design. Despite the use of a whole-body birdcage transmit RF coil, known for a superior homogenous RF profile compared to surface or head only RF transmit coils, the B1+ correction was still essential for calculating accurate T1s and contrast concentrations. The implication of our findings is generalizable to pre-clinical applications at 9.4T or higher. Multi-channel surface transmit coils with B1+ shimming capabilities have shown to be effective in reducing the inhomogeneity (40) but they are generally unavailable for pre-clinical animal scanners.

Following the methodological development for converting enhancement ratios into actual contrast concentration we performed whole brain analysis of contrast uptake. Temporal profiles of the enhancement ratios and actual contrast concentration uptake maps were linearly related. The dynamic contrast concentration maps showed that the time of solute transport from the cisterna magna to the brain occurred within ~10 min from the onset of contrast infusion and CSF-ISF exchange peaked ~40 min after terminating the infusion and then slowly decayed at the rate almost an order of magnitude slower than the initial influx as estimated in the rate constants. In addition there are apparent disproportionate influx and clearance rates of tracers in both sleep and awake states as well (9). Parenchymal uptake and perivascular removal of the contrast solute are taking place concurrently and the total mass in the brain represents the amount of retention as the net effect of both uptake and removal. Maximal mass retention of the contrast was ~20 % of the total infused mass and to interpret this fraction in terms of CSF equivalent displacement volume it translates into ~12 μl ( roughly 13 % of the total CSF in the brain) using available data on CSF flow rate of ~3 μl/min at cisterna magna (41,42). Only a small fraction of the infused CSF solute reached the brain parenchyma because there are multiple CSF efflux pathways from cisterna magna (6) leading out of the brain, and CSF/solute transport does not always include the glymphatic pathway. Known CSF efflux sites outside of the brain include arachnoid villi, cribriform plate (43), and cranial and spinal nerves (44,45). These alternative pathways might be used if access to the glymphatic pathway is restricted (6). For example, CSF-ISF exchange along the peri-vascular space can be more resistive than larger reservoirs of subarachnoid space.

A recent study suggested a possible continuous passage from cisterna magna to lateral ventricles through the interpeduncular cisterns (21) as a shortcut to redirect CSF into the lateral ventricles. Upon evaluation of summed concentration weighted maps in this study, however, no evidence was found to support the existence of this route. Nevertheless, noticeable contrast uptake in the lateral ventricles was apparent in one rat with enlarged ventricles; this was a consequence of enlarged 3rd ventricles allowing contrast into the lateral ventricles which then subsequently seeped into the cleft around the hippocampus. The fact that the contrast was observed in the ventricles signifies that a portion of CSF that would otherwise participate in CSF-ISF exchange and waste clearance was instead delivered to ventricles.

There are several technical limitations in the present study. First, a significant signal drop off from the dorsal to ventral side of the brain is an inevitable consequence of a surface coil receiver, and at low signal-to-noise ratio the unweighted linearization of VFA-SPGR signals in calculating T1 is sensitive to a noise bias. Weighted linear/non-linear least square fitting has been reported to be an effective method in reducing these biases (39,46,47). Second, the sensitivity of detecting contrast concentration is limited by the level of background noise. The steep concentration gradient from the subarachnoid space toward the leading edge of the permeating solute may have excluded some contrast in the total contrast mass calculation. Third, the DCE-MRI signal indirectly measures contrast concentration from the from the surrounding proton T1 relaxation measurements and this correlation has known issues with regards to water compartmentalization (48). The method applied in this article has been confirmed valid both in vitro (49–51) and in vivo (52) but other methods like Gd-14C-DTPA autoradiography and flameless atomic absorption spectrophotometry (53) can be used to further validate the results of this study. Lastly, T2* effect was assumed to be negligibly small in deriving the concentration calculation. T2* effect is a consequence of water proton exchange between spatially varying static magnetic field (B0), or local susceptibility change induced by the paramagnetic contrast agent, resulting in collective dephasing of the water protons and signal loss in the spoiled gradient echo images. While T2* does not affect the pre-contrast tissue T1 calculation, the enhancement ratio can be underestimated if T2* signal loss is substantial within the echo time (54,55). An additional scan (supporting material S2 Figure 1S and Figure 2S) was performed in one female Sprague Dawley rat undergoing the same experimental procedure using a dual echo (TE=4 and 9ms) spoiled gradient echo sequence but T2* maps were extremely noisy and could not measure the values reliably (supporting material S2 Figure 3S and Figure 4S). Therefore voxel-wise T2* with the short echo spacing would add considerable noise to the concentration calculation and further study is needed in evaluating the viability of the T2* correction.

Supplementary Material

Supp info

Figure. 1S. The regions of interest (red) to characterize T2* effects.

Figure. 2S. Signal intensities within ROIs as a function of time at TE=4ms (purple) and TE=9ms (green). The onset of infusion was set to time=0.

Figure. 3S. T2* within the regions of interest. The onset of infusion was set to time=0.

Figure. 4S. Comparison between pre (1^st frame) and post (40 min post infusion) contrast enhancement in T1 weighted images (left) and corresponding T2* images (middle) and 1/T2* difference (right) between pre (average of three frames) and post contrast enhancement.