A new formalism for modelling parameters α and β of the linear quadratic model of cell survival for hadron therapy

Abstract

We propose a new formalism for calculating parameters α and β of the linear quadratic model of cell survival. This formalism, primarily intended for calculating relative biological effectiveness (RBE) for treatment planning in hadron therapy, is based on a recently proposed microdosimetric revision of the single-target multi-hit model. The main advantage of our formalism is that it reliably produces α and β that have correct general properties with respect to their dependence on physical properties of the beam, including the asymptotic behavior for very low and high linear energy transfer (LET) beams. For example, in the case of monoenergetic beams, our formalism predicts that, as a function of LET, (a) α has a maximum and (b) the α/β ratio increases monotonically with increasing LET. No prior models reviewed in this study predict both properties (a) and (b) correctly, and therefore, these prior models are valid only within a limited LET range.

We first present our formalism in a general form, for polyenergetic beams. A significant new result in this general case is that parameter β is represented as an average over the joint distribution of energies E₁ and E₂ of two particles in the beam. This result is consistent with the role of the quadratic term in the linear quadratic model. It accounts for the two-track mechanism of cell kill, in which two particles, one after another, damage the same site in the cell nucleus. We then present simplified versions of the formalism and discuss predicted properties of α and β Finally, to demonstrate consistency of our formalism with experimental data, we apply it to fit two sets of experimental data: (1) α for heavy ions, covering a broad range of LETs, and (2) β for protons. In both cases, good agreement was achieved.

1 Introduction

Physical properties of hadron beams change significantly as particles propagate in patient tissues. This causes the relative biological effectiveness (RBE) to change. Although variations in RBE throughout the treated volume pose a serious challenge to treatment planning, they concurrently present an additional degree of freedom for optimization of a treatment plan that is not available in conventional treatments with high-energy photons. To harness the distinct biological properties of hadron beams, an accurate and reliable model for calculating three-dimensional distributions of RBE throughout the patient anatomy is required.

Several models for calculating RBE of hadron beams, mostly protons, have been proposed in previous studies. All of these models rely on the linear quadratic model of cell survival. The linear quadratic model, however, has limitations. At high radiation doses, it is inconsistent with experimental data that tend to have a constant slope of the logarithm of cell survival versus dose curves, Garcia et al. (2006). The linear quadratic model is therefore considered to be ”inappropriate” for modelling high dose per fraction treatments, such as those used in radiosurgery, Kirkpatrick et al. (2008). It has also been noted that the linear quadratic model poorly fits survival data at low doses, Garcia et al. (2006), Iwata et al. (2006). Overall, published data suggest that the linear quadratic model should not be used at doses below 1–2 Gy or above 8–10 Gy. Several cell survival models have been proposed that improve agreement with experiment at high doses: Scholz et al. (1997), Guerrero and Li (2004), Astrahan (2008), Park et al. (2008), Mckenna and Ahmad (2009), Vassiliev (2012). Some of these models are closely related to the linear quadratic model. For example, implementation of the linear-quadratic-linear model, Scholz et al. (1997) and Astrahan (2008), requires the usual parameters of the linear-quadratic model, α and β, plus an additional parameter, the threshold dose, D_t, beyond which the logarithm of survival is approximated by a linear function of dose.

In the linear quadratic model, two parameters define a survival curve: α representing the single-track mechanism of cell kill, and β representing the two-track mechanism. In the two-track mechanism, the same site within the cell nucleus is damaged twice by two consecutive hits by tracks of two different particles. For this reason β generally depends on the dose rate, because the higher the dose rate, the less time on average the cell has to repair damage from the first hit. Mechanisms involving three or more tracks are neglected, which is one of the reasons for poor performance of the linear-quadratic model at high doses, where multi-track events become more likely. The model proposed by Vassiliev (2012) eliminated this limitation and, at high doses, predicted a constant slope of the logarithm of survival versus dose, which is consistent with experimental findings, Garcia et al. (2006).

The RBE of a hadron beam at a point receiving dose d_h (hadron dose) per fraction, can be calculated if parameters α_h and β_h of the hadron beam at this point are known, Joiner (1989):

$$\mathit{\text{RBE}}=\frac{1}{2d_h}\{\sqrt{{\left(\frac{{\alpha }_{\gamma }}{{\beta }_{\gamma }}\right)}^2+4d_h\frac{{\beta }_h}{{\beta }_{\gamma }}[\frac{{\alpha }_h}{{\beta }_h}+d_h]}-\frac{{\alpha }_{\gamma }}{{\beta }_{\gamma }}\},$$ (1)

where the subscript γ denotes the reference radiation, high energy photons.

Parameters α_h and β_h need to be expressed as functions of physical parameters of a hadron beam at a given location. The most commonly used for this purpose beam parameter is the linear energy transfer (LET). Before we review existing models for α_h and β_h, and their limitations, we will point out that α_h and β_h have the following general properties:

1. At low LET, α_h increases with increasing LET, reaching a maximum at an LET on the order of 30 keV/µm for protons and 100 keV/µm for heavier ions. Then, beyond the maximum, α_h decreases.

2. The α_h/β_h ratio increases monotonically with increasing LET. This happens for two reasons. First, for higher LET beams, fewer particles are needed to deliver a given dose and, therefore, two-track events become less likely than single-track events. Second, as the LET increases, damage to the cell from a track entering its nucleus increases. This property is consistent with the fact that the shoulder of experimental survival curves gradually disappears as LET increases.

The simplest model for α_h and β_h was proposed by Wilkens and Oelfke (2004), Tilly et al. (2005), Wedenberg et al. (2013) and Cometto et al. (2014). In this model α_h is a linear function of LET

$${\alpha }_h(L)={\alpha }_{\gamma }+\lambda L,$$ (2)

and β_h is a constant

$${\beta }_h={\beta }_{\gamma }.$$ (3)

Here, λ is a model parameter and L is the LET. The above model for β_h dates back to the theory of dual radiation action, Kellerer and Rossi (1972). The linear model for α_h does not have property (A). This model was intended, however, for proton beams that have relatively low LET. When Eq. (1) is used for polyenergetic beams, L is replaced with the dose averaged LET, L_d, Wilkens and Oelfke (2004), Cometto et al. (2014)

Chen and Ahmad (2012) proposed a model that has property (A):

$${\alpha }_h={\alpha }_{\gamma }+\frac{1-\text{exp }(-{\lambda }_1{L}^2)}{{\lambda }_{2}L},$$ (4)

This model has two parameters, λ₁ and λ₂. For small LET, α_h increases approximately linearly with increasing LET. Then it reaches a maximum and starts decreasing. However, β_h, was assumed constant, as in Eq.(3), and therefore this model does not have property (B).

In the models proposed by Carabe et al. (2012) and McNamara et al. (2015), α_h is a linear function of LET, as in Eq.(2), but β_h, is given by

$$\sqrt{{\beta }_h}={\lambda }_1+{\lambda }_2{L}_d.$$ (5)

In the Carabe et al. (2012) study, fitting this model to experimental data for proton beams produced λ₁ > 0 and λ₂ > 0. McNamara et al. (2015) fitted the model to a more comprehensive set of experimental data and reported λ₁ > 0 and λ₂ < 0. Both versions of the model have neither property (A) nor property (B). With the fitting parameters reported by Carabe et al. (2012), the α_h/β_h ratio as a function L_d has a maximum. In the model of McNamara et al. (2015), for L_d = − λ₁/λ₂ we have β_h = 0 and an infinite α_h/β_h ratio. Beyond this point (L_d > − λ₁/λ₂), β_h is not defined. Fitted to experimental data for protons, both models are nevertheless fully applicable to proton beams.

Kuperman (2016) revised the modified linear quadratic model of Guerrero and Li (2004) by applying a microdosimetric methodology to account approximately for fluctuations of energy depositions. For low LET, in this model both α_h and β_h, are linear functions of LET, respectively increasing and decreasing with increasing LET. Thus, for low LETs, the model has property (B). The model was intended primarily for proton beams, and its properties for high LET were not investigated.

Finally, in the microdosimetric kinetic model (MKM), Kase et al. (2006), α_h is expressed in terms of microdosimetric parameters and it does have property (A). Parameter β_h, however, is constant (the same for all ions), and therefore the MKM does not have property (B).

In this study we derive expressions for α_h and β_h from a revised version of the single-target multi-hit model proposed by Vassiliev (2012). In this revised model, the definition of a hit was refined. The hit was defined as an ionization cluster within a sensitive volume (SV), or a target, in the cell nucleus. It is characterized by a single parameter, the energy ε₀ transferred to the SV by all inelastic interactions that belong to the cluster. In doing so we followed Good-head et al. (1993) who described initial physical damage in terms of ionization clusters and quantified the severity of damage by cluster energy. This approach is consistent with the principles of microdosimetry where specific energy z determines the biological effect. Following some simplifying assumptions, and using microdosimetric concepts, a probability distribution of the number of clusters was derived in an analytical form. Unlike the classical multi-hit model, in the revised model the distribution of hits is not Poissonian. Hence, the new formulation is designated the Non-Poisson Multi-Hit (NPMH) model. In the NPMH model, the cell survival curve is not linear quadratic. However, the exact expression for the logarithm of cell survival in the NPMH model can be written as a power series:

$$-\text{ln }S={\alpha }_{h}D+{\beta }_h{D}^2+{\gamma }_h{D}^3+\dots ,$$ (6)

from which parameters of the linear quadratic model, α_h and β_h, can be found.

After we derive expressions for α_h and β_h, we review general properties of the solution, and consider in detail several simple examples. The NPMH model was originally formulated in terms of microdosimetric quantities. Therefore, our most general result for α_h and β_h is also written in terms of microdosimetric quantities. For a simple introduction to microdosimetric concepts and terminology, we refer to Vassiliev (2017). In some cases, we also present results written in terms of the LET, by using an approximate relationship between the key microdosimetric parameter of the model and the LET. Our new model correctly predicts how α_h and β_h depend on the LET. In all cases, except one special case, our model has both (A) and (B) properties. The exception is the single-hit system, in which α_h decreases monotonically with increasing LET, and β_h = 0. This, however, is the correct behavior of the single-hit system.

2 Methods and materials

2.1 The NPMH model for polyenergetic beams

As mentioned above, for polyenergetic beams in most models the beam properties are characterized by a single number, the dose average LET, L_d. This, however, is an oversimplification because therapeutic hadron beams usually have broad spectra. For example, spread out Bragg peaks are formed by mixing multiple beam energies, and in scanning beam techniques the energy spectrum broadens towards the end of a particle range, which is where the RBE reaches its maximum. The dose average LET characterizes only the center of an LET distribution but contains no information about the shape of the spectrum, its width, or skewness. Therefore, two very different spectra may have the same L_d, but different RBEs. This contributes to the scatter of experimental RBE data, when it is plotted versus L_d, and ultimately limits the predictive power of a model.

In this study, the radiation field is characterized by fluence spectrum of hadrons Φ(E) at the point of interest. We chose the energy spectrum instead of the LET spectrum, because two hadrons with different energies and/or charges, and therefore different RBEs, may have the same LET, see for example Lappa et al. (1993). We use fluence because by definition, fluence determines the number of particles entering a small volume, ICRU Report 60 (1998) and Vassiliev (2017), such as the cell nucleus or another target volume in the cell. Therefore, Φ(E) is the energy distribution of particles entering the target volume.

In the original study, Vassiliev (2012), in which the NPMH model was introduced, we did not clarify how to apply this model to polyenergetic beams. This is not a straightforward procedure, and we explain it in this section. We have omitted explanations and justifications of the underlying model assumptions since these were provided in the Vassiliev (2012) study, where we also demonstrated the consistency of the model with experimental data for several biological endpoints. In summary, the NPMH model correctly predicts the shape of typical cell survival curves and its variation with LET. This includes a non-zero initial slope, the shoulder, and an invariant slope at high doses. The NPMH model is also applicable to analysis of DNA damage. We have shown that the model is consistent with data on the variation of single and double strand break yields with particle energy for electrons and protons. Finally, in the NPMH model, α_h and β_h have correct general properties, which is discussed in more detail in this paper.

The NPMH model is a modification of the classical multi-hit model where radiation damage is linked to the formation of ionization clusters and the mathematical formalism is based on the microdosimetric principles. Many previous studies, for example, Friedland et al. (2011), Friedrich et al. (2012), Ballarini et al. (2013), and Manganaro et al. (2017) have investigated the connection between energy depositions in an SV and cell survival using various approaches. These studies are similar in that they model the microscopic patterns of energy deposition and molecular-level processes leading to cell inactivation. They utilize advanced computing techniques, such as Monte Carlo. Models of this type provide a good insight into the underlying mechanisms. The NPMH model does not reach the level of complexity of such models. It nevertheless reliably predicts all the essential properties of survival curves and other effects, as we described above. All this is achieved within an analytical formalism that requires only three simple parameters: number of hits, energy per ionization cluster and the size of the SV.

Before we begin, we need to clarify our terminology.

• Track. In this context a track comprises all inelastic interactions of a single primary particle produced by the source, and by all secondary particles it produces, such as delta electrons and nuclear fragments.

• Energy deposition event (EDE). A particle enters the SV, undergoes an inelastic interaction and deposits energy ε > 0 within the SV. If two or more particles that belong to the same track (e.g., they were produced by the same parent particle) enter the SV and both deposit energy, this is counted as one EDE. With this clarification, use of the Poisson distribution for the number of EDEs is fully justified. Instead of EDE, the expression ”track enters the SV” may be used.

• Hit. In the original multi-hit model, the hit was equivalent to an EDE. In the NPMH model, hit is defined as an ionization cluster within the SV. Therefore, in the NPMH model, one EDE can produce more than one hit, or it may produce none.

First, the probability distribution of the number of hits, p(k), is written with use of a total probability equation:

$$p(k)=\sum _{i=0}^{\infty }p(i)p(k|i)=\text{exp }(-a)\sum _{i=0}^{\infty }\frac{a^i}{i!}p(k|i),k=0,1,\dots ,$$ (7)

where p(i) is the probability distribution of the number of tracks entering the SV and depositing energy, i.e., the number of EDEs; p(k|i) is the conditional probability distribution of the number of ionization clusters, k, for a given number of EDEs, i. We assumed that the distribution p(i) is a Poisson distribution, with the average a, which can be calculated as

$$a=\frac{D}{{\overline{z}}_F},$$ (8)

where D is the dose and z̄_F is the frequency-mean specific energy. The total number of hits k is the sum of hits from individual EDEs:

$$k=k_1+k_2+\dots +k_i.$$ (9)

The distribution of a sum is a convolution of individual distributions. If all particles entering the SV had the same energy, the individual distributions would be the same and we could write

$$p(k|i)=p{(k|1)}^{\ast i},$$ (10)

where *i denotes an i-fold convolution. For polyenergetic beams, we need to account for energy distribution of particles. To do so, we again use a form of the total probability equation

$$p(k|i)={\int }_0^{\infty }\mathrm{d}{E}_1\mathrm{\Phi }(E_1)\dots {\int }_0^{\infty }\mathrm{d}{E}_i\mathrm{\Phi }(E_i)p(k|i,E_1,\dots E_i).$$ (11)

Here, we used fluence spectra Φ(E) because, by definition, the fluence gives the total number of particles entering a small sphere, such as the SV. The fluence spectrum, then, gives the energy distribution of particles entering the SV. We normalized the fluence spectra, so that they could be used as probability densities for particle energy

$${\int }_0^{\infty }\mathrm{d}E\mathrm{\Phi }(E)=1.$$ (12)

The conditional distribution p (k|i, E₁, … E_i) is the distribution of the number of hits k that was delivered by i particles that entered the SV with energies E₁, …, E_i. This distribution is a convolution of distributions associated with individual particles (single-particle distributions):

$$p(k|i,E_1,\dots E_i)=p(k_1|1,E_1)\ast \dots \ast p(k_i|1,E_i).$$ (13)

We then assumed that the individual distributions are Poisson distributions, with the average of the distribution, b (i.e., the average number of hits per particle), being a function of particle energy, b = b(E):

$$p(k|1,E_j)=\text{exp }[-b(E_j)]\frac{b^k(E_j)}{k!};j=1,2,\dots ,i.$$ (14)

In that case, in Eq.(13) we have a convolution of Poisson distributions, which is, again, a Poisson distribution but with a different mean value:

$$p(k|i,E_1,\dots E_i)=\text{exp }[-\sum _{j=1}^{i}b(E_j)]\frac{1}{k!}{[\sum _{j=1}^{i}b(E_j)]}^k.$$ (15)

For parameter b(E_j) we can use any of the following three expressions

$$b(E_j)=\frac{{\epsilon }_F(E_j)}{{\epsilon }_0}=\frac{z_F(E_j)}{z_0}=\frac{y_F(E_j)}{y_0},$$ (16)

where ε_F (E), z_F (E), and y_F (E) are, respectively, the frequency-mean energy deposited in the SV (eV), specific energy (Gy), and lineal energy (keV/µm), for a particle of energy E. The last two quantities are closely related:

$$z_F=\frac{y_F}{\pi \rho r^2},$$ (17)

where r is the radius of SV (assumed to be a sphere) and ρ is the mass density of the material within the SV. An advantage of using the lineal energy is that it only weakly depends on the size of the SV. Furthermore, it is approximately linearly related to LET, L(E):

$$y_F(E)\propto L(E).$$ (18)

Considering the relatively large uncertainties in biological data, this approximation may provide adequate accuracy for RBE modelling. In that case, we can use

$$b(E_j)\approx \frac{L(E_j)}{L_0},$$ (19)

The denominators in Eqs.(16) and (19), ε₀, z₀, y₀, and L₀ represent the energy per ionization cluster, a model parameter, in the respective units.

A review of microdosimetric quantities that includes tables of y_F and z_F for several light ions and a number of different SV sizes can be found in Liamsuwan et al. (2014) and Nikjoo et al. (2016).

We need to clarify the difference between z̄_F in Eq.(8) and z_F (E) in Eq.(16). The former is the frequency-mean specific energy measured in a polyenergetic beam, and the latter is the same, but for a beam where all particles have the same energy E, i.e., a monoenergetic beam. If we have only a monoenergetic beam, the two quantities coincide, z̄_F = z_F (E).

We now insert Eqs.(11) and (15) into Eq.(7) and arrive at our main formula:

$$\begin{gathered} p(k)=\frac{1}{k!}\text{exp }(-a)\sum _{i=0}^{\infty }\frac{a^i}{i!}{\int }_0^{\infty }\mathrm{d}{E}_1\mathrm{\Phi }(E_1)\dots {\int }_0^{\infty }\mathrm{d}{E}_i\mathrm{\Phi }(E_i)\times \\ \text{exp }[-\sum _{j=1}^{i}b(E_j)]{[\sum _{j=1}^{i}b(E_j)]}^k. \end{gathered}$$ (20)

Finally, in the multi-hit model, a cell survives if the number of hits is less than n (model parameter). Then, the surviving fraction is

$$S=\sum _{k=0}^{n-1}p(k).$$ (21)

2.2 Calculating α and β

The model is applicable to all charged particles, not only to hadrons. Therefore, we will henceforth not use the subscript h.

It follows from Eqs.(6) and (8) that

$$\alpha =-\underset{D\to 0}{\text{lim}}\frac{\partial }{\partial D}\text{ln }S=-\frac{1}{{\overline{z}}_F}\underset{a\to 0}{\text{lim}}\frac{\partial }{\partial a}\text{ln }S.$$ (22)

Calculating the derivative and taking the limit yield:

$$\alpha =\frac{1}{{\overline{z}}_F}\{1-\sum _{k=0}^{n-1}\frac{1}{k!}{\int }_0^{\infty }\mathrm{d}E\mathrm{\Phi }(E)\text{ exp }[-b(E)]b^k(E)\},$$ (23)

or,

$$\alpha ={\int }_0^{\infty }\mathrm{d}E\mathrm{\Phi }(E)A(E),$$ (24)

where

$$A(E)=\frac{1}{{\overline{z}}_F}\{1-\text{exp }[-b(E)]\sum _{k=0}^{n-1}\frac{1}{k!}{b}^k(E)\}$$ (25)

For monoenergetic beams, the above expression reduces to

$$\alpha =\frac{1}{z_F}\{1-{\mathrm{e}}^{-b}\sum _{k=0}^{n-1}\frac{b^k}{k!}\}$$ (26)

From Eqs.(23) and (26) follows an important general result. For very high LETs, when L ≫ L₀, we have

$$\alpha \approx \frac{1}{{\overline{z}}_F}.$$ (27)

Then it follows from Eq.(8) that, in this case, αD is equal to the average number of particle tracks entering the SV. Therefore, in the high LET limit, the average number of cells killed by the single-track mechanism is equal to the average number of tracks that entered the SV. The role of the multi-track mechanism in cell kill diminishes with increasing LET.

To calculate β, according to Eq.(6), we need to find the second derivative:

$$\beta =-\frac{1}{2}\underset{D\to 0}{\text{lim}}\frac{{\partial }^2}{\partial D^2}\text{ln }S=-\frac{1}{2{\overline{z}}_F^2}\underset{a\to 0}{\text{lim}}\frac{{\partial }^2}{\partial a^2}\text{ln }S.$$ (28)

The result is:

$$\begin{gathered} \beta =\frac{1}{2{\overline{z}}_F^2}\{{[\sum _{k=0}^{n-1}\frac{1}{k!}{\int }_0^{\infty }\mathrm{d}E\mathrm{\Phi }(E)\text{ exp }[-b(E)]b^k(E)]}^2- \\ \sum _{k=0}^{n-1}\frac{1}{k!}{\int }_0^{\infty }\mathrm{d}{E}_1\mathrm{\Phi }(E_1)\text{ exp }[-b(E_1)]{\int }_0^{\infty }\mathrm{d}{E}_2\mathrm{\Phi }(E_2)\text{ exp }[-b(E_2)]\times \\ {[b(E_1)+b(E_2)]}^k\}, \end{gathered}$$ (29)

or,

$$\beta ={\int }_0^{\infty }\mathrm{d}{E}_1\mathrm{\Phi }(E_1){\int }_0^{\infty }\mathrm{d}{E}_2\mathrm{\Phi }(E_2)B(E_1,E_2),$$ (30)

where

$$B(E_1,E_2)=\frac{1}{2{\overline{z}}_F^2}\{\text{exp }[-b(E_1)]\text{ exp }[-b(E_2)]\times [\sum _{k_1=0}^{n-1}\frac{b^{k_1}(E_1)}{k_1!}\sum _{k_2=0}^{n-1}\frac{b^{k_2}(E_2)}{k_2!}-\sum _{k=0}^{n-1}\frac{{(b(E_1)+b(E_2))}^k}{k!}\left]\right\}.$$ (31)

As we discussed in the Introduction, β represents the two-track mechanism of cell kill. This is the fundamental reason why we arrived at a double integral in the expression for β, Eq.(30). It represents an averaging over the joint distribution of two energies, which is given by the product, Φ(E₁)Φ(E₂). The latter implies that E₁ and E₂ are statistically independent. Energies of two particles entering the SV may in principle be correlated. These correlations can be accounted for in our formalism by replacing the product of two fluences by a joint probability distribution f(E₁, E₂). This, however, is unnecessary, because correlations have a very minor effect on the result. Particles correlations are discussed in more detail in Vassiliev (2017), Chapter 6.

For monoenergetic beams, Eq.(31) becomes

$$\beta =\frac{{\mathrm{e}}^{-2b}}{2z_F^2}\{{\left[\sum _{k=0}^{n-1}\frac{b^k}{k!}\right]}^2-\sum _{k=0}^{n-1}\frac{{(2b)}^k}{k!}\}.$$ (32)

In the limit LET→ ∞, we have β = 0. This shows, again, that the role of the two-track mechanism for high LET beams is diminished.

3 Results and Discussion

In this section we will consider three examples: the single-hit (n = 1), the two-hit (n = 2) and the three-hit (n = 3) versions of the model. This will give us a clear idea of how α and β depend on LET and how these dependencies are affected by the model parameter n.

3.1 Modelling α

The single-hit model

The single-hit model is applicable, for example, to modelling the yields of DNA single-strand breaks, Vassiliev (2012). With n = 1, Eq.(25) simplifies to

$$A(E)=\frac{\rho \pi r^2}{{\overline{y}}_F}\{1-\text{exp }[-\frac{y_F(E)}{y_0}\left]\right\}.$$ (33)

As we pointed out earlier, in Eqs.(18) and (19) lineal energy can be approximated by LET, resulting in this case in

$$A(E)\approx \frac{\rho \pi r^2}{\overline{L}}\{1-\text{exp }[-\frac{L(E)}{L_0}\left]\right\}.$$ (34)

For monoenergetic beams, this leads to a simple expression for α

$$\frac{\alpha }{\rho \pi r^2}=\frac{1}{y_F}[1-\text{exp }(-\frac{y_F}{y_0}\left)\right],$$ (35)

or, alternatively

$$\frac{\alpha }{\rho \pi r^2}=\frac{1}{L}[1-\text{exp }(-\frac{L}{L_0}\left)\right].$$ (36)

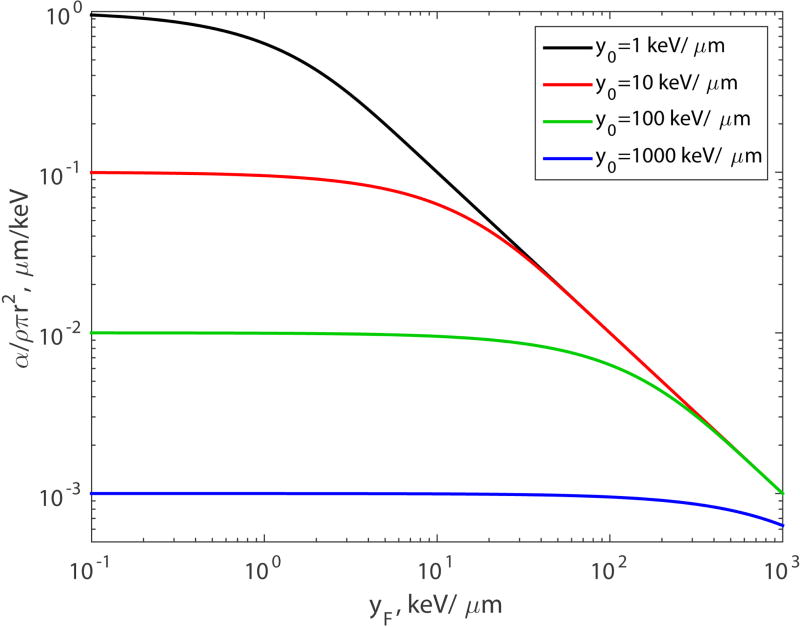
These expressions for α have two fitting parameters, y₀ (or L₀) and ρπr². Parameter α given by Eq.(35) is shown in Fig. 1 for four values of y₀: 1, 10, 100 and 1000 KeV/µm. All four curves start at value 1/y₀ for the lowest y_F, and as y_F increases they all eventually converge to the same 1/y_F line. The latter property is a general result that we derived in the preceding section.

Figure 1.

Parameter α versus y_F for the single-hit model (n = 1).

Replacing lineal energy with LET is straightforward, and henceforth we will not include formulas with LET.

For low LET, when y_F ≪ y₀ or L ≪ L₀, α decreases linearly with increasing y_F

$$\frac{\alpha }{\rho \pi r^2}\approx \frac{1}{y_0}(1-\frac{y_F}{2y_0}).$$ (37)

The two-hit model

In the two-hit model, n = 2, we similarly have

$$A(E)=\frac{\rho \pi r^2}{{\overline{y}}_F}\{1-[1+\frac{y_F(E)}{y_0}\left]\text{ exp }\right[-\frac{y_F(E)}{y_0}\left]\right\},$$ (38)

and for monoenergetic beams:

$$\frac{\alpha }{\rho \pi r^2}=\frac{1}{y_F}[1-(1+\frac{y_F}{y_0}\left)\text{ exp }\right(-\frac{y_F}{y_0}\left)\right].$$ (39)

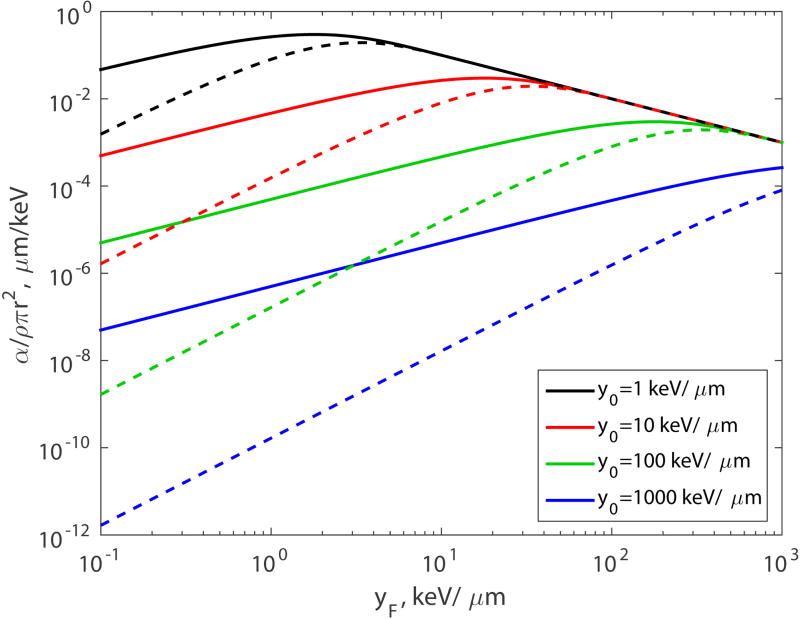
Parameter α given by Eq.(39) is shown in Fig. 2 (solid lines) for four values of y₀: 1, 10, 100 and 1000 keV/µm.

Figure 2.

Parameter α versus y_F for the two-hit model (n = 2, solid lines) and the three-hit model (n = 3, dashed lines).

All four curves, for low LETs, are approximately straight and parallel lines. This suggests a power law dependence. In this case the power is 1. Indeed, for low LET, when y_F ≪ y₀ or L ≪ L₀, α is proportional to y_F:

$$\frac{\alpha }{\rho \pi r^2}=\frac{y_F}{2y_0^2}.$$ (40)

For large LETs, all four curves, again, converge to one line, given by 1/y_F.

The three-hit model

Finally, in the three-hit model (n = 3) we have

$$A(E)=\frac{\rho \pi r^2}{{\overline{y}}_F}\{1-[1+\frac{y_F(E)}{y_0}+\frac{1}{2}{\left(\frac{y_F(E)}{y_0}\right)}^2\left]\text{ exp }\right[-\frac{y_F(E)}{y_0}\left]\right\},$$ (41)

and for monoenergetic beams

$$\frac{\alpha }{\rho \pi r^2}=\frac{1}{y_F}\{1-[1+\frac{y_F}{y_0}+\frac{1}{2}{\left(\frac{y_F}{y_0}\right)}^2\left]\text{ exp }\right(-\frac{y_F}{y_0}\left)\right\}.$$ (42)

Parameter α given by Eq.(42) is shown in Fig. 2 (dashed lines) for four values of y₀: 1, 10, 100 and 1000 keV/µm. Again, for small LETs, we see four approximately parallel straight lines, but with a different slope than in the two-hit model. This is because for small LETs the dependence is now quadratic. That is, if y_F ≪ y₀ or L ≪ L₀, then

$$\frac{\alpha }{\rho \pi r^2}=\frac{1}{6y_0}{\left(\frac{y_F}{y_0}\right)}^2.$$ (43)

The linear-quadratic model underestimates the probability of three hits, because it does not account for the three-track mechanism, where each of the three hits is delivered by different tracks. To account for all multi-track mechanisms, the full version of the NPMH model, Eqs.(20) and (21), should be used.

3.2 Location of maximum α

The location of maximum α in Fig. 2 is determined by the ratio y_F/y₀. Monte Carlo data of Nikjoo et al. (2016) show that y_F is approximately a linear function of LET. For at least relatively light particles (protons, α particles, carbon, oxygen and neon ions) the slope of the linear function decreases with increasing atomic number of the particle. This means that our model predicts that for a fixed value of parameter y₀, increasing the atomic number of the particle results in the maximum α moving to a higher LET. This predicted trend is consistent with experimental data.

3.3 Modelling β

The single-hit model

In the single-hit model, if we insert n = 1 into Eq.(31), we will get β = 0. This is a predictable result, because as we mentioned earlier, β represents the two-track mechanism. In the single-hit model, if the first track delivers a hit, the cell is killed, regardless of what damage, if any, was done by the second track.

The two-hit model

In the two-hit model (n = 2), Eq.(31) takes the form

$$B(E_1,E_2)=\frac{1}{2}{\left(\frac{\rho \pi r^2}{{\overline{y}}_F}\right)}^2\frac{y_F(E_1)}{y_0}\text{exp }[-\frac{y_F(E_1)}{y_0}]\frac{y_F(E_2)}{y_0}\text{exp }[-\frac{y_F(E_2)}{y_0}].$$ (44)

An important property of function B given by Eq.(44) is that it can be written as a product: B(E₁, E₂) = B(E₁)B(E₂). This simplifies calculations for polyenergetic beams because the double integral in Eq.(30) can now be transformed into a square of a single integral over the energy of one particle.

For monoenergetic beams, Eq.(44) leads to a simple formula

$$\frac{\beta }{{\left(\rho \pi r^2\right)}^2}=\frac{1}{2y_0^2}\text{exp }(-2\frac{y_F}{y_0}),$$ (45)

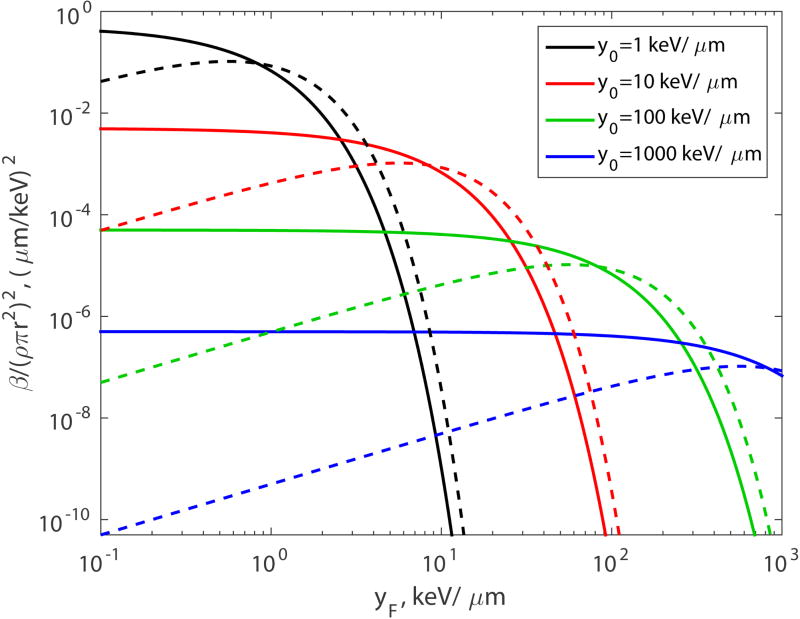
where β decreases exponentially with increasing y_F. Parameter β given by Eq.(45) is shown in Fig. 3 (solid lines) for four values of y₀: 1, 10, 100 and 1000 KeV/µm.

Figure 3.

Parameter β versus y_F for the two-hit model (n = 2, solid lines) and three-hit model (n = 3, dashed lines).

For low LET, when y_F ≪ y₀ or L ≪ L₀, the exponent can be approximated by a linear function

$$\frac{\beta }{{\left(\rho \pi r^2\right)}^2}=\frac{1}{2y_0^2}(1-2\frac{y_F}{y_0}).$$ (46)

Hence, in this case (n = 2 and y_F ≪ y₀), β is approximately a linear function of y_F. For all y_F, β decreases with increasing y_F.

The three-hit model

Finally, in the three-hit model, n = 3, we have for the general case of polyenergetic beams

$$\begin{gathered} B(E_1,E_2)=\frac{1}{4}{\left(\frac{\rho \pi r^2}{y_F}\right)}^2\frac{y_F(E_1)}{y_0}\text{exp }[-\frac{y_F(E_1)}{y_0}]\frac{y_F(E_2)}{y_0}\text{exp }[-\frac{y_F(E_2)}{y_0}]\times \\ [\frac{y_F(E_1)}{y_0}+\frac{y_F(E_2)}{y_0}+\frac{y_F(E_1)y_F(E_2)}{2y_0^2}]. \end{gathered}$$ (47)

which leads to a simpler formula for monoenergetic beams:

$$\frac{\beta }{{(\rho \pi r^2)}^2}=\frac{1}{2y_0^2}\text{ exp }(-2\frac{y_F}{y_0})[\frac{y_F}{y_0}+\frac{1}{4}{\left(\frac{y_F}{y_0}\right)}^2].$$ (48)

Parameter β given by Eq.(48) is shown in Fig. 3 (dashed lines) for four values of y₀: 1, 10, 100, and 1000 keV/µm. In contrast to the two-hit model, in the three-hit model, β as a function of y_F has a maximum. For low LET, when y_F ≪ y₀ or L ≪ L₀, β is approximately a linear function of y_F:

$$\frac{\beta }{{(\rho \pi r^2)}^2}=\frac{y_F}{2y_0^3}.$$ (49)

None of the above versions of the NPMH model, n = 1, 2 or 3 predict that $\sqrt{\beta }$ is a linear function of LET, as some previous studies have postulated.

3.4 The α/β ratio

We pointed out in the Introduction that the α/β ratio should increase monotonically with increasing LET. It is difficult to prove that our model satisfies this requirement for an arbitrary polyenergetic beam. Hence, in this section we will consider only monoenergetic beams and the two- and three-hit versions of the model. The single-hit model is a special case where β = 0.

The two-hit model

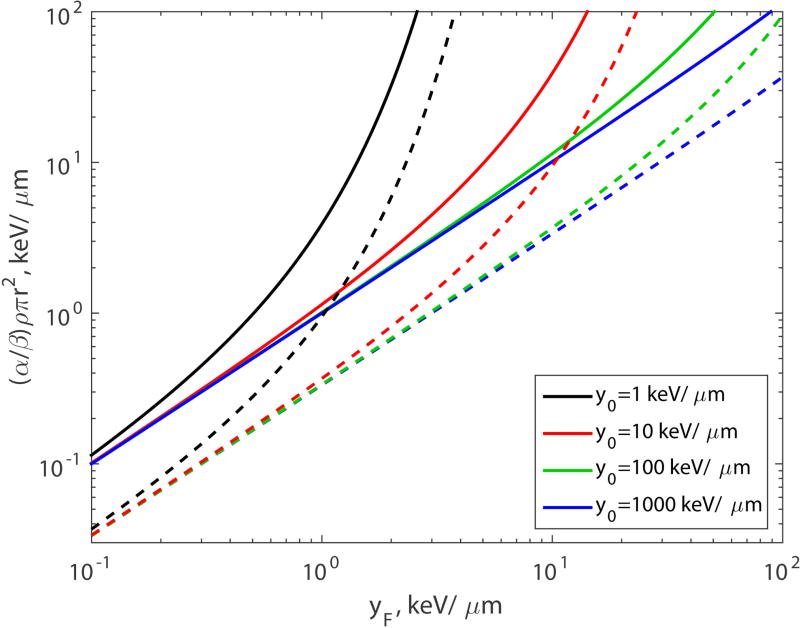
For the two-hit model, n = 2, it follows from Eqs.(39) and (45) that

$$\frac{\alpha }{\beta }\rho \pi r^2=2y_0\left(\frac{y_0}{y_F}\right)\text{ exp }\left(\frac{y_F}{y_0}\right)\left[\text{exp }\right(\frac{y_F}{y_0})-1-\frac{y_F}{y_0}],$$ (50)

which is a monotonically increasing function of y_F. It is shown in Fig. 4, for four values of parameter y₀: 1, 10, 100, and 1000 keV/µm. For small LET (y_F ≪ y₀), it is a linear function:

$$\frac{\alpha }{\beta }\rho \pi r^2=y_F.$$ (51)

Figure 4.

The α/β ratio versus y_F for two-hit model (n = 2, solid lines) and three-hit model (n = 3, dashed lines).

The three-hit model

For the three-hit model the behavior of the α/β ratio is qualitatively similar (see Fig. 4). From Eqs.(42) and (48), for n = 3 we derive

$$\frac{\alpha }{\beta }\rho \pi r^2=2y_0{\left(\frac{y_0}{y_F}\right)}^2\frac{\text{exp }(y_F/y_0)}{1+(1/4)y_F/y_0}\left[\text{exp }\right(\frac{y_F}{y_0})-1-\frac{y_F}{y_0}-\frac{1}{2}{\left(\frac{y_F}{y_0}\right)}^2],$$ (52)

which is a monotonically increasing function of y_F. The function is linear for small LET:

$$\frac{\alpha }{\beta }\rho \pi r^2=\frac{y_F}{3}.$$ (53)

3.5 Fitting experimental data

In this section we apply our model to fit experimental data for α and β. The results we present are purely illustrative, intended only to demonstrate the overall consistency of our model with experimental data. For simplicity, we treat all beams as if they were monoenergetic.

Fitting α

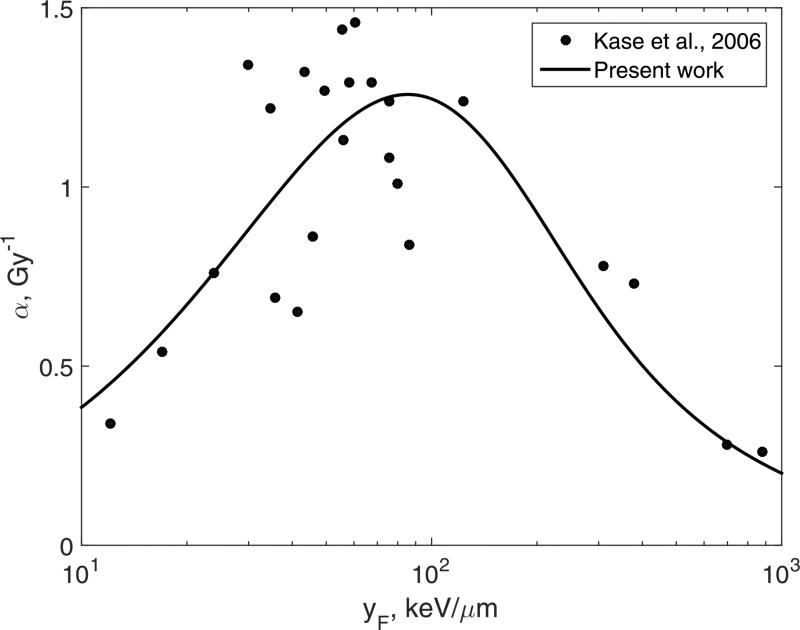
Data reported by Kase et al. (2006) is perfect for our purposes. In that study the key parameter of our model, y_F, was actually measured, and the data spans over two orders of magnitude, with y_F ranging from 0.35 to 880 keV/µm. In this example we will use the data for human salivary gland cells, and exclude measurements taken within a spread-out Bragg peak, so that the beams that we include are approximately monoenergetic.

The best fit was achieved with the two-hit model, n = 2, Eq.(39). The best-fit values of the other two model parameters were as follows: y₀ = 47.7 keV/µm, and r = 226 nm assuming that the density ρ was 1 g/cm³. Kase et al. (2006) used the microdosimetric kinetic model (MKM) to analyze their data. The MKM also involves the concept of an SV, or domain in the MKM terminology. They reported that the radius r of the SV, was 420 nm. This is almost twice as large as our best-fit value. However, we do not consider this difference to be a serious discrepancy because the two models are very different and we used only a subset of data from Kase et al. (2006). The advantages of our model in this case are its simplicity, see Eq.(39), and the clarity of the mechanism.

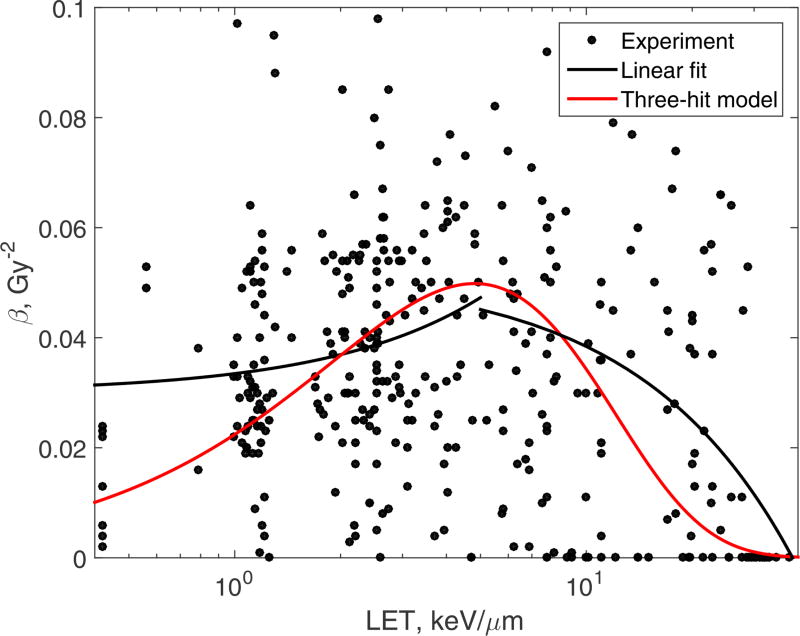
Fitting β

Unfortunately, Kase et al. (2006) did not report on the variation of β with LET, because β was assumed to be constant. We therefore chose for this example experimental data from the recent review by Paganetti (2014). The data are shown in Fig. 6. Our model for β predicts that β either decreases monotonically with increasing LET (the two-hit model) or that it has a maximum (the three-hit model). To determine which of the two cases better describes the experimental data, we first performed a piecewise linear fit of the data. This simply means that we fitted the data with two linear models, one applied to low-LET data (< 5 keV/µm) and the other applied to the rest of the data. Because of the large scatter of the experimental data, we used a robust linear regression algorithm, Huber (1981), that reduces the influence of outliers on the result. The slope of the first linear model (low LET) was (0.0035±0.0013) µm keV⁻¹ Gy⁻², and the slope of the second linear model (high LET) was (−0.0013±0.0005) µm keV⁻¹ Gy⁻². The uncertainties are given as ± one standard deviation. This test suggested that β had a maximum (black lines in Fig. 6). We, therefore used the three-hit model, Eq.(48).

Figure 6.

Experimental β for protons, Paganetti (2014), (circles), the piecewise-linear fit (black lines), and the three-hit model, Eq.(48), (red line), fitted to the experiment.

The best-fit values of the model parameters were: n = 3, L₀ = 3.89 keV/µm, and r = 77.7 nm. The three-hit best-fit result is shown in Fig. 6 with red line. Because of large scatter of the data this figure is intended only to show the general form of the curve predicted by our model in relation to experimental data. The figure suggests that our model behaves more realistically for both small and large LETs. It agrees better with the cluster of data points near LET ≈ 0.4 keV/µm than the linear model does. For large LETs, our model predicts β gradually approaching from above the limit of β = 0, whereas in the piecewise-linear model, β crosses over into the negative region.

Deriving α and β for various tissues

The scope of this paper is limited to modelling the dependence of α and β on LET and the frequency-mean lineal energy y_F. Clinical implementation of our formalism for treatment planning will require addressing another challenging problem: deriving model parameters for various tissues.

In recent years progress has been made in solving this problem. Frese et al. (2011) used a rather simple approach for protons. It is based on the model of Wilkens and Oelfke (2004) where the linear coefficient λ in the expression for α, Eq.(2), was assumed to be the same for all tissues.

Carabe et al. (2012) and McNamara et al. (2015) developed models where α and β are expressed as functions of dose-weighted LET, L_d, and the α/β ratio for the reference radiation, high energy photons. For example, both Carabe et al. (2012) and McNamara et al. (2015) used the following expression for α

$$\frac{\alpha }{{\alpha }_{\text{ref}}}=p_0+\frac{p_1}{{(\alpha /\beta )}_{\text{ref}}}{L}_d.$$ (54)

where p₀ and p₁ are model parameters and the subscript ”ref” denotes the reference radiation. This method relies on the ratios (α/β)_ref for various tissues that have been determined using data accumulated in radiotherapy with high energy photons.

To apply the same strategy to our model, we need to express α and β for a hadron beam as a function of the α/β ratio for high energy photons. Developing this methodology in the general formulation of our model is more appropriate for a separate paper. Here we will present the simplest version of the method, only for α, and applicable only to low LET particles (y_F ≪ y₀). From Eqs.(40) and (51) we have

$${\mathit{\text{RBE}}}_{\text{max}}\equiv \frac{\alpha }{{\alpha }_{\text{ref}}}=\frac{y_F}{{(y_F)}_{\text{ref}}}.$$ (55)

and

$${\left(\frac{\alpha }{\beta }\right)}_{\text{ref}}=\frac{{\left(y_F\right)}_{\text{ref}}}{\rho \pi r^2}$$ (56)

From Eq.(56) we express (y_F)_ref as a function of (α/β)_ref and insert in Eq.(55). We then replace y_F with L and arrive at a formula similar to Eq.(54)

$$\frac{\alpha }{{\alpha }_{\text{ref}}}=\frac{L}{\rho \pi r^2{(\alpha /\beta )}_{\text{ref}}}.$$ (57)

Our model does not have parameter p₀, which makes it more realistic, especially considering that the reported best-fit value of this parameter is ≈0.99, McNamara et al. (2015). In Eq.(54) RBE_max cannot be less than p₀. If we have a radiation beam with an LET significantly lower than that of the reference radiation, in our model the RBE_max will be reduced proportionally, whereas in the model by McNamara et al. (2015) it will remain ≳0.99.

4 Conclusions

Treatment planning in hadron therapy requires tools not only for accurate calculation of three-dimensional distributions of the physical dose but also for calculation of RBE distributions that ideally achieve accuracy comparable to that of the calculated physical dose. The linear quadratic model is currently the most common basis for the latter tools. The present study introduces a new formalism for calculating parameters α and β of the model that removes two important limitations common to prior models.

First, in our formalism physical properties of a hadron beam at a point of interest are characterized by its fluence spectrum Φ(E). The spectrum contains more complete information about the beam physics than does a single quantity, such as the dose average LET used in most models. Hadron beams often have broad energy distributions that can be very complex. Using a single quantity to represent all beam physics imposes an unnecessary limit on achievable accuracy of RBE models. Furthermore, this limit is easily avoidable, because calculating Φ(E) is not principally more difficult than calculating the dose average LET.

Second, our new formalism is built in such a way that it invariably produces α and β that have correct general properties with respect to their dependence on physical properties of the beam, including the asymptotic behavior for very low- and high-LET beams. This makes our model more reliable overall. It is therefore less likely to produce large errors when used for fitting experimental data. As we discussed in the Introduction, prior models lack such overall consistency. This does not mean that those models are invalid. They are usually based on solid experimental data and therefore can be safely used within appropriate dose and LET limits.

Our approach has potential to advance to a new level the accuracy and reliability of modelling RBE for treatment planning in hadron therapy, as well as for analysis of treatment outcomes. With the extensive biological data presently available and with the tools that have been developed for calculating fluence spectra, such as Monte Carlo codes, the next task is applying our approach to analyze the RBE data, determine model parameters and implement these results into routine treatment planning.

Figure 5.

Experimental α for heavy ions, Kase et al. (2006), circles, and the two-hit model, Eq.(39), fitted to the experiment, solid line.