Occurrence and stability of lone pair–π stacking interactions between ribose and nucleobases in functional RNAs

Abstract

The specific folding pattern and function of RNA molecules lies in various weak interactions, in addition to the strong base-base pairing and stacking. One of these relatively weak interactions, characterized by the stacking of the O4′ atom of a ribose on top of the heterocycle ring of a nucleobase, has been known to occur but has largely been ignored in the description of RNA structures. We identified 2015 ribose–base stacking interactions in a high-resolution set of non-redundant RNA crystal structures. They are widespread in structured RNA molecules and are located in structural motifs other than regular stems. Over 50% of them involve an adenine, as we found ribose-adenine contacts to be recurring elements in A-minor motifs. Fewer than 50% of the interactions involve a ribose and a base of neighboring residues, while approximately 30% of them involve a ribose and a nucleobase at least four residues apart. Some of them establish inter-domain or inter-molecular contacts and often implicate functionally relevant nucleotides. In vacuo ribose-nucleobase stacking interaction energies were calculated by quantum mechanics methods. Finally, we found that lone pair–π stacking interactions also occur between ribose and aromatic amino acids in RNA–protein complexes.

INTRODUCTION

The view of the RNA structure has evolved in a few decades from a simplistic ‘two-dimensional’ concept of base-paired helices interspersed with single-stranded unpaired regions, to a variety of complex 3D arrangements associated with many complex functions (1,2). In fact, while an increasing number of functional RNA molecules are identified by biochemical and genetic screens, it is clearly emerging that the space of RNA architectures is vast and largely uncharacterized to date (3,4).

To overcome the electrostatic repulsion due to the negative charge featured by each nucleotide and achieve a compact 3D fold, RNA molecules employ a variety of stabilizing strategies. In addition to the strong edge-to-edge hydrogen bonding interactions between the bases, many other weaker factors contribute to the stability of an overall RNA fold and of specific structural motifs. These include π–π stacking between the nucleobases (5,6), posttranscriptional modifications (7–11), environmental factors such as structural water molecules (12), metal ions (13,14), protonation of nucleobases (15–17) and a variety of base-backbone interactions (18), some of which are probably yet to be revealed.

Focusing on base-backbone interactions in nucleic acids, one involving the O4′ atom of cytosine deoxyribose and a guanine nucleobase was first reported almost two decades ago by Egli and co-workers as a stabilizing structural element of the Z-DNA double-helix structure (19). This interaction was characterized as a non-covalent contact between the O4′ atom lone pair(s) of the sugar and the π cloud of the aromatic system of the nucleobase and was thus defined as a lone pair–π (lp–π) interaction. Recently, a structural survey of the Protein Data Bank (PDB) by Auffinger and coworkers revealed the presence of ‘Z-DNA like’ steps in RNA molecules, involving the O4′ atom of a ribose and the nucleobase of the subsequent nucleotide (20). Instances of lp–π interactions involving the oxygen of a water molecule have also been reported both in RNA, specifically in structures of a ribosomal frame-shifting RNA pseudoknot (21), and in proteins (22). lone pair–π interactions between O4′ of the deoxyribose and aromatic amino acids have also been reported and energetically characterized in the context of DNA–protein π interactions (23) Moreover, instances of oxygen–aromatic contacts in intra-strand base pairs in DNA have also been reported (24). In a broader perspective, stacking contacts between a ribose and a nucleobase parallel the carbohydrate–π contacts described in glycobiology (25–29) and nanobiotechnology (30), and the lp–π interactions between electron-rich atoms and electron-deficient aromatic rings observed in organic compounds, supramolecular assemblies and solid-state structures (31–38).

Although the awareness of the relevance of such lp–π interactions in the context of biomolecular structures is increasing, they still lack comprehensive structural and energetic characterization in the context of RNA. To fill this gap, in this contribution, we present a systematic search of lp–π ribose–base stacking interactions in 699 high-resolution non-redundant RNA structures from a dedicated database (39), complemented by a state-of-the-art characterization of the interaction energies.

We found lp–π ribose–base stacking interactions to be extremely widespread in functional RNAs, with the Z-like steps representing only a small fraction of all cases. We discuss lp–π ribose–base stacking interactions in detail, with a focus on variants involving specific nucleobases; the distribution of the sequence distance between the ribose and nucleobase; and their strategic location in relevant and recurrent RNA structural motifs, active sites, inter-domain and inter-molecular contacts. We also characterize the geometry and energetics of lp–π ribose–base stacking interactions. Finally, we extend the analysis to RNA–protein interactions and show that lp–π stacking contacts are also common between the RNA ribose moiety and the side chain of aromatic amino acids.

MATERIALS AND METHODS

Structural dataset

We started from the non-redundant 3D structure dataset for RNA, version 1.89 by Leontis and Zirbel (39). The 699 structures that have a resolution ≤3.0 Å were collected, and we refer to them as the nrRNA3.0 dataset. For some analyses, we also used a reduced dataset of 221 structures with a resolution ≤2.0 Å that we named the nrRNA2.0 dataset.

Identification of ribose–base lone pair–π contacts

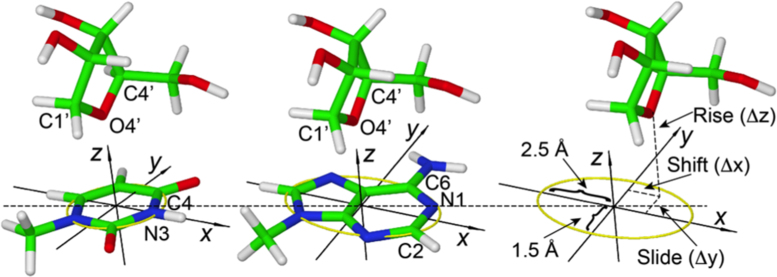
Identification of lp–π ribose–base interactions was achieved by using the geometrical setup shown in Figure 1. The nucleobases of all the entries in the nrRNA3.0 dataset were oriented in a Cartesian frame as follows. The origin of the frame was placed at the geometric center of the heterocycle skeleton, the x-axis passing through the N3 atom for pyrimidines and through the middle point of the N1-C2 bond for purines (see Figure 1). The y-axis formed a 90° angle with the x-axis, with the C6 atom of purines and the C4 atom of pyrimidines lying in the xy-plane at positive y values. The z-axis vector was built as the cross product of the vectors along the x- and y-axes, thus forming a right-handed frame. Orienting the base in the reference frame facilitated definition of the position of the O4′ atom of a ribose with respect to the nucleobase using the three translational parameters Δx(shift), Δy(slide) and Δz(rise) shown in Figure 1.

Figure 1.

Definition of the reference Cartesian frame on the nucleobases and of the shift, slide and rise parameters used to define the position of the O4′ atom of ribose relative to the base. The origin is at the geometrical center of the heterocycle skeleton, the x-axis passing through the N3 atom for pyrimidines and through the middle point of the N1–C2 bond for purines; the y-axis forms a 90° angle with the x-axis, with the C6 atom of purines and the C4 atom of pyrimidines lying in the xy-plane at positive y values; the z-axis is the cross product of the versors (unit vectors indicating the directions) along the x- and y-axes, thus forming a right-handed frame. The yellow circle defines a circle of radius 1.5 Å in the xy-plane of pyrimidines, while the yellow ellipse defines an ellipse in the xy-plane of purines, with minor and major axes equal to 1.5 and 2.5 Å. A ribose and a base are considered to be interacting if the projection of the O4′ atom of the ribose on the xy-plane is within the yellow circle for pyrimidines or the yellow ellipse for purines, with the rise parameter in the –4.0 to +4.0 Å range.

Ribose–base couples were defined as interacting based on two conditions. First, their rise fell in the –4.0 to +4.0 Å range. Second, the projection of the ribose O4′ on the nucleobase plane is within the heterocycle ring. Specifically, for pyrimidines, it had to fall on a circle of radius 1.5 Å centered on the heterocycle; for purines, it had to fall on an ellipse with minor and major axes of 1.5 and 2.5 Å, again centered on the heterocycle, as shown in Figure 1. This procedure allowed us to identify a total of 2015 ribose–base contacts in 270 PDB structures involving all four nucleobases. Of course, choosing cutoff values in a structural search always has some arbitrariness. In the present case, the cutoff values that we chose for the slide and shift were selected to enforce that the projection of the O4′ atom of the ribose on the base plane is within the heterocycle ring. For the ‘rise’, we considered a cutoff of ±4.0 Å. A plot of the distribution of distances of the O4’ atom from the base plane is reported in Supplementary Figure S1. Incidentally, our approach is consistent with the cutoffs adopted in a recently published independent study on the O4′-base interaction in Z-DNA like motifs (20).

Clustering of the selected ribose–base geometries

The clustering method adopted here is based on quantifying similarity between ribose–base structures on the basis of the root-mean-square displacement (rmsd) between the C4′–O4′–C1′ atoms of the ribose moiety, after superimposition of the nucleobases. Only the C4′–O4′–C1′ atoms of the ribose were used to define the rmsd, since these three atoms univocally define the position of the ribose ring relative to the nucleobase, avoiding any complication due to the conformational flexibility of the ribose ring. Of course, the ribose–base structures were initially separated into four subsets based on the specific nucleobase involved in the contact, then pairwise all-by-all superpositions were performed within each subset. The affinity propagation algorithm (40) was used to cluster structures based on the C4′–O4′–C1′ rmsd. The representative of each cluster (the ‘exemplar’ within the affinity propagation algorithm terminology) represents the structure in the cluster having the lowest total distance from other cluster points. The PDB IDs and the residue numbers for the representatives of each cluster are listed in the SI.

Quantum mechanics calculations

The ribose–base interaction energy in the representatives of each cluster from the clustering step was evaluated using quantum mechanics (QM) calculations. Recent studies corroborate that accurate computational techniques can provide important information about the stability and energetics of π–π interactions (5,28,41–46). In nucleic acid structures, quantum chemical calculations have been found indispensable to clarify the strength of H-bonding and stacking interactions between nucleobases observed in experimentally determined structures (5,7,12–15,43–58).

Following a protocol common in the literature (7,12,49,54,59,60), the geometries of the interacting ribose–base were extracted from the PDB file, and the base was truncated at the C1′ atom while the ribose was truncated at the 5′ and 3′ phosphorus atoms. The truncated bonds were capped with a hydrogen atom, as shown in Figure 1. A density functional theory (DFT) approach based on the hybrid PBE0 functional with the triple-ζ TZVP (61,62) basis set, as implemented in the Gaussian 09 package, was used to optimize the position of the hydrogen atoms only. The dihedral angles leading to the 5′H and 3′H hydrogen atoms were frozen in order to avoid the formation of spurious H-bonding contacts with the nucleobase (6).

The ribose–base interaction energy was then evaluated at the coupled cluster level of theory, with iterative inclusion of single and double excitations and perturbative inclusion of triple excitations (CCSD(T)), which is considered the gold standard in electronic structure calculations (63), including stacking interactions in nucleic acids (47,64). The domain-based local pair-natural orbital (DLPNO) (65–67) approximation, as implemented in the ORCA package (68), was used to accelerate calculations. The correlation consistent Dunning cc-pVTZ basis set was used in these calculations (69). The tight PNO settings (TCutPairs = 10⁻⁴, TCutPNO = 3.3 × 10⁻⁷, TCutMKN = 10⁻³) were used to reduce any numerical noise in the calculations. The default SCF convergence criterion NormalSCF (energy change 1 × 10⁻⁶ au) was replaced with the tighter TightSCF (Energy change 1 × 10⁻⁸ au) to achieve better converging wave functions. All the interaction energies are corrected for basis set superposition error with the counterpoise method of Boys and Bernardi (70). Electrostatic potentials were mapped on electron density isosurfaces corresponding to a value of 0.0004 atomic units, and are scaled between –30 and +30 kcal/mol.

In this work, we calculated the interaction energy of the ribose–base pairs, E_int, as in Equation (1):

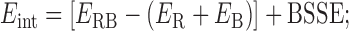(1)

where E_RB is the electronic energy of the ribose–base complex and E_R and E_B are the electronic energies of the isolated ribose and base fragments forming the complex. The geometry of the separated base and ribose was not optimized, which means the isolated base and ribose have exactly the same geometry that they have in the complex. It should be noted that the calculated interaction energies cannot directly be compared to the experimental free energies of RNA folding or stem formation, as they do not include several corrections, such as approximating the solvent with a continuum model and entropy (6). For this reason, we aligned the calculated interaction energies with the H-bond interaction energy in a water dimer, and the average stacking energy of a series of stacked nucleobase pairs was extracted from RNA duplexes whose structure was resolved with a resolution ≤3.0 Å.

To decompose the interaction energy between ribose and nucleobases into contributions due to genuine lp–π interaction and to dispersion (also known as Van der Waals) interaction (71), test calculations were performed on models corresponding to ideal T-shaped geometries of ribose stacked on top uracil, adenine, and for the sake of comparison of benzene and hexafluorobenzene. The BSSE corrected interaction energy for these systems was calculated at the second order M⊘ller-Plesset level of theory, MP2 (72), with the PBE0 functional, and further by addition of Grimme's empirical dispersion term (73), arriving to PBE0-D3 energies. The cc-pVTZ basis set was used, and the empirical correction term was calculated using Becke-Johnson damping.

RESULTS

Statistical and structural analysis of lone pair–π ribose–base stacking interactions

The nucleobases of all the 699 structures in the nrRNA3.0 dataset (see Materials and Methods) were examined to identify lp–π ribose–base interactions using the geometrical setup shown in Figure 1. Interacting ribose–base pairs were defined as those pairs for which the rise of the O4′ atom of ribose is in the –4 to +4 Å range, and its projection on the base plane is in the circle of radius 1.5 Å for pyrimidines and in an ellipse for purines, with major and minor axes of 2.5 and 1.5 Å (see Materials and Methods). This procedure allowed us to identify a total of 2015 ribose–base stacking contacts in 270 PDB structures involving all four nucleobases (1124, 426, 260 and 205 instances for interacting adenine, guanine, cytosine and uracil, respectively). No preference was observed instead for the identity of the base covalently bonded to the stacked riboses.

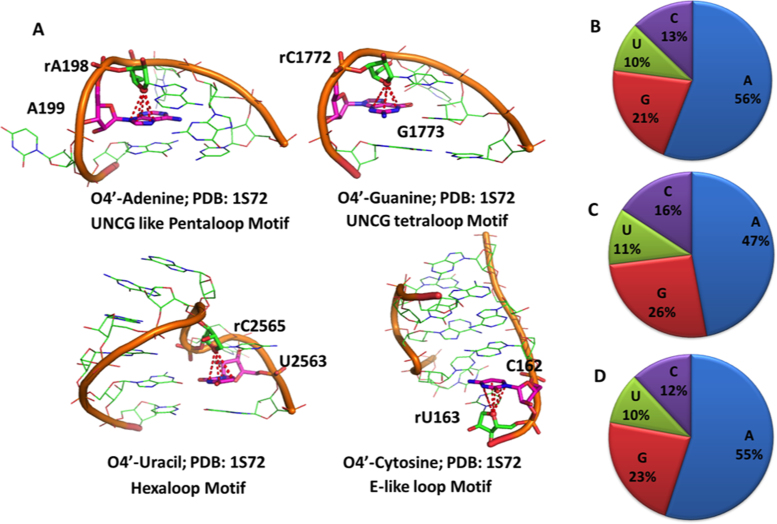
The 270 structures of the nrRNA3.0 dataset featuring lp–π ribose–base interactions include a wide variety of RNA molecules, such as various tRNAs (38 instances), ribozymes and riboswitches (16 and 33 instances) and ribosomes from five different species, which highlights this interaction as being ubiquitous in RNAs with completely different functions. The average RNA length in these structures is 121 residues if ribosomes are included and 48 residues if ribosomes are excluded. As we will show below, such interactions are located outside the regular helical regions, being part of more complex structural motifs. An example of a lp–π ribose-nucleobase stacking interaction in recurrent and well-known RNA structural motifs is given for each nucleobase in Figure 2A. The shown motifs are the UNCG like pentaloop, the UNCG tetraloop, the hexaloop and the E-like loop (74). Further, examples of ribose–base stacking interactions have also been observed in A-minor motifs (see below) and in the UNCG like tetraloop; see Supplementary Figure S2. Of these structural motifs, the UNCG tetraloop has already been discussed by Auffinger et al. in the context of Z-like steps (20). On the other hand, the 429 structures of the nrRNA3.0 dataset that lack lp–π interacting ribose–bases typically represent synthetic fragments folded in single or double helical strands, with an average length as low as 13 nucleotides.

Figure 2.

(A) Examples of ribose–base stacking contacts involving different nucleobases in different structural motifs. (B–D) Percentage of nucleobases involved in ribose–base stacking interactions in different RNA molecules: (B) nrRNA3.0 (non-redundant RNA structure dataset with a resolution ≤ 3.0 Å); (C) as in B) but not including ribosomal structures; (D) subset of nrRNA3.0 with a resolution ≤ 2.0 Å. Number of occurrences corresponding to A, G, C, U are 1124, 426, 260 and 205 respectively in (B), 374, 207, 126 and 88 in (C) and 87, 36, 19 and 16 in (D).

Statistical analysis shows that purines are more frequently involved than pyrimidines in ribose–base interactions (77% vs. 23%), see Figure 2B. This is especially due to the prevalent involvement of A in the interaction, representing 56% of the cases, followed by G in 21% of the cases, while C and U are present in 13% and 10% of the cases, respectively. The over-representation of the ribose-adenine interaction persists if we exclude the ribosomal structures from the dataset, as in Figure 2C, or if a more stringent resolution cutoff of 2.0 Å is used to build the non-redundant dataset, as in Figure 2D.

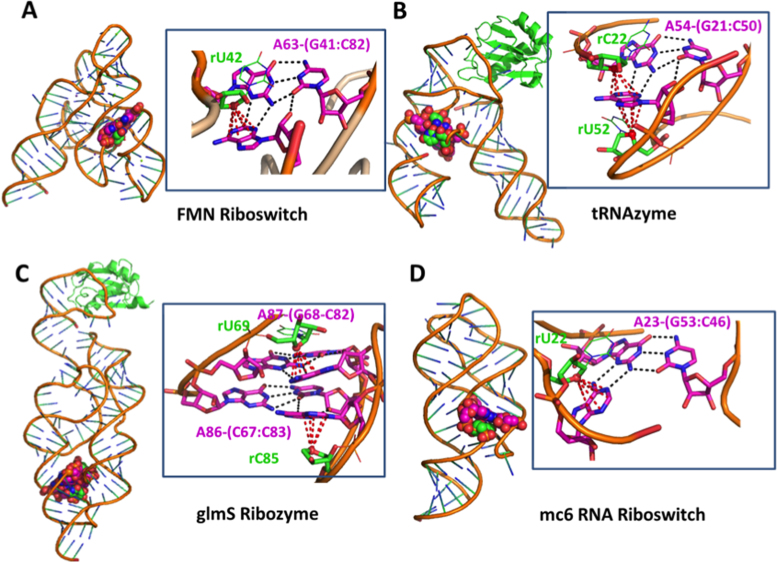
The prevalence of adenines in ribose–base interactions prompted us to investigate the structural context in which ribose-adenine interactions occur, and we found a preponderance of these interactions in the A-minor motif. By restricting this analysis to the structures of the dataset with a resolution ≤2.0 Å (nrRNA2.0), we could verify that approximately half of the ribose-adenine stacking contacts (40 out of 87) are part of an A-minor motif. The A-minor motif is a ubiquitous RNA structural motif that involves the insertion of an adenine into the minor groove of the RNA duplex, and it is known to be relevant in the stabilization of the tertiary structure of RNA molecules (75). Structural analysis of the lp–π ribose-adenine contacts in H. marismortui 23S rRNA (PDB ID: 1S72) revealed that 42% of the contacts (46 out of 109) are part of A-minor motif interactions. In addition, we found ribose-adenine contacts in A-minor motifs in other RNA molecules, including different metabolite-sensing riboswitches, ribozymes, and small RNA molecules. Representative examples are given in Figure 3. Specifically, Figure 3A shows the interaction between the ribose of U42 with A63 in the FMN riboswitch (PDB ID: 3F2Q), with A63 H-bonded via the sugar edge to the G41:C82 base pair. More complex contacts can also be formed, as shown in Figure 3B, reporting A54 of the tRNAzyme (PDB ID: 3CUN) sandwiched between the ribose O4′ atoms of the C22 and U52 nucleotides. Furthermore, we found ribose-adenine contacts also in A-patches (1), which correspond to the stacking of adenines involved in different A-minor motifs; an example of this arrangement is shown in Figure 3C for the glmS ribozyme molecule (PDB ID: 2NZ4). Finally, in Figure 3D, the interaction between the ribose of U22 with A23 of the mc6 RNA riboswitch (PDB ID: 3LA5) is shown, with A23 H-bonded via the Watson-Crick edge to the G53:C46 base pair.

Figure 3.

Examples of A-minor motifs, including a ribose-adenine stacking interaction in different RNA molecules. (A) FMN riboswitch (PDB ID: 3F2Q); (B) tRNAzyme (PDB ID: 3CUN), with an adenine stacked between two riboses; (C) glmS Ribozyme (PDB ID: 2NZ4), featuring an A-patch interaction motif (75). (D) mc6 RNA riboswitch (PDB ID: 3LA5), with an adenine giving a tertiary interaction with the G53:C46 base pair.

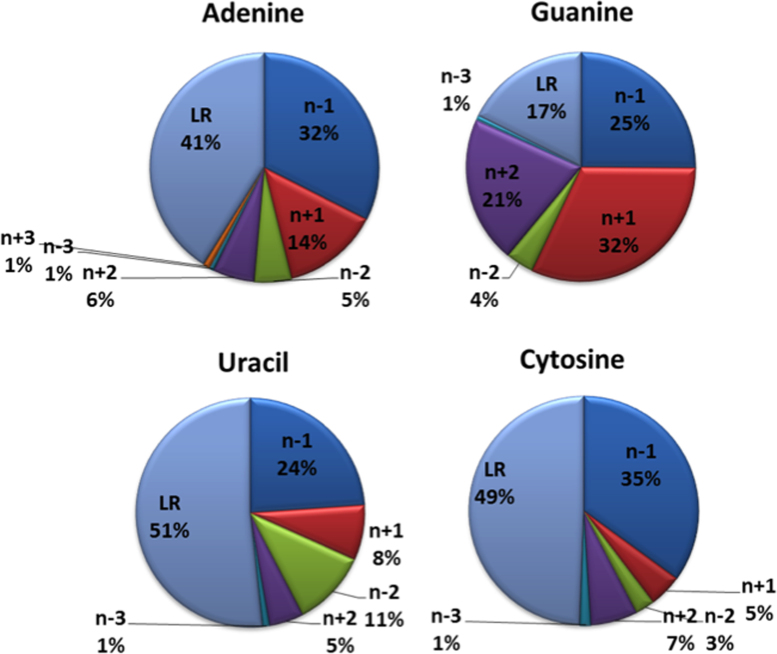
Next, we investigated the sequence distance in the 5′→3′ direction of the RNA chain between the ribose (residue number n) and the nucleobase (residue number n+i) involved in the lp–π interaction. The results of this analysis, reported in Figure 4, show that a relevant fraction of the interactions (between 17% for G and 51% for U) are long range; i.e. they involve a ribose and a base that are at least four residues apart in the corresponding RNA sequence (i ≤ –4 or ≥ 4). In the case of A, these long-range interactions mainly correspond to adenines in the A-minor motifs discussed above. For U and C, a fraction (9%) of these long-range interactions involves the ribose of nucleotide 59 with the variable base (C/U/m⁵C) of nucleotide 48, which is in turn involved in H-bonding with nucleotide 15 in the 100% conserved 15–48-59 tRNA tertiary interaction (12,14,50), see Supplementary Figure S3. Another significant fraction of the interactions (from 10% for C to 25% for G) involves ribose and base moieties that are two residues apart (n + 2 or n – 2). An example of an n – 2 interaction is shown in Figure 2D for the hexaloop structural motif.

Figure 4.

Sequence distance between the ribose(n) and the nucleobase(n±i) moieties involved in stacking interactions, reported for each of the four bases. The residue numbering is in the 5′→3′ direction of the RNA chain. LR refers to the long-range contacts, with a sequence spacing of at least 4 residues (i ≥ 4 or i ≤ 4).

Interactions involving a ribose and a base on contiguous residues (n – 1 or n + 1) represent fewer than half of the total cases (average 46%, from 32% for U to 57% for G). The n + 1 ribose–base interactions include occurrences located in well-known structural motifs, such as the UNCG like pentaloop and the UNCG tetraloop motifs, as shown in Figure 2A. As already mentioned, a recent work described the n + 1 O4′-base interaction in the UNCG tetraloop as a Z-DNA like structural element (20,76). The n – 1 interactions also include well-known structural motifs, such as the E-like loop motif shown in Figure 2A.

We conclude this structural analysis remarking that, in some of the detected ribose–base contacts, a Mg²⁺ ion was bound to the N7 atom of an adenine or a guanine (Supplementary Figure S4), or a modified base is involved in the interaction, as the modified, 5-methyl-cytosine (m⁵C) base already mentioned in the context of tRNA (Supplementary Figure S3). Furthermore, two riboses can interact with opposite sides of the same base; examples of this kind of interaction are shown in Figure 3B, Figure 5C and Supplementary Figure S4. Finally, an analogous search for lp–π stacking interactions between ribose O3′ and O5′ atoms and nucleobases results in a total of only 90 and 144 instances, respectively (see the SI for a complete list).

Figure 5.

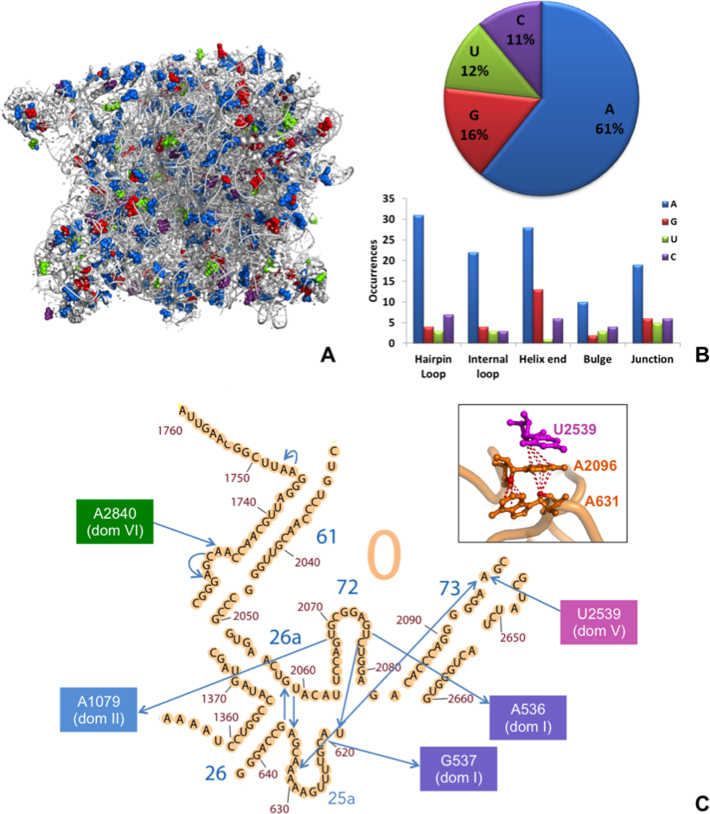
ribose–base stacking contacts in 23S rRNA from H. marismortui. (A) 3D representation (PDB ID: 1S72), with blue, red, green and purple spheres representing adenine, guanine, uracil, cytosine bases involved in ribose–base interactions, respectively. (B) Fraction of different nucleobases involved in the interactions (top) and number of occurrences of bases involved in the interactions in different structural motifs (bottom). (C) ribose–base stacking contacts of Domain 0. In the 2D representation (adapted from http://apollo.chemistry.gatech.edu/RibosomeGallery/), the arrows are directed from the riboses to the nucleobases. A 3D representation of the interactions involving nucleotides A631, A2096 and U2539 (on domain V) is also provided.

23S rRNA, a case-study

In the 3D structure of 23S rRNA from H. marismortui (PDB ID 1S72), we detected a total of 179 ribose–base stacking interactions widespread all over the molecule (Figure 5A). Of these 179 interactions, 109 (61%) involve adenine as a base (Figure 5B). Focusing on the structural context of the bases participating in the stacking interactions, we found that they are consistently located in regions other than a regular double helix (stems). They are indeed observed in hairpin and internal loops, helix ends, bulges and junctions (Figure 5B), consistent with the knowledge that structural motifs other than π–π stacking interactions between nucleobases have an important role outside of A-RNA/B-DNA double helix structures (1,18). Remarkably, interactions involving a base from a hairpin loop usually involve a ribose distant in sequence. In total, 46% (83 out of 179) of the ribose–base interactions in H. marismortui 23S rRNA are long-range interactions, with many of them having the ribose and the base hundreds of residues away in sequence. As an example, 25 interactions involve riboses and nucleobases more than 700 residues apart. These interactions are established between different domains of rRNA, possibly contributing to maintaining its overall 3D fold and functionality. Of these very long-range inter-domain interactions, eight involve the domain V, which is mainly responsible for 23S peptidyl transferase activity. Details are given in Figure 5C for domain 0, the domain at the core of the 23S structure, to which the other six domains are rooted (77). This is a relatively small domain, with its ≅160 nt; however, it features a total of 12 ribose–base stacking contacts, 5 of them established with other domains. A schematic representation of all these interactions is given in Figure 5, together with a 3D representation of a structure detail, i.e., a double intra-domain head-to-tail stacking contact combined with an inter-domain one (from domain V).

Clustering and energy calculations

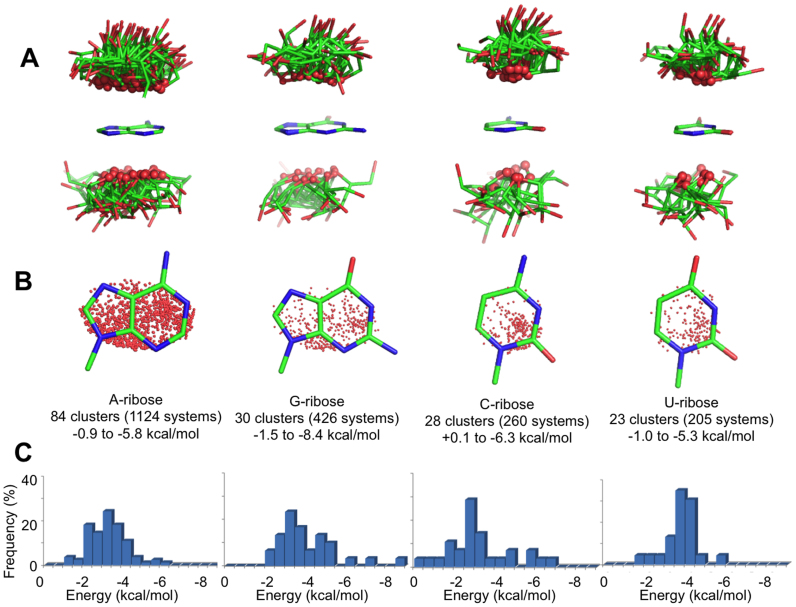
The 2015 O4′-base contacts identified were first grouped by base identity and then clustered to obtain groups of geometrically similar interactions. This resulted in a total of 165 clusters, 84 involving an A, 30 involving G, 28 involving C and 23 involving U as the base. For each cluster, the medoid (i.e. the structure that is ‘least dissimilar’ from all of the others) was selected as a representative structure, and the interaction energy between the ribose and the base was calculated by the ‘gold standard’ CCSD(T) quantum mechanics method within the DLPNO approximation (64) (see Methods for computational details, and see SI for details about the selected PDB IDs and residue numbers). The orientation of the ribose relative to the base is shown in Figure 6A for all the representative structures. Analysis of Figure 6A indicates that in all the structures, the O4′ atom points towards the base, with the ribose ring protruding away, as indicated by the average angle formed by the bisector of the C1′–O4′–C4′ angle with the base plane, 65.2° ± 17.6°. This result shows that the ribose and the base predominantly assume a T-shaped geometry. Furthermore, projection of the O4′ atom on the base plane indicates no clear orientation preference for the O4′ atom over the purine rings, while in the case of pyrimidines, there is a small tendency of the O4′ atom to be on top of the C2 atom (Figure 6B).

Figure 6.

(A) Stick representations of the ribose orientation relative to the base in the 165 structures representative of different interaction clusters, organized by nucleobase identity. The ribose O4′ atoms are shown as small spheres. (B) The projection of the O4′ atom of riboses on the base plane is shown as a red dot. (C) Distribution of the interaction energies calculated for all 165 cluster representatives (kcal/mol).

The DLPNO-CCSD(T) ribose–base interaction energies are near –3 kcal/mol (–2.8 ± 1.0, –3.2 ± 0.9, –3.6 ± 1.5 and –2.7 ± 1.6 kcal/mol for A, U, G and C, respectively) (Figure 6C). In some cases, interaction energies stronger than –5 kcal/mol were calculated due to the presence of an H-bond between a hydroxyl group of the ribose and a donor/acceptor on the nucleobase (see the SI). To compare this interaction energy with that of ‘classical’ base-base stacking, we calculated the interaction energy for the 10 possible combinations of stacked nucleobase pairs. To obtain geometries representative of typical RNA structures, we extracted the geometries of stacked bases from a regular double helix (see the SI for further details). These calculations resulted in an average interaction energy between these stacked bases of –4.7 ± 3.38 kcal/mol (in a range from –0.5 for GG to –12.05 kcal/mol for GC; see the SI), which is only –2 kcal/mol stronger than the average ribose–base interaction. This indicates that the O4′–base interaction can contribute a stabilizing energy contribution comparable to the stacking of nucleobases. To verify that the interaction energy calculated for the representative structure indeed represents the interaction energy of the cluster, we calculated the interaction energy for all 22 structures of a ribose–cytosine stacked-pair cluster. As we show in Supplementary Figure S5, all the structures within the cluster have similar interaction energies, with a standard deviation of ±0.4 kcal/mol. Finally, we remark that solvent effects reduce the strength of the interaction compared to in vacuum calculations. For example, the interaction energy between the classic AU and GC Watson-Crick pairs is reduced from –15.0 and –28.0 kcal/mol in vacuum to –7.9 and –12.5 kcal/mol when solvent effects are included with a continuum solvation model (49). For this reason, the calculated ribose–base stacking interaction energies we reported should be considered as an upper bound limit.

As expected, the presence of a Mg²⁺ ion coordinated to the N7 atom of purines stabilizes the contact; the calculated interaction energies are –9.8 and –11.8 kcal/mol for the (Mg²⁺-G)-ribose and (Mg²⁺-A)-ribose structures of Supplementary Figure S4A and B, whereas the values are –3.1 and –4.2 kcal/mol if the Mg²⁺ ion is omitted in the calculations. A similar stabilization, mediated by metal binding to the N7/O6 atoms of a guanine base in the CpG steps, has been previously described for the Z-DNA structure by Egli and Sarkhel (59). However, we remark that it has been recently shown that the occurrences of Mg²⁺ ions bound to N7 atoms may be related to misinterpreted solvent electronic densities in the X-ray structures (78). Furthermore, methylation of cytosine to 5-methylcytosine stabilizes the ribose–base contact slightly, with the interaction energy increasing in magnitude from –3.0 kcal/mol for ribose-C to –3.8 kcal/mol for the ribose-m⁵C contact (Supplementary Figure S4C). Finally, we also calculated the interaction energy when the base is engaged in a lp–π interaction with two riboses on opposite sides of base plane (Supplementary Figure S4D–F) to check for potential cooperative effects between the two riboses that would reinforce the interaction. In the case of the cytosine complex in Supplementary Figure S4F, the overall interaction energy of C with both riboses is –5.6 kcal/mol, while the interaction energy of the base with the single riboses (calculated in the absence of the other ribose) is –2.4 and –2.8 kcal/mol. This result indicates a negligible cooperative effect of –0.4 kcal/mol (calculated as –0.4 = –5.6 +2.4 + 2.8 kcal/mol).

To clarify the physico-chemical nature of the ribose-nucleobase interaction we refer to the conceptual framework outlined by Hobza and Ran to clarify the nature of the bonding in lp–π electron complexes of water and dimethylether with benzene and 1,2,4,5-tetracyanobenzene (71). They clearly showed that: (i) the T-shaped water/benzene complex is repulsive because of repulsive electrostatic interaction between the lp of water and the negative electrostatic potential on top of the benzene ring. (ii) Decreasing the negative charge at oxygen and increasing the polarizability of the system (e.g. moving from water to dimethylether) provides stabilization even for genuine lp–π interactions. Nevertheless, the substantial part of the stabilization stems from dispersion (or Van der Waals) energy. (iii) Substituting an aromatic ring by electron-withdrawing groups (e.g. moving from benzene to an aromatic ring with electron withdrawing groups, such as 1,2,4,5-tetracyanobenzene or hexafluorobenzene) provides a substantial stabilization of genuine lp–π interactions. In these cases electrostatic interaction contributes significantly to the stabilization energy, with dispersion energy contributing less relevantly.

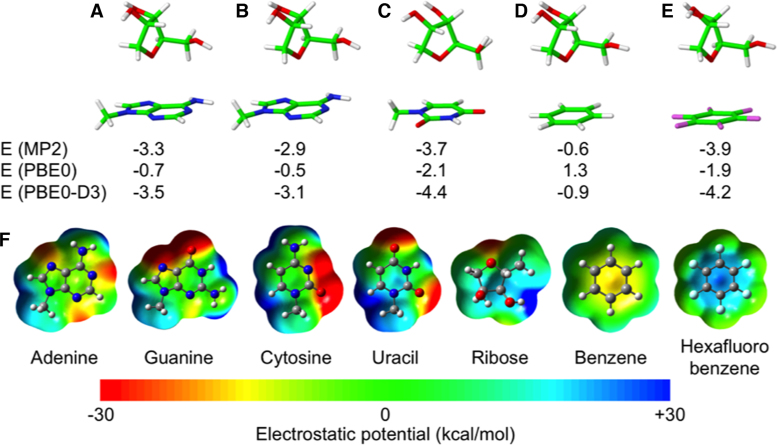
With this background in mind, we performed a series of test calculations using model geometries with the ribose pointing towards the baricenter of the whole heterocycle of a purine (A) (Figure 7A) and towards the center of the 6 membered ring of a purine (A), a pyrimidine (U), benzene, and hexafluorobenzene (Figure 7B–E). In all the cases the bisector of the C1′–O4′–C4′ angle is perpendicular to the aromatic ring, and the O4′ atom is at a distance of 3.5 Å from the plane of the aromatic ring.

Figure 7.

Geometries and energies of model T-shaped geometries corresponding to ribose stacked on top of the baricenter of adenine (A) on top of the center of the 6 membered aromatic ring of adenine (B), uracil (C), benzene (D), hexafluorobenzene (E). (F) electrostatic potential of nucleobases and of bezene and hexafluorobenzene. Electrostatic potentials were mapped on electron density isosurfaces corresponding to a value of 0.0004 atomic units, and are scaled between –30 and 30 kcal/mol. Interaction energies, in kcal/mol, were calculated at the MP2 level and at the DFT level using the PBE0 functional, and at the PBE0-D3 level, which means adding an empirical dispersion energy term to the PBE0 energy.

The energies reported in Figure 7 indicate that at the MP2 level there is substantial stabilization (i.e. lower than –2.5 kcal/mol) for all complexes, except for ribose–benzene, with a stabilization energy of only –0.6 kcal/mol. These results are remarkably different when the simple PBE0 functional is used, with repulsive interaction between the ribose and C₆H₆, and clearly weaker interaction (i.e. higher than –2.5 kcal/mol) in all the other cases. Considering that functionals such at the PBE0 functional are not capable to account for dispersion interaction, the PBE0 interaction energies can be considered a good estimate of the electrostatic interaction energy between the ribose and the aromatic ring. In line with previous discussion on the electrostatic potential of the different systems (71), electrostatic interaction between the ribose and benzene is repulsive, due to the negative electrostatic potential around the O4′ atom and at the center of the benzene ring, see Figure 7F, it is weakly attractive between the ribose and the nucleobases, due to the slightly positive electrostatic potential above the heterocycle skeleton of nucleobases, see Figure 7F, and it is clearly attractive between the ribose and hexafluorobenzene, due to the clearly positive electrostatic potential at the center of the hexafluorobenzene ring. Adding a dispersion term to the PBE0 functional, which is considering the PBE0-D3, results in a remarkable agreement between the MP2 and the PBE0-D3 values, highlighting the stabilizing contribution of dispersion in all cases. Comparison of the PBE0 and PBE0-D3 values indicates that the interaction of ribose and nucleobases has a contribution from both genuine lp–π interaction and dispersion. Further details on the nature of the non covalent interaction between the ribose and the aromatic rings, based on an analysis of the electron density, is reported in the SI.

Stacking interactions between ribose and aromatic amino acids

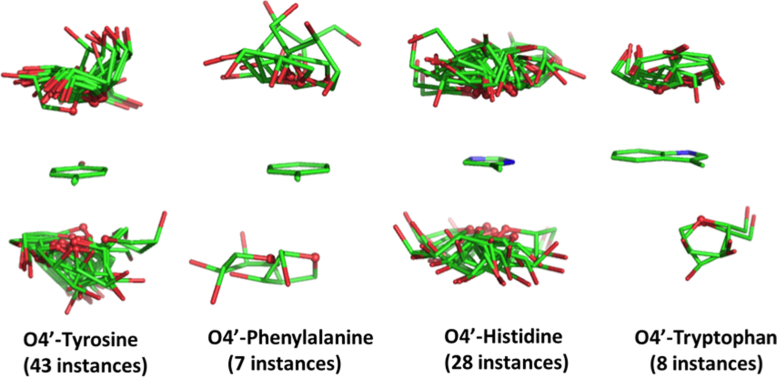
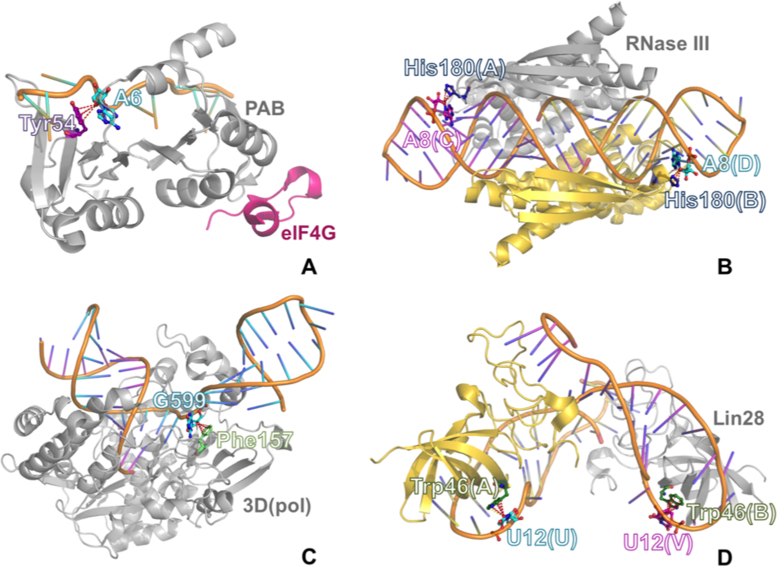
The identification of numerous ribose–base interactions in RNA prompted us to investigate whether analogous interactions can be observed between ribose and the aromatic amino acids in RNA–protein complexes. To this end, we searched the 464 structures in the nrRNA3.0 dataset including proteins for occurrences of lp–π stacking interactions between riboses of RNA and tyrosine, phenylalanine, histidine or tryptophan residues. As a result, we found a total of 86 occurrences of stacking interactions in 36 structures, 43 of them involving a tyrosine, 7 involving a phenylalanine, 28 involving a histidine, and 8 involving a tryptophan (see Figure 8).

Figure 8.

Stick representation of the ribose orientation relative to the side chains of the four aromatic amino acids in the lp–π ribose-amino acid stacking interactions.

Of the total of 86 occurrences, 26 (30%) are established in the ribosome between RNAs and 13 proteins (four from the small and nine from the large subunit). The remaining lp–π ribose-amino acid interactions are found in complexes of RNA molecules with a variety of proteins, including viral RNA polymerases, ribonuclease III, poly(A)-binding protein, aminoacyl-tRNA-synthetases, PIWI proteins, the Lin28 inhibitor of let-7 miRNA, the core protein (CASC3) of the exon junction complex, etc. An example of a lp–π ribose-amino acid stacking interactions for each aromatic amino acid is shown in Figure 9. For each amino acid, the structure with the highest resolution was selected for energy calculations, resulting in interaction energies of –1.6, –1.5, –2.8 and –3.7 kcal/mol for tyrosine, phenylalanine, histidine and tryptophan, respectively. These values are quite similar to those obtained for the ribose–nucleobase interactions. Finally, when histidine was modeled in its protonated form, the interaction energy increased to –12.3 kcal/mol, indicating that protonation can be an energy-modulating agent analogous to metal binding or post-transcriptional modification in nucleobases.

Figure 9.

An example of lp–π ribose-amino acid stacking interactions for each aromatic amino acid: (A) ribose-Tyr stacking contact in a ternary complex between the human translation factors polyadenylate-binding protein-1 (PABP) and eIF4G and a poly(A)(11) RNA (PDB ID: 4F02); (B) ribose-His stacking contact in a complex between A. aeolicus dimeric ribonuclease III (RNase III) and a product double-stranded RNA (dsRNA) (PDB ID: 2EZ6); (C) ribose-Phe stacking contact in the complex between rhinovirus RNA-dependent RNA polymerase (3D(pol)) and synthetic RNA (PDB ID: 4K50); (D) ribose-Trp stacking contact in a complex between mouse dimeric Lin28 and the microRNA (miRNA) let-7 (PDB ID: 3TS0).

DISCUSSION AND CONCLUSIONS

We have found that ribose–base stacking interactions are widespread in RNA molecules and that only a minor subset of them corresponds to the n + 1 ribose–base Z-DNA motif already identified in RNA molecules (20). Remarkably, we have found occurrences of ribose–base stacking interactions in essentially all the RNA molecules that need to adopt a complex 3D structure to be functional. We have also shown that they are preferentially located in structural regions other than regular helices and usually involve ribose and base moieties that are not contiguous (even separated by three or more residues in a significant fraction of cases). Therefore, our analysis clearly emphasizes that the lp–π ribose–base interaction is a structural element that is much more common in RNA molecules than has been considered to date. In addition, we have also shown that the energy of such interactions is not negligible, as it is in fact comparable to an H-bond between two water molecules calculated at the same level of theory, –4.3 kcal/mol, and to the stacking between two bases in a regular double helix, –4.7 ± 3.38 kcal/mol. The structural stabilization of such an interaction, as we have shown, relies on a contribution from genuine lp–π interaction due to the slightly positive electrostatic potential exhibited by the nucleobases above the base plane and the negative electrostatic potential localized around the ribose O4′ atom, and a substantial contribution deriving from dispersion interaction between the whole ribose ring and the nucleobase.

In light of these results, the question arises as to whether these widespread interactions may have a functional role. For the Z-DNA like motifs, they have been suggested to be involved as protein recognition sites in DNA (79–83), and, more recently, they have been proposed to have implications for RNA/protein recognition and immune response (20). As for the other examples of ribose–base interactions we have characterized, it should be noted that several of these interactions are found at key locations in the RNA structures and involve bases that are highly conserved and suggested to be functional by experimental evidence.

One example is the twister ribozyme, recently added to the list of the catalytic RNA family members, which features eight highly conserved nucleobases that stabilize the core of the ribozyme (84). In its 3D structure (PDB ID: 4OJI), we could find three ribose–base interactions, O4′(A7)-A29, O4′(C31)-A40 and O4′(A8)-A28; the latter one involves the A28 nucleobase, whose mutation to G or U causes a significant decrease in the ribozyme activity (84). The above stacking interaction is consistently found in independent structures obtained for the same RNA molecule (PDB IDs: 4RGE, 5DUN (85,86)). Another example pertains to the flexizyme, a 45-nucleotide ribozyme discovered through selection in vitro, which is capable of charging tRNA with various activated L-phenylalanine derivatives (PDB ID: 3CUN) (87). In this structure, we observed a sandwich-like O4′(U52)–A54–O4′(C22) stacking contact with the A54 nucleobase stacked between the ribose moieties of U52 and C22 (also shown in Figure 2B). Again, mutation of A54, the nucleobase involved in the stacking interaction, to U has been shown to decrease this ribozyme activity by 95% (87).

In addition to stabilizing RNA structures, the ribose–base stacking seems to be involved in molecular recognition. It was already reported that the ribose of G34, the first anticodon position in tRNA, stacks against the highly conserved G966 base of 16s rRNA (18), thus possibly playing a role in the tRNA recognition by ribosomes. Analogously, we could observe several other instances of inter-molecular ribose–base stacking interactions. For instance, in the yeast ribosome, two ribose–base interactions were observed between the 5.8S rRNA from the large and 25S rRNA from the small ribosomal subunits (specifically between the riboses of C8/C137 and A1399/U14, respectively, PDB ID: 3U5H). Other examples of inter-molecular ribose–base stacking interactions were detected between the T. tengcongensis glmS ribozyme and its RNA substrate (PDB ID: 2HO7 (88)) and between a herpesvirus RNA element and a poly(A) target (PDB ID: 3P22 (89)). The key locations discussed above complement the many instances of long-range intra-molecular interactions, joining different domains of the same molecules, as shown before for the 23s rRNA.

As recently noted by Grosjean and Westhof in the context of decoding, along the course of evolution, RNA has set up ‘various strategies based, as in any complex molecular system, on the interplay between many weak interactions together with a few strong interactions’ (90). We believe the stacking between riboses and nucleobases to be one of these relatively weak but significant interactions. In this study, we provide the first comprehensive structural overview of this hitherto mostly overlooked interaction, together with a reference system to estimate the energy contribution of similar contacts in newly characterized structures.

Finally, the finding that lone pair–π interactions are also common between riboses and aromatic amino acids suggests a functional role played by this kind of interaction in the process of recognition and complex stabilization between RNAs and RNA-binding proteins.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

King Abdullah University of Science and Technology (KAUST) [to L.C.]; Polish National Science Center (NCN) [2012/04/A/NZ2/00455 to J.M.B.]. Funding for open access charge: King Abdullah University of Science and Technology. For computer time, this research used the resources of the Supercomputing Laboratory at King Abdullah University of Science & Technology (KAUST) in Thuwal, Saudi Arabia.

Conflict of interest statement. Janusz M. Bujnicki is an Executive Editor of Nucleic Acids Research.