Enrichment of dynamic chromosomal crosslinks drive phase separation of the nucleolus

Abstract

Regions of highly repetitive DNA, such as those found in the nucleolus, show a self-organization that is marked by spatial segregation and frequent self-interaction. The mechanisms that underlie the sequestration of these sub-domains are largely unknown. Using a stochastic, bead-spring representation of chromatin in budding yeast, we find enrichment of protein-mediated, dynamic chromosomal cross-links recapitulates the segregation, morphology and self-interaction of the nucleolus. Rates and enrichment of dynamic crosslinking have profound consequences on domain morphology. Our model demonstrates the nucleolus is phase separated from other chromatin in the nucleus and predicts that multiple rDNA loci will form a single nucleolus independent of their location within the genome. Fluorescent labeling of budding yeast nucleoli with CDC14-GFP revealed that a split rDNA locus indeed forms a single nucleolus. We propose that nuclear sub-domains, such as the nucleolus, result from phase separations within the nucleus, which are driven by the enrichment of protein-mediated, dynamic chromosomal crosslinks.

INTRODUCTION

The eukaryotic nucleus is a complex three-dimensional (3D) environment in which genome function depends not only on the linear arrangement of regulatory sequence elements but also on their spatial organization for effective control of gene expression and nucleic acid metabolism (1–3). The spatial organization is in constant flux; individual genes can reposition within the nucleus in response to environmental or developmental cues and the genome can be mobilized in times of genotoxic stress (4–6). The nucleus is composed of a variety of sub-domains or different compartments, each of them with a distinct structure and function. The mechanisms by which sub-nuclear compartments are formed and maintained as well as what determines their composition, size, shape and number at various stages of the cell cycle remain largely unknown. Integration of current advances in microscopy, chromosome engineering, theory and computation enables exploration and validation of the statistical mechanical underpinnings that account for formation and maintenance of different sub-nuclear compartments.

In this paper, we investigate the dynamic organization of the nucleolus, the site of ribosomal RNA synthesis, within the nucleus of budding yeast. The nucleolus is composed of repeated DNA sequences and, as a result, is often not included in large-scale sequencing or chromosome conformation studies (7). The nucleolus can readily be identified as an approximately crescent-shaped structure adjacent to the nuclear envelope and typically opposed to the spindle pole body in G1 stage of the cell cycle (8,9). In addition to housing the ribosomal DNA (rDNA), the nucleolus is a reservoir for cell-cycle regulatory factors such as FEAR and MEN. Upon anaphase onset, several of the regulatory proteins are modified and released from the nucleolus to carry out anaphase. In this study, we focus on rDNA in G1 cells to reduce complexity introduced with building an intranuclear spindle in metaphase. In yeast, rDNA is found in arm 2 of chromosome XII. Albert et al. (10) performed a comprehensive investigation of this chromosome and found that the dynamics of non-rDNA loci consistently followed those of homogeneous, tethered polymer chains. In contrast, the dynamics of the rDNA loci showed a distinctive deviation from such behavior; namely, larger separation with respect to the nuclear center and slower movement. In agreement with these results, Wong et al. (7,11) used polymer models to simulate chromosome XII as a heteropolymer assigning a 10× larger size to the rDNA segments of the chain. This size was used so that the resulting nucleolus occupied roughly one-third of the nuclear volume. Using this minimalistic dynamic model the authors were able to explain a large set of quantitative data reported on yeast nuclear architecture including locus positions, contact frequencies and motion characteristics (11). Although the nucleolus plays a unique role in the organization of the nuclear architecture, to our knowledge no other modeling efforts have included its dynamics in an explicit manner. Few exceptions remain, where the nucleolus is included as a topological constraint within the computational domain (12–14). However, in these works the nucleolus was assumed to be static and uniform.

Stochastic simulations of entropy-driven, bead-spring polymer chain models account for many features of the dynamic properties of chromatin fibers confined within the yeast nucleus (15–19). In this study, we explore key parameters that endow a sub-domain of the genome with characteristics that define the nucleolus. As discussed above, previous work has modeled the nucleolus as a chain of increased diameter (11). This approach provides a physical basis for chain thickening and manifests experimental findings. Here, we take a different approach and introduce crosslinking within or between chains representing chromatin interactions with structural maintenance of chromosomes (SMC) proteins or with a high mobility group protein, HMO1 involved in rDNA transcriptional regulation within the nucleolus (20,21). The model herein is fully reflective of experimentally based, biological parameters including chromosomal DNA properties, nuclear confinement, tethering of chromosome arms to the centromere and telomere sites, and the relative lengths of all 32 chromosome arms (16 chromosomes, 32 arms roughly meta-centric). We translate simulated data from the 3D computational models into equivalent microscope images, to view and analyze experimental images obtained from live cell microscopy. Through these visualization tools and comparison of simulation results and experimental data, we report the statistical mechanics sufficient to account for nucleolar dynamics and conformation due to molecular mechanisms (protein-mediated crosslinking kinetics) that are beyond current experimental resolution.

MATERIALS AND METHODS

Strains and imaging

Budding yeast strains EMS219 (Mat alpha, his5 leu2–3,212 ura3–50 CAN1 asp5 gal2 (form I1 rDNA::leu2 URA3+)), intact rDNA and EMS60-UVR-12 (LEU2+, URA3+ CANS form I1 rDNA), translocated rDNA (22), were transformed with CDC14-GFP:KAN to label the nucleolus to generate DCY1021.1 and DCY1017.2, respectively. DCY1021.1 was transformed using pS01 plasmid to introduce the brn1–9 allele into strain AY1009. DCY1021.1 was transformed to knockout Fob1 and Hmo1 in strains DCY1055.1 and DCY1056.1, respectively. Cells were grown in YPD (1% Yeast extract, 2% Bacto-peptone, 2% Dextrose) with excess adenine. Strains were grown until mid-log phase prior to imaging. Images were acquired at room temperature for wild-type (WT), fob1Δ and hmo1Δ mutant strains (25°C). brn1–9 strains were shifted to 37°C 3 h prior to image analysis. G1 cells were found in the population by visual inspection of bud size. Images were acquired using a Ti-Eclipse inverted microscope (Nikon) with a 100 × Plan Apo 1.4 NA objective (Nikon) and Clara CCD digital camera (Andor) using MetaMorph 7.7 imaging software (Molecular Devices). Single stacks contained 7 Z-planes sections with 300 nm step-size. Image stacks were cropped and maximum intensity projections were created using ImageJ.

Image analysis

Image stacks of single cells were imported into MATLAB using bfopen.m function from the MATLAB Toolbox of the Bio-Formats program suite from the downloads page of the Open Microscopy Environment (http://downloads.openmicroscopy.org/bio-formats/5.5.1/) (23). A custom MATLAB function, mdx_multi_thresh.m, converted the image stack to a maximum intensity projection, padded the image to 200 × 200 pixels with minimum pixel intensity and normalized the image intensities such that minimum intensity is set to 0 and maximum intensity is set to 1. A gradually increasing threshold (0 to 1 using 0.01 increments) was applied to the image, such that intensity values below the threshold were not included in later calculations. At each threshold, the variance of the normalized intensities above the threshold and the normalized area (area of pixels above threshold divided by area total image) was calculated. The mean and S.E.M. of the variances and areas at each threshold was calculated from all cells of a given genotype. The same analysis was performed on simulated images using the MATLAB function dt_cmyk_mmt.m.

Modeling approach

The observed motion of chromatin loci is consistent with those of highly flexible polymers. As a consequence, polymer models have proved valuable in the understanding of chromatin dynamics (14,16–19,24–30). In our approach, chromosome chains are modeled using a bead-spring polymer model where each arm is represented by interacting beads connected via springs following a worm-like chain (WLC) force law (31,32). Each chain is tethered at both the ends representing the tethering of the telomeres to the nuclear membrane and the centromeres to the spindle pole body. This tethering resembles the Rabl configuration observed experimentally (26,33–36). In addition to tethering, chains are confined within the nuclear domain represented by a sphere of radius 1 μm; both constraints reflect in vivo observations of yeast chromosomes (18,36).

The basis of the model is a balance of forces acting on each bead,

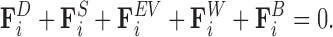(1)

The forces considered in our model are the drag force 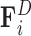opposing the movement of the bead; the spring force 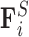capturing bead–bead interactions via an attractive potential; the excluded volume force 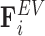that opposes overlapping of two beads; interactions with the cell wall 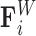that ensures that beads remain within the spherical domain and that beads corresponding to centromere and telomere sites remain fixed to the domain wall; and the Brownian force 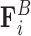that captures the random motion of the beads due to thermal fluctuations. For details of the functional form of these forces and the model parameters, we refer the reader to (17).

Nucleolus modeling

The discretization in our model corresponds to 5 kb of DNA per spring. The total number of beads composing each chromosome arm are determined based on this discretization; for specific numbers see (17). In yeast, rDNA comprise ∼1.8 million bp in length, corresponding to ∼361 beads in our model. Here, we simulate the nucleolus by increasing the size of arm 2 in chromosome XII by 361 beads. The position of these beads is in agreement with experimental observations; however the qualitative observations presented in this study are independent of the location of these 361 beads within arm 2 of chromosome XII. We also investigated variations of the number of beads representing the rDNA, these results are shown in Supplementary Figure S8. In general, nucleolus beads follow the same force laws and have the same parameter values as all other beads in our computational domain; with the exception that dynamic crosslinking among nucleolus beads is introduced, arising from the presence of SMC proteins with preferential affinities to the nucleolus beads. For simulations where the nucleolus is split, the nucleolus beads are divided between arm 2 of chromosome III and arm 2 of chromosome XII, consistent with experiments. Table 1 summarizes modeling assumptions regarding numbers of beads.

Table 1. Summary of number of beads used in each type of simulation.

		Number of beads
Chromosome	Arm	No nucleolus	Single nucleolus	Split nucleolus
III	1	24	24	24
	2	41	41	325
XII	1	31	31	31
	2	186	546	263

All other chromosome arms are discretized as in (17).

Crosslinking

As in (17), we assume a pair-wise binding of beads by introducing a spring-like force between them. This spring force obeys a WLC law, just like the one between neighboring beads in the bead-spring chromatin chain. However, in protein-mediated crosslinks, the springs are 50× stronger. Note that loops are formed when these crosslinks occur between beads in the same chain. We explore several assumptions about crosslinking in the nucleolus and external to the nucleolus:

1. Absence of crosslinks throughout the whole domain. This set of data is used as a baseline comparison with all other simulations.

2. Fixed loops in the nucleolus only. Here, we assume that the 361 beads composing the nucleolus are arranged such that strong WLC springs connect every third, fifth or seventh bead. This results in chain configurations of permanent 3-bead, 5-bead and 7-bead loops, respectively.

3. Dynamic crosslinking in the nucleolus only. We assume stochastic dynamic crosslink formation within the nucleolus, with all beads within the nucleolus available for binding-unbinding kinetics and assume no crosslinks outside the nucleolus. We tune dynamic crosslinking through the use of six parameters, defined below. Unlike single molecule analysis or imaging, this approach enables us to discern how the dynamics of entropic chain fluctuations, together with on and off timescale distributions of the binding protein, influence the strength of interactions within the nucleolus.

4. Preferential dynamic crosslinking internal versus external to the nucleolus. We assume dynamic crosslinking throughout the genome, but with a fraction (1/3, 1/10) of active binding sites external to the fully active nucleolus.

Dynamic looping parameters

1. Barrier. The distance (90 nm) between which two beads must fall in order to be eligible to form a crosslink. Although in our modeling, we are assuming generic crosslinkers, here we choose a value based on experimental work with condensin, which can reach and bind portions of DNA that are at most 90 nm apart (37). However, other values were explored and these results are shown in Supplementary Figure S9.

2. Maximum loop distance. The distance where the WLC spring has a singularity. The bond might start at a larger distance when they form the crosslink, but will quickly move within this distance. This value was chosen based on experimental work suggesting that condensin can stretch to 45 nm (37). As mentioned above, this does not indicate we are only modeling condensin, but rather we are taking these values as reference points.

3. Loop force scale. Applicable in both the uniform looping and dynamic looping cases, this parameter is a coefficient that scales the linear part of the WLC spring; namely, it makes the spring stiffer at shorter length scales.

4. Mean on, Mean off, Standard Deviation on and Standard Deviation off. These parameters (units of time) are the mean and standard deviation for how long a crosslink is active or inactive. In our simulations, we have varied the values for ‘Mean On’ and ‘Mean Off’ (often choosing values so that the ratio Mean On:Mean Off = 9) but have kept both ‘Standard Deviation On’ and ‘Standard Deviation Off’ set to 20% of their respective mean value for all simulations. For example, if ‘Mean On’ = 0.09 s and ‘Mean Off’ = 0.01 s, then ‘Standard Deviation On’ = 0.018 s and ‘Standard Deviation Off’ = 0.002 s.

5. Formation and destruction of links. Due to the dynamic nature of the loop formation and the constantly changing spatial organization of the beads, the pair bonds need to be updated each time step. Bonds might break because one of the beads in the pair became inactive. Bonds can form because two active and available beads might be close enough to form a bond. To do this, we compute the pairwise distance between all beads that are active and not currently bonded, and put the distance in a strictly upper triangular matrix. If all of those distances are larger than the barrier then no more bonds need to be created. Otherwise the smallest value in this matrix means that there will be a dynamic bond formed between the beads corresponding to the row and column of this entry. The bond is made and the corresponding row and column is removed from the upper triangular matrix since a bead can at most dynamically link with one other. This process is repeated until the smallest distance is above the barrier distance. In the end, this matrix does not have to be empty, since the number of available beads might be odd and there are often lone beads that are too far away from the other unattached beads. We also note that, in the case of dynamic looping, it is likely that two beads will be more than the maximum loop distance apart from one another when they first join to form a loop, since the barrier value is larger than the maximum loop distance value. Thus, at every subsequent time step after the initial loop connection is made, the distance between the two beads is halved until that distance is less than the maximum loop distance value.

Microscope simulator

We have created two distinct pipelines—one for experimental images and the other for simulated bead position data. Simulated data go through a program, which we call the microscope simulator, to create images that can be post-processed the same way as images that come from experiments. This allows us to analyze the entire simulation run. This is done by using and extending DataTank, an object-oriented programming environment offering large dataset support and visualization tools made by Adalsteinsson http://www.visualdatatools.com/DataTank. The metric we use is nucleolar area.

1. Experimental input. Images from light fluorescence microscopy are input into the DataTank script. The script takes the max projection of the Z-stack to produce a single image for a given time. We use the Otsu thresholding method (38) to determine the appropriate nucleolar contour threshold for each frame. This gives us a polygonal representation of the boundary and allows us to compute the area for the cell at each frame and compute statistics from the collection of images.

2. Simulated input. When analyzing simulated data, the process is similar, but we must first transform the simulated data into an image. This is the program we refer to as the Microscope simulator and was created as a module in DataTank. This module contains information about how a single point of light spreads and is visualized in 3D; namely, it utilizes a point spread function (PSF) to generate a simulated 3D image. This PSF was captured using the same microscope that the Bloom Lab uses in their experimental work. In the DataTank script, the simulator module takes as input a 3D stack of images coming from a single fluorescent bead along with the x, y, z coordinates from the simulation. The module goes over each simulated data point and shifts the 3D input image to that center and adds together all of those images to form a 3D image. At this point it computes a max projection to create a single 2D image. This is done for every frame of the simulation. After this, we use the same process as for the experimental images, except that the threshold is kept the same for all of the images, at 68% of the maximum light intensity.

Metrics

• Radius of Gyration: The radius of gyration for N nucleolar beads is computed as:

  

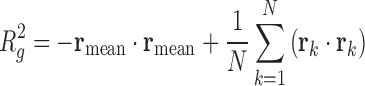
  where 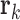is the vector position for individual beads and 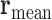is the mean position of all nucleolus beads.

• Expected Value(E[X]): for a log-normal distribution with mean μ and standard deviation σ, the E[X] is:

  
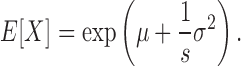
• Coefficient of Variation (CV): for a log-normal distribution with standard deviation σ the arithmetic CV is:

  

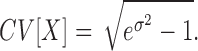
RESULTS

The nucleolus is a heterogeneous and dynamic nuclear sub-domain

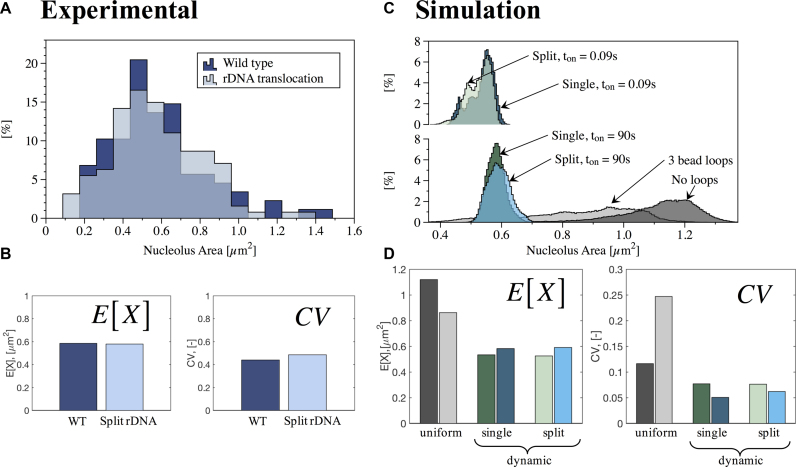
In the yeast cell, 1.8 Mb of a tandem repeat of 9.1 kb (about 180 repeats) resides on the right arm of chromosome XII. This repeat contains the genes for 5S, 5.8S, 18S and 25S rRNA and several transcribed and non-transcribed spacer regions. The repeat array occupies a specific nuclear domain throughout the cell cycle in living yeast. To visualize the nucleolus, we fused several protein components to green fluorescent protein (GFP) including Cdc14 (protein phosphatase), Cbf5 (pseudouridine synthase) and a multiply integrated array of lacO/lacI-GFP (39). Nucleolar protein fusions and integrated lacO arrays occupy a distinct region of the nucleus adjacent to the nuclear envelope and typically opposed to the spindle pole body. We have developed analytical tools to quantitate changes in nucleolar morphology and distribution (see ‘Materials and Methods’ section). Our analysis shows that the distribution of areas occupied by a nucleolar protein (Cdc14-GFP) display a lognormal distribution in WT cells in G1 of the cell cycle (Figures 1A and 2). For each of these distributions, we calculated the E[X] and CV as measures of central tendency and dispersion of the data (Figure 1B).

Figure 1.

Quantitative analysis of nucleolus area in wild-type (WT) and rDNA translocation strains. (A) Histogram of experimental results for WT (88 cells) and rDNA translocation (127 cells). Y-axis is percentage in each bin. (B) Measures of central tendency (Expected value, E[X]) and dispersion (Geometric coefficient of variation, CV) obtained from best fit to lognormal distributions to experimental data in (A). (C) Histogram of simulations results for no crosslinks, uniform crosslinks and dynamic crosslinks, with K_eq = 9 and two different (slow and fast) binding times t_on for single and split nucleolus. Y-axis is percentage in each bin. (D) Measures of central tendency (E[X]) and dispersion (CV) obtained from best fit to lognormal distributions of simulated data in (C). Color code for panels (C) and (D): No crosslinks (dark gray), uniform crosslinks with 3 beads per loop (light gray), dynamic crosslinks, single nucleolus, t_on = 90 s (dark green), dynamic crosslinks, single nucleolus, t_on = 0.09 s (dark blue), dynamic crosslinks, split nucleolus, t_on = 90 s (light green) and dynamic crosslinks, split nucleolus, t_on = 0.09 s (light blue).

Figure 2.

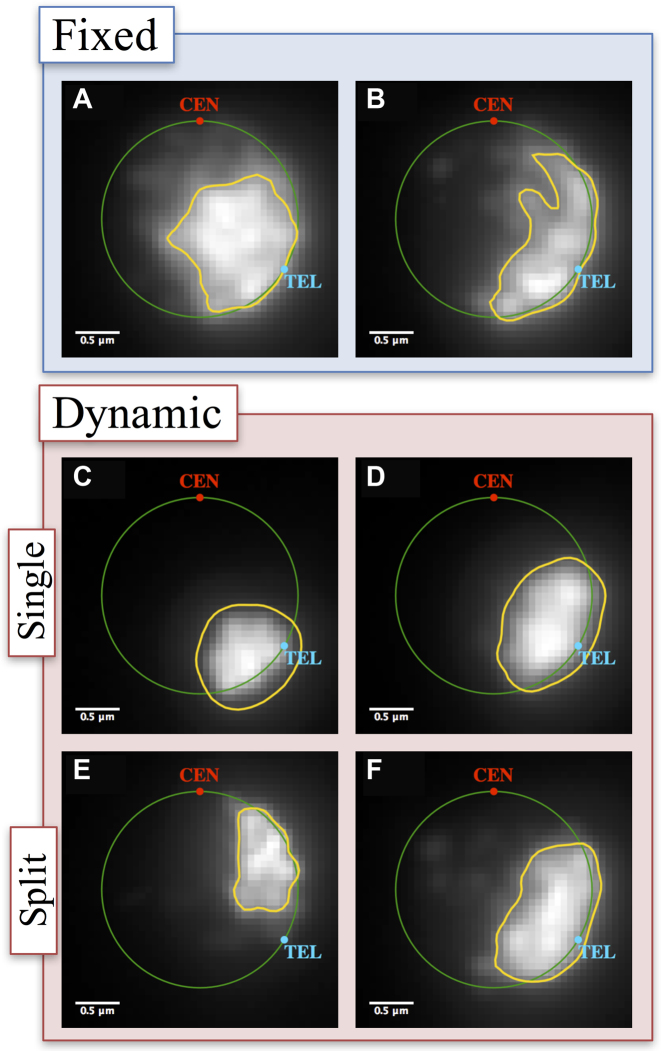
Experimental results for CDC14-GFP of intact and translocated rDNA. Maximum intensity projections of CDC14-GFP in strains with (A) WT (DCY1021.1) and (B) translocated (DCY1017.2) rDNA.

Nucleolar position and morphology is not dependent on rDNA continuity along a single chromosome

In yeast cells, rDNA can be experimentally manipulated through chromosome translocation to split the locus among different chromosomes. We have utilized a strain where the rDNA has been split between chromosome XII and III (Figure 2). Through an engineered chromosome translocation, Mikus and Petes (22) have generated a yeast strain where a translocation between two chromosomes results in splitting the rDNA. Remarkably, the split nucleolus is indistinguishable from the nucleolus in WT cells (Figure 2), similar to that found in cells with rDNA at ectopic sites (40). Figure 1A and B show that the area within the nucleolus, as well as the quantitative analysis of central tendency and dispersion, are comparable between the two biological situations. This finding provides the impetus to explore models that account for the biological merger of rDNA when the gene arrays lie on disparate chromosomes.

Implementation of crosslinks through molecular springs to simulate the nucleolus

To directly compare bead-spring models to experimental data, we convolved beads that occupy the position comparable to the rDNA repeats in chromosome XII with a point-spread function from a fluorescence microscope used to image the nucleolus (see ‘Materials and Methods’ section). The strategy was implemented in DataTank (http://www.visualdatatools.com). Analyses of nucleolus area from simulations also display a lognormal distribution (Figure 1C). Figure 1D shows the resulting measures of central tendency and dispersion. Examples of microscope-simulator images and area thresholds are shown in Figure 3, for different modeling assumptions.

Figure 3.

Qualitative analysis of nucleolus area. Simulation results converted to microscope images (see ‘Materials and Methods’ section). (A) Without crosslinks, (B) uniform, fixed cross-links, (C) dynamic crosslinks for single nucleolus with t_on = 0.09 s, (D) dynamic crosslinks for single nucleolus with t_on = 90 s, (E) dynamic crosslinks for split nucleolus with t_on = 0.09 s and (F) dynamic crosslinks for split nucleolus with t_on = 90 s.

SMC proteins, including condensin (SMC2,4) and cohesin (SMC1,3), are major structural components of eukaryotic chromosomes and are enriched in the nucleolus throughout phylogeny. The proteins comprise small rings (25–50 nm diameter) that function to build chromatin loops, hold sister chromatids together and are the basis for the 3D organization of the chromatin fiber into topologically associated domains (TADs). (41). To simulate rings that physically aggregate remote chromatin domains, we implemented molecular springs in the model that bridge and hold pairs of beads for prescribed statistical durations. This spring force obeys a WLC law, based on polymer models of random coils (42,43) and is the same as the one implemented in the springs between neighboring beads of the bead–spring chromatin chains. In addition, the crosslinking springs are 50× stronger than those connecting neighboring beads. In this way, crosslinking springs represent relatively stiff protein complexes (small persistence length, L_p) while springs between neighboring beads represent chromatin tension blobs (large L_p).

To explore whether introducing crosslinking via simple springs is sufficient to segregate sub-domains in the genome, we implemented simulations with no crosslinks (Figure 4A), permanent crosslinks formed by springs located at fixed locations (uniform crosslinks—Figure 4B) and crosslinks formed by springs whose locations are changed dynamically (dynamic crosslinks—Figure 4C), as described in the ‘Materials and Methods’ section. In Figure 4, for uniform crosslinks we impose chain configurations with 3-bead loops: two looping beads separated by one bead, as described in ‘Materials and Methods’ section. For dynamic crosslinks, we assume stochastic dynamic crosslink formation within the nucleolus, with all beads within the nucleolus available for binding-unbinding kinetics and assume no crosslinks outside the nucleolus (see below for inclusion of crosslinks outside the nucleolus). Several noteworthy differences distinguish the dynamic crosslinks case from the uniform, fixed-loops case. For instance, dynamic crosslinking allows for the possibility of a transient, fluctuating ‘loops within loops’ structure. We tune dynamic crosslinking through the use of six parameters, defined in detail in ‘Materials and Methods’ section. The parameters are the distance (90 nm) between which two beads must fall in order to be eligible to form a crosslink, maximum separation (45 nm) that beads cannot breach when they are bound by a dynamic crosslinking spring, spring force that makes the spring stiffer at shorter length scales (50×) and mean t_on, mean t_off, standard deviation on and standard deviation off. The last four parameters are in seconds and they define the distribution of times at which beads can turn ‘on’ and ‘off’, i.e. are eligible for binding with other active beads. In the model, we have varied the values for t_on and t_off, keeping the equilibrium rate constant, K_eq = t_on/t_off = 9 and have set the standard deviations of both distributions equal to 20% of the mean value for all simulations.

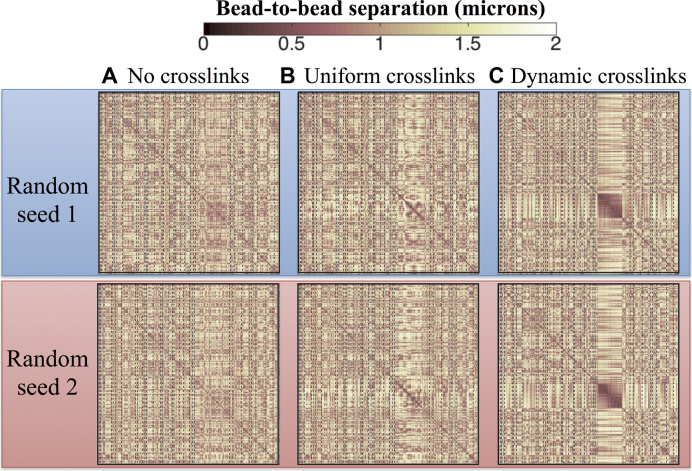
Figure 4.

Contact Maps depicting the average 3D bead-to-bead distance over 15 min. Each plot corresponds to datasets from six independent simulations; however datasets in the same row (top or bottom) use the same random seed and only differ on the type of crosslinking imposed in the nucleolus. Dynamic crosslinking dramatically increases nucleolus connectivity, whereas uniform crosslinking has a far lesser effect. (A) No crosslinks, (B) 3-bead uniform loops, (C) Dynamic crosslinking (K_eq = t_on/t_off = 9, t_on = 0.09 s). X- and Y-axis in each contact map correspond to bead numbers (1–2443), where bead 1 is the first bead in the chain corresponding to arm 1 of chromosome I and bead 2443 is the last bead in the chain representing arm 2 of chromosome XVI.

Crosslinks in the model promote compaction and spatial segregation while dynamic crosslinking promotes connectivity and sub-structure within the nucleolus

Unlike single molecule analysis or imaging, simulation enables us to discern how the dynamics of entropic chain fluctuations, together with permanent versus dynamic crosslinking, influence the strength of interactions within the nucleolus. Figure 4 shows contact maps consisting of average bead–bead distances over a 15-min period. In the absence of crosslinking, the maps in Figure 4A reveal a fairly uniform distribution of bead–bead distances across the genome. Although the average distance is about 1 µm, there is heterogeneity across the genome and different simulations show different distributions (top–bottom Figure 4). Upon introducing static 3-bead looping, Figure 4B shows that the major change is a decrease in average bead–bead distances, from ∼1 µm to ∼600 nm, in the region where the looping was implemented (denoted as the rDNA containing 1.8 Mb of rDNA gene repeats). However, the remaining beads exhibit similar contact statistics as in the non-crosslinking configuration, except for their interactions with beads belonging to the nucleolus region, which show an increase in bead separation (lighter ‘cross’ in the contact maps), indicating enhanced sequestration of the nucleolus. In contrast, fast dynamic crosslinking has a major impact on the behavior of the rDNA cluster (Figure 4C). There is a predominant compaction of bead–bead distance in the dynamic case, down to 300–400 nm among a sub-set of beads (further explored below) within the nucleolar region and less dramatic yet still much closer bead–bead proximity within the rest of the nucleolus relative to the rest of the genome. Furthermore, the distance between the rDNA beads and the rest of the genome increases, corresponding to more enhanced sequestration of the nucleolus. This implies that the rDNA beads are interacting more frequently with themselves and therefore less frequently with the remainder of the genome. This is notable in the perpendicular cross, lighter regions vertical and horizontal from the rDNA, signifying the rDNA bead interactions with unlinked chromosomes. This somewhat non-intuitive impact of weak binding relative to tight binding kinetics has been explored in other biological contexts (J. Newby, J. Schiller, T. Wessler, M.G. Forest, S. Lai, A blueprint for robust crosslinking of mobile species in biogels using third-party molecular anchors with short-lived anchor-matrix bonds, Nature Communications, accepted July 2017), both experimentally and theoretically.

Reduction of crosslinks through in vivo mutational approaches corroborate model predictions

To test the physiological significance of the model, we examined nucleolar morphology (Cdc14-GFP) in strains lacking key proteins reported to crosslink or loop segments of rDNA within the nucleolus. These include condensin (Brn1), Fob1 and Hmo1. Brn1/Barren is the kleisin component of condensin, that bridges SMC 2,4 heads in the protein ring. Fob1 is required for maintenance of the rDNA copy number and regulates the association of condensin with rDNA repeats (44,45). The replication fork barrier within the rDNA is a binding site for Fob1 that together with several other components (Tof1, Csm1 and Lrs4) are responsible for the concentration of condensin within the nucleolus (44). Hmo1 is an abundant high mobility group protein that localizes to the nucleolus and has been proposed to share functions with UBF1 involved in rDNA transcriptional regulation within the nucleolus (20,21). Fob1 and Hmo1 are non-essential genes and were deleted from the genome. In a quantitative genome-wide analysis, Kobayashi and Saskai (46) found no significant change in rDNA copy number in fob1Δ or hmo1Δ strains relative to WT. Brn1 is an essential gene, thus we utilized the temperature sensitive mutant Brn1–9 (47).

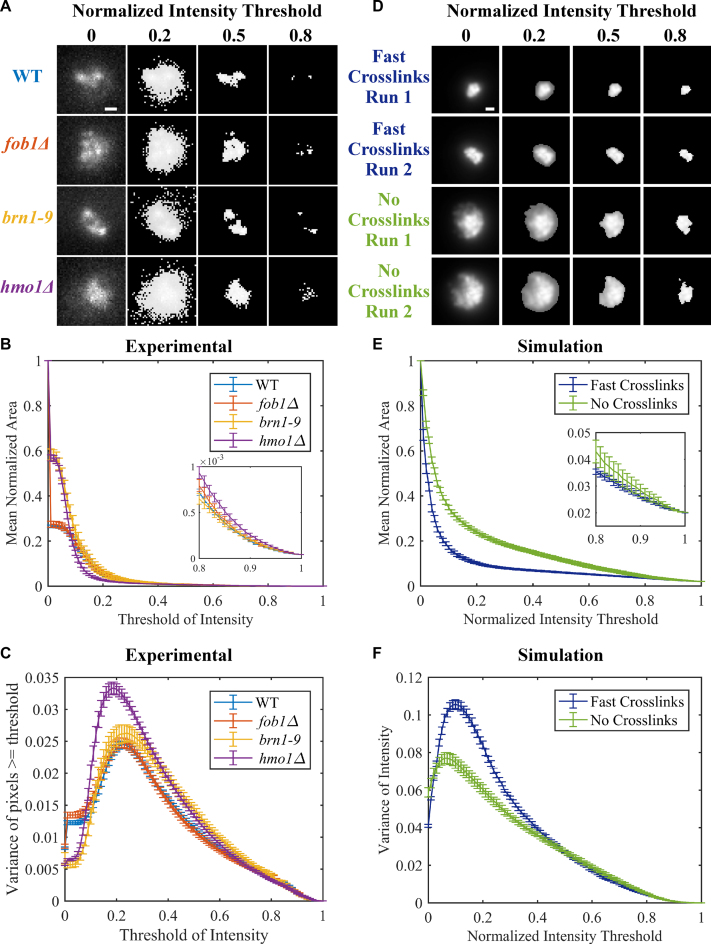
Cdc14-GFP was introduced into these strains for quantitative image analysis of the nucleolus (Figure 5A). Given the diffuse and amorphous nature of the CDC14-GFP signal, we measured the fluorescent signal over 100 imaging thresholds (Figure 5A). Individual images were normalized by subtracting the minimum intensity from all intensity values (giving a minimum intensity of 0) and setting the maximum intensity to 1 (dividing each intensity value by the maximum intensity). We measured the area (Figure 5B) of the normalized fluorescent signal at increasing fractional thresholds from 0 (total image measured) to 1 (brightest pixel only) (48). The nucleolus occupies a larger normalized area in the absence of Fob1, Hmo1 and brn1–9 at thresholds <0.15 and >0.8 (Figure 5B inset). In the absence of Fob1, the nucleolar area is indistinguishable from WT (Figure 5B), as reported in Albert et al., (49). At intermediate thresholds, the fluorescence intensity reflects regions of heterogeneity within the nucleolus where the intensities are heightened due to clustering of a fraction of the repeats (Figure 5A 0.8, mutants). To confirm that the thresholding is an appropriate metric, we examined the model through convolution of simulated fluorescence (Figure 5D). The thresholding metric captures the increased area observed in the absence of crosslinks versus compaction upon crosslinking (Figure 5D) over all thresholds. Thus the crosslinking function provided by key nucleolar components, Brn1, Hmo1 phenocopy simulations of their deletion in the model.

Figure 5.

Area and variance of experimental and simulated nucleolar signals. (A) Representative images of CDC14-GFP in WT, fob1Δ, brn1–9 and hmo1Δ at different fractional intensity thresholds. Images are maximum intensity projections of Z-stacks through the cell. Images were normalized by subtracting minimum pixel value and then dividing by the maximum pixel value for each image. Thresholding of images set all pixels below indicated normalized intensity threshold to 0. Scale bar is 0.5 μm. (B) Normalized area of CDC14-GFP signal over all intensity thresholds. Error bars are S.E.M. WT (n = 179), fob1Δ (n = 70), brn1–9 (n = 41) and hmo1Δ (n = 77). Inset is zoomed in portion of graph from threshold of intensity from 0.8 to 1. (C) Variance of CDC14-GFP signal above the normalized intensity threshold. Error bars are S.E.M. (D) Simulated images of two iterations of fast, dynamics looping and no looping simulations. Images were normalized as in (A). (E) Normalized area of simulated nucleolar signal over all intensity thresholds. Image area was normalized to total image area. Error bars are S.E.M. Fast looping (n = 10), no looping (n = 10). Inset is zoomed in portion of graph from threshold of intensity from 0.8 to 1. (F) Variance of simulated nucleolar signal above the normalized intensity threshold. Error bars are S.E.M.

In addition to the normalized area, we determined the variance of normalized intensity (minimum intensity is 0, maximum intensity is 1) to assess heterogeneity in bead distribution within the nucleolus. The greatest variance is observed in hmo1Δ mutants (Figure 5C). The distribution of clusters is comparable to WT in fob1Δ and brn1Δ mutant situations. In simulation, the greatest variance is observed when fast cross-linking is implemented (Figure 5F). Reduction of crosslinks leads to homogenization of bead distribution. The increased variance in hmo1 mutants in vivo predicts that the binding and release of a crosslinker (e.g. condensin) is more rapid in hmo1 mutants.

Timescales of binding kinetics tune segregation and heterogeneity of the nucleolus

In the previous section, we showed that fast dynamic crosslinking enhances interactions within the active binding domain, leading to enhanced compaction and segregation of the nucleolus relative to permanent or no crosslinking. Here we explore the critical biological parameters involved in dynamic crosslinking, the on and off timescales of binding kinetics between nucleolar beads via the molecular springs and their influence on nucleolar morphology and nucleus-wide genome organization. We simulated three dynamic kinetic regimes, each with K_eq = t_on/t_off = 9, spanning fast to slow (weak to tight) binding with t_on = 0.09, 0.9 and 90 s, shown from left to right in Figure 6. These bead–bead contact maps reveal that faster binding kinetics induces closer bead–bead contacts (progressively darker shades) within the nucleolus. Further, upon closer inspection of Figure 6 left column, fast kinetics induces heterogeneity of bead–bead contacts within the nucleolus, indicative of structure-within-structure in nucleolus morphology, which homogenizes with slower binding (left to right in Figure 6).

Figure 6.

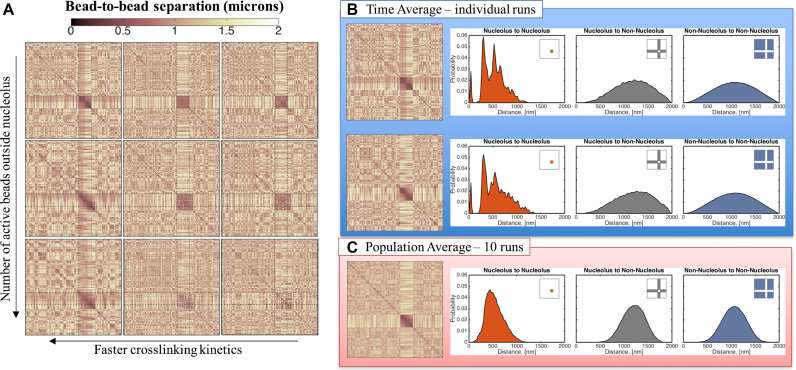
Nucleolus and genome-wide interactions as functions of crosslinking parameters. (A) Faster kinetics (lower t_on) result in more interactions within the nucleolus. From left to right t_on = 0.09, 0.9 and 90 s. Dynamics outside the nucleolus are controlled by the number of beads that are actively crosslinking. From top to bottom: all beads outside the nucleolus are inactive, every tenth bead is active and every third bead is active. All contact maps correspond to an average over 15 min for a single run. All data shown are simulated using the same random noise. (B) Distribution of bead-to-bead distances for dynamic crosslinking with K_eq= 9 and t_on= 0.09 s. Sub-structures within the nucleolus are formed by groups of beads that interact more frequently, leading to the darker regions in the contact maps and the peaks in the distribution functions. Although dynamic, these sub-structures persist over time for a given run (see Supplementary Movie 1) and vary from run to run. Top and bottom panels correspond to the same model parameters but different random seed. (C) The sub-structures are lost in the population averages resulting in a more uniform distribution of bead-to-bead distances within the nucleolus. X- and Y-axis for each contact map correspond to bead numbers, as explained in Figure 4.

Dynamic crosslinking is a segregation mechanism within the nucleus

By allowing a preferential interaction of beads in a specific part of the genome, a crosslink-induced phase separation occurs within the nucleus. In our simulations, one phase consists of beads in the nucleolus and this region is characterized by being denser than the rest of the nucleus. This compaction comes from enhanced interactions among these beads together with reduced interactions with other beads in the genome. To take into account different binding kinetics outside the nucleolus we define the number of ‘actively crosslinking’ beads outside. Figure 6 (top to bottom) shows that as this number decreases (less externally active beads) the nucleolus becomes more compact. As more beads outside the nucleolus participate in binding kinetics the identity of the nucleolus is weakened: less separation between bead–bead contacts within and external, and less compaction and segregation of the nucleolus (Supplementary Figure S4).

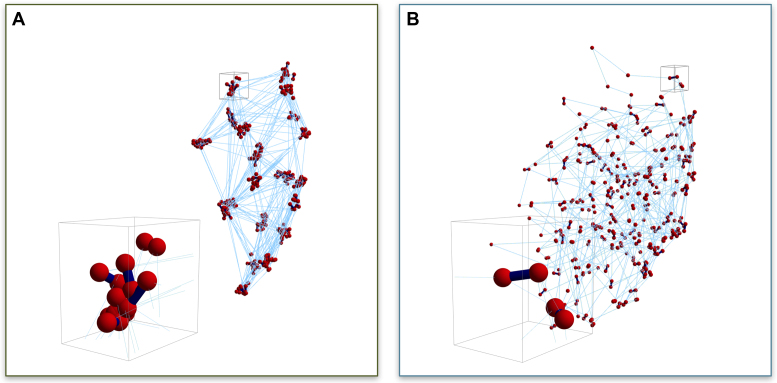
Figure 6A shows that sub-structures are formed within the nucleolus exclusively in the fast kinetics case, t_on = 0.09 s. These sub-structures are formed by clusters of nucleolar beads that reside closer and interact more frequently with members of their cluster, as suggested by the non-uniformity in the contact maps (left column of Figure 4). To amplify this feature, in Figure 6B we show histograms of bead–bead distances for two individual simulations and for a population average over 10 individual simulations, all with t_on = 0.09 s and identical initial data. Note the remarkable similarity of histograms for both individual runs shown (indeed for all 10 individual runs), with striking peaks within the nucleolus bead–bead distances yet with smooth proximity distributions of the population average and all bead-bead statistics involving extra-nucleolar beads. The first peak at ∼10 nm identifies sub-sets of beads tightly and persistently packed (forming clusters) and the second peak at ∼300 nm implies a robust separation between the persistent clusters. To visualize this implied morphology, Figure 7A is a 3D snapshot of all nucleolus beads for an individual run, revealing ∼25 clusters of 10–25 beads each. Distances within these clusters correspond to the leftmost peak in the graphs for individual runs in Figure 6B, while inter-cluster distances correspond to the second and third peaks in the same histograms. Although dynamic, these sub-structures persist in time for each individual run and vary from run to run (see Supplementary Movie 1). We note that these peaks and associated sub-structures are not present in runs with slower dynamics (see Supplementary Figure S3 for t_on = 90, Figure 7A and Supplementary Movie 2). Furthermore, these sub-structures are lost in the population averages that show uniformly distributed bead-to-bead distances within the nucleolus as shown in Figure 6C). That these peaks do not survive population averaging, despite the remarkable similarity in the cluster morphology of both runs in Figure 6A (indeed all 10 runs), is due to the fact that nucleolar beads are randomly distributed in the clusters for each run, so the tight associations of beads in any one cluster for any individual realization are different in every other realization. This result indicates that population averages might obscure a rich set of dynamic structures, which can only be appreciated at the single, live cell level.

Figure 7.

Snapshots of 3D nucleolus simulations. Bead distributions for (A) t_on = 0.09 s and (B) t_on = 90 s. Red symbols (spheres) represent bead positions, dark blue segments (lines) represent transient crosslinks between beads both inter- and intra-chain, light blue (thin) lines represent intra-chain neighboring bead connections. Inserts in (A) and (B) are blow-ups of small volumes around bead clusters.

Dynamic crosslinking within the nucleolus imposes itself on the remainder of the chromosomes as seen in the contact maps. By taking out a large segment of potential interactions (rDNA), contacts between the remainder of the genome occur with greater frequency. This indicates that despite a large block of the chromosome segregated in its own territory, the ability of remaining chromosomes to independently interact, e.g. by different SMC proteins, is not impeded. There is a small increase in the average distance between nucleolus beads and beads outside the nucleolus (Figure 5B and Supplementary Figure S3). These results suggest that dynamic crosslinking, although segregating nucleolar beads, still allows them to explore the nuclear state. There is physiological evidence for nucleolar DNA exiting the nucleus under conditions of DNA damage (5). The simulation indicates that rDNA is constantly able to ‘explore’ the nucleus and perhaps DNA damage takes advantage of this naturally occurring process.

We can divide our simulations along three main conditions: (i) static/uniform versus dynamic crosslinking, (ii) magnitude of dynamic binding-unbinding timescales and (iii) percentage of active-binding domains throughout the nucleus. A summary of these conditions is shown in Supplementary Figure S1 where we compare the statistics of bead–bead separation using best fits to lognormal distributions and their measures of central tendency E[X] and dispersion with respect to the mean (geometric CV). These statistics allow us to quantitate the degree of nucleolar structure. Imposing uniform looping in the nucleolus has little effect in the average bead–bead distance for beads both inside and outside of the nucleolus. Dynamic crosslinking, on the other hand, reduces the average distance between intra-nucleolar beads, while an increase of active beads outside the nucleolus has the opposite effect, i.e. increasing the average intra-nucleolar distance. As more beads outside the nucleolus participate in the crosslinking dynamics, the average separation between nucleolus beads increases (Supplementary Figure S1). This effect is more pronounced in the slow kinetics (t_on = 90 s), which shows bead–bead distances that are comparable with those found in the case where crosslinking was absent throughout the whole nucleus. With more active beads outside the nucleolus, the nucleolar beads are more spread out, indicating that the area increases as nucleolar beads spend more time outside the nucleolus.

Split nucleolus: co-linearity is not required to form a single domain

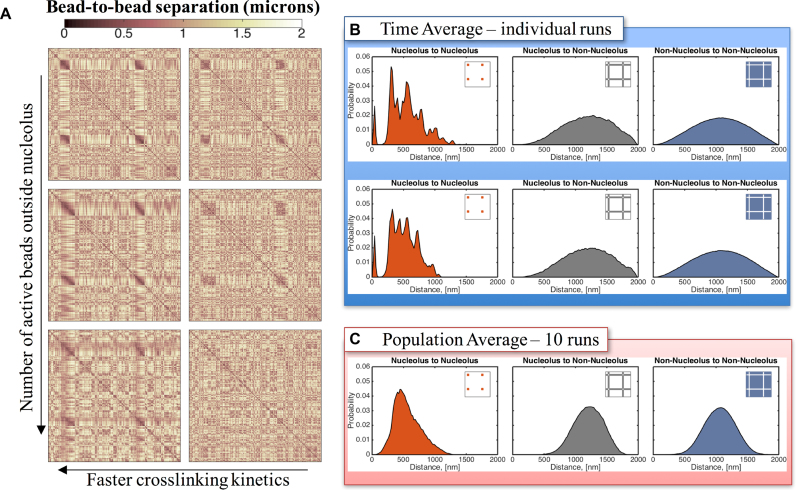
A critical prediction of the model is that the coalescence of beads into a distinct phase is not dependent on their co-linearity, (i.e. contiguous on the same chromosome arm) rather it is a consequence of protein-mediated binding kinetics. To test this in the model, we simulate a split nucleolus by dividing ‘nucleolar beads’ into two different chains as described in the ‘Materials and Methods’ section. The objective of this numerical experiment is to assess whether dynamic crosslinking suffices to create different regions within the nucleus or if co-linearity of such beads is required. Our results indicate that the split chains occupy a single region within the nucleus as shown in the contact maps in Figure 8 and Supplementary Figure S5. In addition, the distance between all nucleolar beads are comparable, consistent with them being in close proximity (Figure 6B). These results suggest that the main driving mechanism in the formation of nucleolar-like regions is a ‘preferential crosslinking’ within that region. In our case, this preferential crosslinking is controlled by the on/off binding dynamics of chromatin domains inside relative to outside the nucleolus.

Figure 8.

Distribution of bead-to-bead distances for split nucleolus. (A) Contact maps show that there is a marked increased in bead interactions within the nucleolus as a function of decreasing the on/off times of binding (left to right). Faster (weak) kinetics results in more interactions. Left column t_on = 0.09 s, right column t_on = 90 s. Active beads outside the nucleolus are introduced to account for binding interactions throughout the nucleus. In the non-nucleolar chromatin, interactive beads are inactive outside the nucleolus (stride zero—top row), every tenth bead is active (stride 10) and every third bead is active (stride 3—bottom row). (B) Sub-structures within the nucleolus are formed by clusters of beads that are closer, interact more frequently and maintain some separation between clusters. These fluctuating sub-structures create darker regions in the contact maps and peaks in the bead–bead proximity histograms within the nucleolus. Although dynamic, these sub-structures persist over time for a given run (see Supplementary Movie 3) and are robust from run-to-run although the nucleolar bead cluster assignments are random. Top and bottom panels correspond to the same model parameters but different random seed. (C) The sub-structures are lost in the population averages, even though the cluster morphology is robust, because of random cluster assignments, resulting in a more uniform distribution of bead-to-bead distances within the nucleolus. X- and Y-axis for each contact map correspond to bead numbers, as explained in Figure 4.

Remarkably, the dynamics observed in our single nucleolus simulations are mirrored by those in the split nucleolus. Namely, faster binding kinetics result in a decrease in the nucleolar area (compare Supplementary Figures S1 and 6) arising from beads within the nucleolus self-associating via sub-structures and interacting less with beads outside the nucleolus (Supplementary Figures S2 and 7). The introduction of crosslinking dynamics outside the nucleolus results, as anticipated, in an increase in nucleolar area. This increase scales with the relative percentage of active external beads versus internal nucleolar beads; all active beads experience increased interactions independent of which chromosome arm they reside in, essentially creating an effective nucleolus dictated by mutual binding affinity. Finally, for slow crosslinking dynamics and large numbers of active beads outside the nucleolus, the resulting distribution of bead–bead distances shows a complete mixing throughout the nucleus, evident in the contact maps shown in Figure 8. We note that this ‘mixing’ effect is more pronounced in the split nucleolus case than in the single nucleolus (compare bottom right of Figures 5A and 7A).

Results discussed above point toward a different understanding of the formation of nucleolar-type regions in the nucleus. As previously noted, the assumption of different polymeric properties for the nucleolar beads results in segregation and slower dynamics of the nucleolus, consistent with experimental results (11). However, this assumption alone does not, and cannot, yield our experimental results for a split nucleolus. Our approach of distinguishing the nucleolar beads not by their polymeric properties but by their binding affinity to certain proteins, recapitulates segregation, slower dynamics and split nucleolus observations. We note, however, that in vivo the most probable scenario is a combination of different non-specific (entropy, polymeric properties, macromolecular crowding, etc.) and specific interactions (e.g. protein-mediated crosslinking).

DISCUSSION

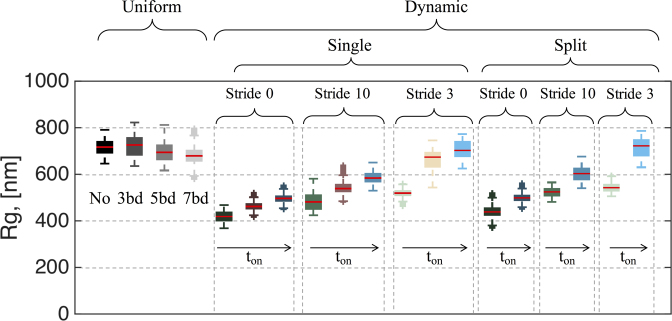
The numerical study presented here suggests that preferential, protein-mediated crosslinking in different regions of the genome results in the self-segregation, compaction and morphology of these regions, with each feature tunable by the timescales of crosslinking. Using bead–spring polymer models, we have shown that the only necessary condition to ‘create’ a nucleolus is that certain beads (which we labeled ‘nucleolar beads’) have binding affinity to each other in a dynamic way. Whether or not the nucleolar beads belong to the same chain, has little effect in the formation of the nucleolus or its dynamics. The important parameters are intra-nucleolar bead interaction kinetics and their relative interaction kinetics with non-nucleolar beads. We control the interaction kinetics via on/off binding timescale distributions and the interactions with other beads through the percentage of active beads outside the nucleolar region. We have summarized the parameter space explored in this study in Figure 9, where the radius of gyration of the resulting nucleolus is used as a metric for nucleolus size.

Figure 9.

Summary of nucleolus size with respect to crosslinking parameters. Radius of gyration, Rg, for each of the parameter values investigated in this study. For single nucleolus dynamics the values for t_on are 0.09, 0.9 and 90 s. For split nucleolus dynamics t_on = 0.09 and 90 s. Increase in ‘on’ time leads to an increase in the nucleolus size. Similarly, increase in the fraction of beads that are active outside the nucleolus (stride) increases the size of the nucleolus. For slow kinetics and comparable number of active beads inside and outside the nucleolus (light blue), there is little difference with respect to the case where no crosslinks are included (black). All dynamic crosslinking simulations have K_eq = 9.

The kinetics of the crosslinking agent relative to the motion of the sub-strate is a major driver of sub-nuclear organization. If the crosslinkers bind and release more rapidly than the chains can relocate, the non-intuitive consequence is that the chains explore less space. When nodes of protein/binding sites arise, they persist for extended time periods. The result is evident in Figure 6 as peaks and valleys in the histogram of bead–bead distances and as a 3D array of bead clusters in the snapshots of nucleolus beads in Figure 7, with persistence revealed in Supplementary movies. The primary peak in the fast-binding histograms represents an increased number of beads interacting within small areas, the array of clusters in Figure 6C. The valleys are a consequence of cluster–cluster separation statistics. Importantly, this heterogeneity is lost if one averages across a population (compare population average versus individual runs, Figure 6). A second consequence of the rapid kinetics relative to chain motion is the increase in distance for a portion of beads (tail toward increasing distance). This can be seen in the increase in CV for dynamic looping. This may have important biological consequences in terms of a mechanism for extending the DNA, thereby facilitating DNA transcription into RNA.

In previous studies, we described some general principles driving nuclear organization during interphase (41). We showed that entropic and/or other non-specific interactions dictate, to first order, the structure and dynamics of the yeast genome. We hypothesized that the role of biochemical and other specific interactions is to modulate this organization by guiding, stabilizing and sustaining cycle-dependent genomic states. One objective of the present work is to validate such hypotheses and indeed we have shown how certain specific interactions (modeled as protein-mediated, dynamic crosslinks) drive the rearrangement into different functional phases within the nucleus. While entropic and other non-specific interactions such as macromolecular crowding (50–53) and viscoelastic phase separation (54,55) promote the association of different regions or compartments, specific interactions are ultimately responsible for shaping and maintaining such compartmentalization.

An emerging concept is that phase transitions play a fundamental role in nucleolar organization (56–59) (60). Many studies have highlighted the role played by proteins and/or RNA in nuclear phase separation (50–59,61,62). Most commonly this behavior is described as liquid–liquid phase transition, where the different compartments behave as ‘liquid drops’ within the nucleoplasm (56,59,61). Within this context of liquid–liquid demixing one can distinguish two phases by their viscous behavior (e.g. different viscosities). However, from a soft matter perspective one can define phase separation in a much broader sense to include behaviors and properties beyond those related to viscosity-based demixing, for example stiffness (elasticity-based demixing), viscoelastic demixing, volume occupancy (swelling), etc. For instance, one can view the nuclear environment as a complex, cross-linked network formed by chromosomes, proteins, RNA and other macromolecular components. This cross-linked network exhibits characteristics observed in gel solutions (e.g. sub-diffusive behavior (18,63,64)). In this view, different levels of gel stiffness characterize different ‘phases,’ each one exhibiting different transport and diffusive properties. However, in this view the boundaries between phases are more nuanced than a scalar-based, viscous demixing picture.

In general, the demixing studies indicate that phase separation occurs via non-specific interactions mainly driven by changes in the concentration of proteins and RNA, while chromosomes play a semi-passive role. Here we set to explore whether or not chromosomes play a more active role in phase separation through the formation of chromosomal regions with preferential, protein-mediated crosslinking. By assuming preferential crosslinking kinetics we effectively modify the local gel properties of the network. In this view, one could consider the nucleolus formation and stability to be characterized as a gel–gel phase separation, where one gel phase, the nucleolus, exhibits properties corresponding to a ‘stiffer’ gel compared to the rest of the genome. In addition, the formation of different phases within the nucleus via crosslinks favors the formation of nuclear compartments through protein-mediated self-organization allowing the development of diverse dynamic structures (65), which gives the genome the ability to rearrange into different functional states according to modifications of the crosslinking mechanisms. These mechanisms can arise from the fast exchange of proteins across different regions in the genome, which has been observed in the nucleolus (66), Cajal (67) and PML bodies (68).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Science Foundation–Division of Mathematical Sciences (DMS) [1410047 to P.A.V., in part]; National Institutes of Health [R37 GM32238 to K.B.]; National Science Foundation [DMS-1412844, DMS-1462992 to M.G.F.]; National Institutes of Health [T32CA201159–01 to J.L.]. Funding for open access charge: National Institutes of Health [R37 GM32238 to K.B.].

Conflict of interest statement. None declared.