Pausing kinetics dominates strand-displacement polymerization by reverse transcriptase

Abstract

Reverse transcriptase (RT) catalyzes the conversion of the viral RNA into an integration-competent double-stranded DNA, with a variety of enzymatic activities that include the ability to displace a non-template strand concomitantly with polymerization. Here, using high-resolution optical tweezers to follow the activity of the murine leukemia Virus RT, we show that strand-displacement polymerization is frequently interrupted. Abundant pauses are modulated by the strength of the DNA duplex ∼8 bp ahead, indicating the existence of uncharacterized RT/DNA interactions, and correspond to backtracking of the enzyme, whose recovery is also modulated by the duplex strength. Dissociation and reinitiation events, which induce long periods of inactivity and are likely the rate-limiting step in the synthesis of the genome in vivo, are modulated by the template structure and the viral nucleocapsid protein. Our results emphasize the potential regulatory role of conserved structural motifs, and may provide useful information for the development of potent and specific inhibitors.

INTRODUCTION

Retroviruses are a unique class of RNA viruses, which reverse-transcribe their genome into a double-stranded DNA intermediate that is integrated into the host genome. During reverse transcription, reverse transcriptase (RT) uses the viral RNA (vRNA) as a template to synthesize an integration competent DNA molecule, performing three different catalytic activities: RNA-dependent DNA polymerization, DNA-dependent DNA polymerization and RNase H degradation (1). The most extensively studied RTs, the ones from the human immunodeficiency virus (HIV) and the Moloney murine leukemia virus (MuLV), are different in their oligomeric state: while HIV-1 RT works as a hetero-dimer, MuLV RT functions as a monomer (2,3). Nevertheless, both subunits in HIV-1 RT (p66 and p51) and the single subunit in MuLV RT display the common structural features of other DNA polymerases (DNAPs), with thumb, palm and fingers subdomains (4). p66 and MuLV RT harbor an additional domain responsible for the enzymes’ RNAse H activity. Previous studies addressing the mechanism of polymerization by RT, using both steady state and pre-steady state techniques (5–10) have delineated kinetics that are, in general, common with other DNA polymerases, and include the following steps: nucleic acid binding to form a binary complex, dNTP binding, a rate limiting isomerization step, nucleotide incorporation, pyrophosphate release and translocation (11). However, the rates of polymerization by RTs are fairly slow and their processivity is poor relative to other DNAPs (12). Interestingly, while both HIV-1 RT and MuLV RT lack the 3′ to 5′ proofreading exonuclease activity present in high fidelity replicative DNAPs, MuLV RT has a much higher fidelity than HIV-1 RT (13–15). In addition, MuLV RT has a lower affinity for dNTPs than HIV-1 RT (16–20), a fact suggested to reflect the large difference in [dNTP] between the cell types specifically infected by lentiviruses and oncoretroviruses (21).

As opposed to most DNAPs which require a single strand DNA (ssDNA) template, and have been found to arrest when confronted with duplex DNA, RT belongs to a small group of polymerases that are capable of efficiently unwinding duplexes in the template during polymerization. This strand displacement (SD) synthesis activity by RT is required for the polymerization on the highly structured vRNA (22) and the removal of RNA fragments which cannot be cleaved by the enzymes RNase H activity (23). In addition, SD synthesis on a DNA duplex is particularly important to complete the plus- and minus-strands by polymerizing on the long terminal repeats (24). Importantly, some of the structural motifs present in the vRNA, such as the trans-activating responsive element, were found to be highly conserved among retroviruses, which may suggest that they serve a functional role (22,25–28). Indeed, previous studies have shown that secondary structure motifs are involved in a number of retroviral processes, such as serving as recombination ‘hotspots’ in the gag, pol and env coding domains of the HIV-1 genome (29).

Although the rates of both displacement and non-displacement DNA synthesis vary for different sites over the template, SD synthesis is, on the average, slower by a factor of 3–4 (30), as compared to primer extension (PE) synthesis. Moreover, in vitro studies demonstrated that the polymerization products of RT show reproducible patterns of early termination events (23,31–33) which, despite a lack of complete understanding on their origin, where generally termed ‘pauses’. Pauses were detected for different RTs, on both RNA and DNA templates, and were found to be enriched at regions of predicted secondary structure and on homopolymeric nucleotide runs (34). Pausing within duplex regions were shown to diminish when the contiguity of base pairing was disrupted by the introduction of single unpaired nucleotides or mismatches (35,36). Interestingly, Klarmann et al. (34) showed that the observed pausing includes at least two sources: (i) RT remaining bound to the primer-template and polymerizing at a greatly reduced rate, and (ii) RT dissociating from the primer-template. However, the nature of the bound but slowly polymerizing species remained unclear. In addition, some controversy exists on the effect that the duplex base pairing energy has on determining the pausing sites. While some reports have found a correlation between pausing position and base pairing energy (32) others have reported a lack of correlation (23,30).

Importantly, the above studies suffer from the inherent limitations of bulk experiments, where averaging over an unsynchronized population can obscure the fine scale molecular dynamics. Moreover, they were constrained in general to short nucleic acid molecules as templates. To overcome these limitations, Kim et al. monitored polymerization by HIV-1 RT on a long DNA template using a single-molecule flow-stretch-based assay, and found that the overall velocity of the enzyme during SD polymerization is greatly diminished (∼9-fold) as compared with the PE velocity (37). Moreover, they found that the mean rate of SD synthesis is dependent on the local GC content in the duplex. Unfortunately, although their work stresses the important of secondary structures in the regulating SD synthesis, their assay did not have the resolution to characterize the dynamics of RT during SD polymerization. In particular, since pauses could not be resolved, it was not possible to separate the effects that GC content and applied force may have on the instantaneous polymerization rate and their effect of the kinetics of pausing.

Single molecule fluorescence studies have shown that HIV-1 RT is able to ‘slide’ on its nucleic acid substrate, rapidly shuttling between the opposite termini of a duplex (38). It was also shown that RT is able to spontaneously ‘flip’ between a polymerization-competent orientation and an orientation that favors Rnase H activity (38,39). The observed sliding and flipping dynamics play a role in the initiation of reverse transcription (40). Moreover, it was shown that sliding of the enzyme is stimulated by binding of non-nucleoside RT inhibitors, and reduced for a resistant-conferring mutant (41), suggesting that modulation of RT’s dynamics can be a part of potential inhibition strategies. These studies, and others (42), describe a highly dynamic picture of the interactions between RT and its substrate, which is particularly interesting in the case of SD polymerization. Footprinting (43,44) and structural studies (1,45) have shown that RT accommodates ∼6 nt of single-stranded RNA or DNA in an active complex, meaning that the unwinding fork is separated from the catalytic site by this distance. Hence, sliding of the enzyme away from the primer strand 3′ terminus can result in reannealing of these nucleotides, a fact that may prevent the enzyme from returning back into alignment. Despite the important insights provided by these single molecule fluorescence studies (38–41), the FRET experiments are limited to probing a short range of interaction, and therefore the role of the dynamics in the processive polymerization of long templates is still not completely understood. Moreover, the relationship between the pauses observed during polymerization in biochemical assays and the sliding dynamics reported by the single molecule experiments has not been established yet.

In vitro, RT is able to perform SD polymerization without accessory proteins (31,46–48), unlike most (but not all (49–51)) DNA polymerases, which require additional factors such as helicases or single strand binding proteins. However, the viral nucleocapsid (NC) protein, with roles in several steps during viral replication (52), has been also shown to serve as an assisting factor in SD synthesis (23,24). NC is a small, highly basic nucleic acid binding protein with one or two zinc fingers, which functions as a nucleic acid chaperone, catalyzing nucleic acids conformational rearrangements so that the most thermodynamically-stable conformations are formed (52–57). This is achieved by the interplay between two seemingly opposing activities: duplex destabilization, mediated by the zinc fingers (58) and strand annealing, driven by the electrostatic attraction that results from NC’s charge density. However, the molecular mechanism by which NC specifically affects SD polymerization by RT, is still unclear.

Here, we use high resolution optical tweezers to elucidate the role of pausing by MuLV RT. By following the polymerization on a DNA template under tension, both in SD and PE modes, we were able to directly observe the individual and abundant pausing events in the polymerization reaction, and to characterize the mechanisms governing them. Our results show that SD polymerization is dominated by its pausing and reinitiation kinetics, which can be controlled by the nature of the structural motifs ahead and by the presence of NC, making them convenient and versatile regulatory targets.

MATERIALS AND METHODS

Molecular constructs for single molecule experiments

DNA sequences used as polymerization templates were amplified by polymerase chain reaction (PCR) from a plasmid that was a generous gift from Daniela Rhodes (MRC, Cambridge, UK), for Sequence 1, and from mouse genomic DNA for Sequence 2 (Supplementary Table S1). Primers used for the amplification reactions are listed in Supplementary Table S2. The constructs were digested using DraIII-HF (New England Biolabs) overnight according to the manufacturer’s instructions. A 10-bp hairpin (Sigma) was ligated to the construct using T4 DNA ligase (New England Biolabs), in a reaction with 1:10 molar excess of the hairpin, at 16°C. The construct was subsequently digested overnight with BglI (New England Biolabs). Two 600-bp DNA handles, each incorporating a specific tag (digoxigenin and biotin, respectively), were generated using commercially purchased 5′-modified primers (Supplementary Table S3) in a standard PCR reaction. Two of the primers were designed to contain repeats of the three DNA sequences recognized by single strand nicking enzymes: Nt.BbvCI and Nb.BbvCI (both from New England Biolabs) on the biotin-tagged handle and on the digoxigenin-tagged handle, respectively. The nicking enzymes generated 29 nt complementary overhangs on each handle. Handles were mixed at equal molar ratios for DNA annealing, creating an ∼1200 bp fragment of annealed DNA handles. The polymerization templates were ligated to the DNA handles using a rapid ligase system (Promega) in 3:1 molar ratio, 30 min at room temperature.

Reagents

MuLV RT and dNTPs were purchased from New England Biolabs and Sigma, respectively. HIV-1 NC was cloned into pET28b, between NdeI and XhoI, to give an N terminal His-tagged construct. This expression plasmid was transformed into BL21 cells which were grown in Luria-Bertani medium until OD₆₀₀ = 0.7, at which time expression was induced with 0.5 mM Isopropyl β-D-1-thiogalactopyranoside (IPTG) and the cells were supplemented with 50 µM Zinc acetate. Cells were grown overnight (20 h) at 16°C, collected by centrifugation and stored at −20°C until further use. Frozen cells were resuspended in purification buffer (500 mM NaCl, 50 mM Tris 8.3, 5 mM imidazole and 5 mM beta-mercaptoethanol). Cells were disrupted, centrifuged at 14 000 rpm and His-tagged protein was captured from the supernatant using a Nickel bead affinity purification column. Bound protein was washed in purification buffer supplemented with 30 mM imidazole and eluted in purification buffer supplemented with 300 mM imidazole. The sample was washed in a 3 kDa centricon in dialysis buffer (200 mM NaCl and 20 mM Tris 8.3) before further purification on a S200 size exclusion column equilibrated and run in dialysis buffer. Elutions containing NC were stored at −80°C.

Optical tweezers

Experiments were performed in a custom-made high-resolution dual-trap optical tweezers apparatus (59), as previously described (60). The only modification from the original design is the use of an advanced Master Oscillator Power Amplifier (MOPA) laser (TA-PRO, Toptica), supplying 3W at 852 nm, which provides better stability and results in lower heating of the sample as compared with previously used lasers. The setup was built at a basement-level room with vibrations below vibration criteria ‘E’. To further isolate the system from building vibrations, a separate concrete slab was poured on the bedrock as the basis for the instrument. On top of this isolated slab, we placed a 24’ thick optical table (Newport, RS-400) seating on 4 pneumatic isolators (Newport, S2000). To minimize vibrations at frequencies of ∼1–3 Hz, at which the pneumatic isolators do not isolate the vibrations from the floor, we chose a short (1.2 × 1.8 m) and thick (60 cm) tabletop, which has mechanical resonances at relatively high values (few kHz), outside the low-frequency region where the isolators do not perform optimally. The room was built with acoustically isolating walls and door, and the walls covered with noise-absorbing foam. In addition, the instrument was designed with all noise-generating equipment (e.g. fan-cooled electronics) placed outside the room, and is remotely operated from an external operating computer that controls activation of the traps, the position of the chamber and the laminar flow buffers. The acoustical noise level is below 33 dBA at full operating conditions. An independent, PID controlled, air-conditioning unit was installed for the setup room, and located outside the lab to minimize acoustical noise. Both the input and return air travel through silencing ducts into/from the lab. With careful tuning of the control parameters, we obtain a stability of 0.1°C, while maintaining at the same time the low level of acoustical noise mentioned above. The beam from the 852 nm is coupled into a polarization-maintaining single-mode optical fiber. The collimated beam propagating out of the fiber, with a waist of w₀ = 4 mm, is split by a polarizing beam splitter (PBS) into two orthogonal polarizations, each directed into a mirror and combined again with a second PBS. One of the mirrors is mounted on a piezoelectric nano-position stage (Nano-MTA, Mad City Labs). A X2 telescope expands the beam, and also images the plane of the mirrors into the back focal plane of the focusing microscope objective (Nikon, Plan Apo VC 60X, NA/1.2). Two optical traps are formed at the objective’s focal plane, each by a different polarization, and with a typical stiffness of 0.3–0.5 pN/nm. The nano-positioning stage allows steering the position of one of the traps. The light is collected by a second, identical objective, the two polarizations separated by an additional PBS and imaged onto two position sensitive detectors (First Sensor). The position of the beads relative to the center of the trap is determined by back focal plane interferometry (61). Calibration of the setup was done by analysis of the thermal fluctuations of the trapped beads (62), which were sampled at 100 kHz. The stability of the instrument was characterized by repetitive unzipping of a DNA hairpin over a 10 min period (Supplementary Figure S8).

Single molecule polymerization experiments

The full polymerization construct was incubated for 15 min on ice with 0.9 μm polystyrene beads (Spherotech), coated with streptavidin (SA) and diluted 1000-fold in RT buffer (RTB; 50 mM Tris–HCl, 75 mM KCl, 3 mM MgCl2, 10 mM DTT, pH 8.3 at 25°C). The SA beads bound to the DNA constructs, together with 0.9 μm anti-digoxigenin (D) coated beads were introduced into the microfluidic channel filled with RTB. Tether formation was performed in situ (inside the experimental chamber) by trapping an SA coated bead in one trap, trapping an 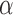D bead in the second trap and bringing the two beads into close proximity to allow binding of the digoxigenin tag in the DNA to the 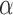D in the bead. After a few seconds, the beads were moved away from each other while monitoring changes in the force. Establishment of a tether is indicated by an increase in force as the traps are separated. In some of the experiments, the polymerization reaction was initiated by flowing activity buffer (RTB with the addition of 1–250 uM dNTP and 200U/ml RT) into the chamber. In other experiments, a laminar flow chamber (u-Flux, Lumicks) was used, with one channel containing RTB and a different one activity buffer. Polymerization was initiated by moving the beads into the activity buffer channel.

Experiments were conducted in a semi-passive mode, in which polymerization takes place with no feedback on the force but where, if the force exceeds a predetermined value, the position of the steerable trap is rapidly changed in a single step and in a direction and magnitude that are expected to restore the measured force to the range of forces that were pre-established (typically, ±1.5 pN of the nominal force). As a result, our polymerization data consist of intervals of passive-mode operation, that are separated by sudden ‘jumps’ in the position of the steerable trap. Segments in the data during which the mirror moves were identified and subtracted from further analysis.

Data analysis

Conversion of the data into physical units

Data were digitized at a sampling rate fs = 2500 Hz, and saved to a disk. All further processing of the data was done with Matlab (Mathworks). Using the calibration parameters previously obtained, the total extension of the tether, 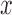, and the force acting on it, 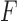, were calculated. From the extension versus time traces, e.g. the one in Figure 1B, we identified the sections in the data containing SD and PE polymerization. Then, the number of base pairs polymerized during SD and PE activity ( 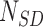and 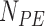, respectively), were calculated as:

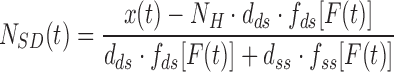and

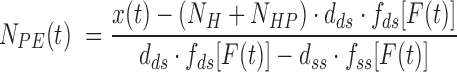where 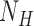= 1200 is the number of base pairs in the dsDNA handles, 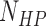is the number of base pairs in the hairpin, 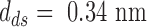the rise per base pair for dsDNA and 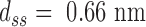the rise per base for ssDNA (63). 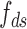and 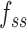are functions describing the extension-over-contour ratio for dsDNA and ssDNA, respectively, as a function of the applied force. For the dsDNA parts, we used an extensible worm-like-chain (eWLC) model, and for the ssDNA parts, a WLC model (64). The persistence length was experimentally determined, for each molecule probed, by fitting force-extension curves.

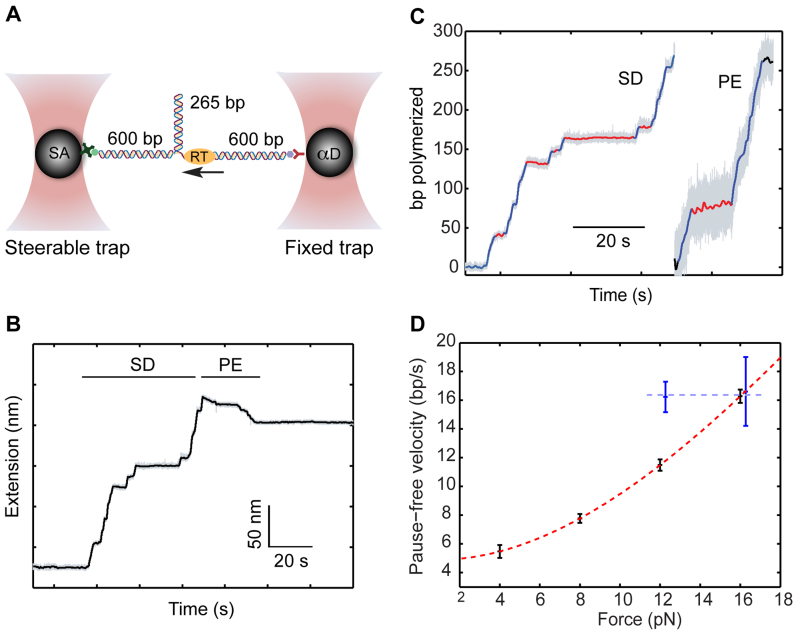
Figure 1.

Following SD and PE polymerization on a substrate under tension. (A) Experimental geometry. A 265-bp DNA hairpin is connected to two 600-bp dsDNA handles, and held under tension in a dual-trap optical tweezers. The 3′-OH terminus of one of the dsDNA handles serves as a primer for elongation. (B) Time-trace of the tether extension as a result of RT DNA polymerization. The extension increases during SD polymerization, and decreases during PE synthesis. (C) The extension changes are converted into the number of base pairs polymerized. A pause-finding algorithm identifies activity bursts (blue) and inactivity events (red). (D) The pause-free velocity of RT is force-dependent during SD activity (red), but independent for PE polymerization (blue). The dashed lines are drawn to guide the eye.

Detection of pauses

The original, 2500 Hz data were low-pass filtered with a third order Butterworth filter with a cutoff f_c = 0.5 Hz, and the residency time in 1-bp windows, 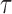, was calculated. Data point corresponding to 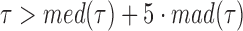, where 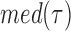and 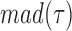are the median and the median absolute deviation of 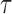, respectively, were considered as belonging to pauses. Finally, pauses shorter than 1 s and polymerization bursts shorter than 2 bp, were eliminated. The performance of the pause-detection scheme was tested using simulated traces (Supplementary Figure S9), revealing ≤2% of false-negatives and ≤4% of false-positives across all the conditions tested.

Calculation of pause density and cumulative pause density

The pause density for a specific dataset (i.e. a specific force and [dNTP]) was calculated by counting the total number of pauses in the dataset that had a duration in a determined duration interval, and then dividing by the total number of base pairs polymerized in the dataset. Cumulative pause densities (e.g. Figures 2B, 3A and B) were obtained by performing a cumulative sum of the pause density.

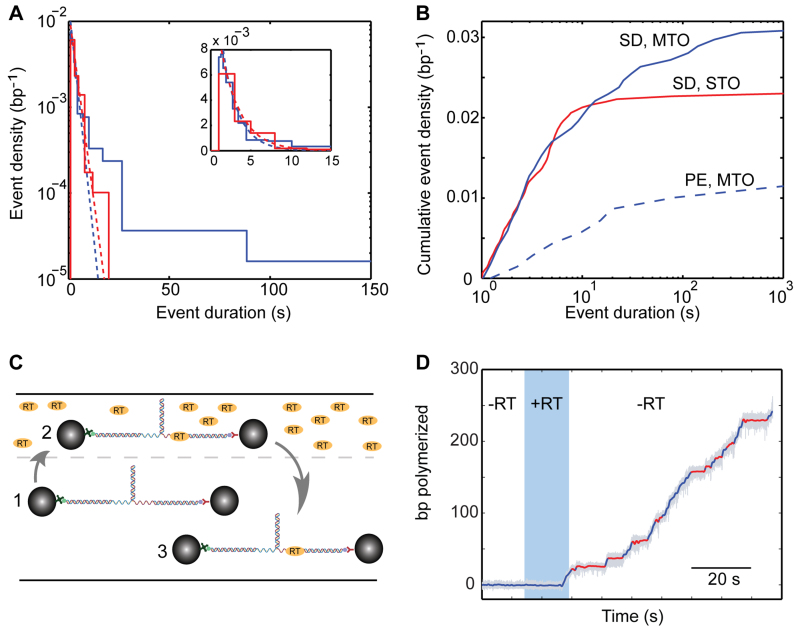
Figure 2.

Two types of inactivity events in the polymerization traces. (A and B) The distribution of event lengths exhibits a long tail, and cannot be described by a single exponential. (A) Distribution of event densities, for SD polymerization in the MTO configuration (blue; F = 12 pN, [dNTP] = 250 μM, N_traces = 29, N_pauses = 267) and STO configuration (red; F = 12 pN, [dNTP] = 250 μM, Ntraces = 45, Npauses = 201). The dashed lines are exponential fits to the short duration region (blue and red for MTO and STO, respectively). Inset: zoom-in into the short durations region, in a linear scale. (B) Cumulative density for SD polymerization in the MTO configuration (blue; F = 12 pN, [dNTP] = 250 μM, N_traces = 29, N_pauses = 267) and STO configuration (red; F = 12 pN, [dNTP] = 250 μM, N_traces = 45, N_pauses = 201), and PE polymerization in MTO (dashed blue; F = 12 pN, [dNTP] = 250 μM, N_traces = 8, N_pauses = 24). (C) A single-molecule single-turnover experiment is implemented by using a laminar flow cell. The substrate is momentarily exposed to activity buffer, containing RT (25 nM) and dNTP to allow the formation of an initiation complex, and then moved to an RT-free region. (D) Typical polymerization trace in a single-turnover experiment. Polymerization starts in the region containing RT (blue shade) and continues in the RT-free region.

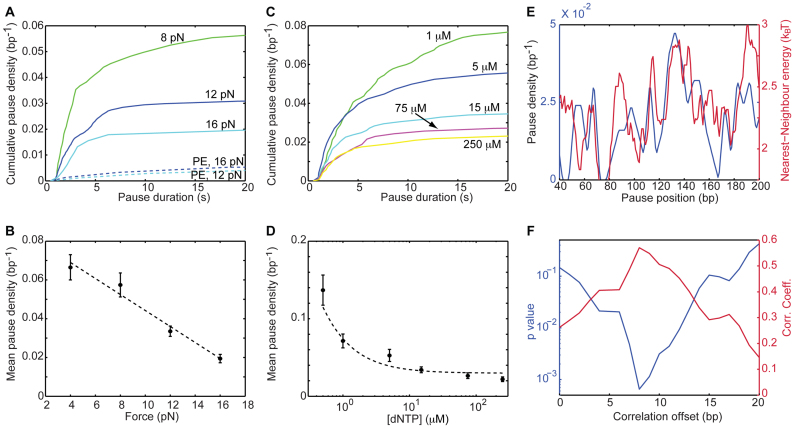
Figure 3.

RT senses the sequence ahead, and enters into the paused-state in a competition with elongation. (A and B) Dependence of the pause density on the applied force. The density of pauses during SD (but not PE) activity is sensitive to the force on the construct. (A) Cumulative pause densities. SD: N_traces = 12,16,13. PE: N_traces = 8,10. (B) The mean density of pauses, showing a linear dependence on the force (r = −0.98, P = 0.01, Pearson's correlation coefficient and P-value, respectively). Data shown as mean ± SEM. The dashed line shows the result of fitting the data to a linear equation (adjusted-r² = 0.96) (C and D) Dependence of the short pause-density on [dNTP]. (C) Cumulative pause densities. N_traces = 13,5,12,9,16. (D) The mean pause density, which stabilizes at saturating [dNTP] (r = −1, P = 0.003, Spearmans's correlation coefficient and P-value, respectively). Data shown as mean ± SEM. The dashed line was drawn to guide the eye. (E and F) The position-resolved pause density correlates with the local strength of the duplex, shifted by 8 bp. (E) Pause density, calculated on 5-bp windows (blue), and strength of the base pair being polymerized, as calculated from the nearest neighbor model and averaged over a 10-bp running window (green). (F) Pearson's correlation coefficient (green) and P-value (blue) for the correlation between pause density and energy, as a function of the offset between them.

Correlations between density and base pairing energy

In order to calculate the correlation between the positions of the pauses along the template, and the local base pairing energy, the following procedure was followed: first, a histogram of the positions of the pauses was calculated, with a bin size B (i.e. we counted the number of pauses detected in the intervals [0, B], [B, 2B], …and [S- B, S], where S is the templates length, and divided by the bin size to obtain the pause density). Next, we calculated the base pairing energy at each position along the template, using the published nearest neighbor parameters (63,65) corresponding to our buffer conditions, and then ‘smoothed’ these energies with a window W, and introduced a shift D, by calculating its mean over the intervals [0+D,W+D], [W +D, 2 W +D]…[S- W+D,S]. Finally, we calculated the correlation between the pause density and the (shifted) base pairing energy, and the P-value of this correlation, using Matlab's ‘corrcoef’ function. The sensitivity of these calculations was checked by repeating them for different choices of B and W (Supplementary Figure S10).

Backtrack detection

In order to quantify the backtracking depth, the original, 2500 Hz extension data were smoothed with a Savitzky–Golay filter and a window size of 501 points. The backtracking depth was defined as the difference between the value of the filtered signal at the time of entering a pause and the minimal value of the filtered signal during the pause, divided by the extension of 2 nt at the specific force. As a control, the same procedure was applied to the signal segments prior to the exposure of the substrate to the activity buffer. Setting a threshold of 3-bp backtrack-depth to be classified as a pause, the fraction of pauses where backtrack is detected is 38% in the data obtained at 16 pN, as compared to only 6% in the control (P < 10⁻⁷).

RESULTS

Direct observation of processive polymerization by MuLV reverse transcriptase

The molecular construct used to study polymerization by RT consists of a 265-bp DNA hairpin that is attached to two ∼600-bp dsDNA handles, each harboring a tag (biotin and digoxigenin, respectively), that allow to tether the complete construct between two microspheres trapped in two separate optical traps (Figure 1A). Stretching this DNA construct results in a unique force versus extension curve (FEC, Supplementary Figure S1). At forces smaller than ∼17 pN the hairpin is folded and the FEC follows the Worm-Like-Chain (WLC) model of polymer elastic behavior characteristic of dsDNA. Once the force increases above ∼17 pN, destabilization of the base pairs in the hairpin results in a series of sudden events involving an increase in extension and a decrease in force. Each of these jumps corresponds to the cooperative opening of a few base pairs. Eventually, the entire hairpin duplex is open and a segment of unstructured ssDNA is held between the handles. Further stretching at this stage exhibits the elastic behavior of a combination of dsDNA and ssDNA. This FEC is reversible and reproducible.

Once the quality of the tether is confirmed by the FEC, we set the force at a predetermined value at which the hairpin is still closed (12 pN, unless otherwise specified) and maintain it at the vicinity of this value using a semi-passive approach (‘Materials and Methods’ section). Next, we introduce a mixture of RT and dNTPs into the experiment chamber ([dNTP] = 250 µM, unless otherwise specified). RT binds to the DNA construct by using the 3′-OH terminus of the dsDNA handle as a primer and engages in SD polymerization of the hairpin. Each catalytic step, i.e. the elongation of the primer by 1 bp, results in an increase of the tether extension, by an amount equal to the addition of both a single base pair and a single nucleotide (Figure 1B). After the first half of the hairpin has been polymerized, the hairpin is completely open and RT continues its activity on the remaining ssDNA, acting in PE polymerization mode. During this stage, each catalytic cycle results in the conversion of a nucleotide into a base pair, hence the extension change per cycle is the result of their extension difference. Since at forces above ∼5 pN the extension of 1 bp of dsDNA is shorter than the extension of 1 nt of ssDNA, polymerization results in a contraction of the tether (Figure 1B). A number of observations support this interpretation of the observed extension changes: first, no change in extension is observed when either RT or dNTPs are omitted. Second, the measured extension changes are in agreement with the size of our construct. Finally, the force-extension curve measured after the putative polymerization shows no hairpin signature and is also well-fitted by a WLC model with a contour length equal to the size of the handles plus twice the size of the hairpin (Supplementary Figure S1). In order to study the kinetics of polymerization, we then convert the measured extension changes into the number of polymerized nucleotides (Figure 1C), using measured parameters for the polymer models of dsDNA and ssDNA (‘Materials and Methods’ section).

Distinct inactive states punctuate the polymerization traces

Figure 1C shows that, for SD- as well as for PE-polymerization, bursts of activity are interspersed with numerous inactive phases, a phenotype that was observed in all of our traces. Since there is a clear separation between them and the activity bursts (Supplementary Figure S2), we used a dwell-time threshold (‘Materials and Methods’ section) to identify these phases and extract them. As shown in Figure 1D, the pause-free velocity during SD activity strongly depends on the applied force. This phenotype, similar to previous reports for other DNA polymerases (37,50,51), suggests that DNA unwinding by RT is, at least partially, a passive process exploiting the spontaneous thermal fluctuations of the hairpin, which are facilitated by the applied force. In contrast, although the range of forces for which it can be reliably characterized is limited, we did not observe a similar force dependence for the velocity of PE-polymerization. RT has been reported to have a relatively low processivity (31) (∼60–70 bp for MuLV RT (12)), so we suspected that one source for the inactive states may involve dissociation and subsequent binding of a new enzyme. Alternatively, the enzyme can still be bound, making these states the result of an off-pathway event in the enzyme's catalytic cycle. Moreover, Figure 2A and B show that a pause duration histogram cannot be fit with a single exponential. This may indicate that recovering from the inactive state is a complex kinetic event, involving more than one energy-barrier crossing. It is also possible that the non-exponentiallity results from the coexistence of more than one inactive state, where perhaps one of them represents the enzyme re-binding times after dissociation. In order to elucidate this point, we exploited a laminar flow cell to expose the construct to the solution containing RT and dNTPs and, once polymerization starts, move it into a channel where dNTP is present but RT is not (Figure 2C). In this single-turnover (STO) assay, polymerization displayed a modified behavior (Figure 2D), with the long-duration tail (>20 s) of the distribution of inactive states largely reduced (Figure 2A and B; red line), as compared with the previous, multiple-turnover (MTO) scheme (blue line). In addition, there was a drastic reduction in the fraction of experiments were polymerization of the complete hairpin was observed, from 62% (122 out of 195) to 17% (12 out of 70). Taken together, this suggests that most of the long (>20 s) inactive intervals represent events of dissociation and rebinding, while a small fraction of these long events, and all the short (<20 s) ones, take place while the enzyme is still bound to its template. Notably, the mean duration of long events (118 ± 24 s, mean ± SEM) is similar to the mean time for polymerization initiation as the construct is first exposed to the activity buffer (99 ± 22 s), lending further support for our interpretation. Hence, in what follows we refer to the short events as bona fide pauses in RT’s activity and to the long ones as reinitiation events, and analyze each of these separately.

Entry into the paused-state is modulated by the stability of the fork ahead

Pausing is significantly less frequent during PE polymerization (Figure 2B), indicating that the presence of the hairpin stimulates entry into the paused state. In addition, the density of pauses during SD- (but not PE-) polymerization decreases as the applied force is increased (Figure 3A and B) in agreement with the stability of the duplex ahead affecting the pause entry, and suggesting that the probability of entering the pause increases as translocation becomes more difficult. Interestingly, pause density decreases also as the concentration of dNTP is increased (Figure 3C and D), and stabilizes to a value of ∼0.02 bp⁻¹ as the dNTP concentration becomes saturating. This is consistent with previous studies which showed that binding of a cognate nucleotide, which induces the fingers and thumb domains to close around the primer terminus, significantly stabilizes the enzyme (38).

These results indicate that entry into the pause is an event in kinetic competition with productive elongation. In such case, one would expect that the local, sequence resolved pause density will be correlated with the local strength of the duplex. Indeed, Figure 3E shows that the local pause density and the strength of the base pair being polymerized, as calculated from a nearest-neighbor model (63,65), are correlated. However, this correlation is maximized (r = 0.57, P = 6·10⁻⁴; Pearson correlation coefficient, P-value), when the energy is calculated with an offset of ∼8 bp (Figure 3F). Interestingly, although we observed a correlation for the pause density with the base pairing energy, no enrichment of specific nucleotides in the set of pausing positions could be found (Supplementary Figure S3), suggesting that the correlation truly reflects an energy effect, and is not the result of interactions with specific sequence motifs. Remarkably, control experiments with a different sequence (Sequence 2, Supplementary Table S1), also resulted in a significant correlation (r = 0.4, P = 0.04), for a similar offset of 8–10 bp (Supplementary Figure S4a and b), and the same was observed also for other forces (Supplementary Figure S4c and d). No significant correlation exists between the pause density measured for the first sequence and the nearest-neighbor energies of the second, or vice versa (Supplementary Figure S4e and f), and no significant correlation was measured for the pauses during PE activity (Supplementary Figure S4g and h).

Note, that since we monitor in our experiments the extension of the tether, and not directly the position of RT, the existence of such an offset is very surprising. In a simple model (Supplementary Figure S5a), our reaction coordinate can be traced to the position of the fork, and no offset is expected. How can we rationalize our results, which seemingly indicate that RT can ‘sense’ the sequence ahead? One possibility, is that ‘unwinding’ of the dsDNA and ‘release’ of the unwound ssDNA strands are spatially separated (Supplementary Figure S5b). That is, when a base pair is unwound by RT, the resulting strands are not immediately ‘released’, thus increasing the extension of the tether, but remain bound to RT as two strands of ssDNA, for eight additional cycles of incorporation and translocation by RT. In this case, the reaction coordinate measures the position of the last released nucleotide, and there is an offset with the position of the unwinding fork. A similar model was proposed for the unwinding of RNA by the HVC NS3 helicase, where it was shown that unwinding and release are not only spatially uncoupled but are also asynchronous (66,67). However, this model has also implications for the elongation of RT under force, as characterized by the pause-free velocity: If both strands of DNA are bound by the enzyme, thereby preventing their release, the fork will be actually shielded from the mechanical force and no force effect should be expected for the force on the velocity, in contradiction to the force-dependent pause-free velocity we measured. Hence, we favor a model where there is no uncoupling of unwinding and release, i.e. a base pair unwound is immediately released thus increasing the extension, but where there is an additional interaction between RT and the template strand DNA, ∼8 nt ahead of the unwinding fork, that modulates allosterically the SD polymerization reaction (Supplementary Figure S5c).

RT backtracks during the pauses, and its recovery requires opening of the fork

Figure 4A indicates that the time to recover from the paused state, measured as the mean pause length, depends on the force applied on the hairpin. Moreover, fitting the pause length data to an exponential dependence of the form 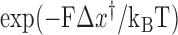, where 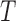is the temperature, 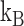is the the Boltzmann's constant and Δx^† is the distant to the transition state, results in Δx^† = 0.17 nm. This distance, which is a fraction of the extension change as 1 base pair opens under force, suggests that the rate limiting step in recovery from the pause involves opening of a single base pair and that, although still bound to the substrate, RT is displaced from the fork during the pause, allowing some degree of reannealing of the DNA that then impedes recovery from the pause, back to processive elongation.

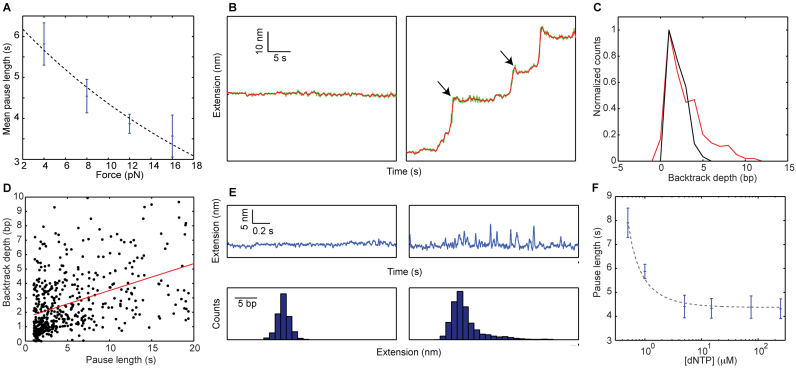
Figure 4.

Recovery from the paused state indicates backtracking of RT. (A) Increasing the force shortens the pause recovery times. Mean recovery time versus force, for [dNTP] = 250 μM (blue). N_traces = 13,12,16,13. Error bars indicate SEM. (r = −0.96, P = 0.04, Pearson's correlation coefficient and P-value, respectively). The dashed line shows the result of fitting the data to an exponential equation. (B) Backtracking events (arrows) as RT enters into pauses are observed for data collected at 16 pN (right panel), but not in the control segments before the exposure to the activity buffer (left panel). The raw data, sampled at 2.5 kHz, was lowpass filtered to 10 Hz (green) and 2.5 Hz (red). (C) Histogram of backtracking depth for all pauses collected at 16 pN (red, N = 524), and all the control segments at the same force (black, N = 75). (D) Backtracking depth and pause duration are correlated. (r = 0.43, P = 7 × 10⁻²³, N = 524) (E) Transient excursions involving extension changes of a few nm are observed during a pause (right panels), but not in the control (left panels). The data was lowpass filtered to 10 Hz. The lower panels show histograms of the instantaneous tether extension. (F) Mean recovery time versus [dNTP], for F = 12 pN (blue). N_traces = 5,13,5,12,9,16. Error bars indicate SEM. (r = −0.94, P = 0.02, Spearmans's correlation coefficient and P-value, respectively). Dashed-black lines are drawn to guide the eye.

Previous studies have described two different conformational changes of HIV-1 RT on its substrate. The enzyme was shown to ‘flip’, changing its binding orientation (38,39), and to ‘slide’, moving along the substrate away from the primer end (38). While it is possible that these two types of dynamics are affected by the presence of the hairpin, the former, which involves positioning of the enzyme to support Rnase-H activity, is rare in DNA/DNA primer/templates (39). Hence, we hypothesized that the observed pausing events involve ‘backtracking’ of RT from the polymerization site, in a manner analogous to previous observations for RNAPs (68–72), but not reported for DNAPs. If that is the case, one would expect to directly observe a reduction in the extension of the tether as RT enters into a pause. It is important to note that, in contrast to previous single-molecule experiments with RNAP where the enzyme was attached to one of the beads, in our experiments backtracking will change the tether extension only as long as it is accompanied by a closing of the hairpin. Since, according to footprinting experiments (44), there are ∼6 nt of ssDNA protected by RT (and an additional 2 bp melted ahead of the enzyme (73)), backtracking of the enzyme can result in some or all of these 8 base pairs reannealing to their complementary strand. Up to 8 bp, for each bp of backtracking the tether extension will be reduced by the extension of 2 ssDNA nucleotides (∼ 1 nm at 16 pN), but further backtracking will result in no extension change. So, backtracking (even if very deep) can only result in an extension reduction of no more than ∼8 nm. Notably, at forces ≥8 pN, when the resolution of our data is high enough, we have been able to observe the backtracking by RT during SD polymerization, and Figure 4B shows examples of such backtracking at the beginning of pauses for typical 16 pN traces. Next, we applied an automatic algorithm (‘Materials and Methods’ section) to characterize in an unbiased manner all the backtracking events at the different forces, and compared the results to a control measurement obtained by applying the same algorithm to the portions of the trace that precede the exposure to the activity buffer (Figure 4C). The tail at the positive side of the distribution represents the backtracking events that can be reliably identified. Setting a 3-bp threshold (i.e counting only events >3 bp as backtracks), the fraction of pauses where backtracks were detected is 38% in the data, as compared to only 6% in the control (P < 10⁻⁷; N = 524 and 75 for data and control, respectively.). Close observation of the 16 pN data reveals that >95% of the measured backtracking events are ≤8 nm, as expected.

In addition, the backtracking depth and the pause length are correlated (Figure 4D), as expected for a diffusional recovery process and in agreement with the theory of Ref. (74), lending further support for our interpretation. Similar results were obtained also for 8 and 12 pN (Supplementary Figure S6). Finally, assuming that the pauses represent backtracking events, recovery from them is a complex process, with a distribution of durations not necessarily described by an exponential function as in Figure 2. As shown in Ref. (74), the distribution of recovery times can be approximated by a t^−3/2 decay. Indeed, Supplementary Figure S7 shows that such a curve is consistent with our distribution of pause durations and results in a better fit (with a single fitting parameter) than a single-exponential function (with two fitting parameters).

Remarkably, monitoring the extension of the tether during a pause at high temporal resolution also reveals a rich dynamics of ‘excursions’ into higher extensions (Figure 4E), which likely reflect recovery attempts, i.e. diffusional runs that result in partial unwinding of the reannealed fork. Interestingly, although such dynamics must be present also during RNAP pauses induced by backtracks, to the best of our knowledge no experimental evidence has been reported for their observation.

Finally, the recovery time from the pauses is also modulated by [dNTP] (Figure 4F), and displays saturation at saturating concentrations, in agreement with a stabilizing effect of nucleotide binding (38). Taken together, these results suggest that RT enters into a backtracked state, promoted by the presence and stability of the duplex ahead, and its recovery from this state back to a polymerization-competent conformation is inhibited by the duplex regained contacts, but facilitated by dNTP binding.

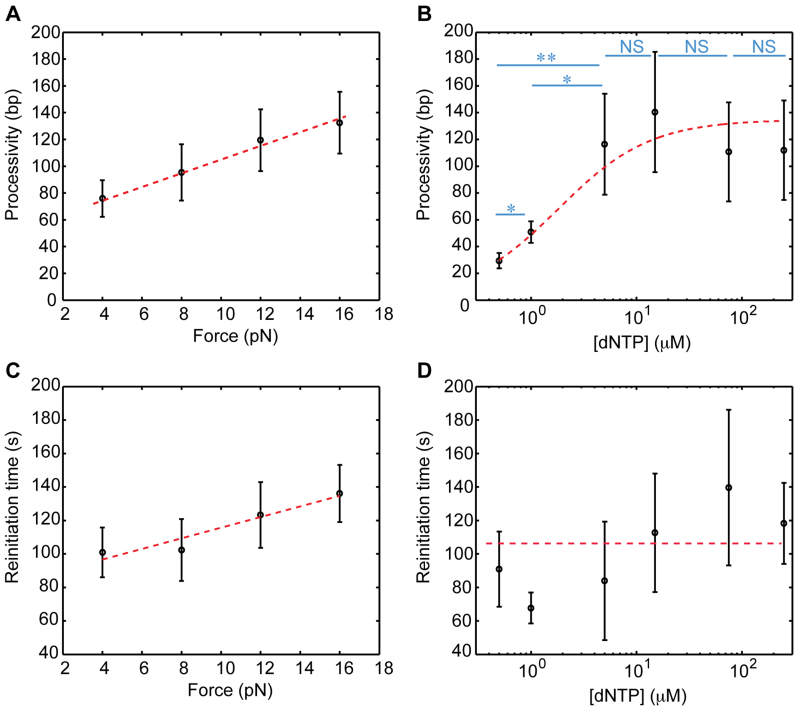
RT’s processivity and reinitiation time are modulated by the duplex ahead

The density of long inactive states, identified above with dissociation of RT followed by reinitiation, allows us to calculate the processivity of RT, and the mean duration of these states represents the reinitiation time. The measured processivity is higher during PE activity (240 ± 75 bp) as compared to SD activity (121 ± 22 bp; mean ± SEM). Moreover, we find that SD processivity increases monotonically with the applied force, and increases with increasing [dNTP], but stabilizes at saturating [dNTP] (Figure 5A and B). This suggests that dissociation, too, is modulated by a kinetic competition with elongation, either as an independent pathway or via the paused state as an intermediate. Interestingly, the reinitiation time is independent of [dNTP] (Figure 5D), but depends on the force applied on the hairpin (Figure 5C). However, in this case force acts as an inhibitor, making the reinitiation times longer as the force is increased. Crystal structures have shown that duplex DNA in complex with RT is strongly bent, by more than 40°, as it passes under the thumb domain (2,45,75). This implies that initiation may be inhibited by force due to the additional mechanical work that is required to form the bent structure on a substrate under tension. Remarkably, extrapolating our data to zero tension (either by a linear function or an exponential one), reveals that the tension-free, mean reinitiation time is ∼70 s. Given that the processivity of RT is much shorter than the long genome it reverse-transcribes (12), reinitiation events are very frequent in vivo, and many of them will take place on a structured template. Such long reinitiation times mean that the time required to complete polymerization of a complete genome is dominated by the reinitiation events, and that reinitiation may be an important target for the regulation of RT by additional cellular or viral factors, such as NC.

Figure 5.

Dissociation and reinitiation. (A) The processivity during SD activity increases with increasing force applied on the template (r = 0.97, P = 0.02, Pearson's correlation coefficient and P-value, respectively. N_traces = 22,30,37,42, based on all data at saturating [dNTP], i.e. 20, 75 and 250 uM). (B) The processivity also increases with increasing [dNTP], up to a saturation value. (*P < 0.05. **P < 0.001. NS = not significant. N_traces = 5,13,5,12,9,16). (C) Reinitiation is inhibited by tension on the substrate (r = 0.95, P = 0.04, Pearson's correlation coefficient and P-value, respectively. N_traces = 22,30,37,42). (D) dNTP binding does not affect the reinitiation time (r = 0.77, P = 0.1, Spearmans's correlation coefficient and P-value, respectively. N_traces = 5,13,5,12,9,16). All data shown as mean ± SEM. The dashed lines are drawn to guide the eye.

Nucleocapsid modulates the reinitiation of reverse transcription

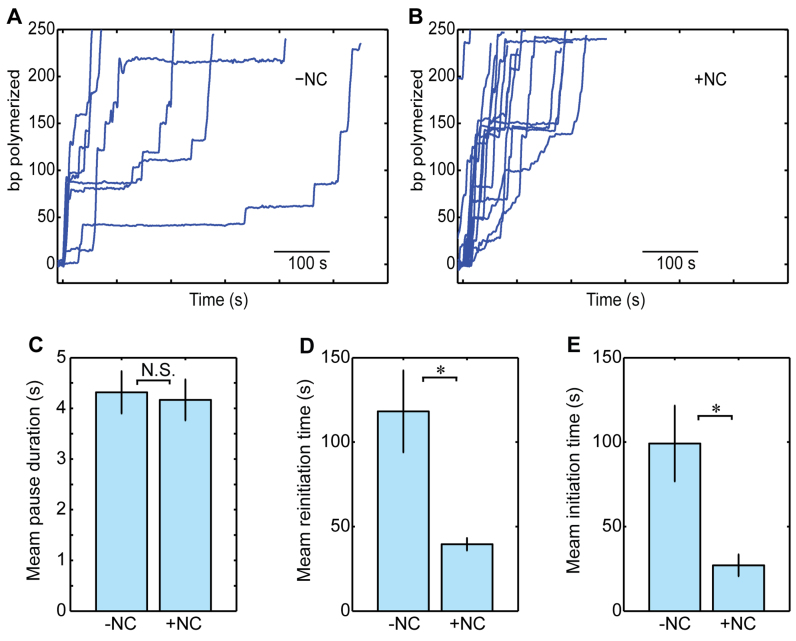
To clarify the role of NC in the kinetics of pausing and reinitiation during SD polymerization, we repeated the experiments when NC was added to the activity buffer (Figure 6A and B). In the presence of NC, only a small increase was observed in the pause-free rate of SD polymerization (12.5 ± 0.9 bp/s with NC versus 10.4 ± 0.8 bp/s without NC; mean ± SEM. P = 0.06, t-test), and no significant effect was detected in the total density of inactive events (0.036 ± 0.003 bp⁻¹ versus 0.031 ± 0.003 bp⁻¹). In addition, the duration of the pauses was not affected by NC (4.2 ± 0.4 s versus 4.3 ± 0.4 s; Figure 6C). In contrast, NC had a strong effect on the reinitiation time (39.6 ± 4 s versus 118.2 ± 24 s; P = 0.03, two-sample t-test; Figure 6D). Interestingly, the initiation time (the time to polymerization upon the first exposure to RT) is modulated by NC in a similar way (27 ± 6 s versus 99 ± 22 s; P = 0.01, two-sample t-test; Figure 6E). These results indicate that NC must interact with RT, its template or both to shorten the initiation and reinitiation times. However, since as described above, NC had no effect on the duration of short pauses, which are sensitive to the stability of the DNA duplex, we favor a scenario where NC interacts directly with RT, consistently with previous reports (76–79).

Figure 6.

Nucleocapsid modulates reinitiation of RT. (A and B) Typical polymerization traces without (A) and with (B) NC, at F = 16 pN and [dNTP] = 250 uM, low-pass filtered to 0.25 Hz. (C) The mean duration of the backtracking pauses is not affected by NC. Shown as mean ± SEM. N_traces = 29, 14. (D) The mean reinitiation time is significantly affected by the presence of NC. (Shown as mean ± SEM. P = 0.03, two-sample t-test. N_traces = 29,14) (E) A similar effect is observed in the mean time for the first initiation event. (Shown as mean ± SEM. P = 0.03, two-sample t-test. N_traces = 42, 21).

DISCUSSION

Here, we use optical tweezers to elucidate the role of pausing by MuLV RT. By following the polymerization of single enzymes on a DNA template, both in SD and PE modes and in a broad range of mechanical and chemical conditions, we were able to resolve the abundant inactive events in the polymerization reaction. Our data indicate that RT spends most of the time required to synthesize a long and structured molecule in inactive states, highlighting the importance of elucidating the mechanisms controlling these states and their kinetics. Two types of such states were identified: the more abundant are shorter and take place without dissociation of RT from its substrate, while longer pauses are the result of dissociation and reinitiation events.

The force and [dNTP] dependence of the pause density reveals that RT enters a paused state in a step that competes with the SD elongation reaction. This competition may arise in a simple way: in a typical elongating complex, RT is bound to a primer/template complex accommodating ∼8 nt of single-stranded nucleic acid template beyond the polymerization site. Hence, during SD polymerization, the duplex ahead is destabilized by ∼8 bp beyond the polymerization site. As a result, there is an energetic competition between two states: the elongating complex, where the ssDNA is bound to RT, and a state where the ssDNA reanneals to its complementary sequence and RT is displaced backward on the substrate, i.e. a paused state which is a backtracked state. A stronger base pairing energy will tilt the equilibrium toward the paused state, whilst force on the hairpin, which adds an additional energetic cost to the formation of the backtracked state, favors the elongation state. A dNTP bound at the active site adds to the interaction energy of the elongating complex, thus reducing the probability of backtracking. Alternatively, as suggested for the replicative DNAPs of T4 and T7, this may be the result of the regression pressure generated by the fork, which could distort the template strand at the polymerase active site (50).

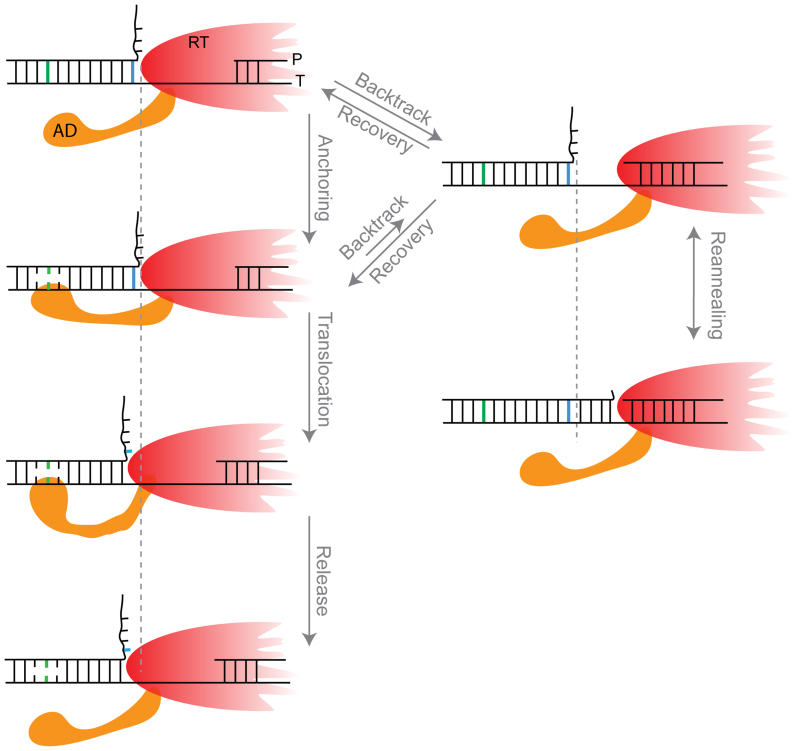
Remarkably, our data indicate that entry into the pause is modulated by the strength of the duplex ∼8 bp ahead. A possible model to explain this result postulates that ‘unwinding’ of the dsDNA and ‘release’ of the unwound ssDNA strands are spatially separated, i.e. when a base pair is unwounded by RT, the resulting strands do not immediately increase the length of the tether, but remain bound to RT as two strands of ssDNA for eight additional cycles of incorporation and translocation by RT (Supplementary Figure S5b). However, this model implies that the interactions of RT with both ssDNA strands will isolate the unwinding fork from the effect of the external force thereby making the pause-free velocity force-independent, in contradiction with our results. Hence, to accommodate all our findings, we propose a model (Figure 7 and Supplementary Figure S5c) where a certain region in RT, which we denote the ‘anchor domain’ (AD) contacts the template strand, about 8 bp ahead of the unwinding fork (i.e. ∼16 bp from the polymerization site). In this model, AD binds only ssDNA, likely by exploiting a thermal fluctuation that opens a bubble in the dsDNA, and this interaction results in an increase in the rate of translocation by the ‘body’ of the enzyme, either by an allosteric effect or via the partial destabilization of the fork as a result of opening a bubble 8 bp ahead. Failure to form the AD interaction impedes or slows down the translocation and, since there is a kinetic competition between elongation and backtracking, induces a backtracking pause. Since a stronger duplex at the point of anchoring inhibits formation of this contact, and therefore promotes backtracking, there will be a correlation between the strength of the anchor point's base pairing energy and the pause density, as observed.

Figure 7.

A possible model for RT backtracking and recovery. The anchor domain (AD) contacts the template, in ssDNA form, ∼8 bp ahead of the fork. This interaction modulates both the rate of elongation and the rate of entering a backtracked state by RT. Upon backtracking, the hairpin reanneals, thus making the recovery time dependent on the fork dynamics.

Notably, the model predicts that the pause density will depend on the base pairing energy at the anchoring point (which indirectly affects the elongation by modulating the energetics of AD binding) and also on the base pairing energy at the fork (which directly affects the elongation rate). Since a correlation is observed for the former, but no significant correlation is observed for the latter, it seems that the modulation via AD binding is stronger. Based on this observation, one may argue that elongation is not significantly affected by the local strength of the fork and therefore no effect for the local sequence is observed. However, the force-dependence of the pause-free velocity indicates that there is a strong effect for the force on the elongation rate. These seemingly contradicting facts can be reconciled if the rate of entering the backtracked state is higher in the absence of the AD contact than it is in its presence (i.e. anchoring prevents backtracking). Then, the effect of the AD is double: the base pairing energy at the AD contact point modulates AD binding, and therefore the elongation rate. In addition, the pause entry rate, with which this elongation rate competes, depends also on whether the AD is bound.

Clearly, such a scenario requires the existence of an additional binding site for DNA or RNA on RT. Although not detected in the crystal structures, prepared with short primer/templates, previous studies have shown that such interactions are possible and demonstrated the formation of a ternary complex of RT, a primer/template and an additional single-stranded molecule (80). The authors of these studies also suggested that a positively charged patch in the surface of HIV RT may be involved in nucleic acid binding, and a similar positively charged region was also found in the surface of MuLV RT (2). Although these additional interactions were suggested in the context of the strand-transfer step (73,81), our results indicate that they may be relevant also for polymerization.

Entry into the pause is accompanied by a conformational change that enables a partial reannealing of the duplex, and our data supports the identification of this conformation change as backtracking events: first, while it is possible that the conformation of this complex is different from the elongation-competent conformation, and that lost contacts between RT and the template contribute to the observed reannealing of the fork, the existence of reannealing events that are as long as 8 bp (similar in size to the ssDNA protected by RT in the canonical state) indicates that the enzyme’s active site must be displaced from the primer’s 3′ end in this configuration. Otherwise, this will imply that there is no separation between the active site and the fork, an unphysical possibility. Next, in previous studies of replicative DNA polymerases, it was proposed that the regression pressure generated by the DNA fork upstream of the polymerase shifts the equilibrium of the complex to an exonuclease conformation (50). A similar scenario in RT’s case will imply that, during the pause, RT is in an alternative but stable configuration, for example the ‘flipped’ conformation observed by Liu et al. (38) for HIV RT. However, the broad distributions of measured backtrack depths and recovery-attempts sizes, and the correlation between depth and recovery time, indicate that during the pauses RT is in an ensemble of states, each allowing reannealing of a different number of base pairs and therefore involving a different degree of displacement. In addition, previous studies have shown similar patterns of DNAse protection conferred by RTs engaged in PE and SD polymerization (82,83). Since our data show that RT spends most of the reaction time during SD polymerization in the paused state, the measured patterns of protection correspond to the paused state too, and indicate that RT is displaced while conserving a relatively similar structure as the elongating complex. Taken together, these results indicate that RT’s displacement takes place along the template, and represent backtracked states. Finally, the recovery time distribution we measured is well described by a t^-3/2 dependence, as expected for the recovery from a backtracking process (74).

Recovery from the backtracked state requires unwinding the duplex, as demonstrated by the force dependence of the recovery time. If the enzyme slides back from the active site, and has no energy input in the absence of hydrolysis, it can only realign with the 3′ OH end of the primer by a diffusional process, a process analogous to the backtracking recovery in RNA polymerases, where the polymerase needs to realign, via thermal diffusion, with the nascent RNA. How will the existence of the hairpin affect this recovery? During SD polymerization, RT is in a complex where the duplex ahead is destabilized by ∼8 bp beyond the polymerization site. If the enzyme backtracks from the DNA fork, these base pairs can reanneal. Then, since it is unlikely that RT can actively unwind the duplex with no energy source, we expect the recovery time to be modulated by the spontaneous opening of the hairpin. Remarkably, our measurements of Δx^† during recovery indicate that the process is dominated by unwinding of a single base pair, suggesting that every single forward step during backtrack recovery is affected by the presence of the fork, in agreement with the prediction (74) that backtracks, even if very long in time, will go back in general only a few base pairs. This model, of a diffusing RT and a thermally fluctuating hairpin, is similar to models proposed for the recovery of backtracked RNA polymerases in the presence of a nucleosome, that must thermally unwrap to allow realignment with the nascent RNA (70,74,84).

Our results show that the existence and nature of a structured template ahead of the polymerization site modulate also the processivity of the enzyme. After dissociation, RT must reinitiate to continue polymerization. We found that the time required to reinitiate is independent of [dNTP], but depends on the tension on the template. Previous studies have suggested that HIV-1 RT reinitiates by binding non-specifically to DNA, and sliding into alignment of its active site with the primer end (38). Hence, there is much in common between backtracking events (sliding without dissociation) and reinitiation events (sliding after dissociation and binding at a non-specific site), and in both cases the presence of the hairpin can be an obstacle for realignment. However, there are a number of important differences: In the case of backtracking, which always starts with an enzyme backtracked by a single base pair from its position in the elongating complex, most of the excursions will be short and RT will remain in the vicinity of the hairpin (74), and therefore most steps in the diffusion will be affected by the hairpin. In contrast, after dissociation RT can bind non-specifically in any location along the dsDNA handle. Enzymes that bind at a very short distance from the hairpin will be affected by its presence but, for most of the binding locations, the time required to realign will be dominated by the diffusion time into the vicinity of the primer end, and will not be affected by the presence of the hairpin. If an average rate is calculated over all the possible binding position along the extended DNA molecule, the contribution of the former outweighs the one from the latter (85), making the rate of reinitiation independent of the opening of the hairpin, i.e. force-independent. (The moderate inhibitory effect we observe for the force on the reinitiation might be a result of the effect of the force on the binding time, since tension can inhibit the formation of a complex where DNA is in a bent conformation). The differences outlined above rationalize also the dNTP dependence: the reinitiation time, dominated by the diffusion time over long regions of DNA, is independent of dNTP. The backtrack recovery, faster and mostly affected by the local effects in the vicinity of the duplex, is also affected by the stabilizing effect of binding a cognate nucleotide once alignment is reached, and therefore [dNTP] dependent.

NC significantly shortens the time required for RT to form a new initiation complex after dissociation. Since NC binds preferentially single-stranded nucleic acids, it is tempting to postulate that the shortening of the initiation time is the result of an effective increase in the hairpin’s opening probability by the binding of NC, i.e. by the effect of NC acting as a nucleic acid chaperon. However, such scenario is unlikely, as it will imply that the rate limiting step in realignment is coping with the duplex, and not the long diffusion time. Hence, our results support a direct interaction between RT and NC, and are consistent with two possible scenarios: first, it is possible that formation of a complex between RT and NC, with its high affinity for nucleic acids, results in an increase in the binding rate to DNA, in line with previous reports on the recruitment of RT by NC (76) and others that showed that NC promotes the efficient synthesis of long products by its aggregation/condensation but not its helix-destabilizing activity (77). Alternatively, it is possible that NC decreases the dissociation of RT from the DNA in the sliding phase, i.e. stabilizes the RT-DNA complex, as was previously described (78,79).

Taken together, our results show that the existence and nature of a structured template ahead of the polymerization site induce entry into a paused state and dissociation, and modulate the recovery from these non-productive states. Given the highly structured genome (22), the kinetics of these pausing and recovery events can have a profound effect on the efficiency and timing of the replication process, and may represent an attractive target for its inhibition.

AVAILABILITY

The data that support these findings are contained within the Article or Supplementary Data files, or available from the authors upon request.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Israel Science Foundation [1750/12 to A.K.]; Israeli Centers of Research Excellence Program [I-CORE, Center no. 1902/12 to A.K.]; European Commission [293923 to A.K.]; Mallat Family Fund. Funding for open access charge: I-CORE (902/12).

Conflict of interest statement. None declared.