Modeling the Multiple Facets of Speciation-with-Gene-Flow toward Inferring the Divergence History of Lake Whitefish Species Pairs (Coregonus clupeaformis)

Abstract

Parallel divergence across replicated species pairs occurring in similar environmental contrasts may arise through distinct evolutionary scenarios. Deciphering whether such parallelism actually reflects repeated parallel divergence driven by divergent selection or a single divergence event with subsequent gene flow needs to be ascertained. Reconstructing historical gene flow is therefore of fundamental interest to understand how demography and selection jointly shaped genomic divergence during speciation. Here, we use an extended modeling framework to explore the multiple facets of speciation-with-gene-flow with demo-genetic divergence models that capture both temporal and genomic variation in effective population size and migration rate. We investigate the divergence history of replicate sympatric species pairs of Lake Whitefish (normal benthic and dwarf limnetic) characterized by variable degrees of ecological divergence and reproductive isolation. Genome-wide SNPs were used to document the extent of genetic differentiation in each species pair, and 26 divergence models were fitted and compared with the unfolded joint allele frequency spectrum of each pair. We found evidence that a recent (circa 3,000–4,000 generations) asymmetrical secondary contact between expanding postglacial populations has accompanied Whitefish diversification. Our results suggest that heterogeneous genomic differentiation has emerged through the combined effects of linked selection generating variable rates of lineage sorting across the genome during geographical isolation, and heterogeneous introgression eroding divergence at different rates across the genome upon secondary contact. This study thus provides a new retrospective insight into the historical demographic and selective processes that shaped a continuum of divergence associated with ecological speciation.

Introduction

Historical changes in the geographical distribution of species have been an important driver of diversification across many taxa (Coyne and Orr 2004). In particular, the pronounced climatic variations that occurred during the late Pleistocene caused major shifts in the distribution ranges of many species. These shifts are responsible for the divergence of ancestral lineages that survived in different glacial refugia, and then possibly came into secondary contact during interglacial periods (Bernatchez and Wilson 1998; Avise 2000; Hewitt 2001). The signature of postglacial recolonization is still apparent in well-known terrestrial and aquatic suture zones, where multiple contacts between expanding postglacial lineages tend to overlap and form hybrid zones hotspots (Hewitt 1996, 2000, 2004; Swenson and Howard 2005; Bierne etal. 2011; April etal. 2013).

In some cases, secondary contacts have resulted in the sympatric enclosure of previously allopatric, partially reproductively isolated lineages, for instance within postglacial lakes (reviewed by Taylor 1999). This sympatric coexistence should have facilitated gene flow compared with parapatric populations, eventually leading to complete genetic homogenization of the original glacial lineages. This is not the case, however, for several north temperate freshwater fishes in which sympatric glacial lineages have further diverged into phenotypically differentiated and reproductively isolated species pairs following secondary contact (Bernatchez and Dodson 1990; McPhail 1992; Taylor and Bentzen 1993; Schluter 1996; Wood and Foote 1996; Taylor 1999). These cases of ecological speciation have been hypothesized to reflect adaptive responses to minimize competitive interactions and outbreeding depression through ecological niche segregation and hybridization avoidance among previously allopatric lineages (Bernatchez etal. 2010).

The evolutionary processes responsible for the phenotypic diversification of these incipient sympatric species remain contentious, especially with regards to the relative contributions of genetic differences that evolved in allopatry compared with more recent genetic changes occurring in sympatry (Bierne etal. 2013; Welch and Jiggins 2014). To gain a more thorough understanding of how divergence unfolds at the molecular level, it is crucial to simultaneously take into account the historical demographic events that accompanied divergence and the subsequent genetic exchanges that occurred in sympatry. Genome-wide polymorphism data now provide the opportunity to infer complex demographic histories (Gutenkunst etal. 2009; Excoffier etal. 2013; Butlin etal. 2014) and investigate the evolutionary processes leading to the formation of nascent sympatric species.

Many aspects of populations’ evolutionary history are influenced by demography, such as the rate of lineage sorting and gene exchange (Sousa and Hey 2013). Several approaches have been developed to infer the history of population divergence from genetic data obtained from contemporary populations. These methods usually rely on demographic models capturing the effects of population size, splitting time, and migration between two populations exchanging genes (Hey and Nielsen 2004, 2007; Becquet and Przeworski 2007). An important facet of the speciation process which is usually not taken into account by demographic models is that a significant proportion of the genome may be affected by selection (Barton and Bengtsson 1986; Feder etal. 2012; Nosil 2012; Harrison and Larson 2016; Wolf and Ellegren 2017). Two different selective processes that generate heterogeneous genome divergence can be distinguished. One occurs during contact episodes and corresponds to selection acting on genomic regions involved in reproductive isolation and local adaptation (Harrison 1990; Wu 2001; Payseur 2010). The second occurs through the action of background selection and selective sweeps (Hill and Robertson 1966; Smith and Haigh 1974; Charlesworth etal. 1997), which remove linked neutral diversity within populations during periods of reduced gene flow (Cruickshank and Hahn 2014). Although the barrier effect of speciation genes is equivalent to a local reduction in effective migration rate (m_e) (Barton and Bengtsson 1986; Feder and Nosil 2010), linked selection rather corresponds to a reduction in effective population size (N_e) that locally accelerates lineage sorting in the genome (Charlesworth 2009). Based on this, it is possible to capture the barrier effect of speciation genes by allowing for varying rates of introgression among loci (Roux etal. 2013, 2016; Sousa etal. 2013; Tine etal. 2014), and to capture the effect of linked selection by allowing loci to experience varying rates of genetic drift (Sousa etal. 2013; Roux etal. 2016). This provides a framework in which the effects of heterogeneous selection and gene flow can be considered separately or simultaneously to identify the simplest divergence scenario that best explain the data, thus avoiding overparametrization issues.

North American Lake Whitefish (Coregonus clupeaformis) represents a valuable model to study the role of past allopatric isolation on recent, sympatric ecological divergence. The Saint-John River drainage (southeastern Québec, northeastern Maine), where benthic (normal) and limnetic (dwarf) Whitefish sympatric species pairs occur in different lakes, corresponds to a suture zone where two glacial lineages (Atlantic/Mississippian and Acadian) have been hypothesized to have come into secondary contact during the last glacial retreat on the basis of mitochondrial DNA phylogeography (Bernatchez and Dodson 1990). Given the historical hydrology of the region whereby there was a limited temporal window during which different lakes could be colonized by fish before becoming isolated (Curry 2007), and the absence of limnetic (dwarf) Whitefish in allopatry, the most likely scenario is that of an independent phenotypic divergence that occurred in each lake (Bernatchez 2004). In some lakes, phenotypic divergence between sympatric dwarf (limnetic) and normal (benthic) populations is still partly associated with the mitochondrial DNA lineages characterizing the different glacial origins of the sympatric populations (Pigeon etal. 1997). Dwarf whitefish are most often associated with the Acadian mitochondrial lineage and are only found in sympatry with the normal species. Moreover, fish from the Acadian lineage have a normal phenotype outside the contact zone, which supports the hypothesis that the dwarf phenotype has been derived postglacially from an Acadian genetic background within the contact zone and independently in each lake (Bernatchez and Dodson 1990, 1991; Bernatchez etal. 2010). The evolution of further phenotypic divergence in sympatry suggests that character displacement may have been facilitated by the contact between genetically differentiated lineages (Bernatchez 2004). Moreover, the different dwarf–normal species pairs found in the contact zone are arrayed along a continuum of phenotypic differentiation, where smaller lakes exhibit higher morphological differentiation, which closely mirrors the potential for niche segregation and exclusive interactions within lakes (Lu and Bernatchez 1999; Rogers etal. 2002; Landry etal. 2007; Rogers and Bernatchez 2007; Landry and Bernatchez 2010). This continuum is also evident at the genomic level, with increased baseline genetic differentiation and larger genomic islands of differentiation being found from the least to the most phenotypically and ecologically differentiated species pair (Renaut etal. 2012; Gagnaire, Pavey etal. 2013). Finally, quantitative trait loci (QTL) underlying adaptive phenotypic divergence on complex and polygenic quantitative traits (e.g., behavioral, morphological, physiological, and life history traits) map preferentially to genomic islands of differentiation (Renaut etal. 2012; Gagnaire, Normandeau etal. 2013; Gagnaire, Pavey etal. 2013), suggesting that selection acting on these traits contribute to the barrier to gene flow. Despite such detailed knowledge on this system, previous studies did not allow clarifying how the genomic landscape of dwarf–normal divergence in each lake has been influenced by the relative effects of directional selection on these QTLs and postglacial differential introgression. Consequently, it is fundamental to elucidate the demographic history of the dwarf–normal whitefish species pairs to disentangle the evolutionary mechanisms involved in their diversification.

The main goal of this study was to use a genome-wide single nucleotide polymorphism (SNP) data set to infer the demographic history associated with the recent phenotypic diversification of replicate sympatric dwarf and normal Lake Whitefish species pairs. Using RAD-seq SNP data to document the Joint Allele Frequency Spectrum (JAFS) in each species pair, we specifically test for the role of temporal and genomic variations in the rate of gene flow for each species pair separately, controlling for both effective population size and migration. We then performed historical gene flow analyses among lakes to determine how the different scenarios independently inferred within each lake collectively depict a parsimonious evolutionary scenario of diversification. Finally, we document how the complex interplay between historical contingency, demography, and selection jointly shaped the continuum of divergence among sympatric whitefish species pairs.

Materials and Methods

Sampling and Genotyping

We used RAD-sequencing data from Gagnaire, Pavey etal. (2013) to generate a new genome-wide polymorphism data set. Previous studies based on these data (Gagnaire, Pavey etal. 2013; Laporte etal. 2015) only focused on a subset of 3,438 SNPs that were included in the Lake Whitefish linkage map (Gagnaire, Normandeau etal. 2013). Here, we used the total amount of sequence data (1.7 × 10⁹ reads of 101 bp) to document genome-wide variation in all five sympatric species pairs that are still occurring in five isolated lakes from the Saint-John River basin (fig. 1). For each pair, 20 normal and 20 dwarf individuals were used for RAD-sequencing, but five individuals that received poor sequencing coverage were removed from the data set. Consequently, the following analyses were performed with 195 individuals, each having an average number of 8.7×10⁶ of reads.

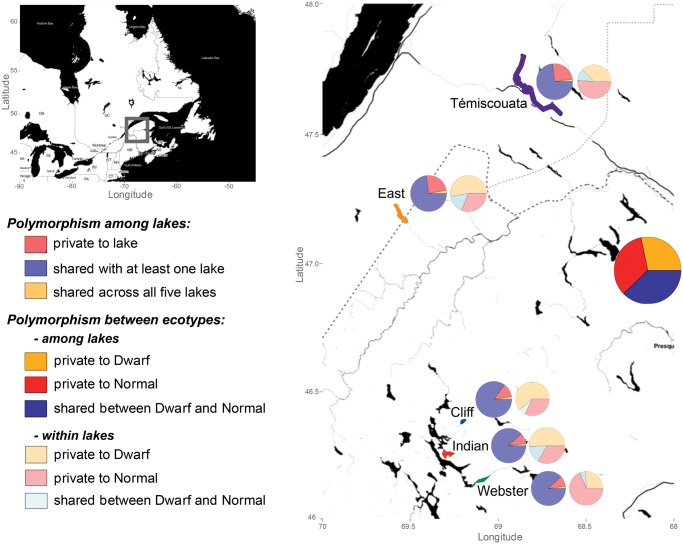
Fig. 1.

—Geographic locations of the lakes where sympatric whitefish species pairs were sampled, and overview of the extent of shared versus private polymorphism. Pie charts illustrate the amount of shared and private SNPs among lakes as well as between species among or within lakes.

We also sequenced six European Whitefish (Coregonus lavaretus), a sister species closely related to the North American Lake Whitefish, to provide an outgroup for identifying ancestral and derived alleles at each polymorphic site within the Lake Whitefish. European Whitefish were sampled in Skrukkebukta Lake (Norway, 69°34′11.6″N–30°02′31.9″E), which also harbors postglacial sympatric whitefish species pairs (Amundsen etal. 2004; Østbye etal. 2006). RAD libraries were prepared for three individuals from each ecotype population, using the same procedure as for American Lake Whitefish (Amundsen etal. 2004; Østbye etal. 2006).

The C. lavaretus raw sequence data set was filtered using the same criteria as for C. clupeaformis (Gagnaire, Pavey etal. 2013). After sequence demultiplexing, the reads were trimmed to a length of 80 bp to avoid sequencing errors due to decreasing data quality near the end of reads. We then used the Stacks pipeline (v1.24) for de novo RAD-tags assembly and individual genotyping (Catchen etal. 2013). We empirically determined an optimal set of assembly parameters to Ustacks, in order to 1) adjust haplotype divergence between alleles at the same locus to the within-population diversity, 2) take into account the possibility of introgression between differentiated populations, whereas 3) controlling for false allelic variation due to hidden paralogy. A minimal coverage depth of 5× per allele (m = 5) and a maximal number of six mismatches between two haplotypes at a same locus within individuals (M = 6) were set. We then allowed a maximal number of six mismatches between individuals in Cstacks (n = 6) to merge homologous RAD-tags from different samples. Finally, we used the program Populations to export a VCF file containing the genotypes of all individuals.

Several filtering steps were then performed with VCFtools v0.1.13 (Danecek etal. 2011) to remove miscalled and low-quality SNPs, as well as false variation induced by the merging of paralogous loci. We first removed SNPs with >10% missing genotypes in each C. clupeaformis population. A lower exclusion threshold of 50% was used for C. lavaretus to retain a maximum of orthologous loci in the outgroup. We then filtered for Hardy–Weinberg disequilibrium within each population using a P value exclusion threshold of 0.01. Finally, we merged the filtered data sets of dwarf and normal populations within each lake together with the European whitefish outgroup and kept only loci that passed the previous filters in all three samples. This resulted in five lake-outgroup data sets containing 14,812, 22,788, 5,482, 26,149, and 14,452 SNPs for Témiscouata, East, Webster, Indian, and Cliff lakes, respectively. Finally, we determined the most parsimonious ancestral allelic state for loci that were monomorphic in the outgroup but polymorphic in C. clupeaformis, defining the allelic state in the outgroup as the ancestral allele (Tine etal. 2014). The resulting oriented SNP data sets contained 11,985, 11,315, 5,080, 13,905, and 9,686 SNPs for Témiscouata, East, Webster, Indian, and Cliff lakes, respectively, that were used to build the unfolded JAFS of each lake, using custom perl and R scripts. Because the amount of SNPs was limited for Webster Lake possibly due to lower quality samples, this species pair was not considered for the subsequent demographic inferences to avoid potential biases due to a lack of resolution of its JAFS. In the four retained lakes, the JAFS was projected down to 13 individuals (i.e., 26 chromosomes) per population to avoid remaining missing genotypes and optimize the resolution of the JAFS.

Inferring the History of Divergence with Gene Flow and Selection

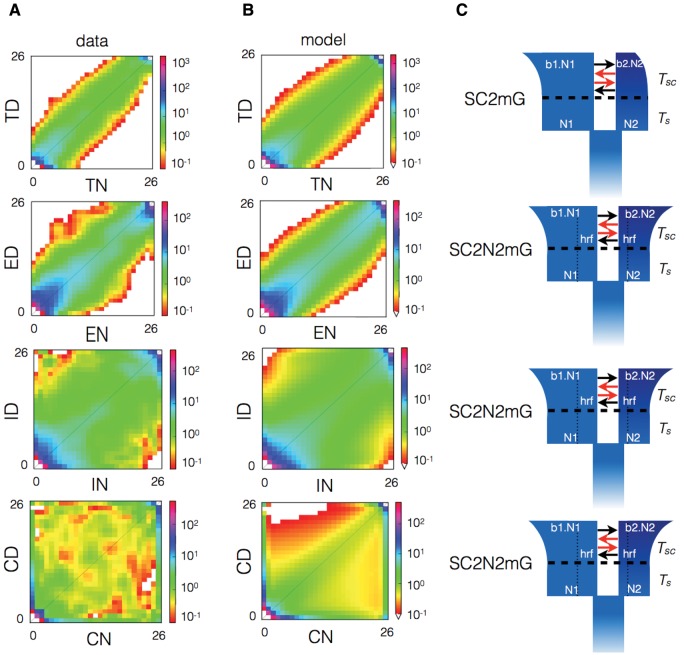
Because the different lakes have been isolated from each other for ∼12,000 years (Curry 2007), we analyzed their JAFS separately. The demographic and selective histories of the four species pairs were inferred using a custom version of the software ∂a∂i v1.7 (Gutenkunst etal. 2009). We considered 26 models (fig. 2) that were built to extend four basic models representing alternative modes of divergence: Strict Isolation (SI), Isolation-with-Migration (IM), Ancient Migration (AM), and Secondary Contact (SC). Each model consists of an ancestral population of size N_ref that splits into two populations of effective size N₁ and N₂ during T_S (SI, IM), T_AM+T_S (AM), or T_S+T_SC (SC) generations, possibly exchanging migrants during T_S (IM), T_AM (AM), or T_SC (SC) generations at rate m_e12 from population 2 (normal) into population 1 (dwarf), and m_e21 in the opposite direction. These models were extended to integrate temporal variation in effective population size (-G) by enabling exponential growth using current-to-ancient population size ratio parameters b₁ (for dwarf) and b₂ (for normal) to account for expansions or bottlenecks. Variation in effective population size across the genome due to Hill–Robertson effects (Hill and Robertson 1966)—that is, local reduction in N_e at linked neutral sites due to the effect of background (Charlesworth etal. 1993) and positive selection (Smith and Haigh 1974)—was modeled by considering two categories of loci (-2 N) occurring in proportions Q and 1-Q in the genome. In order to quantify a mean effect of selection at linked sites, we defined a Hill–Robertson scaling factor (hrf), relating the effective population size of loci influenced by selection (N′₁=hrf × N₁ and N′₂=hrf × N₂) to that of neutral loci (N₁ and N₂). Then, models of divergence with gene flow were extended to account for heterogeneous migration across the genome by considering two categories of loci (-2 m). In addition to a first category of loci evolving under effective migration rates m_e12 and m_e21 and occurring in proportion P in the genome, we considered a second category of loci that occur in proportion 1-P, experiencing different effective migration rates m_e’12 and m_e’21 (Tine etal. 2014). The proportion P was identical in the two diverging populations (same for Q). Because migration and drift influence gene flow during the whole divergence period in the IM model, the effects of heterogeneous migration and population effective size are difficult to dissociate. Therefore, these effects were estimated jointly only within the AM and SC models, in which a strict isolation period helps uncoupling the effects of migration and drift (i.e., -2N2m extensions were considered in addition to -2 N and -2 m models, fig. 2). In these cases, the proportions 1-P and 1-Q corresponded to different sets of loci in the genome. All models with heterogeneous gene flow were also implemented to allow for population growth (i.e., -2NG, -2mG, and -2N2mG). Finally, in order to take into account potential errors in the identification of ancestral allelic states, predicted JAFS were constructed using a mixture of correctly oriented and mis-orientated SNPs occurring in proportions O and 1-O, respectively. The JAFS of mis-oriented variants was obtained by reversing the model spectrum along its two axes (Tine etal. 2014).

Fig. 2.

—The 26 models implemented in this study. The models implemented here represent extensions of the four classical models of divergence: “Strict Isolation” (-SI), “Isolation with Migration” (-IM), “Ancient Migration” (-AM) and “Secondary Contact” (-SC). Briefly, T_S corresponds to the duration of complete isolation between diverging populations and T_AM and T_SC correspond to the duration of gene-flow in AM and SC models, respectively. The first extension of these four models accounts for temporal variation in effective populations size (-G models), allowing independent expansion/contraction of the diverging populations. The last categories correspond to “Heterogeneous gene flow” models, which integrate parameters allowing genomic variations in effective migration rate (-2 m), effective population size (-2 N) or both (-2m2N) to account for genetic barriers and selection at linked sites.

The 26 models were fitted independently for each lake using successively a hot and a cold simulated annealing procedure followed by “BFGS” optimization (Tine etal. 2014). We ran 25 independent optimizations for each model in order to check for convergence and retained the best one (supplementary table S3, Supplementary Material online) to perform comparisons among models based on Akaike information criterion (AIC). Our comparative framework thus addresses overparametrization issues by penalizing models which contain more parameters. By allowing comparisons among nested models of increasing complexity, it also provides a means to independently evaluate the effect of accounting for temporal or genomic variation in migration rate or effective population size. A conservative threshold was applied to retain models with $\mathrm{\Delta }AI{C}_i=AI{C}_i-AI{C}_{min}\le 10,$since the level of empirical support for a given model with a$\mathrm{\Delta }AI{C}_i>$10 is essentially none (Burnham and Anderson 2002). For each lake, the difference in AIC between the worst and the best model ${\mathrm{\Delta }}_{max}=AI{C}_{max}-AI{C}_{min}$ was used to obtain a scaled score for each model using:

$$model\mathrm{ }score=\frac{({\mathrm{\Delta }}_{max}-\mathrm{\Delta }AI{C}_i)}{{\mathrm{\Delta }}_{max}}$$ (1)

such that for each lake the worst model takes a score of 0 and the best model takes a score of 1. Therefore, the model score could be used to more easily compare the retained models among lakes. In order to evaluate the relative probabilities of the different models within each lake, we also computed Akaike weights ($w_{AIC}$) following equation (2), where R corresponds to the total number of models considered (R = 26).

$$w_{AIC}=\frac{e^{\frac{(-\mathrm{\Delta }AI{C}_i)}{2}}}{\sum _{i=1}^R{e}^{\frac{(-\mathrm{\Delta }AI{C}_i)}{2}}}.$$ (2)

To estimate parameter uncertainty, we used the Godambe information matrix method from ∂a∂i v1.7. Nonparametric bootstrapping was used to generate 1,000 bootstrapped data sets to estimate confidence intervals (CIs) using the standard-error of maximum likelihood estimates (se).

Finally, we converted estimated demographic parameters into biologically meaningful units in order to compare informative parameter values among lakes (e.g., timing and strength of gene flow). These estimates were only used for indication and comparative purpose, since we were missing crucial information about the per generation mutation rate in Lake Whitefish. We used the optimal multiplicative scaling factor theta between model and data to estimate the ancestral effective population size (N_ref) before split for each lake:

$$N_{ref}=\frac{\theta }{4L\mu }$$ (3)

with μ being the mutation rate (fixed at 10⁻⁸ mutations per site per generation) and L the effective length of the genome explored by our RAD-Seq experiment and estimated as:

$$L=\frac{zy80}{x}$$ (4)

where x is the number of SNPs that were originally detected from y RAD-tags of 80 bp present in the initial data set, and z is the number of SNP retained for ∂a∂i analyses in the lake considered. Estimated times in units of 2N_ref generations were converted into years assuming a generation time of 3.5 years (i.e., the average between 3 and 4 years for sexual maturity in dwarf and normal whitefish, respectively) (Chebib etal. 2016). Estimated migration rates were divided by 2N_ref to obtain the proportion of migrants received by each population every generation.

Patterns of Shared Ancestry and Admixture among Lakes

We also searched for signatures of shared ancestry and gene flow among replicate species pairs to provide a broader understanding of the divergence history in whitefish. The four lake-specific data sets used for demographic inferences were merged together with the Webster Lake data set, added here to get a more thorough understanding of the system as a whole. Only polymorphic loci that were retained after filtering in all five lakes were considered (42,558 SNPs in total, without the outgroup). For each lake, we determined the fraction of private polymorphisms, the fraction of SNPs shared with at least one other lake or shared across all five lakes. We then measured the proportion of SNPs that were shared between species and private to each species within each lake, as well as among lakes.

To visualize the overall genetic structure and relationships among lakes and species, we performed a discriminant analysis of principal components (dAPC) in Adegenet v2.0.0 (Jombart etal. 2010). We first imputed missing genotypes within each population using a Random Forest regression approach (Poland etal. 2012). Imputation was performed using ten iterations with 150 trees using the randomForestSRC v1.6.1 package in Stackr v.0.1.5 (Gosselin and Bernatchez 2016) and imputed subdata sets were subsequently merged to perform the dAPC.

Finally, we used TreeMix v1.12 (Pickrell and Pritchard 2012) to infer historical relationships among populations. This method uses the covariance structure of allele frequencies between populations and a Gaussian approximation for genetic drift to build a maximum likelihood graph relating sampled populations to their common ancestor, taking migration events into account to improve the fit to the inferred tree. Migration events between populations are modeled in TreeMix by discrete mixture events. Such events may either reflect gene exchange between populations within lakes and/or genetic correlations between geographically isolated populations of the same species, due to the retention of shared ancestral polymorphism among populations from different lakes following their geographic isolation. In order to avoid interpreting spurious migration signals, we focused on the main events of gene flow that received the highest weights (Pickrell and Pritchard 2012), which likely correspond to the largest admixture proportions. We thus allowed a maximum of six migration events to be inferred among branches of the whitefish population tree. For this analysis, we used a 20% missing genotype rate per population without imputing missing genotypes to avoid potential biases in the covariance matrix.

Results

Comparisons among Divergence Models

For each of the four sympatric whitefish species pairs retained for historical divergence analyses (fig. 1), 26 alternative divergence models of increasing complexity were fitted to polymorphism data and compared with each other. This comparative framework enabled us to account for four different aspects of gene flow, that were considered separately or in combination. This includes temporal variation in effective population size (N_e) and migration rate (m), but also genomic heterogeneity in these parameters to capture selective effects (fig. 2). The four JAFS obtained highlighted the continuum of divergence existing among lakes (fig. 3A and supplementary fig. S1, Supplementary Material online). Namely, the density of shared polymorphisms located along the diagonal decreased from the least divergent (Témiscouata and East) to the most divergent (Indian and Cliff) species pairs, whereas the variance of SNP density around the diagonal increased accordingly. In addition, nonshared polymorphisms (i.e., private SNPs) located on the outer frame of the spectrum were mostly found in Indian and Cliff lakes, which were also the only lakes where differentially fixed SNPs between dwarf and normal whitefish were observed.

Fig. 3.

—Historical demography of the Lake Whitefish species pairs. (A) Observed joint allele frequency spectrum (JAFS) for normal (-N; x axis) and dwarf (-D; y axis) populations for each of four lakes (T = Témiscouata, E = East, I = Indian, and C = Cliff), obtained by projection of empirical data to 13 diploid individuals per population. For each JAFS, the color scale indicates the number of SNPs falling in each bin defined by a unique combination of the number of derived allele observed in normal and dwarf populations. (B) Predicted JAFS of the fittest model for each lake. (C) Representation of the fittest model for each lake.

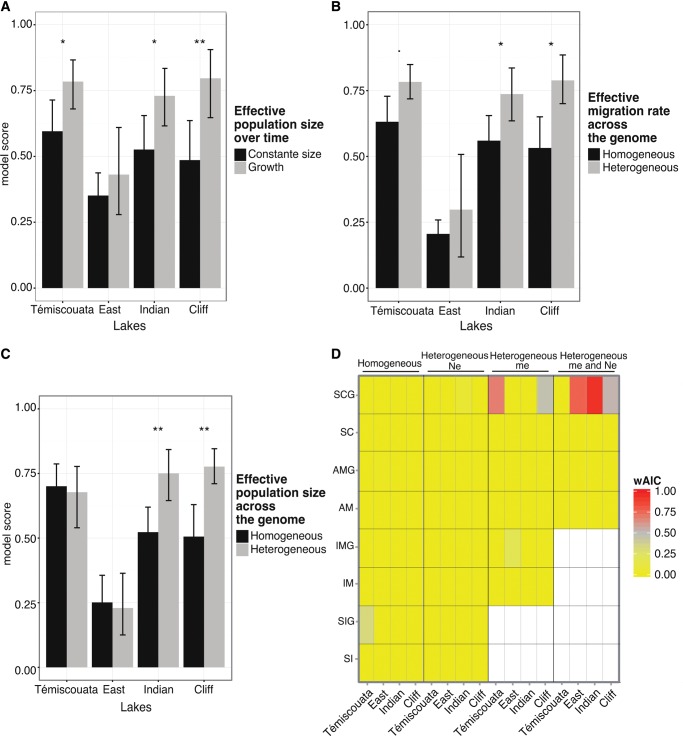
The comparison of model scores within and among lakes showed the importance of considering temporal changes in effective population size. Models including population growth (-G models) generally provided better fits to the data for Témiscouata, Indian and Cliff lakes (Mann–Whitney U test, P = 0.002; P = 0.011, and P = 0.0001, fig. 4A). Similarly, accounting for heterogeneous migration rates across the genome (-2 m models) improved the average model scores for each lake, although not significantly in East Lake (U test, P = 0.016; P = 0.063, and P = 0.029 for Témiscouata, Indian, and Cliff lakes, respectively) (fig. 4B). Moreover, models integrating heterogeneous effective population size at the genomic level (-2 N models) provided significant improvements for the two most divergent species pairs from Indian and Cliff lakes (U test, P = 0.010, and P = 0.005, respectively) (fig. 4C).

Fig. 4.

—Model comparisons. Barplots showing the effect of taking into account a particular demographic or selective aspect in the models, assessed using model scores, with (A) the effect of including temporal variation in population effective size (-G), (B) heterogeneous migration rates among loci (-2 m) and (C) heterogeneous effective population sizes among loci (-2 N). The vertical bars indicate the variance of model scores within a given category of models and asterisks represent significant differences in average model scores between the compared categories of models. (D) Heat-map of the weighted AIC ($w_{AIC}$) showing the relative weights of the 26 models for each lake. The color scale corresponds to $w_{AIC}$ values ranging from 0 to 1. Warmer colors indicate the best models.

For each lake, we performed model selection based on the AIC to penalize model likelihood by the number of parameters to avoid overfitting. Applying a criterion of $\mathrm{\Delta }AI{C}_i\le 10$ for model selection, we retained two best models for Témiscouata (SC2mG and SIG), Indian (SC2N2mG and SC2NG), and Cliff (SC2N2mG and SC2mG) lakes and four best models for East Lake (SC2N2mG, IM2mG, AM2N2m, AMG$)$ (supplementary tables S1 and S2, Supplementary Material online). Akaike weights ($w_{AIC}$) were >0.5 for the highest ranked model of each lake (fig. 4D;supplementary tables S1 and S2, Supplementary Material online). For Témiscouata, the best model was a secondary contact with heterogeneous migration contemporary to population size change (SC2mG; $w_{AIC}=0.68$). The other three species pairs received the highest support for a secondary contact model with heterogeneous migration rate and effective population size contemporary to population size change (SC2N2mG;$\mathrm{ }{w}_{AIC}=0.77$ in East, $w_{AIC}=0.94$ in Indian, and $w_{AIC}=0.53$ in Cliff). Comparisons between the JASF predicted under the best models and the data showed variable patterns in the distribution of residuals depending on lakes (supplementary fig. S1, Supplementary Material online), which were most likely due to model departure from the real (and probably more complex) evolutionary history of species pairs.

Inference of Model Parameters

The inferred proportion of correctly oriented markers in the unfolded JAFS (parameter O) ranged from 95.4% to 99%, suggesting that the vast majority of ancestral allelic states were correctly inferred using the European Whitefish as an outgroup (supplementary tables S1 and S2, Supplementary Material online).

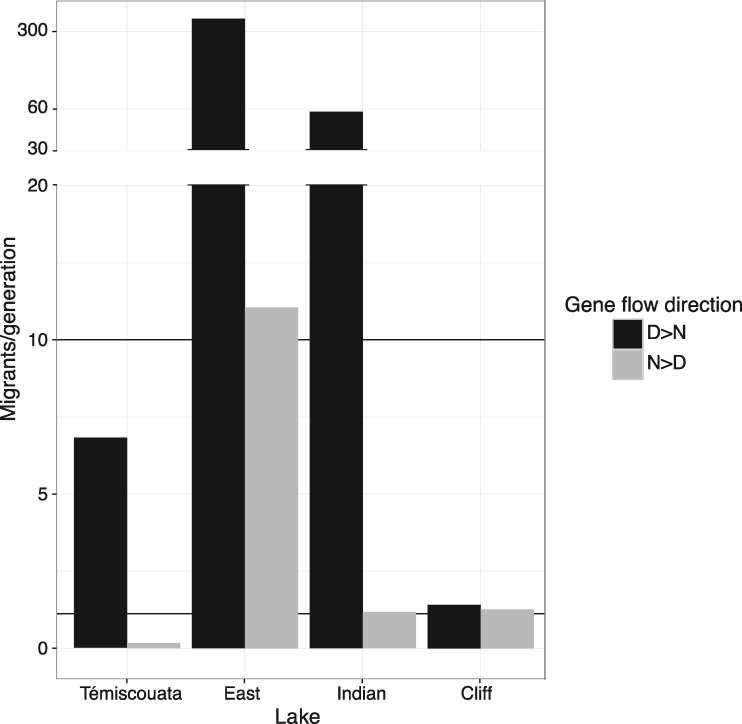
Considering only the highest ranked model for each lake, some general patterns emerged from the comparisons of inferred model parameters among lakes. First, differences in effective population sizes between dwarf and normal whitefish were inferred after splitting from the ancestral population, especially in Indian and Cliff lakes where inferred N_e showed no overlap in CIs between dwarf and normal (supplementary tables S1 and S2, Supplementary Material online). When such differences were observed, N_e was larger for dwarf compared with normal whitefish. Taking into account population growth in the four lakes revealed quite similar patterns of temporal population size changes with recent demographic expansions being found in all populations except for normal whitefish in Lake Témiscouata. A more pronounced demographic expansion was generally inferred for dwarf compared with normal whitefish, and the contemporary effective population size was also larger in dwarf than in normal populations in the four lakes (nonoverlapping CIs, supplementary table S4, Supplementary Material online). The contemporary number of migrants exchanged per generation from one population to the other, estimated using the weighted mean effective migration rate in each direction [i.e., average effective gene flow = N×b × (P×me+1−P×me′)], revealed more pronounced gene flow from dwarf to normal populations in all lakes except Cliff (fig. 5).

Fig. 5.

—Asymmetrical effective gene flow between normal and dwarf whitefish within lakes. Bar plot of the effective number of migrants per generation in both directions from dwarf to normal (black) and reciprocally (gray), obtained from estimated parameters of the fittest model for each lake, using the average gene flow formula (average gene flow=N×b × (P×m_e + (1−P)×m_e’) in each direction.

The highest ranked model for East, Indian, and Cliff lakes included heterogeneous effective population size at the genomic level (figs. 3C and 4; supplementary table S1, Supplementary Material online). The fraction of the genome with a reduced N_e (Q) was estimated to ∼16% in East Lake, 40% in Indian and Cliff lakes, and the proportion of reduction in N_e in those fractions of the genome (i.e., the Hill–Robertson factor, hrf) was ∼11%, 20%, and 17% for East, Indian, and Cliff lakes, respectively.

Time parameters, namely the duration of allopatric isolation (T_S) and secondary gene flow (T_SC), were converted into years. Estimated durations of allopatric isolation periods revealed a recent and similar divergence history in all five lakes (Ts was ∼30,000; 36,000; 29,000; 32,000 years for Témiscouata, East, Indian, and Cliff lakes, respectively, supplementary table S2, Supplementary Material online). The inferred time of secondary contact coincided roughly with the last glacial retreat following the Wisconsinian glaciation, which happened between 18,000 and 11,000 years before present (7,200; 19,600; 8,500; and 9,200 ybp for Témiscouata, East, Indian, and Cliff lakes, respectively, supplementary table S2, Supplementary Material online).

Comparisons of Genetic Variation among Lakes

Only a small proportion (2.5%) of the 42,582 SNPs that were genotyped in all lakes (including a fifth species pair from Webster Lake) corresponded to polymorphic loci that are shared across all five lakes (i.e., “shared across all five lakes” category; fig. 1). Reciprocally, ∼25% of the SNPs were private to Témiscouata or East lakes, whereas Webster, Indian, and Cliff lakes each had ∼10% of private SNPs. The majority of the loci were segregating in at least two (but less than five) lakes (fig. 1). When combined over the five lakes, a higher proportion of the loci were private to normal compared with dwarf populations. Within lakes, the highest proportions of SNPs private to normal whitefish were found in Témiscouata (51%) and Webster (69%). The three other lakes displayed the opposite pattern with higher proportions of SNPs private to the dwarf populations. Shared variation within lakes represented only 6–16% of the SNPs.

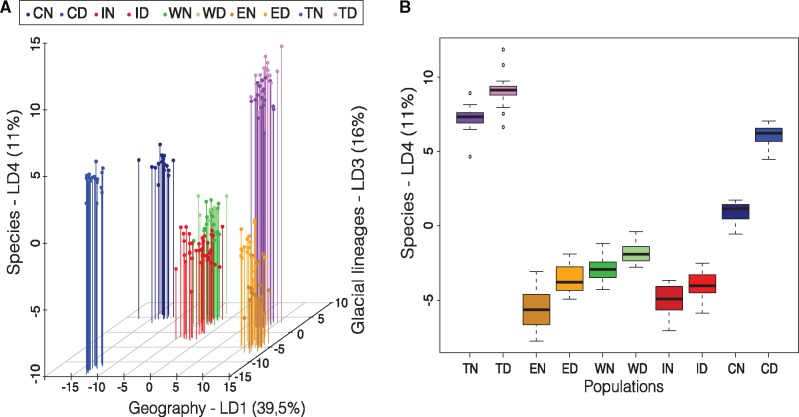
Partitioning genetic variation within and among lakes using a dAPC revealed distinct signals along the four first axes (fig. 6A). On the first axis (LD1, explaining 39.5% of the variance), populations clustered by lakes according to their geographical distribution, roughly separating the three southernmost lakes (Webster, Indian, and Cliff, negative coordinates) from the two northernmost lakes (Témiscouata and East, positive coordinates). The second axis (LD2, explaining 22.5% of the variance, not shown here but see supplementary fig. S2, Supplementary Material online) mostly separated dwarf and normal whitefish from Cliff. The third axis (LD3, explaining 16% of the variance) tended to separate species pairs by shifting normal whitefish of Mississippian/Atlantic origin toward positive coordinates and dwarf whitefish of Acadian origin toward negative coordinates, except for East Lake. The two most extreme populations values on that axis corresponded to normal species from Cliff Lake, the least introgressed relict of the Mississippian/Atlantic lineage (Lu etal. 2001; Gagnaire, Pavey etal. 2013), and the dwarf species from Cliff Lake associated with the Acadian lineage. Finally, the fourth axis (LD4, explaining 11% of the variance) separated the dwarf and normal species from each lake, thus illustrating the shared ancestry between species among lakes (fig. 6B).

Fig. 6.

—Genetic structure and relationships among lakes and species. (A) Discriminant analysis of principal components (dAPC) of the different lakes (Cliff, Indian, Webster, East, Témiscouata) for either Dwarf or Normal whitefish (D or N), representing 3D relationships among populations. The first axis (LD1, 39.5%) captures the geographical signal of differentiation among lakes. The third dAPC axis (LD3, 16%) separates species pairs according to their residual genetic promixity to ancient glacial lineages represented by the least introgressed populations from Cliff Lake. Positive coordinates represent populations with high proportions of Atlantic ancestry whereas negative coordinates reflect increased proportions of Acadian ancestry. The fourth axis (LD4, 11%) tends to separate species pairs within each lake. The second dAPC axis LD2 is not shown here to avoid partial redundancy with LD1, but is provided as a Supplementary Material online. (B) Boxplot of individual coordinates along the fourth dAPC axis (LD4), highlighting the divergence parallelism between species among lakes.

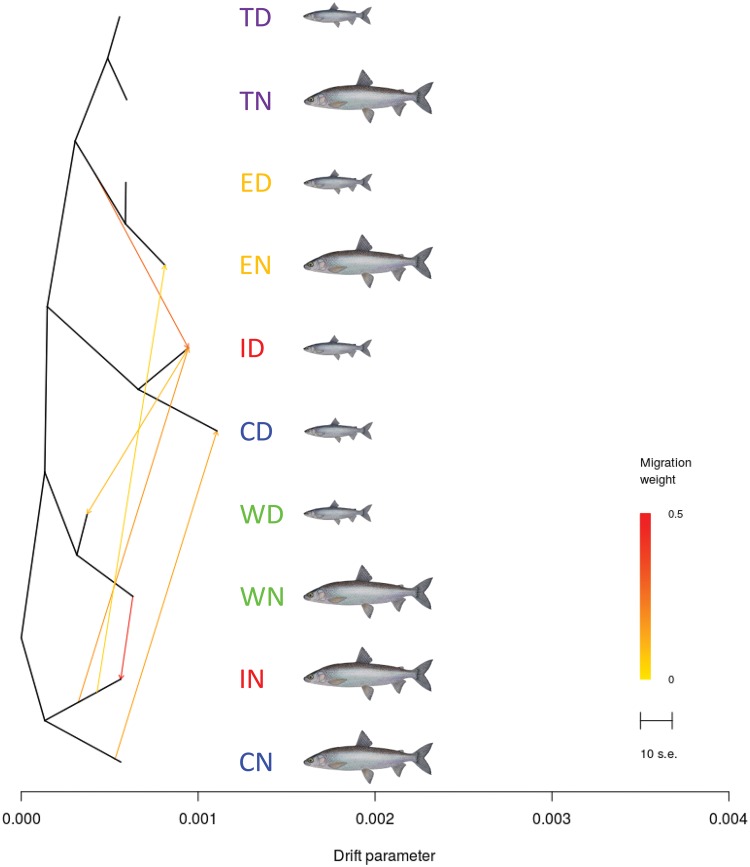
The genetic relationships among populations analyzed with TreeMix revealed two levels of signal (fig. 7 and supplementary fig. S3, Supplementary Material online). The first level was directly linked with genetic distance between the different populations of dwarf and normal whitefish. The population tree rooted with the normal population from Cliff (the most divergent population that best reflects the ancestral state of the Mississippian/Atlantic lineage (Lu etal. 2001; Gagnaire, Pavey etal. 2013), clearly separated normal whitefish from Cliff (CN) and Indian (IN) and dwarf whitefish from Cliff (CD) and Indian (ID), which were grouped together separately from all other populations. The clustering of CN with IN as that of CD and ID most likely reflect their shared ancestral polymorphism associated with their glacial lineage origin (Mississippian/Atlantic lineage for CN and IN; Acadian for CD and ID) (Lu etal. 2001). The second level of signal (geographic signal) grouped population pairs by lake in the remaining part of the tree, most likely reflecting the effect of gene flow following secondary contact between glacial lineages in each lake (Gagnaire, Pavey etal. 2013).

Fig. 7.

—Shared ancestral genetic variation between allopatric populations and admixture events between sympatric species pairs. The least introgressed normal whitefish population from Cliff Lake was used to root the tree. Horizontal branch lengths are proportional to the amount of genetic drift in each branch, and the scale bar indicates 10 times the average standard error (SE) of the entries in the covariance matrix between pairs of populations. Color scale indicates the weight of inferred migration events.

Inferred migration links were represented by arrows, the color of which indicates their relative weights (fig. 7). Migrations links between sympatric species pairs for Cliff and Indian lakes suggested contemporary gene flow (i.e., consecutive to the colonization of the postglacial lakes) between dwarf and normal populations within each of these two lakes. Other migration links between allopatric populations of the same species (i.e., populations from different lakes which have been isolated since the lakes formation) illustrated the genetic proximities (i.e., shared ancestry) of species from distinct lakes. For instance, dwarf whitefish from Webster (WD) was related to dwarf whitefish from Indian lake (ID), and the same link was found between the normal populations of these lakes (WN and IN). Finally, the ancestral population of East Lake was related with dwarf whitefish from Indian Pond, whereas normal whitefish from East Lake (EN) was linked to normal whitefish from Indian Lake, thus supporting a common genetic background between the normal populations of East and Indian lakes.

Discussion

The observed patterns of genomic differentiation among replicated dwarf/normal Lake Whitefish species pairs provide new insights into the divergence history of a well-studied model of ecological speciation (Bernatchez etal. 2010). The first approach implemented here relied on inferring the divergence history of each species pair separately, using the JAFS as a summary statistics of genome-wide differentiation. In order to maximize the amount of available information, each JAFS was oriented using the closely related European whitefish as an outgroup species, thus providing increased power to detect demographic processes that generate asymmetric distributions of derived variants around the diagonal of the JAFS.

The secondary contact (SC) scenario provided the best fit to the observed data for all of the four species pairs used for historical divergence analyses. Therefore, our ability to detect the secondary contact was apparently not affected by the small degree of genetic divergence between the least differentiated species pairs. Using simulations, Roux etal. (2016) recently showed that the power to detect the SC scenario can be high when the period of isolation is long relative to the duration of secondary contact, which was the case here. Moreover, secondary contacts are expected to leave detectable signatures on the JAFS (Alcala etal. 2016), since the erosion of past allopatric divergence by secondary gene flow typically generates an excess of shared intermediate frequency alleles.

A scenario of secondary contact is concordant with past phylogeograhic studies performed in the early days of mtDNA studies (Bernatchez and Dodson 1990, 1991; Pigeon etal. 1997), but provided much deeper insights into the evolutionary history of whitefish radiation. The geographic area where sympatric whitefish species pairs occur corresponds to a well-known suture zone where glacial lineages have come into contact in several freshwater species, as they were recolonizing from different refugia after the Wisconsinian glaciation (Curry 2007; April etal. 2013). In Lake Whitefish, this zone corresponds to a phylogeograhic transition between Acadian and Atlantic/Mississippian mitochondrial lineages (Bernatchez and Dodson 1990; Pigeon etal. 1997). Interestingly, the Allegash River basin (including the studied lakes), which represents the core of this contact zone, is the only area where sympatric populations of Lake Whitefish are observed. Moreover, no dwarf population, either in allopatry or sympatry, has been reported outside this region (Bernatchez and Dodson 1990). Therefore, phenotypic and ecological divergence, and in particular the occurrence of dwarf whitefish, is tightly linked to this secondary contact zone.

The frequency of Acadian and Atlantic/Mississippian mitochondrial lineages within lakes was partly associated with the level of phenotypic divergence between dwarf and normal whitefish, with variable amounts of mitochondrial introgression being found among lakes (Bernatchez and Dodson 1990; Pigeon etal. 1997). At one extreme, the least phenotypically divergent pair from East Lake is fixed for the Acadian mitochondrial haplogroup in both dwarf and normal whitefish, which has previously been interpreted as a support for sympatric divergence in this particular lake (Pigeon etal. 1997). Although our inferences based on the JAFS could not definitely rule out the IM model (IM2mG, $w_{AIC}=0.19$), we obtained much stronger evidence in favor of the secondary-contact scenario in this lake (SC2N2mG, $w_{AIC}=0.77$). A possible explanation for the loss of the Atlantic/Mississippian haplogroup in East Lake involves a stronger recent demographic expansion in the dwarf population following secondary contact, which may have contributed to the fixation of the Acadian lineage. Indeed, the preferential direction of introgression between hybridizing populations with asymmetrical N_e is expected to occur from the larger to the smaller population (Beysard etal. 2012). This is consistent with the inferred asymmetrical direction of the effective gene flow from dwarf to normal populations (fig. 5). This is also supported by a similar scenario in the neighboring Témiscouata Lake, which harbors the second least divergent species pair. Témiscouata Lake is also dominated by the Acadian haplogroup, but a small proportion of normal whitefish in this lake is still associated with the Atlantic/Mississippian lineage. Since we also inferred an expansion of the dwarf population (but not in normal whitefish) following secondary contact in this lake, it is likely again that this demographic imbalance explains the predominance of Acadian mitochondrial haplotypes in the northern part of the contact zone. At the other extreme, Cliff Lake where species divergence is the most pronounced shows differential fixation of Acadian and Atlantic/Mississippian haplotypes in dwarf and normal populations, respectively (Bernatchez and Dodson 1990). Thus, there is a perfect association in this lake between glacial lineage origin and phenotypic divergence, which was also attributed to a secondary contact in our demographic inferences. Similarly to East Lake, Indian Lake harbored both dwarf and normal populations fixed for the Acadian haplogroup (Lu etal. 2001). However, our analysis of the JAFS also confirmed that two distinct glacial lineages have come into contact in this lake. Such a partial concordance is typically expected when secondary contact occurs between incompletely reproductively isolated species (Taylor and Donald McPhail 2000).

A Shared History of Divergence before Independent Evolution within Lakes

The global analysis including all five pairs simultaneously helped clarifying the extent to which replicate whitefish species pairs share a common history of divergence. The secondary contact scenario implies that the different species pairs are derived from the same two glacial lineages, as partly supported by mitochondrial data (Bernatchez and Dodson 1990; Pigeon etal. 1997). However, whether whitefish species pairs share a common history before secondary contact has never been assessed using nuclear markers.

Grouping populations based on their overall genetic similarities with Treemix produced two different types of grouping in the population tree. Populations from the three least divergent species pairs were grouped by lake (i.e., TN grouped with TD, EN with ED, and WN with WD), whereas populations from the two most divergent species pairs were grouped by ecotypes (i.e., IN with CN, and ID with CD). This complex picture likely reflects the relative importance of gene flow between species within lakes and genetic drift among lakes, and is in itself insufficient to distinguish contemporary admixture from shared ancestry during lakes colonization. Inferring migration events among populations enabled us to detect contemporary gene flow between sympatric dwarf and normal whitefish within Indian and Cliff lakes. However, the other inferred links connecting populations of the same species but from different lakes (i.e., isolated populations) rather indicated shared genetic variation due to common ancestry. Namely, inferred links between Webster and Indian indicated the sharing of ancestral variation between WN and IN (and therefore with CN), as well as between WD and ID (and therefore with CD). This supports the view that the different populations of each species in these three lakes, which are not physically connected today thus hampering any gene flow, were genetically similar before being isolated in their respective lakes. An additional link inferred between EN and IN (IN being connected with WN and CN) confirmed that normal whitefish from East Lake share ancestral variation with other normal populations from the southern part of the contact zone. This provides further evidence that the secondary contact inferred in East Lake has occurred between the same two glacial lineages as for the other lakes, despite the lack of Atlantic/Mississippian mitochondrial lineage in this lake. Finally, the ancestral population from East Lake was linked to the dwarf population from Indian (and therefore to WD and CD), indicating that both populations from East Lake share much of the ancestral variation originating from the Acadian lineage. This is also consistent with the genetic swamping hypothesis proposed for explaining the lack of mitochondrial polymorphism in this lake.

The analysis of overall diversity patterns performed with the dAPC (fig. 6) was a complementary way to disentangle remaining signals of genetic differentiation between glacial lineages (axis 3) from genetic differentiation among lakes (axis 1). On the third axis, the projection of dwarf and normal populations from Cliff Lake indicated the positions of the two least introgressed populations (and closest to their ancestral genetic background) of our data set. Therefore, they could be used to define an Acadian (negative coordinates) and an Atlantic/Mississippian (positive coordinates) reference for comparisons with other lakes. Interestingly, both populations from East and Indian lakes occupied intermediate positions, which is concordant with a higher proportion of Acadian ancestry in these lakes, as suggested by mitochondrial data (Pigeon etal. 1997).

In summary, the most parsimonious overall scenario supported by our analyses corresponds to a secondary contact for all lakes, with variable contributions of Acadian and Atlantic/Mississippian lineages due to demographic contingencies. The secondary contact was concomitant to population expansions in both glacial lineages, which were detected for most lakes. This is broadly consistent with the idea that the two glacial lineages were undergoing spatial expansions after the last glacial retreat, which provoked a secondary contact at the origin of parallel genetic divergence patterns across whitefish species pairs. Our results also support that population expansions were generally more pronounced for dwarf relative to normal populations, still reflected today by the higher contemporary abundance of dwarf whitefish in all lakes (Bernatchez L, unpublished data). This demographic imbalance also impacted the main direction of gene flow, which was more pronounced from dwarf to normal populations than the reverse. As a consequence, an important amount of shared ancestral polymorphism between dwarf and normal populations (fig. 1) most likely corresponds to genetic variation coming from gene exchanges due to introgression between lineages, in addition to incomplete lineage sorting.

An Extended Framework for Inferring Speciation-with-Gene-Flow

The concept of speciation-with-gene-flow embraces a large diversity of divergence scenarios with regards to the timing of gene flow, which in turn pertains to different modes of speciation that have long been recognized in the speciation literature (Coyne and Orr 2004). Diverging populations can experience temporal variations in effective size and migration rate, which both influence the temporal dynamics of gene flow. Consequently, demographic inference methods that account for these temporal variations have the potential to provide an improved understanding of the historical demographic events that shaped the unfolding of speciation.

For the Lake Whitefish as for other species with a pan-Arctic distribution, the history of divergence has been strongly impacted by quaternary climatic oscillations (Bernatchez and Wilson 1998). Glaciations have drastically restricted the area of species distribution provoking geographic isolation among bottlenecked populations (Bernatchez etal. 1989; Ambrose 1998; Aoki etal. 2008), whereas interglacial periods have allowed secondary contacts between populations expanding from their glacial refugia (Hewitt 2001). Here, accounting for temporal variation in migration rate and N_e allowed us to determine that the secondary contact between whitefish glacial lineages has occurred contemporarily with population expansions. This later point is of prime importance for understanding the evolution of reproductive isolation, since bottlenecked populations undergoing demographic expansions are more likely to carry and even fix deleterious alleles (Luikart etal. 1998; Peischl etal. 2013; Lohmueller 2014), which could later translate into substrate for genetic incompatibilities upon secondary contact. Indeed pronounced postzygotic incompatibilities between dwarf and normal whitefish representing different glacial lineages have been documented despite relatively small overall genomic divergence between them (Lu and Bernatchez 1998; Rogers and Bernatchez 2006; Dion-Côté etal. 2014). Moreover, such genetic incompatibilities may associate by coupling to form stronger barriers to gene flow (Barton and de Cara 2009; Bierne etal. 2011), as proposed in Gagnaire, Pavey etal. (2013).

Another important aspect of divergence-with-gene-flow relates to the extent to which the previously described demographic effects interact with selection. The speciation genomics literature has been increasingly integrating the influence of selective processes in historical divergence models (Roux etal. 2013; Sousa etal. 2013; Tine etal. 2014), and more generally, in the analytical approaches to relate genomic divergence patterns to the underling evolutionary processes (Cruickshank and Hahn 2014). These selective effects can be separated in two broad categories. First, genetic barriers caused by local adaptation and reproductive isolation loci can resist introgression, hence reducing the effective migration rate at linked loci (Barton and Bengtsson 1986; Feder and Nosil 2010). The second category embraces the effect of positive (e.g., selective sweeps) (Smith and Haigh 1974) and background selection (Charlesworth etal. 1993), which cause local reductions in genetic diversity at both selected sites and linked neutral sites. These later selective effects rather correspond to a reduction in the N_e of the genomic regions influenced by selection, irrespective to the role that they play in the speciation process. Since gene flow depends both on N_e and migration rate, both types of selective effects are likely to impact genomic divergence patterns during speciation. Here, we captured these effects separately using divergence-with-gene-flow models that take into account in a simple way the effects of genetic barriers and linked selection.

Accounting for variation in effective migration rate across the genome generally improved the fits to empirical data whatever the model considered (fig. 4B), and the best models for all lakes also included heterogeneous migration rates. This suggests that the rate of introgression between whitefish glacial lineages has been highly variable across their genome since the beginning of secondary contact, as reported previously in other species (Tine etal. 2014; Le Moan etal. 2016; Rougemont etal. 2017). Moreover, integrating heterogeneous N_e in the models also improved model scores for the two most divergent species pairs (Cliff and Indian, fig. 4C). Therefore, our results also support the view that linked selection has influenced the patterns of genomic divergence in whitefish sympatric species pairs. As proposed in earlier studies, this mechanism may be particularly efficient in low-recombining chromosomal regions (Cruickshank and Hahn 2014). Some of our models (e.g., SC2m2N and AM2m2N) combined both genome-wide variation in N_e and m_e, as already developed within an ABC framework (Roux etal. 2016). The rationale behind this is that only models that both contain a period of isolation and gene flow enable to dissociate the influence of both sources of chromosomal variation, since only linked selection is at play during periods of geographic isolation. However, it is currently unclear how much the signal contained in empirical polymorphism data can retain distinct signatures for these two selective effects. This will need to be addressed using simulations.

In summary, as for most models, our models remain simplifications of a probably more complex reality. Yet our approach illustrates the need to take into account both temporal and genomic variations in effective population size and migration rates when inferring the history of speciation. The 26 divergence models considered here enabled us to evaluate a large diversity of scenarios, taking each effect separately an in combination with other to improve the inference of the divergence history while controlling for model complexity.

Understanding the Divergence Continuum in Whitefish

Lake Whitefish nascent species pairs offer a rare opportunity to understand the influence of selection and historical demography on a continuum of phenotypic and genomic divergence associated with speciation. Previous works have provided mounting evidence for the role of selection in shaping genetic and phenotypic divergence across this continuum (Rogers etal. 2002; Landry etal. 2007; Bernatchez etal. 2010; Renaut etal. 2012; Gagnaire, Pavey etal. 2013; Laporte etal. 2015). However, the role played by historical demography has never been fully resolved since previous studies largely depended on mitochondrial DNA alone.

Our study brings new evidence supporting previous findings based on mitochondrial DNA that the onset of this young radiation matched the last glacial period (Bernatchez and Dodson 1990, 1991). Using a mutation rate of 10⁻⁸ mutations per site per generation and a generation time of 3.5 years, the average divergence date between glacial lineages was 41,600 ybp (SD 8,100). This is consistent with a previous study based on mitogenome sequencing (Jacobsen etal. 2012) that estimated the divergence time between 20,000 and 60,000 ybp. This corresponds to the late Wisconsin glacial episode, starting 85,000 years ago, during which the Laurentide ice sheet covered the studied region in eastern North America, with a maximum ice extent occurring ∼25,000 ybp (Curry 2007). The average time of secondary contact obtained here, was dated to 11,200 years (SD 5,700), which also corresponds to the glacial retreat period, at which the lakes were colonized by the two glacial lineages from eastern (Acadian) and western (Atlantic/Mississipian) glacial refuges (Curry 2007). Therefore, the inferred timing of divergence and secondary contact between glacial lineages matches relatively well the chronology of the climatic events in eastern North America.

Our results suggest that demographic differences among lakes have contributed to shaping the divergence continuum observed among the five lakes. Introgression rates tended to be higher in the least divergent species pairs, resulting into a weaker genetic differentiation. Yeaman etal. (2016) recently showed that the formation of genomic islands by erosion of divergence following secondary contact depends on the amount of linkage disequilibrium (LD) among selected loci and the intensity of effective migration. Here, we showed that effective migration rate was generally higher in the least differentiated lakes (Témiscouata and East), whereas at the same time, increased LD among genomic islands has been documented in the most divergent lakes (Gagnaire, Pavey etal. 2013). Therefore, the divergence continuum likely implies both the antagonistic effects of divergent selection maintaining LD and introgression eroding past divergence.

Our study also provides new insights on the role of linked selection in shaping patterns of genomic divergence observed among the whitefish species pairs. Namely, we inferred that some genomic regions have experienced a reduction in N_e, as predicted under the effect of selection at linked sites (Cruickshank and Hahn 2014). The increasing proportion of genomic regions affected by Hill–Robertson effects, from the least to the most divergent lakes, indicated that the divergence continuum among lakes was also influenced by linked selection.

In the light of those observations, along with previous studies on this system, we propose that the continuum of genetic divergence in whitefish species pairs is the evolutionary result of a complex interplay between 1) genetic divergence between glacial lineages through lineage sorting and mutation accumulation, 2) reduced introgression in genomic regions involved in reproductive isolation due to the accumulation of incompatibilities, 3) divergent selection on phenotypes maintaining LD, and 4) the independent contingency of demographic events among lakes. The heterogeneous landscape of species divergence in the whitefish system was thus likely built by a combination of selective and demographic factors. Our inferences allowed us to disentangle part of this complex interplay, although many aspects remain to be clarified. In particular, whether selection at linked sites also plays a role in facilitating the accumulation of incompatibilities during allopatry isolation will need to be scrutinized into more details, as well as the role of such incompatibilities in facilitating the divergence of quantitative polygenic traits following secondary contact. This could be achieved by testing the effect of divergence on quantitative traits with and without the joint action of selection against hybrids. Indeed, a model mixing components of allopatric speciation, with the accumulation of genetic incompatibilities (e.g., underdominant mutations) and sympatric speciation (i.e., local adaptation involving divergent selection on quantitative traits), would differ from the coupling hypothesis model which mostly considers local adaptation loci of relatively strong effect (Bierne etal. 2011). We argue that this kind of models could be relevant for some systems in which sympatric speciation after admixture, or parallel hybrid speciation, has been inferred without explicitly testing a single divergence event with recent secondary gene flow (Kautt etal. 2016; Meier etal. 2017). We also believe that demographic inferences approaches should systematically include basic scenarios of divergence, extended by models with increasing levels of complexity to address demographic and selective effects separately and then combined, and not only focus on the a priori history of the system. To conclude, this study illustrates the potential benefits of applying a modeling framework to disentangle the relative role of demography and selection, toward elucidating the complexity of species divergence in any other taxonomic group.

Availability

The source code for demographic inferences and documentation are available on Github (https://github.com/crougeux/Dadi).

Supplementary Material

Supplementary data are available at Genome Biology and Evolution online.