Cell-to-cell variability and robustness in S-phase duration from genome replication kinetics

Abstract

Genome replication, a key process for a cell, relies on stochastic initiation by replication origins, causing a variability of replication timing from cell to cell. While stochastic models of eukaryotic replication are widely available, the link between the key parameters and overall replication timing has not been addressed systematically. We use a combined analytical and computational approach to calculate how positions and strength of many origins lead to a given cell-to-cell variability of total duration of the replication of a large region, a chromosome or the entire genome. Specifically, the total replication timing can be framed as an extreme-value problem, since it is due to the last region that replicates in each cell. Our calculations identify two regimes based on the spread between characteristic completion times of all inter-origin regions of a genome. For widely different completion times, timing is set by the single specific region that is typically the last to replicate in all cells. Conversely, when the completion time of all regions are comparable, an extreme-value estimate shows that the cell-to-cell variability of genome replication timing has universal properties. Comparison with available data shows that the replication program of three yeast species falls in this extreme-value regime.

INTRODUCTION

In all living systems, the duration of DNA replication correlates with key cell-cycle features, and is intimately linked with transcription, chromatin structure and genome evolution. Dysfunctional replication kinetics is associated to cancer and found in aging cells. Eukaryotic organisms rely on multiple discrete origins of replication along the DNA (1,2). These origins are ‘licensed’ during the G1 phase by origin recognition complexes and MCM helicases, and can initiate replication during S phase (3). Once one origin is activated (‘fires’), a pair of replication forks are assembled and move bidirectionally. In one cell cycle, one origin already activated or passively replicated cannot be activated again (2). Origins have specific firing rates, possibly connected to the number of bound MCM helicase complexes (4), and their specificity determines the kinetics of replication during S phase, or ‘replication program’.

To investigate genomic replication kinetics, DNA copy number can be measured with microarray or sequencing, as a function of genome position and time (see, e.g. (5–7)). Based on such high-throughput replication timing data, it is possible to infer origin positions and the key parameters for a mathematical description of the replication process (see, e.g. (5,8,9)). Recent methods also allow to extract the same information from free-cycling cells (10). The mathematical modeling of genome-wide replication timing data shows that replication kinetics results from the stochastic mechanism of origin firing (3,6). In other words, replication timing originates from individual probabilities of origin firing (and their correlations with genome state (11–13)). In such models, firing rate of individual origins determine the kinetic pattern of replication along the chromosomal coordinate, and fork velocity is typically assumed to be nearly constant along the genome (in absence of blockage).

Evidence of this stochasticity directly from single cells (which should give access to relevant correlation patterns) is less abundant. Importantly, replication timing patterns observed in population studies can be explained by stochastic origin firing at the single-cell level (14). Stochastic activation of origins leads to stochasticity of termination and cell-to-cell variability of the total duration of replication of a chromosome, a genomic region, or the whole S-phase (6), with possible repercussions on the cell cycle. This raises several questions, including how the individual rates and spatial distribution of origins cooperate to generate variability in replication timing, the extent of such variability, and whether it is possible to identify specific regimes or optimization principles in terms of cell-to-cell variability. However, such questions have not been systematically addressed in the available models.

A series of pioneering studies (15,16) has used techniques of extreme-value theory to derive the distribution of replication times in the particular case where each locus of the genome is a potential origin of replication, as in the embryonic cells of X. laevis. These efforts allowed to clarify the possible optimization principles underlying the replication kinetics in such organisms.

Here, we extend this approach to the widely relevant case of discrete origins with fixed positions (2,17,18) using a modeling framework for stochastic replication to investigate the cell-to-cell variability of the duration of S-phase (or of the replication of any genomic region such as one chromosome). We use analytical calculations based on extreme-value theory and simulations, employ experimental data to infer replication parameters and identify the main features of empirical origin strengths and positions, and their response to specific changes.

MATERIALS AND METHODS

Model

We make use of a 1D nucleation-growth model (19) of stochastic replication kinetics with discrete origin locations x_i, similar to models available in the literature (5,20). Activation of origins (firing) is stochastic, and is described as a non-stationary Poisson process. The firing rate A_i(t) of the origin located at x_i is a function of time, A_i(t) = λ_it^γθ(t), where θ(t) is the step function, and λ_i and γ are constants (5,15,21). We assume that the parameter γ and the fork velocity 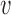are common to all origins, whereas λ_i, which reflects the specific strength of each origin, is origin dependent. The probability density function (PDF) f_i(t) of the firing time t for the i-th origin, given that the origin fires during that replication round, can be obtained as 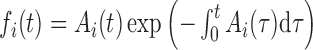, which gives

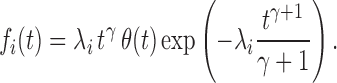(1)

When γ > 0, i.e. when the firing rate increases with time, f_i(t) is a stretched exponential distribution. When γ = 0, the firing rates are constant and the process is stationary, so A_i(t) = λ_i and .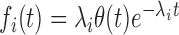

Once an origin has fired, replication forks proceed bidirectionally at constant speed, possibly overriding other origins by passive replication. When two forks meet in an inter-origin region, replication of that region is terminated. The length of the i-th region is defined as d_i = x_{i + 1} − x_i; the time when its replication is completed is T_i. The duration of the S phase T_S is the time needed for all inter-origin regions to be replicated.

Fits

Empirical parameters were inferred through fitting experimental data from refs. (6,7,22,25) on DNA copy number as a function of position and time with the model. The positions of replication origins were obtained directly from the literature and considered fixed (6,7,22,25). The fits are performed by minimizing the distance between the replication timing profiles in the model and in the experimental data. This is carried out by updating the global parameters (γ and ) and the local parameters (λ_i, i ∈ {1, 2, ..., n}) iteratively (see Supplementary Text). The parameters from these fits are presented in Supplementary Table S1.

Simulations

Our theoretical calculations (described below) allow to obtain the cell-to-cell variability of T_S in special regimes. We compare simulations using the complete information on the locations and strengths of all origins fitted from the data, with randomized chromosomes having similar properties. In these randomized chromosomes we consider the inter-origin distances d_i and the strengths λ_i as independent random variables. They are drawn from probability distributions recapitulating their empirical mean and variability. More precisely, from the fitted parameters we fix the mean 〈d〉 and the standard deviation σ_d of the distance, and the mean 〈λ〉 and the standard deviation σ_λ of the strength. The actual distances d_i and strengths λ_i are then drawn by sampling from two gamma distributions

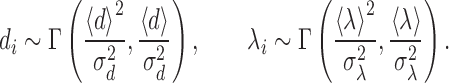(2)

The gamma distribution Γ(a, b) (parametrized in terms of a shape parameter a and a rate parameter b) has PDF p(x)∝x^{a − 1}exp (−bx). It yields positive values, with mean a/b and variance a/b², and it is the maximum-entropy distribution with fixed mean and fixed mean of the logarithm. We verified that the assumption of a gamma distribution was in line with empirical data (Supplementary Figure S1).

To explore the full range of parameters, we also used stochastic simulations, which were performed both (i) with the precise origin locations and strengths fitted from the data, and (ii) with d_i and λ_i drawn randomly as described above. To avoid the boundary effects of linear chromosomes, we consider circular chromosomes with n origins, unless specified otherwise (boundary effects are discussed in the Supplementary Text and Supplementary Figure S2, and do not affect our main conclusions.)

To analyze the biologically relevant regimes, we considered replication kinetics data on different yeast species, from refs. (6,7,22,25), ran simulations with such parameters, and compared with the theoretical predictions using the empirical values for σ_d, σ_λ and mean origin positions and strengths.

RESULTS

The S-phase duration is the result of a maximum operation on the stochastic replication times of inter-origin regions

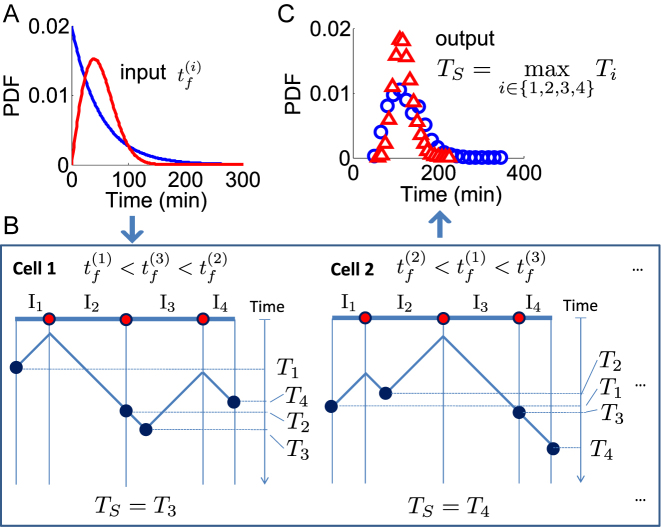
We start by discussing how the stochastic nature of single-origin firing affects the total replication timing of a chromosome. Figure 1A and B illustrates this process. In each cell, a chromosome is fully replicated when the last inter-origin region is complete. In other words, the last-replicated region sets the completion time for the whole chromosome. Consequently, the total duration is the maximum among the replication times of all inter-origin regions (16). For simplicity, we first consider the case of a genome with only one chromosome. The duration of the S phase is therefore T_S = max (T₁, T₂, ..., T_n) where n is the number of inter-origin regions. The stochasticity of the replication time T_i of each inter-origin region makes the S-phase duration T_S itself stochastic, thus giving rise to cell-to-cell variability, which can be estimated by the model (Figure 1C). In the case of multiple chromosomes, the same reasoning applies to the last-replicated inter-origin region over all chromosomes.

Figure 1.

The S-phase duration is the maximum between the stochastic termination time of all inter-origin regions. The illustration considers replication of one linear chromosome with three origins. (A) The activation of each origin is stochastic, and the firing time 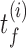follows a given phenomenological distribution. (B) In each cell, each origin randomly chooses a firing time from this distribution. The last replicated inter-origin region, which may be different in different cells, determines the total duration of the S phase. In the sketch, red circles indicate origins. Dark blue circles indicate the latest replicated loci for each inter-origin region. Some origins (e.g. the one between I₂ and I₃ in cell 1) may be replicated passively, and never fire in some realization. (C) The stochastic model generates a distribution of S-phase durations, which expresses the cell-to-cell variability. The parameters used in the plots are: chromosome length L = 300 kb, fork velocity 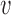= 1 kb/min, firing exponent γ = 0 (blue line in (A) and blue circles in (C)) or 1 (red line in (A) and red triangles in (C)), origin locations x₁ = 50 kb, x₂ = 150 kb and x₃ = 250 kb, origin strength λ_{1, 2, 3} = 0.02 min ⁻¹ (for γ = 0) or 6.3 × 10⁻⁴ min ⁻² (for γ = 1).

A theoretical calculation reveals the existence of two distinct regimes for the replication program

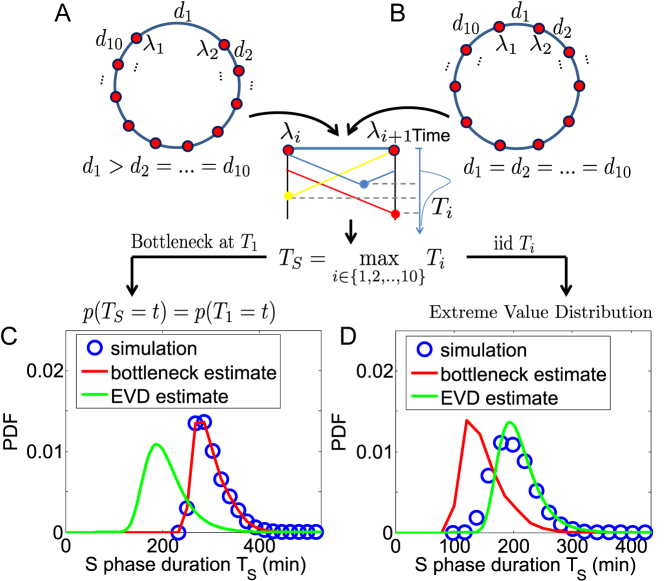
It is possible to estimate the distribution of T_S analytically, starting from the distribution of T_i. Two distinct limit-case scenarios can be distinguished. In the first scenario, a specific inter-origin region r is typically the slowest to complete replication and thus represents a ‘replication bottleneck’. In this case, T_S is dominated by T_r, meaning that T_S ≈ T_r. T_r is identified as the one which is largest on average. Figure 2A shows an example chromosome with 10 origins with the same strength, where one inter-origin distance (d₁) is much larger than the others. Owing to this disparity, T₁ is very likely the maximum among all T_i, and is therefore the region determining T_S. In this scenario, which we term ‘bottleneck estimate’, the distribution of T_S will be approximately the same as that of the bottleneck T_r (Figure 2C).

Figure 2.

Analytical estimates indicate the existence of two replication regimes. (A) If a single ‘bottleneck’ inter-origin region (labelled by the index 1 in panels A and B) is typically the last to complete replication, T_S will be typically equal to T₁ (inter-origin distances in the example are d_i = 167 kb for all origins except d₁ = 500 kb). (B) If the replication times of all inter-origin regions are comparable, and they are considered independent and identically-distributed (iid) random variables, the distribution of T_S can be obtained by extreme-value-distribution (EVD) theory (inter-origin distances are d_i = 200 kb). Simulations of the model (blue circles), when one inter-origin distance is much larger than the others (C), and when all inter-origin distances and strengths are comparable (D), agree with the corresponding analytical calculations (red and green curves). (Origin number n = 10 origins, fork velocity 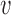= 1 kb/min, origin strength λ_i = 0.02 min ⁻¹.)

In the second scenario, each inter-origin region has a similar probability to be the latest to complete replication. In this case, every inter-origin region contributes to the distribution of T_S. Since T_S = max (T₁, T₂, …, T_n), we apply the well-known Fisher–Tippett–Gnedenko theorem (23,24), which is a general result on extreme-value distributions (EVD). In order to use this theorem, we make the following two assumptions: (i) T₁, T₂, …, T_n are statistically independent, i.e. each inter-origin replication time is an independent random variable, incorporating the essential information about origin variability and rates; (ii) T_i follows a stretched-exponential distribution, independent of i, i.e.

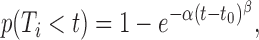(3)

when t > t₀, while p(T_i < t) = 0 when t ≤ t₀. The (positive) parameters α, β and t₀, effectively describe the consequences of the model parameters 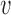, γ, inter-origin distances (d₁, d₂, ..., d_n) and origin strengths (λ₁, λ₂, ..., λ_n) on completion timing of inter-origin regions (see below and Supplementary Text), and can be obtained by fitting the distribution of replication time for a typical inter-origin region (obtained from simulations) with Eq. (3).

Our fits show that Eq. (3) is a remarkably good phenomenological approximation of the distribution of T_i (see Supplementary Text and Supplementary Figure S3), thus justifying assumption (ii) above. Note that the fitted stretched exponential form also incorporates effectively the coupling existing between different inter-origin regions. Indeed, neighboring regions are correlated since they use a pair of replication forks stemming from their common origin. Moreover, even distant inter-origin regions can share the same fork if they are passively replicated. In order to justify the assumption (i), we tested the effect of the correlation between different regions, by sampling T₁, T₂, …, T_n from the distribution in Eq. (3) independently and then taking their maximum 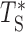. We verified that the difference between the distribution of 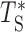and that of T_S obtained from simulation (where the correlations are present) is small. Therefore, the effect of these relatively short-ranged correlations can be, to a first approximation, neglected at the scale of the chromosomes and of the genome, and described by the effective stretched-exponential form (see Supplementary Figure S4).

Based on these assumptions, we can use the Fisher–Tippett–Gnedenko theorem and derive the following cumulative distribution function for T_S as a function of the number of origins n and the parameters α, β and t₀ (the calculation is detailed in the Supplementary Text):

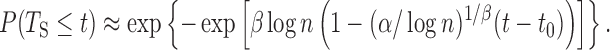(4)

Equation (4) gives a direct estimate of the distribution of the S-phase duration in this second scenario, which we term ‘extreme-value’ or ‘EVD’ regime. The resulting distribution is universal, since it does not depend on the detailed positions and rates of the origins, and depends in a simple way on the parameters α, β, t₀ and n. Although the extreme-value estimate should apply to the case of large n, the approximation Eq. (4) holds to a satisfactory extent also for realistic values, when n is order 10 (see Supplementary Figure S12). We also derived approximate analytical expressions for α, β and t₀ as functions of the parameters 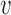, γ, for a ‘typical’ region characterized by 〈λ〉 and 〈d〉 under the assumption of negligible interference from non-neighbor origins (see Supplementary Text).

The procedure by which we apply Eqs. (3) and (4) is the following. Given inter-origin distances and origins strengths assigned arbitrarily or inferred from empirical data, the simulation of the replication of a chromosome gives the distribution of T_i and T_S. A fit of the distribution of T_i from simulation using Eq. (3) gives the parameters α, β and t₀. Finally, the EVD estimate for the distribution of T_S, can be obtained from Eq. (4), and compared with the distribution of T_S form simulations. This procedure can be seen as a variant of the method introduced in (15,16) applicable to the case of discrete origins (see Discussion).

Figure 2B shows one example where one circular chromosome has 10 origins with identical strengths and identical inter-origin distances. The estimated distribution of S-phase duration from Eq. (4) is well-matched with the simulated one (Figure 2D). Figure 2 also shows how the bottleneck estimate works for the opposite scenario, and compares simulations with both estimates in the two different regimes. Similar to Figure 2, Supplementary Figure S5 shows the existence of the two regimes in presence of a single origin affecting the two neighboring inter-origin regions. In the bottleneck regime, these two regions replicate much later than the others, because their common origin is much weaker than the other origins; the S-phase duration is then dominated by their replication time. This case also illustrates how the bottleneck regime may not be limited to a single inter-origin region. Finally, Supplementary Figure S6 shows the distribution of the inter-origin completion times T_i in the cases presented in Figure 2 and Supplementary Figure S5. This analysis illustrates how extra peaks in the right tail of T_i distribution relate to the failure of the extreme-value estimate for the distribution of S-phase duration. These examples indicate that, as expected, the presence of outliers in the values of T_i (exceedingly slowly-replicating regions) is responsible for the onset of the bottleneck behavior.

The extreme-value regime is robust to perturbations increasing the replication timing of a local region

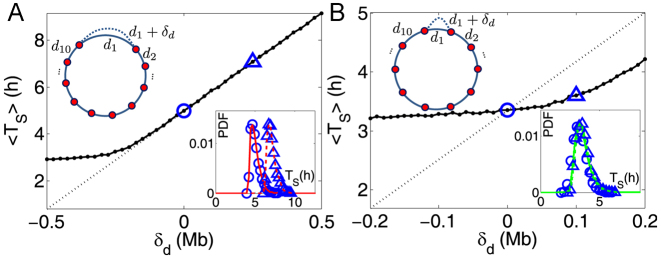
Origin number, origin strengths and inter-origin distances can be perturbed due to genetic change (DNA mutation or recombination), over evolution, and due to epigenetic effects such as binding of specific agents. We can compare the robustness of the two regimes identified above to perturbations of these parameters. We consider in particular the elongation of a single inter-origin distance d_i↦d_i + δ_d (similar results to those reported below are obtained for a perturbation affecting the strength of a single origin, see Supplementary Figure S7). In such case, the change of T_i is approximately equal to δ_d/2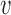. In the bottleneck regime, if the perturbed inter-origin region is the slowest-replicating one, 〈T_S〉 increases linearly with δ_d with slope 1/2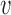, and the distribution of T_S shifts by a delay δ_d/2 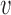(Figure 3A). In the extreme-value regime, instead, there is no single bottleneck inter-origin region, and the change of T_S with the perturbation turns out to be much smaller than δ_d/2 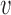(Figure 3B). Notice that in both regimes the variability of the S-phase duration around its average is not affected sensibly (insets of Figure 3).

Figure 3.

Effects of perturbations of a single inter-origin region on S-phase duration. (A) The bottleneck inter-origin region of the chromosome shown in Figure 2A is perturbed by increasing its length by δ_d (i.e. d₁ → d₁ + δ_d). The black solid line with points is the average S-phase duration, which increases linearly with δ_d. The black dotted line, with slope 1/(2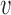), is a guide to the eye. The inset shows that the perturbation shifts the distribution of T_S by δ_d/2 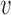(circles are simulations for the unperturbed chromosome, and triangles correspond to δ_d = d₁/2; the two curves are the analytical estimates in the bottleneck regime). (B) The same perturbation as in (A) is performed on an inter-origin region of the chromosome shown in Figure 2B, which lies in the EVD regime. Symbols are as in (A). The distribution of T_S is robust to this perturbation.

In summary, the bottleneck region is ‘sensitive’ to the specific perturbations considered, since termination of replication is highly dependent on a single inter-origin region, while the EVD regime is ‘robust’, as the effect of small local perturbations can be absorbed by passive replication from nearby origins (6).

Diversity between completion times of inter-origin regions sets the regime of the replication program

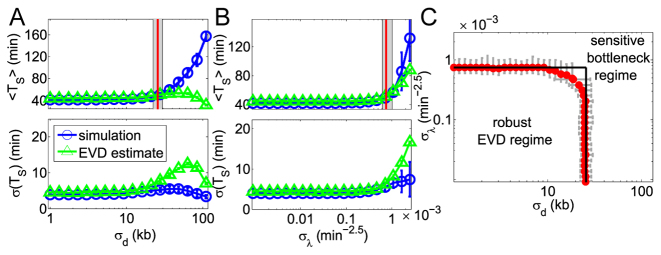
The cases discussed above (Figure 2) recapitulate the expected behavior in case of high versus small variability of the typical completion time of different inter-origin regions. One can expect that if the variability of the inter-origin distances is large, or origin strengths are heterogenous, it will be more likely to produce a bottleneck region, which in turn will trivially affect replication timing. Conversely, the replication program will be in the extreme-value regime if the completion times of all regions are comparable. In order to show this, we tested systematically how average and variability of T_S change with the variability of inter-origin distances and origin strengths in randomly generated genomes. In this analysis, origin spacings and strengths are assigned according to the prescribed probability distributions shown in Eq. (2), with varying parameters (see the Methods for a precise description of how chromosomes are generated).

Figure 4 shows the results. Importantly, we find that the regimes defined above as extreme cases apply for most parameter sets, and there is only a small region of the parameters where we find intermediate cases. Specifically, two parameters, the standard deviations σ_d and σ_λ, of the inter-origins distances and the origin strengths respectively, are sufficient to characterize the system. Figure 4A indicates that as long as σ_d is smaller than a threshold (∼30 kb), the average 〈T_S〉 and the standard deviation σ(T_S) of the replication time are approximately constant. In this regime, the extreme-value estimate matches well the simulation results. When σ_d exceeds the threshold, the average of T_S increases and its standard deviation decreases with large fluctuations. In this other regime, both 〈T_S〉 and σ(T_S) deviate from the EVD estimate. Figure 4B shows that varying σ_λ at fixed origin positions produces a similar behavior (although with smaller deviations from the EVD estimates).

Figure 4.

The variabilities of the inter-origin distances, σ_d, and of the firing strengths, σ_λ, set the replication regime. (A, B) Average S phase duration (top panels) and its standard deviation (bottom panel) as functions of σ_d (panel A) or σ_λ (panel B), obtained by simulations of the model (blue circles and lines) and by the EVD estimate (green triangles and lines). Fifty samples of inter-origin distances and origin strengths are chosen according to the distributions in Eq. (2). Red lines indicate the transition points where the simulated 〈〈T_S〉〉 is 20% larger than at σ_d = 0 and σ_λ = 0. The border lines of the grey area show the transition points for 〈〈T_S〉〉 + σ (〈T_S〉) and 〈〈T_S〉〉 − σ (〈T_S〉) respectively. (C) Phase diagram separating the EVD and bottleneck regimes. Red transition points with error bars (obtained with the method shown in (A) and (B)) form an approximate rectangle phase boundary. Parameters: fork velocity 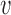= 1.81 kb/min, origin number n = 20, γ = 1.5, 〈d〉 =28.13 kb, 〈λ〉 =6.17 × 10⁻⁴ min ^−2.5, σ_λ = 0 (A) and σ_d = 0 (B).

This analysis shows an emergent dichotomy between these two regimes, which depends on the distribution of T_i (i.e. both inter-origin distances and origin firing rates). In principle, more complex situations where e.g. a subset of many comparably ‘slow’ inter-origin regions dominates S-phase timing is possible, but this situation is very rare (and negligible) if origin rates and positions are generated with the criteria used here (given by Eq. 2). De facto, under these prescriptions, motivated by empirical properties of origin positions and strengths, only the two regimes defined above as extreme cases were observable. For example, one can imagine a situation where each chromosome are, separately, in the EVD regime, but the replication of one of the chromosomes takes considerably longer than the others on average, which may lead the S-phase duration to be in the bottleneck regime. However, we find that this situation is essentially never found if origin rates and positions have empirically relevant values (i.e. for all realizations with empirical means and variances of inter-origin distances and origin firing rates). Qualitatively, this will always be the case if the distribution of T_i shows a single mode, and there are very few, or just one exceptional late-replicating region.

This behavior suggests to define ‘critical values’ of σ_d and σ_λ, separating the extreme-value regime from the bottleneck regime, as follows. We define the 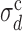, at fixed σ_λ, as the value of σ_d at which 〈T_S〉 (possibly averaged over many samples of the origin configuration too, denoted 〈〈T_S〉〉) is 20% larger than at σ_d = 0 and σ_λ = 0. The results presented here do not depend appreciably on this threshold and do not change much if we define 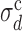as the value of σ_d at which 〈T_S〉 is 20% off the prediction of the EVD theory. The same definition holds for 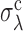at fixed σ_d. Surprisingly, 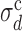turns out to be independent of σ_λ, and 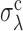independent of σ_d. The resulting ‘phase diagram’, shown in Figure 4C, separates the space of parameters into an approximately rectangular region where the EVD estimate is precise, and an outer region where heterogeneities dominate, which is identified with the bottleneck regime.

We can give a simple argument for why this phase diagram is approximately rectangle-shaped. Intuitively, a large σ_d increases the probability of extracting a very large value for d, and a large σ_λ increases the probability of extracting a very small λ. In a realization of a randomized chromosome, such rare events may generate an extremely slow-replicating region acting as the bottleneck. Clearly, drawing an extreme value for only one of the two variables is sufficient to generate the bottleneck region, giving rise to the two sides of the rectangle. For values of the variances of both variables that are below the individual thresholds, drawing a large d and small λ jointly makes the upper-right region of the rectangle rounded. However, such joint extreme draws in the same inter-origin region are very rare, because the two variables are drawn independently, so the rounded upper-right corner is very small, as visible in Figure 4C.

The yeast replication program is just inside the EVD regime and likely under selection for short S-phase duration

The results of the previous section indicate that the standard deviations of the origin distances and of the strengths are the most relevant parameters determining the regime of the distribution of the S-phase duration across cells. We inferred the parameters from replication timing data of the yeasts S. cerevisiae (6), L. kluyveri (7) and S. pombe (22). Such fits fully constrain the model parameters: fork velocity 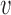, γ, start of the S phase t₀, origin strengths λ_i and inter-origin distances d_i, from which we calculated 〈d〉, 〈λ〉, σ_d and σ_λ, and simulated the duration of S phase and replication time of each chromosome (see Supplementary Text and Supplementary Figures S8–S10). In these simulations we consider circular chromosomes with n origins, and boundary effects are tested in the Supplementary Text and Supplementary Figure S2, and do not affect our main conclusions, indicating that, according to the model, the partition of the genome into the empirical number of unconnected chromosomes has little effect on the statistics of S-phase duration. The values of γ that were obtained as best fits of the empirical data (Supplementary Figure S8) were in line with previous analyses (e.g. (5,6)). In addition, we found that the standard deviation of the predicted S-phase duration decreases with the parameter γ (Supplementary Figure S9), which agrees with the finding of previous studies focused on X. laevis (15,16).

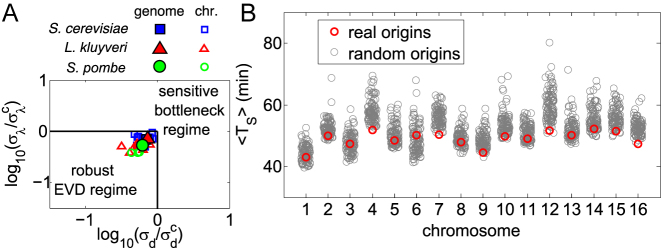
This analysis indicates that the whole-genome values of σ_d and σ_λ measured for S. cerevisiae, L. kluyveri and S. pombe place these genomes within the extreme-value regime. Rescaling σ_d and σ_λ by the crossover values 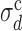and 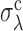respectively makes it possible to compare data with different mean T_S. This comparison (Figure 5A) shows that not only the genomic but also most of chromosomal parameters of L. kluyveri, S. cerevisiae and S. pombe are located in the extreme-value regime. With the fitted parameters, most of chromosomes and genomes are found in the extreme-value regime (as an example, see Supplementary Figure S10). Interestingly, all chromosomes (and the full genome) lie close to the transition line. This may be a consequence of the presence of competing optimization goals, such as replication speed (or reliability) and resource consumption by the replication machinery (16).

Figure 5.

The replication program of yeast is in the robust regime. (A) Symbols are the parameters of S. cerevisiae (blue squares), L. kluyveri (red triangles) and S. pombe (green circles), inferred from fits with replication timing data from (6,7,22) respectively (see Supplementary Table S1). Filled symbols correspond to the whole genome, hollow symbols to each chromosome. (B) For each chromosome of S. cerevisiae, the average S-phase duration (y axis) is compared (by simulations of the model) between empirical origin positions and firing strengths (red circles) and randomized origins with empirically fixed distributions (grey circles).

Furthermore, we considered data of two S. cerevisiae mutants. In one mutant, three specific origins in three different chromosomes (6, 7 and 10) were inactivated (6). The inactivation of a specific origin slows down the replication of the nearby region, which might cause a bottleneck. Our results show that this origin mutant is still in EVD regime (Supplementary Figure S13). Importantly, in this case the model should be able to make a precise prediction for the replication profile of the chromosomes where one origin is inactivated. Supplementary Figure S14 shows the prediction on the replication profile of origin mutant strain based on the parameters fitted from the data of wild-type strain (except that the three inactivated origins are deleted from the origin list). The model prediction is in fairly good agreement with data. The mismatch between prediction and data in some regions (but not others) is an interesting feature revealed by the model, and may result from experimental error or gene-expression adaptation of the mutants (6). The other mutant strain that we considered is isw2/nhp10, from the study of Vincent and coworkers (25), who analyzed the functional roles of the Isw2 and Ino80 complexes in DNA replication kinetics under stress. This study compares the behavior of wild type (wt) strain and a isw2/nhp10 mutant in the presence of MMS (DNA alkylating agent methyl methanesulfonate) and found that S-phase in isw2/nhp10 is extended compared to the wt strain because the Isw2 and Ino80 complexes facilitate replication in late-replicating-regions and improve replication fork velocity. In agreement with these findings, the model fit of the data shows that isw2/nhp10 mutant has more inactive origins and smaller fork velocity. Such conditions may facilitate the onset of a bottleneck regime in the mutant compared to the wt strain. We found that S. cerevisiae wt strain treated with MMS still falls in the extreme-value regime. Conversely, some chromosomes (e.g. 13 and 15) of the isw2/nhp10 mutant are in the bottleneck regime, and in this case, the whole genome (entire S-phase), is driven in the bottleneck regime (see Supplementary Figure S15). Strikingly, the model makes a good prediction on the replication profile of the isw2/nhp10 mutant, using origin firing strengths and the γ values fitted from the wild-type strain experiments, and just adjusting two (global) parameters replication speed and an overall factor in all origin firing rates (Supplementary Figure S16). This provides a good cross-validation of the applicability of the model in a predictive framework.

A further question is whether we can detect signs of optimization in the duration of chromosome replication. Figure 5b compare the S-phase durations obtained from simulations of the model in two cases: (i) by using the origin positions and strengths from empirical data (see Supplementary Figure S10), and (ii) by using a null model with randomized parameters (both origin strengths and inter-origin distances) drawn according to Eq. (2), and preserving the empirical mean and variance. The results show that for some of the chromosomes the average replication timing T_S is close to the typical one obtained from randomized origins (e.g. chromosomes 1, 3, 5, 6, 8, 11, 13 in S. cerevisiae). For other chromosomes (e.g. 2, 4, 7, 10, 12, 15, 16 in S. cerevisiae) the empirical average T_S is instead very close to the minimum reachable within their ensemble of randomizations. Remarkably, chromosomes with higher average replication timing in the randomized ensemble seem to be more subject to pressure towards decreasing their average T_S (Supplementary Figure S11). This result suggests that the whole replication program may be under selective pressure for fast replication.

DISCUSSION

The core of our results are analytical estimates that capture the cell-to-cell variability in S-phase duration based on the measurable parameters of replication kinetics. Extreme-value statistics has been applied to DNA replication before (15,16), but only to the case of organisms like X. laevis, where origin positions are not fixed and there is no spatial variability of initiation rates. To our knowledge, this method has not been applied systematically to fixed-origin organisms such as yeast. More specifically, (15) explores the case of a perfect lattice of equally spaced discrete origins with fixed and equal firing rates, but does not address the role of the variability of inter-origin replication times due to randomness in firing rates and inter-origin distance, which is relevant for fixed-origin organisms. Another difference is that the authors of (15,16) derive the coalescence distribution starting from their model, while here we assume a stretched-exponential, motivated by data analysis. Since their distribution is more complex (although the model is simpler), EVD estimate leads to a formula linking the parameters of the Gumbel distribution to the initiation parameters in the form of an implicit equation, that needs to be solved numerically. Conversely, the assumption that the shape of the distribution of T_i is given (and estimated from data), gives an explicit relationship between the parameters describing the T_i distribution and the Gumbel parameters, leading to simpler formulas and applicability to the case of discrete origins with different spacings and firing rates. The parameters of the T_i distribution have then to be related to the microscopic parameters (See Supplementary Text).

It is important to note that an approach based on extreme-value distribution theory is general (16). Simulations (including the model used here) are based on specific assumptions that are often not simple to test and many models on the market use slightly different assumptions. Instead, the extreme-value estimates are robust to different shades of assumptions used in the models available in the literature, and thus more comprehensive. Our estimates reveal universal behavior in the distribution of S-phase duration. There is a prescribed relation between mean and variance of S-phase duration, defining a ‘scaling’ behavior for its distribution. Such universality has been observed in cell-cycle periods and cell size (26,27). Qualitatively, we expect the same universality to hold in a regime when origins have <100% efficiencies, and some may not fire at all during S-phase. Origins that fire only in a fraction of the realizations are accounted for in our simulations, but they entail second-neighbor effects that are not currently accounted in our estimates.

There are hundreds of origins in a genome, but our analysis shows that the relevant parameters to capture the overall behavior are the means and variances of inter-origin distances and origin firing rates. Specifically, we find that two regimes describe most of the phenomenology, and they depend on the values of these effective variables. Importantly, the regimes identified here differ from those identified in (15), which just identify a critical spacing between discrete (equally spaced) origins, for which replication timing starts to be linear with inter-origin distance.

The notion that the last regions to replicate may tend to be different in every cell (our ‘extreme-value’ regime) has been proposed already by Hawkins et al. (6). The opposite regime where some specific regions tend to always replicate last (‘bottleneck region’), has been proposed for mammalian common fragile sites (28). Such regions of slow replication, pausing and frequent termination have also been described in yeast (6,29–31). These studies make it plausible to think that both extreme-value and bottleneck regimes may apply to yeast, despite our analysis based on replication kinetics data indicating some pressure towards the extreme-value regime. Another important case for what concerns replication termination is the rDNA locus, which cannot be analyzed in replication kinetics data based on microarrays/sequencing data due to its repetitive nature (∼150 identical copies in yeast). However, the large inter-origin distances, pseudo-unidirectional replication and epigenetic control of origin firing in this locus (32) make it a good candidate for the last sequence to replicate in yeast.

Importantly the model used here is similar to a set of previous studies, which have tested this approach and validated it with experimental data (3,5,6,8,15,33). Our analysis of S-phase duration in single cells is generic, and expected to be robust to variations of model details. The mutant data sets analyzed here also support the predictive power of the model in presence of perturbations and parameter changes, and hence validate the use of the model in a predictive framework. Our predictions are compatible with the available values for average S-phase duration, which can be roughly estimated through flow cytometry (6,7), and corresponds well to the values obtained by the model (around 60 min for S. cerevisiae, ref. 6). Other yeast studies found smaller values in other conditions (34), which would be interesting to study with the model. Additionally, we provide a prediction for the cell-to-cell variability of S-phase duration, which is an important step of the cell cycle. Indeed, completion of replication needs to be coordinated with growth and progression of the cell cycle stages (35,36). Cell-to-cell variability in replication kinetics makes the S phase subject to inherent stochasticity. Experimentally, measuring the cell-to-cell variation of the S-phase duration is a challenge. While some studies exist using mammalian (cancer) cell lines (37), they currently do not have the precision needed to allow a quantitative match with models. However, we expect that such measurements will become available in the near future, thanks to rapidly developing methods of single-cell biology (38). Our predictions define some key properties of the replication period that may be tested with, e.g., single-cell studies in budding yeast, using the parameters available from replication kinetics studies. In this model the S phase is (by itself) a ‘timer’, so its connection to cell size homeostasis must be affected by external mechanisms (35). S-phase duration has been measured on single E. coli cells, and found to be unlinked to cell size (39). Interestingly, our predictions of S-phase duration and variability as a function of chromosome copy numbers (Supplementary Figure S12) might apply to cancer cell lines with different levels of aneuploidy (37). Finally, there is the possibility of applying this framework to describe relevant perturbations (40,41). This could also help elucidate how response to DNA damage affects the replication timing and its variability across cells.

Intriguingly, we also found evidence of bias towards faster replication in empirical chromosomes compared to randomized ones. Thus, our overall findings support the hypothesis of a possible selective pressure for faster replication, and against bottlenecks. Other approaches have assumed optimization for faster replication and looked for optimal origin placement (42) or found other signs of optimality in similar data (5). Our results are in line with these findings, and isolate a complementary direction for such optimization. All these considerations support the biological importance of replication timing of inter-origin regions and its variability. However, the sources of the constraints remain an open question. Clearly, overall replication speed can increase indefinitely by increasing origin number and initiation rates. However, there are likely yet-to-be-characterized tradeoffs in these quantities, that prevent this from happening, and force the system to optimize the duration of replication in a smaller space of parameters. The molecular basis for such constraints likely lies at least in part in the finite resources available for initiation complexes (4).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

LabEx CALSIMLAB [ANR-11-LABX-0037-01 to Q.Z.] constituting a part of the ‘Investissements d’Avenir’ program [ANR-11-IDEX-0004-02]. Funding for open access charge: LabEx CALSIMLAB [ANR-11-LABX-0037-01].

Conflict of interest statement. None declared.