Resolving sugar puckers in RNA excited states exposes slow modes of repuckering dynamics

Abstract

Recent studies have shown that RNAs exist in dynamic equilibrium with short-lived low-abundance ‘excited states’ that form by reshuffling base pairs in and around non-canonical motifs. These conformational states are proposed to be rich in non-canonical motifs and to play roles in the folding and regulatory functions of non-coding RNAs but their structure proves difficult to characterize given their transient nature. Here, we describe an approach for determining sugar pucker conformation in RNA excited states through nuclear magnetic resonance measurements of C1΄ and C4΄ rotating frame spin relaxation (R_1ρ) in uniformly ¹³C/¹⁵N labeled RNA samples. Application to HIV-1 TAR exposed slow modes of sugar repuckering dynamics at the μs and ms timescale accompanying transitions between non-helical (C2΄-endo) to helical (C3΄-endo) conformations during formation of two distinct excited states. In contrast, we did not obtain any evidence for slow sugar repuckering dynamics for nucleotides in a variety of structural contexts that do not undergo non-helical to helical transitions. Our results outline a route for significantly improving the conformational characterization of RNA excited states and suggest that slow modes of repuckering dynamics gated by transient changes in secondary structure are quite common in RNA.

INTRODUCTION

Many regulatory RNAs undergo large conformational changes in response to a wide range of cellular cues to effect diverse functional outcomes (1–3). For example, protein-induced changes in RNA structure help direct the hierarchical assembly of ribonucleoprotein complexes such as the ribosome (4,5) and spliceosome, (6) while ligand-dependent changes in the structure of riboswitches underlie their ability to regulate gene expression (7,8). Conformational dynamics also allow ribozymes to assume the many different conformations required during their multi-step catalytic cycles (9–11). Understanding RNA conformational flexibility is also critical to achieving a predictive understanding of RNA folding (12–14) and for implementing structure-based approaches in RNA-targeted drug discovery (15–17).

Considerable effort has been directed toward the development of biophysical methods for characterizing the dynamic properties of RNA three-dimensional (3D) structure (7,18–21). These studies have exposed a variety of reoccurring motional modes in RNA including local motions of unpaired nucleotides and sugar repuckering dynamics at the ps–ns timescale, (22–25), collective motions of helical domains at the ns–μs timescale (26–29) and large-scale changes in secondary structure at timescales slower than ms (30,31). Recent developments in the application of nuclear magnetic resonance (NMR) relaxation dispersion (RD) techniques (32,33) to study conformational exchange in nucleic acids have uncovered another ubiquitous motional mode involving the transient reshuffling of base pairs in and around non-canonical motifs resulting in localized changes in secondary structure on the μs–ms timescale (34–38). These studies indicate that many RNAs exist in dynamic equilibrium with alternative secondary structures that are lowly populated (population typically <15%), short lived (lifetimes typically shorter than milliseconds), and that are rich in non-canonical motifs. These conformational states are often referred to as ‘excited states’ (ESs) (33,38) and are increasingly implicated in the mechanisms of regulatory RNAs where they can potentially function as fast conformational switches (34–37,39–42) or act as intermediates during RNA tertiary folding (14,38,43).

Characterizing the 3D structures of RNA ESs is crucial for elucidating their biological roles, for evaluating their suitability as targets in RNA-directed drug discovery, and for rigorously mapping out the entire RNA dynamic structural landscape. Techniques based on NMR RD can be used to detect RNA ESs and to determine their thermodynamic population, rates of exchange with the dominant ground state (GS) and chemical shifts, which in turn carry structural information. Thus far, NMR RD studies have targeted nuclei in the nucleobase and sugar moiety whose chemical shifts are primarily sensitive to base pairing and the glycosidic torsion angle (χ) (36,37). Analysis of these RNA ES chemical shifts aided by secondary structure prediction and mutations designed to trap or inhibit ESs have led to several proposed RNA ES structures all of which feature local reshuffling of bases in and around non-canonical motifs (see Figure 1A) (34,35).

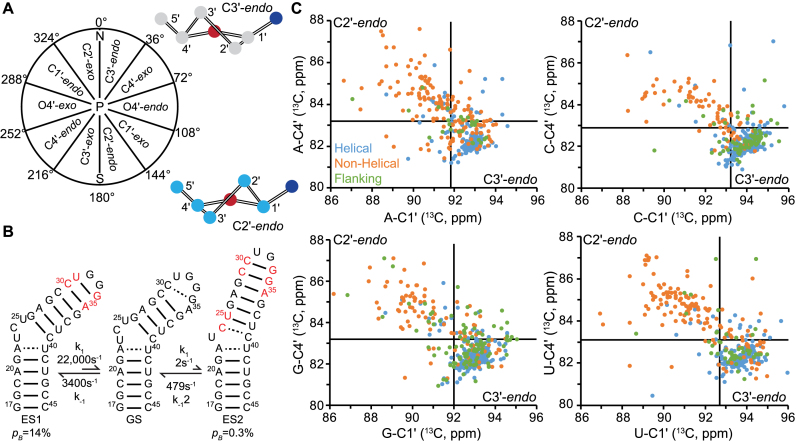
Figure 1.

C1΄ and C4΄ chemical shifts as probes of sugar pucker. (A) The different sugar pucker conformations defined by a pseudorotation angle, P. (B) Chemical exchange between the TAR ground state (GS) and two excited states (ES1 and ES2). Shown are the populations (p_B) and forward (k₁) and reverse (k_-1) rate constants obtained from Lee et al. (35). Nucleotides highlighted in red are expected to undergo sugar repuckering from C2΄-endo in the GS to C3΄-endo in ES1 or ES2 as they transition from non-helical to helical conformations. (C) C1΄ versus C4΄ chemical shift correlations obtained from the BMRB (54) for nucleotides classified as helical (blue), non-helical (orange) and flanking (green) based on the available RNA secondary structure. Plots shown for adenosine (N = 376), cytidine (N = 434), guanosine (N = 489) and uridine (N = 381). See Supplementary Figure S2 and Table S2 for chemical shift distributions. Solid lines indicate the upper boundaries for C3΄-endo chemical shift ranges as obtained based on the average and standard deviation of observed chemical shifts for helical nucleotides. The lower right quadrant represents the C3΄-endo sugar pucker; the upper left quadrant represents C2΄-endo pucker; the lower left quadrant likely represents C3΄-endo with low χ-angle (−130 ± 20°); and the upper right quadrant likely represents C3΄-endo with trans γ dihedral angle, or C2΄-endo with syn χ-angle.

Current NMR RD methods target nuclei that provide limited information regarding the sugar pucker and phosphodiester backbone conformation (34–37). As a result, there is still a great deal of uncertainty regarding even the secondary structure of these transient species. In addition, RNA ESs are proposed to be unusually rich in non-canonical motifs and it remains unclear whether these structures feature unusual sugar pucker and/or backbone conformations which could contribute to unique functional properties or provide distinguishing features for RNA-targeted drug discovery. Most if not all of the proposed RNA ESs feature nucleotides transitioning between unpaired and paired conformations. We hypothesized that such changes in base pairing could be coupled to changes in sugar pucker as nucleotides transition between non-helical (C2΄-endo) and helical (C3΄-endo) conformations (Figure 1A). This would in turn lead to sugar repuckering dynamics that is many orders of magnitude slower than is normally observed in RNA GSs (24,25,44–47) Indeed, the only RD NMR study employing Carr-Purcell-Meiboom-Gill (CPMG) and selectively C2΄/C4΄ ¹³C labeled nucleotides examining the ribose moiety provided evidence for slower μs timescale sugar repuckering dynamics for select nucleotides in a GCAA tetraloop (48). The origin of these slow sugar repuckering and whether they are a general mode of RNA dynamics remains to be determined.

Here, we developed an approach that combines NMR measurements of C1΄ and C4΄ rotating frame spin relaxation (R_1ρ) RD for determining sugar pucker conformation in RNA ESs using uniformly ¹³C/¹⁵N labeled RNA samples. Application to the transactivation response (TAR) element of human immunodeficiency virus type 1 (HIV-1) (49) exposed μs and ms timescale sugar repuckering dynamics that are coupled to non-helical to helical transitions accompanying formation of two distinct ESs. Our results provide new insights into the structure of RNA ESs and suggest that slow modes of repuckering dynamics gated by transient changes in secondary structure are quite common in RNA.

MATERIALS AND METHODS

Sample preparation

All RNA samples were prepared by in vitro transcription using T7 RNA polymerase (New England Biolabs Inc.) and synthetic DNA templates (Integrated DNA Technologies Inc.) with the T7 promoter sequence (TTAATACGACTCACTATA). Uniformly and residue type labeled samples were prepared by replacing the natural abundance nucleotides with uniformly ¹³C,¹⁵N-labeled nucleotide triphosphates (Cambridge Isotope Laboratories, Inc.). Samples were purified using a 33 × 52 cm, 20% (w/v) polyacrylamide (29:1) gel with 8 M urea and 20 mM Tris borate 1 mM ethylenediaminetetraacetate followed by electro-elution (Whatmann, GE Healthcare) in 40 mM Tris Acetate 1 mM ethylenediaminetetraacetic acid (EDTA) and ethanol precipitation. The RNA pellets were dissolved in water and the concentration adjusted to 60–100 μM before it was annealed by heating at 95°C for 10 min followed by rapid cooling on ice. Samples were buffer exchanged using a centrifugal concentrator (3 kDa molecular weight cutoff, Amicon Ultra EMD Milipore) into NMR buffer (15 mM sodium phosphate, 25 mM sodium chloride, 0.1 mM EDTA, pH 6.4) with a final concentration of 1.0–1.4 mM RNA. Samples were then flash frozen, lyophilized overnight and then resuspended in 100% D₂O (EMD Milipore).

To improve spectral resolution in the congested sugar spectra and maximize the number of sites with adequate resolution for RD measurements, we prepared four type labeled TAR samples in which only one type (A, C, G or U) of the nucleotide triphosphates used in in vitro transcription was replaced with a uniformly ¹³C,¹⁵N- nucleotide triphosphate (Supplementary Figure S1). All experiments were performed in 100% D₂O given the close proximity of the majority of ribose ¹H chemical shifts to water (4.7 ppm). We note that type labeling of samples was critical to the measurement of the near comprehensive RD dataset reported in this study.

Sugar pucker chemical shift relationships

Studies comparing density functional theory (DFT) predicted and experimentally measured values have shown that the ¹³C chemical shifts of the ribose ring can be used to determine the sugar pucker (50–53). In particular, C1΄ and C4΄ chemical shifts can be used to coarsely differentiate C2΄-endo and C3΄-endo sugar puckers. Here we expanded upon previous studies by examining a total of 65 RNA entries in the Biological Magnetic Resonance Data Bank (BMRB) (54) with complete or near complete (>80%) ¹³C assignments of ribose chemical shifts to confirm the relationship between C1΄ and C4΄ chemical shifts and sugar pucker (see Supplementary Table S1). We chose to use RNA secondary structure to probe chemical shift trends, since there are often few direct constraints on the sugar puckers in NMR structures, noting that most helical nucleotides adopt the C3΄-endo sugar pucker while non-helical nucleotides (e.g. bulges and apical loops) are expected to predominantly adopt a C2΄-endo sugar pucker (55,56). It should be noted that there can be some errors in chemical shift referencing and even misassignments in BMRB entries (57). Therefore, each entry was evaluated according to the method outlined by Aeschbacher et al. (57) which utilizes the highly conserved C1΄ and C3΄ of the 3΄-end cytidine to establish systematic referencing errors. In the event that this was not possible (e.g. due to absence of 3΄-end cytidine), we used the added criteria of average C1΄ values <89 ppm and C4΄ values <79 ppm to determine if chemical shifts were improperly referenced. Each entry was then assigned a secondary structure identification code: helical (any base paired nucleotide with both neighbors also engaged in base pairing interactions), non-helical (loops and bulges) and flanking (base paired nucleotides adjacent to non-helical elements) based solely on secondary structure. Terminal ends and modified bases were excluded from analysis. The average and standard deviation of C1΄ and C4΄ chemical shifts for nucleotides classified as helical were used to define the boundaries C3΄-endo sugar pucker on C1΄, C4΄ correlation plots for each base type as shown in Figure 1C (see Supplementary Figure S2 and Table S2 for exact values).

NMR experiments

Resonance assignments

All NMR assignment experiments were performed on a Bruker Avance III 600-MHz NMR spectrometer or Bruker Avance III 700-MHz spectrometer equipped with a 5-mm triple-resonance cryogenic probe. The NMR assignments of HIV-1 TAR aromatic and C1΄-H1΄ were previously published (27). Resonances in UUCG-ES2-TAR were assigned using 2D ¹H-¹³C Heteronuclear Single Quantum Coherence (HSQC), ¹H-¹⁵N and HCN through-bond correlation experiments, and 2D ¹H-¹H Nuclear Overhauser Effect Spectroscopy (NOESY) experiments. 3D HCCH-total correlation spectroscopy (TOCSY) experiments were used to unambiguously assign the ribose resonances of both HIV-1 TAR and UUCG-ES2-TAR (58). Type labeled samples were used to reduce spectral crowding and to allow for more facile assignment of resonances. Finally, ¹H-¹H double quantum filtered correlation spectroscopy (COSY) was used to qualitatively assess sugar pucker in UUCG-ES2-TAR based on cross peak intensity and ³J_H1΄,H2΄ scalar couplings. Both C2΄-endo and C1΄-exo have ³J_H1΄,H2΄ ∼ 10 Hz, however, it is common practice to refer to nucleotides with ³J_H1΄,H2΄ ∼ 10 Hz, or a strong cross peak as C2΄-endo (24,59,60).

¹³C R_1ρ relaxation dispersion

¹³C RD experiments were conducted on 600 MHz and 700 MHz Bruker Avance III spectrometers equipped with cryogenic probes at 10, 25 and 35°C using 1.0–1.4 mM type labeled HIV-1 TAR samples in in 15 mM sodium phosphate 25 mM NaCl, 0.1 mM EDTA, pH 6.4 and 100% D₂O. On- and off-resonance RD profiles were measured using various spin lock offsets (ω₁) and spin lock powers (Ω) listed in Supplementary Table S4 for each spin of interest and six to nine unique delay times. We used the previously described 1D R_1ρ experiment (61) which broadens the range of spin lock powers that can be used relative to conventional 2D R_1ρ which is typically limited to powers >1000 Hz due to the difficulty in aligning many spins with a broad range of chemical shift frequencies along their distinct effective fields (61–63). The 1D experiment uses selective Hartmann-Hahn polarization transfers to excite specific spins of interest and collect data in a 1D manner (63). Because only one spin is aligned along its effective field, it is possible to use significantly weaker RF fields for a full range of 150–3500 Hz (61).

The lowest spin-lock power attainable is predominately limited by ∼3× the largest homonuclear scalar coupling which for C4΄ corresponds to 3 × ¹J_C4΄C5΄ ∼130 Hz (63). By using a continuous low spin-lock RF field rather than hard 180° pulses, it is also possible to suppress or eliminate unwanted C–C interactions in uniformly ¹³C/¹⁵N labeled samples (23,64). Consistent heating throughout a given experiment is maintained by a heat-compensation element that applies far off-resonance ¹H and ¹³C/¹⁵N spin-locks for a given amount of time (T_max-T_relax), where T_max is the longest time delay and T_relax is the time delay in a given scan (61).

When using uniformly labeled nucleotides, care must be taken to avoid Hartman-Hahn matching conditions owing to sizable homonuclear ¹³C-¹³C scalar couplings between ribose atoms (¹J_C4΄-C3΄ ∼ 38 Hz, and ¹J_C4΄C5΄ ∼ 43 Hz) (65). The maximum efficiency of Hartman-Hahn transfer between coupled spins I and S is given by:

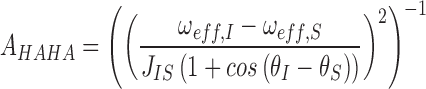where, ω_eff,X = (ω₁² + Ω_X²)^1/2 is the effective spinlock strength at spin X, J_IS is the scalar coupling constant, ω₁ is the applied spin lock field strength, Ω_x frequency offset relative to spin X, with 0 being on resonance and θ_X = arctan(ω₁/Ω_X) is the tip angle of the magnetization of spin X with respect to the static magnetic field. This results in a maximum when ω₁ = −0.5*(δ_I-δ_S) where δ_I and δ_S are the observed chemical shifts of I and S. Since C1΄ is only coupled to C2΄ which is >17ppm upfield shifted, it is possible to avoid Hartmann-Hahn conditions by not sampling offsets near 1000–1300 Hz. C4΄, however, is coupled to both C5΄ and C3΄. C5΄ is on average 17 ppm upfield shifted and Hartmann-Hahn conditions can be avoided by not sampling offsets near 1000–1300 Hz. On the other hand, C3΄ is only 7–10 ppm upfield shifted and therefore offsets of 500–700 Hz must also be avoided (Supplementary Figure S2B).

R_1ρ data analysis

Peak intensities at each delay time were calculated using NMRPipe, (66) which were then fit to a mono-exponential function using an in-house python script to determine the rotating frame relaxation rate, R_1ρ. Standard Monte Carlo simulations (500 iterations) were used to estimate error. Exchange parameters were determined by fitting experimental R_1ρ values to numerically simulated R_1ρ values given by the Bloch-McConnell equations at each Ω and ω₁ values. Residual sums of squares were minimized with a bounded least-squares algorithm yielding best-fit exchange parameters (67). The uncertainty in the exchange parameters was calculated as the standard error of the fit (68). All data was fit to a two state model with initial magnetization aligned along the average effective field, (69) with the exception of A35-C4΄ and C30/24-C4΄ discussed below.

Prior studies showed that A35 experiences both μs (ES1) and ms (ES2) exchange such that the ES1 contributions to RD can be minimized by increasing the temperature to 35°C, effectively pushing ES1 exchange into the fast exchange limit (69). The RD profiles measured for A35-C4΄ at 25°C could be satisfactorily fit assuming a three-state model yielding exchange parameters that are consistent with ES1 and ES2 (Supplementary Table S5). The best fit model was obtained when the population and exchange rate for ES2 were fixed (see Supplementary Table S5 for exact values), as determined by Akaike information criterion (70) and Bayesian information criterion (70). The resulting −2.1 ppm and −2.5 ppm upfield shift observed for A35-C4΄ is consistent with C2΄-endo to C3΄-endo sugar repuckering on both the μs and ms timescale. The ES2 exchange contribution to A35-C4΄ RD was verified by repeating RD experiment at 35°C where the ES1 contribution is minimized (35). A two-state fit to the RD profiles yielded the same population and chemical shift for the ms exchange to those obtained using the three-state at 25°C.

RESULTS AND DISCUSSION

C1΄ and C4΄ chemical shifts as reporters of sugar pucker

Thus far, RD measurements on the sugar moiety have primarily focused on the anomeric C1΄ which enjoys superior spectral resolution and which can be selectively irradiated to suppress unwanted C1΄-C2΄ interactions in uniformly ¹³C/¹⁵N labeled samples (33,35,36,71). The C1΄ chemical shift can show modest variations with sugar pucker (typically <2 ppm) but it exhibits a stronger dependence on the glycosidic torsion angle χ (72–76). Because A-form helical Watson–Crick (C3΄-endo) nucleotides tend to favor an anti conformation (χ = −161 ± 19°), while C2΄-endo nucleotides tend to favor a high anti conformation (χ < −140°), C1΄ RD data can indirectly report on changes in sugar pucker accompanying ESs formation (55,56). However, the enrichment of ESs with non-canonical motifs and mispairs, which often have unusual χ-angles, (55,56) can easily lead to variations in C1΄ chemical shift solely due to changes in the χ-angle which could be misinterpreted as changes in sugar pucker. Due to these limitations, C1΄ RD studies have not provided definitive information regarding changes in sugar pucker that might accompany formation of RNA ESs.

The remaining ribose carbon chemical shifts (C2΄-C5΄) strongly depend on sugar pucker making them good RD probes of sugar pucker in RNA ESs (73–76). However, in practice, severe spectral congestion complicates RD measurements for C2΄ and C3΄ (Supplementary Figure S1) while relaxation contributions from geminal protons complicate RD measurements for C5΄. Some of the above problems can be addressed through specific ¹³C-labeling of C2΄ and C4΄ (48). However, the site-labeled nucleotide triphosphates are not commercially available. As an alternative approach, we targeted C4΄ which enjoys better spectral resolution and a chemical shift predominantly determined by the sugar pucker, with a very weak dependence on the χ-angle (76). As we show here, C4΄ R_1ρ RD data can be reliably and conveniently measured in uniformly ¹³C/¹⁵N residue-type labeled RNA samples without the need for specialized labeling of the nucleotides (Supplementary Figures S1 and 2).

Prior studies have shown that C1΄ and C4΄ chemical shifts alone (57) or in combination with C5΄ (50,52,75) can be used to distinguish C3΄-endo and C2΄-endo conformations in RNA. These studies have shown that C3΄-endo nucleotides tend to have downfield shifted C1΄ and upfield shifted C4΄ chemical shifts placing them in the lower right quadrant of a C1΄,C4΄ correlation plot whereas C2΄-endo nucleotides tend to have upfield shifted C1΄ and downfield shifted C4΄ chemical shifts placing them in the upper right quadrant of the correlation plot (Figure 1C).

To verify these trends, we conducted a survey of over sixty chemical shift assignment entries in the biological magnetic resonance bank (BMRB) (Figure 1C, Supplementary Figures S2 and 3) (54). As shown in Figure 1C, ∼83% of helical nucleotides (base paired nucleotides that are flanked by base paired nucleotides) have chemical shifts that fall within a narrow range in the lower right quadrant of the C1΄-C4΄ correlation plot as expected for nucleotides with a C3΄-endo conformation and anti χ-angles (Figure 1C). As expected, deviations from the C3΄-endo region are more prevalent for base paired nucleotides flanking unpaired motifs such as bulges and apical loops most likely due to variations in the χ-angle (Figure 1C, Supplementary Figure S3 and Table S3). Only 8% of helical nucleotides fall outside the lower right quadrant without an obvious structural explanation; some of these cases could reflect misassignments or improper referencing (57). On the other hand, most (53%) non-helical nucleotides (defined as unpaired nucleotides) fall in the upper left, C2΄-endo, quadrant of the C1΄, C4΄ correlation plot and have broader chemical shift distributions relative to helical nucleotides reflecting a broader range of sugar puckers. Approximately 25% of non-helical nucleotides fall within the C3΄-endo region and likely reflect nucleotides that stack in a helical manner without base pairing in non-canonical motifs such as internal loops, three-way junctions and GNRA tetraloops (see Supplementary Figure S3 and Table S3).

There were noteworthy exceptions to the above linear trend (Supplementary Figure S3 and Table S3) most of which represent mispairs, their neighbors and non-canonical motifs that can have unique backbone and/or χ angles. In particular, deviations into the lower left quadrant (6%) represent C3΄-endo nucleotides with upfield shifted C1΄ resonances due to a high anti χ-angle relative to the normal anti (χ = −161 ± 19°) conformation (Figure 1C and Supplementary Figure S3) (72–74,76). Deviations into the upper right quadrant (6%) can include C2΄-endo nucleotides with a downfield shifted C1΄ due to a more anti/syn χ-angle, (73,74,76) or C3΄-endo nucleotides with downfield shifted C4΄ due to variations in the backbone geometry.

These results show that together, C1΄ and C4΄ chemical shifts provide a robust reporter of sugar pucker, especially when interpreted in concert with the RNA secondary structure. It is also clear from our survey of the BMRB that certain nucleotides with unusual backbone conformations and/or that adopt nan-canonical geometries can prove challenging to interpret unambiguously and could potentially even lead to erroneous results if not considered within the broader context of the RNA ES secondary structure. This emphasizes the importance of obtaining models for the ES secondary structure for helping identify such non-canonical motifs using a broad set of RD measurements, secondary structure prediction programs and mutations/single atom substitutions. (34–36)

Absence of slow sugar repuckering in helical nucleotides

We carried out C1΄ and C4΄ R_1ρ RD measurements to characterize the sugar puckers in two previously characterized ESs (35,71) in the transactivation response element (TAR) from the human immunodeficiency virus type 1 (HIV-1) (Figure 1B). Prior R_1ρ RD studies (35,71) targeting the anomeric sugar (C1΄) and base (C2, C6, C8 and N1/N3) nuclei showed that TAR exists in dynamic equilibrium with two short-lived and low-populated ESs referred to as ES1 and ES2 (Figure 1B). ES1 has a relatively large population (p_B = 14%), exhibits exchange kinetics on the μs timescale (k_ex = k₁ + k_-1 ∼ 25 000 s⁻¹), and involves the reshuffling of base pairs within the apical loop (Figure 1B). (34) ES2 has a lower population (p_B = 0.4%), exhibits slower exchange kinetics on the ms timescale (k_ex ∼ 500 s⁻¹), and features a larger rearrangement in secondary structure that reshuffles nucleotides in both the bulge and apical loop resulting in the formation of an extended upper helix containing multiple non-canonical mispairs (Figure 1B) (35). Dynamics toward either ES1 or ES2 results in nucleotides transitioning between non-helical and helical conformations that could result in coupled changes in sugar pucker.

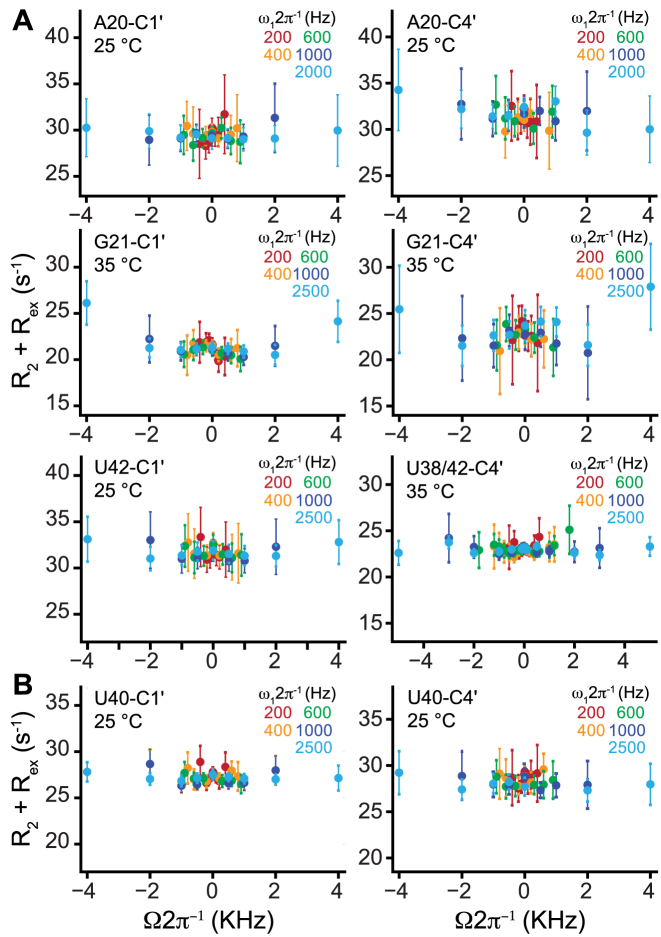
We first carried out C1΄/C4΄ R_1ρ RD experiments on helical nucleotides that do not experience changes in secondary structure or base pairing on forming either ES1 or ES2. The R_1ρ experiment measures the exchange contribution (R_ex) to intrinsic transverse relaxation (R_2,int) arising due to chemical exchange with an ES. The experiment entails measuring R_2,eff = R_2,int + R_ex as a function of varying continuous wave spin lock power (Ω) and offset (ω₁). The resulting RD profiles, showing the variation of R_2,eff with spin lock power and offset frequency, can be fitted to extract exchange parameters of interest, including the population of the ES (p_B), the exchange rate (k_ex = k₁ + k_-1), and the difference in chemical shift between the GS and ES (Δω = ω_ES – ω_GS) which carries information regarding changes in structure (32,77). For these experiments, we prepared residue-type (A, G, C and U) ¹³C/¹⁵N labeled TAR samples to alleviate spectral crowding in the C4΄-H4΄ correlation spectra allowing optimal measurements of C1΄ and C4΄ RD data (Supplementary Figure S1).

Based on an available NMR structure (1ARN Honglue: Should be 1ANR), (78) dynamic ensemble, (79) and C1΄/C4΄ chemical shifts (Supplementary Figure S4), Watson–Crick base pairs in TAR predominantly adopt the C3΄-endo conformation. As shown in Figure 2A, all of the C1΄ and C4΄ RD profiles measured for these helical nucleotides (A20, G21, U38 and U42) were flat, showing no evidence for μs-ms conformational exchange. Flat RD profiles were also observed when lowering (10°C) or increasing (35°C) the temperature (Supplementary Figure S6A), which may be expected to move the exchange rate into the range of RD detection. Flat RD profiles were also observed for junctional nucleotides U40 (Figure 2B) and C39 (Supplementary Figure S6B). Therefore, helical nucleotides with C3΄ sugar puckers that do not experience changes in base pairing upon forming ES1 or ES2 do not undergo slow μs-ms sugar repuckering dynamics detectable by NMR RD.

Figure 2.

No detectable slow sugar repuckering in HIV-1 TAR at nucleotides that do not undergo conformational changes when forming excited states. Shown are representative C1΄ or C4΄ off-resonance R_1ρ RD profiles collected on 600 and 700 MHz (¹H frequency) spectrometers for (A) helical (B) junctional nucleotides showing the absence of chemical exchange. Error bars represent experimental uncertainty determined by propagation of error determined based on a Monte Carlo analysis of monoexponential decay curves and the signal to noise. The sample conditions were 1.0–1.4 mM TAR in 15 mM sodium phosphate 25 mM NaCl, 0.1 mM EDTA, pH 6.4 and 100% D₂O.

μs timescale C2΄-endo to C3΄-endo repuckering

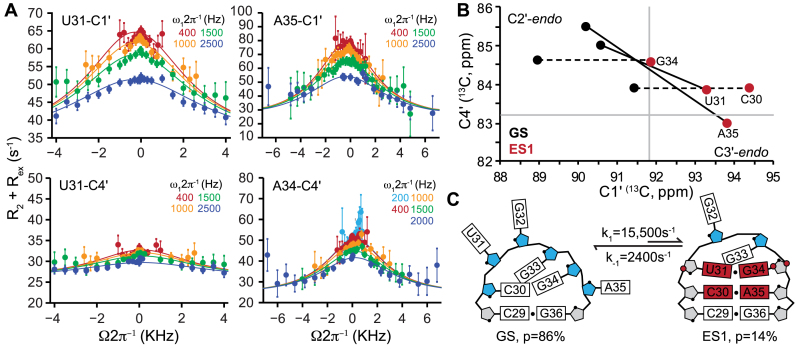
Next, we examined apical loop nucleotides that undergo changes in base pairing upon forming ES1 (Figure 1B). In the TAR GS, (78,79) apical loop nucleotides C30, U31, G34 and A35 are unpaired (non-helical) and adopt a predominantly C2΄-endo sugar pucker conformation. This is consistent with the GS C1΄ and C4΄ chemical shifts (Supplementary Figure S4). These nucleotides are proposed to form non-canonical mispairs in ES1 where they are likely to adopt a C3΄-endo conformation (see Figure 3C) (71). Indeed, we observed significant C1΄ and/or C4΄ RD for these apical loop nucleotides (Figure 3A and Supplementary Figure S7). Fitting of the individual RD data to a two-state model yielded similar p_B and k_ex parameters across the different sites, consistent with a concerted chemical exchange process involving formation of a single ES. Indeed, global fitting of the sugar RD data yielded exchange parameters (p_B = 14 ± 1% and k_ex = 18 000 ± 400 s⁻¹, see Supplementary Table S5) that are in excellent agreement with those determined previously for ES1 using a different set of RD data (p_B = 13.0 ± 0.2% and k_ex = 25 000 ± 700 s⁻¹) (35,71). The slightly slower k_ex can be attributed to use of 100% D₂O as compared to 90% H₂O 10% D₂O in the previous study and/or possibly other small differences in sample conditions.

Figure 3.

Microsecond timescale sugar repuckering in HIV-1 TAR tied to ES1 formation. (A) Representative examples of C1΄ and C4΄ off-resonance R_1ρ RD profiles collected on a 600 MHz (¹H frequency) spectrometer and 25°C for nucleotides involved in ES1 exchange. The sample conditions were 1.0–1.4 mM HIV-1 TAR in 15 mM sodium phosphate 25 mM NaCl, 0.1 mM EDTA, pH 6.4 and 100% D₂O. Solid lines represent global fits of the C1΄ and C4΄ RD data. Error bars represent experimental uncertainty determined by propagation of error determined based on a Monte Carlo analysis of monoexponential decay curves and the signal to noise. (B) Plot of ES1 C1΄ and C4΄ chemical shifts deduced from R_1ρ RD measurements showing transitions toward the helical C3΄-endo sugar pucker. Solid gray lines indicate the C2΄-endo / C3΄-endo boundaries (see Supplementary Table S2 for exact values). Dashed lines indicate nucleotides for which only C1΄ RD could be measured. (C) Secondary structure of the TAR apical loop in GS and ES1. Nucleotides with C2΄-endo (blue) and C3΄-endo (gray) based on sugar chemical shifts. Nucleotides that undergo changes in secondary structure are in red. The red circle on G34-C1΄ indicates a change in χ-angle from anti to syn conformation. Red circles on U31-C4΄, and G34-C4΄ indicate an increase in γ dihedral angle relative to the A-form helix.

The R_1ρ RD experiment can be used to determine the difference between the GS and ES chemical shifts (Δω = Ω_ES − Ω_GS) which can in turn be used to determine the chemical shift of the ES (32). However, for fast exchanging systems in which k_ex > 10 × Δω the sign and magnitude of delta omega can be difficult to measure reliably (32,69). We have demonstrated in prior studies that despite the fast rate of exchange (k_ex/Δω ∼ 7.5), the C1΄ and aromatic RD data could be used to reliably measure the sign and magnitude of Δω for TAR ES1 (69). This was also the case in our current study including C4΄ (Supplementary Figure S7) when carrying out two-state analysis of the C1΄ and/or C4΄ RD data.

The ES1 C1΄ and/or C4΄ chemical shifts for C30 and A35 obtained from two-state analysis of the RD data differ significantly from the GS (Figure 3B) and fall within the C3΄-endo region, consistent with a transition from a predominantly non-helical C2΄-endo conformation in the GS to a helical C3΄-endo conformation in ES1. The ES1 chemical shifts for U31 and G34, which form a tetraloop closing base pair in ES1, also differ significantly from their GS counterparts consistent with a change from C2΄-endo to C3΄-endo (Supplementary Figure S7). The C4΄ chemical shifts of these nucleotides did not fall within the C3΄-endo quadrant; rather they fall within the upper right quadrant consistent with placement of these nucleotides as closing tetraloop base pairs in ES1 as observed in our BMRB survey (Figure 1C and Supplementary Figure S3). Importantly, the unpaired nucleotides G32 and G33, which predominantly adopt C2΄-endo sugar pucker in the GS, remain unpaired in ES1, and correspondingly show no signs of RD (Supplementary Figure S6C) (see below). This shows that even flexible nucleotides with C2΄-endo sugar pucker that do not experience transitions between non-helical and helical environments upon forming an ES do not spontaneously undergo slow μs-ms sugar repuckering dynamics.

These results provide evidence for μs timescale sugar repuckering between a major (population ∼86%) C2΄-endo and minor (population ∼14%) C3΄-endo sugar conformations that are coupled to localized transitions in RNA secondary structure that lead to formation of an ES.

ms timescale C2΄-endo to C3΄-endo repuckering

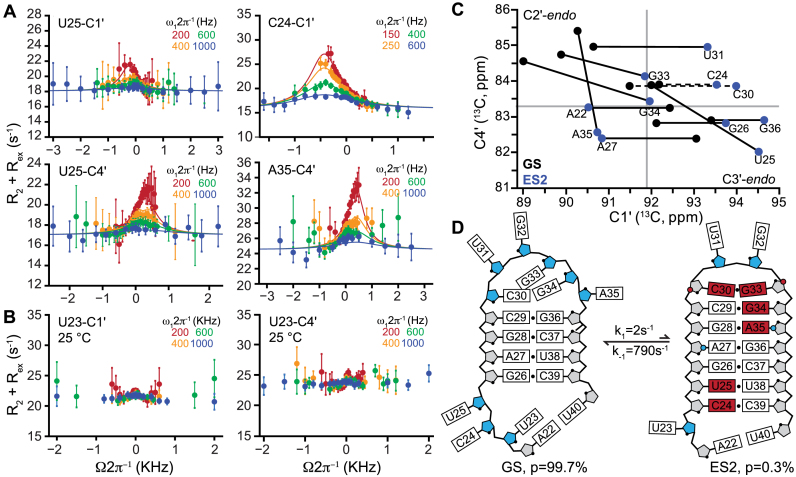
Next, we measured RD for bulge and upper stem nucleotides that experience changes in secondary structure when forming ES2. Most experiments were performed at 35°C in order to push exchange with ES1 to the fast limit and thereby suppress its contributions to the measured RD as described previously (35). Once again, we observed significant RD for C1΄ and/or C4΄ at nucleotides (C24, U25, C30, G33, G34 and A35) that transition between a non-helical to helical conformation upon forming ES2 (Figure 4A). The sugar RD data could be satisfactorily combined in a global fit to yield exchange parameters (p_B = 0.30 ± 0.02% and k_ex = 800 ± 80 s⁻¹, see Supplementary Table S5) that are in excellent agreement with those reported previously for ES2 using a different set of RD data (p_B = 0.40 ± 0.05 and k_ex = 474 ± 69 s⁻¹) (35). Due to the slower exchange, the sign and magnitude of the chemical shift can reliably be determined in the case of ES2 as evidenced by the clear positioning of the off-resonance RD profiles (Figure 4A and Supplementary Figure S8). The ES2 C1΄ and/or C4΄ chemical shifts for C24, U25, C30, G33, G34 and A35 differed significantly from their GS counterparts and fall within the C3΄-endo quadrant (Figure 4C), with minor deviations toward the upper right quadrant again observed for the apical loop closing base pair (G33-C4΄). Therefore, these nucleotides undergo much slower sugar repuckering dynamics on the ms timescale between a predominantly (population ∼99.6%) C2΄-endo conformation in the GS and an exceptionally low populated (population ∼0.4%) C3΄-endo conformation in ES2 (Figure 4D).

Figure 4.

Millisecond timescale sugar repuckering tied to ES2 formation. Representative C1΄ and C4΄ off-resonance R_1ρ RD profiles collected on a 600 MHz (¹H frequency) spectrometer and 35°C for nucleotides involved in ES2 exchange. The sample conditions were 1.0–1.4 mM HIV-1 TAR in 15 mM sodium phosphate 25 mM NaCl, 0.1 mM EDTA, pH 6.4 and 100% D₂O. Error bars represent experimental uncertainty determined by propagation of error determined based on a Monte Carlo analysis of monoexponential decay curves and the signal to noise. Solid lines represent global fits of the C1΄ and C4΄ RD data (see main text, Supplementary Table S5). Shown are RD profiles for nucleotides that (A) experience non-helical to helical transitions and (B) profiles observed for U23 which maintains a C2΄-endo conformation in both GS and ES2. (C) Plot of C1΄ and C4΄ chemical shifts of ES2 deduced from R_1ρ measurements showing transitions toward the helical C3΄-endo sugar pucker. Solid gray lines indicate C2΄-endo/C3΄-endo boundaries (see Supplementary Table S2 for exact values) Dashed lines indicate nucleotides for which the magnitude of C4΄ chemical shift could not be measured due to overlap. (D) Secondary structure of the TAR upper stem in GS and ES2. Nucleotides with C2΄-endo (blue) and C3΄-endo (gray) in ES2 as deduced using the RD-derived sugar chemical shifts are highlighted. Nucleotides that undergo changes in secondary structure are in red. The blue circles on A27-C1΄ and A35-C1΄ indicate a decrease in χ-angle relative to A-form helix. Red circles on C30-C4΄, and G33-C4΄ indicate an increase in the γ dihedral angle relative to A-form helix.

In ES2, A27 and A35 form tandem GA mispairs, which in the (GAGC)₂ sequence context, are characterized by C3΄-endo sugar pucker and a high anti (∼ −140°) χ-angle for the adenosine nucleotides (80). In the GS, A27 has a typical anti χ-angle (−160°) and C3΄-endo sugar pucker, while A35 has a high anti χ-angle and a C2΄-endo sugar pucker (Supplementary Figure S4) (78,79). Therefore, the observation of RD at A27-C1΄ but not A27-C4΄ can be attributed to a change in χ-angle while maintaining the C3΄-endo sugar pucker of the GS (Supplementary Figure S4). In contrast, the observation of RD at A35-C4΄ but not A35-C1΄ likely reflects a change in sugar pucker from C2΄-endo to C3΄-endo sensed by C4΄ RD but not C1΄ RD because the change in chemical shift due to sugar repuckering is effectively neutralized by the additional change in the χ-angle. These results show the advantages of combining C1΄ and C4΄ RD data to obtain structural information on RNA ESs and also highlight pitfalls when relying solely on C1΄ RD data. They also emphasize the importance of obtaining secondary structural models for the ES to aid the interpretation of the C1΄ and C4΄ chemical shifts in terms of sugar pucker.

As expected, no RD was observed for U38 and C39 (Supplementary Figure S6), which maintain a helical conformation in both the GS and ES2. The lack of detectable C1΄ and C4΄ RD for bulge residue U23 is also consistent with the sugar maintaining a predominantly C2΄-endo conformation in both the GS and ES2 (Figure 4B), as verified based on analysis of chemical shifts and ³J_H1΄H2΄ coupling constants in an ES2 trapped mutant (see below). Taken together, the RD data pinpoint slow sugar dynamics specifically to nucleotides that experience changes in base pairing upon forming an ES and otherwise provide no evidence for slow modes of repuckering dynamics in a variety of structural contexts.

Confirming the excited state sugar puckers using an ES2-stabilizing TAR mutant

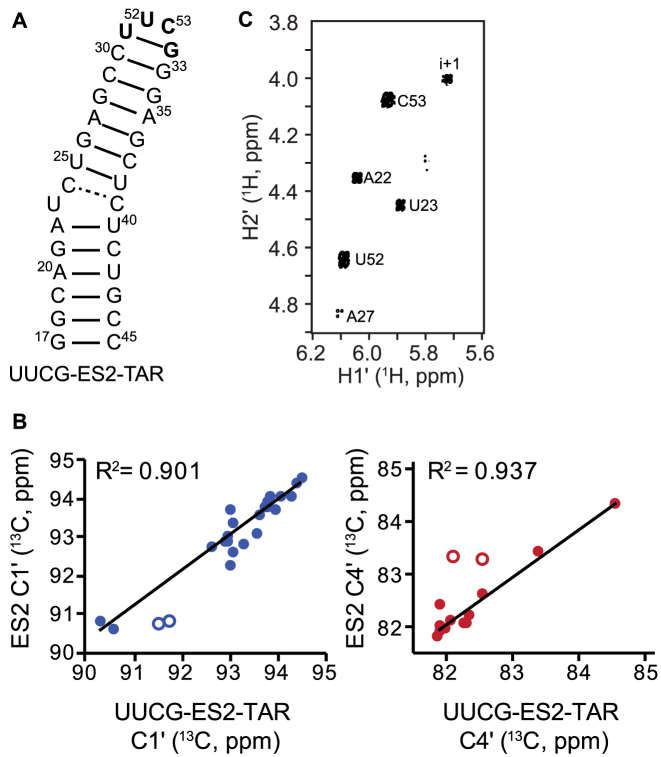
To verify the sugar puckers of the TAR ES2 deduced based on C1΄ and C4΄ RD, we analyzed the sugar pucker conformation of a previously described (81) TAR mutant (UUCG-ES2-TAR) which traps the ES2 conformation (Figure 5A). The mutant replaces U31 and G32, which form the apical loop in ES2, with a stable UUCG tetraloop, (81) thus trapping the rest of the molecule in an ES2-like conformation (Figure 5A). This mutant was previously shown to adopt an ES2 conformation based on the agreement between the mutant GS chemical shifts and those measured for ES2 in HIV-1 TAR using RD (81).

Figure 5.

Confirming R_1ρ-derived sugar puckers using an ES2-stabilizing mutant. (A) Secondary structure of ES2-mutant trap, UUCG-ES2-TAR, in which the extended upper helix is stabilized by replacing U31 and G32 with the highly stable UUCG tetraloop shown in bold. (B) Correlation plot comparing the C1΄ (blue) and C4΄ (red) chemical shifts measured in the UUCG-ES2-TAR mutant and TAR ES2 using RD measurements. Open circles indicate nucleotides with no detectable C1΄ or C4΄ RD, most likely due to low population of ES2 and/or small magnitude of Δω (|Δω| < 1 ppm). These points were excluded from the R² calculation. (C) ¹H,¹H DFQ-COSY spectrum collected on a 600 MHz (¹H frequency) spectrometer confirming a C2΄-endo conformation for A22 and U23 in ES2. Sample condition was 1.8 mM UUCG-ES2-TAR in 15 mM sodium phosphate 25 mM NaCl, 0.1 mM EDTA, pH 6.4 and 100% D₂O.

We observed excellent agreement between the ES2 C1΄ and C4΄ chemical shifts determined using RD and those measured for UUCG-ES2-TAR (Figure 5B). This suggests that nucleotides in UUCG-ES2-TAR adopt sugar puckers similar to those in ES2. Next, we confirmed the sugar pucker conformation in UUCG-ES2-TAR using ¹H-¹H double quantum filtered correlation spectroscopy (DQF-COSY) (24,59,60). In this experiment, strong cross peaks are observed for nucleotides with C2΄-endo sugar pucker due to sizeable ³J_H1΄H2΄ ∼ 10 Hz. Conversely, nucleotides with C3΄-endo sugar pucker have ³J_H1΄H2΄ < 2 Hz resulting in weak cross peaks that are often not observable (24).

As expected, we did not observe any cross peaks for nucleotides (C24, U25, C30, G33, G34, A35) that are proposed to adopt a C3΄-endo conformation in ES2 (Figure 5C). A weak cross peak was observed for A27 suggesting that although it is predominantly C3΄-endo, it may have some C2΄-endo character as well. Strong cross peaks were observed for U52 and C53 of the UUCG tetraloop consistent with pure C2΄-endo. The weaker cross peaks observed for bulge nucleotide U23 and the flanking nucleotide A22 are also consistent with a predominantly C2΄-endo conformation. These results help confirm that the slow motions sensed by C1΄ and C4΄ RD data represent slow transitions between C2΄-endo and C3΄-endo sugar conformations that accompany formation of TAR ES2.

Our studies suggest that there is a strong correlation of the glycosidic torsion angle, sugar pucker and the geometry of the base pairing interactions. Non-helical nucleotides transitioning to helical conformations consistently repucker to a C3΄-endo sugar pucker. This is accompanied by a decrease in χ-angle for nucleotides engaged in base pairing interactions with Watson–Crick like geometry. However, the glycosidic torsion angle can vary independently of sugar pucker in cases where the new base pairs occupy a non-Watson–Crick geometry. This is exemplified by the sheared tandem GAs’ in ES2, which have a C3΄-endo sugar pucker but retain C1΄ chemical shifts consistent with a high anti-χ angle more common to C2΄-endo sugar pucker. Future studies should more broadly examine correlations between the backbone, glycosidic angle and sugar pucker when transitioning between ground and excited states of RNA.

CONCLUSION

The combination of C1΄ and C4΄ R_1ρ RD data can be used to probe the sugar and backbone conformation of RNA ESs using uniformly ¹³C/¹⁵N labeled RNA samples. Application of this methodology to HIV-1 TAR exposed μs-ms sugar repuckering dynamics, which are several orders of magnitude slower than ps-ns sugar repuckering dynamics normally observed in RNA. These slow changes in sugar pucker accompany localized changes in secondary structure in which nucleotides transition between non-helical and helical conformations upon forming ESs. The results support the previously proposed TAR excited state secondary structures, (34,35) and provide new structural information about the backbone and sugar pucker conformations. Furthermore, the results confirm that the C3΄-endo sugar pucker is still preferred in helical regions of TAR ESs despite being unusually rich in non-canonical motifs. Our results provide no evidence for slow sugar repuckering in the absence of changes in secondary structure. This was the case for nucleotides in a variety of contexts including A-form helices, junctional base pairs and unpaired nucleotides. This strongly implies that the slow nature of the observed sugar puckering dynamics arises due to the energy barrier associated with breaking base pairs during secondary structural transitions rather than the barrier associated with changing the sugar pucker itself. By providing unique information regarding the sugar pucker and backbone conformation, the combination of C1΄ and C4΄ RD based method outlined in this work should greatly enhance the NMR conformational characterization of RNA ESs.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

US National Institutes of Health [PO1 GM0066275 to H.M.A.]. Funding for open access charge: US National Institutes of Health [PO1 GM0066275].

Conflict of interest statement. H.M.A.-H. is an advisor to and holds an ownership interest in Nymirum, an RNA-based drug-discovery company.