How proteins bind to DNA: target discrimination and dynamic sequence search by the telomeric protein TRF1

Abstract

Target search as performed by DNA-binding proteins is a complex process, in which multiple factors contribute to both thermodynamic discrimination of the target sequence from overwhelmingly abundant off-target sites and kinetic acceleration of dynamic sequence interrogation. TRF1, the protein that binds to telomeric tandem repeats, faces an intriguing variant of the search problem where target sites are clustered within short fragments of chromosomal DNA. In this study, we use extensive (>0.5 ms in total) MD simulations to study the dynamical aspects of sequence-specific binding of TRF1 at both telomeric and non-cognate DNA. For the first time, we describe the spontaneous formation of a sequence-specific native protein–DNA complex in atomistic detail, and study the mechanism by which proteins avoid off-target binding while retaining high affinity for target sites. Our calculated free energy landscapes reproduce the thermodynamics of sequence-specific binding, while statistical approaches allow for a comprehensive description of intermediate stages of complex formation.

INTRODUCTION

The question of how DNA-binding proteins locate their targets—navigating through billions of base pairs to find the single site where they perform their actual function—is critical for the understanding of a range of fundamental biological phenomena, from epigenetic regulation to chromosomal organization to orchestration of transcription. Sequence-specific binding essentially depends on two main components: thermodynamic, dictated by the relative affinity for a selected site on the DNA, and kinetic, dependent on the dynamic formation of transient complexes during the search process (1). The sequence-specific recognition results from a complex interplay of factors such as electrostatic attraction, hydrogen bonding, hydrophobic interactions and sequence-dependent DNA deformability (2). Due to small (often in the range of 2–3 kcal/mol (3–6)) energetic differences between specific and non-specific association, consensus sequences and protein–DNA complex geometries have repeatedly proven difficult to predict without prior knowledge. Nevertheless, modern knowledge- and physics-based prediction algorithms can predict binding motifs with reasonable accuracy (7,8), in particular if complex formation is not coupled to a large conformational change in either of the binding partners (9,10).

At the same time, recent years have seen remarkable progress in the molecular description of dynamic target search on DNA, revealing the mechanisms of facilitated diffusion encompassing a mixture of several distinct search modes. A number of single-molecule studies (11–13) along with theoretical and simulational reports (14–17) reinforced the widely accepted view that most DNA-binding proteins find their target by advantageously combining 1D sliding, hopping and 3D diffusion. In this way, the protein can utilize the slow 1D sliding mode to systematically scan along relatively short sequences without detaching from the DNA strand, and periodically unbind to quickly move to remote sites on DNA in the 3D hopping/diffusion mode. By tuning its non-specific affinity for DNA during evolution, the protein is hence able to adjust the proportion of time spent in the 1D and 3D search modes. Depending e.g. on the abundance and separation of target sites, such an adjustment allows to optimize the target search time on large genomes (18–20).

This picture, however, becomes less clear as the description of target search approaches atomic resolution. Though several notable studies shed light on the dynamic properties of protein–DNA complexes on both target and off-target sequences (21–24), the molecular mechanism of dynamic sequence sampling, i.e. how loosely-bound proteins discern target and off-target sequences upon encounter, remains largely elusive. In particular, it is unclear to what extent the transiently bound protein can quickly identify and skip over sequences that do not resemble their targets. Also, the choice of proper strand orientation—since none is preferred a priori—requires the protein to tumble and flip in the 1D search mode, as underscored by several reports (25–27). In part due to the high computational cost, few in silico studies explicitly addressed the issue of dynamic association and formation of the native protein–DNA complex, exclusively using simplified coarse-grained models with varying spatial resolution (16,17,23). In the advent of petascale computing, however, the modelling of dynamic complex formation is becoming increasingly feasible, as has already been shown for protein-ligand interactions (28).

At mammalian telomeres—the chromosomal termini comprising thousands of tandem repeats of the hexanucleotide 5΄-TTAGGG-3΄ motif—this sequence search problem becomes even more intriguing. Here the target sites for the two telomeric dsDNA-binding proteins, telomere repeat-binding factors 1 and 2 (TRF1/TRF2), are immediately adjacent to each other and restricted to a small region of the chromosome. After TRF1 and TRF2 localize to telomeres, they thus do not remain bound to a single site but slowly move between neighboring repeats, which allows them to homodimerize and form the shelterin—a higher-order protein assembly that maintains functionality and structural integrity of telomeres. Indeed, in a recent article Lin et al. showed that TRF1 diffuses on bare telomeric DNA, with diffusion 17-fold slower and residence times 31-fold longer than on random λ-DNA (12). The dynamic nature of TRF1 on telomeric tracts in the cellular environment was highlighted in another report (29).

In this work, we employ feature-length MD simulations to provide a comprehensive description of DNA binding and sequence recognition of the TRF1 homeodomain on both target and off-target DNA sequences. Using computational mutagenesis, we describe two opposing mechanisms allowing TRF1 to achieve sequence specificity and accelerate the scanning of DNA sequence by balancing between increased affinity for the target sequence and low affinity for off-target sites. We then investigate the thermodynamics of the TRF1–DNA complex on the actual telomeric sequence by computing free energy maps that capture the sequence-dependent differences in affinity and predict the existence of additional binding sites, simultaneously reproducing experimental data with high precision. By running a total of 180 μs parallel unbiased simulations, we were able for the first time to observe spontaneous formation of a sequence-specific protein–DNA complex with atomic resolution, gaining novel insight into consecutive stages of sequence recognition from initial association to direct base readout. Finally, we used data reduction and statistical inference methods to quantitatively analyze the massive amount of simulation data in order to extract intermediates of the binding process, identify residues involved in the initiation of binding, as well as quantify the kinetics of flipping and specific complex formation. Since TRF1 assumes a homeodomain fold similar to many sequence-specific transcription factors (30,31), we believe that these conclusions are widely applicable in the field of protein–DNA interactions.

MATERIALS AND METHODS

System setup

All simulated models involving the TRF1 DNA-binding domain (DBD; residues 379–430, capped on both termini) were based on the X-ray structure of the DBD bound to telomeric double-stranded (ds) DNA found in PDB entry 1W0T. All fully atomistic simulations employed a periodic, effectively infinite dsDNA model built using the ideal B-DNA parameters as implemented in the X3DNA package (32), with 20 base pairs corresponding to two full turns of B-DNA double helix. Such an approach has been successfully used by several groups so far (33–36), allowing to bypass common problems associated with the behavior of DNA termini and excessive elasticity of short DNA oligomers complexed with proteins. Due to a mismatch between the periodicity of telomeric 5΄-TTAGGG-3΄ tandem repeats and the helical pitch (10–10.5 bp), the periodic sequence (5΄-GGTTAGGGTTAGGGTTAGGG-3΄) consisted of three tandem repeats and two additional GC pairs. A native structure of the specific TRF1–DNA complex was obtained by superimposing phosphorus atoms in the X-ray structure with the artificially created 20-bp periodic model.

Simulation details

For all free energy simulations, a cubic 6.62 nm × 6.62 nm × 6.62 nm box was used in which the protein–DNA complex was solvated with 8695 TIP3P water molecules. For spontaneous binding simulations, we employed a rectangular 6.5 nm × 6.5 nm × 6.62 nm box containing the protein, DNA and 8217 TIP3P water molecules. The number of K⁺ and Cl⁻ ions was adjusted to maintain a physiological salt concentration of 0.154 M and neutralize the net charge of the system. All simulations were performed in Gromacs 4.5 (free energy) or 5.0.4 (spontaneous binding) (37). The Amber99sb-parmbsc0 force field was used (38), and temperature was maintained at 300 K using the stochastic velocity rescaling thermostat with a time constant of 0.1 ps. In order to use the 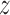-coordinate as the reaction coordinate, in free energy simulations the 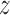axis vector length was constrained to a fixed value using the semi-isotropic coupling scheme; besides that, pressure was maintained at 1 bar using the Berendsen barostat with a time constant of 2.0 ps. Particle Mesh Ewald (PME) summation was used for the calculation of electrostatic interactions, and van der Waals interactions were cut off at 1.0 nm.

DNA-binding affinity of TRF1 mutants

The umbrella sampling/WHAM approach was used for the calculation of free energy profiles in the radial direction, in analogy to our previous work (39). The distance between DNA phosphorus atoms and core residues of the protein (12 residues closest to the protein COM during an equilibrium simulation) projected onto the XY-plane (r-distance) was used as the reaction coordinate. Initial frames for individual windows were generated from a 1-μs steered MD simulation in which the center of the restraining potential was changed at a constant velocity in the radial direction from the starting value of 1.55 nm up to 3.0 nm, with a force constant of 2500 kJ/mol nm². From this trajectory, 30 frames were extracted that corresponded to geometries in 0.05-nm intervals along the reaction coordinate. These geometries were then used to assess the effect of single amino acid mutations on the thermodynamics of specific and non-specific TRF1–DNA binding.

In the simulations, an inverse telomeric sequence (5΄-CCCTAA-3΄ repeats) was used as a model non-specific target, and in this case initial geometries for umbrella sampling were obtained by mutating all 40 DNA bases in the original 30 frames (extracted from steered MD trajectories) using the X3DNA package, as described below. Overall, a total of 12 free energy profiles were obtained for the wild-type protein and five mutants (R380A, V418A, K421A, D422A and R425A) with respect to the standard (5΄-TTAGGG-3΄ repeats) and inverse (5΄-CCCTAA-3΄ repeats) telomeric sequence. Amino acid mutations were introduced by simple deletion/renaming of existing atoms. The number of ions was then adjusted to ensure charge neutrality. All modifications described above were followed by energy minimization, and 500 ns simulations were carried out in each US window, yielding a total of 180 μs. 100 ns at the beginning of each trajectory in individual US windows was discarded to allow the systems to adjust to any introduced changes. Importantly, the use of a single steered MD trajectory results in desirable error cancellation, allowing us to capture relatively minor changes in the behavior of all systems considered with high sensitivity.

Free energy along the DNA major groove

The free energy along the major DNA groove (i.e. in close vicinity to the DNA) was calculated using the umbrella sampling (US)/weighted histogram analysis (WHAM) method (40,41). To generate initial frames for individual US windows along the DNA helix, a rotation-translation matrix was used to propagate the protein in 69 steps along a helical path about the main axis of the DNA helix, as defined by standard B-DNA geometry. This approach is different from the one used in the recent study by Marklund et al., where helical movement along the major groove was enforced by pulling in the helical direction (35), but similar to that of Furini et al. (33). DNA bases in frames generated along the standard telomeric sequence (target, 5΄-GGGTTAGGGTTAGGGTTAGG-3΄) were then mutated using X3DNA to create a corresponding set of frames along the inverse telomeric sequence (model off-target, 5΄-CCCTAACCCTAACCCTAACC-3΄). After energy minimization, the PLUMED plugin (42) was used to restrain the protein in its initial position along the Z-axis with a force constant of 200 kJ/mol nm². This Z-coordinate was defined with respect to a single base pair not involved in protein binding (1.6 nm below the lowest US window) whose position in space was restrained in the Z-direction. In addition, one-sided harmonic potentials were added to prevent the COM of DNA from diffusing away in the XY-plane, in order to avoid periodic boundary artifacts. To ensure that the obtained free energy profile captures the effect of DNA sequence, spontaneous dissociation from non-native interfaces was prevented by adding a one-sided harmonic potential with a force constant of 500 kJ/mol nm² at protein–DNA COM XY-distance of 1.55 nm. For the purpose of subsequent analyses, a proper equilibrium distribution was recovered using a weighting factor of 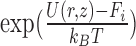, where U(r, 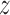) is the applied biasing potential and F_i is the free energy associated with the constraint in ith window as calculated by the WHAM algorithm.

For both DNA orientations, a set of 750-ns simulations in each umbrella sampling window was ran. For the standard orientation, additional data from 1000-ns simulations performed with a larger force constant (500 kJ/mol nm²) that did not yield proper histogram overlap were also included in the construction of free energy maps and subsequent calculations. Hence, the total simulation time used to construct the profiles along the DNA was greater than 170 μs.

Spontaneous binding and spawning

To study spontaneous binding of TRF1 to telomeric DNA, 50 systems have been prepared in which the protein was placed randomly in the simulation box containing a periodic DNA molecule. All systems were solvated with identical number of ions and water molecules and, after energy minimization, 50 equilibrium simulations were ran from thus obtained geometries. 20 trajectories have been propagated for 4 μs each, and another 30 for 2 μs each, yielding a total of 140 μs. From the resulting trajectories, sampled at each 25 ns, a subset of 77 frames has been identified that captured geometries close to the native protein–DNA complex, and additional seventy seven 500-ns long simulations were ran starting from these frames (later referred to as ‘spawning’ simulations). Geometries were chosen based on an mRMSD criterion. The mRMSD parameter was defined so as to take into account the relative position of 10 phosphate atoms from the DNA backbone (5 bp at the protein–DNA interface) and 15 Cα atoms from the DNA-binding helix, indicative of the overall geometry of the native complex. Then, mRMSD was calculated as the lowest RMSD value for this subset of atoms with respect to any consecutive chain of five phosphate pairs among 20 possible alignments (in geometry corresponding to the reference 1W0T X-ray structure), since there are 20 possible sites at which the protein–DNA complex can be formed, or 40 if both orientations are possible. If mRMSD was lower than 0.175 nm, the respective frame was accepted as a starting point for the spawning simulations. Since the procedure was aimed at generating trajectories that bind in a sequence-specific manner, only the standard orientation of the DNA duplex (5΄-TTAGGG-3΄) and not the inverse sequence (5΄-CCCTAA-3΄) was considered when applying the criterion. By this virtue, the original 50 trajectories have equal a priori probabilities of binding in either orientation, while the spawning trajectories are strongly biased towards the standard one and were hence excluded from analyses in Supplementary Figure S10.

RESULTS AND DISCUSSION

Positive and negative selection mechanisms balance between target recognition and avoidance of off-target binding

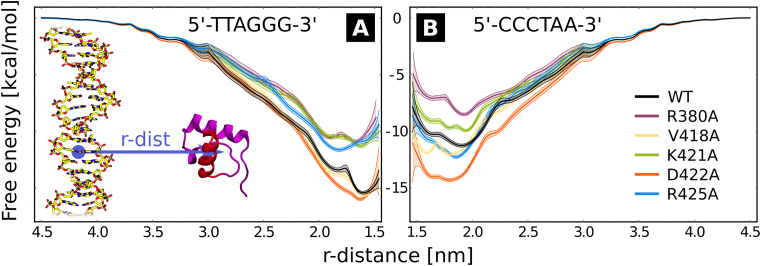
To characterize the role of individual amino acids in sequence-specific binding of TRF1 to DNA, we calculated how the free energy of TRF1–DNA association is affected by individual single amino acid mutations. To this end, we ran a set of umbrella sampling simulations using an effectively infinite telomeric dsDNA, i.e. composed of tandem 5΄-TTAGGG-3΄ repeats joined via the periodic boundary of the system, to model the native TRF1–DNA complex, and employed the inverse telomeric sequence (5΄-CCCTAA-3΄) as a model for off-target chromatin sites. The choice of a single off-target sequence was kept consistent throughout the study (see Supplementary Figure S1 for a schematic illustration and Materials and Methods for full details of system preparation workflow). While being inherently arbitrary, the use of the inverse telomeric sequence allows for a more natural interpretation of the results; moreover, virtually no sequence-specific variation in DNA-binding affinity has been observed on this off-target sequence, as will be shown below.

The free energy profiles, shown in Figure 1, illustrate the changes in the binding affinity induced by mutations at five residues located at the protein–nucleobases interface: R380A, V418A, K421A, D422A and R425A, at the target (A) and model off-target sequence (B). Due to a combination of electrostatic attraction with the DNA sugar-phosphate backbone and base-specific hydrogen bonding, all basic amino acids—R380, K421 and R425—increase the affinity for the target site, as shown by the less negative binding free energy of the respective alanine mutants (purple, green and cyan line in Figure 1A) compared to the wild-type protein (black line). At the off-target sequence (Figure 1B) only the non-specific electrostatic attraction remains at play, so that these residues show mixed behavior: R380 and K421 enhance and R425 decreases the binding affinity, although in case of K421 and R425 the effect of the mutation is minor (1–2 kcal/mol) compared to the target sequence. This defines the intuitive ‘positive selection’ of binding sites, where individual amino acids significantly increase the affinity for the target sequence while having a smaller or random impact on off-target binding. On the contrary, D422 and—to some extent—V418 can be similarly viewed as ‘negative selectors’. Such residues have virtually no effect on the stability of the native complex, as shown by the red and yellow lines in Figure 1A, but make off-target binding significantly less favorable mostly due to electrostatic repulsion (D422) or unmatched hydrophobic contacts (V418). Indeed, the absolute DNA-binding affinity of the D422A mutant is high and quantitatively similar for both target and off-target sites, with estimated values of −16 and −14 kcal/mol, respectively. This shows that, counterintuitively, D422 is not indispensible for strong binding to telomeric tracts; however, its deletion would result in almost equally strong binding to non-telomeric DNA. In fact, the almost identical shape of red and black curves in Figure 1A stems from the fact that on the target sequence, favorable h-bonding of D422 with the amino group of cytosine (see closeup of the binding interface in Supplementary Figure S2) cancels out its repulsive interaction with negatively charged phosphates; hence, the D422A mutation does not alter the affinity for the target sequence. On the other hand, the corresponding curves are separated in in Figure 1, because such a cancellation no longer occurs on the off-target sequence and in the wild-type protein the electrostatic repulsion prevails, which makes binding to off-target sites strongly unfavorable. Since the D422A mutation increases the affinity for the off-target sequence, we conclude that D422 is solely needed to avoid binding strongly to off-target sites. Apart from thermodynamical considerations, strong off-target binding would also significantly slow down the process of sequence search, so that acidic residues might help avoid kinetic trapping in non-specific complexes. As clearly revealed by a systematic search through all h-bonded nucleobase-amino acid pairs found in the PDB database (Supplementary Figure S3), the specific recognition of cytosine by acidic residues is quite frequent (more than 8% of instances), suggesting that this mechanism might be commonly employed by a large portion of protein–DNA complexes, possibly even in the prototypical c-Myb protein where a similar contact is found (43).

Figure 1.

Free energy profiles of DNA-TRF1 interaction as a function of intermolecular distance, calculated with respect to the target sequence (left) and the inverse sequence, used as a model off-target site (right). Between 4.5 and 3.0 nm, i.e. in the non-specific range, the free energy corresponds to the entropy-corrected Debye–Huckel energy, scaled appropriately in cases where mutations changed the net charge on the protein. Shaded areas show the standard error.

A more careful inspection of the profiles reveals the existence of two free energy minima, associated with two distinct binding modes—tight and loose—at distances of 1.6 and 1.85 nm, consistently with the findings of our previous work (39). As particularly visible in case of R425A, mutations of amino acids at the recognition interface typically shift the binding equilibrium towards the more loosely bound state. The D422A mutation, though, appears to abolish the distinction between the two modes, since the discussed cancellation of attractive and repulsive interactions requires a direct contact between D422 and the cytosine residue. This suggests that besides the aforementioned ‘negative selection’, D422 is also responsible for locking the bound protein in place, hence ensuring stable binding in the native complex.

2D maps reveal the roughness of the free energy surface along telomeric and off-target sequences

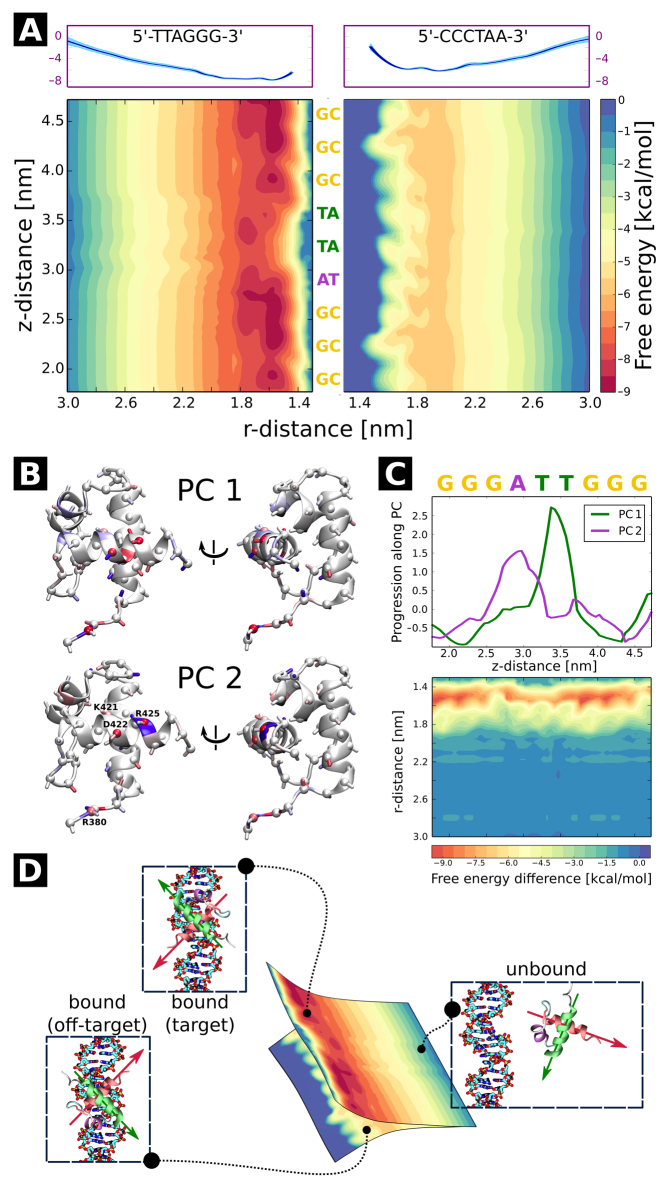
To obtain a comprehensive picture of the binding thermodynamics and diffusion of TRF1 on telomere repeats, we computed the full free energy landscape of the TRF1–DNA interaction in the radial (r) and axial (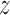) direction. For the construction of this free energy map, we employed radial profiles calculated based on initial structures from a spontaneous association trajectory that started from an unbound state and led to a complete reconstitution of the native complex, described in next section. This approach is different from the one used above, where initial frames for free energy calculations were obtained from a steered MD simulation in which the protein was pulled away from the DNA. We note that by extracting these initial ‘seeding’ frames from equilibrium simulations, we were able to avoid hysteresis associated with the use of non-equilibrium pulling forces and achieve better sampling of the transiently bound states, eventually obtaining a more reliable free energy values, as will be shown below. The radial profiles, shown in Supplementary Figure S4, were then merged with profiles obtained from umbrella sampling simulations of the bound state translated along the helical path in the DNA major groove, in a way that ensures that the effect of sequence-specific interactions is also captured at larger radial distances (see Materials and Methods). The resulting free energy landscapes shown in Figure 2A illustrate the free energy surface as sensed by TRF1 diffusing parallel (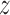-direction) and perpendicular (r-direction) to the DNA main axis, at both the target (left panel) and off-target sequence (right panel). Due to the periodicity of the telomeric sequence, the free energy function along the z-direction is periodic with a period of ca. 2.0 nm, so that the obtained profiles cover the entire telomeric tract. At large distances, the two profiles correspond to physically identical situations, as they describe loose interaction of the protein with the same—just differently oriented—DNA strand. When the protein approaches the DNA molecule, it has to assume one of the two distinct orientations, thus encountering either its target telomeric sequence or the inverse one, used as a model off-target sequence; see schematic description in Figure 2D.

Figure 2.

(A) 2D free energy of the TRF1–DNA interaction as a function of the radial (r) and axial (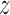) coordinate, with respect to standard/target (left) and inverse/off-target (right) telomeric sequence. Radial profiles used to construct the plot are shown in the top panels. See Materials and Methods and Supplementary Figure S4 for details. (B, C) Principal component analysis of h-bonding patterns along the telomeric sequence. As seen from the projections (upper panel of C), the first principal component (PC1) describes the change in h-bonding patterns when the protein moves from the G triplet to the T pair, while PC2 corresponds to the G→A switch. In panel B, blue color indicates an increase and red a decrease in capability of the protein residues to form h-bonds with the bases (sphere), DNA backbone (ribbon) and other amino acids (stick) as the protein moves to the free energy barrier region; see SI Methods for details. In bottom panel of C, a differential free energy map is shown to isolate the contribution of sequence-specific effects. (D) Orientational selection upon formation of the protein–DNA complex. The two 2D profiles are physically identical at large distances, but as the protein approaches the DNA, it has to assume one of the two possible orientations, which can be illustrated as choosing one of the two free energy profiles.

By comparing the two free energy profiles in the radial direction, shown in the upper panel of Figure 2A and Supplementary Figure S4, one can estimate the difference in binding affinity for target and off-target sequences as equal to 1.74 kcal/mol. It matches the value of 3.4k_BT (2.0 kcal/mol) reported for the predominantly monomeric TRF1 protein based on single-molecule measurements (12), proving that our approach allows to reliably quantify such minor differences. Also the absolute affinity towards the target sequence estimated using our approach (−9.0 kcal/mol) agrees well with the value obtained experimentally (−9.2 kcal/mol) (44). This confirms that ‘seeding’ frames extracted from equilibrium simulations yield more reliable results than these obtained from steered MD simulations, with the latter yielding relative and absolute values of 4 and −14 kcal/mol, respectively. For details of the calculation and comparison with other force field variants—CUFIX correction that aimed to improve the description of lysine–carboxyl and lysine–phosphate interactions (36) as well as the recently released parmbsc1 designed to replace the parmbsc0 variant (45)—see SI Methods and Supplementary Figure S5.

As seen from the free energy surface for the target sequence (left panel of Figure 2A), two free energy basins of ca. −8.5 kcal/mol (a small one at 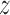= 1.95 nm and a broad one at 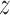between 2.2 and 2.8 nm) exist in close vicinity to DNA, so that—surprisingly—the TRF1–DNA interface appears to allow for binding at multiple sites along the telomeric sequence, not only the one observed crystallographically ( 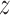= 1.9). This can be explained based on the computational mutagenesis data presented above, as in both low free energy basins D422 directly faces the amino groups of the three consecutive cytosine bases, and both nucleobase-binding arginines—R380 and R425—can also easily form h-bonds with their counterparts on DNA. On the other hand, at the main free energy barrier for diffusion along the DNA ( 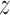in the range of 3.0–3.7 nm) the recognition helix of TRF1—including D422 and R425—interacts unfavorably with adenine and thymine bases. Simultaneously, the minor groove-bound R380 anchoring the protein to DNA partially dissociates upon encountering GC pairs, which expose a different h-bonds acceptor (A)/donor (D) pattern in the minor groove (ADA instead of AA).

To describe the link between binding affinity and changes in hydrogen bonding patterns in a more direct manner, we performed principal component analysis (PCA) to see how the h-bonding patterns change as the protein progresses along the helical path on the DNA. The results are shown in Figure 2B and C. In the figure, the first two components—PC1 and PC2—represent changes in h-bonding capabilities of the DNA strand as the protein crosses the free energy barrier. As seen from the projections in Figure 2C, the first component, peaking at ca. 3.4 nm, corresponds to the protein moving from G/C pairs (low PC1 values) to T/A pairs (high PC1 values), while the major change in component 2 describes the movement of the protein from G/C pairs to the A/T pair along the periodic 5΄-TTAGGG-3΄ sequence. Figure 2B and C shows that upon moving from the free energy basin (1.8 nm <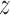 < 2.8 nm) to the barrier region (2.8 nm < 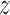< 3.8 nm), R380 and R425 cease to form sequence-specific h-bonds with base pairs, as indicated by red spheres, and instead interact with the backbone, as shown by the blue coloring of the ribbon (for R425 this is true only for PC2, i.e. when R425 faces the adenine base). A similar but much less pronounced pattern can also be seen in case of K421. On the contrary, the loss in h-bonding capability by the negative selector D422 residue is not compensated by a different DNA binding mode, but rather by forming additional h-bonds with neighboring amino acids (blue stick in PC1). In consequence at least two protein residues engage in an intramolecular salt bridge instead of binding with DNA, thus decreasing the binding affinity at off-target sites.

In the opposite orientation, i.e. at the inverse telomeric sequence (right panel of Figure 2A), TRF1 encounters a free energy barrier that prevents it from approaching the DNA strand at distances shorter than 1.6 nm. As a result, the free energy surface is visibly smoother than at the target strand, in line with experimental observations (46) and theoretical predictions (47) that put an upper limit of 2k_BT on efficient 1D sequence search. The estimated difference in roughness between the two landscapes (1.5 kcal/mol) is also in excellent agreement with the experimentally derived value of 2.8k_BT (12). While the profile shows no significant variation in affinity for individual sites along the sequence, the easily seen ripple-like patterns along the 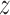-coordinate illustrate the non-specific ‘lock-in’ mechanism responsible for aligning the protein in discrete positions when the protein closely approaches the DNA strand. This effect stems from non-specific interactions of phosphate moieties in the DNA backbone with positively charged amino acids that contribute to the rigidity of the protein–DNA complex. Supplementary Figure S6 shows that the lock-in is significantly less pronounced on the off-target sequence than on the target one, which probably serves to optimize the target search time: both increased equilibrium intermolecular distance (1.6 versus 1.9 nm) and looser lock-in should facilitate the diffusion along the DNA on off-target sequences, effectively improving search efficiency (19,48).

To further investigate the dynamic behavior of a single TRF1 DNA-binding domain on both the telomeric tracts and an off-target DNA strand, we ran a set of Brownian dynamics (BD) simulations in which the protein is modeled as a point particle whose stochastic motion around the DNA is governed by the effective potential shown in Figure 2A. In the simulations a reflective barrier was used to mimic the effect of DNA geometry, so that at r < 2.0 nm the protein entered a helical groove on the DNA strand, as illustrated in Supplementary Figure S7. Importantly, this simplified description neglects certain aspects of protein–DNA complex formation that are inherently multi-dimensional, such as binding or flipping kinetics, and discussion of these is hence deferred until the last section of the article. The coarse-grained model, however, remains informative as it can predict general characteristics of large-scale motion of TRF1 DBDs on telomeric and non-telomeric tracts that cannot be trivially inferred from free energy profiles alone. Indeed, Supplementary Figure S7A shows that on the target sequence, TRF1 exhibits significant processivity, i.e. is capable of sliding along relatively long stretches of DNA without detaching from the major groove. The observed processivity was noticeably lower on off-target sequences, where dissociation from the major groove successfully competes with sliding within the groove, allowing the protein to rapidly switch orientations as it scans through off-target sites. Nevertheless, translation along the DNA axis was still coupled with rotation on the off-target sequence, in line with what was observed for a range of DNA-binding proteins (46). Moreover, we found that experimentally determined residence times—ca. 15 s on telomeric and 1.8 s on random λ DNA (12)—match the results of our BD simulations, in which the protein approached the 3.0 nm mark once during 12.8 s simulations on the target and three times during 3.2 s simulations on the off-target sequence. Unfortunately, we were unable to reproduce experimental differences in diffusion rate along the DNA strand since standard BD cannot properly model processes dominated by subdiffusive motion (49), as found to be the case for TRF1 (12).

Equilibrium simulations correctly reproduce the crystal structure of the native complex

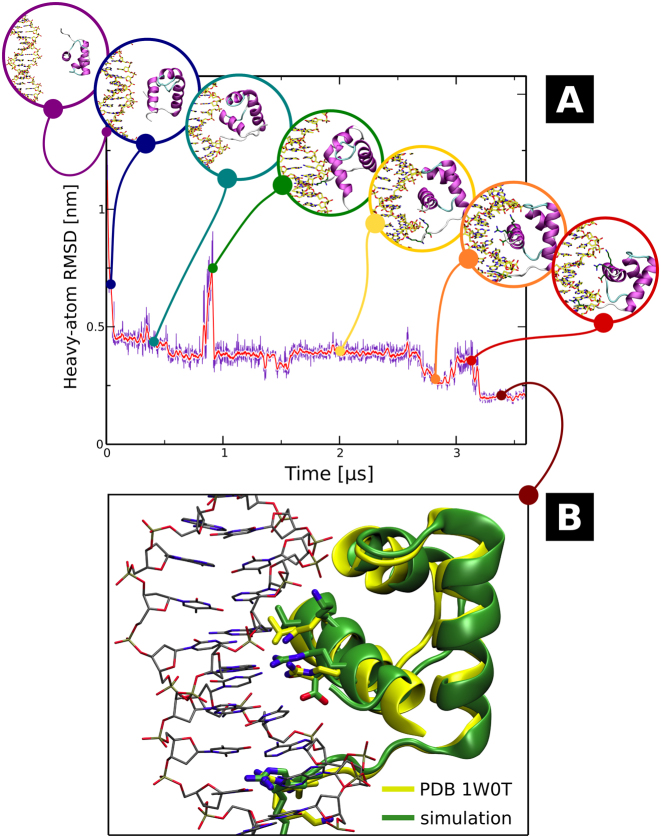
To date, most computational studies that attempted to asses the stability of protein–DNA complexes were based either on enforced dissociation (35,50,51) or bound state-/implicit solvent-based models (52–54), which significantly restricted the exploration of conformational space and—consequently—proper reconstruction of the free energy landscape. To overcome this common problem, we ran a set of 50 extensive (total of 140 μs) equilibrium simulations seeded from random unbound states to observe the spontaneous formation of protein–DNA complexes without imposing any initial bias. By subsequently spawning additional equilibrium trajectories from spontaneously formed pre-bound structures (see Materials and Methods), we were able to obtain a native-like complex that resembles the crystallographically resolved structure with root-mean square deviation (RMSD) equal to 1.95 Å.

Figure 3, as well as Movie S1, show the time evolution of RMSD with respect to the target site, along with snapshots of intermediate binding poses assumed during the search (Figure 3A) and the final structure superimposed with the crystal structure from PDB entry 1W0T (Figure 3B). Even though the initial association was very rapid, consistently with the steep slope in the free energy profile along the radial direction—with first direct protein–DNA contacts formed within the first 2 ns of the trajectory—upon first encounter the DNA-binding helix directly faced the minor groove (blue circle in Figure 3A) and required additional 50 ns to move to the neighboring major groove position (cyan). This particular transition was relatively fast, though, as in many trajectories the initially formed minor groove-bound state remained stable over several μs. In this major groove-bound pose, the positively charged K379 and R380 in the flexible linker tail were able to sample the vicinity of the minor groove; in effect, after another ca. 300 ns K379 inserted into the minor groove, anchoring the protein in place so that the DNA-binding helix could sample the adjacent nucleobases in the major groove. However, access to the major groove was hindered by the formation of a stable salt bridge between R380 and D422, so that close to the 850 ns timestamp the protein rotated and almost dissociated from the interface (green). In this state, TRF1 remained bound only via the minor groove-inserted K379 that now acted as a pivot, allowing the protein to return to the previous pose (yellow). At the 2.69 μs timestamp, K379 was substituted in the minor groove by R380, which also led to the formation of base-specific hydrogen bonds by R425 and D422 within the next 150 ns (orange). Due to suboptimal packing, the protein moved away from this binding pose at the 3.0 μs timestamp (red), and rebound at a neighboring target site after rotating slightly around the still bound R380, quickly reestablishing the correct interface with nucleobases. Eventually the native-like complex, shown Figure 3B, remained stable at RMSD close to 0.2 nm, i.e. similar to that observed in equilibrium simulations initialized from crystalographically derived structures.

Figure 3.

(A) Time evolution of RMSD values in the spontaneous association trajectory. Intermediate geometries assumed by the forming protein–DNA complex, discussed in detail in the main text, are shown in circles. The additional ‘spawning’ simulation started at 3.125 μs and was propagated for another 500 ns. (B) Geometry of the spontaneously formed TRF1–DNA complex (green) superimposed with the X-ray structure taken from PDB entry 1W0T (yellow). For full trajectory, see Movie S1.

The above description clearly underscores several general aspects of homeodomain-like protein binding to DNA. Firstly, the basic disordered tails—with their ability to remain stably bound to AT pairs in the minor groove—may enable the DNA-binding domain to locally sample the local base pattern by rotation around the single-residue pivot, in addition to their apparent role in facilitating the ‘hopping’ mechanism of DNA search reported previously (55) and in line with recent reports (56,57). Secondly, jumps that significantly change the binding pose are fast compared to the time spent by the protein in intermediate states, and often triggered by rapid fluctuations in the behavior of single residues. Finally, the binding process indeed involves multiple metastable intermediates even when the DNA-binding domain aligns itself correctly in the first place, providing many possible checkpoints to ensure sequence compatibility.

Collective trajectory analysis allows to identify intermediate states and quantify the kinetics of binding

To better understand the factors governing the formation of native-like complexes, we first inspected the trajectories in which the protein was found in a pre-bound state, i.e. the ones from which frames were selected for additional 500-ns spawning simulations. The trajectories, visualized in SI Movies 2–9, allow to generalize the conclusions inferred from the description of the single binding event above. In particular, as seen in SI Movie 2, the formation of a stable insertion mode by R380 (close to the 2 μs timestamp) that drives further stabilization of the entire domain (at the 3 μs timestamp) is only possible when R380 interacts with AT pairs in the minor groove, confirming the important role of the basic disordered tail in preliminary search for potential binding sites. Indeed, SI Movies 2–6 show that in absence of a stable R380-minor groove contact, the protein can easily hop between sites on DNA as a whole (at timestamps 0.75 μs in SI Movie 3, 1 μs in SI Movie 4, 0.75 μs in SI Movie 5, and 1 μs in SI Movie 6), sampling the sequence at a relatively fast pace. In several cases (SI Movies 3–6) R380 fails to locate to the minor groove at all, instead remaining bound to an acidic residue on the protein surface and facing the major groove, suggesting that the major-minor groove transition is an important rate-limiting step in formation of the bound complex. In absence of the anchoring interaction, the complex is often stabilized by non-specific contacts via the upper loop portion of the protein and the C-terminal end of the DNA-binding helix (see e.g. SI Movie 7), allowing R380 to find its way to the correct binding site. In contrast, stable binding of R380 to AT pairs in the minor groove anchors the protein in a single position (SI Movies 2 and 7), allowing it to transiently unbind to adjust its binding mode (at the 3 μs timestamp in SI Movie 7 and 2 μs timestamp in SI Movie 8). This initial binding ensures that the DNA-binding helix, shown in blue, directly faces the three consecutive CG pairs in the telomeric sequence, so that the formation of remaining specific contacts is plausible.

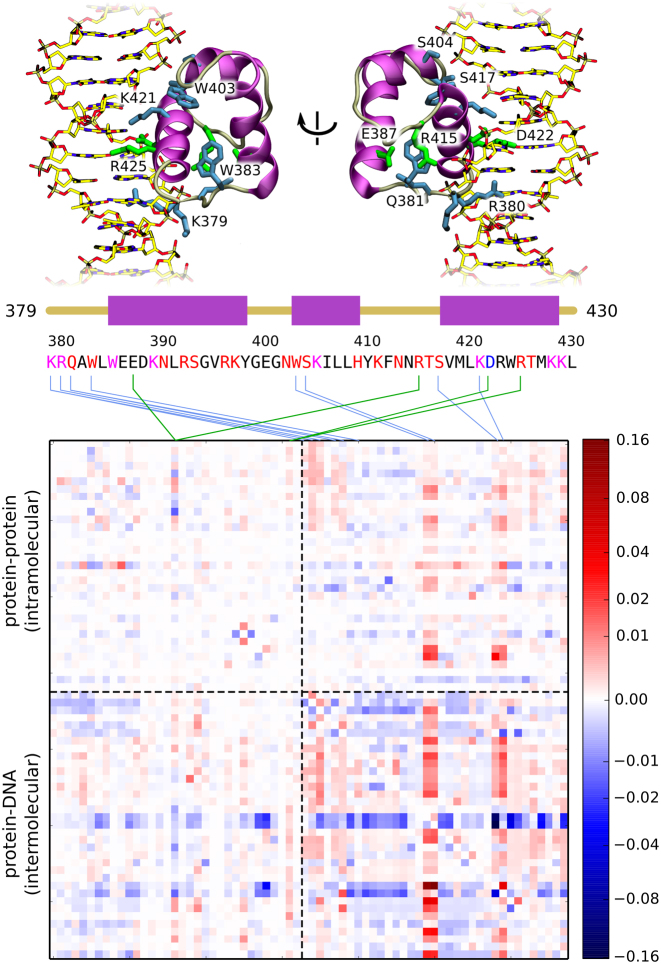
In order to identify interactions that are critical for the initiation of native complex formation, we additionally quantified causal relationships between the existence of individual hydrogen bonds (see SI Methods and Supplementary Figure S8) by employing the concept of transfer entropy (58). This quantity measures how much additional information about the evolution of some observable i can be obtained from previous values of another observable j, compared to only knowing the historical values of i. In other words, transfer entropy tells us whether knowledge of previous values of j improves our ability to predict future values of i, and hence measures the (directional) causality between i and j. In practice, it is more convenient to use a derived quantity, the normalized directional index D_{j → i} (see SI Methods and an article by Kamberaj and van der Waart (58) for an in-depth technical discussion). By construction, positive values of the matrix element D_ij indicate that j is the causal factor and i responds to its changes after a chosen lagtime τ. Due to normalization, directional index between any two observables D_{j → i} attains values from −1 to 1, and is antisymmetric with respect to swapping of the observables, i.e. D_{j → i} = −D_{i → j}, as the sign reflects the direction of causality. A value of 0 indicates no net causal effect, however it does not necessarily mean that the two observables are not correlated. In addition, the directional index alone does not indicate whether a causal relationship corresponds to a positive or negative correlation between i and j, and this information has to be supplied from elsewhere, e.g. from the time-shifted correlation matrix. In the calculated directional index matrix, shown in Figure 4, individual observables correspond to the intra- (observables 1-33) and intermolecular (observables 34–68) hydrogen bonds. Interestingly, instead of single matrix elements, one can easily identify whole columns that are dominated by positive values. Such a pattern indicates that single ‘early’ hydrogen bonds (here mapped onto the protein sequence using blue lines for inter- and green lines for intramolecular contacts) induce an extensive rearrangement of the contact map, likely associated with the formation of a native-like protein–DNA complex. Among the identified key h-bonds, the strongest signal corresponds to four residues that form a patch on the upper portion of the protein–DNA backbone interface: W403, S404, S417 and K421 (see top panel of Figure 4), indicating that initial protein–DNA contacts made by these residues facilitate subsequent refinement of the structure of the complex, as well as reshape the intramolecular h-bonding pattern. By comparison with the time-shifted correlation matrix (Supplementary Figure S9), one can note that binding of these residues to the DNA backbone is highly cooperative, i.e. positively correlates with binding of neighboring residues, as well as facilitates the interaction of R380—previously implicated in anchoring the protein to the potential binding site—with the DNA strand. This observation is consistent with the above description of spontaneous binding events, in which the upper portion of the protein could stabilize the pre-bound complex, thus allowing the basic residues in the disordered tail to sample the sequence in the minor groove. Another cluster of residues with large directional index values can be found on the N-terminal end of the domain, i.e., in the basic disordered tail region. Here the initial binding of K379, R380, Q381 and W383 to DNA can again be seen to promote the formation of the protein–DNA interactions in the DNA-binding helix region, as well as prevent the formation of other potentially non-specific contacts. Certain intramolecular contacts also seem to affect the binding process, e.g. the D422–R425 salt bridge that forms both in the unbound and tightly bound state but often dissociates in weakly bound structures due to interactions of R425 with the backbone, or the E387–R415 pair in which the arginine can switch between two potential binding partners: the glutamate and the DNA backbone, as illustrated by strong anticorrelation in Supplementary Figure S9.

Figure 4.

Directional index matrix describing causal relationships between the existence of individual protein-protein (intramolecular) and protein–DNA (intermolecular) h-bonds. Matrix columns with high absolute values are mapped onto the protein sequence, with green lines corresponding to intra- and blue to intermolecular h-bonds. Letter coloring in the protein sequence denotes the type of h-bonding with DNA: magenta corresponds to h-bonding with both the bases and the backbone, red—only with the backbone, and blue—only with the bases. In the top panel, selected residues are shown in the context of the native complex. Non-linear scaling was employed for visualization purposes. See Supplementary Figure S8 for a full list of h-bonds used in the analysis.

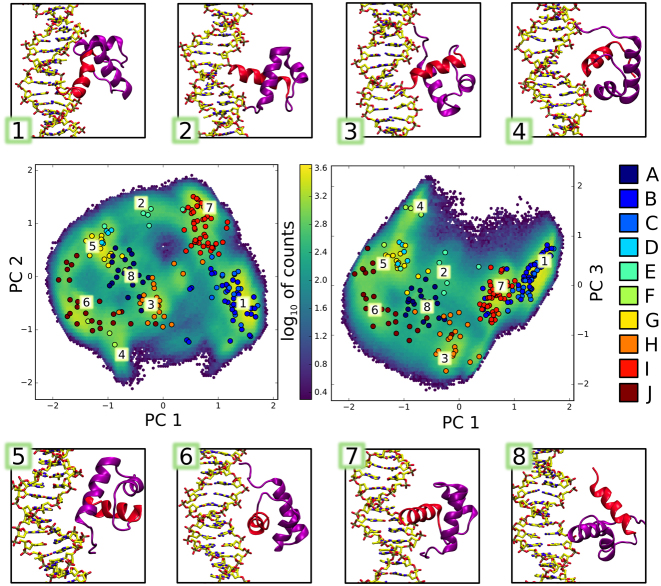
To identify other intermediates involved in the binding process, we then built a Markov state model (MSM) that allows to identify binding pathways from large amounts of simulation data. To this end, we described the protein–DNA system using a set of generalized coordinates relevant to binding, including intermolecular distances, mRMSD values, relative orientations of the binding partners and frequently occurring h-bonds (see SI Methods and Supplementary Figure S8 for a detailed explanation). The selected coordinates were subject to dimensionality reduction via principal component analysis (PCA) to facilitate further processing. The resulting data was then clustered into so-called microstates to produce discrete-state trajectories used for the construction of the MSM, and spectral clustering with PCCA+ allowed to identify 10 kinetically connected (slowly interconverting) macrostates.

These states can be intuitively interpreted from Figure 5, where cluster centers are projected onto the plane spanned by principal components 1/2 and 1/3 and color-coded according to their assigned macrostate A–J. The heavily populated rightmost side of the graph—represented by sample structures 1 and 7—corresponds to native-like complexes in the standard orientation, with two underlying free energy basins (yellow blobs in the 2D histogram in Figure 5) differentiating between the loosely-bound state, in which the DNA-binding helix is oriented horizontally, and the tightly bound state, in which the helix fits into the major groove at an angle (see also Supplementary Figure S2). The left side of the graph, on the other hand, is partially populated by native-like complexes in the inverse orientation, exemplified by structures 4 and 6. Between these extremes, a pool of transient, intermediate states can be found, in which the tips of both N- and C-terminal α-helix point towards the DNA grooves (sample structures 2, 3 and 5), or the N-terminal helix enters the major groove (structure 8). Although the states identified by the PCCA+ algorithm allow to distinguish between intermediates formed during binding, they are diffuse and structurally not well-defined, and hence provide only a rough estimate of interconversion rates between different loosely-bound states. Supplementary Table S1 summarizes mean first passage times (MFPTs) between individual macrostates calculated using an improved MSM-based procedure proposed by Suarez et al. (59). From these values, one can see that many overlapping macrostates interconvert rapidly, within tens of nanoseconds, while more distant intermediates (such as those captured in states E, F and G) equilibrate within the timescale of several microseconds. This shows that the during the search process, the protein often becomes trapped in multiple metastable states, as shown already in case of trajectories corresponding to native-like complex formation. Using the same algorithm, we were able to estimate the MFPT for the assembly of a specific TRF1–DNA complex (defined by the existence of three aminoacid-nucleobase h-bonds formed by R380, D422 and R425), starting from radial distance of 4.0 nm, as equal to 34 μs. This value agrees well with the scarcity of tightly bound complexes in our set of simulations that were much shorter individually, but totaled 180 μs (140 μs random + 40 μs spawning) over 127 runs. Using the same approach to calculate the MFPTs for flipping, i.e. the mean time required to switch from a sequence-specific complex to the bound complex in the inverse orientation and undergo the reverse transition, we obtained values of 88 and 11 μs, respectively.

Figure 5.

Intermediate states (1–8) formed by the TRF1–DNA complex in unbiased association simulations. Aggregated simulation data is shown as 2D log histograms projected onto the planes of greatest variability (principal components 1/2 and 1/3). Circles correspond to cluster centers identified by the clustering algorithm, and are colored according to macrostate assignments by the PCCA+ method.

CONCLUSIONS

In this article, we present a comprehensive study of the dynamic DNA sequence recognition and protein–DNA complex formation by the TRF1 homeodomain in fully atomistic detail, based on extensive (over 0.5 ms in total) MD simulations. In particular, our computational mutagenesis analysis shows how TRF1 targets specific sites on the DNA by combined use of positive and negative selectors, i.e. residues that increase the affinity for target and decrease the affinity for off-target sites, respectively. The calculated prevalence of similar base-amino acid contacts in the PDB database suggests that the identified negative selection mechanism is also at play in other sequence-specific DNA-binding proteins. This finding also exemplifies the notion that in order to bind any target with high precision, one cannot solely optimize the affinity for this single target but has to mind other possible targets as well. Such a picture is particularly relevant in the context of protein–DNA recognition, with DNA-binding proteins often searching through billions of potential binding sites.

This process of sequence search on both target and off-target sequences was described here in such detail for the first time, with the calculated free energy maps yielding both relative and absolute values of binding affinity and free energy landscape ruggedness in excellent agreement with reported experimental findings. We show that TRF1 can use its unstructured basic tail to sample the sequence even at a distance, and plausibly forms a stable complex with DNA at more than one site along the telomeric sequence. The stability of these complexes is provided by both advantageous h-bonding with nucleobases and the ‘lock-in’ mechanism that depends on direct contacts between basic residues and DNA backbone phosphates. The results of Brownian dynamics of TRF1 on the calculated free energy landscapes suggest that at telomeric tracts, TRF1 mostly follows the helical path along the major groove of DNA, while at off-target sites the propagation along the groove is often interrupted by dissociation events.

To more directly study the dynamical aspects of complex formation, the above free energy calculations were complemented by a series of equilibrium simulations initialized in the unbound state. Most importantly, these simulations were able to reproduce the native TRF1–DNA complex, yielding RMSD of 1.95 Å with respect to the X-ray structure. To our knowledge, this marks the first observation of spontaneous formation of a sequence-specific protein–DNA complex in fully atomistic MD simulations, thus adding to the growing body of biologically relevant processes that can be reproduced in silico in an unbiased way. A detailed inspection of this spontaneous binding trajectory, as well as several trajectories that led to the formation of non-specific complexes, provided novel insight into the process of dynamic sequence search. In particular, the N-terminal basic tail was observed to sample the minor groove in search for AT pairs, providing a means of sequence interrogation at the early stage of complex formation. When anchored to the minor groove via the side chains of lysine or arginine, the protein could perform a more detailed—though still dynamic—sampling of the local nucleobase sequence. Indeed, the anchored protein domain rapidly dissociated and rebound at neighboring sites, ultimately finding the correct binding pose. While the early recognition allows the protein to speed up the search by skipping roughly half of potential binding sites, further acceleration is provided by the negative selection mechanism described above.

Subsequent steps of complex formation were revealed by the transfer entropy analysis, which helped identify a subset of residues forming ‘early’ hydrogen bonds that promote the alignment of the DNA-binding helix in the major groove and lead to direct base readout. Finally, Markov state model analysis of the spontaneous binding trajectories allowed to capture intermediate states of binding in which the binding partners are not aligned properly. These slowly interconverting metastable states—with lifetimes on the order of several microseconds—might actually slow down the complex formation, and indeed in a majority of the 2–4 μs-long equilibrium simulations the protein did not find the correct binding pose in either orientation. Hence, although the initial protein–DNA association occurs rapidly, the convolved pathway that leads to the formation of a native complex resulted in a relatively long calculated MFPT for sequence-specific binding, on the order of 34 microseconds. Orientational flipping was found to occur on a similar timescale, with MFPTs of 88 and 11 μs for orientation switch from standard to inverse and from inverse to standard, respectively.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Polish Ministry of Science and Higher Education [0059/DIA/2014/43]; Foundation for Polish Science (FNP) Homing Plus Programme, co-financed from the European Union's Regional Development Fund within the Operational Programme Innovative Economy [HOMING PLUS/2011-4/3]; PL-Grid Infrastructure and the TASK Computational Center (in part). Funding for open access charge: Polish Ministry of Science and Higher Education [0059/DIA/2014/43] and Gdansk University of Technology.

Conflict of interest statement. None declared.