Model-based and design-based inference goals frame how to account for neighborhood clustering in studies of health in overlapping context types

Abstract

Accounting for non-independence in health research often warrants attention. Particularly, the availability of geographic information systems data has increased the ease with which studies can add measures of the local “neighborhood” even if participant recruitment was through other contexts, such as schools or clinics. We highlight a tension between two perspectives that is often present, but particularly salient when more than one type of potentially health-relevant context is indexed (e.g., both neighborhood and school). On the one hand, a model-based perspective emphasizes the processes producing outcome variation, and observed data are used to make inference about that process. On the other hand, a design-based perspective emphasizes inference to a well-defined finite population, and is commonly invoked by those using complex survey samples or those with responsibility for the health of local residents. These two perspectives have divergent implications when deciding whether clustering must be accounted for analytically and how to select among candidate cluster definitions, though the perspectives are by no means monolithic. There are tensions within each perspective as well as between perspectives. We aim to provide insight into these perspectives and their implications for population health researchers. We focus on the crucial step of deciding which cluster definition or definitions to use at the analysis stage, as this has consequences for all subsequent analytic and interpretational challenges with potentially clustered data.

1. Background

Human experience takes place in multiple overlapping contexts, including geographic contexts such as neighborhoods and cities, organizational contexts such as schools and clinics, and social contexts such as families and friendship networks. Though the variability of health-relevant exposures and outcomes within and between these contexts has long been a focus of study (Mooney, Knox, & Morabia, 2014; Morabia, 2014; Pincus & Stern, 1937), in recent years, research teams have increasingly had opportunities to link measures from more than one type of context within the same study population (Box 1).

Box 1. The Role of the Intra-Class Correlation in Selecting a Cluster Definition.

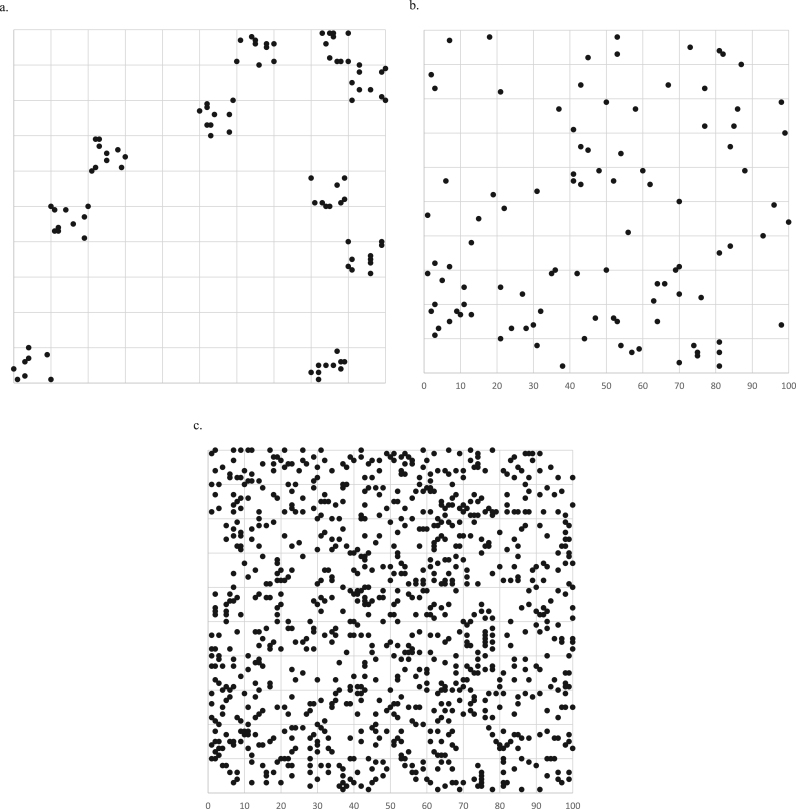
Either perspective might turn to tools such as the intra-class correlation (ICC) to quantify how distinct clusters are with respect to the health outcome of interest (Merlo, Chaix, Yang, Lynch, & Rastam, 2005). An ICC that is distinct from zero (or one with a 95% confidence interval that excludes zero) might be used to justify a particular cluster definition by some with a model-based perspective (Snijders and Bosker, 2012b, Snijders and Bosker, 2012c, Snijders and Bosker, 2012d). The ICC may also be used by those with either perspective to point to areas of potential interest for substantive investigation. Because the ICC correlation within clusters, any decision that relies on ICC values may be reversed when the same study data are used to investigate a different outcome. Similarly, a pilot study and a full scale study might reach different conclusions about the need to account for clustering, even though each used the same sampling strategy to study the same outcome. Thus, the design effect will depend not only on the sampling strategy but also on the population sampled and the outcome itself. For example, among students there may be stronger clustering of standardized test scores by classroom due to influence of the teacher and of processes by which students of similar abilities are assigned to the same classroom, whereas school-level clustering may be stronger for physical activity outcomes due to shared physical fitness facilities and physical education policies. To visualize this phenomenon, it may help to consider a sparse sample (Fig. 2b), where the social contexts will often be unique or shared by few participants. Low power would result in wide confidence bounds around the ICC, and we would be unlikely to exclude zero (however, even when power is low to detect whether the ICC for the outcome is distinguishable from zero, there may be sufficient power to detect an association with one of the measured cluster characteristics). By contrast, in a dense sample (Fig. 2c) there is greater statistical power to distinguish the ICC from zero, and more opportunity to investigate the contributions of both measured and unmeasured characteristics of shared environments.

The integration of multiple context types into our research reflects the multiplicity of overlapping contexts that shape our social experience and related health risks. Health-relevant sorting into neighborhoods (Bischoff & Reardon, 2013), schools (Reardon & Owens, 2014), clinics (Sarrazin, Campbell, Richardson, & Rosenthal, 2009), and workplaces (Goh, Pfeffer, & Zenios, 2015) has been well-documented in the literature, complicating our ability to study the implication of changing such contexts for our health. Beyond physical contexts there are social networks and affinity groups that affect the health of individuals. The numerous overlapping contexts in which individuals are embedded result in correlations within “clusters” (a term that we will use for brevity to indicate the spatial units, institutional settings, or other macro-units to which individuals in a study population are indexed via a cluster identifier). The availability of repeated measures over time in longitudinal studies bring further complexity as well as value (Leckie, 2009). One or more of the clusters may take on particular salience because of the study design or context characteristics available for linkage (Fig. 1). Doing so makes salient the often implicit tensions between two inferential perspectives labeled as model-based and design-based.

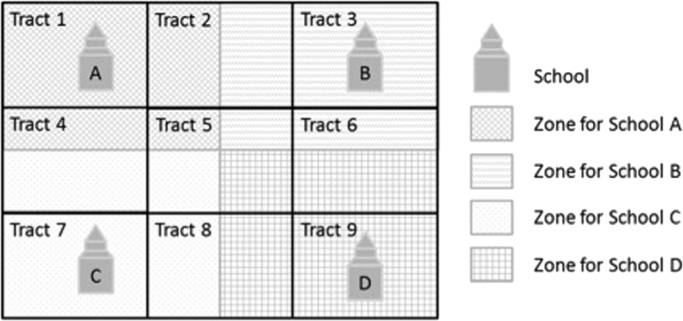
Fig. 1.

A schematic diagram of overlapping sources of clustering. Subjects recruited from schools A and D are both clustered in schools and in an overlapping subset of census tracts. Which, if any, of these clustering sources does an analyst need to account for? Notes: This study recruited students from schools A and D, then measured neighborhood conditions in census tracts referring to students in those tracts (1, 2, 4, 5, 6, 8, and 9). Does the analyst need to account for clustering on tracts, on schools, or both? How should we decide, noting that the clusters are overlapping and not hierarchical? A design-based perspective would emphasize the recruitment setting, indicating that inference about students in general must account for clustering of students within schools. A model-based perspective would emphasize whether clustering is important to approximating the probability model generating the observed data.

This paper identifies two common perspectives and their implications when considering a clustering-based analytic approach (e.g. by using random effects or cluster robust standard errors) for studies linking context to health. As such analytic approaches have become easier to implement in standard statistical software (Diez Roux, 2000; Singer, 1998), how specifically to analyze clustered data, and whether hierarchical or cross-classified techniques are truly necessary, should be considered carefully (Mitchell, 2001). Attention to what have been called “model-based” and “design-based” inference goals (Snijders and Bosker, 2012c, Sterba, 2009), and the tensions between perspectives and within each perspective, can elucidate how we decide on which cluster definition (or definitions) to account for, a decision that in turn affects all subsequent analytic and inferential steps. We aim to provide insight into these perspectives and their implications for an applied population health research audience. We first discuss distinguishing features of each perspective, and then turn to how they offer divergent guidance under the increasingly common circumstance of having more than one type of context available to account for non-independence (Fig. 1).

Consider, for example, an investigation of swimming skills (Hulteen et al., 2015) among children in a given city, with relevance to both physical activity (Fisher et al., 2005) and drowning risk (Brenner et al., 2009). The investigative team systematically samples schools within the city, and then children within those schools, such that sampling probabilities are known. Suppose also that residents of some neighborhoods have received frequent marketing of private swimming lessons at their local swimming pool (for the sake of illustration, we suppose this is unmeasured, as would often be the case for local social norms or other behaviorally-relevant characteristics of context). Empirically, it might be that residual clustering in the outcome is greater based on neighborhood than by school. Exposures of interest addressed by the investigative team across several empirical manuscripts are defined at the individual (e.g., gender), school (e.g., physical education hours/week), and neighborhood level (e.g., area-based socioeconomic indicators). A team that adopts a design-based perspective would be attentive to sampling weights and inference to the city population, but might not require adding a random effect to account for within-neighborhood clustering because that clustering is a reflection of the clustering truly present in the city (rather than being investigator-imposed). By contrast, the model-based perspective would primarily be focused on specification of the model, accounting for neighborhood clustering if the processes shaping the skills of two children within the same neighborhood are not considered independent; the model-based team might consider an unweighted analysis using adjustment as a possibly more efficient alternative to a weighted analysis. Both perspectives are flexible, and ideally the advantages of each will be considered, but we posit that being able to name and distinguish them will help to avoid confusion.

2. Distinguishing features of, and selected tensions within, a model-based perspective

A model-based perspective emphasizes the processes producing outcome variation, and observed data are used to characterize that data-generating process. This is the majority perspective in statistical textbooks, including those focused specifically on multi-level modeling (Snijders & Bosker, 2012d). Attention is paid to minimizing bias and maximizing efficiency, and if weighting is used it is often for these purposes. Crucially for the topic at hand, a model-based inference perspective primarily considers independence of observations with respect to residual correlations in the observed data. Measured cluster-level characteristics may be of interest to explain such residual correlations, in which case a model structure is specified and the parameters estimated accordingly, or there may simply be an interest to account for the variance structure because the assumption about observations’ independence does not hold.

Even before we consider the contrast with a perspective focused on design-based inference, it is worth mentioning two tensions among those seeking to make model-based inference. First, in decisions on whether to condition on clusters, some may prefer a strategy specified a priori, while others may look to the data to guide the structure of the model. Often, the two strategies are blended, starting with an a priori strategy and then using sensitivity analyses to explore modifications to that strategy as colleagues and reviewers suggest them. A similar tension can be noted in deciding which variables to include as covariates: a strategy informed by expert knowledge and optimized to address the causal question of interest has clear strengths, but exploration of the data may suggest a simpler model that would serve just as well or a more complex model that fits the data better (which may come along with risks of overfitting the data). Investigators with model-based inference goals differ also in whether they view the implementation and interpretation challenges of more complicated models as inherently problematic due to the potential for user error, or as opportunities to enhance training and interdisciplinary partnerships. We will return to divergent views of model complexity as we conclude our discussion of analytic implications of model-based and design-based perspectives.

2.1. Key features of a design-based perspective, and potential relevance to multiple sampling strategies

A design-based perspective emphasizes generalizability of estimated parameters to a well-defined finite population. This perspective is more commonly invoked by those designing and using complex survey samples or within institutions such as municipal health departments that have responsibility for health in a particular locality. From a design-based perspective, the distributional assumption about the data-generating process made using a model-based approach are replaced by the introduction of empirical randomness from the random sampling design. Thus, from a design-based perspective, greatest concern about “non-independence” would arise if sampling probabilities are not independent. Non-independent sampling probabilities could arise, for example, in a two-stage sampling design or with respondent-driven sampling. Knowing that an adjacent member of the population has been sampled is informative for guessing whether I, too, will be sampled.

There are designs other than complex survey samples in which sampling probabilities can be correlated, suggesting the design-based perspective has wider relevance than may be at first assumed. For example, a convenience or purposive sample that recruits through institutional settings may have unequal but unknown sampling probabilities, in which case information about the target population from other sources can help to characterize any divergence from what would be expected in a census or simple random sample, designs in which all observations in the underlying population are equally likely to get into the analytic dataset.

In most real-world studies, even those with a random sampling plan, study refusals and missing data create a mismatch between the characteristics of those included in the analysis and those targeted for recruitment. A study planned to include a simple random sample of the target population may nonetheless find that refusals or missing data are common within certain clusters. Weighting can be used to maximize the correspondence of analytic results with what would be expected for the entire target population (Lee & Forthofer, 2005). If an association varies in strength across demographic groups, some of which were less likely to be in the sample, those individuals who were unlikely to be in the sample are assigned higher weights; the weighted result is shifted toward the average for that group as compared to the unweighted result (Chaix et al., 2011). Thus, from a design-based perspective, weights are often used to better approximate a representative sample taken from a specific finite population. Integration of survey weights with mixed models and other approaches continues to be an active topic for methods development (Carle, 2009, Rabe-Hesketh and Skrondal, 2006, Si et al., 2015).

2.2. What makes us question the assumption of independence?

Human health has individual-level causes, but these are not the only opportunities to intervene if we seek to improve the health of populations. The distributions of health within and between populations are shaped by factors that lie above the individual and influence individuals’ actions and interactions within societies. Examples of these factors include political factors, the economy and corporate practices, local built environments, and the social structure. These macrosocial factors create differential access to resources and opportunities and influence the level and distribution of health and disease within and between populations. Thus, as humans we are embedded in social structures, creating organized complexity (Jacobs, 1961).

Despite the importance of various contexts for human lives, in many studies this fades to the background and is not explicitly investigated or accounted for in our statistical analyses. There are two common triggers for discussion of whether we need to account for non-independence in health studies, based on different considerations of when clustering could represent a threat to study validity.

First, as emphasized under a model-based perspective, we may have an awareness of (and possibly an interest in explaining) shared variability in the health outcome arising from how subjects are clustered within a population. Research teams might characterize geographic clusters through data linkage or through audits of the local environment (e.g., systematic observation of streets, parks, or stores). Often such studies rely on the availability of the participant’s home address, which researchers subsequently geocode. Administrative units such as US census tracts are commonly used, in which case characteristics will be identical for those living in the same census tract, and may be correlated for those living in adjacent census tracts (Diez Roux et al., 1997). Likewise, linkage to institutional records may allow characterization of school environments, workplaces, clinical settings, and other contexts. Characterizing contexts makes the possibility of residual correlations within clusters more salient, as we realize that we have not necessarily captured all relevant aspects of shared experience among individuals in the same cluster.

Second, as emphasized under a design-based perspective, inference about a finite population from a finite sample requires assuming the sample represents the population, and accounting for any correlations that may have been induced by the sampling strategy.The central limit theorem implies that with a sufficiently large random sample, inferences about the sample are likely to recapitulate inferences about the population. However, researchers frequently enroll subjects in clusters to gain efficiency. For example, in a two-stage sampling design, the target population is partitioned into clusters, often based on geographic units (e.g. census tracts) or institutional settings (e.g. high schools). Subject recruitment then takes place within a subset of these clusters. A schematic representation of this approach is shown in Fig. 2a, wherein grid cells represent clusters and subjects are recruited from 10 of the 100 potential clusters. Cluster-based sampling has logistical advantages during the process of data collection relative to a simple random sample. However, the assumption that such clustered samples fully represent the overall population is more tenuous.

Fig. 2.

Schematic representation of observations within clusters differing in density and sampling strategy. Notes: Panel (a) shows a balanced sampling pattern with 10 dots sampled by design within each of 10 randomly selected clusters, a situation often handled through the use of weights or so-called “fixed effects” (dummy indicator variables for all clusters except for an omitted reference cluster). Panel (b) shows a sparse, unbalanced pattern of 100 dots arranged randomly across 100 clusters, resulting in few observations per cluster (including some clusters with zero observations). Panel (c) shows an unbalanced pattern 1000 dots within 100 clusters.

These two triggers for the need to consider clustering have been recognized and discussed extensively in prior literature. However, they have typically been discussed separately. Whereas literature focused on model-based inference has focused on estimating parameters from a probability model which could have generated the data (Snijders and Bosker, 2012d, Sterba, 2009), literature focused on sampling has taken a design-based perspective, emphasizing inference to a finite population (crucially considering how one should account for sample selection). While the model-based perspective suggests accounting for clustering in the structure of our model (e.g., through cluster robust standard errors or random effects), the design-based perspective often instead deploys weights or other strategies with the goal of accounting for sampling probabilities (thus more closely aligning estimates and standard errors with what we would expect to see in the target population). Both strategies may be combined in a hybrid framework, such that both perspectives are accommodated at the cost of increased model complexity.

Yet examining these two perspectives separately may provide insight into alternative goals we could pursue with the same data, and doing so highlights divergent implications when deciding which cluster type to account for or whether clustering must be accounted for analytically at all.

2.3. Sampling within clusters matters for both perspectives

Whatever our perspective, sampling within clusters shapes our situation in three ways.

First, random sampling within clusters for statistical efficiency (Scheaffer, Mendenhall III, & Ott, 1996) generally ensures that each cluster will have multiple observations. Because people are clustered in reality, sampling at random with respect to clusters typically results in a lower and less balanced number of observations per cluster, as shown in Figs. 2b and 2c. In the context of multi-level modeling, a balanced data structure is one with the same number of observations in each cluster. For example, a study that sampled a total of 100 adults within 10 selected ZIP codes would have a mean of 10 observations per ZIP code. If instead the study had sampled 100 adult residents at random from 100 ZIP codes (or, to be even more extreme, across the nearly 42,000 possible ZIP codes in the US), we would have several ZIP codes with zero observations, and many others would have only one participant in this sparse sample. The density of observations within clusters does not change how important attributes of clusters are for health in the underlying population. However, multiple observations per cluster (a minimum of 2) are necessary to disentangle the between group and within group variance, and for this purpose a balanced design will be desirable. Further, observations that are concentrated within fewer clusters make the measurement of cluster-level predictor variables more feasible via geographic information systems (GIS) (Vine, Degnan, & Hanchette, 1997), ecometric measurement (Mooney, Bader, et al., 2014; Mujahid, Diez Roux, Morenoff, & Raghunathan, 2007), or institutional data linkage (Jutte, Roos, & Brownell, 2011). On the other hand, inclusion of a larger, geographically dispersed sample of clusters may enhance variation of characteristics under study, thus addressing concerns about statistical power and multicollinearity that plague many place-based investigations.

Second, sampling within clusters can exaggerate similarities within clusters if differences in equipment, calibration, or data collection personnel are present between clusters. For example, if fitness testing is conducted within schools (Rundle et al., 2012), differences in the ways that students are incentivized using grades or in the method of recording results (e.g., by peers versus by teachers) may induce differential measurement error. This error could make the scores more similar for students at the same school than would be expected based on the similarity of their underlying fitness levels.

Third, sampling within clusters embeds some particular definition of a cluster into our study design, despite the multiplicity of potential factors on which clustering occurs and potential definitions of those clusters. Humans are simultaneously clustered by residential neighborhood, workplace or school, physician, friendship group, and any number of other social and physical contexts with potential relevance for their health. The design of randomized studies can also embed a particular cluster definition into the design (Liao, Zhou, & Spiegelman, 2015; Raudenbush, 1997; Saville & Wood, 1991).

3. Selecting a cluster definition using different perspectives

In some studies of context and health, there is only one source of clustering considered. Perhaps geographic units such as postal codes were prominent in our sampling strategy and characterized through linkage to spatial data. The research team would likely agree easily that postal code “neighborhoods” should be used to account for clustering.

However, different perspectives can be revealed when there is more than one defensible way to identify how individuals are clustered (Fig. 1). For example, consider an investigation of childhood obesity in relation to neighborhood characteristics conducted as part of a study in which subjects were sampled through schools (Gordon-Larsen, Nelson, Page, & Popkin, 2006). A design-based perspective would emphasize the sampling strategy and any investigator-induced structure in the sampling probabilities that would result. Inference about students in the finite population of students attending the schools from which the sample was drawn must account for sampling of students within schools. A model-based perspective would instead emphasize accounting for clustering that helps to approximate the probability model generating the observed data, whether by school or by neighborhood or both.

3.1. Socially connected individuals may share common factors

We have just noted that clustered sampling tends to make our choice of a cluster identifier obvious: the primary sampling unit. Indeed, if sampling was intended to characterize the population of clusters, a two-level mixed effects model is appealing because of the parallel between the data collection and analytic approaches. However, investigators with a model-based perspective may be tempted to at least consider other cluster definitions. The common practice of geocoding home addresses (Rushton et al., 2006) and grouping the addresses within neighborhoods, often defined using postal codes or other administrative units (Riva, Gauvin, & Barnett, 2007), made such geographic units a popular option. Furthermore, some For geographic research, some researchers have taken steps to combine administrative units after review to create more meaningful groupings (Sampson, Raudenbush, & Earls, 1997), but ultimately each observation is in one and only one group. Even for spatial analyses where predictors have been collected for personalized neighborhood boundaries (Lovasi, Grady, & Rundle, 2012), accounting for clustering is often handled through a return to reliance on administrative boundaries that can be used to define random effects or to construct cluster robust standard errors. Likewise, linkage to data on workplace, school, clinic, or other health-relevant settings raises the salience of both modeled and residual clustering of health outcomes within such settings, even if they were not accounted for during sampling.

Such a search for potential clustering may be productive, and perhaps should be pushed even further. Having found a defensible and readily available cluster definition, we may benefit from further delving into other sources of non-independence that are not so easily measured, such as approaches that more continuously account for the distance between observations spatially (Chaix et al., 2005, Rainham et al., 2010) or across social networks (Luke & Harris, 2007). Choosing the most readily measured definition (such as postal code) might obscure the more complex ways in which individual are socially interconnected. While the design-based perspective might view this merely as a missed opportunity for substantive investigation (and not required to appropriately account for investigator-induced clustering of sampling probabilities), a model-based perspective would call into question whether a model structure that ignores this source of non-independence is misspecified and thus suspect.

More generally, in our complex and socially integrated real world, there is no guarantee that the within-group correlation observed in sampled clusters in a cluster-based sample is stronger than correlation within alternative geographic or organizational groups. The model-based perspective suggests that adjusting analytically only for sample-based clusters would be insufficient (due to misspecification of the model), particularly if an alternate form of clustering empirically shows stronger within-group residual correlation. By contrast, the design-based perspective is concerned with clustering that the sample design creates by deliberately oversampling within some units. It is concerned with units that are literally not independently sampled. It seeks to remove this investigator-induced dependency. The approach acknowledges that people may be alike because of membership in other geographic or social groups but that this is not investigator-induced. It warrants study with whatever means best illuminates whether and why people within groups are alike but it should not be equated with, or confused as being the same as, non-independence that the investigator creates.

A potential compromise position is to account for multiple types of clustering, using tools such as cross-classified mixed models (Diez Roux, 2002). Cross-classified models are gaining increasing use in fields such as education research (Rasbash, Leckie, Pillinger, & Jenkins, 2010) and in population health research (Carroll-Scott et al., 2015, Dunn et al., 2015, Milliren et al., 2017), but have additional potential for use. Yet the potential ways that observations may be clustered can easily overextend what we can handle given sample size and implementation challenges. If we adopt the design-based perspective, we may declare that we have done enough by accounting for our sampling methods, and that although further clustering may be of interest, it need not be accounted for in analyses where non-independence is merely a nuisance. Indeed, some robustness to model misspecification, such as omitted interaction terms, is a key advantage of adopting a design-based perspective (Lee & Forthofer, 2005) and a potential justification for the efficiency “costs” inherent to many weighted analyses (Bollen, Biemer, Karr, Tueller, & Berzofsky, 2016). (In contrast, from a model-based perspective we would be more focused on the implications for model efficiency and uncertainty, and on evaluating whether accounting for clustering results in more appropriate standard errors and 95% confidence intervals.) Thus, a design-based perspective relieve us from chasing additional ways to account for residual clustering in our data.

Regardless, once clusters have been defined, the definition has implications for how analyses proceed.

3.2. Implications of cluster definition for analysis of clustered data

There are several analytical techniques commonly used to analyze clustered data, including mixed-effect models, generalized estimating equations (GEE), and cluster robust standard errors (Cerin, 2011, Hubbard et al., 2010, Subramanian and O’Malley, 2010). GEE is a population-based approach based on a quasilikelihood function and provides the marginal or “population averaged” estimate of the parameters, whereas the mixed or “mixed-effect” model employs random effects to capture variation between clusters and provides a conditional or “cluster-specific” estimate of the parameters for individual-level predictors. An approachable overview and comparison of analytic choices following cluster sampling has been presented for the context of built environment and physical activity research (Cerin, 2011). For those who would like more detailed guidance there are a number of excellent texts (Gelman & Hill, 2007; Raudenbush & Bryk, 2002a; Snijders & Bosker, 2012d). While in some cases a design-based approach using weights might only estimate simple statistics such as means and ratios, a design adjusted variance estimator using Taylor linearization can be employed to account for design-based features, more of a hybrid (Graubard & Korn, 2002).

An investigator’s decision to employ one technique over another is potentially a function of the research question. Of note, the choice of cluster definition may be more consequential than the estimator choice (Zorn, 2006), though additional examination of this question is needed. For some questions in which variance partitioning (Brunton-Smith et al., 2017, Dundas et al., 2014, Leckie et al., 2014, Leckie and Goldstein, 2015; Merlo, 2014; Næss & Leyland, 2010) or cluster-level prediction (Brunton-Smith et al., 2017, Cerda et al., 2008, Croon and van Veldhoven, 2007, Steele et al., 2017) play a key role, mixed models have clear advantages. Likewise questions that pertain to variance partitioning across more than two levels (Browning et al., 2003, Sarkar et al., 2013) would point toward the use of mixed models over GEE and cluster robust standard errors. Often, however, the research focus is on estimating fixed effects relevant to a hypothesized context-health association, and the conclusions would likely be robust to the modeling approach (Cerin, 2011; Stephen W. Raudenbush & Bryk, 2002b). For individual-level predictors, on the other hand, there is a key distinction between the conditional estimates from mixed models and the marginal estimates from GEE. While conditional estimates are expected to be farther from the null than marginal estimates in logistic models or other generalized forms used for categorical outcomes (Hosmer and Lemeshow, 2000, Snijders and Bosker, 2012a), there is mathematical equivalence of marginal and conditional estimates for linear models of a continuous outcome.

An alternative of using dummy indicator variables as “fixed effects” comparing each of the clusters to an excluded reference cluster can also be considered, and due to efficiency implications this is usually considered when the number of clusters is relatively low (Cerin, 2011; G. S. Lovasi & Goldsmith, 2014).

Further, the selection of a cluster definition, which as discussed above can be informed by a model-based or design-based perspective, becomes even more important if one is reporting parameter estimates that are conditional on cluster. Mathematically, this distinction is fairly inconsequential when using linear models for continuous predictors, but it becomes more important when working with logistic or other generalized mixed models(Hosmer & Lemeshow, 2000; Mood, 2010; Snijders and Bosker, 2012a, Snijders and Bosker, 2012d).

4. When is it necessary to account for clustering?

Most analysts would agree that we will gain nothing from efforts to account for clustering in datasets that are extremely sparse with respect to a given potential cluster definition (i.e., most clusters have only one observation) (Clarke, 2008, Rasbash et al., 2010).

However, when multiple observations per cluster exist, the decision becomes more complicated. Even when there are several observations per cluster (Fig. 2c), a given outcome may not be strongly patterned by cluster. Moreover, the decision is neither purely theoretical nor purely empirical, but must balance both substantive and statistical considerations (Snijders & Bosker, 2012d). Mixed models or GEE approaches may be attractive if such divergence is detected, particularly because of their robustness to unbalanced designs with observations missing at random conditional on cluster (Ghisletta & Spini, 2004). However, from a design-based inference perspective (Lee & Forthofer, 2005), some emphasize that independent sampling probabilities justify analytic approaches that do not explicitly account for potentially health-relevant clustering in social contexts.

Analysts may empirically check if the outcome variable has an ICC that is distinguishable from zero, as introduced briefly above. Even those favoring a priori specification of how the model will account for clustering, coauthor or reviewer suggestions may warrant an empirically-informed response. The ICC can be approximated even if the outcome variable is dichotomous (Merlo et al., 2006; Ridout, Demetrio, & Firth, 1999). While often ICC is evaluated for the outcome variable, examining the ICC for model residuals is common as well, and is arguably even more closely aligned with the question of whether there is unexplained non-independence in our data. If the ICC for our outcome is estimated as zero, there is no variation between groups beyond what would be expected by chance. We may then have little to gain by explicitly accounting for clustering. However, what ICC we consider as substantially greater than zero is dependent on the research context and the dataset; small but statistically significant ICCs may easily result from the use of ‘Big Data’ (Mooney, Westreich, & El-Sayed, 2015). Point estimates and confidence intervals (Snijders & Bosker, 2012b) thus may be more informative than p-values alone, and researchers may find comparisons to an r² statistic helpful when interpreting the magnitude of an ICC. Both the ICC and r² are describing a portion of variance explained (by the cluster-level identifier or by covariates in a regression model, respectively), and for both of these we would expect to occasionally note values as low as 2% (ICC or r² of 0.02) as statistically distinguishable from zero, and explaining 5% or more of the outcome variance (an ICC or r² ≥ 0.05) is considered important (Subramanian & O’Malley, 2010) and occasionally much higher ICCs are noted in health research (J Merlo, Wagner, Ghith, & Leckie, 2016; Rodriguez and Goldman, 1995, Rodriguez and Goldman, 2001).

4.1. Is there any harm to accounting for clustering when it is not necessary?

Beyond standard recommendations to check model assumptions and use best practices to account for our study design, should we routinely scan for clustering within spatial units such as postal codes in health studies? Such human health characteristics as we are likely to use as outcomes typically cluster to a small extent within spatial units, though often with an ICC below 0.10 (Subramanian & O’Malley, 2010). Non-health outcomes such as housing abandonment, in contrast, may have a neighborhood ICC above 0.50 (Morckel, 2015).

There are several concerns that may be raised with regards to an overly simplistic approach to clustering. First, if we account for clustering within our most readily measured cluster definitions, we may deflect attention from the other social measures that would offer valuable insights but which are more challenging to measure. We often assume that the clusters themselves are independent, despite potential adjacencies or other ties (Chaix et al., 2005). We also assume that we are not ignoring important substructures within our clusters--though this is less of a problem for robust standard error approaches (Heagerty and Lumley, 2000, Lumley and Heagerty, 1999) which can account only for a single specified cluster definition, but allow arbitrary correlations between observations within clusters. Thus, while we tend to discuss a multi-level model as though it has dismissed any concerns about non-independence, from a model-based perspective the decision to use a multi-level model only modifies the approach to make different, and hopefully more plausible and innocuous, assumptions about independence of our sampling probabilities and model residuals. A limited selection of dependency structures, such as the autoregressive form commonly used in longitudinal investigations, is available for consideration (Hosmer & Lemeshow, 2000; Singer & Willett, 2003). It should be emphasized that our greatest ambivalence about identifying the appropriate approach to account for clustering comes from concerns about unmeasured sources of variance. From a model-based perspective, we worry that our residuals are not independent and identically distributed, as usually assumed, because of unmeasured causes. Yet our hypotheses are more often about variables we have measured.

But concerns can also be raised due to the complexity of accounting for clustering if doing so is unnecessary, and the complexity is particularly notable for cross-classified models. There is a tradeoff between model complexity (without which we risk model misspecification) and primary attention to the sampling strategy (which have efficiency costs, but may relieve somewhat our dependence on the model specification) (Lee & Forthofer, 2005). The easy availability of mixed models in standard software means that they can be used casually by users who may not be attentive to the subtleties of careful implementation. Sensitivity analyses comparing results between simpler and more complex approaches may be helpful in fostering transparency and an understanding of robustness of the results. Underappreciated complexity that is already part of our logistic modeling (Mood, 2010) gets exaggerated in the context of mixed effects modeling (Jones & Subramanian, 2013). When our research question, perspective, and data structures point toward the use of mixed models, their distinct advantages should be embraced. However, perfunctory use of such models to defend against non-independence concerns, especially when simpler approaches would be adequate to address the research question, may open the door to user error in interpretation or implementation. Nonetheless, there may be untapped potential to use mixed models to address new question types, particularly those focused on modeling variance (Brunton-Smith et al., 2017, Leckie et al., 2014, Leckie and Goldstein, 2015) or on group-level prediction (Lüdtke et al., 2008).

In response to complexity, training investigators to use a range of modeling approaches well is appealing, allowing the choice of approach to be shaped by considerations of what is most appropriate. However, in a reality inhabited by investigators with varying levels of analytic sophistication and understanding, guidance as to when a simpler approach can be viewed as sufficient is valuable. The design-based perspective seems more readily to endorse a simple approach as sufficient,one which accounts for sampling probabilities, and then explores as a substantive research problem whether and to what extent people within theoretically relevant are more alike and why.

5. Conclusions

Some caution is clearly warranted to make sure we are appropriately accounting for clustering with awareness of our perspectives and with attention to what is needed to address our research questions. Table 1 summarizes some key contrasts between the model-based and design-based perspectives. Whereas a model-based perspective emphasizes the probability model generating the data, a design-based perspective emphasizes the need to account for how the data were sampled. However, these perspectives only occasionally surface as a clear difference of opinion about how to proceed. Indeed, given that both our modeling strategies and our sampling are always imperfect aspects of each perspective are often co-mingled in teaching and in practice (Gelman and Hill, 2007, Snijders and Bosker, 2012d, Sterba, 2009). However, since investigative and mentorship teams may span multiple perspectives, attention to each is warranted, and may be particularly important as we select a cluster definition.

Table 1.

Summary of the contrasting perspectives on accounting for non-independence described here.

	Model-based	Design-based
Goal of accounting for clustering	Better approximating the probability model for the data generating process	Accounting for sampling strategy to allow inference to a finite population of interest
Implications for analysis	A tendency toward more complexity, potentially including cross-classified models to avoid misspecification	A tendency toward less complexity, focused attention on accounting for sampling may be seen as sufficient
Cluster definition source	Relatively more emphasis on the a priori structure of the data generating process, or empirical analysis suggestive of residual clustering	Relatively more emphasis on the investigator-controlled and empirically-informed model relating cluster membership to sampling probabilities
Key analytic technique(s)	Multi-level models, generalized estimating equations or cluster robust standard errors	Models incorporating complex sampling weights, which may include multi-level models or generalized estimating equations

Note: While we emphasize for clarity the divergent implications of the model-based and design-based perspectives, both perspectives are flexible and there is much potential for overlap and integration

Ethics approval

Ethics approval is unnecessary. No human subjects’ data was used for this paper.