RSAT matrix-clustering: dynamic exploration and redundancy reduction of transcription factor binding motif collections

Abstract

Transcription factor (TF) databases contain multitudes of binding motifs (TFBMs) from various sources, from which non-redundant collections are derived by manual curation. The advent of high-throughput methods stimulated the production of novel collections with increasing numbers of motifs. Meta-databases, built by merging these collections, contain redundant versions, because available tools are not suited to automatically identify and explore biologically relevant clusters among thousands of motifs. Motif discovery from genome-scale data sets (e.g. ChIP-seq) also produces redundant motifs, hampering the interpretation of results. We present matrix-clustering, a versatile tool that clusters similar TFBMs into multiple trees, and automatically creates non-redundant TFBM collections. A feature unique to matrix-clustering is its dynamic visualisation of aligned TFBMs, and its capability to simultaneously treat multiple collections from various sources. We demonstrate that matrix-clustering considerably simplifies the interpretation of combined results from multiple motif discovery tools, and highlights biologically relevant variations of similar motifs. We also ran a large-scale application to cluster ∼11 000 motifs from 24 entire databases, showing that matrix-clustering correctly groups motifs belonging to the same TF families, and drastically reduced motif redundancy. matrix-clustering is integrated within the RSAT suite (http://rsat.eu/), accessible through a user-friendly web interface or command-line for its integration in pipelines.

INTRODUCTION

Transcription factor binding motifs (TFBMs, simply called motifs below) are models describing the binding specificity of a transcription factor (TF). Such motifs are generally obtained by aligning the sequences of several binding sites, and summarizing the nucleotide frequencies per position. Motifs are commonly represented as position-specific scoring matrices (PSSMs) (1) and visualized as sequence logos (2). Although the adequacy of PSSMs has been questioned for some particular TF classes (3–6), e.g. in cases of dependencies between adjacent nucleotides, they are still the most widely used method to represent the binding specificity of a TF. Thousands of PSSMs are available in private or public databases, such as JASPAR (7), TRANSFAC (8), Cis-BP (9), FootprintDB (10), HOCOMOCO (11), which constitute key resources to interpret functional genomics results. A well-known issue with these databases is motif redundancy (12), resulting from various causes: (i) for a given TF, multiple PSSMs can be built from different collections of sites characterized with alternative methods (i.e. DNase-Seq, SELEX, protein-binding microarrays (PBMs), ChIP-seq); (ii) the binding specificity is often conserved between TFs of the same family; (iii) some databases contain PSSMs obtained from orthologous TFs in different organisms; (iv) some unrelated TFs recognize similar DNA motifs.

In addition to this intra-database redundancy, inter-database redundancy and the exponential growth of motif collections are becoming major issues. Indeed, the development of high-throughput methods to characterize genome-wise TF binding locations (e.g. ChIP-seq, ChIP-exo) has led to an explosion of motifs, with a fast expansion of databases (e.g. JASPAR almost doubled in size between 2014 (590 motifs) and 2016 (1092 motifs)) (12). In parallel, some individual studies targeting many TFs (13,14) produce motif collections as large as the classical reference databases. This constant increase in the number of motifs and redundant collections represents a real challenge for the community. Which collection to use? How important is the overlap between the different collections? Efforts to collect and integrate numerous up-to-date collections into a single metadatabase like FootprintDB (10) or cis-BP (9) are critical for the community. These metadatabases however do not deal yet with the redundancy issue, and keep increasing in size. This now constitutes a bottleneck, by drastically increasing the time needed to compare motifs or to scan sequences with a complete motif database.

Analysis of high-throughput datasets (e.g. from ChIP-seq experiments) also produces sets of redundant motifs. It is common practice to simultaneously run multiple de novo motif discovery tools, in order to benefit from their complementarity (15–18). While some motifs could be discovered exclusively by a given tool, most will be found independently by different tools, hence producing redundant motifs with small variations in length and/or nucleotide frequencies at some positions. Some of these variations may be important biologically, but remain undetected when inspecting unordered collections of motif logos.

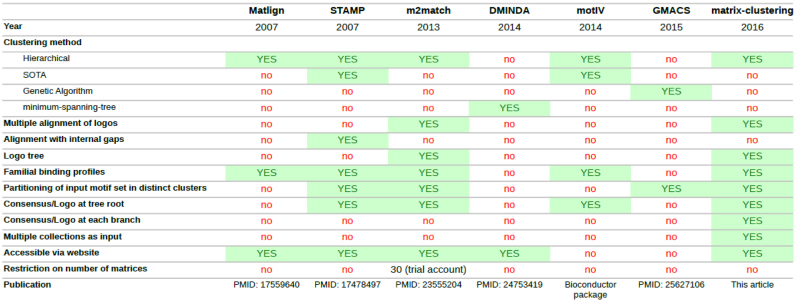
Motif redundancy can be automatically reduced by identifying sets of similar motifs and clustering them. Quantifying the similarity between motifs is nevertheless far from trivial. Many efforts have been done to develop statistical methods and to find adequate comparison metrics between motifs, each one with its own strengths and drawbacks (19–36). Despite this intensive research activity to refine motif similarity metrics, no general consensus has emerged about the best one. Currently, a handful of tools are available for motif comparison: STAMP (22,37), TomTom (23), MATLIGN (26), macro-ape (27), DMINDA (35), DbcorrDB (34) and RSAT compare-matrices (38). Other tools are specialized in motif clustering: STAMP (22), m2match (25), MATLIGN (26), GMACS (28), DMINDA (35) and motIV (Bioconductor package) (see Table 1 for a comparison of their capabilities). However, each of these tools presents some limitations: analysis based on a single metric, restricted number of input motifs, static visualization interfaces.

Table 1. Features of software tools available to perform clustering of PSSMs.

We have developed matrix-clustering within the RSAT suite (39), motivated by the crucial need for a tool to cluster similar motifs, align them to facilitate visual comparison, explore each cluster in a dynamic way, and reduce redundancy either automatically or in a supervised, user-friendly way. We first show with two case studies that matrix-clustering simplifies the interpretation of motif discovery results, and that a dynamic view of aligned logos can reveal biologically relevant motif variants. We then consider two applications encompassing complete databases, which show that the program regroups motifs bound by TFs of the same family, and can be used to explore the complementarity between multiple motif collections. This approach paves the way towards creating systematic non-redundant motif collections.

MATERIALS AND METHODS

Overview

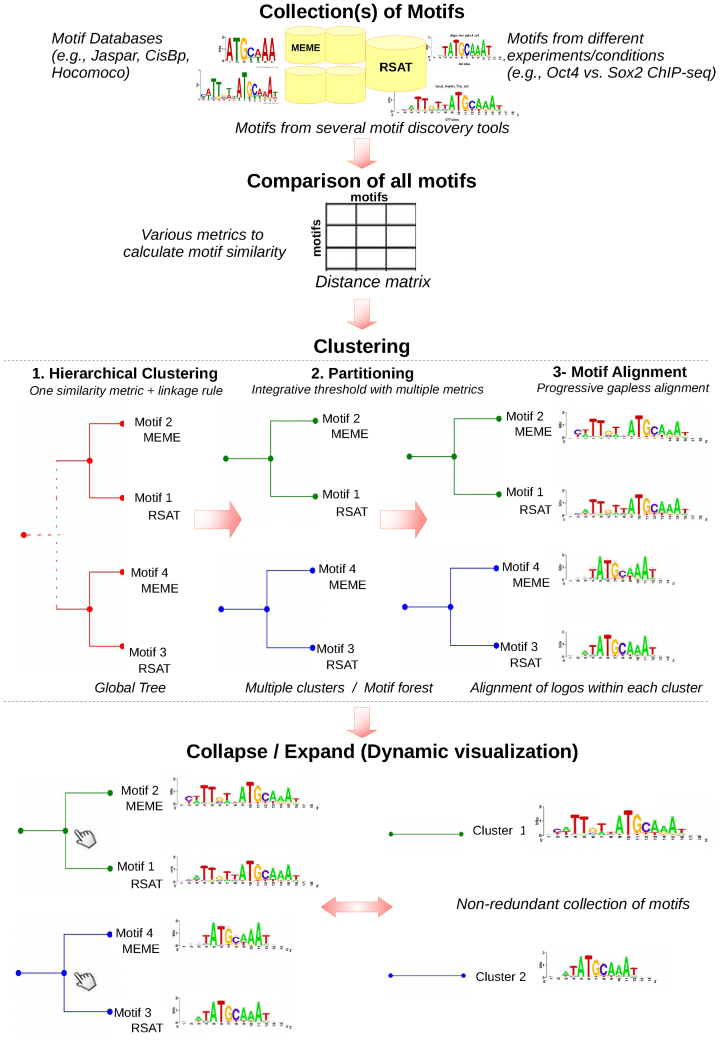
matrix-clustering first computes a matrix of similarity between each pair of input PSSMs, runs hierarchical clustering to build a complete motif tree, which is then partitioned to generate motif clusters (Figure 1), based on a combination of thresholds on one or several motif similarity metrics. Within each cluster, PSSMs are then aligned. The results are displayed on a dynamic user-friendly web report enabling to collapse or expand trees at will.

Figure 1.

Schematic flow chart of the matrix-clustering algorithm. The program takes as input one (or several) collection(s) of PSSMs, and calculates the motif similarity using several metrics. One of these metrics is used to group the motifs with hierarchical clustering. A threshold consisting in a combination of metrics is used to partition the global tree in a set of cluster-specific trees. Each resulting tree then serves as a guide to progressively align the PSSMs. The PSSMs at the root of each tree are exported as non-redundant motifs. The trees can be collapsed or expanded at each node dynamically on the resulting web page.

Input formats and processing time

matrix-clustering receives as input one or several collections of PSSMs (provided as separate files) with an associated ‘collection name’ (e.g. several PSSM collections obtained from different analyses or databases). This program supports different file formats: TRANSFAC (default), MEME, HOMER, JASPAR, etc., and has no restriction on the number of input PSSMs, but users should be aware that the processing time increases drastically with the number of motifs (time complexity is approximately quadratic, see Supplementary Figure S1). For small collections of motifs, the running time enables matrix-clustering usage via the website (e.g. 7 min for the first case study with 66 motifs). Large datasets can be treated with a stand-alone installation of the RSAT suite.

PSSM comparison

Similarity between each pair of input PSSMs is calculated with the RSAT tool compare-matrices (38,39), which can compute multiple similarity metrics in a single run: Pearson correlation (cor), sum of squared distances (SSD), Mutual Information, Information correlation (Icor), Euclidean Distances (dEucl), Sandelin–Wasserman Similarity (SW), as well as width-normalized versions of some metrics obtained by dividing the total length of the alignment by the number of columns where the two PSSMs overlap: normalized correlation (Ncor), normalized information content correlation (NIcor), normalized Euclidian distance (NdEucl) (see Supplementary Notes for the mathematical formulae). Each possible offset is tested for each pair of PSSMs in both orientations, and the program returns the best matching alignment.

Hierarchical clustering

To build the global hierarchical tree encompassing all input PSSMs, the user must select one motif similarity metric (to make the motif-to-motif distance matrix) and one linkage method (average, complete or single). Some metrics directly measure distances (dEucl, SSD, SW); for the metrics measuring similarities (e.g. cor, with a range from –1 to +1), the values are first transformed into dissimilarities (i.e. Dcor = 2 – r, where r is the correlation coefficient).

Identification of motif clusters by tree partitioning

As the RSAT program compare-matrices (38) can return several metrics simultaneously, any combination of these can be selected to define thresholds for the partitioning step, thereby enabling to combine their respective advantages. The global tree is traversed in a bottom-up way and, for each intermediate node, the selected metrics values are computed from all pairs of descendent leaves according to the chosen linkage rule (single, average, complete). Whenever an intermediate node fails to satisfy any of the threshold values, a new cluster is created by separating its two children branches.

Progressive alignment of the PSSMs

Once the global tree is partitioned, each resulting cluster tree is used as a guide to progressively align the PSSMs. They are first orientated (direct or reverse) and then shifted relative to each other. Note that this algorithm does not insert internal gaps. This process produces one multiple alignment for each internal node of each tree, ending with a root alignment that encompasses all the PSSMs of a cluster.

Branch-wise PSSMs, logos and consensus sequences

Once the PSSMs of each cluster tree have been aligned, matrix-clustering calculates for each internal node a branch-wise PSSM by summing (default) or averaging the frequencies of the descendent aligned motifs. It then generates the corresponding consensus sequences and logos. Branch-wise PSSMs introduced here are a generalization of the so-called familial binding profiles (FBP) (37).

Dynamic visualization of the clusters

The clusters are displayed as a PSSM forest, i.e. a collection of trees (one per cluster) with a PSSM associated with each leave. A unique feature of matrix-clustering is that trees can be browsed dynamically: each branch can be collapsed by clicking, and it is replaced by the logo of the branch PSSM, thereby enabling to produce customized motif trees (Figure 1).

Cross-coverage of motif collections

When two or more motif collections are given as input, the cross-coverage indicates the percentage of the PSSMs from one collection that co-occur in clusters with PSSMs from another collection. The coverage of collection A by collection B (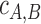) is the number of PSSMs from A co-clustered with PSSMs from B (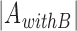), divided by the total number of motifs in A ().

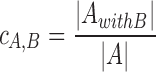Reciprocally, the coverage of collection B by collection A is computed as follows.

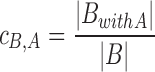This asymmetrical comparison provides a more realistic interpretation of the importance of the intersection relative to the respective sizes of collections (e.g., a comparison between smaller and bigger databases). The cross-coverage is displayed as a heatmap, and a Venn diagram is drawn for each pair of collections. The percentage of specific motifs to each collection is also indicated.

PSSM datasets of the case studies

Case studies 1 and 2: in order to illustrate the clustering of ab initio discovered motifs, we used 359 PSSMs obtained with the RSAT tool peak-motifs (15,40) from 12 TF ChIP-seq peak-sets (41). We also collected the PSSMs obtained by analysing one ChIP-seq peak set with MEME-ChIP (16) and Homer (42).

Case studies 3 and 4: for full database clustering, we analysed 24 taxon-specific collections from 18 databases (Supplementary Table S1): vertebrates (JASPAR (7), HOCOMOCO mouse and human (11), Cis-BP (9), Jolma 2013 ‘HumanTF’ (4), Jolma 2015 ‘HumanTF_dimers’ (13), Uniprobe (43), Fantom5 ‘novel’ motifs (44), hPDI (45), epigram (46), Homer (42), Encode (47)), plants (JASPAR, Athamap (48), Cis-BP, ArabidopsisPBM (49) and Cistrome (14)) and insects (OntheFly (50), JASPAR, dmmpmm and idmmpmm (51), Cis-BP (9), FlyFactorSurvey (52), DrosphilaTF (53)).

Implementation

matrix-clustering is implemented in Perl and R. The Logo trees are implemented in HTML5 with the D3 JavaScript library (54) (http://d3js.org/).

RESULTS

We have developed matrix-clustering to deal with the increasing number of motifs and reduce the inherent redundancy within collections. It takes as input one or more collections of PSSMs, measures the similarity between them using several motif comparison metrics, builds a similarity tree by hierarchical clustering, splits the initial tree to obtain one tree per cluster, generates a consensus and a logo for each branch of each tree, computes branch-wise PSSMs, and generates different graphical representations, including a dynamic visualization enabling flexible customization of the display (Figure 1).

Choice of the default clustering parameters

Parameters of matrix-clustering were chosen based on a detailed comparison between clusters of 374 PSSMs from HOCOMOCO human TFBMs (11) and their classification in 21 families taken from the TFClass database (55). We tested four alternative similarity metrics (cor correlation, Ncor normalized correlation, Icor information correlation, and NIcor normalized information correlation), three linkage rules (single, average or complete), incremental series of partitioning threshold values on each metric (by step of 0.05), as well as combined thresholds applied on a metric and its normalized version (Ncor + cor or NIcor + Icor). Based on this study, we defined the default parameters: the motif-to-motif similarity matrix is computed using Ncor with a minimal alignment width of 5 columns, the motif tree is built with the average linkage rule, and the partitioning criterion combines thresholds on two metrics: cor ≥ 0.6 and Ncor ≥ 0.4. The detailed results of the systematic evaluation, as well as the parameters used for each program, are described in the Supplementary Notes.

Case study 1: identification of TF binding motif variants within motifs discovered with multiple tools in ChIP-seq datasets

It is common practice to perform ab initio motif discovery with several algorithms and to consider the motifs found by several approaches as robust predictions. Yet, some motif variants can be found only by a particular algorithm. This first case study aims at comparing motifs detected in ChIP-seq peaks with three motif discovery tools: RSAT peak-motifs, Homer and MEME-ChIP. We re-analysed the ChIP-seq peaks for the Oct4 TF (also named Pou5f1) in mouse embryonic stem cells (ESC) from Chen et al (41).

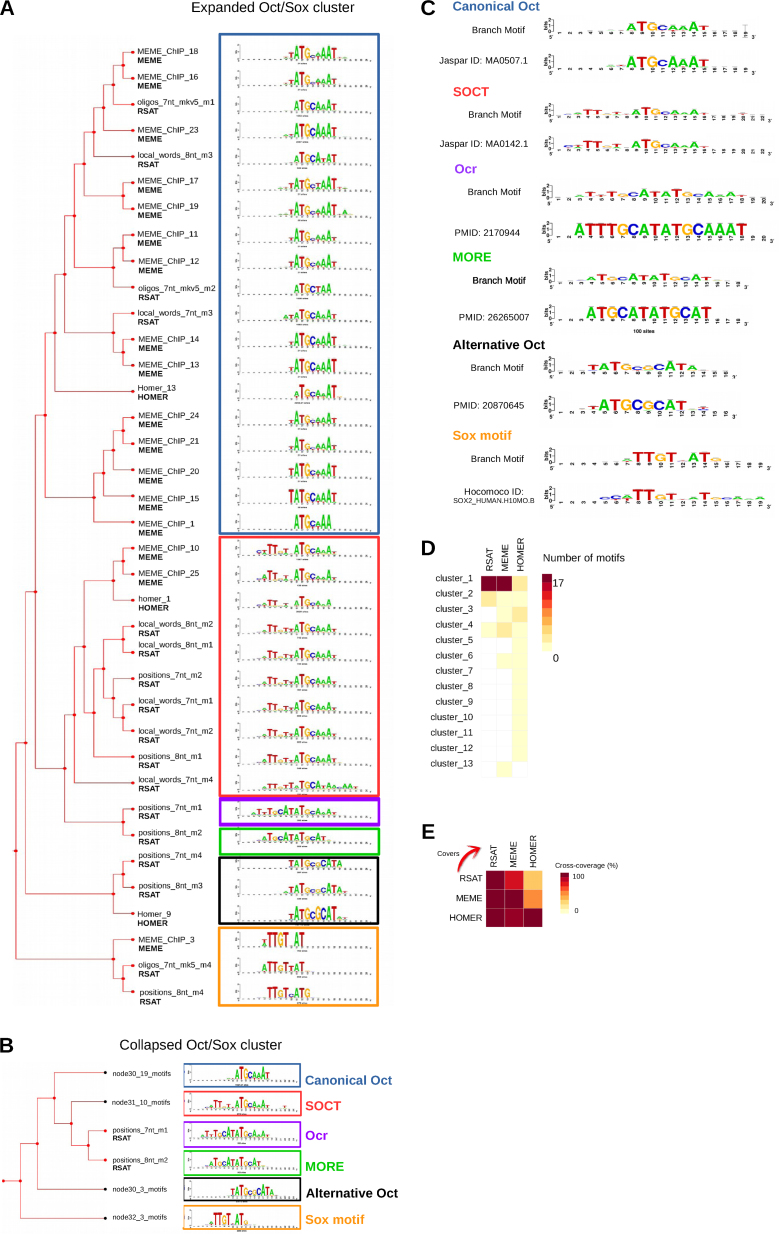
Altogether, the three tools produced 66 motifs: 22 discovered by RSAT peak-motifs, 25 by MEME-ChIP and 19 by Homer. matrix-clustering separated these 66 PSSMs into 13 clusters (Supporting website). The largest cluster regroups 37 PSSMs corresponding to Sox, Oct and other Oct-like motifs (Figure 2A). Since the name of the source collection is automatically displayed besides each logo (spelled RSAT for RSAT peak-motifs, MEME for MEME-ChIP, HOMER for Homer), we readily identify the robust motifs discovered by multiple tools, as well as motif variants detected by a single algorithm.

Figure 2.

Clustering of PSSMs discovered in the Oct4 ChIP-seq peaks using several motif discovery tools. The Oct4 peaks identified by Chen et al. (41) were submitted to three de novo motif discovery programs: RSAT peak-motifs, MEME-ChIP and Homer. All discovered PSSMs were clustered simultaneously by matrix-clustering. (A) Hierarchical tree corresponding to cluster_1 (37 motifs), where different Oct motif variants and Sox2 motifs are highlighted with different coloured boxes. The leaves are annotated with the name of the submitted motif and the name of its collection (RSAT, MEME, HOMER). (B) Reduced tree showing six non-redundant motifs, obtained after manual curation of the cluster_1, by collapsing the branches. (C) Annotation of the six non-redundant variants (‘branch PSSMs’) based on alignments to reference motifs (see main text). When available in databases (JASPAR or HOCOMOCO), the ID of the reference motif is indicated. Otherwise, it is replaced by the PMID of the publication mentioning the motif. (D) Heatmap summarizing the number of motifs from each collection found in each cluster. (E) Heatmap of the cross-coverage between each collection.

We manually collapsed the cluster tree and identified six non-redundant motifs (Figure 2B) for which we searched for similarities in JASPAR vertebrates and HOCOMOCO Human (Figure 2C).These six motifs correspond to the canonical Oct4 (blue box on Figure 2A and B), Sox2 (orange), the composite SOCT (Sox+Oct) motif (red) (56), an alternative configuration of Oct4 (black) (57), a palindromic Oct homodimer (more palindromic oct factor recognition element, MORE) (green) (58), and an octamer-repeat (Ocr) (purple) (59). Of note, these last two motifs were only found by RSAT peak-motifs (Figure 2B).

The contributions of the respective motif discovery tools to the clusters are unbalanced. While RSAT contributes to three clusters shared with MEME and HOMER, MEME raised one single-PSSM cluster (singleton) and HOMER six (Figure 2D). The cross-coverage between the tools (Figure 2E) confirms that RSAT and MEME show high overlap, whereas the HOMER motifs are quite dissimilar from those obtained with the other tools. Of note, many PSSMs only found by Homer are actually of low-complexity (2-residue repeats) and are not likely to correspond to bona fide TFBMs.

Altogether, this case study demonstrates that matrix-clustering can guide and accelerate human-based reduction of a highly redundant collection of motifs, produced by running several motif discovery tools on the same sequence set. The clustering moreover highlights the existence of TFBM variants and combinations (e.g. homodimers, heterodimers).

Case study 2: identification of exclusive or shared motifs between various ChIP-seq experiments

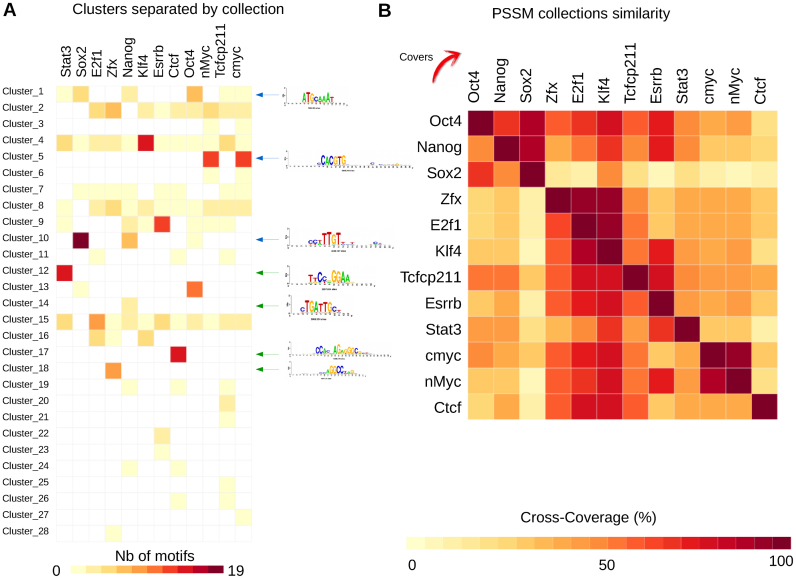
We extended our previous analysis to the 12 TFs studied by Chen et al. (41) in order to identify common and set-specific motifs among the ChIP-seq peak sets. We ran RSAT peak-motifs on each peak set separately and obtained 359 PSSMs, regrouped by matrix-clustering into 28 clusters (Supporting website).

Some clusters contain set-specific motifs, e.g. Stat3 (cluster_12), Nanog (cluster_14), Ctcf (cluster_17) and Zfx (cluster_18) (Figure 3A). Other clusters contain motifs found in two or more peak sets: the Sox (cluster_10), Myc (cluster_5) and Oct motifs (cluster_1) are respectively found in three (Oct4, Sox2 and Nanog), two (nMyc and CMyc) and six (Oct4, Sox2, Nanog, Stat3, Tcfcp2l1, cMyc) peak sets (Figure 3A). These TFs are known to cooperatively regulate common target genes, explaining why their motifs are found across multiple peak sets (41,56). The cross-coverage heatmap (Figure 3B) provides a global view of the content similarity between motif collections. This representation confirms that PSSMs discovered in Oct, Sox and Nanog peak sets are highly similar, consistent with the fact that these TFs co-occur in shared enhancers (41). This is also the case for the cMyc and nMyc motifs, as well as for E2f1 and Zfx, which are functionally related as histone genes regulators (60). By contrast, the motifs discovered in CTCF peak sets are mostly specific to this collection. This case study shows that handling multiple motif collections (a feature unique to matrix-clustering) can highlight their similarities and differences.

Figure 3.

Clustering of 12 sets of PSSMs discovered in mouse ESC TF ChIP-seq peaks. (A) Matrix showing the cluster composition by motif collection. Examples of motifs found in one or several collections (and their corresponding logos) are indicated with green and blue arrows, respectively. (B) Heatmap showing the cross-coverage between the 12 motif collections corresponding to the ESC TF peak-sets.

Case study 3: complete database analyses highlights relationships between motif clusters and TF families

We evaluated whether a clustering of complete motif databases enables (i) to identify redundancy between motifs, and (ii) to regroup PSSMs from the same TF family. TFs are classified in families according to their DNA-binding domains (55,61), which usually recognize similar binding sites. TFs belonging to the same families are thus often associated with similar TFBMs, which constitute a source of redundancy.

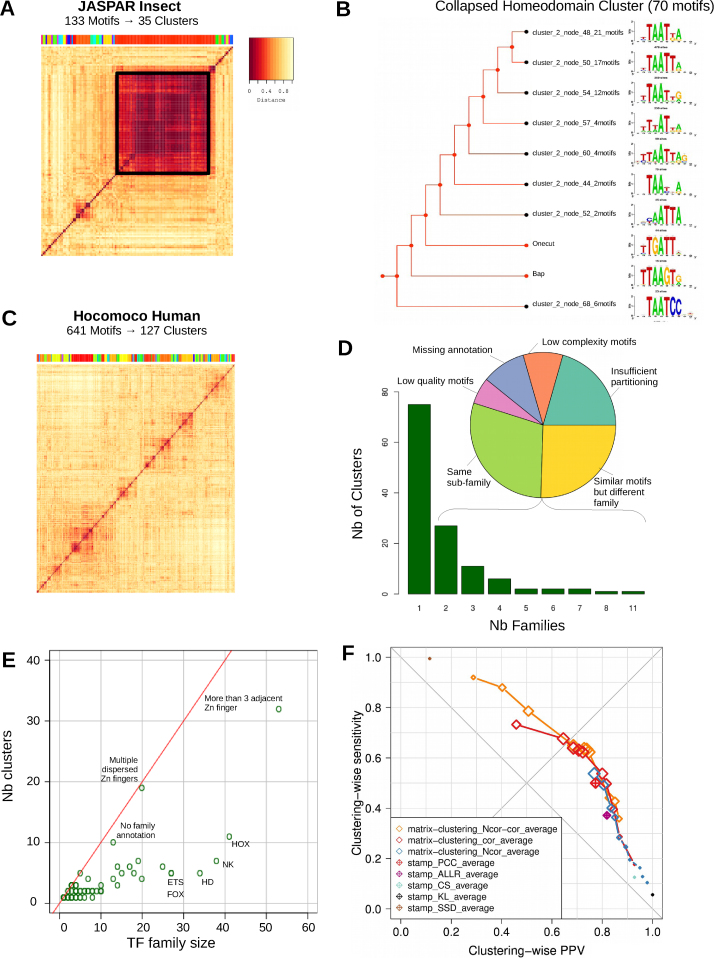
We clustered the complete set of taxon-specific motifs from JASPAR (vertebrates and insects), and species-specific motifs from HOCOMOCO (human and mouse). The clustering of JASPAR insects (133 motifs grouped in 35 clusters) reveals a large cluster of 70 PSSMss (Figure 4A; Supporting website) encompassing almost half of the database. This corresponds to homeodomain-containing TFs, whose TFBMs are characterized by the core consensus 5΄-TAAT-3΄ (62). The dynamic browsing capabilities of matrix-clustering enable to manually reduce these 70 PSSMs to 10 distinct motifs (Figure 4B). The numerous members of this family in the insect database reflect a bias in the content, as most of these PSSMs result from a single analysis covering many homeodomain TFs analyzed with bacterial one-hybrid system (62).

Figure 4.

Clustering of complete Insect and Human motif databases. (A) Heatmap representing the similarity (Ncor) between all 133 PSSMs of JASPAR Insects. The 35 clusters found are indicated with a colored bar above the heatmap. The black square emphasizes the large cluster (almost half of the PSSMs) containing the very similar Homeodomain motifs. (B) The 70 Homeodomain motifs were manually reduced by collapsing the tree branches into ten motifs. The collapsed tree is displayed along with the corresponding aligned branch motifs. (C) Heatmap representing the similarity (Ncor) between all 641 PSSMs of HOCOMOCO Human. (D) Repartition of the clusters formed from HOCOMOCO Human with TF families. The bar plot indicates that most clusters are composed of a single TF family. The pie chart illustrates the reasons for observing multiple TF families in a single cluster. (E) Scatterplot comparing the number of members of each TF family as a function of the number of covered clusters. The name of the families with more than 20 members are shown. (F) Scatterplot showing the trade-off between sensitivity and specificity by clustering PSSMs from the same family with either matrix-clustering or STAMP, using different parameters to compute similarities between each pair of input matrices, build the trees and define the clusters. For matrix-clustering, the curves denote a series of tests performed with different threshold values on the same similarity metric. For STAMP, the number of clusters is defined automatically. Dot sizes are proportional to the Adjusted Rand Index (ARI). The ideal clustering would be in the top-right corner.

By contrast in vertebrates, the 641 human PSSMs of HOCOMOCO are reduced to 127 small clusters (Figure 4C). We obtained similar results for JASPAR vertebrates and HOCOMOCO mouse collections (Supplementary Figure S2A and B, Supporting website). As HOCOMOCO includes the information about TF families imported from TFclass (55), we analyzed the correspondence between clusters produced by matrix-clustering and these TF families. The majority of the clusters (77 out of 127) indeed regroup motifs bound by TFs from a single family (Figure 4D). Furthermore, most of the other clusters actually regroup TFs belonging to different families of the same class. The remaining clusters encompass TFs from different classes but nevertheless bound to similar motifs, and thus correctly grouped by matrix-clustering.

Reciprocally, for each TF family we counted the number of covered clusters (Figure 4E, Supplementary Figure S3). Among the 78 families from HOCOMOCO, 29 are consistently packed in a single cluster, 10 in two clusters, and 16 in three clusters. On the other extreme, some TF families are split into many clusters, in particular the Zinc finger families (e.g. for the family ‘Factors with multiple dispersed zinc fingers’, each PSSM comes as a separate cluster). This dispersion is perfectly consistent with the well-known properties of these TFs: the sequence bound by each Zinc finger domain is determined by the four specific amino acids entering in contact with the DNA (63).

As above mentioned, we explored the impact of clustering parameters on the correspondence between clusters of PSSMs from Human HOCOMOCO (11) and the families of the bound TFs (see section ‘Choice of the default parameters’ and Supplementary Notes). The best correspondence, as measured by both Adjusted Rand Index (ARI) and geometric accuracy (Acc), was achieved with Ncor as matrix-to-matrix comparison metric, average linkage rule to build the tree, and a partitioning combining thresholds on Ncor (≥0.4) and cor (≥0.6) (Figure 4F).

This case study demonstrates how matrix-clustering can handle large collections of PSSMs and automatically reduce their redundancy within a database, while correctly regrouping motifs from TFs belonging to the same family.

Case study 4: comparison and integration of multiple motif databases

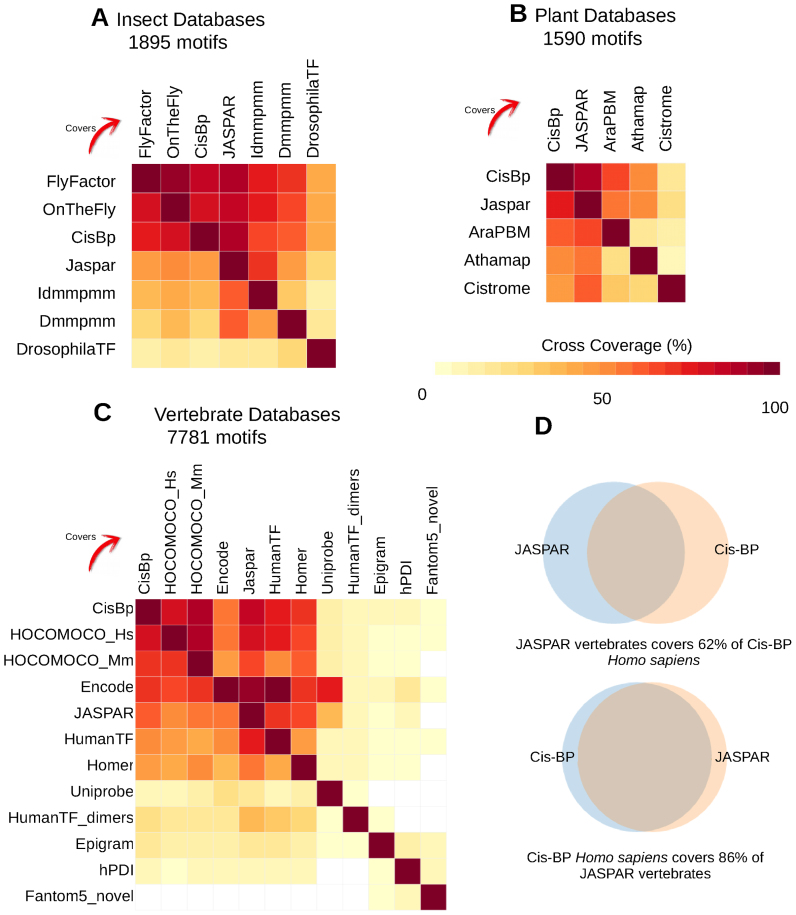
To evaluate inter-database redundancy and to automatically produce a non-redundant motif set, we clustered 24 motif collections and measured their cross-coverage (see Supplementary Table S1 and Material and Methods for the complete list of collections).

We first merged these public databases to obtain three taxon-specific collections for insects (7 databases; 1895 PSSMs), plants (5 databases; 1590 PSSMs) and vertebrates (12 databases; 7781 PSSMs), respectively. We then applied matrix-clustering and obtained 354 clusters for insects (19% of the total merged PSSM collection), 306 for plants (19%) and 1757 for vertebrates (33%) (Supporting website). In order to obtain non-redundant motifs whilst preserving specificity, we used more stringent partitioning criteria than the default (cor ≥ 0.8 and Ncor ≥ 0.65): the threshold on correlation ensures that the clustered motifs are highly similar and the additional threshold on normalized correlation selects the alignments covering most of the motif lengths, in order to separate composite motifs (e.g., bound by a TF dimer) from their elementary components.

We then explored the mutual overlap between the original collections by computing the cross-coverage (Figure 5). For the insect databases, Cis-BP, OnTheFly, FlyFactorSurvey and JASPAR are the most similar to each other, while DrosophilaTF is drastically different from all of them (Figure 5A), likely because this collection was built by selecting motifs discovered exclusively on Drosophila promoters, and whose binding factors are unknown (53).

Figure 5.

Cross-coverage of public motif databases. Several full public collections were merged and clustered, separately by taxa. The heatmaps of the cross-coverage between each collection is plotted for (A) seven insect collections, (B) five plant databases and (C) twelve vertebrate databases. The heatmaps show the cross-coverages for each pair of databases. Note that the heatmaps are not symmetrical because the numbers of motifs in the different databases differ. (D) Venn diagrams showing the asymmetry of cross-coverage between two databases with different sizes.

For the plant databases, JASPAR and Cis-BP are most similar to each other (Figure 5B), which is coherent with Cis-BP being an integrative motif collection encompassing other public collections (including JASPAR). The three other databases focus on sets of motifs characterized by specific experimental methods (PBM for ArabidopsisPBM, binding sites curated from literature for Athamap, DAP-seq for CisTrome).

Regarding vertebrates, five databases have a similar content (HOCOMOCO human and mouse, JASPAR, cis-BP, Jolma 2013 ‘HumanTF’), which is explained by the integration of HOCOMOCO and JASPAR in Cis-BP, as well as by the similarity of the original datasets used to build the TFBMs (mostly public ChIP-seq, Selex-seq and PBM), yet with different algorithms (Figure 5C). Note that the cross-coverage is not reciprocal since the number of motifs and the motif diversity differ among these databases. For example, JASPAR includes 62% of the content of Cis-BP, whereas the latter encompasses 86% of JASPAR motifs (Figure 5D). We observed that the motif diversity is not proportional to the database size (e.g. the 641 JASPAR vertebrate PSSMs cover 82% of the 1800 Cis-BP Human PSSMs). In contrast, the contents of the remaining databases differ considerably according to the different methods and data used to build the motifs: a single type of data (Uniprobe, derived from PBMs only), restricted numbers of sites (hPDI, 17 sequences per motif on average), data from ChIP-seq experiments targeting histone marks in different cell types (epigram), or motifs modelling TF dimers (Jolma 2015 ‘HumanTF_dimers’). The low cross-coverage of Fantom5 collection of ‘novel’ motifs is consistent with the definition if this database, which is restricted to motifs without any match in reference databases (44).

In summary, this case study highlights how matrix-clustering can be used to automatically reduce motif redundancy across multiple databases into non-redundant taxon-wise motif collections (available as Supporting files 1–3 and on the Supporting website) encompassing several thousands of PSSMs. The concise representation provided by the cross-coverage heatmap enables to intuitively grasp the overlap between each pair of individual collections.

Comparison with alternative motif clustering tools

RSAT matrix-clustering is the only tool supporting dynamic browsing of motif trees with custom collapse/expansion of branches, and providing multiple ways to inspect the results: motif forest with branch motifs at each level of each tree, similarity heatmap, searchable table of motifs and clusters, comparison between multiple collections with contingency tables summarizing relationships between clusters and collections, as well as cross-coverage between collections. See Table 1 for a list of features supported by existing motif clustering tools. This flexibility has a cost in computing time (see Supplementary notes for a comparison of time efficiency between STAMP and matrix-clustering).

Figure 4F shows a comparison between the performances of matrix-clustering and STAMP, based on three evaluation criteria: the abscissa indicates the positive predictive value (PPV), i.e., the proportion of a motif cluster that belongs to the same TF family, whereas the ordinate indicates the sensitivity (Sn), i.e., the proportion of a motif family found grouped in the same cluster. The size of the symbol is proportional to the Adjusted Rand Index (ARI), a single-valued metric capturing the global correspondence between the clusters and the TF families (see Supplementary Notes for the detailed formulae). A perfect correspondence would reach the top-right corner. The result closest to this ideal is achieved by matrix-clustering with the double threshold on Ncor and cor (orange empty diamonds), which supersedes the single-metric thresholds on Ncor (blue diamonds) or cor (red diamonds). STAMP results are represented by a single symbol (crossed diamond) per metric rather than a curve, since it partitions the tree based on an automatic, non-tunable criterion. The best result returned by STAMP is obtained with the average linkage on Pearson correlation coefficient (PCC). Interestingly, this result is inferior to matrix-clustering result with the same metric (cor) and linkage rule. All the other metrics supported by STAMP return poorer results. In particular, the Kullback–Leibler metric (KL) generates almost one cluster per motif, therefore reaching a trivial result with maximal PPV (each cluster matches a single TF family) but a very poor sensitivity (clusters only cover a tiny fraction of each family). The Sum of Square Distance (SSD) metrics has the opposite bias: it produces only two clusters, which results in a very high sensitivity (almost all the members of a given TF family are comprised in either of these clusters) but a weak PPV (since each cluster regroups many families, cluster membership is not informative).

We furthermore submitted our case studies 1 and 3 to several motif clustering tools (using default parameters): STAMP (22), m2match (25), Matlign (26) and Gmacs (28). This analysis was restricted to case studies 1 and 3, since no other tool currently supports the clustering of multiple collections. The results are detailed in the Supplementary Notes.

Performances of clustered and unclustered matrices to predict binding sites

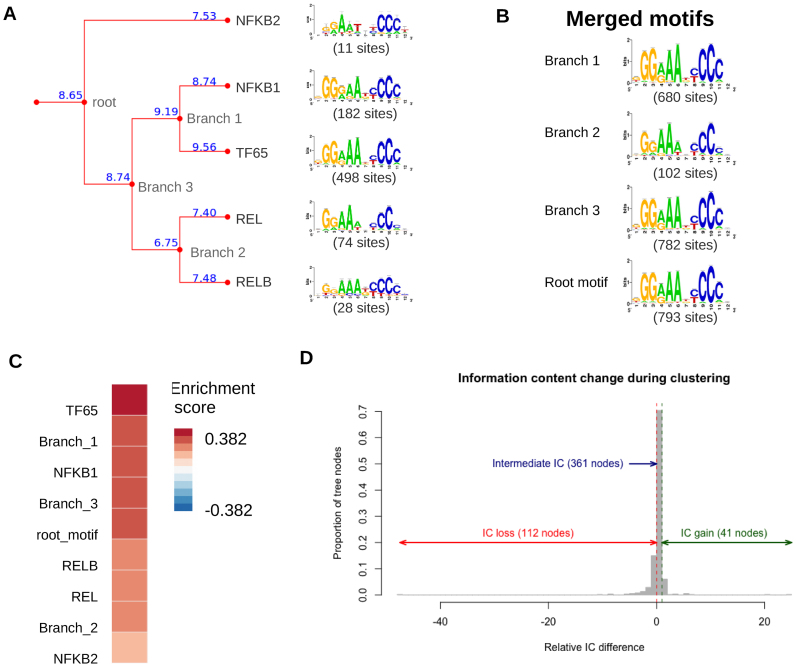
Motif clusters are built from motifs differing by their lengths, numbers of sites and information content (IC). By summing up the information from several matrices, clustered motifs are expected to gain sensitivity at the cost of specificity. We wondered whether merged motifs at each node of a tree would perform better or worse to predict TFBSs than the original motifs (the leaves). We focused on an illustrative cluster regrouping the five motifs of Human HOCOMOCO NF-kappaB-related factors (TFClass 6.1.1) and the merged motifs produced at each level of the tree (Figure 6A and B). The original matrices were built based on various kinds of experiments, with numbers of sites varying from 11 (NFKB1) to 498 (TF65). Figure 6A shows that for this cluster, the IC of the branch motifs takes an intermediate value between those of the two original motifs.

Figure 6.

Information content and predictive power of the unclustered and clustered motifs. (A) Clustering of five HOCOMOCO human motifs bound by NF-kappaB-related factors. The blue numbers at the tree branches indicate the information content of each PSSM. The number of sites used to build each matrix is indicated in parenthesis. (B) Logos of the merged motif at each level of the tree. (C) Enrichment of predicted NFKb binding sites for original and merged (branch + root) motifs in ChIP-seq peaks for RelA in Hodgkin Lymphoma Cell Line (GEO entry GSM1556331) (64). (D) Distribution of IC relative differences measured during the clustering of 519 human TFBMs from HOCOMOCO.

We measured the enrichment of predicted binding sites in ChIP-seq peaks for the RelA TF (GEO GSM1556331) (64) for the five original matrices and the merged motifs corresponding to each branch of the tree. The heatmap (Figure 6C) shows an enrichment score (NWD, defined in (65)) relative to random peaks of the same sizes. The motifs are sorted by decreasing enrichment. The motif with the highest enrichment is TF65, the original matrix encompassing the largest number of sites (498). The second-ranking matrix is the branch matrix that regroups TF65 and NFκB1, the two motifs with the largest number of sites. All the other motifs, built from 11, 28 and 74 sites respectively, show poorer performances than the branch and root motifs.

This example suggests that clustered motifs do not supersede the motifs from which they were merged, in particular when these motifs were built from hundreds of ChIP-seq peaks, such as TF65. However, a systematic analysis reveals that this observation admits exceptions. Indeed, we extended this analysis by comparing the IC of each merged motif with the two original motifs along the trees resulting from the clustering of all the Human TFBMs from the HOCOMOCO database. The distribution of relative IC differences (Figure 6D, see Supplementary Notes for the formulae) shows that in most cases (361/514) the IC of the merged motif has an intermediate value between the respective ICs of the two original motifs. However, we also observed 41 cases of IC gain and 112 cases of IC loss (i.e. the merged motif has respectively a higher or lower IC than either of its children). Two illustrative examples of IC gain and loss are shown in Supplementary Figure S4. In this example the IC gain comes from the merging between two motifs respectively built from 1230 and 27 sites. Although the second motif only contributes a tiny proportion of sites for the merged matrix, it increases the information content because it adds three columns at the motif end, resulting in additional IC computed from these only 27 sites (Supplementary Figure S4B green rectangle). We also observed IC gain when a short motif is merged with a larger one (e.g., alignment of a monomer with a dimer). By contrast the IC loss is mainly observed when two motifs are highly similar except for one or a few positions (Supplementary Figure S4C, red rectangle), where the fusion between two conserved positions (e.g., a C in one motif and a G in the second one) leads to a less informative column in the merged matrix (C or G).

DISCUSSION

With the advent of large-scale experimental approaches to uncover TF binding specificity such as ChIP-seq, Selex-seq and PBMs, the number of TFBMs has recently exploded, and motif redundancy is becoming a critical bottleneck for sequence analyses. Although many software tools are available to measure motif similarity, only a few tools are truly specialized in motif clustering. A basic survey of motif clustering tools and their functionalities (Table 1) revealed many limitations that prompted us to develop matrix-clustering.

A key feature that distinguishes matrix-clustering from the other tools is its dynamic interface to browse clustered PSSMs. This feature substantially facilitates the manual control of cluster visualization and reduces the time for human analysis of motif sets. Notably, this visualization has enabled us to identify the Ocr motif in the Oct4 ChIP-seq peaks (Figure 2). This motif was already present in our previous analysis of the same dataset (15), but we had not been able to detect this subtle variation among all other unclustered motifs. We thus expect that this dynamic visualisation of motif clusters will be beneficial to both experts and non-experts users. Furthermore, matrix-clustering dynamic interface can be used and integrated in the website of motif databases.

Our method relies on hierarchical clustering with a bottom-up partitioning. The tree is thus segmented based on the similarity between all the descendant PSSMs of each branch, which strongly differs from the usual cut-off at an arbitrary height of the tree. We evaluated an alternative segmentation method called dynamic tree cut, which relies on tree topology to produce balanced clusters (66), but we kept our approach because it allows to cut the tree based on motif similarity rather than on the sole tree topology. One caveat of hierarchical clustering is to produce ‘frozen’ clusters, when nodes regrouped early in the tree cannot be relocated in later steps (28). Note that some motif clustering tools avoid this problem by using iterative assignment algorithms, such as k-medoids (28), and that STAMP circumvents it by refining the tree a posteriori (22). Our quantitative evaluation based on HOCOMOCO TF families however shows that appropriately chosen thresholds on multiple metrics achieve better results than such methods. Partitioning thresholds can further be tuned to reach the desired granularity of clusters. Based on the systematic evaluation of HOCOMOCO motifs, we used default thresholds (Ncor > = 0.4 and cor > = 0.6) to group the TF binding variants and motifs from the same TF family within the same cluster. However, in order to favor specificity and obtain non-redundant collection of motifs (case study 4), stringent thresholds can be used (Ncor > = 0.65 and cor > = 0.80).

Several databases like JASPAR and HOCOMOCO already provide non-redundant collections, obtained by a time-consuming manual curation, which will become complicated to maintain with the increasing number of motifs. Of note, in motif databases, the term non-redundant denotes the restriction to one PSSM per TF (7). However, distinct TFs may also bind very similar motifs (e.g. Oct4, Oct9 and Oct11), and in some cases a same TF might bind to alternative motifs (e.g., TF complexes, or multi-domain TFs). In this study, the term non-redundant refers to a single PSSM summarizing a set of highly similar motifs, independently of the binding TF.

Reducing the size of motif collections is becoming crucial to limit the processing time of tools relying on full motif databases (e.g., motif enrichment, motif comparisons, identification of regulatory variants). As a proof-of-concept, we have shown that matrix-clustering can be used to compare full collections, but also to drastically reduce inter-database redundancy: in case study 4 we produced non-redundant motifs collections that reduced the insect, plant and vertebrate collections to 19%, 19% and 32% of their original sizes, respectively. We thus expect that meta-databases, such as footprintDB (10) or Cis-BP (9) could benefit from matrix-clustering to offer non-redundant motif collections.

Non-redundant motif collections would reduce computing time when scanning large sequence sets with large collections of PSSMs. However, it should be noted that merged motifs resulting from clustering are by definition less specific than the original motifs, more so if they have a poor quality. Still, for motifs built from a few binding sites, a merged motif could be more specific (Figure 6 and Supplementary Notes). We suggest that merged PSSMs could be used to represent a group of similar motifs to reduce computing time for tasks affected by motif redundancy (e.g. comparison of discovered motifs with reference databases). For more precise tasks, such as TFBS prediction, they can be suboptimal.

The possibility to cluster several collections simultaneously makes matrix-clustering a versatile tool, as demonstrated by the four case studies considered (identification of motif variants, integration of motifs found by multiple motif discovery tools, comparison of motifs obtained from many collections). The same tool could be used to compare motifs obtained for different experimental conditions. Given the compatibility with many PSSMs formats (TRANSFAC, MEME, HOMER) and its Web access, matrix-clustering will be of interest to the broad community of biologists and bioinformaticians involved in the analysis of regulatory sequences.

AVAILABILITY

The tool matrix-clustering is freely available on the RSAT Web servers (http://www.rsat.eu/) (39). It can also be downloaded with the stand-alone RSAT distribution to be used on the Unix shell, allowing its inclusion in automated pipelines. The complete results of the case studies are available on the supporting website: http://teaching.rsat.eu/data/published_data/Castro_2016_matrix-clustering/.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

French Agence Nationale pour la Recherche iBone [ANR-13-EPIG-0001-04]; EchiNodal [ANR-14-CE11-0006-02]; CONACyT-Mexico grant [Fellowship 391575 to J.A.C.M.]; PhD grant of J.A.C.M. from the Ecole Doctorale des Sciences de la Vie et de la Santé, Aix-Marseille Université. Funding for open access charge: French Agence Nationale pour la Recherche ORICHOICE [ANR-14-CE10-0019-03].

Conflict of interest statement. None declared.