Quaternary interactions and supercoiling modulate the cooperative DNA binding of AGT

Abstract

Human O⁶-alkylguanine-DNA alkyltransferase (AGT) repairs mutagenic O⁶-alkylguanine and O⁴-alkylthymine adducts in single-stranded and duplex DNAs. The search for these lesions, through a vast excess of competing, unmodified genomic DNA, is a mechanistic challenge that may limit the repair rate in vivo. Here, we examine influences of DNA secondary structure and twist on protein–protein interactions in cooperative AGT complexes formed on lesion-free DNAs that model the unmodified parts of the genome. We used a new approach to resolve nearest neighbor (nn) and long-range (lr) components from the ensemble-average cooperativity, ω_ave. We found that while nearest-neighbor contacts were significant, long-range interactions dominated cooperativity and this pattern held true whether the DNA was single-stranded or duplex. Experiments with single plasmid topoisomers showed that the average cooperativity was sensitive to DNA twist, and was strongest when the DNA was slightly underwound. This suggests that AGT proteins are optimally juxtaposed when the DNA is near its torsionally-relaxed state. Most striking was the decline of binding stoichiometry with linking number. As stoichiometry and affinity differences were not correlated, we interpret this as evidence that supercoiling occludes AGT binding sites. These features suggest that AGT's lesion-search distributes preferentially to sites containing torsionally-relaxed DNA, in vivo.

INTRODUCTION

O⁶-alkylguanines and O⁴-alkylthymines form in DNA exposed to alkylating agents. Both adduct types are mutagenic and carcinogenic, while O⁶-alkylguanine residues are cytotoxic as well (1,2). In human cells, O⁶-alkylguanine residues are repaired by the O⁶-alkylguanine DNA alkyltransferase (AGT, also known as methylguanine methyltransferase, MGMT; EC 2.1.1.63) (2,3). This enzyme has received much attention because, in addition to its normal roles, it also protects tumor cells against DNA-alkylating drugs (2,4–6). Trials with AGT-inhibitors are underway, with the aim of improving the clinical efficacy of chemotherapeutic alkylating agents (7–9).

Human AGT is a small protein (Mr = 21 519), expressed constitutively in normal cells and over-expressed in some tumors (2,5). It is a monomer in vitro, and it binds DNA with modest affinity, moderate cooperativity, high protein density (1 protein/4 bp) and very little DNA sequence- or O⁶-alkylguanine specificity (2,10–12). This lack of specificity raises an important question: how does AGT carry out its search for DNA lesions? AGT is active in repair of a wide range of O⁶-alkylguanines (2,13), and models based on crystal structures show that O⁶-benzylguanine can be contained completely within the active site (14,15). These results support the idea that only one protein molecule is required for the alkyltransfer step of the reaction. On the other hand, repair of free alkylguanine bases is dramatically slower than that of alkylguanines in polymeric DNA (16), and cooperativity appears to be important for equilibrium binding to lesion-containing and lesion-free DNAs (12,17). Cooperativity also appears to be important for the kinetics of lesion search and repair on polymeric DNA in vitro (12,17). The relevance of cooperative binding to in vivo functions of AGT is strongly suggested by the finding that protein mutations that disrupt cooperativity in vitro also make living cells sensitive to the alkylating agent MNNG (18). In addition, as previously described (19,20) and briefly discussed below, cooperative binding has the potential to provide a lesion-search mechanism that does not require high sequence- or O⁶-alkylguanine-specificity. These features justify work leading to a better understanding of the cooperative DNA binding mechanisms of AGT.

Crystal structures of AGT and AGT–DNA complexes are available (3,14,21,22) and they provide insight into the interactions and functions of AGT. Important results include the finding that the protein occupies a DNA contour spanning ∼8 bp, roughly twice the site-size that one monomer occupies to the exclusion of others (17); that the base under surveillance is flipped out of the duplex stack into the active site pocket (21,22); and that in spite of this DNA-allosterism, the protein conformation is little-changed (3,21). The available AGT–DNA structures contain either single AGT molecules or AGT molecules bound to well-separated DNA sites on double-stranded (ds) DNA (3,21,22) and thus do not replicate features of cooperative AGT assemblies, or complexes formed with single-stranded (ss) DNA.

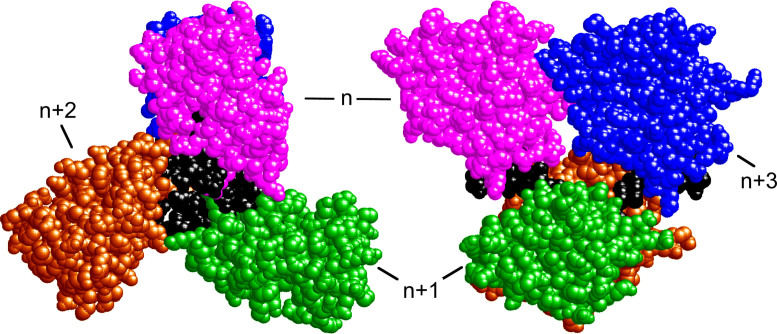
To aid thinking about the DNA-interactions of AGT, we built models that use the structure of a 1:1 AGT–dsDNA complex as the repeating motif and that replicate the 1 protein/4bp (and 1 protein/4 nt) binding densities found experimentally (23). A representative model structure, containing four AGT molecules bound to single-stranded DNA, is shown in Figure 1. Such models account for protein crosslinking and mutagenesis data (18,24), the DNA-length dependencies of binding cooperativity values (17,23) and the distributions of cooperative cluster sizes observed on relaxed dsDNAs (20). Recently the structure of a DNA-complex containing Mycobacterium tuberculosis OGT protein was reported (19). This enzyme has structural and sequence similarities to AGT (2), and its protein–DNA complex contains two OGT molecules in a nearest-neighbor arrangement similar to the one that we have proposed for AGT (20). It seems possible that some protein-interactions are conserved within the family of alkyltransferase-like proteins.

Figure 1.

Model of an AGT–DNA complex with single-stranded DNA. Left: end-view, oriented with protein N-termini toward the reader. Right: side-view with protein N-termini oriented toward the left. Subunits are numbered for reference. The repeating unit of this structure contains one molecule of AGT (colors) plus 4 nt of DNA (black). Coordinates were derived from the structure of Daniels et al. (21), as described by Adams et al. (24). This model features extensive contact between proteins n and n+3, but no direct contact between nearest neighbors.

Among the intriguing features of the models that we have proposed are the high protein-densities that can be attained and the extensive contacts between proteins at positions n and n+3 in the cooperative array (see Figure 1 for designations). These features allow us to make predictions about the mechanisms of cooperative binding that are relevant to lesion search. First, unobstructed DNA sites are needed for formation of cooperative assemblies, so DNA–DNA contacts that are present in supercoiled DNA will be found to inhibit binding. Second, both nearest-neighbor and long-range protein–protein contacts contribute to binding cooperativity, and both require precise juxtaposition of protein neighbors. Accordingly, binding cooperativity will depend strongly on the helical twist and the torsional flexibility of the AGT–DNA complex. Third, although there are three nearest neighbor contacts for each long-range n-to-n+3 contact in the cooperative unit, the larger n-to-n+3 interaction surface will make the dominant contribution to cooperative free energy. Tests of these predictions and their roles in AGT's lesion search are discussed below.

MATERIALS AND METHODS

Reagents

Agar, yeast extract and tryptone were obtained from Midwest Scientific. T4 polynucleotide kinase and Escherichia coli topoisomerase I were purchased from New England Biolabs. [γ-³²P]ATP was from ICN Radiochemicals. All other biochemicals were from Sigma.

Proteins

Human AGT, with wild-type sequence except for a C-terminal (His)₆–tag replacing residues 202–207, was encoded on plasmid pQE-hAGT, (21). The sequence was confirmed by sequencing plasmid DNA from candidate clones (performed by Seqwright DNA Technology Services). Proteins were expressed in XL1-blue E. coli (Stratagene) and purified by Talon^® chromatography as described (21). This protein has been shown to bind short single- and double stranded-DNAs with stoichiometries and affinities that are within error the same as that of wild-type AGT (11). Further, the residues identified as lying in the protein–protein interaction interface do not include the C-terminal (His)₆ tag (24). Minor contaminants were removed and proteins were transferred into storage buffer (20 mM Tris (pH 8.0 at 20°C), 250 mM NaCl, 1 mM DTT) by passage through Sephadex G-50. AGT solutions were stored frozen at −80°C until needed. AGT concentrations were measured spectrophotometrically using ε₂₈₀ = 3.93 × 10⁴ M⁻¹cm⁻¹ (11). The samples used here were >95% active in DNA binding (17) and in repair of short DNAs containing O⁶-methylguanine lesions (20).

Nucleic acids

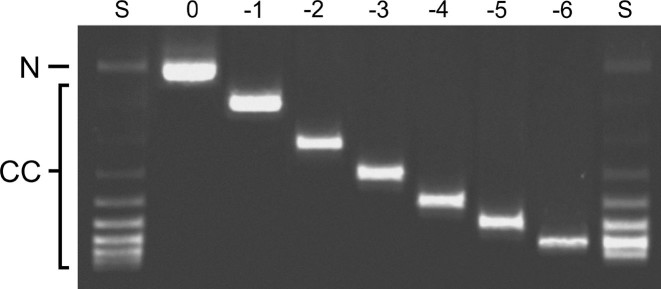
Oligonucleotides of 13 and 16 residues (sequences shown in Table 1) were purchased from The Midland Certified Reagent Company Inc. DNA samples for EMSA experiments were labeled at 5΄ termini with ³²P (25). Unincorporated [γ- ³²P]ATP was removed by buffer exchange using Sephadex spin columns equilibrated with 10 mM Tris (pH 8.0 at 21°C). DNA duplexes were prepared by annealing purified 5΄-labeled oligonucleotides with slight excess of the complementary unlabeled strands. Single-stranded DNA concentrations were measured spectrophotometrically using extinction coefficients provided by the manufacturer. Negatively-supercoiled pUC19 plasmid DNA, was obtained from New England Biolabs. This preparation was relaxed with E. coli topoisomerase I, and individual topoisomers were resolved by electrophoresis in 1.4% agarose gels (24). Linking difference values (ΔLk) were assigned by band counting (26), using the relaxed circular form as a reference with ΔLk = 0. Isolated topoisomer DNAs were purified using a polymerase chain reaction Clean-up kit from Qiagen, followed by dialysis against buffer containing 10 mM Tris (pH 8.0 at 20°C), 1 mM ethylenediaminetetraacetic acid. Plasmid DNA concentrations were measured spectrophotometrically, using ε₂₆₀ = 1.31 × 10⁴ M⁻¹cm⁻¹ (per base-pair).

Table 1. Macromolecules.

Identity	Sequence/Structure	MWa
AGT protein	monomer	21 519
Single-stranded 13-mer	5΄-GAC TGA CTG ACT G-3΄	3974
Double-stranded 13-mer	5΄-GAC TGA CTG ACT G-3΄	7909
	3΄-CTG ACT GAC TGA C-5΄
Single-stranded 16-mer	5΄-GAC TGA CTG ACT GAC T-3΄	4881
Double-stranded 16-mer	5΄-GAC TGA CTG ACT GAC T-3΄	9762
	3΄-CTG ACT GAC TGA CTG A-5΄
pUC19 plasmid	Duplex DNA	1 659 730

^aCalculated from sequence.

Electrophoretic mobility shift assays

Binding buffers contained 10 mM Tris (pH 7.6 at 20°C), 1 mM DTT, 100 mM KCl, 0.1 mg/ml BSA. Samples were equilibrated at 20 ± 1°C for 1 h. Duplicate samples tested with longer incubations gave indistinguishable results, indicating that equilibrium had been attained (not shown). Electrophoresis was carried out as described (17) using 15% polyacrylamide gels. Autoradiographic images were captured on storage phosphor screens (GE Healthcare), detected with a Typhoon phosphorimager and bands were quantified with Image-Quant software (GE Healthcare).

Sedimentation equilibrium analyses

AGT protein and DNAs were dialyzed against 10 mM Tris (pH 7.6 at 20°C), 1 mM DTT, 100 mM NaCl. Analytical ultracentrifugation was performed at 20°C in a Beckman XL-A centrifuge using an AN60Ti rotor, with scanning at 260 nm. Equilibration was considered complete when scans taken 6h apart were indistinguishable. For large (plasmid-size) DNAs, the concentration of protein-free DNA molecules became negligible well before all available protein binding sites were occupied. Over a wide range of [protein], such systems contain mixtures of free protein and protein–DNA complex, with the weight-average molecular weight of the complex increasing smoothly with [protein] until saturation was approached. These systems were analyzed with Equation (1).

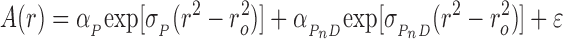(1)

For short DNAs with small numbers of protein-binding sites, cooperative binding was described by the simple mechanism nP + D ⇆ P_nD in which free protein (P) and DNA (D) are in equilibrium with saturated complex (P_nD) but intermediates with sub-saturating stoichiometries were not present at significant concentrations. The radial distribution of absorbance for this system at sedimentation equilibrium (SE) is given by Equation (2).

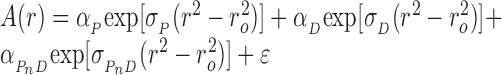(2)

In these equations, A(r) is the absorbance at radial position r and α_P, α_D and α_PnD are absorbances of protein, DNA and protein–DNA complex at the reference position, r_o and ε is a baseline offset that accounts for radial position-independent differences in the absorbances of different cell assemblies. The reduced molecular weights of AGT protein, DNA and protein–DNA complexes are given by σ_P = M_P(1 - 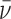_P ρ)ω²/(2RT), σ_D = M_D(1 - 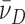ρ)ω²/(2RT) and 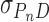= (nM_P + M_D)(1 - 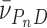ρ)ω²/(2RT). The molecular weights of protein and DNA are M_P and M_D respectively, n is the protein:DNA ratio of the complex; ρ is the solvent density, ω the rotor angular velocity and R is the gas constant and T the temperature (Kelvin). The partial specific volume of AGT and the density of sample buffer were calculated using the program SEDNTERP (27). The partial specific volumes of duplex and single stranded DNAs at 0.1M NaCl (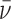_ds = 0.55 ml/g; 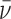_ss = 0.502 ml/g) were estimated by interpolation of the data of Cohen and Eisenberg (28). Partial specific volumes of protein–DNA complexes were calculated using Equation (3).

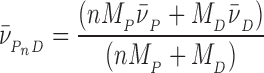(3)

SE data were interpreted using sequence molecular weights for AGT and DNAs given in Table 1.

Analysis of binding data

For binding plasmid DNAs, AGT-stoichiometries were inferred from observed weight-average molecular weights of complexes. The concentration of bound protein was determined from input DNA concentration as [P]_bound = n[P_nD] and free protein calculated from [P] = [P]_input – [P]_bound. The binding density ν = [bound AGT]/[lattice residue], where lattice residues nt or bp, as appropriate. The relationship of binding density (ν) to [P] was analyzed using the McGhee-von Hippel isotherm (29). Although the original version of this isotherm was given in the Scatchard form, relating ν/[P] to ν, the version that we have used (Equation 4) separates variables [P] and ν. This avoids problems associated with least-squares fitting to the Scatchard formulation (30).

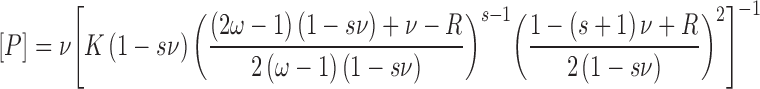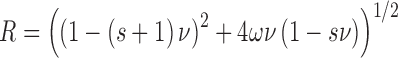(4)

Here K is the association equilibrium constant and ω the cooperativity parameter (the equilibrium constant for transfer of a protein molecule for an isolated binding site to one immediately adjacent to a bound protein, or from a singly-contiguous site to one that is doubly-contiguous (29)). The occluded site size (the size of the site, in base pairs or nucleotides, that one protein molecule occupies to the exclusion of others) is represented by s.

Binding to 13mer and 16mer duplexes was detected by EMSA, using ³²P-DNAs (typically ∼0.1 nM) (31,32). Cooperative binding resulted in apparently single-step saturation of DNA molecules (described below), allowing free protein concentration to be calculated using [P] = [P]_input – n[P_nD]. Here [P_nD] is the concentration of AGT–DNA complex and n is the stoichiometry, determined in separate experiments by SE analysis. The binding density ν = [bound AGT]/[lattice residue], where lattice residues are bases (in single stranded DNAs) or base-pairs (in duplex DNAs). The relationship of free protein concentration [P] to binding density (ν) was analyzed using the short-lattice form of the McGhee-von Hippel isotherm (29,33), here given in a form that separates terms in ν from [P] (Equation 5).

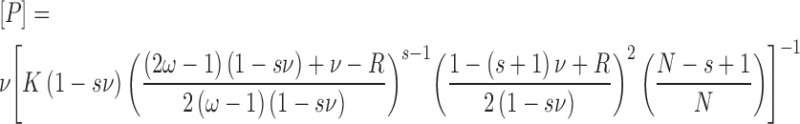(5)

Here terms are defined as in Equation (4), and the DNA length (nt or bp as appropriate) is represented by N. Binding parameters were determined by fitting these relationships to the data. These equations were originally cast in the Scatchard form (ν/[L] as a function of ν) (26,30). Traditional Scatchard plots of binding data are provided as Supplementary Data (Supplementary Figures S1 and 2). Error ranges cited are 95% confidence limits of the corresponding parameters.

RESULTS

A strategy for parsing the contributions of two cooperative mechanisms

Two distinct types of protein–protein interactions are present in AGT arrays like that shown in Figure 1. Those between nearest neighbors occlude little-to-no protein surface, while those between proteins in relative positions n and n+3 occlude ∼1100Ų (24). The contributions of these two different types of interactions to ensemble-average cooperativity values are poorly understood. Here we use a strategy based on differences in the length of DNA substrate needed to support each interaction mode, to resolve the cooperativity factors (34).

The McGhee-von Hippel theory was developed to analyze homogeneous protein–nucleic acid interactions (29,33). When binding is heterogeneous, Equation (5) returns ensemble-average values for K and ω. (Recall that K is the equilibrium association constant for protein–DNA interaction, and the cooperativity parameter, ω, is the equilibrium association constant for transfer of a protein molecule for an isolated binding site to one immediately adjacent to a bound protein, or from a singly-contiguous site to a doubly-contiguous one (29). Averaging complicates analysis when the goal is to characterize one interaction (or a subset of interactions) within a larger ensemble. This characteristic has been noted, and several investigators have developed expressions that account for more than one binding mode (33,35–37). The alternative approach that we take relies on the observation that AGT binds short DNAs with densities near 1 protein/4 bp (or 1 protein/4 nt on single stranded substrates) but has very low affinity for partial binding sites of 1–3 bp (nt) (17,23,38). Thus, a 13mer DNA should accommodate three closely-bound AGT molecules, with no room for a fourth (needed to make the n-to-n+3 contact), while 16mer DNAs accommodate four AGT molecules, and thus one n-to-n+3 contact (17,23). A comparison of binding cooperativities on these templates tests the idea that the interactions stabilizing the 4:1 complex (nearest neighbor and n-to-n+3 contacts) differ quantitatively from those stabilizing the 3:1 complex (nearest-neighbor contacts only). In addition, a comparison of cooperative interactions on single-stranded and duplex DNAs tests whether cooperative contacts are affected by those important differences in DNA secondary structure.

AGT binding stoichiometries with 13mer and 16mer DNAs

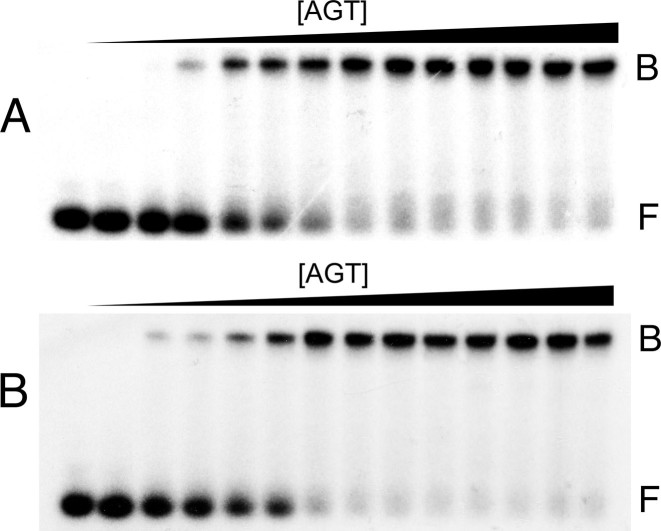
The DNA sequences used were repeats of the 5΄-GACT-3΄ sequence motif (and its complement for duplex DNAs; Table 1), designed to minimize differences in protein–DNA contacts in samples containing DNAs of different length. We previously found that AGT binds cooperatively to single-stranded and duplex 16mer DNAs, forming 4:1 complexes with both DNAs (17,23,24). Parallel experiments were carried out to establish the stoichiometries of complexes formed with single- and double-stranded 13mer DNAs. As shown in Figure 2, AGT formed well-resolved, stable, single complexes from free DNA without accumulation of other species that could be detected by EMSA using ³²P-labeled DNAs. These results justify use of SE analysis to determine stoichiometries. SE analyses (Figure 3) returned weight-average molecular weights of 67 386 ± 1869 for complexes formed with single-stranded DNA and 69 137 ± 1583 for those formed with duplex DNA. These values are consistent with stoichiometries of 2.96 ± 0.09 for single-stranded and 2.85 ± 0.07 for duplex 13-mer DNAs, respectively. The formation of these complexes from free DNA without significant accumulation of lower-stoichiometry species (c.f., Figure 2) indicates that these binding interactions are positively cooperative (11).

Figure 2.

Discrete complexes form when AGT binds single-stranded and duplex 13-mer DNAs. Electrophoretic mobility shift assays (EMSAs) were performed at 20 ± 1°C. Panel A: titration of single-stranded 13 nt DNA (2.1 nM) with AGT (ranging from 0 μM to 9.6 μM) to form the low-mobility cooperative complex. The equilibration buffer was 10 mM Tris (pH 7.6 at 20°C), 1 mM DTT, 100 mM KCl, 0.1 mg/ml BSA. Samples were resolved in a 15% native polyacrylamide gel cast and run as described. Band designations: F, free DNA; B, bound DNA. Panel B: Titration of unmodified double stranded 13 bp DNA (1.6 nM) with AGT (ranging from 0 μM to 9.5 μM). Reaction and electrophoresis conditions were as described for Panel A, above. Band designations: F, free DNA; B, bound DNA.

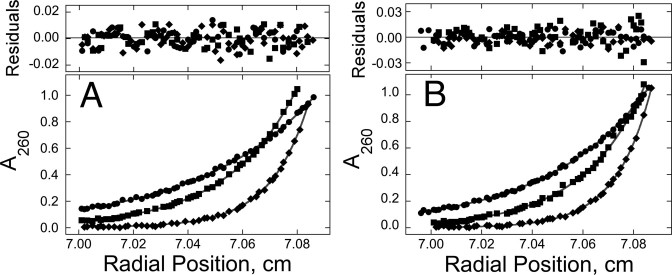
Figure 3.

Sedimentation equilibrium (SE) analyses of samples containing AGT and 13mer DNAs. Panel A: data for binding to single-stranded DNA. Samples contained 2.2 μM DNA and 12.1 μM AGT. Radial scans taken at 20 000 rpm (), 26 000 rpm (▪) and 35 000 rpm (♦) are shown with vertical offsets for clarity. The smooth curves correspond to a global fit of Equation (2) to a dataset including these scans and ones obtained at [AGT] = 18.2 μM. Panel B: data for binding to double-stranded DNA. Samples contained 2.0 μM DNA and 11.0 μM AGT. Radial scans taken at 20 000 rpm (), 26 000 rpm (▪) and 35 000 rpm (♦) are shown with vertical offsets for clarity. The smooth curves correspond to global fits of Equation (2) to a dataset that includes these scans and ones obtained at [AGT] = 16.5 μM. For both analyses the small residuals, symmetrically-distributed about zero (upper panels) indicate that the cooperative nP + D ⇆ PnD model is compatible with the mass distributions of DNA. These analyses returned n = 2.96 ± 0.09 for single-stranded and 2.85 ± 0.07 for duplex 13-mer DNAs, respectively.

Resolving the contributions of two cooperative mechanisms

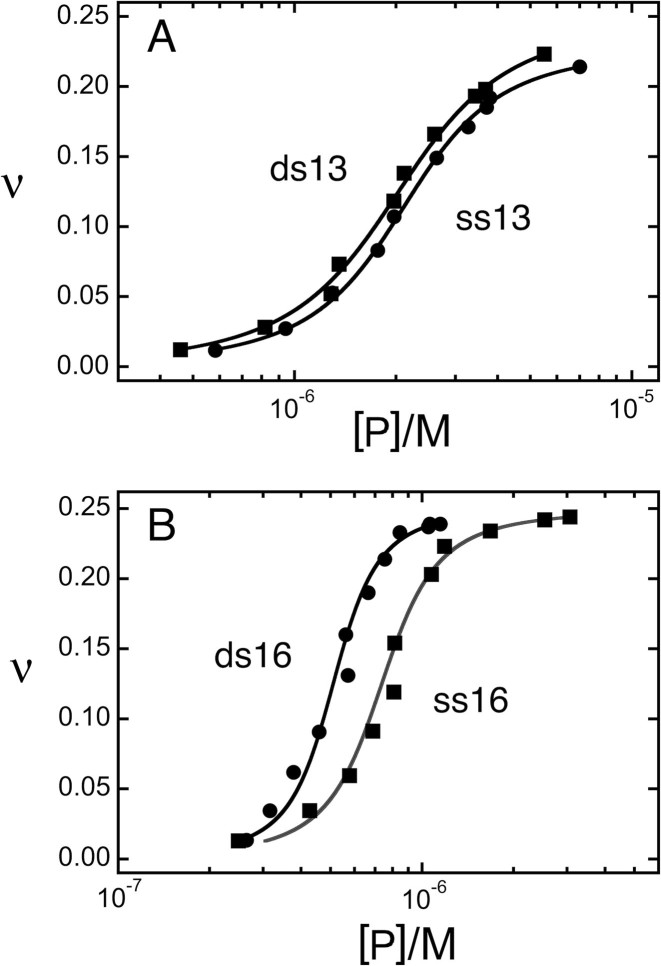
Thirteen-mer and 16mer DNAs were titrated with AGT and binding was detected by EMSA (examples shown in Figure 2). Figure 4 shows the relationship of free protein concentration [P] to binding density (ν) graphed and analyzed using Equation (5). Graphs of this data following the Scatchard convention are shown in Supplementary Figure S1. Parameters returned by these analyses are summarized in Table 2. They show that intrinsic affinities (K) for duplex DNAs were marginally greater than those for the corresponding single-stranded DNAs. Single-stranded 13mer and 16mer DNAs gave similar K-values (∼18 400 M⁻¹), as did duplex 13mer and 16mer DNAs (∼23 000 M⁻¹). These values are consistent with previous measurements made using different DNAs (11,17,23) and suggest that the number of monomers in the complex has little effect on association constant.

Figure 4.

Determination of ensemble average binding affinities for 13 nt, 13 bp, 16 nt and 16 bp DNAs. DNAs (∼3 × 10⁻⁹ M) were titrated with AGT protein (0 ≤ [AGT] ≤ 5.2 × 10⁻⁵M) in buffer consisting of 10 mM Tris (pH 7.6), 1 mM DTT, 1 mM EDTA, 100 mM NaCl. Free and bound DNA species were resolved by native electrophoresis (EMSA) as described for Figure 2. Each dataset is derived from two or more independent titrations. The smooth curves are fits of Equation (5) to the data.

Table 2. Binding parameters^a.

DNA	K ave (l/mol)	ωave	s (bp/AGT or nt/AGT)
Single-stranded 13-mer	18 000 ± 1200	33.9 ± 2.7	4.3 ± 0.04
Double-stranded 13-mer	22 900 ± 1800	27.1 ± 2.7	4.18 ± 0.06
Single-stranded 16-mer	18 800 ± 3300	91.0 ± 16.2	4.01 ± 0.02
Double-stranded 16-mer	23 700 ± 6200	102.6 ± 28.6	3.94 ± 0.06

^aSamples equilibrated at 20 ± 0.1°C in 10 mM Tris (pH 7.6), 1 mM DTT, 100 mM KCl, 5% glycerol.

A different pattern was found for the cooperativity parameter. There, single-stranded and duplex 13mers gave similar values (ω_ss,13 = 33.9 ± 2.7; ω_ds,13 = 27.1 ± 2.7) and single-stranded and duplex 16mers gave similar values (ω_ss,16 = 91.0 ± 16.2; ω_ds,16 = 102.6 ± 28.6). As described, these values are ensemble-averages. The structural model shown in Figure 1 predicts that three nearest neighbor (nn; n-to-n+1) interactions and one long-range (lr; n-to-n+3) interaction stabilize the 4:1 complex. The simplest way in which nearest neighbor and long-range interactions could contribute to overall cooperativity is if they were independent (i.e. their free energies were additive). On this basis, the average cooperative free energy for forming the 4:1 complex on 16mer DNAs is:

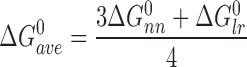(6)

and the long-range (n-to-n+3) component is given by:

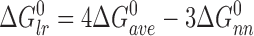(7)

Here, 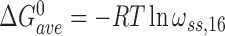and 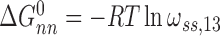for single-stranded substrates while 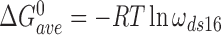and 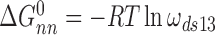for duplex substrates. Interaction-specific values for ω and free energies resolved using Equation (6) are shown in Table 3. Nearest neighbor cooperative interactions, while weak, are not negligible, while long range (n-to-n+3) interactions are considerably stronger than might be expected from a simple inspection of ensemble average cooperativity values. Possible roles of these interactions in stabilizing AGT cooperative complexes, and implications for its lesion search are discussed below.

Table 3. Resolved cooperativity and free energy values.

DNA	ω16	ω13	ΔG°ave (cal/mol-deg)	ΔG°nn (cal/mol-deg)	ΔG°lr (cal/mol-deg)	ωlr
Single-stranded	91.0 ± 16.2	33.9 ± 2.7	−2627 ± 104	−2052 ± 51	−4353 ± 574	1760 ± 232
Double-stranded	102.6 ± 28.6	27.1 ± 2.7	−2697± 152	−1921 ± 62	−5023 ± 797	5567 ± 884

Supercoiling modulates AGT stoichiometry

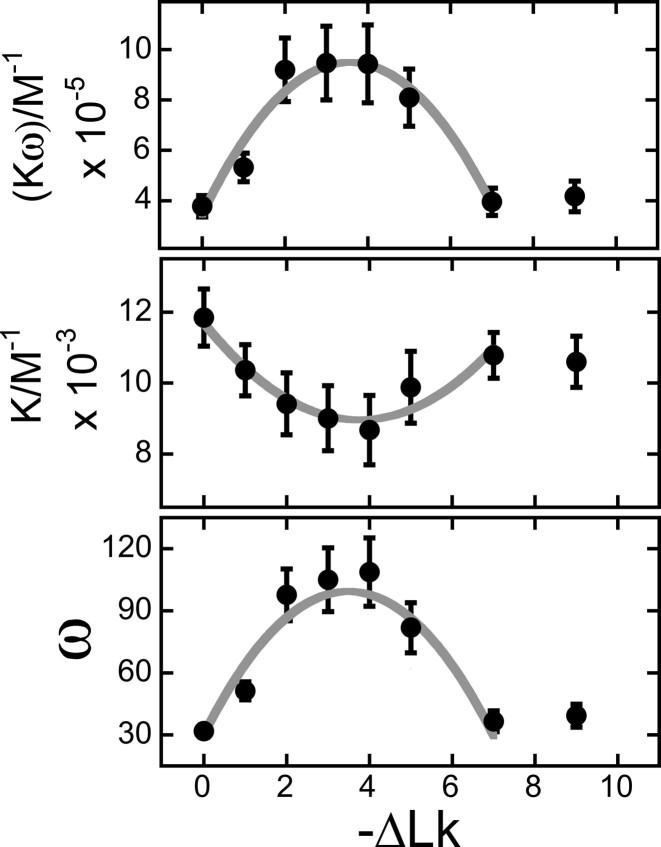
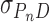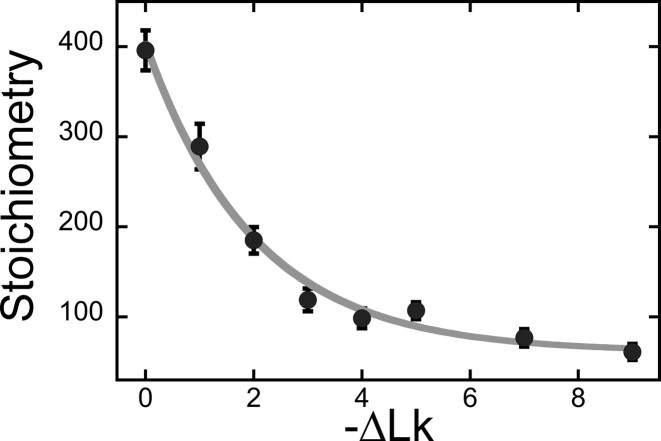
To test the possibility that DNA supercoiling might influence the binding stoichiometry of AGT, individual topoisomers of plasmid pUC19 were obtained by preparative electrophoresis (Figure 5) and incubated with AGT as described. Samples were analyzed at SE (Figure 6) using Equation (1) and binding stoichiometries were inferred from using the monomer molecular weights of AGT and DNA. A wide range of AGT concentration was tested (see below). Constant values of 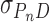with increasing [AGT] indicated the attainment of binding saturation. Shown in Figure 7 are upper-limit AGT stoichiometries for topoisomers (0 ≥ ΔLk ≥ −9), obtained at binding saturation. The limiting stoichiometry obtained for ΔLk = 0 (395 ± 22 AGT/DNA) corresponds well with one previously found for binding to linearized pUC19 DNA (402 ± 15 AGT/DNA; (24)). The striking decrease in limiting stoichiometry with linking number indicates that either the product (K•ω) or the number of accessible binding sites per DNA molecule, or both, are reduced as DNA becomes underwound. Based on the modest effects of ΔLk on K•ω (shown below), we propose that stoichiometry is limited by a reduction in the number of available binding sites. One possible mechanism for this effect is that interwinding makes DNA segments unavailable for AGT binding. This feature, and its relevance to lesion search, are discussed further, below.

Figure 5.

Electrophoretic resolution of purified topoisomers. Closed circular pUC19 DNA was relaxed with Escherichia coli topoisomerase I and resolved into constituent toposiomers by preparative electrophoresis, as described in ‘Materials and Methods’ section. Here individual topoisomers are shown resolved on a 1.4% agarose gel, stained with ethidium bromide and photographed with UV transillumination. The gel lanes are labeled S (source DNA prior to purification), and with linkage differences with respect to relaxed DNA (0 to −6). The positions of bands containing relaxed circular DNA (N) and closed circular DNA (CC) are indicated in the left margin.

Figure 6.

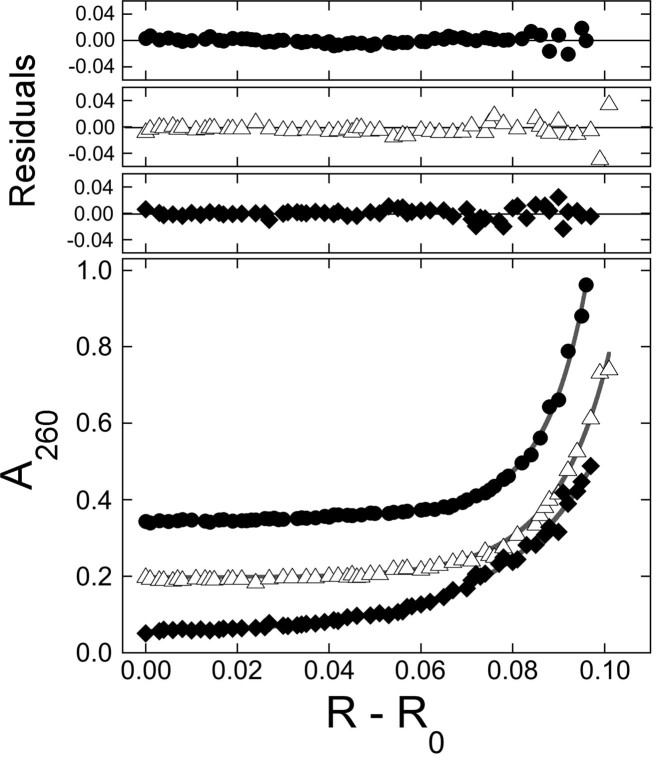
SE analyses of representative AGT-pUC19 DNA mixtures. Samples were centrifuged to equilibrium at 3000 rpm and 4°C, as described in ‘Materials and Methods’ section. Equation (1) was used to fit radial absorbance distributions for samples containing ∼11 nM DNA and ∼8.5 μM AGT. Samples contained DNAs of ΔLk = −1 (), of ΔLk = −2 (△) and ΔLk = −5 (♦). Absorbance values were offset vertically to improve visual clarity. The smooth curves correspond to fits of Equation (1) to these data. Small, symmetrically-distributed residuals (upper panels) indicate that the two-species model represented by Equation (1) was consistent with the mass distributions of DNA in these samples.

Figure 7.

Dependence of saturating stoichiometry on linking difference. Samples contained individually purified pUC19 topoisomers (8–12 nM) and 24 μM AGT in buffer containing 10 mM Tris (pH 7.6), 1 mM DTT, 1 mM EDTA, 100 mM NaCl. Stoichiometries were inferred from the weight-average reduced molecular weights of AGT–DNA complexes, measured at SE, as described in the ‘Materials and Methods’ section.

Supercoiling modulates both the association constant and cooperativity

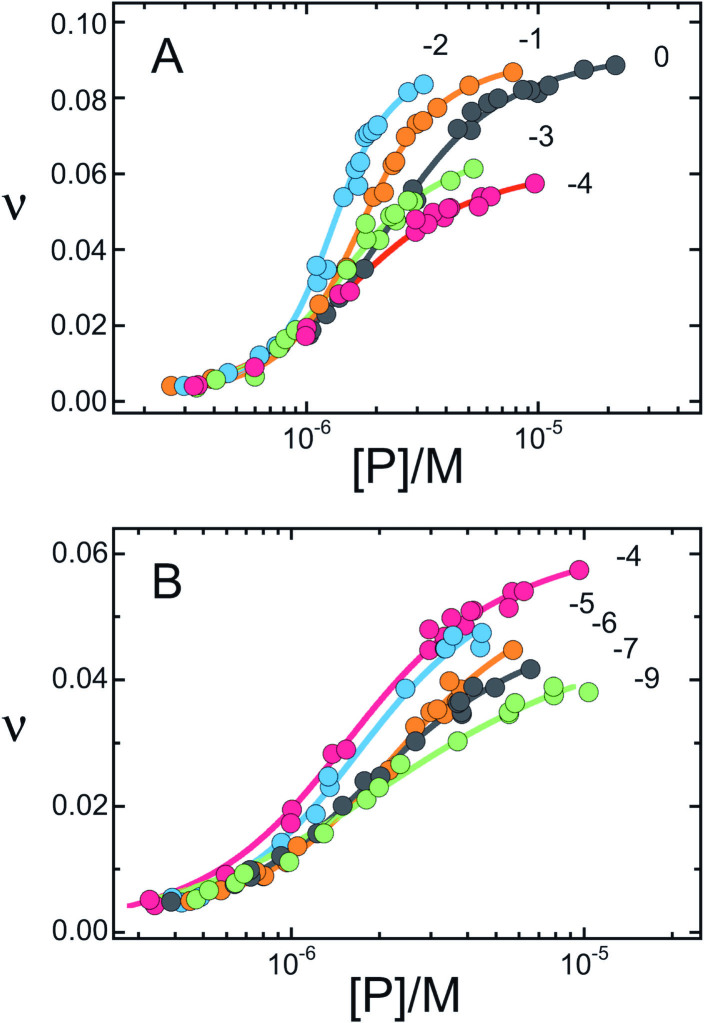
The dependence of limiting stoichiometry on linking number might be a consequence of changes in binding affinity. To test this notion we used the infinite lattice form of the McGhee-von Hippel equation (Equation 4) to estimate association constants and cooperativity parameters for AGT binding to individual topoisomers of plasmid pUC19. Graphs of this function are shown in Figure 8A and B. The clustering of values near the ordinate suggests that association constants for all topoisomers were similar at low binding densities. The decrease in the range of binding density values (ν) with decreasing ΔLk is consistent with the decrease in saturating stoichiometry with ΔLk shown in Figure 6 (this is easily seen when data are graphed according to the Scatchard convention as shown in Supplementary Figure S2). This feature supports the idea that DNA-interwinding reduces the number of available binding sites.

Figure 8.

AGT binding to isolated pUC19 DNA topoisomers. Binding densities (ν) were calculated from weight-average reduced molecular weights of AGT–DNA complexes, measured at SE, as described in ‘Materials and Methods’ section. Linking differences with respect to relaxed form DNA are indicated by the numbers near each curve. The smooth curves are fits of the long-chain version of the McGhee-von Hippel equation (Equation 4) to the data. Binding parameters (K, ω) returned by these analyses are given in Figure 9.

The relationships of K and ω values to ΔLk shown in Figure 9 were derived from fits of Equation (4) to the binding data shown in Figure 8. Values of ω go through a maximum and values of K go through a weak minimum near ΔLk = −3.5. Tests using fixed values of K or ω gave similar distributions for the remaining fitted variables with ΔLk (not shown); this argues that the relationship of K to ω is not evidence of underconstrained curve fitting (see (30) for a discussion of this problem). Thus, we interpret the effect on ω as evidence of a requirement for correct torsional juxtaposition of AGT monomers while that on K as evidence that torsional distortion of DNA influences AGT–DNA contacts. Values of the product K•ω go through a maximum near ΔLk = −3.5. This feature is noteworthy. Since greater stoichiometries were obtained with DNAs of 0 ≥ ΔLk ≥ −3, it indicates that the availability of binding sites (and not binding affinity) is the dominant factor in determining overall stoichiometry. In experiments shown here, DNA with the greatest affinity for AGT (ΔLk ∼−3.5), accommodates ∼125 AGT molecules (Figure 3), corresponding to a net unwinding of ∼−10 degrees/AGT with respect to relaxed DNA. This is slightly greater than values of −7.1 degrees ≥ twist ≥ −9 degrees found in topoisomerase assays and cluster-size analyses (20,24). However these assays are not completely equivalent. In topoisomerase and cluster-size assays, the DNA is relaxed at binding equilibrium. In the topoisomer-binding assays shown here, torsional stress is always present and may influence binding density.

Figure 9.

Dependence of K, ω and K•ω on linking difference, ΔLk. These parameters were obtained by fitting Equation (4) to the binding data shown in Figure 8. The error bars represent 95% confidence limits. The product K•ω is a measure of the ensemble-average affinity of an AGT monomer for its DNA substrate. The minimum of K for −5 < ΔLk < −3 indicates that protein–DNA contacts are marginally less stable on slightly-underwound DNA than they are on the relaxed form. The maximum of ω for −5 < ΔLk < −2 indicates that protein–protein contacts are most stable on slightly-underwound DNA.

DISCUSSION

Cooperative protein interactions play important roles in many cellular processes involving DNA. These include replication and repair (17,39,40), transcription (41,42) and packaging (43,44). An important subset of these interactions gives complexes containing just one kind of protein. Examples include complexes containing the E. coli CAP protein (45), human interferon-inducible protein IFI16 (46), single-strand binding proteins (47–49) and RecA protein (50). Several AGT- and alkyltransferase-like-proteins have also been found to belong to this class, including human and Saccharomyces cerevisiae AGTs ((17), M. G. Fried unpublished results), M. tuberculosis OGT (51) and Schizosaccharomyces pombe ATL (15). While this list is far from exhaustive, we suspect that cooperative binding may be a characteristic of AGT-family proteins.

Structure-specific interactions require accurate juxtaposition of molecular surfaces. With this in mind, we predicted that differences in torsional stiffness of single- and double-stranded substrates would produce differences in binding cooperativity within AGT assemblies. For small complexes on unconstrained DNAs, we envisioned three non-exclusive scenarios. (i) Torsional flexibility might facilitate protein–protein interaction, strengthening cooperativity on single-stranded substrates relative to those on duplex. (ii) Protein-binding might reduce the number of conformations available to single-stranded DNA to a greater degree than it does for duplex. A corresponding entropy difference would appear as reduced binding cooperativity on single-stranded substrates. (iii) Torsional flexing of DNA might cause transient misalignment of protein-protein interfaces, weakening cooperative interactions on single-strands in comparison with the torsionally-stiffer duplex. Resolved long-range and nearest neighbor cooperativities tested these possibilities.

Nearest-neighbor cooperativities for single- and double-stranded 13mers were not significantly different (Table 3), indicating that on the shortest length scale, differences in torsional stiffness between single- and double-stranded DNAs were not large enough to produce observable differences in cooperativity. In contrast, long-range (n-to-n+3) cooperativity values were significantly different, with ω_lr (double-stranded) ∼3-fold greater than ω_lr (single-stranded). This outcome rules out mechanism (i) and supports the idea that mechanisms like (ii) and (iii) reduce cooperativity values on single-stranded substrates in comparison to those seen with duplex.

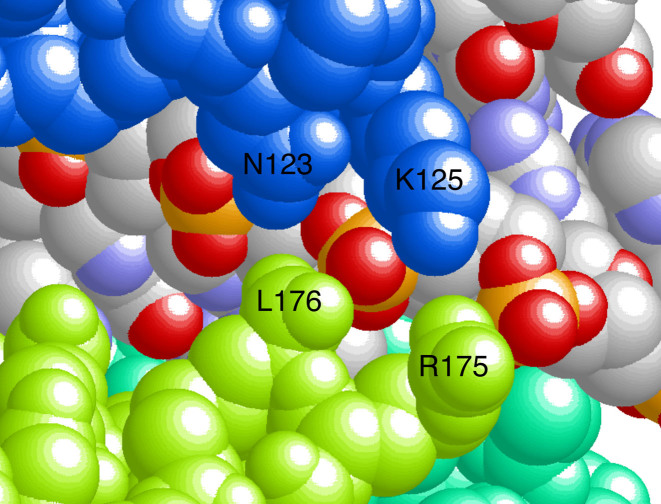
Parsing the ensemble-average cooperativity, ω_ave, into long-range and nearest-neighbor components revealed a significant contribution from nearest-neighbor interactions. This is important because nearest-neighbor contacts are numerically dominant in AGT clusters. In complexes with 2 or 3 proteins they are the only protein–protein interaction, and in larger complexes they are more frequent, by a factor of 3, than long range contacts. The physical basis for the short-range cooperativity is not currently known. Current models predict little-or-no direct nearest-neighbor contact (Figure 1), but overlap along the DNA contour allows neighboring proteins to ‘share’ contacts with the sugar-phosphate backbone (Figure 10). Shared backbone contacts have been seen in other protein–DNA complexes (c.f., (52)) and are likely to be a common feature when proteins bind with high density. Since AGT binding widens the minor groove by ∼3Å compared to undistorted B-DNA (3,21), the binding of one protein may position the DNA backbone for interaction with the neighboring protein. As nearest-neighbor cooperativity values are similar for single-stranded and duplex DNAs (Table 2), the sharing of DNA-backbone contacts may be a common feature of AGT complexes with both single-stranded and duplex DNAs.

Figure 10.

Do shared DNA-backbone contacts mediate cooperative interaction? This view of our current model of the cooperative assembly ((24); see also Figure 1) emphasizes a portion of the AGT–DNA interface. Two protein nearest-neighbors (colored blue and light green) and a segment of the shared DNA surface are shown, as well as a small segment of a third protomer (green). DNA atoms are colored according to the CPK convention (oxygen, red; phosphorus, orange-yellow; nitrogen, light blue; carbon, gray). The residue numbers of amino acid side chains that share DNA contacts are indicated.

The long-range interaction is more than twice as strong than a nearest-neighbor contact, consistent with the larger (∼1100 Ų) n-to-n+3 interface (compare ΔG°_lr and ΔG°_nn values in Table 3). Alanine-scanning across both sides of the n-to-n+3 interface gave mutant proteins with reduced binding cooperativities (18,53). These characteristics support models in which the long-range n-to-n+3 interaction is mediated by specific protein-contacts formed when AGT molecules bind DNA.

Changing the twist of a DNA substrate by altering its linking number (Figure 5) should change the torsional relationship of adjacent proteins and thus, the average cooperativity. We used a SE binding assay with purified single topoisomers to test this prediction. This is, to our knowledge, the first time this general approach has been used. We found that values of 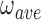were sensitive to DNA twist, going through a maximum at ΔLk ∼−3.5 and then decreasing; this maximum suggests that AGT proteins come into optimal alignment at this linking difference. The association constant (K) varied weakly in phase with cooperativity, but with opposite sign (Figure 9). While we do not know the origin of the dependence of K on ΔLk, its contribution to K•ω should weaken binding specificity for underwound DNA sites. The net result is a ∼2-fold preference for slightly-underwound DNA (σ ∼−0.013); this may make a modest contribution to AGT transfer into genomic regions containing relaxed or nearly relaxed DNA.

A more striking effect is the decrease in limiting stoichiometry with linking difference (Figure 7). As the change in limiting stoichiometry does not correlate with change in affinity (K•ω), it most likely reflects a change in the number of available binding sites. How might DNA-underwinding reduce this number? One possibility is that binding sites are occluded when supercoiling brings DNA segments together. In B-DNA, the minor groove binding sites of AGT should face the neighboring segment every 10.4–11 bp. This is less than the repeat length of the dominant n-to-n+3 AGT interaction (16 bp), and so this site-occlusion mechanism might be expected to destabilize cooperative complexes containing four or more proteins. If the resulting affinity for interwound regions is sufficiently low, it will be observed as a reduction in binding stoichiometry. Destabilization of complexes in interwound regions should direct protein redistribution to non-interwound segments, until those are filled. This is a prediction that can be tested with purified molecules, in vitro. This mechanism has the potential to contribute to AGT-translocation in vivo, and it has the potential to regulate the binding of other proteins that form cooperative complexes on DNA.

AGT binds DNA sites containing O⁶-alkylguanine with modest affinities and low specificities (e.g. short duplex DNAs with single O⁶mG residues gave K_6mG/K_unmodified ≤ 10, when compared with unmodified control DNA of the same sequence (11,12)). DNA repair by AGT is also insensitive to sequence context and, within broad limits, to the identity of the substrate O⁶-alkyl group (3,54,55). These results argue against lesion-search mechanisms that are driven by differences in equilibrium binding affinity. An alternative mechanism that we favor uses cooperative binding, chromatin remodeling and topoisomerase activity to drive AGT's lesion search (3,11). On relaxed DNA, cooperative AGT complexes attain high binding densities (∼1 protein/4 bp on short oligos (Table 2) and ∼1 protein/6.9 bp on relaxed pUC19 plasmid (Figure 3)). Thus, only modest protein displacement is needed for AGT molecules to test every base-pair within a cooperative complex. Kinetic analyses show rapid AGT movement along the DNA contour during repair reactions (12). In addition, a kinetic preference for repair near 5΄ DNA ends, in comparison to 3΄ ends, was found with single-stranded substrates, but not duplex DNAs (21). Together these results suggest that protein displacement along the DNA contour, and directional movement on single stranded DNAs, is part of the lesion-search mechanism.

The formation of cooperative clusters requires sections of unoccupied DNA. Under our standard in vitro conditions, ω-values like those described here result in cooperative clusters containing ∼7 AGT molecules that span ∼30 bp (20) These clusters would fit into the ‘spacer’ DNA between nucleosomes, or in open regions near DNA-replication or transcription complexes. On this basis we expect AGT to partition into DNA regions that have been made available by chromatin remodeling, and have been torsionally relaxed by topoisomerase action. These functions move with replication forks through the genome, so the coupling of AGT binding to DNA relaxation and/or chromatin remodeling could ensure that much of a cell's DNA complement could be examined by AGT during a single replication cycle, without requiring lesion-specific binding.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institute of General Medical Sciences [GM-070662 to M.G.F.]; Department of Molecular and Cellular Biochemistry, University of Kentucky. Funding for open access charge: Department of Molecular and Cellular Biochemistry, University of Kentucky.

Conflict of interest statement. None declared.