In Vivo Multiscale and Spatially-Dependent Biomechanics Reveals Differential Strain Transfer Hierarchy in Skeletal Muscle

Abstract

Biological tissues have a complex hierarchical architecture that spans organ to subcellular scales and comprises interconnected biophysical and biochemical machinery. Mechanotransduction, gene regulation, gene protection, and structure-function relationships in tissues depend on how force and strain are modulated from macro to micro scales, and vice versa. Traditionally, computational and experimental techniques have been used in common model systems (e.g., embryos) and simple strain measures were applied. But the hierarchical transfer of mechanical parameters like strain in mammalian systems is largely unexplored in vivo. Here, we experimentally probed complex strain transfer processes in mammalian skeletal muscle tissue over multiple biological scales using complementary in vivo ultrasound and optical imaging approaches. An iterative hyperelastic warping technique quantified the spatially-dependent strain distributions in tissue, matrix, and subcellular (nuclear) structures, and revealed a surprising increase in strain magnitude and heterogeneity in active muscle as the spatial scale also increased. The multiscale strain heterogeneity indicates tight regulation of mechanical signals to the nuclei of individual cells in active muscle, and an emergent behavior appearing at larger (e.g. tissue) scales characterized by dramatically increased strain complexity.

Graphical abstract

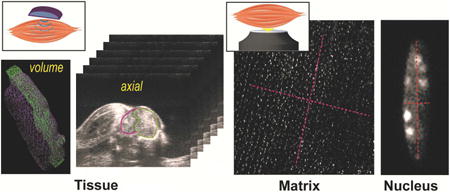
1. Introduction

Biological tissues have a complex hierarchical structure ranging from organ to subcellular (e.g., chromatin) spatial scales. The central organelle of gene expression, the nucleus, is physically linked to the cell exterior through several structural elements including nucleoskeletal, cytoskeletal, and plasma membrane proteins. Physical connections therefore enable direct mechanical regulation of the cell and nucleus from the local molecular structure of the extracellular matrix (ECM)¹. Also, the active components inside cell, e.g. actomyosin and microtubule machinery, are responsible for tight regulation of local subcellular functions important for cell contraction, division, reorganization and migration. The ECM, consisting of several macromolecules (e.g., collagens and proteoglycans), along with the embedded cells, form a complex architecture in which specific organ functions emerge. The spatial mechanical regulation at various hierarchical level can trigger the biochemical pathways, a process called mechanotransduction or mechanoregulation. Mechanotransduction at the cell-ECM interface and in the cytoskeletal structure has been investigated in the context of cancer cell metastasis, wound healing, development and stem cell differentiation². There is increasing evidence of nuclear mechanotransduction, as mechanical forces at the organ and tissue levels can be transferred to the nucleus via physical links from the macro- to micro-scale to orchestrate intranuclear strain dynamics and chromatin architecture reorganization³. Therefore, the tissue-level mechanical forces and strain can modulate the accessibility of specific genes to transcription proteins at a high spatial precision⁴.

An alternative hierarchical mechanoregulation mechanism can be viewed as the emergence of complexity from micro- to macro- scale, in contrast to the aforementioned macro- to micro-mechanoregulation. For example, mutations in a single gene can also alter the cellular, tissue, and organ scale structures and functions. Those mutations can disrupt the translation of several key proteins, thus compromising the function of healthy tissues. This paradigm of internal gene disruption altering organ scale structure indicates an existing micro- to macro-scale mechanoregulation. A classic example includes the mutation in lamin A/C gene, which is known to cause altered production of lamin proteins, thus perturbing the structural support of the nuclear membrane. Functionally, this mutation causes a plethora of diseases collectively known as laminopathies that lead to a weak musculoskeletal system and premature aging, characterized by a greatly decreased production of essential ECM proteins⁵.

In both mechanoregulation modalities, macro- to micro- or micro- to macro-, although several factors have been identified to be the key regulators at multiple scales of the, the detailed and comprehensive mechanism of this complex process remains elusive especially in vivo. Specifically, the influence of spatial deformation patterns on the activation of mechanoregulators and their respective mechanochemical pathways is not clearly understood. Computational and experimental approaches have been employed to many tissue types to investigate multiscale and spatial mechanoregulation mechanisms. Computational research has thoroughly investigated how continuum mechanics, molecular mechanics, or a combination of both can explain the multiscale force transfer and downstream chemical pathway activation in soft tissues (e.g. skeletal muscle^6–8, cardiovascular system^9,10 and articular cartilage^11,12). Experimental paradigms have used isolated single cell mechanics, tissue equivalents, or in situ studies to probe multiscale strain transfer and mechanotransduction mechanisms in the ECM, cell, and nucleus^13,14. To elucidate the mechanical information transfer at different hierarchical levels, the deformation is typically quantified as displacement or strain, allowing for the comparison of values at different scales to gain mechanistic insight at a controlled loading scenario^13,14. One primary limitation of those previous studies is that they quantify the ECM, cellular, or nuclear strain using rudimentary strain measurement approaches, i.e., quantification of bulk linear measurements, areas, or volumetric strains and aspect ratios. Therefore, the intra spatial details of the deformation are lost¹⁵. While a few in situ studies have tried to overcome this limitation by measuring spatial strain distributions in the chondrocyte nucleus¹⁵ and fibroblast cytoplasm¹⁶, they are limited to probing so only at a single scale. Therefore, quantification of multiscale spatial strain distribution at a high resolution in vivo is required to further our understanding of the inherent complexity of mechanotransduction.

The objective of this study is to quantify the spatial distribution of mechanical strain at different length scales to probe how mechanical information is connected between the tissue to the inner nuclei of embedded cells via the matrix. Specifically, we used murine skeletal muscle as an in vivo model for probing this relationship. Skeletal muscle was chosen because the biomechanics of the tissue are relatively well understood from previous studies¹⁷, and because the tissue deforms easily near the skin surface, facilitating in vivo investigation compared to other deep tissues such as the heart or cartilage. To apply a controlled mechanical loading, murine hind limb skeletal muscle was activated using a neuromuscular stimulation system integrated with multiple imaging modalities. In one set of experiments, the organ-scale deformation was imaged using ultrasound, and the spatial strain distribution was quantified. In a separate set of experiments, tissue and nuclear deformation were simultaneously imaged using optical microscopy, allowing us to quantify spatial strain distributions at smaller scales. The spatial strain was measured using an iterative hyperelastic warping technique based on the imaging data¹⁵. We validated this technique at all scales using known forward deformations. The spatial strain distributions were also compared with the limited capability of bulk strain measurements to gain novel insights into the heterogeneity of intra multiscale biomechanics ranging from centimeter to micron scales. The results are discussed from a multiscale mechanobiology perspective and have the potential to advance in vivo biomechanics research for a variety of biomedical applications.

2. Materials and Methods

2.1 Neuromuscular stimulation of mouse hind limb

All animal experiments were performed under Institutional Animal Care and Use Committee (IACUC) approved protocols. C57BL/6J male mice were purchased from Jackson Laboratories (n=5 for ultrasound experiments, n=5 for optical microscopy experiments, age=12 weeks). The anterior compartment of hind leg skeletal muscle was stimulated using a neuromuscular stimulation (NEMS) unit (300 PV Empi) with a modified technique described previously¹⁸. The bulk leg movement of the mouse was restricted using a custom-made fixture to simulate controlled loading (Figure 1A). Animals were anesthetized with 1-3% isoflurane (Kent Scientific, Torrington, CT) in 100% oxygen and remained unconscious during muscle stimulation. A small incision was made on the dorsal side of the hind leg and the skin was removed to expose the anterior compartment muscles. The thin fat layer covering the tibialis anterior muscle was also removed. Copper electrodes were placed directly over the deep fibular nerve, a distal branch of the common peroneal nerve that is located anterior to the fibular head. A milliampere range current stimulated the tibialis anterior and the extensor digitorum longus muscles. While the constraints prevented dorsiflexion of the ankle, full extension of digits confirmed the stimulation of both muscles. We acquired ultrasound and optical microscopy images using same biomechanical stimulation settings without stimulation (undeformed) and with stimulation (deformed). Animals were sacrificed post-experiment by anesthetic overdose and subsequent cervical dislocation.

Figure 1. Experimental setup for neuromuscular stimulation of tibialis anterior muscle with simultaneous imaging.

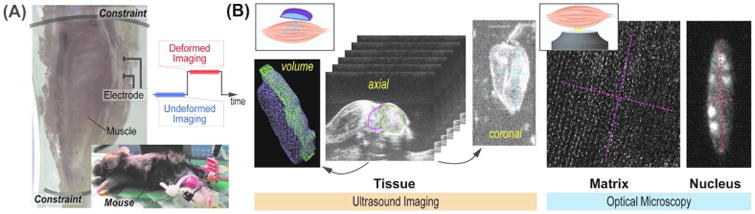
(A) Schematic of the experimental setup for active murine neuromuscular stimulation in vivo. Two plastic fixtures were applied on the hind limb, and the stimulation was applied at the deep fibular nerve. The tibialis anterior muscle deformed as a result of this stimulation and the deformation was maintained until the end of imaging. (B) Three-dimensional ultrasound image stacks were acquired in the axial plane of the limb. The image stacks were used to reconstruct coronal plane images. Volume renderings were used to volumetrically mask the tibialis anterior muscle, and were used to calculate the volumetric strain. Linear marker lines (light blue dotted lines in coronal image) were drawn across the muscle section to quantify linear bulk strains. Optical microcopy enabled visualization of tissue and nucleus images at two separate magnifications. Similar linear bulk strains were quantified from marker lines (pink and red dotted lines) for tissues and nuclei.

2.2 Ultrasound imaging of tissue deformation

For tissue scale imaging, a high frequency ultrasound (Vevo2100, FUJIFILM VisualSonics) was used to acquire sequential axial plane images, that were combined into 3D volumes of the hind limbs. After application of ultrasound gel and fixing the electrodes in place, a 50 MHz center frequency transducer (30 μm axial and 70 μm lateral resolution; VisualSonics microscan transducer MS700) scanned a 2.0 cm distance (154 μm step size) over the tibialis anterior muscle. The complete ultrasound scan deformed state takes around 10 seconds, a period during which the stimulation was applied. Images in the coronal plane were reconstructed using a custom MATLAB script (Figure 1B). The transverse and coronal undeformed and deformed images were then compared to quantify the organ scale strain.

2.3 Microscopy of matrix and nuclear deformation

For optical microscopy, the live nuclei were stained by dipping the muscle in 1× PBS mixed with NucBlue Live ReadyProbes Reagent (Thermo Fisher Scientific Inc.) for 35 minutes, followed by thorough washing. 3D imaging was performed using an inverted confocal microscope (Nikon Eclipse Ti A1R) at two different magnifications (10× and 40×) by maintaining the same field of view. These two magnifications were used to visualize the tissue and the detailed features of nuclei, respectively. After finding the appropriate field of view, we captured z-stack images in the unstimulated state at 40×, followed by 10× (Figure 1B). Stimulation was then started and z-stack images were captured intra-stimulation at 10×, followed by 40×. The complete microscopy scan in the deformed state takes around 90 seconds, during which the stimulation was applied. The undeformed and deformed images were then compared to quantify the tissue and nuclear strain as described in the following sections.

2.4 Quantification of bulk strain

To quantify the volumetric tissue strain, volumetric masking of the tibialis anterior muscle was performed (n=5) using VevoLAB software (FUJIFILM VisualSonics). The tibialis anterior was visually isolated in each acquired ultrasound volume and a perimuscular outline was manually segmented to render a volumetric region of interest. Volumetric strain was quantified as ε_vol = abs[(deformed volume-undeformed volume)/deformed volume], where ‘abs’ represents absolute value. To quantify linear strain at the tissue scale, the coronal plane corresponding to the wedge shaped anatomical feature observed in transverse planes (indicated by pink arrow in Figure 2) was used. Surface to surface strain (major axis and minor axis) was quantified using the maximum distances in the coronal plane (n=5). Linear strain was quantified as ε_lin,tissue = abs[(deformed length in tissue-undeformed length in tissue)/deformed length in tissue]. To quantify matrix scale strain, marker nuclei were chosen in the field of view. Linear distances were measured along the contraction axis, as well as its orthogonal axis (n=5). Linear strain was quantified as ε_lin,matrix = abs[(deformed length in matrix-undeformed length in matrix)/deformed length in matrix]. For nuclei, the surface-to-surface strain was quantified along major and minor axes using similar linear measurements. Same as before, linear strain was quantified, ε_lin,nucleus = abs[(deformed length on nucleus-undeformed length in nucleus)/deformed length in nucleus]. Total 12 nuclei from 5 different samples were analyzed.

Figure 2. Heterogeneous strain distribution across length scales revealed by iterative hyperelastic warping.

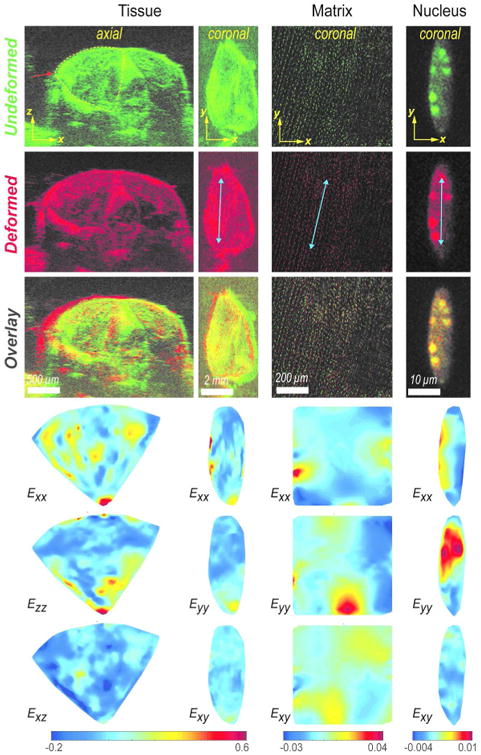
The undeformed (green) and deformed images (red) were used to quantify strain distributions. The overlay is shown to visually compare the undeformed and deformed images directly; the spatial offset indicates the deformed position. In tissue scale axial section, the xz plane is perpendicular to axis of contraction and x is the primary axis of extension. In tissue scale coronal plane, y is the primary direction of contraction (along the myofibers) and x is the primary direction of extension (across the myofibers). In matrix and nucleus scales, y is also the primary direction of contraction (along the myofibers) and x is the primary direction of extension (across the myofibers) in coronal plane. In coronal plane for all scales, the E_xx, E_yy, and E_xy strain components with respect to the xy coordinate system, and in axial plane only for tissue, the E_xx, E_zz, and E_xz strain components with respect to the xz coordinate system, represents the primary strain measure obtained from the iterative hyperelastic warping. These primary strain measures were further used to derive other strain measures. Blue arrows in deformed images show the primary direction of muscle contraction.

2.5 Quantification of spatial strain by iterative hyperplastic warping

The spatial strain distribution for all scales was obtained using an iterative hyperelastic warping technique developed previously¹⁵. The technique uses the local difference in image intensity to match a discretized template image with a target image, thereby obtaining the displacement map required for complete registration. During the image analysis process, spatial averaging in the form of Gaussian blurring is used to avoid local minima which would stop the global image registration prematurely. The displacement undergoes postprocessing to quantify spatial parameters, such as Green- Lagrangian strain (e.g. E_xx, E_yy, and E_xy). An effective two-dimensional hydrostatic strain related to volume change was computed as E_hyd=(E_xx+ E_yy)/2. The first deviatoric strain related to shape change was calculated as E_xx-E_hyd. The analysis was performed over multiple datasets (n=5 for tissue, n=5 for matrix, n=6 for nucleus).

2.6 Validation of iterative hyperelastic warping

To assess the validity of the iterative hyperelastic warping technique at all scales, we applied known forward displacement maps on respective images. The displacement maps quantified by iterative hyperelastic warping were compared to the known displacement map applied in the forward simulation.

2.7 Statistics

The strain in the tissue scale showed more variance than the matrix and nucleus scales (i.e. heteroscedasticity), and thus nonparametric statistical tests were applied. Kruskal-Wallis oneway analysis of variance (ANOVA) was to used test any statistically significant strain difference between the groups. Pairwise comparison between groups were performed using Wilcoxon-Mann-Whitney test. The difference was considered statistically significant for p < 0.01. The coefficient of determination (R²) was calculated using linear regression and paired t-test was applied for validation study data. Minitab 17 (Minitab Inc.) was used for all statistical tests.

3. Results

3.1 Spatial strain pattern across length scales

Strain maps at various length scales from organ to nucleus exhibited widely varying and spatially heterogeneous deformation (Figure 2). In order to align strain results with the predominantly y direction of active muscle contraction and for visualization comparable to physical contraction, strains are presented as E_xx, E_yy and E_zz. The deformation features observed from the undeformed and deformed images (Supplementary Video 1-4) were captured in the strain map. In tissue scale, in the coronal plane xy, mostly negative (contraction) E_yy can be observed in the primary direction of contraction y (along the myofibers) and mostly positive E_xx (extension) can be observed in the direction of extension x (across the myofibers). At the tissue scale, the transverse section showed that the superficial portion of the tibialis anterior was compressed up to 20% strain, while the deeper portion expanded up to 20% along z direction. In the direction of extension x, strains of 20% or even higher were observed. The shear strain caused by heterogeneous organ deformation at different regions, was also found to be significant. Those spatial strain maps showed that a complex deformation pattern existed even across one single muscle while it was stimulated, in contrast to a uniform shortening as we initially expected. Similar behavior can be visualized at the matrix scale, mostly contraction along primary direction of contraction y and extension along the orthogonal direction x was visualized. However local variations can be observed, thus elucidating spatially varying strain response. In nucleus scale, no obvious strain directionality was observed. Random localized regions of extension and contraction was visualized.

Deformation measure across the length scales showed significantly different magnitude of strain at various scales (Figure 3). Derived strain measures, i.e. hydrostatic, deviatoric, along with shear strain were computed to visualize overall volumetric change, shape change and induced shear in contrast to directional strains. The derived strain distribution along the coronal section shows the variability and magnitude of strain across scales. (Figure 3A). It is evident from these plots that though most of the tissue was compressed by 5% (with a peak of -0.05), a large distribution occurred towards both positive and negative values, further illustrating the spread in the spatial nature of the strain. The deviatoric and shear strains were mostly centered around zero, though a distribution of strain was still visible.

Figure 3. Strain magnitudes and heterogeneity decrease with spatial scale.

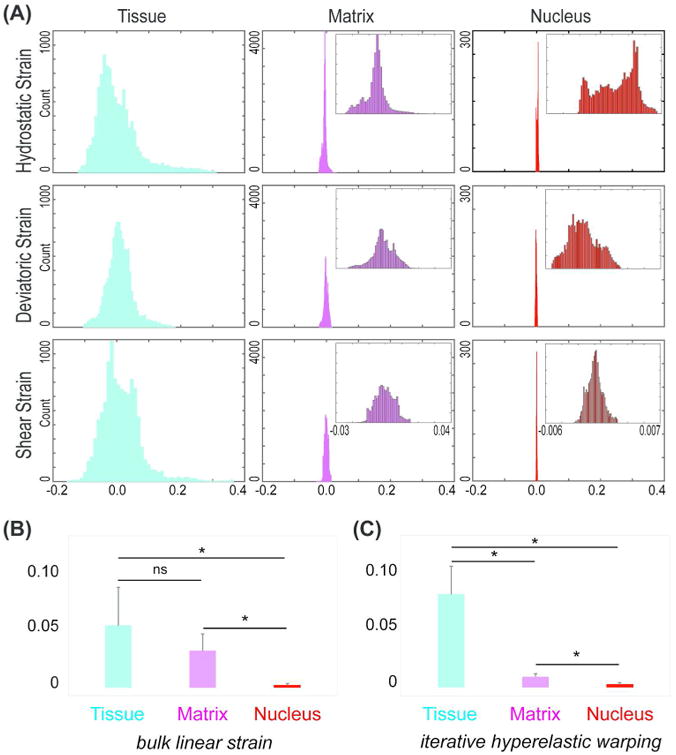
(A) At tissue, matrix, and nuclear scales, decreased distributions were observed for hydrostatic, deviatoric, and shear strains. (B) Bulk linear measurement based strain over all scales. Absolute strain measures were averaged over multiple samples. Data represents mean with standard deviation as error bar. Statistically significant differences were observed between tissue-nucleus and matrix-nucleus scales (*p < 0.01) but not between tissue-matrix scales. (C) Iterative hyperelastic warping based hydrostatic strain over multiple scales. For each sample, the mean of absolute values over all elements was computed. Multiple sample means were averaged to generate the data shown as mean with standard deviation as error bar. Statistically significant differences were observed between tissue-nucleus, matrix-nucleus and tissue-matrix scales (*p < 0.01).

The strain values decreased by one order of magnitude at the matrix scale compared to tissue scale. The undeformed and deformed images (Supplementary videos 1-4) revealed that at the matrix scale there were also localized regions of tensile and compressive strains. Though the shear strain was still centered near zero, the hydrostatic and deviatoric strains were significant (peak at -0.01). This suggests that in addition to the volumetric changes incurred at the organ scale, there was a significant shape change occurring at the tissue scale. In the nuclei, this effect was even more prominent. Although the strain values dropped by one more order of magnitude in nuclei, the hydrostatic and deviatoric strain values were both significant. This further suggests that at this small scale the volumetric and shape changes were both significant (peaks at 0.005 and -0.004, respectively).

3.2 Bulk strain measurement versus spatial strain pattern

Iterative hyperelastic warping not only reveals spatial strain difference in individual scales, but also indicates overall strain difference across scales, which is not captured by bulk strain measurements. In all cases, the absolute value of the strain was used to average over multiple samples. In tissue scale, the bulk volumetric measurement showed 16.5 ± 14.2% strain experienced by the muscle, while the linear measurement based strain computation predicted 5.2 ± 3.2% strain (Figure 3B). Thus, the volumetric and linear measurements showed discrepancies in the measurement. Average spatial hydrostatic strain in tissue scale was quantified to be 7.8 ± 2.3% (Figure 3C), a little higher than that found by bulk linear measurement but lower than bulk volumetric measurements. At the matrix scale, we quantified approximately 3.1 ± 1.4% strain from linear measurement based techniques, which was not commensurate with the lower average spatial hydrostatic strains (0.9 ± 0.3%). The nucleus showed very small strain values as observed from the deformation pattern, and was quantified as 0.3 ± 0.1% from the bulk linear measurement and a similar 0.3 ± 0.1% from spatial averaging. Therefore, bulk strain measurements give contradictory results at the tissue and matrix scales. An interesting observation was that though the bulk measurements did not show any significant strain difference between tissue and matrix scales (Figure 3B), the iterative hyperelastic warping did (Figure 3C).

3.3 Validation and sensitivity analysis

The iterative hyperelastic warping technique was validated at all scales with known forward displacements and is demonstrated by plotting the computed displacement against data known forward displacement data (Figure 4). The iterative hyperelastic warping technique quantified the spatial displacement accurately (characterized by R², slope of fitted trendline m, and p value computed from paired t-test) at all scales. Details are as follows - Tissue: R² = 0.98, m = 0.97, p < 0.0001; Matrix: R² = 0.99, m = 0.99, p < 0.0001, Nucleus: R² = 0.95, m = 1.02, p < 0.0001. Even for ultrasound images, which are known to suffer from spatial white noise and reflection artifacts, R² = 0.98 was achieved.

Figure 4. Validation studies indicate that known forward displacements matched iterative hyperelastic warping generated displacement values.

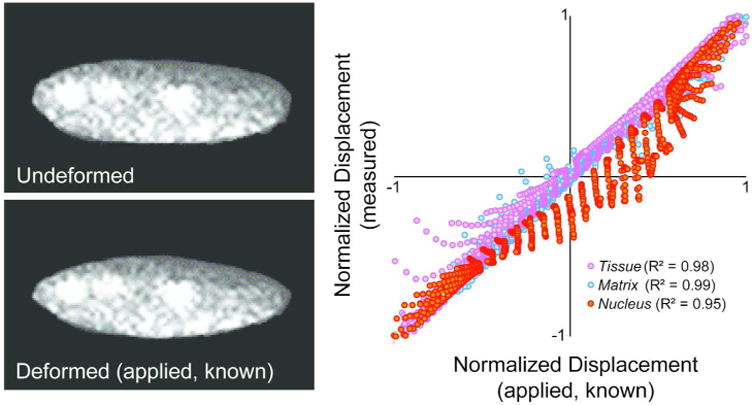
At all scales, the statistically significant correlations were found between known and computed displacement maps, characterized by R² ≥ 0.950, slope 1.00, p < 0.0001.

4. Discussion

This study quantified multiscale deformation in skeletal muscle in vivo and reveals the complex strain transfer across scales. The results show that there is much variability of deformation in each individual scale, and that as we move to a macro scale (i.e. subcellular to tissue regions), the deformation and its variability is magnified. Previous in situ studies in cartilage showed that on shear loading the strain in the nucleus in amplified compared to the strain in tissue¹⁵. Another study reported that on compressive loading of cartilage, in the superficial zone, strain in chondron is attenuated thus showing a protective mechanism¹⁹. However, in deeper zone, chondron strain was amplified. Thus, depending on the loading mode and functionality of the specific tissues, mechanisms may exist to shield the subcellular region from external deformations or amplified to facilitate triggering tissue-specific mechanotransduction pathways. Those previous studies and the results from the present study indicate that in skeletal muscle similar protective mechanisms may exist to shield the nucleus from an actively deforming and mechanically demanding environment, thus providing a tight regulation of gene expression in nucleus. It is known that in skeletal muscle the nuclei of healthy cells remain at the periphery regions of the myofibers¹⁷. On occurrence of injuries, the nuclei migrate to the center, and then migrate back after muscle recovery. This further suggests that the location and organization of nuclei in skeletal muscle may be designed in a way that the nuclei experience minimal deformation induced by the actomyosin contraction machinery in the central region of myofibers. As this protective mechanism may be encoded in the perinuclear space or at the nuclear membrane, further investigation is warranted.

Increasing strain in tissue compared to matrix gives another set of novel mechanistic insight which indicates that strain is amplified from the cell to tissue scale. The basic mechanism of muscle contraction was mediated by the contraction of the acto-myosin assembly. Therefore, the effect at the subcellular scale was the direct consequence of the acto-myosin contraction machinery, though we did not measure that. Thus the subcellular and nuclear strains are locally dependent on molecular machinery and highly regulated. At increasingly larger scales, more passive elements start contributing in the deformation response. Matrix scale strain most likely emerges from the subcellular- and cellular-scale strain through several passive elements, which do not directly interact with acto-myosin contraction machinery. Furthermore, the tissue scale strain was demonstrated to be higher than the matrix scale strain. This indicates that at a larger scale, further emergent properties may be affected by more passive elements, i.e., ECM and their architecture and other connected tissues, i.e. tendon. A model mechanism of such passive element-dominated behavior and resultant emergent properties is proposed (Figure 5). This kind of emergent behavior is most likely observed in skeletal muscle because its primary function is to orchestrate movement through contractions which require more complex and higher deformation (order of centimeter) than that is induced by simple molecular level machinery (order of nanometer).

Figure 5. Proposed model for strain amplification and heterogeneity at larger spatial scales.

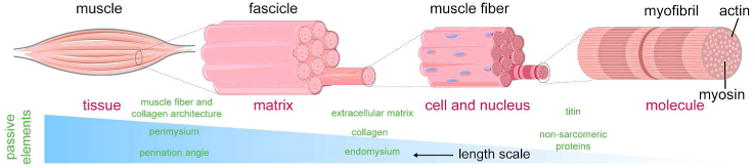
At the molecular level, a nanometer scale acto-myosin sliding mechanism creates a piconewton scale force. At the cell and nuclear level, strains depend mostly on the actions of the molecular scale. This allows the strain to be locally dependent on molecular machinery and highly regulated. At increasingly larger scale, many individual acto-myosin units combine to work to generate a higher amount of force. However, the addition of passive elements at each hierarchical level determines the strain at higher levels and depends on the geometry and combined material properties of the active and passive elements and force at that scale. Thus, at the subcellular level, passive titin and non-sarcomere proteins add to the acto-myosin active machinery. At the tissue scale, it is further added by other passive elements, such as extracellular matrix, collagen, and endomysium, and finally, at the organ scale, by perimysium and other geometrical factors, such as collagen architecture and pennation angle. Thus, from small to large scale, apparent ‘emergent behavior’ appears.

The iterative hyperelastic warping technique can successfully quantify the strain over multiple length scales with different image data types as illustrated in this work. At the tissue scale, hyperelastic warping has been successfully applied on MRI and CT images, and in ultrasound images to quantify spatial strain^20,21. Speckle tracking has also been attempted to quantify deformation using ultrasound images²², but it is limited by lower accuracy and poor resolution. Iterative hyperelastic warping depends on the texture of images, and is limited only by the quality of images acquired. As implemented in this work, this technique can reliably quantify the strain in both the transverse plane and the reconstructed coronal plane using ultrasound images, even though the latter has lower spatial resolution. In the nucleus, this technique has been used before in situ¹⁵, but this is the first work where the iterative hyperelastic warping is used in nucleus and tissue level strain quantification in vivo. The previous multiscale in situ studies suffer from the loss of the full complexity of the in vivo system. In vivo biomechanics have been investigated at organ and tissue scales, via bulk and spatial measurements using ultrasound^22–25 and MRI^26–29 in several organ types. However, the investigation of cell level mechanics in vivo is a new research area, with a few studies available on lower order lifeforms (e.g. in drosophila³⁰ and nematode³¹ embryos). In mice, cell mechanics have been studied spatially and temporally in chondrocytes using controlled loading of cartilage joints^32,33, but the researchers used simple cell geometry based measurements to probe the cell mechanics and thus lack any spatial details of deformation. It was clearly observed that bulk measurement of strain does not give meaningful information, is prone to user dependent errors and sometimes leads to discrepancies in the strain measurements. Spatial strain quantification at is an automated technique to understand detailed mechanics, and is important to quantify as the detailed spatial mechanics can affect the biomechanical phenomena in the local microenvironment.

Although the stimulation experiments were performed in almost similar biomechanical settings, each imaging modality (i.e. ultrasound and optical microscopy) required specific adjustments in the stimulation settings and particular imaging configurations. The applied stimulation was just enough to start muscle contraction, but any stronger stimulation was avoided in order to avoid fatigue in the muscle. The stimulation was confirmed visually by observed hind-limb digit extension. This threshold was observed to be at 1.5-2.0 mA for optical microscopy experiments, but at ∼45-50 mA for ultrasound imaging. This may be due to the applied ultrasound gel acting as a poor electrical conductor. Regardless, the present study can be supplemented with future multiscale computational biomechanics studies to further illustrate the strain transfer pattern we observed.

The response of the tibialis anterior muscle was imaged by ultrasound at a given transverse plane before, during, and after stimulation. While there is a possibility of muscle fatigue while the muscle remained stimulated, we observed that for the given time interval we used to maintain deformation, the muscle did not show any fatigue response, thus confirming that sequentially performing optical imaging at two different magnifications is valid and can be used for comparing nuclear strain to tissue strain.

This study opens avenues for the growing field of research in multiscale in vivo biomechanics, specifically at the nucleus, cell, and tissue scales. Future research directions include the investigation of the temporal response of skeletal muscle to repeated cyclic loading, which can reveal viscoelastic behavior of the skeletal muscle in vivo. Finally, investigating the effect of aberrant nuclear phenotypes on multiscale strain can provide novel insights on the role that genetics play in maintaining muscle mechanical homeostasis.

Conclusion

Multiscale biomechanics of skeletal muscle was experimentally investigated in vivo. A combination of ultrasound and optical microscopy was used to image the neuromuscular stimulation in organ, tissue and nucleus scales. An iterative hyperelastic warping technique quantified the spatial strain in different scales and showed complex strain transfer pattern over scales, that could not be achieved using traditionally used simple geometric strain measurement techniques. The results suggest complex emergent phenomena at larger scales, that are derived from molecular mechanism combined with materials properties at several scales, and protective nature at subcellular scale that leads to controlled regulation of transcription machinery in the nucleus.