INFERENCE FOR SOCIAL NETWORK MODELS FROM EGOCENTRICALLY SAMPLED DATA, WITH APPLICATION TO UNDERSTANDING PERSISTENT RACIAL DISPARITIES IN HIV PREVALENCE IN THE US

Abstract

Egocentric network sampling observes the network of interest from the point of view of a set of sampled actors, who provide information about themselves and anonymized information on their network neighbors. In survey research, this is often the most practical, and sometimes the only, way to observe certain classes of networks, with the sexual networks that underlie HIV transmission being the archetypal case. Although methods exist for recovering some descriptive network features, there is no rigorous and practical statistical foundation for estimation and inference for network models from such data. We identify a subclass of exponential-family random graph models (ERGMs) amenable to being estimated from egocentrically sampled network data, and apply pseudo-maximum-likelihood estimation to do so and to rigorously quantify the uncertainty of the estimates. For ERGMs parametrized to be invariant to network size, we describe a computationally tractable approach to this problem. We use this methodology to help understand persistent racial disparities in HIV prevalence in the US. We also discuss some extensions, including how our framework may be applied to triadic effects when data about ties among the respondent’s neighbors are also collected.

1. Introduction

There is growing interest in the statistical modeling of network data across a wide range of fields: from the study of political coalitions in the social sciences, to protein-protein interaction networks in genetics and the spread of infectious diseases in epidemiology. In some cases, it is possible to observe the complete network of interest, but in others the network must be sampled. Estimating network models from sampled data raises some unique issues. While progress has been made in developing a general framework for statistical inference (Handcock and Gile, 2010), there is a need for feasible methods that can be used with common network sampling designs in different fields.

In this paper we present a framework for inference from egocentrically sampled network data, a network sampling design that is common in the social and population sciences. Egocentrically sampled network data contain very limited information about network structure: for those individuals in the sample, only information about their immediate partners in the network is observed, and even that information is often limited to non-identifying demographics. The work was motivated by a specific question in the field of HIV epidemiology—Does network structure help explain the persistent racial disparities in HIV prevalence in the United States?—but it has the potential for wide application given the simplicity of collecting egocentrically sampled network data in the population sciences.

The HIV epidemic in the US is now in its third decade. While the rate of transmission has dropped, the racial disparities in HIV prevalence have become entrenched. An African American today is 10 times more likely than a white American to be living with HIV/AIDS. The disparity begins early in life (Morris et al., 2006), and persists through to old age (NCHH-STP, 2013), and is evident among all risk groups: heterosexuals, men who have sex with men (MSM), and injection drug users. The disproportionate risks faced by heterosexual African-American women are especially steep. In 2010, the most recent year for which statistics are available (NCHH-STP, 2012), the annual rates of heterosexually acquired infections by demographic subgroup were roughly 33, 19, 7 and 1 per 100,000 persons for African-American women and men and White women and men, respectively. Similar disparities are found among other sexually transmitted infections, both bacterial and viral (Morris et al., 2006), and for the older reportable STIs, like gonorrhea and syphilis, they stretch back to the earliest reports in the 1960s. (NCDC, 1967)

Empirical studies repeatedly find that these disparities cannot be explained by systematic differences in individual behavior, such as higher numbers of partners or rates of injection drug use, or lower condom use (Hallfors et al., 2007, for example). Nor have race-linked biological differences been identified that could explain disparities across this wide range of pathogens. What all of these infections do share, however, is an underlying transmission network. This network can channel the spread of infection in the same way that a transportation network channels the flow of traffic, with emergent patterns that reflect the connectivity of the system, rather than the behavior of any particular element.

A growing body of work is therefore focused on the role that network structure may play in explaining these disparities. Descriptive analyses and simulation studies (Laumann et al., 1992, 1994; Morris, 1993a; Morris and Kretzschmar, 1997) have focused attention on two structural features: homophily and concurrency. Homophily is the strong propensity for within-group partner selection. It is a common pattern for many social attributes, though not all. (For example, most sexual partnerships are cross-sex rather than same-sex.) When present, homophily leads to clustered, segregated networks. Concurrency is non-monogamy—having partners that overlap in time. While there is a very strong norm of monogamy in sexual partnerships, deviations from the norm occur. When present, concurrency increases network connectivity by allowing for the emergence of stable network connected components larger than dyads (pairs of individuals).

The hypothesis is that these two network properties together can produce the sustained HIV/STI prevalence differentials we observe: differences in concurrency between groups are the mechanism that generates the prevalence disparity, while homophily is the mechanism that sustains it. To test this hypothesis, we need to assess the strength and significance of observed concurrency differentials and homophily by race, and to evaluate whether the observed network mechanisms predict differentials in network exposure by race and sex that are consistent with the differentials in observed HIV prevalence.

Statistical models for social networks, like exponential-family random graph models (ERGMs), let us test for these effects, and we can simulate from them to predict network exposure; but these models must first be fit to available data that can support broad population-level inference. Our main statistical challenge is, therefore, to fit network models (ERGMs in particular) to egocentrically sampled data, and to obtain rigorous measures of uncertainty of these fits; to do so in a computationally feasible manner, for when the population of interest is very large or its size is unknown. We elaborate on these models and these data in turn.

1.1. Exponential-family random graph models

Exponential-family random graph models (ERGMs) are a popular and, importantly for us, parsimonious, class of stochastic models for graphs in general and for social networks in particular. (Frank and Strauss, 1986; Wasserman and Pattison, 1996; Hunter and Handcock, 2006) An ERGM expresses the probability of an observed graph y as an exponential family:

$${Pr}_{\mathit{g}}(\mathit{Y}=\mathit{y};\mathit{x},\mathit{\theta })\equiv exp\{{\mathit{\theta }}^{\top }\mathit{g}(\mathit{y},\mathit{x})\}/{\kappa }_{\mathit{g}}(\mathit{\theta },\mathit{x}),\mathit{y}\in \mathcal{Y}.$$ (1.1)

It is specified by the sample space 𝒴 of possible networks (configurations of relationships) and a sufficient statistic vector g(y, x), which is a function of the whole network y and possible covariates x, and whose elements are selected to represent features of the network that are of substantive interest or believed relevant to the generative process of the relationships in the network (e.g., count of monogamous actors to represent monogamy and count of ties within an exogenously defined group to represent homophily); and it is parametrized by its vector of natural parameters θ. The normalizing constant κ_g(θ, x) ≡ Σ_y′∈𝒴 exp{θ^⊤g(y′, x)} is usually intractable when the choice of g(y, x) induces dependence among the relationship states.

Analogously to Pr_g(·; x, θ), we define E_g(·; x, θ) and var_g(·; x, θ), as, respectively, the expectation and the variance under this ERGM process; and let μ_g(θ, x) ≡ E_g{g(Y, x); x, θ}, the smooth and invertible (Brown, 1986, Thm. 3.6, for example) mapping from the natural to the mean-value parameters of this model; call its inverse θ_g(μ, x) ≡ (θ s.t. μ_g(θ; x) = μ).

Estimating θ facilitates inference about the social forces that shape the network as well as principled simulation of complete networks whose features are similar, on average, to those of the network observed. In the case of sampled network data in particular, it would allow recovering possible full networks from which the sample may have been drawn. Therefore, θ is our target of inference.

1.2. Egocentrically sampled data

Network data are distinguished by having two units of analysis: the actors and the links between the actors. This gives rise to a range of sampling designs that can be classified into two groups: link tracing designs (e.g., snowball and respondent driven sampling) and egocentric designs. Much of the recent literature has focused on developing model- or design-based inference for link tracing designs. (Thompson and Frank, 2000; Salganik and Heckathorn, 2004; Volz and Heckathorn, 2008; Snijders, 2010; Handcock and Gile, 2010; Tomas and Gile, 2011; Illenberger and Fltter, 2012; Pattison et al., 2013) Our work focuses on the egocentric designs that are more commonly used in the social sciences, but are less well developed statistically.

Egocentric network sampling comprises a range of designs developed specifically for the collection of network data in social science survey research. The design is (ideally) based on a probability sample of respondents (“egos”) who, via interview, are asked to nominate a list of persons (“alters”) with whom they have a specific type of relationship (“tie”), and then asked to provide information on the characteristics of the alters and/or the ties. The alters are not directly observed. Depending on the study design, alters may or may not be uniquely identifiable, and respondents may or may not be asked to provide information on one or more ties among alters (the “alter” matrices). Alters can, in theory, also be present in the data as an ego or as an alter of a different ego; the likelihood of this depends on the sampling fraction and the network’s topology.

In this work, we focus on the minimal egocentric network study design, in which alters cannot be uniquely identified and alter matrices are not collected. The minimal design is more common, and the data are more widely available, for three reasons.

Confidentiality and alter identification

If the relationship of interest is sensitive, requiring full identification of the alters is likely to reduce respondent disclosure, and knowledge of alter–alter ties by the respondent may be unreliable. In addition, Institutional Review Boards often forbid the collection of identifiable data about the alters, as the alters have not given informed consent for their personal information to be collected. The minimal egocentric design allows for representative data to be collected in such contexts, with less intrusion and full consent. In public health research on HIV and other STIs, for example, egocentric study designs make it possible to conduct empirical research on how individual sexual behavior influences the population structure of infection transmission networks. There is a growing international archive of public data from such studies, with comparable surveys now available from over 50 different countries as far back as the early 1990s (MEASURE DHS, 2000–2014; Tanfer, 1991; Laumann et al., 1992; Udry, 2003; NSFG, 2002, 2006–2011, for example).

Time cost of alter matrix collection

The number of potential alter–alter ties grows quadratically with the number of alters nominated by the ego, quickly making data collection burdensome for the respondent, and difficult to justify in surveys that must serve multiple needs. As a result, even the less sensitive forms of social network data tend to be collected using the minimal egocentric design. Perhaps the best known example is the egocentric friendship network data collected annually by the General Social Survey since 1985 (Burt, 1984), which was used in the landmark study of the decline in American friendship and social support networks as described in Bowling Alone (Putnam, 2000).

Compatibility with established methods for survey sampling for population-based inference

While in theory, the “seed nodes” for a link-traced sample could be chosen at random from the population of interest, the real strength of these designs is the ability to sample from hidden or inaccessible populations, where no sampling frame is available, and this is the application context in which they are most often used. Egocentric designs, by contrast, sample egos using standard sampling methods, and the sampling of links is implemented through the survey instrument. As a result, these methods are easily integrated into population-based surveys, and, as we show below, inherit many of the inferential benefits.

This sampling design has immediate implications for the scope of models that can be fit. For example, lack of information on alter–alter ties means that triadic (friend-of-a-friend) effects are not identifiable, and the lack of information on alter degree means that degree assortativity (a correlation between degrees of linked actors) (Gupta et al., 1989) also cannot be identified. These limitations must be kept in mind when drawing inferences, but they are not likely to undermine the specific inferences we draw here. Further discussion can be found in Section 8.2.

Despite the widespread availability of the minimal egocentrically sampled network data, statistical methods for analyzing them are still relatively undeveloped. Early work focused on descriptive methods for analyzing “mixing matrices”, cross-tabulations of ego–alter dyads by actor attributes (Marsden, 1981; Morris, 1991), or bivariate associations between ego attributes and alter summary statistics (Marsden, 1987; Admiraal, 2009). van Duijn, van Busschbach, and Snijders (1999) used a multilevel (mixed effects) model to analyze factors affecting changes over time in such networks based on repeated observations on same relations over time, and conditioning on the initial time point’s relationships. More recent work has focused on the key topic of recovering whole network attributes from egocentric data (Gjoka, Smith, and Butts, 2014b, e.g., clique size distributions), but does not provide a framework for inference.

Handcock and Gile (2010) established a general framework for model-based inference for networks based on sampled data that allows for egocentrically sampled data as a special case: when only dyads incident on those in the sample are observed (Koskinen, Robins, and Pattison (2010) developed a similar approach in a Bayesian framework.) Unfortunately, their likelihood approach is infeasible for our problem for three reasons. First, it requires fitting an ERGM to a network of the size equal to that of the population from which the egos were sampled, which is, often, on the order of millions, and possibly unknown. Second, it assumes uniquely identified alters: one can identify when one ego nominates another ego and when two egos nominate the same alter. For most egocentrically sampled data (including all of the studies cited above), alters are not identified. Although a likelihood can be derived for this case too, it requires integration over the space of networks that produce exactly the observed dataset—a more complex constraint. Third, if the data come from a complex (even just weighted) design, ignorability of the sampling process might not hold, requiring nested integration over the sampling process as well.

Krivitsky, Handcock, and Morris (2011) described how the sufficient statistic needed to fit certain ERGMs may be derived from egocentrically sampled data and used to simulate networks consistent with egocentric observations. This approach has been used in applied contexts (Morris et al., 2009; Goodreau et al., 2010; Smith, 2012). What remains lacking, however, is a general, rigorous framework for ERGM inference for such data, and we turn to the pseudo-MLE (PMLE)¹ (Binder, 1983; Pfeffermann, 1993, for example) approach to do this.

Outline

The rest of the article proceeds as follows. In Section 2, we describe the notation and the sampling framework for egocentrically sampled network data, and in Section 3, we specify an ERGM subfamily amenable to being fit to such data. The pseudo-MLE of θ—calculated by obtaining a design-based estimator of the ERGM sufficient statistic of the network of interest and fitting the ERGM to that—and its asymptotic properties are derived in Section 4, along with a method for quantifying its uncertainty. An overview of implementation issues and of a validating simulation study are given in Sections 5 and 6, respectively, with the details left to the supplemental article (Krivitsky and Morris, 2016). Finally, in Section 7, we apply our developments to the question of the impact of network structure on persistent racial disparities in HIV prevalence in the US.

2. Notation and sampling

Let N be the population being studied: a very large, but finite, set of actors whose relations are of interest, and let x_i be a vector of attributes (e.g., age, sex, race) of an actor i ∈ N, with x_N (or just x, when there is no ambiguity) being the attributes of actors in N. Let 𝕐(N) ≡ {{i, j}: (i, j) ∈ N × N ∧ i ≠ j} (distinct unordered pairs of actors) be the set of dyads (potential ties) in an undirected network of these actors. Then, let 𝒴(N, x) ⊆ 2^𝕐(N) (set of subsets of potential ties) be the set of networks (sets of ties) of interest. 𝒴(·, ·) may incorporate exogenous constraints, which we discuss in Section 3.2. For a network y ∈ 𝒴(N, x), let y_i,j ≡ y_j,i be an indicator function of whether a tie between i and j is present in y and y_i = {j ∈ N: y_i,j = 1}, the set of i’s network neighbors.

Throughout, y will refer to what we will call the population network: a fixed but unknown network of relationships of interest.

2.1. Egocentric data

Now, let e_i be the “egocentric” view of network y from the point of view of actor i (“ego”). It comprises ${\mathit{e}}_i^{\mathrm{e}}\equiv {\mathit{x}}_i$: i’s own attributes, and ${\mathit{e}}_i^{\mathrm{a}}\equiv {({\mathit{x}}_j)}_{j\in {\mathit{y}}_i}$: an unordered list (technically, a multiset) of attribute vectors of i’s immediate neighbors (“alters”), but not their identities (indices in N). For convenience, we refer to the kth attribute/covariate observed on ego i and its alters as $e_{i,k}^{\mathrm{e}}\equiv x_{i,k}$ and ${\mathit{e}}_{i,k}^{\mathrm{a}}\equiv {(x_{j,k})}_{j\in {\mathit{y}}_i}$.

Then, (e_i)_i∈N (e_N for short) represents the egocentric census, the information retained by the minimal egocentric sampling design discussed in Section 1.2. The information about y contained in an egocentric sample of actors S ⊆ N can then be represented as e_S ≡ (e_i)_i∈S.

2.2. Sampling design considerations

In the following developments, we will assume that egocentric observations are sampled using a conventional sampling design, with N as the sampling frame, though as we discuss in Section 5, this is not critical in practice. The proposed methods can be applied to more complex—stratified, for example—designs, but here, we focus on simple probability designs, and designs that can be approximated with simple probability designs. Specifically, let inclusion probabilities π_i ≡ Pr(i ∈ S), for i ∈ N, and assume that a weight $w_i\propto {\pi }_i^{-1}$ is observed for each ego i ∈ S, but only up to proportion: Σ_i∈N w_i is not known. In our application, in particular, w_S incorporate both stratification for oversampling and post-stratification to account for missing reports, making inclusion probabilities π_i difficult to obtain.

Analogously to the ERGM process, we will use E_S(·) and var_S(·) to refer to the expectation and the variance under the sampling process.

3. Egocentric ERGMs

Even if the whole population is observed (i.e., S = N, a census), not every ERGM can be fit to such data, and we turn to the notion of sufficiency to identify those that can. Define an ERGM of the form (1.1) to be egocentric if both its sufficient statistic and its sample space constraints (if any) can be recovered from an egocentric census. We discuss them in turn.

3.1. Egocentric statistics

We call a network statistic g_k(·, ·) egocentric if it can be expressed as

$$g_k(\mathit{y},\mathit{x})\equiv {\sum }_{i\in N}{h}_k({\mathit{e}}_i),$$ (3.1)

for some function h_k(·) of egocentric information associated with a single actor. For the egocentric observations e_i of the form defined in Section 2.1, the space of egocentric statistics includes dyadic-independent (Hunter et al., 2008b) statistics that can be expressed in the general form of g_k(y, x) = Σ_(i,j)∈y f_k(x_i, x_j) for some symmetric function f_k(·, ·) of two actors’ attributes; and some dyadic-dependent statistics that can be expressed as g_k(y, x) = Σ_i∈N f_k{x_i, (x_j)_j∈yi} for some function f_k(·, ···) of the attributes of an actor and their network neighbors. Table 1 gives their representations in terms of of h_k(·), along with some examples. Such egocentric statistics induce at most Markov graph dependence (Frank and Strauss, 1986) and are local by the definition of Krivitsky et al. (2011).

Table 1.

Examples of egocentric statistics for undirected networks. x_i,k may be a dummy variable indicating i’s membership in a particular exogenously defined group. h_k(e_i) that sum over ties are halved because each tie is observed egocentrically twice: once at each end.

Statistic	gk(y, x)	hk(ei)
General sum over ties	Σ(i,j)∈y fk(xi, xj)	$\frac{1}{2}{\sum }_{\mathit{z}\in {\mathit{e}}_i^{\mathrm{a}}}{f}_k\left({\mathit{e}}_i^{\mathrm{e}},\mathit{z}\right)$
Number of ties in the network	|y| ≡ Σ(i,j)∈y 1	$\frac{1}{2}\mid {\mathit{e}}_i^{\mathrm{a}}\mid$
weighted by actor covariate xi,k	Σ(i,j)∈y(xi,k + xj,k)	$\frac{1}{2}\left(e_{i,k}^{\mathrm{e}}\mid {\mathit{e}}_i^{\mathrm{a}}\mid +{\sum }_{z\in {\mathit{e}}_{i,k}^{\mathrm{a}}}z\right)$
weighted by difference in xi,k	Σ(i,j)∈y|xi,k − xj,k|	$\frac{1}{2}{\sum }_{z\in {\mathit{e}}_{i,k}^{\mathrm{a}}}\mid e_{i,k}^{\mathrm{e}}-z\mid$
within groups identified by xi,k	Σ(i,j)∈y 1xi,k=xj,k	$\frac{1}{2}{\sum }_{z\in {\mathit{e}}_{i,k}^{\mathrm{a}}}{1}_{e_{i,k}^{\mathrm{e}}=z}$
General sum over actors	Σi∈N fk {xi, (xj)j∈yi}	$f_k\left({\mathit{e}}_i^{\mathrm{e}},{\mathit{e}}_i^{\mathrm{a}}\right)$
Number of actors with d neighbors	Σi∈N 1|yi|=d	$1_{\mid e_i^{\mathrm{a}}\mid =d}$
weighted by actor covariate xi,k	Σi∈N xi,k1|yi|=d	$x_{i,k}{1}_{\mid {\mathit{e}}_i^{\mathrm{a}}\mid =d}$

As one might expect from the discussion in Section 1.2, statistics measuring triadic closure, degree assortativity, and 4-cycles are not egocentric under this sample design. However, some of them (and thus the ERGMs that use them) may be egocentric under different egocentric sampling designs, which we discuss in Section 8.2.

Other statistics that are not egocentric include the average number of neighbors of an actor—g_k(y, x) = 2|y|/|N|—because the corresponding $h_k({\mathit{e}}_i)=2\times \frac{1}{2}\mid {\mathit{e}}_i^{\mathrm{a}}\mid /\mid N\mid$ depends on the network size, which is information not contained in e_i. (That is, an individual cannot see exactly how big the network of interest is.) The latter are thus not local by the definition of Krivitsky et al. (2011). (This does not mean that the mean degree parameter itself cannot be estimated from egocentric data, only that our inferential results might not apply.)

3.2. Egocentric sample space constraints

We call the sample space 𝒴(·, ·) of an ERGM egocentric if it can be expressed as

$$\mathcal{Y}(N,\mathit{x})\equiv \left\{\mathit{y}\in 2^{\mathbb{Y}(N)}:{\mathrm{\Pi }}_{i\in N}\mathscr{H}({\mathit{e}}_i)\ne 0\right\},$$

for some indicator function ℋ(·) that depends only on egocentric information associated with a single actor. For example, $\mathscr{H}({\mathit{e}}_i)=1_{\mid {\mathit{e}}_i^{\mathrm{a}}\mid \le d}$ would constrain y ∈ 𝒴(N, x) so that no actor has more than d ties; and, given a binary actor attribute x_i,k (e.g., sex), $\mathscr{H}({\mathit{e}}_i)={\mathrm{\Pi }}_{z\in {\mathit{e}}_{i,k}^{\mathrm{a}}}{1}_{e_{i,k}^{\mathrm{e}}\ne z}$ would force all of the ties to be between groups defined by x_i,k, modeling a bipartite network (if, say, the focus were on heterosexual partnerships).

For the remainder of this paper, we will fix ℋ(e_i) = 1 so that 𝒴(N, x) = 2^𝕐(N): our data include same-sex ties, and statistics g(·, ·) with free parameters can be used to model the above-described features more flexibly. Also, hard constraints are less well understood, and techniques such as network size adjustment needed for the computational approach described in Section 5.2 have not been developed for even the simpler ones.

4. Inference

Our inferential goal is to fit ERGMs to unobserved networks based on egocentric samples from them: to recover the parameters that would have been estimated had an ERGM been fit to fully observed y. Because y and x are fixed, we will drop them from g(y, x) (i.e., g) and others from now on, unless it is to emphasize the dependence.

Most treatments of ERGM estimation treat θ as a parameter of a superpopulation process of which y is a single realization; and the maximum likelihood estimator (MLE) θ̂ is obtained by solving the score equation

$$\text{sc}(\widehat{\mathit{\theta }})\equiv \mathit{g}(\mathit{y})-{\mathit{\mu }}_{\mathit{g}}(\widehat{\mathit{\theta }})=\mathbf{0},$$ (4.1)

which has a unique solution θ̂ = θ_g{g(y)}. When the likelihood contains an intractable normalizing constant κ_g(·) (which also makes μ_g(·) and θ_g(·) intractable), Monte-Carlo Maximum Likelihood Estimation (MCMLE) techniques of Geyer and Thompson (1992), as applied to ERGMs by Hunter and Handcock (2006), can be used. The variance of θ̂ is then typically estimated by the inverse of the simulated negative Hessian of the log-likelihood.

In contrast, we treat θ as a finite population parameter, defined implicitly for the unobserved population network y as the solution to (4.1). The inverse-negative-Hessian is not the correct variance for this estimation problem: whereas it reflects, loosely, the uncertainty in estimates due to the stochasticity of the generative process for the network’s ties, we treat the network as a fixed, unknown, finite population, so it is not a source of uncertainty in the first place. Rather, uncertainty comes from having to estimate g from an egocentric sample e_S. Indeed, if S = N, (3.1) gives g exactly, so var_S(θ̂) = 0. (We do address the superpopulation case in Section 8.3.)

Our inferential approach is, therefore, to obtain an estimator for g based on the available data, then substitute it into (4.1), solving it to obtain a pseudo-MLE θ̃. We derive it, and its properties, as follows.

4.1. Pseudo maximum likelihood estimation

Following Binder (1983), substituting (3.1) into (4.1) gives a score equation of the form of Binder’s eq. 2.6. Binder’s Assumptions (a), (c), and (d) (open parameter space, smoothness, and continuity of variance, respectively) are guaranteed by finite exponential family proprieties of ERGMs. Assumption (b) calls for an asymptotically normal estimator of the population total g and a consistent estimator of its variance. We treat them in turn.

A consistent, asymptotically normal estimator for g

For our design, we use the inverse-probability weighted estimator (Hájek estimator) scaled to the population size. (Hájek, 1971) With y, x, and therefore g being fixed, and letting $w.\equiv {\sum }_{i=1}^{\mid S\mid }{w}_i$,

$$\stackrel{\sim }{\mathit{h}}({\mathit{e}}_S)\equiv {\sum }_{i\in S}{w}_i\mathit{h}({\mathit{e}}_i)/w.$$ (4.2)

is a design-consistent—if slightly biased—estimator of h̄ ≡ g/|N|, the population mean contribution of each actor to the sufficient statistic. (Fuller, 2011, p. 61) Scaling it to the population size, g̃(e_S) ≡ |N|h̃(e_S) is then a design-consistent estimator for the population network statistic g. Provided the joint distribution of [w_i, w_ih(e_i)] under the sampling process in Section 2.2 is not degenerate and the fourth moments of w_i and h(e_i) are finite, Fuller (2011, Thm. 1.3.8, pp. 58–61) gives

$${\mid S\mid }^{\frac{1}{2}}(\stackrel{\sim }{\mathit{g}}({\mathit{e}}_S)-\mathit{g})=\mid N\mid {\mid S\mid }^{\frac{1}{2}}(\stackrel{\sim }{\mathit{h}}({\mathit{e}}_S)-\overline{\mathit{h}})\stackrel{d}{\to }{\text{MVN}}_p(\mathbf{0},{\mid N\mid }^2{\mathit{\sum }}_{\mathrm{H}}),$$

where

$${\mathit{\sum }}_{\mathrm{H}}\equiv {\mu }_w^{-2}\left(\overline{\mathit{h}}{\overline{\mathit{h}}}^{\top }{\mathit{\sum }}_{w,w}-\overline{\mathit{h}}{\mathit{\sum }}_{w,w\mathit{h}}-{\mathit{\sum }}_{w\mathit{h},w}{\overline{\mathit{h}}}^{\top }+{\mathit{\sum }}_{w\mathit{h},w\mathit{h}}\right),$$ (4.3)

with μ_w ≡ E_S(w_i), the expected sampling weight, and

$$\left[\begin{array}{cc}{\mathit{\sum }}_{w,w}& {\mathit{\sum }}_{w,w\mathit{h}}\\ {\mathit{\sum }}_{w\mathit{h},w}& {\mathit{\sum }}_{w\mathit{h},w\mathit{h}}\end{array}\right]\equiv {\mathit{\sum }}_{[w,w\mathit{h}]}\equiv {var}_S\left(\left[\begin{array}{c}{w}_i\\ w_i\mathit{h}({\mathit{e}}_i)\end{array}\right]\right).$$

A consistent estimator for Σ_H

Provided the fourth moments of w_i and h(e_i) are finite, by the Weak Law of Large Numbers, the sample variance ${\stackrel{\sim }{var}}_S\{{[w_i,w_i\mathit{h}({\mathit{e}}_i)]}^{\top }\}$ consistently estimates Σ_[w,wh], h̃(e_S) consistently estimates h̄, and w̄ ≡ w_·/|S| consistently estimates μ_w. Substituting them into (4.3) gives such an estimator; call it Σ̃_H.

Then, the PMLE θ̃ = θ_g{g̃(e_S)} solving $\stackrel{\sim }{\text{sc}}(\stackrel{\sim }{\mathit{\theta }})=\stackrel{\sim }{\mathit{g}}({\mathit{e}}_S)-{\mathit{\mu }}_{\mathit{g}}(\stackrel{\sim }{\mathit{\theta }})=\mathbf{0}$ is a consistent, asymptotically normal estimator of θ (Binder, 1983):

$${\mid S\mid }^{\frac{1}{2}}(\stackrel{\sim }{\mathit{\theta }}-\mathit{\theta })\stackrel{d}{\to }{\text{MVN}}_p\left(\mathbf{0},{\{{\nabla }_{\mathit{\theta }}{\mathit{\mu }}_{\mathit{g}}(\mathit{\theta })\}}^{-1}{\mid N\mid }^2{\mathit{\sum }}_{\mathrm{H}}{[{\{{\nabla }_{\mathit{\theta }}{\mathit{\mu }}_{\mathit{g}}(\mathit{\theta })\}}^{-1}]}^{\top }\right).$$ (4.4)

Notably, θ_g{g̃(e_S)} is defined for every g̃(e_S) in the convex hull of g(𝒴; x) (the set of sufficient statistics attainable in the model’s sample space), so θ̃ is defined even when, say, g̃(e_S) estimates a fractional number for a network statistic that is a count (like |y|), and MCMLE can be used in this situation without modification. (Hummel, Hunter, and Handcock, 2012)

4.2. Variance estimation

In addition to the estimator for Σ_H, the variance in (4.4) calls for an estimator of ∇_θμ_g(θ). In practice, it can be approximated by ∇_θμ_g(θ̃), which can be estimated as a byproduct of the likelihood maximization using MCMLE (e.g., Hunter and Handcock, 2006, eq. 3.5): for a minimal exponential family, ∇_θμ_g(θ) = −E_g{∇_θ sc(θ); θ} = E_g{sc(θ) sc(θ)^⊤; θ} = var_g{g(Y ); θ}, so ∇_θμ_g(θ) can be approximated by the sample variance–covariance matrix of g(Y) simulated at θ̃. That is,

$${var}_S(\stackrel{\sim }{\theta })\approx {[{\stackrel{\sim }{var}}_{\mathit{g}}\{\mathit{g}(\mathit{Y});\stackrel{\sim }{\mathit{\theta }}\}]}^{-1}({\mid N\mid }^2{\mathit{\sum }^{\sim }}_{\mathrm{H}}/\mid S\mid ){[{\stackrel{\sim }{var}}_{\mathit{g}}\{\mathit{g}(\mathit{Y});\stackrel{\sim }{\mathit{\theta }}\}]}^{-1},$$ (4.5)

an estimator of the form of Binder (1983, eq. 3.4).

5. Implementation

Section 4 leads to the following procedure:

1. Estimate the sufficient statistic of the ERGM with g̃(e_S).

2. Obtain θ̃, using MCMLE to solve $\stackrel{\sim }{\text{sc}}(\stackrel{\sim }{\mathit{\theta }})=\mathbf{0}$.

3. As a byproduct of Step 2, obtain ${\stackrel{\sim }{var}}_{\mathit{g}}\{\mathit{g}(\mathit{Y});\stackrel{\sim }{\mathit{\theta }}\}$.

4. Estimate var_S(θ̃) as described in Section 4.2.

For the simulation study and the analysis that follow, we use, mainly, the R (R Core Team, 2013) package ergm (Hunter et al., 2008b; Handcock et al., 2014) for fitting and simulating from ERGMs. The extensions to fit ERGMs to egocentrically sampled data have been implemented in a new R package, ergm.ego, under development for public release. We also use the R package sna (Butts, 2008) to calculate network connected component sizes.

Some additional implementation challenges arise as well.

5.1. Reconstructing x_N from sampled data

Formally, our procedure depends on x being observed completely (i.e., a census), or, at least, its distribution being known to a very high degree of accuracy. Step 2’s MCMLE, in particular, requires sampling over the space of possible population networks, conditional on all actor attributes, and its implementation requires constructing a network having actor attributes x_N, which is unobserved. While this may seem like a major obstacle, in practice it is not: for i ∈ S, x_i are observed directly, and for the remainder, only a distribution of x is needed: actors having the same x_i are interchangeable.

Therefore, in the analyses performed here, we use the design-based estimator of the finite-population distribution of x_N: we replicate each x_i for i ∈ S as close to |N|w_i/w_· times as possible. This has consequences, which we illustrate in the simulation study in Section 6 and the supplemental article (Krivitsky and Morris, 2016, App. B).

5.2. Scalable estimation

The procedure also calls for fitting an ERGM to a network of size |N|. While possible in principle, this is often a computationally infeasible task. For example, the “population” of the NHSLS study we consider below is all individuals aged 18 through 59 and living in the US at the time of the study (1992)—hundreds of millions—and naively fitting an ERGM to a smaller subnetwork is unlikely to produce meaningful estimates due to non-projectivity of ERGMs with dyadic dependence (Shalizi and Rinaldo, 2013). We work around this using the network-size-invariant parametrization of Krivitsky et al. (2011): by adding an offset term, some ERGMs can be adjusted so that fitting them to networks having similar structure and composition but different sizes produces the same parameter estimates. We thus construct a “scaled-down” pseudopopulation of interest, N′, and fit the adjusted model to it, thus approximating the θ̃ that would have been obtained by fitting to the full N. This adjustment is not applicable to every network feature of every possible ERGM, but its applicability to a given model can be verified by simulation. Further details are given in the supplemental article (Krivitsky and Morris, 2016, App. A).

Thus, using the network-size-invariant parametrization, and estimating x_N from x_S, the procedure does not require any information not in e_S.

6. A simulation study

To evaluate the properties of our estimators we performed a simulation study, constructing a large population network with known ERGM parameters and simulating egocentric samples from it, using two sampling designs: unweighted and weighted. The sampling weights have a range similar to the NHSLS, oversample some groups of actors (A and C), and are correlated with a continuous covariate used in the model (x_i,2). For each sample, we calculated point estimates and standard errors in order to assess their accuracy and the coverage of Wald confidence intervals. Details and full results are given in the supplemental article (Krivitsky and Morris, 2016, App. B).

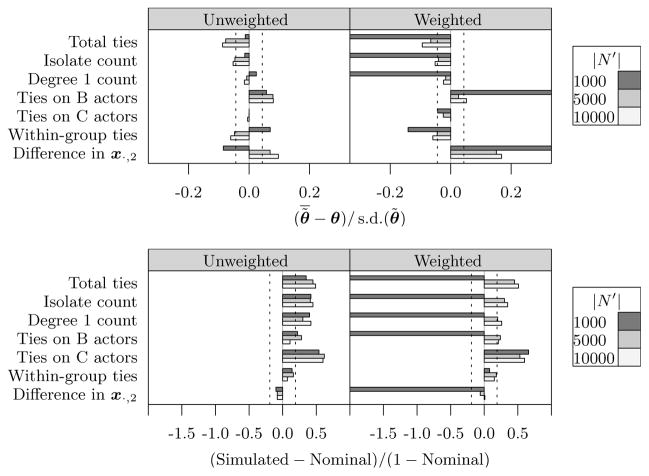
Selected bias and coverage results for sample size |S| = 1,000 are shown in Figure 1. The unweighted sampling estimates display some bias, though it does not appear to have a systematic pattern as a function of |N′| or model term. None of the estimated biases are greater than 10% of the standard deviation of θ̃ under repeated sampling; that is, bias accounts for less than 1% of the mean squared error (MSE) of the estimator.

Fig 1.

Simulated bias in the point estimates, relative to simulated standard deviation (top); and 95% confidence interval coverage, relative to the miss probability of 5% (bottom) for |S| = 1,000. Dashed lines are level 0.05 critical values: 95% of the results should fall between them, if the estimator is unbiased / has nominal coverage.

The weighted sampling estimators are, as one would expect, highly biased for smaller |N′|. For the largest |N′|, the bias tends to approach that of the unweighted, and the most biased parameter’s (Difference in x_·,2) bias is less than 20% of its standard deviation (≈ 4% of MSE). A possible reason why it is the most biased is that egos with small x_i,2 are by design severely undersampled, which means that there will exist many samples where the full range of x_·,2 is not represented. This is likely to be less problematic in real-world applications like the analysis in Section 7, where continuous covariates (like age) have an explicit range of interest.

Overall, we found the standard errors for both weightings to be conservative, overestimating the simulated standard deviation by between 1% and 20% (in a few cases). The resulting confidence interval coverage is consistent with these observations: for almost all terms, the intervals are somewhat conservative for both sampling designs (given sufficient |N′|).

We replicated the study for |S| = 2,000, and found that the biases decrease (both absolutely, and relative to their standard deviation, which is, itself, smaller), and the standard errors became more accurate as well. The coverage remains somewhat conservative. (Krivitsky and Morris, 2016, App. B.2)

This study demonstrates parameter recovery for when the egocentric ERGM on observed actor attributes is the “true” model (though dropping the assumption that the whole x_N is observed). We discuss the issue of model misspecification in Section 8.2.

7. Understanding persistent racial disparities in HIV prevalence in the US

We now return to our motivating questions: 1) How strong is the race homophily in the the population? 2) Are there differences in the propensity towards monogamy and concurrency for the races and the sexes? And, 3) What impact do these network features have on overall network connectivity and differentials in network exposure by race and sex?

7.1. Data

The National Health and Social Life Survey (NHSLS) of 1992 (Laumann et al., 1992, 1994) was undertaken at the start of the AIDS epidemic in the US. The objectives of the study included obtaining the data on sexual behavior necessary to predict the long term trajectory of HIV and AIDS prevalence, and to understand the disparities in HIV prevalence by race that had already begun to emerge. The survey collected, among other information, a representative egocentric sample of sexual partnerships of a stratified sample of residents of the US aged 18–59 (inclusive). A rich set of socio-demographic attributes was collected, including the respondent’s age, sex, race/ethnicity, and respondents were asked for similar information about all of their sexual partners from the previous twelve months.

For this analysis, we focus on modeling the cross-sectional network of ongoing sexual partnerships of persons aged 18–59. Some reported partners were outside this age range, and a small number of respondents had turned 60 by the time they were interviewed. We exclude these partnerships and persons, as well as those with missing data on the necessary attributes (race, sex, and age, for both ego and alter). More appropriate handling of missing actor data in egocentrically sampled networks is subject for future research. These exclusions lead to dropping 75 egos and 215 alters, leaving 3,357 egos and 2,555 alters in the sample for analysis. The ego degree distribution for the analytic sample was not significantly different from the full sample.

The NHSLS study used a stratified multistage cluster sample, with oversampling of Black households. The public dataset includes weights that account for both stratification and attribute-based non-response, so we approximate the design by an independent weighted sample.

7.2. Methods and models

We divide the respondents into three racial/ethnic categories: White, Black, and Other. While the primary contrast of interest here is between Whites and Blacks, a non-negligible fraction of egos reported other identifications for themselves and their alters. These cannot be dropped in a network analysis, as they can serve as connecting elements that influence the measures of interest.

Homophily is operationalized as an edge covariate, and is defined as concordance in actor attributes in a partnership, as reported by ego. We focus on homophily by sex and race in this analysis, allowing for differential homophily by race. Concurrency is operationalized at the actor level, and is defined as actor degree greater than 1. For modeling purposes, we fit a monogamy term to capture these effects, defined as actor degree equal to 1, again allowing for group-specific propensities for monogamy. This produces more stable estimates, especially for smaller groups with very low rates of reported concurrency.

We fit a sequence of nested models to test the network hypothesis for the racial disparities in HIV prevalence. Model 1 serves as a baseline, fitting the observed mean degree for each sex by race, as well as the prevalence of heterosexual mixing. It has terms for the main effects for each sex and each race, and a homophily term for sex. Since this is a largely heterosexual population, we expect the sex homophily term will be strongly negative, but same-sex partnerships are not precluded. This model assumes partners are selected at random with respect to race, and there is no propensity for monogamy in sexual partnerships. Model 2 tests homophily by race by adding a term for each race to capture the prevalence of within-group mixing. We expect these terms to be large and positive. Model 3 tests heterogeneities in the propensity for monogamy by adding a term for each sex by race to capture the prevalence of persons with exactly one partner. We expect these terms to be positive, given the strong norm of monogamy in sexual partnerships, but we also expect there to be significant differences by race and sex. Since the group-specific mean degrees have been fit by the baseline terms, lower coefficient values on the monogamy terms will imply higher prevalence of concurrent partners.

We evaluate the goodness of fit of each model using the following criteria:

Reproducing observed degree distributions

We compare the observed degree distribution to 100 realizations of complete networks from each specified model. In principle, we can evaluate the goodness of fit to any egocentric statistics that are not already in the model, following the general approach of Hunter, Goodreau, and Handcock (2008a). We choose the degree distribution because it is a primary determinant of network connectivity. A model that does not fit the degree distribution well is unlikely to produce the unobserved network connectivity that we wish to infer.

Reproducing whole network patterns consistent with observed HIV incidence

We simulate complete networks from the fitted models, which allows us to evaluate whether the micro-level processes specified by each model produce non-egocentric macro-level outcomes (network connectivity and exposure) that are consistent with observed epidemiological data. We measure overall network connectivity using the connected component size distribution. The propensity for monogamy in Model 3 is expected to increase the number of components of size 2 (mutual monogamy) and decrease the number and size of the larger components. We measure network exposure at the actor level, using the probability of membership in components of size 3 or greater. This represents the risk of indirect exposure: an actor with only one partner will have little direct exposure, but by virtue of the network she or he may still be exposed to her or his partner’s other partner(s) and beyond. Under the network hypothesis, only Model 3 is expected to produce differentials in network risk exposure that are consistent with the observed disparities in HIV incidence.

Robustness of conclusions to additional predictors

The models we consider are, of course, not intended to be complete specifications of the network process, as they exclude many factors that are known to influence sexual behavior and partner selection. For our purposes, the question is whether our results are robust to the inclusion of these factors, which would depend on whether the factors are correlated to race and sex, or interact with them in relevant ways. A good example to consider is age, as it influences both degree and partner selection patterns, and we examine its effects by adding to Model 3 terms to capture the impact of age on both degree distribution and partner selection. If the addition of these terms renders the monogamy-bias or homophily terms nonsignificant, it would suggest that there is an age mechanism that underlies these biases, and the marginal impacts in Model 3 are due to differences in age composition by race.

The population network would have had |N| ≈ 147 million persons (Population Estimates Program, 2001), so we take advantage of the scaled-down approach mentioned in Section 5.2. Based on reasoning detailed in the supplemental article (Krivitsky and Morris, 2016, App. C.1), we select, conservatively, |N′| ≈ 45,000 ≈ 13.4 × |S|, or 44,859 after rounding the scaled sampling weights. This network size is also used in the simulation results we report. Notably, this may be overly conservative in practice: we obtained very similar results in a pilot analysis using |N′| ≈ 15,000.

Verification of the assumption that our models are amenable to network-size- invariant parametrization is given in the supplemental article (Krivitsky and Morris, 2016, App. C.4).

7.3. Results

We report the model fits in Table 2. Model 1 results are consistent with expectations. There is a significant and strong propensity for heterosexual ties, and a slightly higher mean degree for men than women. There are no significant differences in mean degree by race. In Model 2, the results are consistent with the network hypothesis: all of the race homophily terms are large and significant. In Model 3, the results are again consistent with the hypothesis: there is a strong propensity for monogamy in all groups, but the propensity is relatively higher among White men and women. The difference between Whites and Blacks is significant for men (contrast diff. = 1.17, s.e. = 0.32, P-value < 0.001), but not for women (diff. = 0.45, s.e. = 0.51, P-value > 0.3). Women have higher rates of monogamy than men in all groups, especially among Blacks, but these differences are not statistically significant.

Table 2.

Coefficients and standard errors for the three models. Coefficients reported are in the presence of an edge count offset of −log(44859) = −10.71.

Model	1	2	3
	Main	+ Mix.	+ Monog.
Actor activity by sex
Female	0.02 (0.10)	−0.99 (0.19)***	−1.88 (0.31)***
Male	0.46 (0.10)***	−0.55 (0.20)**	−1.18 (0.25)***
Same-sex partnership	−4.49 (0.21)***	−4.50 (0.20)***	−4.52 (0.21)***
Actor activity by race
White		0 (baseline)
Black	−0.09 (0.07)	−0.58 (0.29)*	−0.30 (0.38)
Other	−0.03 (0.07)	0.83 (0.33)*	0.93 (0.42)*
Race homophily by race
Black		5.13 (0.35)***	5.15 (0.38)***
Other		2.06 (0.35)***	2.04 (0.35)***
White		2.25 (0.34)***	2.32 (0.36)***
Monogamy by sex and race
Black Female			1.80 (0.47)***
Other Female			2.51 (0.67)***
White Female			2.25 (0.31)***
Black Male			0.99 (0.24)***
Other Male			1.40 (0.31)***
White Male			2.16 (0.25)***

Significance levels: 0.05 ≥ * > 0.01 ≥ ** > 0.001 ≥ **

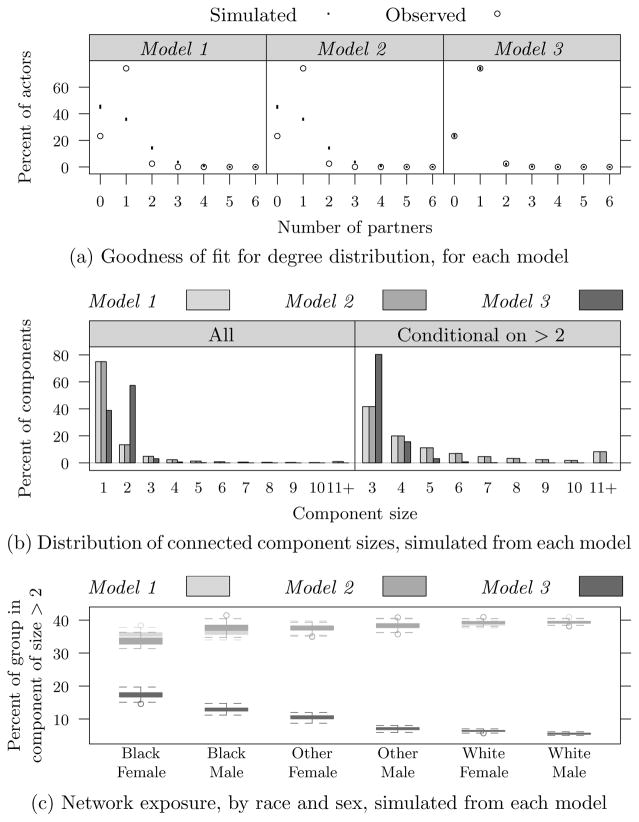
The goodness of fit for each model is shown in Figure 2a. The first two models do a very poor job fitting the observed degree distribution: both underestimate the fraction of persons with only one partner and overestimate both the fraction with no partner, and more than one partner. The data clearly indicate a strong propensity for monogamy, and Model 3 captures this well. Because there are race and sex-specific monogamy terms in Model 3, it provides a good fit for all groups. (A more detailed breakdown and discussion are given in the supplemental article (Krivitsky and Morris, 2016, App. C.2).)

Fig 2.

Simulation results based on 100 realizations from each of the fitted models: (a) goodness-of-fit plot, comparing simulated degree frequencies (dot plot) to that observed in the data; (b) simulated network component size distributions, averaged over each simulation; and (c) simulated distribution of the proportions of individuals of each race and sex who are in components of size 3 or greater. (Because of the large |N′| used in the simulation, there is little variability percent-wise between realizations in (a).)

The overall network connectivity predicted by each model can be seen in Figure 2b. The plot shows the distribution of component sizes produced by each model. The first two models are, again, similar: both predict that about three quarters of the components are size 1 (isolated actors), and the ties distributed to the remaining actors produce components with sizes that can reach 100 or more. By contrast, Model 3 predicts that the modal component is size 2 (mutual monogamy), that only about 20% of the actors are isolates, and the maximum component size attained in the 100 simulated realizations has fallen to only 6. Monogamy thus has the expected effect: it dramatically reduces the connectivity in the overall network.

The differential network risk exposure by race and sex predicted by each model can be seen in Figure 2c. This plot shows the group-specific distributions of the probability of belonging to a component of size 3 or more for each model. Models 1 and 2 produce very similar results: overall network exposure probabilities are about 40%, and the race-specific differences are small, with lower probabilities of exposure predicted for Blacks than Whites. Since lower probabilities of exposure imply lower transmission risks, this pattern is the opposite of what we expect given the HIV/STI prevalence disparities. Adding the differential monogamy terms in Model 3 reverses the predicted network exposure risk differentials for both sexes, producing a pattern that is consistent with the observed racial disparities in HIV/STI prevalence, and consistent with the network hypothesis.

Note that within each racial group, women are more likely than men to be in components of size 3 or more. This is because 3 is by far the most common component size predicted among those not mutually monogamous (≈ 80%, as seen in Figure 2b), and coupled with the higher rates of concurrency among men than women this means that these components typically comprise 1 man and 2 women. This a good example of the somewhat counterintuitive logic of network exposure in infectious diseases: your exposure is not just a function of your own behavior, but also a function of your partner’s. In countries with generalized heterosexual HIV epidemics, such as those in sub-Saharan Africa, concurrency is similarly gendered, and women’s HIV prevalence is typically much higher then men’s (40% higher across this particular region (UNAIDS, 2014)).

Model 3 is clearly the best fit, and it predicts network exposure risks that are consistent with the observed disparities in HIV prevalence by race and sex. Per Section 7.2, we augmented it with several age-related terms. The results, given in the supplemental article (Krivitsky and Morris, 2016, App. C.3), are that age effects are generally significant, but that the key homophily and monogamy-bias results reported for Model 3 are robust.

8. Discussion

There are many challenges in developing rigorous inference for ERGM estimates from egocentrically sampled network data: the stochastic dependence in networks can be complex, the information present in an egocentric sample is limited, and the use of the data is often secondary. We have proposed a technique to conduct statistically valid ERGM inference under these conditions, using pseudo-maximum-likelihood estimation and exploiting exponential family proprieties. This makes it possible to estimate the parameters of a class of statistical models defined by the structural properties of a network that can be observed from an egocentric sample, test hypotheses of interest, assess goodness of fit, and conduct principled simulation from a superpopulation of networks having properties similar to those observed. By making use of a network-size-invariant parametrization for the ERGMs of interest, this can be done even when the target population is very large or even unknown. The result is a general statistical framework for leveraging whole network information from an efficient minimal sampling design.

As with all inferential frameworks, ours rests on a set of approximations and assumptions, and comes with limitations, some of which may be addressed in future research:

8.1. Data considerations

x is sampled

Per Section 5.1, we had constructed x_N′ by extrapolating from the sample, but we did not take this into account in our inference. Our simulation study suggests that the inference is still valid (conservative, in fact), but this issue can be addressed more rigorously. Recall that we only require the joint distribution of x_N\S, not their individual values. Fortunately, the distribution for demographic attributes such as sex, age, ethnicity, and geographic location is often known to a very high degree of precision—from a national census, for example; and it could be used to construct an x_N′ with virtually no sampling variation. In fact, the weights in the NHSLS data in Section 7 had been calculated through post-stratification to reflect the population, so, in our analysis, this had already been done for us.

Alternatively, uncertainty from x being sampled may be incorporated into the inferential procedure: in particular, Fellows and Handcock (2012) propose an exponential-family model for jointly modeling actor attributes and ties. Provided the sufficient statistic associated with actor attributes could be recovered from egocentric data, our results should be applicable.

Stratified and cluster sampling

We approximated the sampling design of the NHSLS study with that of Section 2.2: a simple probability sample. A more accurate estimate of var_S(θ̃) could be obtained by substituting into (4.5) an estimate of var_S{h̃(e_S)} that better reflects the design than Σ̃_H/|S| does. And, for small N, finite-population correction can be used.

Measurement error

In our application, we assumed that the responses were accurate: that, for example, the male respondents did not overreport their partnerships and female respondents did not underreport. While the discrepancy in the number of lifetime partners reported by men and women is well-established in the literature (Morris, 1993b), the magnitude of the discrepancy declines with the length of the recall period (Hamilton and Morris, 2010). In the NHSLS data used here, there is almost perfect correspondence between the weighted total number of ongoing heterosexual partnerships reported by women and men (1366 and 1388, respectively), which suggests some internal validity to the reports.

8.2. Model considerations

Misspecification

The potential for model misspecification is particularly serious for egocentric inference. This is not because of the inferential approach as such: our asymptotic results guarantee that for an egocentric ERGM, the PMLE (say, θ̃_E) consistently estimates the parameters (θ_E) that would have been obtained had the same model been fit to the full population network, with variability of θ̃_E under repeated sampling accurately quantified. Rather, this is because of how the data limit the scope of the models that can be estimated: even where the “true” model specification is known and is an ERGM (say, with coefficients θ_T), it might not be estimable (identifiable) with the available data. Therefore, the question about the impact of misspecification in egocentric inference reduces to the question of whether substantive conclusions drawn based on the coefficients in θ_E are different from those that would be drawn from the corresponding coefficients of θ_T, were it estimable.

While assessing general misspecification through traditional goodness-of-fit approaches is uniquely challenging in the context of egocentric data constraints, it is still possible to assess some aspects of model specification this way, as we have done in Section 7.2. Others can be tested by validating model predictions against specific hypotheses, for example, demonstrating that the disparities in network exposure predicted by the model are consistent with the observed disparities in HIV prevalence only when both of the hypothesized network features (homophily and monogamy bias) are included. But, this still leaves open the question of whether unobserved higher-order (such as triadic or degree-assortative) effects significantly influence the overall network structure, and potentially alter the impacts of the observed network features on the outcomes of interest.

In general, the potential impact of specific unobserved features could be examined through simulation. One could construct or simulate networks whose egocentric statistics match those inferred from the data but which also possess the specific hypothesized higher-order properties, such as more transitivity than predicted by simulating from θ̃_E obtained from the egocentric submodel alone. Estimating the “true” MLE θ̂_T and the egocentric submodel’s MLE θ̂_E (≈ θ̃_E, by construction) based on these networks and comparing their common elements should provide information about what biases may have been introduced by omitting the higher-order terms.

In our application, we did not use simulation to address this question, because the specific alternative hypothesized network effects in this case can be assessed more directly. For example, one might wish to consider how unobserved triadic effects or degree-based mixing might influence the conclusions we have drawn. Both effects would clearly influence the overall network structure in ways that might alter the spread of an infectious disease—positive/negative triadic effects might cluster/disseminate prevalence, and assortative/disassortative degree-based mixing would have similar effects. But, both of these are also examples of network configurations that can be produced by other mechanisms that, in our case, are observable in egocentric data. In particular, a triangle would have to contain at least one tie between nodes of the same sex. Given the very low prevalence of same-sex sexual ties observed in our population level data, the potential for triangles is very limited, and our models capture this through negative sex homophily even if the data preclude us from identifying specific triadic biases (positive or negative) beyond that. Similarly, one of the most striking features of the HIV prevalence disparities in this application is the lack of correlation with observed activity levels (degree). This would be predicted by degree-disassortative mixing, which we cannot observe in egocentric data. However, we do observe and model a mechanism that would produce degree-disassortative configurations: the systematically higher monogamy bias among women, combined with disassortative mixing on sex. In both cases, therefore, we are producing strucural configurations—that we cannot directly observe—by representing mechanisms that are well grounded in the science, observable, and statistically testable.

In other application settings, where explicitly triadic mechanisms may be at work, friendship networks where such triadic mechanisms can be empirically distinguished from homophily (Goodreau et al., 2009, in particular), suggest that misspecification bias is a bigger problem for estimates of triadic effects than estimates of homophily. That is, unaccounted-for homophily can lead to upward bias in the triadic closure coefficients, but the converse does not hold: unaccounted-for triadic closure does not appear to affect homophily coefficients substantively, and certainly not to the point of, e.g., turning assortative into disassortative mixing or vice versa. Whether this is a general property of the model, or an empirical feature of social networks, is a topic for future research.

One may also be interested in considering potential confounders for the effect of race on the observed racial homophily: for example, homophily on socioeconomic status and residential segregation may both play a role, and (in the United States) both are associated with race and ethnicity. However, this would not alter the main finding that racial homophily contributes to HIV prevalence disparities by race: from the pathogen’s point of view, it does not matter why a particular group structure has emerged, only that it has.

Ultimately, the underlying generative process for the network is outside of the scope of models that we consider for other reasons as well. (Airoldi, Blei, Fienberg, Goldenberg, Xing, and Zheng, 2008, Panel Discussion) The model we consider here is a model only for the static relations, but the underlying process is dynamic. Representing these dynamics would require models for tie formation and dissolution (Krivitsky and Handcock, 2014), and may also require models for random nodal attributes, nodal entry and exit (Airoldi et al., 2008, Blei), and (depending on research goals) the underlying utility functions that represent nodal preferences (Airoldi et al., 2008, Shalizi). This means that our methodology is subject to the usual limitations in terms of causal inference.

Expanding the scope of the model

We can consider a number directions for explanding the scope of these models, subject to data availability.

Directed and bipartite networks

Our development was aimed at undirected relations on unipartite networks, but the general inferential technique should be applicable to directed relations, provided each ego’s in-ties, as well as out-ties, are observed, and to bipartite networks.

Triads and other higher-order terms

We note in Section 3.1 that whether an ERGM term is egocentric—whether it can be identified given available data—is a function of the egocentric survey design: what information does e_i contain? Though less common, information about alters’ connections is sometimes available in an egocentric design through solicitation of alter–alter ties. Smith (2012) and Gjoka, Smith, and Butts (2014a) consider this case for estimating clique size distributions and for reconstructing plausible networks, though not for ERGM inference. Other variations and extensions include studies that collect egocentric-like data but allow some individuals appearing twice in the data to be matched, e.g., couple studies (where the two individuals with a link are recruited together and each is asked about their alters), or a one-wave snowball sample. In epidemiology, such data may be collected in more focused studies of networks of men who have sex with men (MSM) and injecting drug users (IDUs)—where triadic effects may be highly relevant. (Dhanjal et al., 2011; Trotter et al., 1995)

In such studies, e_i would contain some additional information, and the set of statistics expressible in the form of (3.1) would expand accordingly. For example, the transitive ties statistic (a non-degenerate analogue of the triangle count) counting the number of ties (i, j) such that at least one path i − k − j exists, i.e.,

$$g_k(\mathit{y},\mathit{x})=\sum _{(i,j)\in \mathit{y}}\underset{k\in N\backslash \{i,j\}}{max}{\mathit{y}}_{i,k}{\mathit{y}}_{k,j}$$

can be expressed in the form of (3.1) as

$$h_k({\mathit{e}}_i)=\frac{1}{2}\sum _{j\in {\mathit{y}}_i}\underset{k\in {\mathit{y}}_i\backslash \{j\}}{max}{\mathit{y}}_{j,k},$$

which depends only on the set of i’s immediate neighbors (i.e., y_i) and which of those neighbors, j and k, are connected to each other (i.e., y_j,k). (Krivitsky and Kolaczyk (2015) derive this form in a different context.) The pseudo-MLE inferential argument then applies directly.

Dynamic network models

Minimal egocentric surveys often do include temporal information on the ties—such as duration of ongoing and recent partnerships—and inference for dynamic network models based on such data is the focus of ongoing work. (Krivitsky, 2012)

Non-egocentric ERGM terms

Expressability in the form (3.1), is sufficient but not strictly necessary for the estimation: for example, the global clustering coefficient (3 × (# of triangles)/(# of 2-stars)) cannot be so expressed, but both its dividend and its divisor can (given alter–alter data), so the Delta Method or a resampling method can be used to obtain an estimator and its variance. At the same time, such model terms would tend not to be local (Krivitsky et al., 2011)—a given dyad’s state would be conditionally dependent on the whole network, rather than some reasonable social neighborhood of the actors involved—causing difficulties in interpretation and network-size adjustment.

Network-size invariance

Our implementation utilizes the network-size-invariant parametrization of Krivitsky et al. (2011) primarily to facilitate computation—to allow us to fit the model to an “microcosm” N′ of the population N.

This parametrization also facilitates interpretation by giving us parameter estimates invariant to our choice of |N′|, which was the original motivation for its development. It is highly likely that this scaling could be extended to bipartite networks, and Krivitsky and Kolaczyk (2015) propose a size adjustment for ERGM mutuality terms that could be used for egocentric data on directed networks, along with an approach that holds promise for triadic effects. The discussion in the supplemental article (Krivitsky and Morris, 2016, App. A.1) may provide some guidance for developing and testing such adjustments in the future.

In general, an ERGM specification is not guaranteed to have a meaningful size-invariant parametrization. But, size invariance is not strictly necessary for our framework: given sufficient computing power, one may dispense with N′ and estimate parameters on N directly, with inferential results and ability to simulate from the fit networks consistent with the observed data unaffected.

8.3. Inferential considerations

Bias

Our simulation study in Section 6 and the supplemental article (Krivitsky and Morris, 2016, App. B) shows our estimators to be slightly biased. There are four likely sources of bias: (i) sampling variation of x; (ii) biasedness of the Hájek estimator (4.2) for h̄; (iii) nonlinearity of the mapping θ_g(·) and Jensen’s Inequality (analogous to that in logistic regression (Firth, 1993)); and (iv) scaled-down approximation, particularly for weighted samples. Biases (i)–(iii) decrease in sample size |S|, while bias (iv) decreases in |N′|.

We attempted to reduce (ii) using jackknife, with little noticeable improvement in the simulation studies, suggesting that it is not a major source of bias in this case. Judging by the small difference between the biases from the higher values of |N′| considered (found in the supplemental article (Krivitsky and Morris, 2016, App. B.2)), (iv) likely becomes negligible reasonably quickly: the estimates converge to a nonzero bias. We believe this remaining bias to be primarily due to (i) and (iii).

Unfortunately, while a technique like nonparametric bootstrap jointly resampling w_i and e_i can be used for bias reduction and uncertainty estimation alike, this is likely to be computationally prohibitive: whereas every resample of bootstrap or jackknife for (ii) requires merely recalculating a weighted average, culminating in a single ERGM fit using the debiased h̃(e_S), for (i) and (iii), every resample requires refitting an ERGM to a large network. At the same time, it may be possible to reduce (iii) using the penalized likelihood approach of Firth (1993). All this is subject for ongoing work.

Inference for a superpopulation

Lastly, in our framework, the population network y is fixed and unknown and θ_g {g(y)} is a finite population property to be estimated. In some applications, it may be more meaningful to view Y as being drawn from a superpopulation (e.g., ERGM) parametrized by θ, and then observed egocentrically. Although deriving rigorous asymptotics of this generative process may not be feasible, the variance of the estimator is straightforward: whatever the generative process for Y, g̃{e_S(Y)} remains an asymptotically unbiased estimator of g(Y) for any given Y, under repeated egocentric sampling from Y. Then, Law of Total Variance gives

$$\begin{gathered} {var}_{S\circ \mathit{g}}[\stackrel{\sim }{\mathit{g}}\{{\mathit{e}}_S(\mathit{Y})\};\mathit{\theta }]={\mathrm{E}}_{\mathit{g}}({var}_S[\stackrel{\sim }{\mathit{g}}\{{\mathit{e}}_S(\mathit{Y})\}\mid \mathit{Y}];\mathit{\theta })+{var}_{\mathit{g}}({\mathrm{E}}_S[\stackrel{\sim }{\mathit{g}}\{{\mathit{e}}_S(\mathit{Y})\}\mid \mathit{Y}];\mathit{\theta }) \\ \approx {\mathrm{E}}_g({var}_S[\stackrel{\sim }{\mathit{g}}\{{\mathit{e}}_S(\mathit{Y})\}\mid \mathit{Y}];\mathit{\theta })+{var}_{\mathit{g}}\{\mathit{g}(\mathit{Y});\mathit{\theta }\}, \end{gathered}$$

which, for an ERGM superpopulation and the sampling process (S) being independent of the network (Y)—something likely to hold in social surveys—reduces to

$$\begin{gathered} {var}_{S\circ \mathit{g}}(\stackrel{\sim }{\mathit{\theta }})\approx {\stackrel{\sim }{\mathit{V}}}^{-1}({\mid N\mid }^2{\mathit{\sum }^{\sim }}_{\mathrm{H}}/\mid S\mid +\stackrel{\sim }{\mathit{V}}){\stackrel{\sim }{\mathit{V}}}^{-1} \\ \approx {\stackrel{\sim }{\mathit{V}}}^{-1}({\mid N\mid }^2{\mathit{\sum }^{\sim }}_{\mathrm{H}}/\mid S\mid ){\stackrel{\sim }{\mathit{V}}}^{-1}+{\stackrel{\sim }{\mathit{V}}}^{-1}, \end{gathered}$$

for $\stackrel{\sim }{\mathit{V}}={\stackrel{\sim }{var}}_{\mathit{g}}\{\mathit{g}(\mathit{Y});\stackrel{\sim }{\mathit{\theta }}\}$, and if E_g (var_S[g̃{e_S(y)}|Y]; θ) is approximated by |N|² Σ̃_H/|S|. However, while the variance of the parameter estimates may be estimated thus, the normality of g(Y) under the superpopulation is not guaranteed. If the superpopulation process is an ERGM, it can be tested as a side-product of the estimation.