Abstract
I develop a model of insurer price-setting and consumer welfare under risk-adjustment, a policy commonly used to combat inefficient sorting due to adverse selection in health insurance markets. I use the model to illustrate graphically that risk-adjustment causes health plan prices to be based on costs not predicted by the risk-adjustment model (“residual costs”) rather than total costs, either weakening or exacerbating selection problems depending on the correlation between demand and costs predicted by the risk-adjustment model. I then use a structural model to estimate the welfare consequences of risk-adjustment, finding a welfare gain of over $600 per person-year.
1. Introduction
It is widely known that insurance markets can suffer from market failures caused by adverse selection (Akerlof 1970, Rothschild and Stiglitz 1976). Efficiency is achieved when consumers purchase goods that they value more than the social cost of providing those goods. In many markets, competition induces efficiency by ensuring that goods are priced according to their marginal cost. In many health insurance markets, however, adverse selection and pricing regulations work to distort equilibrium prices, causing them to diverge from the first-best (and also the second-best) prices that induce consumers to sort efficiently across health insurance contracts (Einav, Finkelstein, and Cullen 2010). In the extreme, adverse selection can cause some types of insurance products to cease to exist (Cutler and Reber 1998). Due to wider variation in the levels of coverage available to consumers, this adverse selection problem is likely to be more severe in the Health Insurance Marketplaces (Marketplaces) established by the Affordable Care Act (ACA) than in other, more widely studied settings such as the employer and Medicare markets. In fact, recent research suggests the potential for complete market unraveling in a Marketplace-like setting (Handel, Hendel, and Whinston 2015).
While adverse selection in insurance markets has been widely studied both empirically and theoretically, the literature on regulations and policies typically used to combat selection problems is less well-developed. With respect to health insurance markets, the literature has largely focused on only three solutions to the sorting problems caused by adverse selection: restricting the contract space, subsidizing adversely selected plans, and allowing premiums to vary by expected cost (Cutler and Reber 1998; Einav, Finkelstein, and Cullen 2010; Bundorf, Levin, and Mahoney 2012; Geruso 2016, Handel, Hendel, and Whinston 2015). One of the most widely implemented solutions to the adverse selection problem, transfers or subsidies based on enrollee health status typically known as risk adjustment, has received less attention.1 Risk adjustment is typically viewed as being used to combat supply-side selection problems, known as cream-skimming, where insurers distort insurance contracts to attract healthy enrollees (Glazer and McGuire 2000, Brown et al. 2014, Newhouse et al. 2015).2 While these distortions and the power of risk adjustment to combat them are important, in this paper I show that risk adjustment transfers can also have significant effects on sorting and welfare in a fixed contract setting where inefficiency is due to consumers choosing the “wrong” plan rather than cream-skimming insurer behavior. The choice of plan tier in the Marketplaces or the choice between HMO and PPO plans in Medicare Advantage represent such settings.
In the first part of this paper, I present a conceptual framework for evaluating the effect of imperfect risk adjustment transfers on prices and sorting in competitive health insurance markets like the Marketplaces. The framework is based on the model of Einav, Finkelstein, and Cullen (2010). The key innovation is to divide health care spending into two dimensions: the risk adjustment transfer payment attached to the individual (“adjusted costs”) and the difference between total spending and the risk adjustment transfer payment (“residual costs”). Risk adjustment transfers are typically based on risk scores calculated for each enrollee using demographics and diagnoses from health insurance claims. The risk scores act as proxies for the enrollees’ total expected medical spending in an average health plan. A regulator uses these risk scores to enforce transfers from plans attracting low risk enrollees to plans attracting high risk enrollees. These transfers effectively cause the average level of adjusted costs to be equal across all plans (i.e., flatten the “incremental average adjusted cost curve”), leaving only residual costs to generate any heterogeneity in average net-of-risk adjustment spending across plans. Residual costs are typically practically important: Risk adjustment models used in the Medicare Advantage market explain only about 12% of the variation in spending, and models used in the Marketplaces explain 30–40% of spending. However, in most markets it is unknown how much residual costs vary across plans, the key parameter for determining the extent of the adverse selection problem in a market with risk adjustment.
After developing the model, I use a series of graphical representations, building on those presented in Einav, Finkelstein, and Cullen (2010) and Einav and Finkelstein (2011), to develop intuition for how risk adjustment affects sorting and welfare. The model and figures provide intuition for an important and novel conceptual point: The effect of risk adjustment on equilibrium prices and sorting is determined by the joint relationship between risk scores (i.e. adjusted costs), spending, and demand for the adversely selected plan. This joint relationship differs from the typical metric used to evaluate risk adjustment policies, the relationship between risk scores and spending. Importantly, I show that this implies that if in a market a given health plan is adversely selected on total spending but advantageously selected on the risk score, risk adjustment transfers can result in fewer, rather than more, enrollees choosing the adversely selected plan, effectively exacerbating the problem it is meant to address. Such a setting is possible because risk adjustment is imperfect and only captures certain dimensions of spending and preference heterogeneity causes different dimensions of spending to have different correlations with demand.3 This is a novel and important conceptual point that to my knowledge has not previously been made in the risk adjustment or adverse selection literatures.4
In the second part of this paper, I investigate the efficiency consequences of standard risk adjustment transfer policies empirically using rich administrative health insurance claims and enrollment data from a large employer that includes individual-level medical spending as well as all of the pieces of information necessary to compute the risk scores used in Marketplace risk adjustment policies. I combine the rich claims and enrollment data with a structural model of consumer health plan choice to estimate consumer risk preferences and the correlations between risk preferences, risk scores, and total spending for a sample of employees. I then use this joint distribution of preferences, risk scores, and spending combined with an algorithm developed by Handel, Hendel, and Whinston (2015) to simulate equilibrium plan prices and consumer sorting with and without risk adjustment in the context of a Marketplace where consumers are required to enroll in either a less comprehensive Bronze plan or a more comprehensive Platinum plan.5 I simulate the actual risk adjustment transfer policy being implemented in the Marketplaces along with a few counterfactual policies. I use these simulations to estimate the consequences of risk adjustment for prices, sorting, and, ultimately, welfare in the Marketplaces.
The simulations suggest that there will be significant adverse selection in the Marketplaces. I replicate the result of Handel, Hendel, and Whinston (2015) that with no risk adjustment transfers, the market fully unravels, and all consumers enroll in the less comprehensive Bronze plan. I then simulate prices and sorting under the Marketplace risk adjustment policy and find that, despite its imperfection at explaining costs at an individual level, it undoes a significant portion of market unraveling. The equilibrium premiums of the two plans converge, and over 60% of market participants enroll in the more comprehensive Platinum plan. I also test several counterfactual risk adjustment policies, finding that risk adjustment based on demographics only has no effect on market unraveling and that when combined with reinsurance the effects of risk adjustment are augmented, producing Platinum plan enrollment exceeding 80%. Welfare calculations indicate that the welfare consequences of risk adjustment in this setting are far from trivial, with the Marketplace risk adjustment transfer policy improving welfare by $600–$700 per person, per year, or around 20% of total health care costs among employees of the firm I study.6 These findings are largely robust to various assumptions about the ability of consumers to predict their future health care costs.
This paper provides an important contribution to the literature on regulations used to combat adverse selection problems. Specifically, this paper generalizes previous models of adverse selection with risk adjustment developed by Shi (2014) and Glazer, McGuire, and Shi (2014) to allow for preference heterogeneity to cause the relationship between demand and risk scores to differ from the relationship between demand and total costs. This generalization is important as it reveals that risk adjustment does not always increase enrollment in the adversely selected plan as implied by the less-general models. This paper also adds to the growing set of graphical representations of the welfare economics of health insurance markets. The graphical representation introduced by Einav, Finkelstein, and Cullen (2010) has proven influential among researchers and policymakers due to its ability to describe a fairly complex theoretical concept in a simple and intuitive framework. Recently, their model has been used to estimate welfare changes due to the reform of Massachusetts' individual health insurance market (Hackmann, Kolstad, and Kowalski 2015) and the ACA (Kowalski 2014). The model has also been generalized to allow for imperfect competition by Mahoney and Weyl (2014) and information frictions by Spinnewijn (2016) and Handel, Kolstad, and Spinnewijn (2015). These papers both consider the consequences of risk adjustment within the Einav, Finkelstein, and Cullen (2010) framework, showing that imperfect competition and behavioral frictions can result in risk adjustment worsening rather than improving consumer welfare. I add to their work by introducing a new dimension to the Einav, Finkelstein, and Cullen framework: The interaction between preference heterogeneity and risk adjustment imperfections. This extension produces the insight that risk adjustment imperfections alone can result in risk adjustment exacerbating rather than improving adverse selection problems, even without imperfect competition or behavioral frictions.7
The empirical results in this paper also represent a significant contribution in that they show that despite their imperfections, risk adjustment transfers have economically large effects on equilibrium prices and sorting in a Marketplace setting.8 In fact, in the setting studied here, risk adjustment proves critical for the market to function efficiently. Additionally, when combined with reinsurance, the effects of risk adjustment transfers are enhanced. While risk adjustment also likely affects other welfare-relevant margins such as the design of the contracts in the market (Glazer and McGuire 2000), the extent to which insurers inefficiently invest resources in cream skimming behaviors, and the extent of reclassification risk or the level of “fairness” in the market, these results suggest that risk adjustment also plays an empirically important role with respect to the efficient sorting of consumers across a fixed set of contracts in a market.
The paper proceeds as follows. Section 2 develops a simple model of a competitive health insurance market with risk adjustment and presents the graphical framework to provide intuition for the relationship between risk adjustment, prices, and sorting, focusing on the importance of the joint relationship between adjusted costs, total spending, and demand for the adversely selected plan. Section 3 discusses the data used for estimation. Section 4 outlines the structural model used to estimate the joint distribution of risk preferences, total costs, and adjusted costs. Section 5 presents the results of the simulations of equilibrium under risk adjustment, and Section 6 concludes.
2. Theoretical Framework
The model developed here builds on the models developed in Einav, Finkelstein, and Cullen (2010) and Bundorf, Levin, and Mahoney (2012). The key innovation of the model is that total plan spending on an individual is divided into two components: adjusted costs and residual costs. Consumers are required to choose one of two insurance contracts, an enhanced contract (E) and a basic contract (B). These contracts could be differentiated based on coverage or on other dimensions such as quality or the size of the provider network. All consumers face the same price for each contract. Consumers are distinguished by their health risk, θ, and preferences, ε. Let νj (θi, εi) represent consumer i’s valuation of plan j in dollars, so that Δν(θi, εi) = νE (θi, εi) − νB (θi, εi) represents consumer i’s willingness-to-pay for E relative to B. Let P represent the difference in the price for E and the price for B, P = PE − PB. Under these assumptions, consumer i chooses to purchase E if and only if Δν(θi, εi) ≥ P.9
Plans are assumed to set prices equal to the average cost of their enrollees.10 Let cj (θi) represent the (expected) monetary cost to plan j of enrolling a consumer with health risk θi. The average costs of Plans E and B can thus be described as
| (1) |
| (2) |
Given these assumptions, in equilibrium the premium differential, P, will be equal to the difference between Plan E and Plan B’s average costs, or the incremental average cost (IAC):11
| (3) |
Two factors cause the premium differential, P*, to vary: selection and benefit differences. Benefit differences affect premiums because plan costs may differ for a specific enrollee. Selection affects premiums because the average cost of a plan with sicker enrollees will be higher than the average cost of a plan with healthier enrollees.
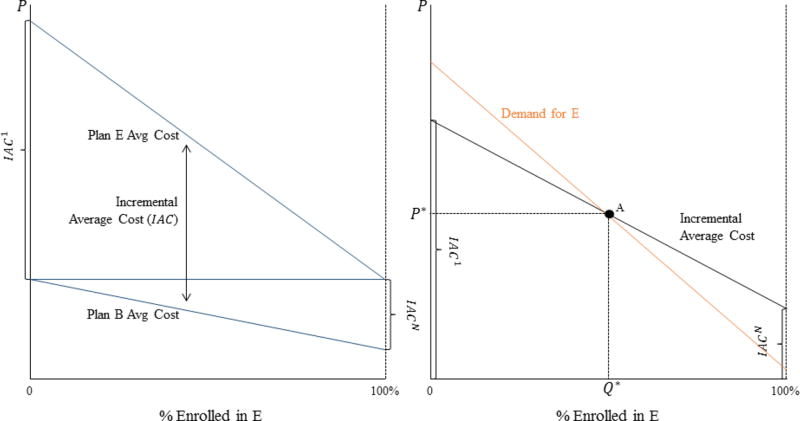
Figure 1 illustrates equilibrium prices and sorting under this model. This figure builds on the figures of Einav, Finkelstein, and Cullen (2010) by illustrating the equilibrium in a market where consumers choose between two plans with endogenous prices rather than a market where consumers choose between purchasing insurance and remaining uninsured. To simplify presentation, in the figure it is assumed that plans have identical benefits, i.e. cE (θi) = cB (θi)∀θi, and that willingness-to-pay for E is increasing in health risk, i.e. .12 In both panels of Figure 1, enrollment in E is increasing along the x-axis. The left panel shows how ACE (P) and ACB (P) change as enrollment in E increases. Both fall because the positive relationship between cost and willingness-to-pay for E implies that the marginal consumer enrolling in E is lower cost than E's enrollees and higher cost than B's enrollees. Recall that it is the difference between these two lines, the incremental average cost, that determines the equilibrium price differential, P. The relationship between enrollment in E and the IAC can be seen in the right panel of Figure 1. In the figure, the IAC is defined by the difference between the cost of the first consumer to enroll in E and the average cost of all other consumers, IAC1, on the left and the difference between the average cost of all consumers and the cost of the last consumer to enroll in E, IACN, on the right. The equilibrium in this setting occurs at Point A, where the demand curve crosses the IAC curve. This is where the sorting of individuals across plans induced by P results in P* = Δ AC (P*), the competitive equilibrium.13
Figure 1. Equilibrium Sorting with Adverse Selection.
Notes: In both panels, enrollment in Plan E is increasing along the x-axis, and the price differential is on the y-axis. The left panel describes the average cost of individuals enrolled in Plan E and Plan B as a function of enrollment in E. The difference between the lines defines the incremental average cost curve shown in the right panel. The right panel illustrates the equilibrium price differential and sorting where the demand curve crosses the incremental average cost curve. The figure illustrates the case where Plan E is adversely selected.
2.1 Risk Adjustment
To incorporate risk adjustment transfers into the model, I introduce the concept of adjusted costs. Risk adjustment transfers are based on individual-level characteristics and typically take the following form: ti = cAdj(ri) − c̄.14 Plans pay/receive ti when enrolling i. cAdj(ri) represents i’s adjusted cost, which is a function of i’s risk score, ri, and c̄ is the average cost among all enrollees in the market. The adjusted cost, cAdj(ri), is typically equal to .15 I define the “residual” cost for enrollee i in plan j to be equal to the difference between the total cost for enrollee i and the adjusted cost for enrollee i: .
In most markets, ri is calculated by multiplying a vector of predictors, Xi, known as “risk adjusters” by a vector of risk adjustment coefficients, β:
| (4) |
For demographic-based risk adjustment, Xi consists of a set of age-by-sex-cells. For diagnosis-based risk adjustment, Xi consists of age-by-sex cells and indicators for a set of clinical condition categories.16 The coefficients, β, are typically estimated via a linear regression of total spending, ci, on the risk adjusters, Xi, in a large health insurance claims dataset. Thus, ri is the linear projection of the risk adjusters on ex-post spending in the estimation dataset, and adjusted costs, cAdj(ri), are the dimensions of spending explained by the risk adjusters.17 Under the assumption of fixed contracts, with risk adjustment plan average costs are
| (5) |
| (6) |
Where is the average adjusted cost for the individuals enrolled in plan j: . This implies that the equilibrium price differential is
| (7) |
| (8) |
| (9) |
Where is the average residual cost for plan j. Also, let be the incremental average residual cost.
As before, reflects differences in the cost to Plan E from enrolling individual i and the cost to Plan B from enrolling the same consumer. This difference will be reflected in the incremental average residual cost because the residual cost is equal to the total cost minus the adjusted cost and enrollee i′s adjusted cost is the same no matter which plan she enrolls in. However, whereas before P* also reflected selection on total costs as reflected in the incremental average cost, reflects selection on residual costs only. The difference here is that the adjusted costs compensate the plans for some portion of the difference in total costs. I now turn to a series of graphical representations to provide intuition for how this difference affects equilibrium prices and sorting.
2.2 Risk Adjustment and Equilibrium in Pictures
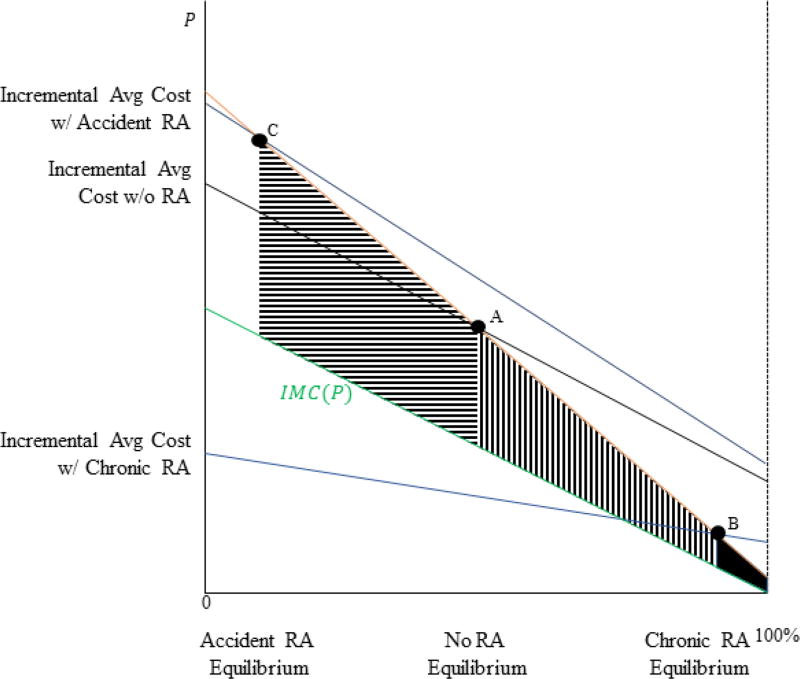
Consider a setting where medical spending can be decomposed into three components: Chronic spending (c), acute spending (a), and accident-induced spending (d). Denote this decomposition as ci = cc,i + ca,i + cd,i. Chronic spending can be thought of as spending that is persistent from year-to-year. An example might include treatment for diabetes. Acute spending, on the other hand, can be thought of as non-persistent spending stemming from some underlying health condition. Examples could include heart attacks or strokes. Finally, accident-induced spending is non-persistent and not related to underlying health status. Examples could include car accidents or sports injuries. This particular decomposition was chosen purely to illustrate the concepts described in Section 2.1.
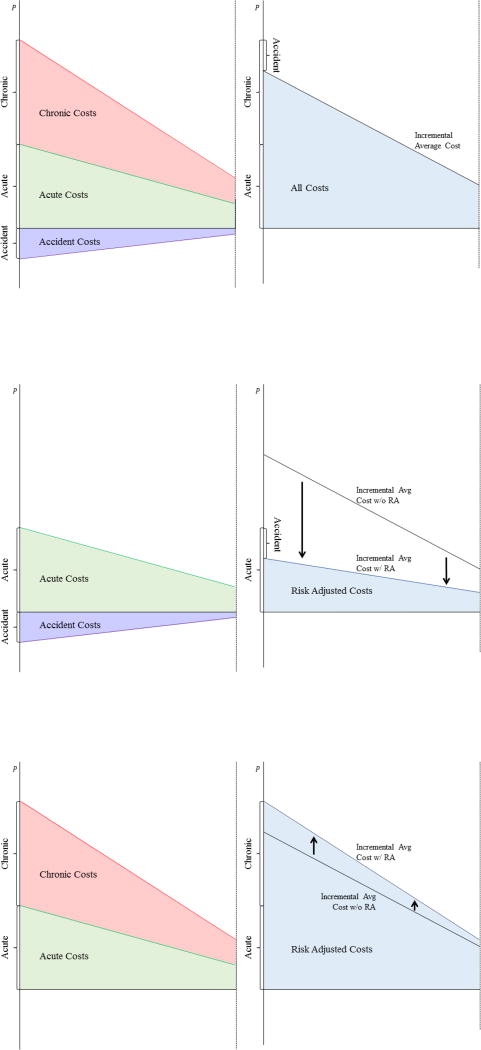
Assume that people with the highest chronic and acute spending exhibit the highest willingness-to-pay for E, but the people with the highest accident-induced spending exhibit the lowest willingness-to-pay for B.18 This could result in a situation like the one shown in the top panel of Figure 2. In the figure, enrollment in Plan E is increasing along the x-axis. The right panel duplicates the right panel of Figure 1, showing the incremental average cost curve. The left panel breaks the incremental average cost into the three components of total medical spending. At any given price, incremental average chronic and acute costs are positive, indicating higher costs in Plan E, but incremental average accident-induced costs are negative, indicating higher costs in Plan B. Incremental average total costs are the sum of the three components. Advantageous selection into E on accident-induced costs offsets a portion of the adverse selection into E on chronic and acute costs, resulting in the incremental average cost curve being lower than it would be without these costs.
Figure 2. Decomposition of Incremental Costs.
Notes: In all panels, enrollment in Plan E is on the x-axis, and the price differential is on the y-axis. The left panels decompose the incremental average cost into three dimensions: chronic, acute, and accident. The right panels show how these three dimensions combine to form the incremental average cost curve.
Recall that the incremental average cost with risk adjustment is equal to the incremental average residual cost: ΔACRA(P) = ΔACRes(P). Consider the following two cases. First, assume that the risk adjusters only predict chronic costs: . The middle panel of Figure 2 illustrates the effect of risk adjustment in this case. Chronic costs are eliminated from the total incremental average cost, and the new incremental average cost curve with risk adjustment is based only on acute costs and accident-induced costs. The right panel of the figure shows that in this case the incremental average cost curve is shifted down and the slope becomes less steep. Second, assume that the risk adjusters only predict accident-induced costs: . The bottom panel of Figure 2 illustrates the effect of risk adjustment in this case. Accident-induced costs are eliminated from the incremental average cost, and the new incremental average cost curve is based only on acute and chronic costs. The right panel shows that in this case risk adjustment causes the incremental average cost curve to shift upwards and become steeper.
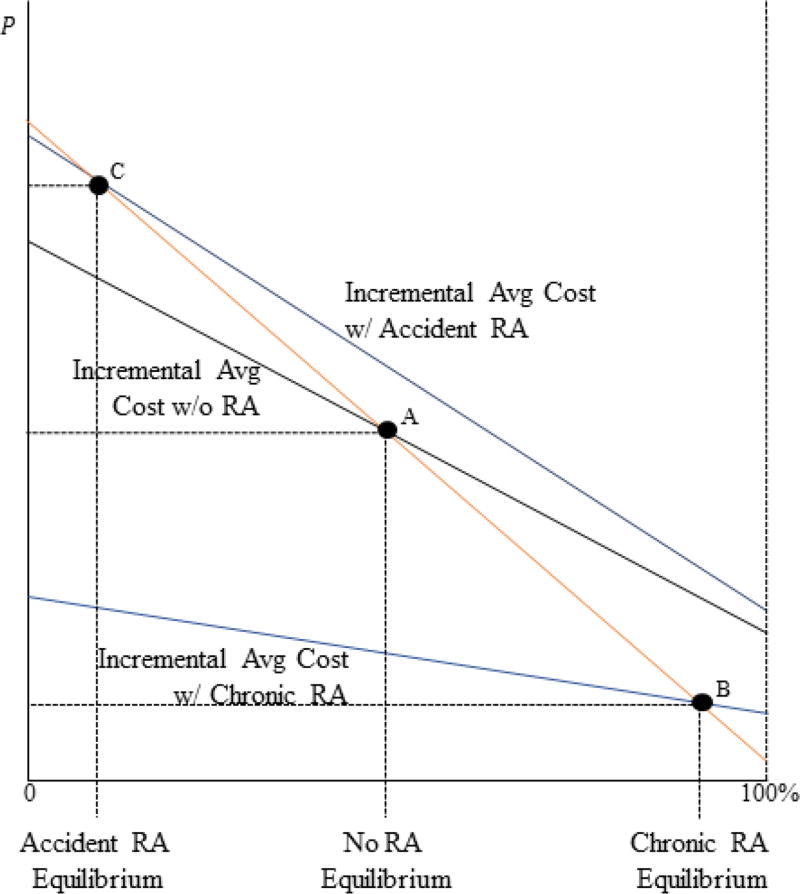
Figure 3 illustrates the effects of risk adjustment on equilibrium sorting and prices. The figure includes three incremental average cost curves. The middle curve represents the case with no risk adjustment. The bottom curve represents Case 1, where the risk adjusters predict chronic costs. The top curve represents Case 2, where the risk adjusters predict accident-induced costs. For each case, the equilibrium occurs where the relevant incremental average cost curve crosses the demand curve. With no risk adjustment, equilibrium occurs at Point A. For Case 1 (Case 2), equilibrium occurs at Point B (C). When risk scores predict chronic costs, risk adjustment increases enrollment in Plan E and decreases the incremental price, and when risk scores predict accident-induced costs, risk adjustment decreases enrollment in Plan E and increases the incremental price. The heterogeneous effects of risk adjustment are due to differences in the relationship between demand and adjusted costs under the different payment systems. If E is adversely selected on the risk score (marginal E enrollees have lower risk scores than average E enrollees; middle panel of Figure 2) then risk adjustment increases enrollment in E. However, if E is advantageously selected on the risk score (marginal E enrollees have higher risk scores than average E enrollees; bottom panel of Figure 2) then risk adjustment decreases enrollment in E, even if E is adversely selected on total costs.
Figure 3. Equilibrium under Various Risk Adjustment Policies.
Notes: In the figure, enrollment is on the x-axis and the price differential is on the y-axis. The figure shows the incremental average cost curve in three settings: no risk adjustment, risk adjustment where adjusted costs equal accident costs, and risk adjustment where adjusted costs equal chronic costs. The equilibrium in each setting occurs where the orange demand curve crosses the incremental average cost curve. The figure illustrates the three equilibria.
2.2.1 Relationship between Adjusted Costs and Demand
The figures and the model show that risk adjustment can either increase or decrease enrollment in the adversely selected plan (E), depending on the relationship between adjusted costs and demand. This relationship merits further discussion. The relationship is a function of two factors. First, it depends on which dimensions of medical spending are captured by the risk score. This is a choice of the regulator. Second, it depends on the relationships between the captured dimensions of spending and willingness-to-pay for E. These relationships are behavioral parameters that depend on how the plans in the market are differentiated.
To see how risk adjustment will affect sorting in the Health Insurance Marketplaces created by the ACA, consider the two choices made by consumers in the Marketplaces. First, consumers choose a plan tier. Across tiers, plans are differentiated by cost sharing. Consumers will choose a tier based on their predicted out-of-pocket spending and risk preferences. Thus, the relationship between willingness-to-pay for higher tiers and a particular dimension of spending is likely to be related to the predictability of the dimension of spending and the relationship between that dimension and risk aversion. For dimensions of spending that are highly predictable, demand is likely to be increasing in spending. For dimensions of spending that are fairly unpredictable, the relationship with demand will depend more on the relationship between the dimension of spending and risk aversion. For these less predictable dimensions, the directions of the relationships between willingness-to-pay and spending are ambiguous and likely to be relatively weak. The case of accident-induced spending explored in the figures above represents an example of such a dimension.
The second choice made by consumers is the choice of a plan within a tier. Within a tier, plans are differentiated mostly by their provider networks. As above, assume there are two plans, E and B. Plan E includes a prestigious hospital, and Plan B does not. Willingness-to-pay for access to the prestigious hospital is heterogeneous, though overall higher-spending consumers exhibit higher demand for access to the hospital. In this case, the relationship between a particular dimension of medical spending and willingness-to-pay for E is not necessarily related to the predictability of the dimension of spending. Instead, the relationship depends more strongly on the relationship between the dimension of spending and a consumer's preference for access to the prestigious hospital. The direction and strength of these relationships between preferences for access to the hospital and individual dimensions of medical spending are unknown and could vary greatly across dimensions of spending. It could easily be the case that a risk adjustment model that is optimized to undo adverse selection across tiers may exacerbate selection problems within a tier. Indeed, Shepard (2016) provides evidence that in the Massachusetts subsidized Marketplace, willingness-to-pay for a plan that includes a prestigious academic medical center is highly correlated with dimensions of spending not explained by the chronic-disease risk adjusters used in that market. Additionally, Cabral, Geruso, and Mahoney (2014) provide evidence that in Medicare in the early 2000s the marginal MA enrollees were less costly but had higher risk scores than average TM enrollees, implying that MA was advantageously selected on total costs but adversely selected on adjusted costs on the margin, similar to the setting depicted in the bottom panel of Figure 2. This suggests that risk adjustment actually decreased enrollment in the adversely selected plan (TM) and increased enrollment in the advantageously selected plan (MA), the opposite of the intention of the program.
Due to the endogeneity and manipulability of many potential risk adjusters, the regulator's choice of which risk adjusters to include in a payment system necessarily consists of a cost-benefit analysis of each individual risk adjuster. The costs consist of distortions due to “upcoding” as well as any endogeneity between plan spending and plan payment that reduces the plan's incentives to constrain costs (Geruso and Layton 2015, Geruso and McGuire 2016). The benefits consist of limiting the consequences of adverse selection as shown here. The model and the figures suggest that for the case of across-tier adverse selection, risk adjusters that explain the more predictable dimensions of spending from the consumer's point of view will have the largest benefit because they will result in consumers with high levels of demand for more comprehensive coverage having high risk scores. This is the intuition behind the use of indicators for chronic conditions in most risk adjustment models. For the case of within-tier adverse selection, on the other hand, the largest benefit will come from risk adjusters that are related to dimensions of spending that are correlated with demand for wider choice of providers or for prestigious hospitals. It is difficult to know ex ante what those dimensions of spending are. More generally, if the regulator desires to increase enrollment in adversely selected plans, she should focus on selecting risk adjusters that produce larger risk scores among consumers who exhibit high levels of demand for those plans rather than focusing on selecting risk adjusters that are most highly correlated with total spending.
2.3 Efficiency
The model and figures show that if Plan E is adversely selected on adjusted costs, then risk adjustment will result in higher enrollment in Plan E. However, higher enrollment in E is not necessarily efficient in all cases. Efficiency requires that a consumer enroll in Plan E if and only if her willingness-to-pay for Plan E over Plan B exceeds the incremental marginal cost of enrolling her: Δν(θi, εi) ≥ Δc(θi) = cE (θi) − cB (θi). Risk adjustment does not affect the efficiency criteria. The social cost of enrolling consumer i in plan j is invariant to any transfers across plans: The social cost of consumer i choosing Plan E will always exceed the social cost of i choosing B. Risk adjustment just changes how those costs are distributed across plans in the market and, thus, the prices plans charge.
Individuals sort across plans according to their willingness-to-pay, Δν(θ, ε). At the same time, efficiency requires them to sort according to their incremental marginal cost, . It is important to note that in this environment whether there is risk adjustment or not there is only one tool to induce sorting, and thus affect welfare: the incremental price, P. Risk adjustment affects efficiency by altering the equilibrium value of P, thus causing market participants to re-sort across plans. As shown above, the extent and direction of this re-sorting depends on the relationship between willingness-to-pay for E and adjusted costs. The welfare consequences of this re-sorting, on the other hand, depend on the joint distribution of Δν(θi, εi) and Δc(θi).19
The special case Δc(θi) where and demand vary linearly with P (i.e. no preference heterogeneity) is shown in Appendix Figure A1, where the relationship between Δc(θi) and demand is represented by the green incremental marginal cost curve, IMC(P). In this case, the welfare loss from adverse selection with no risk adjustment is described by the combination of the solid black area and the vertically striped area. With risk adjustment where risk scores capture chronic spending, the remaining welfare loss from adverse selection is described only by the solid black area, implying a large welfare improvement from risk adjustment. However, with risk adjustment where risk scores capture accident-induced costs, the welfare loss from adverse selection is described by the combination of the three shaded areas, implying a large welfare loss from risk adjustment.20
In the figure (and in the empirical case studied below), the incremental marginal cost curve is everywhere below the demand curve, implying that it is optimal for the entire market to enroll in Plan E. In reality, however, a variety of factors such as moral hazard or preference heterogeneity can result in the incremental marginal cost curve crossing the demand curve. When this occurs, the welfare consequences of risk adjustment are even more ambiguous, as risk adjustment could result in “too many” individuals enrolling in the more comprehensive plan (see Einav and Finkelstein 2010).
3. Data and Setting
For the empirical analysis, I use administrative health insurance claims data from a large employer in the Truven Marketscan Database from 2006–07.21 During this period, the firm offered its employees a choice of two PPO plans: a basic plan (Plan B) and a more comprehensive, enhanced plan (Plan E). These plans differ only in cost sharing, and the contracts did not change between 2006 and 2007. The cost-sharing rules for each plan are found in the left columns of Table 2. For non-ER medical spending, Plan E has a lower deductible, coinsurance rate, and out-of-pocket maximum. With respect to medical spending from ER visits and prescription drug spending, cost sharing is identical in the two plans.22 The only differences between the plans are the cost sharing parameters for medical spending and the plan premiums. Unfortunately, neither the premiums nor the employee contribution to the premiums are available in the data. Because the employee contribution is a critical piece of the empirical model described below, I follow Kowalski (2015) and Geruso (2016) and estimate the contribution from the data. I discuss the estimation process in the Section 4.2.1.
Table 2.
Cost-sharing Parameters for Firm and Simulation Plans
| Firm | Simulations | |||
|---|---|---|---|---|
| Basic | Enhanced | Bronze | Platinum | |
|
|
||||
| Deductible | 500 | 300 | 4500 | $0 |
| Coinsurance | 20% | 10% | 20% | 20% |
| OOP Max | 4750 | 2600 | 6500 | 1500 |
| Drug copay | Generic = $10 Brand=$5 | Generic = $10 Brand=$5 | Included in medical deductible, coinsurance, OOP max | |
Notes: Table shows cost-sharing parameters for plan options at the firm and for plan options in the Marketplace simulations. Firm parameters are used to create fij (OOP) for estimation of the choice model, simulation parameters are used to create fij (OOP) for Bronze and Platinum plans in the simulations. Under all plans, consumers pay the full cost of care up to the deductible, then they pay the coinsurance rate up to the out-of-pocket max. Beyond the out-of-pocket max, the consumer pays nothing. For the firm plans, drug coverage is not part of the price schedule, but coverage is identical in the two plans. For the simulations, drug spending is included with other medical spending in the non-linear price schedule. In the firm plans, ER visits and preventive visits are free of charge, but these visits make up only a small portion of total medical expenditures, so they considered to be priced with other medical spending.
Around 50,000 employees enrolled in these plans during the time period, along with 76,000 dependents. For all individuals in the data, I observe their plan choice and administrative health insurance claims for each year during which they enroll in a plan. As is common in this type of data, I do not observe employees who choose not to enroll in a plan. In order to simplify estimation, I limit the sample in the following ways. First, I include only employees who enroll no dependents. This permits me to avoid making assumptions about the (unobserved) family structure of the employee contribution to the premium. Second, I limit the sample to employees who are continuously enrolled throughout the sample period.23
The left columns of Table 1 show observed characteristics of the employees in the sample. The Marketscan database includes minimal demographic information about the employees. The average age among the employees in my sample is around 41, and 60% of the employees are male. About 8% of the sample is defined as “new” employees, meaning they were not enrolled in a plan during 2006. The average total annual health care costs among the employees in the sample is around $3,900.
Table 1.
Summary Statistics
| Estimation Sample | Cost Model Sample | Simulation Sample | ||||
|---|---|---|---|---|---|---|
|
|
||||||
| Full sample |
Incumbent Employees |
New Employees | ||||
|
|
||||||
| Male | 0.6 | 0.6 | 0.67 | 0.49 | 0.6 | |
| New | 0.08 | n.a. | n.a. | n.a. | n.a. | |
| Age: | ||||||
| mean | 41.16 | 41.61 | 35.95 | 34.98 | 41.5 | |
| 1st Pcntl | 21 | 22 | 20 | 1 | 22 | |
| 25th Pcntl | 32 | 32 | 26 | 17 | 32 | |
| 50th Pcntl | 45 | 42 | 34 | 38 | 42 | |
| 75th Pcntl | 50 | 50 | 46 | 51 | 50 | |
| 99th Pcntl | 62 | 62 | 61 | 63 | 62 | |
| Total costs: | ||||||
| mean | $3,875.44 | $3,998.5 | $2,422.19 | $3,631.99 | $3,792.1 | |
| 1st Pcntl | $0 | $0 | $0 | $0 | $0 | |
| 5th Pcntl | $0 | $0 | $0 | $0 | $0 | |
| 25th Pcntl | $73 | $90 | $0 | $174.89 | $85 | |
| 50th Pcntl | $857 | $910 | $368 | $802.84 | $900 | |
| 75th Pcntl | $3,016 | $3,136 | $1,811 | $2,885.19 | $3,109 | |
| 95th Pcntl | $15,789 | $16,167 | $9,019 | $13,906.53 | $15,097 | |
| 99th Pcntl | $52,385 | $53,019 | $28,672 | $43,720.05 | $47,342 | |
| Expected costs: | ||||||
| mean | $3,959.34 | $4,028.07 | $3,147.69 | n.a. | $3,804.45 | |
| 1st Pcntl | $317.64 | $332.65 | $283.52 | n.a. | $29.42 | |
| 5th Pcntl | $479.48 | $496.89 | $354.11 | n.a. | $65.83 | |
| 25th Pcntl | $1,073.26 | $1,111.25 | $757.62 | n.a. | $780.63 | |
| 50th Pcntl | $2,071.85 | $2,132.63 | $1,461.67 | n.a. | $1,792.84 | |
| 75th Pcntl | $4,119.02 | $4,207.45 | $3,041.46 | n.a. | $3,932.96 | |
| 95th Pcntl | $12,201.57 | $12,368.52 | $9711.7 | n.a. | $12,600.92 | |
| 99th Pcntl | $30,161.83 | $30,407.75 | $22,785.8 | n.a. | $33,447.02 | |
| Total cost risk scores: | ||||||
| mean | 0.91 | 0.93 | 0.71 | 0.89 | 0.92 | |
| 1st Pcntl | 0.15 | 0.15 | 0.15 | 0.1 | 0.15 | |
| 5th Pcntl | 0.18 | 0.18 | 0.15 | 0.14 | 0.18 | |
| 25th Pcntl | 0.31 | 0.33 | 0.23 | 0.27 | 0.32 | |
| 50th Pcntl | 0.53 | 0.55 | 0.38 | 0.51 | 0.54 | |
| 75th Pcntl | 0.98 | 1 | 0.77 | 0.99 | 1.01 | |
| 95th Pcntl | 2.65 | 2.73 | 2.13 | 2.59 | 2.74 | |
| 99th Pcntl | 6.19 | 6.28 | 4.5 | 5.87 | 6.18 | |
|
| ||||||
| N | 9,133 | 8,420 | 713 | 12,177,930 | 25,398 | |
Notes: Summary statistics for Estimation Sample, Cost Model Sample, and Simulation Sample. All samples come from Truven Marketscan dataset from choice years 2006–08. Estimation and Simulation Samples are from one large firm in Marketscan dataset where employees choose between 2 PPO plans. Samples are restricted to single-coverage employees enrolled for all 365 days of the year prior to and year of plan choice to ensure that costs can be predicted using full set of information. Estimation sample is restricted to employees from choice year 2007. Cost model sample is formed by first taking all individuals in Marketscan during at least 300 days of both 2006–2007. Expected costs calculated by finding mean of the estimated cost distribution. Expected costs are not shown for the cost model sample because the purpose of the cost model sample is to generate the expected cost distributions for the other samples.
4. Empirical Model
Three variables are required to simulate equilibrium prices and sorting under risk adjustment: individual preferences, total costs and adjusted costs. As shown in the model in Section 2, preferences are necessary in order to determine which plan each consumer will join under a given price, and total costs and adjusted costs are required in order to estimate plan costs under a given allocation of consumers across plans. In this section, I discuss how I recover the joint distribution of these three variables.
4.1 Total Costs and Adjusted Costs
Because the data include the universe of health insurance claims for each individual in the sample, total costs under each employee's chosen plan are observed. I assume that total costs are invariant to plan choice (i.e. no moral hazard). This assumption is common in this literature and not unreasonable in this setting where the two insurance contracts are fairly similar (see Handel (2014), Handel, Hendel, and Whinston (2015), Handel and Kolstad (2015), and Geruso (2016)).
I calculate each individual's adjusted costs using the same methods used by regulators. Under standard risk adjustment policies, adjusted costs are a linear function of individuals' risk scores and the average cost in the population. Risk scores are assigned using the following formula:
Ri represents person i’s “raw” risk score; Xi represents a vector of “risk adjusters,” or variables that predict an individual’s spending; and β represents a vector of risk adjustment coefficients, estimated via linear regression using a large sample of individual health insurance claims. R̄ and represent the average raw risk score and the average product of X and β, respectively. Different risk adjustment models use different groups of variables. The risk adjustment models used in the policies I simulate in Section 5 include dummy variables for age-by-sex cells and a set of indicators for chronic conditions called Hierarchical Condition Categories (HCCs). HCCs are based on diagnoses found in health insurance claims. When the diagnoses are from the prior (current) year, the model is referred to as a “prospective” (“concurrent”) model. Details about these models can be found in Appendix A.1.
For each individual in the sample, I use software provided by CMS to map the diagnoses found in an individual's health insurance claims to HCCs and to combine HCCs with the pre-estimated coefficients, β, to generate risk scores. I then use the risk scores to generate adjusted costs by multiplying the normalized risk score times the average cost in the population, , as described in Section 2.2.24 This definition of adjusted costs relies on the subtle but important assumption that individuals would receive the same diagnoses in a setting with or without risk adjustment.25
4.2 Preferences
Unlike total costs and adjusted costs, preferences are unobserved and must be estimated. Conceivably, preferences (i.e. willingness-to-pay) could be estimated by observing how employees respond to an exogenous shift in plan prices (Einav, Finkelstein, and Cullen 2010). However, in my data prices are constant across individuals, so I specify a structural model of consumer demand for health insurance to estimate preferences using a method similar to that used in Handel (2014) and Geruso (2016). The sole purpose of this model is to allow me to extract estimates of consumer willingness-to-pay for the enhanced plan relative to the basic plan, a necessary parameter for the counterfactual simulations I perform below of markets with and without risk adjustment. While this method has its drawbacks, it provides a reasonable way to estimate consumer willingness-to-pay. I start by assuming that employees value plans based on the following von-Neuman Morgenstern expected utility function:
Four variables enter into the employee’s utility function: the employee's distribution of expected out-of-pocket costs if enrolled in plan j, fij(OOP); wealth, Wi; the premium, Pj; and an indicator for whether employee i was enrolled in plan j during the previous period, 1[jit = ji,t−1]ijt. The remaining factor affecting individual choice is the shape of ui. I assume that employees’ preferences follow the following constant absolute risk aversion (CARA) utility function where xij represents employee i’s consumption under plan j:
The shape of each employee’s CARA utility function is defined by her coefficient of absolute risk aversion, γi, with larger values of γi implying higher levels of risk aversion. I define employee consumption, xij, as
Consumption is a function of initial wealth, the premium, expected out-of-pocket costs, a switching cost incurred if the employee chooses a different plan in year t than in year t − 1, and an i.i.d. preference shock, εijt, with mean με and variance .26 Because the two plans available to the employees of the firm vary only in their financial characteristics, I argue that this specification comes quite close to fully characterizing employee choices, though there are a number of reasons why the model may produce preference estimates that incorporate non-welfare-relevant features, which I discuss in Section 4.2.5 below. With all of the components of this model, I can determine each employee's choice of plan under different levels of the price differential, P, from the model above. This will allow me to back out each individual's willingness-to-pay for Plan E relative to Plan B. As most of the components of the model are unobserved, they require some form of estimation. I now discuss how I estimate each component.
4.2.1 Plan Premiums: Pj
In the dataset the employee contribution to the premium is not observed. To estimate the contribution, I recognize that most employers follow a simple pricing rule based on the average cost of individuals enrolled in a plan during the prior year (see Handel (2013) and Geruso (2016)). I assume that for the firm I study, the premium for employees without dependents is equal to the average cost among the employees without dependents enrolled in the plan during the prior year plus some loading factor, . I calculate using the claims data from the prior year. I then assume that the employer sets the employee contributions equal to 20% of the full premium of each plan (Kaiser Family Foundation 2013). Note that for estimation of the choice model it is not important for the premiums of each plan to be accurately estimated. Instead, it is just important that the premium differential P be correct. Given the assumptions, I estimate this premium differential as:
To address the possibility Pt that is incorrectly estimated, I also include a plan specific intercept for Plan E in xij. Because all individuals pay the same prices, this intercept will capture both any idiosyncratic preference for Plan E and any bias in the estimate of P.
4.2.2 Switching Costs: ηi
There is extensive empirical evidence that individuals face substantial switching costs when choosing to move between health plans (Sinaiko and Hirth 2011, Handel 2013, Polyakova 2015). There are many reasons for this phenomenon such as the time and hassle costs of researching a new plan, attachment to a network of providers, or just pure inattention or laziness.27 Here, the source of the switching cost is unimportant. It is included in the model to allow me to estimate consumer preferences when facing an active choice of health plans, the setting I will simulate in Section 5, as opposed to a passive choice of health plans, the setting I observe for most of the employees in the employer data. In order to separately identify switching costs, η, from persistent heterogeneity in preferences captured by γ, I follow Handel and Kolstad (2015) by exploiting the fact that some employees in the data were not previously enrolled in a plan. While I do not observe why these enrollees are enrolling for the first time, I know that they should not face a switching cost when making their choice. To account for observable differences between “new” and “incumbent” enrollees, I allow η to vary with observable demographic characteristics. Specifically, I assume that
Effectively, I compare the choices of new and incumbent enrollees with similar demographics to estimate the switching costs. The important assumption here is that, conditional on age and gender, new and incumbent enrollees are similar with respect to unobserved variables that affect both risk preferences and switching costs.
4.2.3 Out-of-Pocket Cost Distributions: Fij(OOP)
Estimation of the expected utility model requires an estimate of each employee’s distribution of expected out-of-pocket costs in each plan, Fij(OOP). I construct this distribution directly from a larger sample of administrative health insurance claims from the Marketscan Database. I refer to this sample as the cost model sample. Summary statistics for this sample are found in Column 4 of Table 1, and I describe it in detail in Appendix A.2. I divide the individuals in this sample into cells where all individuals in a cell had similar health status in year t − 1. The cells are based on predictive measures of each individual’s health care cost risk generated by sophisticated predictive modeling software developed by Verisk Health and used by health insurers and large employers to predict the costs of their enrollees.28 The software uses information such as diagnoses and utilization found in insurance claims data from year t − 1 to generate predictions of individual spending in year t, λi. These predictions differ from the predicted spending implied by the risk adjustment risk scores. The risk adjustment risk scores are based only on information about a subset of diagnosis groups and demographics. λ is based on the entire set of information available in the health insurance claims. This includes past utilization, spending, and information on diagnosis groups beyond those used to generate the risk adjustment risk scores. This implies that λ includes some portion of the “private information” that individuals possess about their future spending that is not accounted for by the risk adjustment model.
In order to ensure that the estimate of each employee's cost distribution is as precise as possible, I split the large sample of claims into 500 cells based on λ. To ease computation, I take a random sample of 1,000 individuals from each λ cell. For each cell, I fit a log-normal distribution with a point mass at zero to the actual medical spending of the individuals in the cell in year t and allow the log-normal parameters to vary with age and gender. The log-normal parameters plus the point mass at zero fully describe the estimates of each employee's distribution of expected total medical costs. I then use the simple cost-sharing rules for each plan to map each employee's expected total medical spending to expected out-of-pocket costs to form Fij(OOP).29
To construct Fij(OOP), I use the larger cost model sample of claims rather than the smaller sample including only the employees of the firm I study because there is a trade-off between cell size and the number of cells. With a larger number of cells I capture more of the private information about individuals’ future costs. However, larger cells necessarily imply fewer individuals in each cell, resulting in less accurate estimation of the parameters describing Fij(OOP). Using the larger cost model sample avoids this trade-off by increasing the total number of individuals in the sample. The cost of using the cost model sample rather than just using the claims of the employees of the firm I study to estimate Fij(OOP) is the requirement of an additional assumption: Individuals in the cost model sample and the choice model sample are similar with respect to any relevant variables not used to form the cells. Given the large amount of sophisticated information (i.e., λ) used to form the cells and the large number of cells, I argue that this assumption is reasonable. Additionally, in Table 1 I show that the range of risk scores is similar for the cost model and estimation samples, implying that there are similar individuals in the samples. Table 1 also shows that for the estimation and simulation samples the average expected cost produced by the cost model is quite similar to the average realized cost among employees in the sample, implying that the estimates are unlikely to be systematically biased.
4.2.4 Risk Preferences: γi
Each employee's coefficient of absolute risk aversion, γi, is the final component of the choice model. I estimate this parameter as follows: Because the two plans available to the employees in my sample differ only in cost sharing and premiums, if the employees are all risk neutral and Fij(OOP) and Pj are known, their optimal choices can easily be recovered by calculating the mean of each employee’s distribution of expected out-of-pocket costs in each plan, adding that mean to each plan’s premium, and then comparing the two sums. Whichever plan has the lower total cost (premium plus out-of-pocket costs) would be the optimal choice. Call this choice the risk-neutral optimal choice. The intuition behind the identification of γi is that under the assumption that Fij(OOP) is observed, an employee’s deviation from the risk-neutral optimal choice describes her level of risk aversion (Cohen and Einav 2007). For example, if an employee faces a higher total cost in Plan B than in Plan E, but she chooses Plan E anyway, she must be risk averse, and the size of the cost difference identifies the extent of her risk aversion. This method is also used by Handel (2013) and Geruso (2016).
To ensure the joint distribution of demand, total costs, and adjusted costs is fully characterized, I allow γi to vary with a set of demographic variables, Yi, along with a set of variables, Zi, related to an employee's health risk, including total ex-post realized costs, ci, as well as risk adjustment risk scores, ri, to capture any correlation between preferences and adjusted costs. Specifically, I assume that γi can be described as follows:
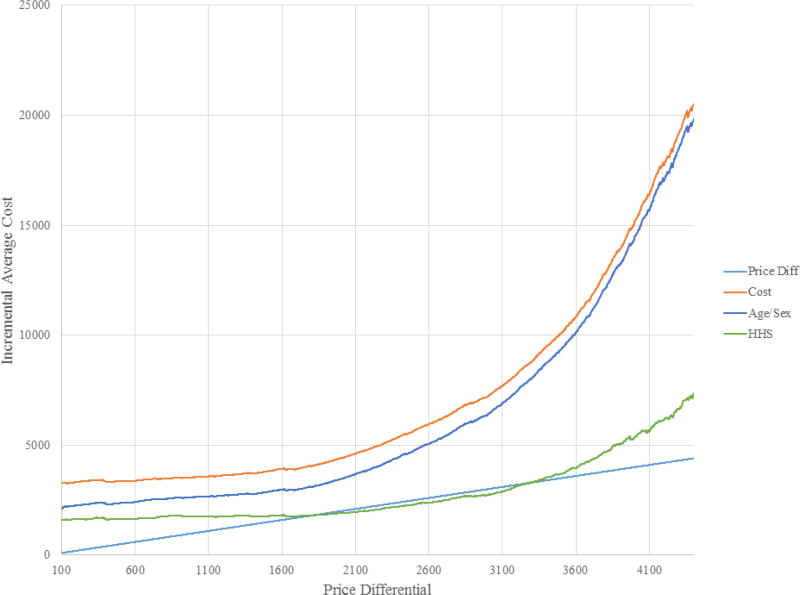
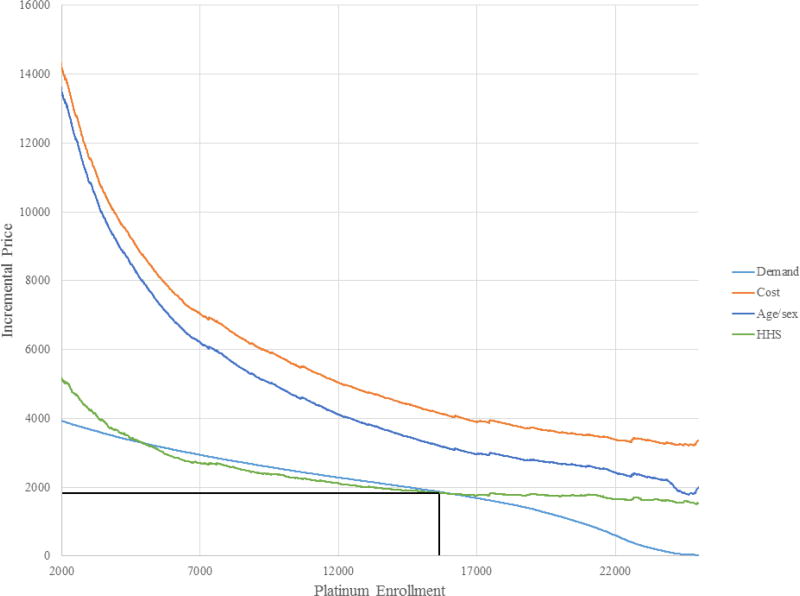
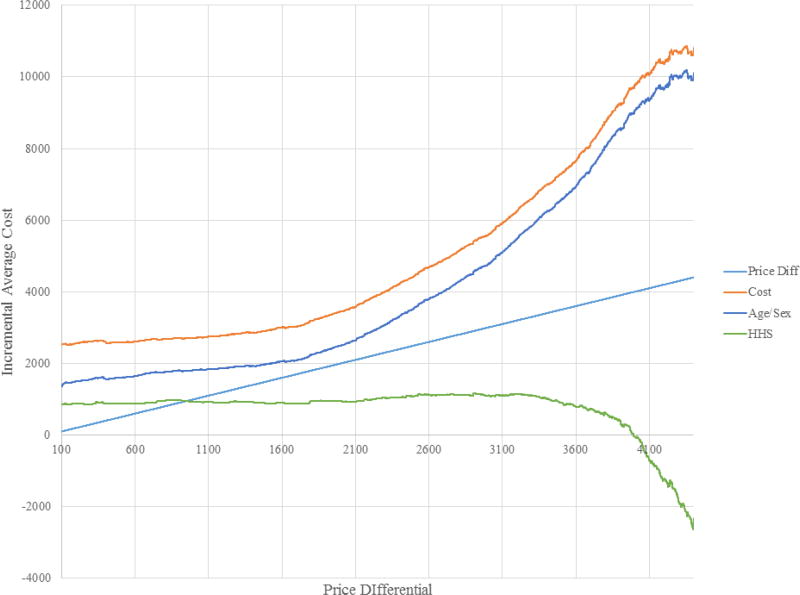
Allowing γi to vary with ci is motivated by previous research that has shown that the correlation between risk preferences and cost risk can influence the degree and direction of selection in equilibrium (see Finkelstein and McGarry (2006), Cohen and Einav (2007), and Handel, Hendel, and Whinston (2015)). The inclusion of ri in the risk preference equation is motivated by the graphical analysis above. Recall that the equilibrium consequences of risk adjustment depend on the relationship between demand and adjusted costs. Thus, in order to accurately simulate equilibrium prices and sorting under risk adjustment, it is critical that the model fully captures this relationship. Because demand is a function of γi, it is necessary to allow γi to vary by the risk scores that determine adjusted costs. In fact, if this relationship is not allowed for in the estimation of γi, the counter-intuitive situation illustrated in Figure 4 where risk adjustment results in a larger price differential and fewer individuals enrolling in Plan E would be missed in the simulations.
Figure 4. Equilibrium Search.
Notes: Figure shows search for equilibrium in setting where sample individuals required to choose between Bronze and Platinum Plans. Light blue line is the 45-degree line. Orange line represents incremental average cost (IAC) curve with no risk adjustment, blue line represents IAC with demographic risk adjustment, gray line represents IAC with prospective risk adjustment, gold line represents IAC with concurrent risk adjustment, and green line represents IAC with HHS-HCC risk adjustment. IAC with no and demographic risk adjustment is everywhere above 45-degree line implying complete market unraveling where everyone enrolls in Bronze plan. Prospective, concurrent, and HHS risk adjustment IACs cross 45-degree line, implying an interior equilibrium exists. Equilibrium is at lowest P where IAC crosses 45-degree line. Concurrent results in the lowest price differential. Prices, enrollment, and welfare can be found in Table 4.
4.2.5 Limitations
While this demand specification characterizes the choices of consumers quite nicely, it does rely on a few important assumptions. First, I assume that when making their choices between the two plans, employees are using the same distribution of expected out-of-pocket costs that I assign to them. While it is possible that individuals know more than what I am able to predict, it is unlikely that they know much more. On the other hand, it is also possible that individuals know much less than the model suggests. To deal with this problem, I perform two sets of robustness checks using alternative specifications of Fij(OOP). In the first set of robustness checks, I test the sensitivity of my results to forming Fij(OOP) using 50 or 1000 cells based on λi instead of 500. In the second set, I allow consumers to have private information by forming a new distribution of expected costs, Gij(OOP) = α oopij + (1 − α)Fij(OOP), where oopi is i’s out-of-pocket cost in plan j based on i’s actual realized costs. I set α equal to .05, .10, .15, .20, and .25.
This still leaves open the possibility that rather than just using limited information in a rational manner, individuals actually use sophisticated information but they do so irrationally. There is evidence for this type of behavior (Abaluck and Gruber 2011, Handel and Kolstad 2015). It is important to note, however, that “mistakes” will likely at least partially be captured as risk preferences in this model. This is not a problem for using the joint distribution of demand, total costs, and adjusted costs to simulate competitive equilibria with and without risk adjustment. However, it does present a problem for inference about the welfare consequences of risk adjustment because the area below the demand curve and above the incremental marginal cost curve may not actually represent consumer surplus (Handel, Kolstad, and Spinnewijn 2016).
4.2.6 Model Estimation and Results
I estimate the parameters of the model using a simulated maximum likelihood approach similar to the method used by Handel (2014) and Geruso (2016) and outlined in Train (2009). Details of the estimation procedure can be found in Appendix A.3. Table 3 presents the results of the estimation procedure. The estimates of the coefficient of absolute risk aversion are similar to estimates in the health insurance literature (Handel 2013; Geruso 2016). The average estimate of this parameter in the sample is 6.3*10−4. To aid interpretation, this level of risk aversion implies that the average employee in the sample would be indifferent between the status quo and a gamble where she will win $100 or lose $94 with equal probability. Perhaps more importantly, the estimates imply that risk aversion is negatively correlated with total costs, negatively correlated with prospective risk adjustment risk scores, and positively correlated with concurrent risk adjustment risk scores.30 If taken literally, this implies that controlling for the risk scores, employees with high levels of total spending have lower levels of risk aversion. This result is similar to the finding of Handel, Hendel, and Whinston (2014) and is consistent with the notion of the “worried well.”
Table 3.
Choice Model Results
| Parameter Estimate | Parameter Std Error | |
|---|---|---|
| Enhanced Shifter | −178.22 | 34.87 |
| Switching Cost - Intercept | 1585.74 | 407.39 |
| Switching Cost - Age Coeff | 21.91 | 12.84 |
| Switching Cost - Fem Coeff | −359.24 | 258.70 |
| CARA - Intercept | 1.0* 10−3 | 1.7*10−4 |
| CARA - Log expend | −3.2*10−5 | 1.7*10−5 |
| CARA - Age Coeff | −8.4*10−6 | 3.9*10−6 |
| CARA - Age*Log expend | 4.2*10−7 | 3.5*10−7 |
| CARA - Fem Coeff | 2.3*10−5 | 6.4*10−5 |
| CARA - Pros Risk Coeff | −3.1*10−5 | 2.1*10−5 |
| CARA - Conc Risk Coeff | 2.7*10−6 | 1.5*10−5 |
| Preference Shock - Std Dev | 20.07 | 231.50 |
| Mean CARA | 6.3* 10−4 | |
| Median CARA | 6.2*10−4 | |
| Mean Switching Cost | 2424.70 | |
| Median Switching Cost | 2418.24 |
Notes: Results from simulated maximum likelihood estimation of choice model described in the paper. Enhanced shifter is a plan-specific intercept for the Enhanced Plan. Switching costs are estimated by comparing the choices of switchers and those of new enrollees of similar age and gender. CARA intercept represents the coefficient of absolute risk aversion for a zero year-old with total predicted cost and risk adjustment risk scores of zero. Log expend coefficient describes how CARA parameter varies with the log of total realized costs. Pros and conc risk coefficients describe how CARA parameter varies with risk adjustment risk scores. Mean CARA parameter implies that average individual in the sample would be indifferent between the status quo and a lottery that offered $100 with 50% probability and $95 with 50% probability.
The average estimated switching cost is close to $2,500. While this is quite large, it is consistent with other estimates in the literature (Handel 2013, Handel and Kolstad 2015). To put this estimate in context, this implies that consumers are willing to forgo savings of around 60% of average health care costs in the sample in order to remain in their current plan. Such large switching costs imply that simulations of active and passive choices will produce substantially different results, making it critical for me to estimate this parameter separately from employee risk aversion.
5. Counterfactual Simulations
In order to simulate competitive equilibria with and without risk adjustment, I first expand the sample to form a new simulation sample. The simulation sample includes all single-coverage employees from 2005–07, rather than only the employees enrolled in 2006–07. The sample is restricted in the same ways as the choice model sample described above (i.e. must be enrolled for all 365 days of the year, etc.). For this sample, total costs and risk scores for each individual are calculated or estimated as described in Section 4. Summary statistics for this simulation sample can be found in the final column of Table 1.
I simulate competitive equilibria with and without risk adjustment in an environment similar to the state and federal Health Insurance Marketplaces created by the ACA. Specifically, each individual is required to choose either a Bronze plan or a Platinum plan where the two plans are vertically differentiated in that they only differ in cost sharing and premiums. The Platinum plan is much more comprehensive than the Bronze plan. Plan cost sharing is described by standard non-linear price schedules where individuals pay the full cost of all care received up to a deductible, then some portion of each additional dollar of care up to an out-of-pocket maximum. The exact price schedules can be found in columns 3 and 4 of Table 2. The simulated Platinum (Bronze) plan has a deductible of $0 ($4500), a coinsurance rate of 20% (20%), and an out-of-pocket maximum of $1500 ($6500). The cost-sharing parameters were chosen using the 2014 version of the actuarial value calculator provided by the Department of Health and Human Services.31 The choice to use the most and least comprehensive plans available on the Marketplace in the simulation was deliberate. In order to capture the most accurate picture of adverse selection on the Marketplace, the simulation should include these two options.32
In the simulations, individuals choose the plan that gives them the highest expected utility, where expected utility is defined as in Section 4.2. In order to calculate each individual's expected utility under each plan, risk preferences and the distribution of expected out-of-pocket costs are required. Risk preferences are assigned to each individual according to the estimated parameters from the model above and presented in Table 3. The distributions of expected out-of-pocket costs for the new Platinum and Bronze plans are estimated using techniques similar to those described in Section 4, with the key difference being that the expected out-of-pocket cost distributions include prescription drug costs, which they did not in the previous section due to the fact that the two employer plans had identical cost sharing for drugs.33 I estimate each individual’s expected utility in plan j with premium Pj by taking Q draws from the out-of-pocket cost distribution Fij(OOP) and plugging them into the following expression:
I can then determine which plan person i will choose given a price differential P.34
5.1 Correlations
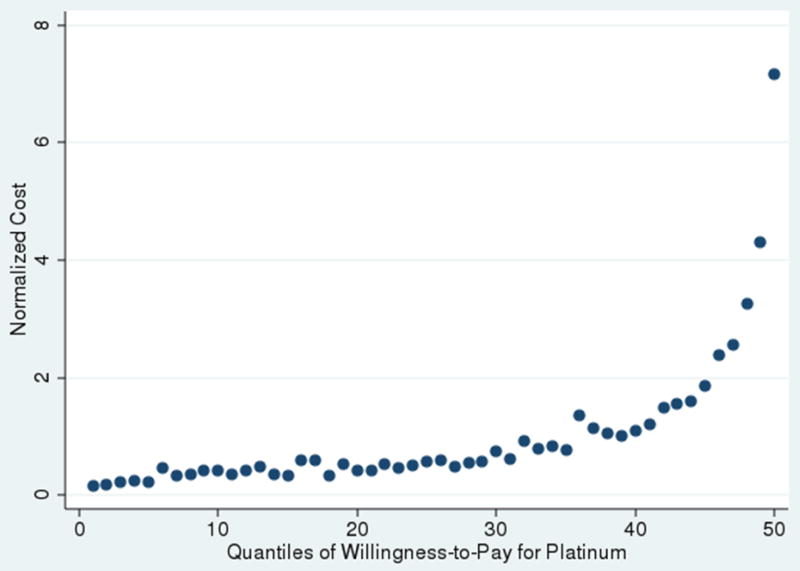
As shown in Section 2, the effect of risk adjustment on prices is revealed by the relationships between demand for the Platinum plan and total costs and demand for the Platinum plan and adjusted costs (i.e. whether the Platinum plan is adversely or advantageously selected on total and adjusted costs). If both relationships are positive, then risk adjustment will result in a smaller price differential and higher enrollment in the Platinum plan. Before moving to the simulations of equilibrium with and without risk adjustment, I present these relationships graphically. Appendix Figure A2 shows the relationship between willingness-to-pay for the Platinum plan and total costs. Quantiles of willingness-to-pay for Platinum over Bronze are on the x-axis, and a normalized measure of total costs (total cost divided by average cost) is on the y-axis. The relationship is positive (i.e. total cost is increasing in willingness-to-pay) and is stronger at higher levels of willingness-to-pay. This implies that as the price differential decreases, the marginal Platinum enrollee will have lower total cost than the average Platinum enrollee. In other words, the Platinum plan will be adversely selected.
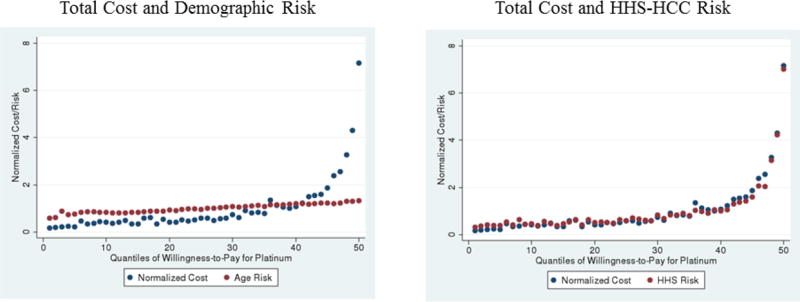
Appendix Figure A3 shows the relationships between willingness-to-pay and the risk scores from the two types of risk adjustment simulated below, demographic and diagnosis-based. I show the relationship between willingness-to-pay and the risk score rather than adjusted costs because adjusted costs are a linear function of the risk score, implying that the relationships will be identical. It is clear that the relationship between willingness-to-pay for the Platinum plan and both types of risk score is also positive. This implies that as the price differential decreases, the marginal Platinum enrollee will have a lower risk score than the average Platinum enrollee (i.e., the Platinum plan will be adversely selected on the risk score). The model and figures in Section 2 suggest that because the relationships between demand and total costs and demand and adjusted costs are both positive, in this setting risk adjustment will result in a smaller price differential and increased enrollment in the Platinum plan. It is interesting to note, however, that the relationship between willingness-to-pay and adjusted costs is quite different for demographic-based risk adjustment (left panel of Figure A3) than for diagnosis-based risk adjustment (right panel of Figure A3. Compared to diagnosis-based risk adjustment, demographic-based risk adjustment does a relatively poor job of capturing the costs of the highest cost/highest demand enrollees. This suggests that demographic-based risk adjustment will likely have less of an effect on equilibrium prices and sorting than diagnosis-based risk adjustment.
5.2 Welfare
In order to assess the welfare consequences of risk adjustment in the simulations, I follow Einav, Finkelstein, and Cullen (2010) and use a certainty equivalent concept. The certainty equivalent, eij, is defined as the value, e, that makes individual i indifferent between paying e and facing the uncertain loss under insurance plan j. I calculate the certainty equivalent for individual i under plan j by finding the value of eij that makes the following expression true:
The certainty equivalent is convenient because it provides a way to determine i’s valuation of the insurance plan in dollars. Given an individual's certainty equivalent under each plan, I can calculate individual i’s willingness-to-pay for the Platinum plan in dollars by subtracting eiB from eiP: WTPiP = eiP − eiB. The willingness-to-pay for the Platinum plan incorporates the difference in out-of-pocket costs paid by i and the difference in uncertainty under the two plans. It represents consumer surplus from i moving from the Bronze plan to the Platinum plan.
Total welfare, however, must also account for changes in the costs paid by the insurer. Because the difference in out-of-pocket costs under the two plans just represents a transfer from the insurer to the consumer, it does not affect total welfare. Only the decreased uncertainty will impact total welfare. Thus, the change in total welfare from i moving from the Bronze plan to the Platinum plan is
Where is the plan cost from enrolling i in plan j, making i’s incremental marginal cost. ΔWi represents the incremental welfare improvement from moving i from the Bronze to the Platinum plan. This implies that the change in total welfare resulting from a move from a setting with no risk adjustment to a setting with risk adjustment is equal to
Where is i’s expected utility under plan j given the equilibrium prices with risk adjustment and is i’s expected utility under plan j given the equilibrium prices without risk adjustment. The intuition for this measure is that welfare only changes when individuals move from one plan to another, and when an individual moves, welfare either increases or decreases by ΔWi, depending on whether i is moving from Bronze to Platinum or Platinum to Bronze. It is important to note, however, that this welfare metric makes the critical assumption that my estimates of willingness-to-pay for the Platinum plan are equal to consumer valuation of the plan. In practice, this may not always hold due to behavioral biases (Handel 2013; Spinnewijn 2017; Handel, Kolstad, and Spinnewijn 2015).
5.3 Equilibrium
In order to simulate equilibrium prices and sorting in this environment, I first need to establish an equilibrium concept. Handel, Hendel, and Whinston (2015) show that in this setting, the competitive equilibrium can be found using the following algorithm where PP and PB represent the premiums of the Platinum and Bronze plans, = PP − PB, ACP (P) and ACB (P) represent the average plan costs of enrollees in the Platinum and Bronze plans given price differential P, ACP and ACB represent the average plan costs of the entire population in the Platinum and Bronze plans, and Δ AC(P) = ACP (P) − ACB (P):
If ΔAC(P) < P ∀P then the entire market enrolls in the Platinum plan and PP = ACP
If ∃P such that P = ΔAC(P) then the equilibrium value of P is equal to P* = min(P: P = ΔAC(P)) and consumers sort according to willingness-to-pay
If ΔAC(P) > P ∀P then the entire market enrolls in the Bronze plan and PB = ACB
Figure 4 illustrates the equilibrium search with no risk adjustment. P is on the x-axis. The light blue line represents the 45-degree line, and the orange line represents ΔAC(P). If there is an interior equilibrium, it will be where ΔAC(P) = P. It is clear that there is no interior equilibrium in this setting and that ΔAC(P) > P for all values of P. This implies that in equilibrium, the entire market enrolls in the Bronze plan and PB = ACB. This is also known as market unraveling and is the same result found by Handel, Hendel, and Whinston (2015). In this setting, the correlation between demand and total costs is so strong that there is no price differential at which any part of the market enrolling in the Platinum plan would result in a competitive equilibrium where both plans earn zero profits.
5.3.1 Risk Adjustment
With risk adjustment, the equilibrium concept remains the same, but the relevant plan average costs change. Risk adjustment is implemented as described in Section 2 by assuming the regulator gives each plan the following transfer
where R̄j represents the average risk score of the enrollees in plan j, R̄ represents the average risk score in the entire market, and P̄ represents the average premium in the market. This is analogous to the individual-level risk adjustment framework developed in Section 2. With risk adjustment, equilibrium is where the premium differential is equal to the incremental average risk adjusted cost, ΔACRA(P) = ΔAC(P) − (Tp(P) − TB(P)). The algorithm for finding the competitive equilibrium remains the same, except ΔAC(P) is replaced with ΔACRA(P). Note that for both plans because when the entire market is enrolled in the same plan Tj = 0.
I simulate two types of risk adjustment: demographic, based on age-by-sex cells, and the HHS-HCC diagnosis-based model being implemented in the Marketplaces.35 Figure 4 illustrates the equilibrium search under these two forms of risk adjustment. Again, the light blue line represents the 45-degree line and the orange line represents ΔAC(P). The dark blue and green lines represent ΔACRA(P) under demographic and HHS-HCC risk adjustment, respectively. Both risk adjustment policies shift the incremental average cost curve down, though HHS-HCC risk adjustment has a much larger effect than demographic-based risk adjustment. It is interesting to note, however, that much of the HHS-HCC model's improvement seems to occur in the middle of the cost distribution, with the incremental average cost curve still sloping up sharply at the far right of the figure, where the sickest individuals are the only ones enrolled in the Platinum plan (though much less sharply than under demographic risk adjustment). Under demographic risk adjustment, ΔACRA(P) > P for all values of P and the entire market still enrolls in the Bronze plan. In other words, demographic risk adjustment has no effect on equilibrium prices or sorting in this setting. However, under HHS-HCC risk adjustment ΔACRA(P) crosses the 45-degree line, implying that there exists an interior equilibrium. With HHS-HCC risk adjustment, there are in fact multiple points where P = ΔACRA(P). Recall that according to the algorithm, the competitive equilibrium value of P, P*, is the smallest value of for P which P = ΔACRA(P). According to the algorithm then, under the Marketplace risk adjustment policy P* = $1,806.
Appendix Figure A4 illustrates the equilibrium allocations of individuals across plans in a more familiar way, similar to the figures in Section 2. In this figure, enrollment in the Platinum plan is on the x-axis. Again, the orange, dark blue, and green lines represent the incremental average cost curve under no risk adjustment, demographic risk adjustment, and HHS-HCC (Marketplace) risk adjustment, respectively. The light blue line reflects demand or willingness-to-pay for the Platinum plan relative to the Bronze plan. For HHS-HCC risk adjustment, the equilibrium price P* is at the smaller of the two points where the green incremental average (risk adjusted) cost curve crosses the light blue demand curve. The equilibrium price and Platinum enrollment under HHS-HCC risk adjustment are highlighted with the black lines. Recall that with no risk adjustment or demographic risk adjustment, the entire market enrolls in the Bronze plan. The figure shows that under Marketplace HHS-HCC risk adjustment, a substantial portion of the market, over 60%, will enroll in the Platinum plan.
The results of these simulations can also be found in Table 4. The table shows that diagnosis-based risk adjustment compresses the premiums of the Platinum and Bronze plans and undoes a substantial portion of market unraveling. Changes in welfare due to risk adjustment are presented in column 5. The welfare calculations suggest that individuals in this market would place a high value on diagnosis-based risk adjustment, over $600 per person per year. This suggests huge welfare gains from risk adjustment, around 20% of average total health care costs in this population.
Table 4.
Equilibrium Prices, Sorting, and Welfare with Uniform Pricing
| No Reinsurance | |||||
| Price Differential | Bronze Price | Platinum Price | % in Platinum | Change in Welfare | |
|
| |||||
| No Risk Adjustment | n.a. | $1,969 | n.a. | 0.0% | n.a. |
| Age/sex Risk Adjustment | n.a. | $1,969 | n.a. | 0.0% | $0 |
| HHS Risk Adjustment | $1,806 | $1,992 | $3,799 | 63.4% | $627 |
|
| |||||
| Reinsurance | |||||
| Price Differential | Bronze Price | Platinum Price | % in Platinum | Change in Welfare | |
|
| |||||
| No Risk Adjustment | n.a. | $1,969 | n.a. | 0% | n.a. |
| Age/sex Risk Adjustment | n.a. | $1,969 | n.a. | 0% | $0 |
| HHS Risk Adjustment | $946 | $2,502 | $3,449 | 82.0% | $775 |
Notes: Table shows equilibrium price differential (price of Platinum – price of Bronze), prices, proportion enrolled in Platinum plan, and change in welfare from no risk adjustment case to case with indicated type of risk adjustment. Bottom panel adds reinsurance where reinsurance reimburses 85% of an individual’s plan costs above $60,000 and is funded with an actuarially fair per capita premium. Equilibrium found using algorithm described in the text. If there is no interior equilibrium, there is no price differential, and only the price of the plan in which the entire market enrolls is shown. Types of risk adjustment include age/sex which uses only demographic variables to predict costs, and HHS which is a concurrent model that uses a different set of diagnosis groups and allows for higher risk scores for Platinum enrollees and a penalty factor for the Platinum plan. Welfare calculated by the certainty equivalent concept discussed in the paper.
5.3.2 Reinsurance
Risk adjustment is not the only adverse selection-related component of the payment systems used to determine payments to health plans in the Marketplaces. Another prominent component of health plan payment is reinsurance. Reinsurance typically reimburses plans for costs incurred by extremely high cost individuals. Because these individuals are likely to disproportionately choose plans with better coverage, reinsurance is likely to also have an effect on prices and sorting. In fact, it may be complementary to risk adjustment: Recall that Figure 4 showed that HHS-HCC risk adjustment flattened the incremental average cost curve for much of the middle of the distribution of willingness-to-pay for the Platinum plan but that a sharp uptick in the slope of the cost curve remained for the upper portion of the distribution. Because the sickest, highest-cost consumers who are most likely to trigger reinsurance payments are most likely in this part of the distribution, reinsurance may be able to complement risk adjustment by flattening this portion of the cost curve. Previous work suggests reinsurance performs well on various metrics of the performance of health plan payment systems with respect to adverse selection problems (Geruso and McGuire 2016; Layton et al. 2017).
To determine the consequences of reinsurance for prices and sorting, I perform an additional set of counterfactual simulations. During the first three years, the Marketplaces featured a reinsurance policy as well as HHS-HCC risk adjustment.36 The initial proposed reinsurance policy reimbursed health plans for 80% of an enrollee's plan costs above a threshold of $60,000 and below a cap of $250,000. Insurers were expected to purchase private coverage for costs exceeding $250,000, with a coinsurance rate of 85%. I simulate equilibrium prices and sorting under each form of risk adjustment combined with reinsurance. I simulate reinsurance by assuming that for each enrollee, plans receive a payment equal to 85% of any plan costs exceeding $60,000 within a year. The simulated reinsurance program is funded with a uniform actuarially fair per capita premium equal to the expected per capita reinsurance payment in the market, making the policy budget neutral.37 The equilibrium results with reinsurance are found in Table 4 and in Appendix Figure A5. The figure and table show that even with reinsurance, both when there is no risk adjustment and with demographic risk adjustment, the market still fully unravels and everyone enrolls in the Bronze plan. In other words, reinsurance alone is not enough to undo unraveling. With HHS-HCC risk adjustment, however, the incremental average (risk adjusted) cost curve is even flatter than it was without reinsurance. The effects of reinsurance are especially apparent for the highest cost/highest willingness-to-pay enrollees at the far right of the figure.38 The results in the table indicate that when HHS-HCC risk adjustment is combined with reinsurance, enrollment in the Platinum plan increases relative to the simulation without reinsurance with 82% of enrollees choosing the Platinum plan. The additional gains from reinsurance when combined with HHS-HCC risk adjustment are non-trivial, around $150. This finding complements the findings of Zhu et al. (2013), Geruso and McGuire (2016), and Layton, Ellis, and McGuire (2015) that suggest that when combined with risk adjustment, reinsurance can substantially weaken plans' incentives to cream-skim healthy enrollees. Additional results for another component of the health plan payment system, age-based pricing, are found in Appendix A.4.
5.3.3 Robustness
Number of cells
As discussed in Section 4.2.5, the results of the choice model estimation and the simulations depend on the assumption that Fij(OOP) is specified correctly. Up until this point, I have assumed that individuals know which of the 500 cells in λi they belong to. I now test the robustness of the results to using 50 or 1,000 cells instead of 500. The parameter estimates change very little as I vary the number of cells. The mean coefficient of absolute risk aversion is increasing in the number of cells, but only slightly. The mean switching cost, on the other hand, is decreasing in the number of cells, but again by a relatively small amount.
Despite the similar parameter estimates, it is possible that changing the number of cells could have large effects on the simulation results. This is due to the fact that Fij(OOP) plays a large role in individuals' choices in the simulations, so changing it could influence the equilibrium results. Equilibrium prices and sorting with 50 and 1,000 cells can be found in Tables A1 and A2. Results are shown with and without reinsurance. Equilibrium prices and sorting are virtually identical with 50, 500, or 1,000 cells.
Private Information
Despite the fact that λi incorporates a great deal of information from claims data into a sophisticated prediction of each individual's costs, it may be the case that some individuals have additional private information about their future spending. For example, a woman who intends to get pregnant during the next year may not have anything in her prior insurance claims suggesting her intention. In this case, the individual will know more about her future costs than λi would suggest. To allow for this possibility, I allow individuals to have 5%, 10%, 15%, 20%, or 25% of Fij(OOP) based on their actual realized costs in the next year. Again, the parameter estimates vary little across specifications.
Equilibrium prices and sorting with 10% and 20% private information can be found in Tables A3 and A4. Interestingly, when there is just a little private information, the HHS-HCC risk adjustment model no longer undoes market unraveling. Under this policy, the entire market enrolls in the Bronze plan. This is quite different from the case with no private information where the HHS-HCC risk adjustment policy resulted in a significant portion of consumers choosing the Platinum plan. Tables A3 and A4 also show equilibrium when reinsurance is combined with risk adjustment and individuals have private information about their future health care costs. Interestingly, the results here are similar to the case with no private information. This implies that reinsurance captures a substantial portion of the relationship between the private information and demand. This result also suggests that the finding that when combined with reinsurance risk adjustment is quite powerful at undoing the effects of adverse selection is robust to assumptions about the structure of individuals' distributions of expected costs. In the presence of private information, reinsurance may thus be a critical component of the payment system.
6. Conclusion
The trade-off between choice and adverse selection is a recurring theme in health economics. In the absence of choice, there is no potential for adverse selection because the costs of all consumers are combined in one risk pool. However, there is also no potential for efficiency gains from competition or from accommodating preference heterogeneity. Risk adjustment presents an opportunity to limit adverse selection problems by pooling a portion of consumers' costs across plans while still allowing choice and competition. Even the imperfect forms of risk adjustment studied in this paper appear to be able to eliminate a substantial portion of the welfare loss caused by adverse selection in a competitive environment similar to the Marketplaces.
While the results in this paper are compelling, they are limited by some important caveats. First, the estimates of consumer preferences used in the simulations are based on a highly parametric structural model. Because the data do not include any premium variation (or even the premiums themselves), I am unable to provide reduced form estimates of an individual's willingness-to-pay for insurance. While the setting in which the individuals choose plans is quite simple and potentially easily characterized, the process by which consumers make choices in the real world is complex. There is evidence of important behavioral frictions in health plan choice (Abaluck and Gruber 2011, Handel 2013, Handel and Kolstad 2015), and although I attempt to control for perhaps the most important of these, inertia, in my estimation, it is controlled for imperfectly and makes up only one of many potential frictions. Additionally, my sample of employees is probably not representative of the individuals likely to enroll in plans through the Marketplaces. The sample is probably higher income and more risk averse than the low income and previously uninsured individuals likely to enroll in a Marketplace plan.
Additionally, throughout this study, the assumptions of a strong mandate and no moral hazard were maintained. If there were moral hazard, equilibrium pricing and sorting results would likely be similar, but the welfare consequences of risk adjustment would not be so extreme. This is due to the fact that with moral hazard it would not be optimal for the entire market to enroll in the Platinum plan. This possibility is related to the discussion of moral hazard in Einav and Finkelstein (2011). Additionally, if the mandate is weak and consumers can opt out of the market, the equilibrium consequences of risk adjustment could be quite different. As shown in the simulations, risk adjustment raises the premium of the Bronze plan. If the mandate is weak, this could result in healthy consumers dropping out of the market entirely, potentially resulting in the entire market unraveling. This issue is beyond the scope of this paper, but presents a promising area for future research. Here, I just point out that a large portion of the individuals participating in the Marketplaces receive substantial subsidies that are based on the price of the second-cheapest Silver Plan. This implies that for a large segment of the market, the absolute prices of the Bronze and Silver Plans don't actually matter; all that matters is the difference between the Bronze or Silver Plan price and the Platinum plan price, which is consistent with the simulations presented here. However, because subsidies are based on the price of the second-cheapest Silver Plan, and the simulations in this paper show that risk adjustment is likely to substantially increase the equilibrium price of that plan, risk adjustment may result in larger subsidy payments than would otherwise be incurred, resulting in the program not being “budget neutral” as policymakers claim.
Despite the potential limitations, however, consumer choice is likely to follow similar patterns to those shown in the counterfactual simulations. Therefore, the effect of risk adjustment on equilibrium prices, sorting, and welfare while perhaps not perfectly estimated, is likely to be substantial. This is true not only in the Marketplaces but also in Medicare Part D where premiums are set competitively, some portions of the contracts are fixed, and demand is correlated with adjusted costs (Polyakova 2015). When combined with its potential beneficial effects on cream-skimming problems (Glazer and McGuire 2000), this makes risk adjustment a powerful tool for ameliorating adverse selection problems and improving welfare within competitive insurance markets. As these markets mature and data becomes available, it will be interesting to observe the correlations between demand, costs, and adjusted costs and the effects of risk adjustment in practice.
Acknowledgments
I am indebted to my advisers, Randy Ellis, Tom McGuire, and Keith Ericson, for their guidance and support in the preparation of this paper. I thank Claudia Olivetti helping me obtain access to the data for this project at the National Bureau for Economic Research. I am also grateful to Martin Andersen, Colleen Carey, Francesco Decarolis, Mike Geruso, Daria Pelech, Mark Shepard, and Julie Shi for useful comments and suggestions. I thank Mike Geruso and Ben Handel for incredibly helpful methodological advice. I also thank participants at the Healthcare Markets Conference at the Kellogg School of Management, the 2014 Biennial Meeting of the American Society of Health Economists, and the Health Economics Student Seminar at Department of Health Care Policy at Harvard Medical School for comments and suggestions. I gratefully acknowledge financial support from the Institute for Economic Development at Boston University and the National Institute of Mental Health (R01 MH094290, T32-019733).
Appendix
A.1 Risk Adjustment Model Estimation
In this paper I simulate risk adjustment with two different risk adjustment models: demographic and HHS-HCC. In this appendix, I explain how the weights are estimated for these models. With model k, each individual is assigned a risk score by multiplying a set of risk adjusters, , by a set of risk adjustment weights, βk:
For the demographic model, consists of a set of age-by-sex cells. For the HHS-HCC model, , consists of the same age-by-sex cells plus a set of Hierarchical Condition Categories (HCCs). HCCs are indicator variables equal to one if an individual receives a diagnosis that maps to the HCC. All diagnoses come from the administrative health insurance claims from the current year. Each of the over 14,000 ICD-9-CM diagnoses map to one of 264 HHS HCCs. For the HHS model, a subset of the HCCs are chosen for inclusion in the model based on explanatory power and concerns about gaming.
All models are estimated using data from the Truven Health Analytics Marketscan Commercial Claims and Encounters database by RTI International. For some subset of the individuals in the dataset (usually those enrolled in a fee-for-service health plan), the total annual healthcare costs, ci, are calculated and HCCs are assigned. The risk adjustment weights are then estimated via the following linear regression of individual costs on the risk adjusters:
The estimated weights are then normalized by dividing by the average cost in the sample:
All of the risk scores assigned in this paper use pre-estimated weights from software provided by HHS.
The estimation of the HHS-HCC weights varies slightly in the definition of ci. Instead of using total costs, the HHS-HCC model is estimated using “plan liability” costs. Plan liability costs are defined by finding an individual's out-of-pocket costs based on her total costs and some standard non-linear cost sharing schedule found using the HHS actuarial value calculator. Because actuarial value varies by plan tier, plan liability costs also vary. This results in 5 separate models, one for each tier in the Marketplaces. In the simulations, this implies that an individual's risk score depends on whether she enrolls in the Bronze or the Platinum plan, with risk scores generally being higher in the Platinum plan. Because of this, the HHS-HCC transfer formula includes an adjustment for the actuarial value of the plan relative to the enrollment-weighted average actuarial value in the market:
I implement this adjustment in the simulations of the HHS-HCC model.
A.2 Expected Out-of-Pocket Cost Distributions
In order to estimate the choice model discussed in Section 4, I construct an estimate of each individual’s distribution of expected costs. Estimation of this distribution is likely to be more accurate with a larger dataset. Because the firm sample is relatively small, in order to estimate the cost distributions I augment the sample using data on 12,177,930 individuals from the Marketscan Database to form the cost model sample.39 The cost model sample consists of all individuals in Marketscan from 2006–07 enrolled in a PPO plan for at least 300 days of year t and year t + 1. The characteristics of the cost model sample are found in column 4 of Table 1. The cost model sample is validated by comparing costs predicted by the cost model to actual costs among the employees in the sample.
As explained in Section 4, an individual's expected out-of-pocket distribution, Fij(OOP), is estimated based on a predictive measure of the individual's future out-of-pocket costs, λit. This measure is calculated using sophisticated predictive modeling software from Verisk Health, and it incorporates virtually all of the information available from the individual's health insurance claims from the prior year. Unfortunately, for the new enrollees who were not enrolled in a plan during the prior year, the information necessary to calculate λit is not available, so a different method for estimating Fij(OOP) is necessary. I follow Handel and Kolstad (2013) by calculating λi,t+1 for each new enrollee using data from the current year. I then use the estimate of λi,t+1 to determine the probability that an individual with a predicted cost of λi,t+1 was in each of the 500 cells of λit at time t. I then determine the parameters of the individual's expected out-of-pocket cost distribution, Fij(OOP), by multiplying the individual's probability of being in a given cell in time t, given that the individual has predicted cost λi,t+1 in time t + 1, by the estimated parameters for the cells. This produces a Bayesian estimate of the individual's expected out-of-pocket cost distribution, given λi,t+1.
A.3 Model Estimation
Estimation begins by fixing the parameter vector, Φ, and taking a draw of the error term, εs, which is assumed to follow a normal distribution. Next, Q draws are taken from each employee's expected total cost distribution and run through each plan's cost-sharing parameters to simulate Fij(OOP) for each employee i and plan j. Each employee's expected utility from plan j is then estimated by averaging the CARA utility function over the Q draws from F_{ij}(OOP):
where
Given the draw of the error term εs and the expected utility estimates for each plan they imply, I could simulate each employee's choice by comparing the expected utilities for Plan E and Plan B and assigning employee i to the plan with higher expected utility, i.e. an accept-reject simulator. However, the accept-reject simulator can cause problems in the estimation process due to flat portions of the likelihood function where no employees choose to move from one plan to the other and undefined portions of the log-likelihood function due to some individuals having a zero probability of enrolling in one of the plans. Both of these problems could potentially be solved by including a larger number of draws of the random components; however, for both issues to be fully resolved, the number of necessary draws would approach infinity. Instead, I use a smoothed accept-reject simulator. The simulator I use was developed by Handel (2014) and simulates the probability that the employee will choose each plan according to the following function:
The form of the simulator ensures that the estimated probability increases (decreases) when the accept-reject simulator would increase (decrease) and that the probability lies between zero and one. As the smoothing parameter, τ, becomes large, the simulator becomes identical to the accept-reject simulator.
The probability of choosing each plan is calculated for each draw, s, of the the error term. To find the simulated probability that the employee chooses plan j, given the draw from the parameter distribution, I average over the smoothed values,
The simulated log-likelihood function is then defined as
dij is equal to one if the employee actually chose plan j and zero otherwise. The likelihood function is quite intuitive in that it will achieve its maximum where the simulated probability that each employee chose plan j is as close to one as possible when the employee actually chose plan j and as close to zero as possible otherwise. I use standard numerical techniques to find the parameter vector, Φ, that maximizes the likelihood function. In the actual estimation I set Q=50, S=75, and τ =2.
A.4 Age-based Pricing
In addition to risk adjustment and reinsurance, another component of the health plan payment system that can affect the consequences of adverse selection is the set of premium rating rules. If premiums are allowed to vary at the level of the individual and there is no private information, then competition will cause insurers to charge each consumer her incremental cost, and consumers will sort efficiently. Throughout the paper, I've assumed that insurers are not permitted to price discriminate and that they must charge all consumers the same price for a given product and enroll any consumer who wishes to purchase the product. I now relax that assumption to allow for age-based pricing. The ACA allows for premiums in the Marketplaces to vary by age as long as they remain within a 3:1 ratio. Because age-based pricing causes the prices paid by enrollees to be closer to their expected costs, this policy has the potential to undo some of the adverse selection problems resulting from uniform pricing that I study in this paper. This suggests that the effects of risk adjustment may not be as large in practice due to this regulation. In fact, Shi (2014) finds that welfare in a simulated Marketplace is highest when risk adjustment is combined with age-based prices. To study this question, I implement age-based pricing as it is implemented in the Federal Health Insurance Marketplace. In the Federal Marketplace, plans submit one price that applies to a 21 year old. An individual's price is this price multiplied by an age-specific weight assigned by HHS. For example, the weight for a 25 year-old is 1.004, the weight for a 40 year-old is 1.278, and the weight for a 64 year-old is 3.0.40
The results from simulations including the HHS-mandated age-curve can be found in Table A5. Interestingly, the results are largely unchanged from the uniform price case. The bolded case in Table A5 with the age-curve, reinsurance, and HHS-HCC risk adjustment is the full policy being implemented in the Marketplaces. It is clear that this policy goes a long way toward undoing the problems cause by adverse selection with 82% of the market enrolling in the Platinum plan, resulting in a welfare gain of over $700 per person, per year.
Figure A1. Welfare Loss under Various Risk Adjustment Policies.
Notes: In the figure, enrollment is on the x-axis and the price differential is on the y-axis. The figure shows the incremental average cost curve in three settings: no risk adjustment, risk adjustment where adjusted costs equal accident costs, and risk adjustment where adjusted costs equal chronic costs. The equilibrium in each setting occurs where the orange demand curve crosses the incremental average cost curve. The figure also presents the green incremental marginal cost curve. Welfare loss is represented by the area between the demand curve and the incremental marginal cost curve at the equilibrium enrollment point.
Figure A2. Correlation between Willingness-to-Pay for Platinum and Total Costs.
Notes: In the figure, 50 quantiles of willingness-to-pay are on the x-axis and normalized total medical spending (spending divided by average spending) is on the y-axis. Willingness-to-pay is generated using the expected utility model presented in the text along with the parameters of the model estimated using the choice model. A positive correlation between willingness-to-pay and total costs implies that as the price differential between Platinum and Bronze decreases, the marginal Platinum enrollee will have a lower cost than the average Platinum enrollee, i.e. the Platinum plan will be adversely selected.
Figure A3. Correlations between Willingness-to-Pay and Risk Scores.
Notes: In the figures, 50 quantiles of willingness-to-pay are on the x-axis and normalized total medical spending (spending divided by average spending) and risk scores are on the y-axis. Willingness-to-pay is generated using the expected utility model presented in the text along with the parameters of the model estimated using the choice model. Risk scores are calculated using information from the health insurance claims data. This information is passed through software from HHS to produce the risk scores. The software multiplies a vector of diagnostic- and demographic-based variables generated from the claims data by a vector of pre-estimated risk adjustment weights. A positive correlation between willingness-to-pay and total costs implies that as the price differential between Platinum and Bronze decreases, the marginal Platinum enrollee will have a lower cost than the average Platinum enrollee, i.e. the Platinum plan will be adversely selected. A positive correlation between willingness-to-pay and the risk score implies that as the price differential between Platinum and Bronze decreases, the marginal Platinum enrollee will have a lower risk score than the average Platinum enrollee, i.e. the Platinum plan will be adversely selected on adjusted costs.
Figure A4. Equilibrium Price Differentials and Sorting under Different Types of Risk Adjustment.
Notes: Figure shows equilibrium in setting where sample individuals required to choose between Bronze and Platinum Plans. Light blue line is the demand curve. Orange line represents incremental average cost (IAC) curve with no risk adjustment, blue line represents IAC with demographic risk adjustment, and green line represents IAC with HHS-HCC risk adjustment. Enrollment in Platinum Plan is on x-axis. IAC with no and demographic risk adjustment is everywhere above 45-degree line implying complete market unraveling where everyone enrolls in Bronze plan. Prospective, concurrent, and HHS risk adjustment IACs cross 45-degree line, implying an interior equilibrium exists. Equilibrium is at lowest P where IAC crosses 45-degree line. Concurrent results in the lowest price differential. Equilibrium price and enrollment in Platinum are highlighted by dotted lines. Prices, enrollment, and welfare can be found in Table 4.
Figure A5. Equilibrium Price Differentials and Sorting under Different Types of Risk Adjustment (with Reinsurance).
Notes: Figure shows search for equilibrium with reinsurance in setting where sample individuals required to choose between Bronze and Platinum Plans. Light blue line is the 45-degree line. Orange line represents incremental average cost (IAC) curve with no risk adjustment, blue line represents IAC with demographic risk adjustment, and green line represents IAC with HHS-HCC risk adjustment. All lines include reinsurance. IAC with no and demographic risk adjustment is everywhere above 45-degree line implying complete market unraveling where everyone enrolls in Bronze plan. Prospective, concurrent, and HHS risk adjustment IACs cross 45-degree line, implying an interior equilibrium exists. Equilibrium is at lowest P where IAC crosses 45-degree line. Concurrent results in the lowest price differential. Prices, enrollment, and welfare can be found in Table 4.
Table A1.
Equilibrium Prices, Sorting, and Welfare with Uniform Pricing (1000 cells)
| No Reinsurance | ||||||
| Price Differential | Bronze Price | Platinum Price | % in Platinum | Change in Welfare | ||
|
| ||||||
| No Risk Adjustment | n.a. | $1,969 | n.a. | 0.0% | n.a. | |
| Age/sex Risk Adjustment | n.a. | $1,969 | n.a. | 0.0% | $0 | |
| HHS Risk Adjustment | $1,858 | $1,972 | $3,830 | 63.2% | $676 | |
|
| ||||||
| Reinsurance | ||||||
| Price Differential | Bronze Price | Platinum Price | % in Platinum | Change in Welfare | ||
|
| ||||||
| No Risk Adjustment | n.a. | $1,969 | n.a. | 0% | n.a. | |
| Age/sex Risk Adjustment | n.a. | $1,969 | n.a. | 0% | $0 | |
| HHS Risk Adjustment | $929 | $2,521 | $3,450 | 82.2% | $832 | |
Notes: Table shows equilibrium price differential (price of Platinum – price of Bronze), prices, proportion enrolled in Platinum plan, and change in welfare from no risk adjustment case to case with indicated type of risk adjustment. All simulations use choice model parameters and expected out-of-pocket cost distributions with 1,000 cells of λi. Bottom panel adds reinsurance where reinsurance reimburses 85% of an individual’s plan costs above $60,000 and is funded with an actuarially fair per capita premium. In all cases, prices vary by age according to the HHS age curve. Equilibrium found using algorithm described in the text. If there is no interior equilibrium, there is no price differential, and only the price of the plan in which the entire market enrolls is shown. Types of risk adjustment include age/sex which uses only demographic variables to predict costs, and HHS which is a concurrent model that uses a different set of diagnosis groups and allows for higher risk scores for Platinum enrollees and a penalty factor for the Platinum plan. Welfare calculated by the certainty equivalent concept discussed in the paper. Case in bold represents the full pricing policy currently being implemented in the Marketplaces.
Table A2.
Equilibrium Prices, Sorting, and Welfare with Uniform Pricing (50 cells)
| No Reinsurance | |||||
| Avg Price Diff | Avg Bronze Price | Avg Platinum Price | % in Platinum | Change in Welfare | |
|
| |||||
| No Risk Adjustment | n.a. | $1,969 | n.a. | 0% | |
| Age/sex Risk Adjustment | n.a. | $1,969 | n.a. | 0% | $0 |
| HHS Risk Adjustment | $2,042 | $1,978 | $4,025 | 52% | $468 |
|
| |||||
| Reinsurance | |||||
| Avg Price Diff | Avg Bronze Price | Avg Platinum Price | % in Platinum | Change in Welfare | |
|
| |||||
| No Risk Adjustment | n.a. | $1,969 | n.a. | 0% | |
| Age/sex Risk Adjustment | n.a. | $1,969 | n.a. | 0% | $0 |
| HHS Risk Adjustment | $938 | $2,507 | $3,445 | 81.7% | $723 |
Notes: Table shows equilibrium price differential (price of Platinum – price of Bronze), prices, proportion enrolled in Platinum plan, and change in welfare from no risk adjustment case to case with indicated type of risk adjustment. All simulations use choice model parameters and expected out-of-pocket cost distributions with 50 cells of λi. Bottom panel adds reinsurance where reinsurance reimburses 85% of an individual’s plan costs above $60,000 and is funded with an actuarially fair per capita premium. In all cases, prices vary by age according to the HHS age curve. Equilibrium found using algorithm described in the text. If there is no interior equilibrium, there is no price differential, and only the price of the plan in which the entire market enrolls is shown. Types of risk adjustment include age/sex which uses only demographic variables to predict costs, and HHS which is a concurrent model that uses a different set of diagnosis groups and allows for higher risk scores for Platinum enrollees and a penalty factor for the Platinum plan. Welfare calculated by the certainty equivalent concept discussed in the paper. Case in bold represents the full pricing policy currently being implemented in the Marketplaces.
Table A3.
Equilibrium Prices, Sorting, and Welfare with Uniform Pricing (10% Private Info)
| No Reinsurance | |||||
| Price Differential | Bronze Price | Platinum Price | % in Platinum | Change in Welfare | |
|
| |||||
| No Risk Adjustment | n.a. | $1,969 | n.a. | 0.0% | n.a. |
| Age/sex Risk Adjustment | n.a. | $1,969 | n.a. | 0.0% | $0 |
| HHS Risk Adjustment | n.a. | $1,969 | n.a. | 0.0% | $0 |
|
| |||||
| Reinsurance | |||||
| Price Differential | Bronze Price | Platinum Price | % in Platinum | Change in Welfare | |
|
| |||||
| No Risk Adjustment | n.a. | $1,969 | n.a. | 0% | n.a. |
| Age/sex Risk Adjustment | n.a. | $1,969 | n.a. | 0% | $0 |
| HHS Risk Adjustment | $988 | $2,511 | $3,499 | 83.0% | $787 |
Notes: Table shows equilibrium price differential (price of Platinum – price of Bronze), prices, proportion enrolled in Platinum plan, and change in welfare from no risk adjustment case to case with indicated type of risk adjustment. All simulations use choice model parameters and expected out-of-pocket cost distributions with 10% private information about future health care costs. Bottom panel adds reinsurance where reinsurance reimburses 85% of an individual’s plan costs above $60,000 and is funded with an actuarially fair per capita premium. In all cases, prices vary by age according to the HHS age curve. Equilibrium found using algorithm described in the text. If there is no interior equilibrium, there is no price differential, and only the price of the plan in which the entire market enrolls is shown. Types of risk adjustment include age/sex which uses only demographic variables to predict costs, and HHS which is a concurrent model that uses a different set of diagnosis groups and allows for higher risk scores for Platinum enrollees and a penalty factor for the Platinum plan. Welfare calculated by the certainty equivalent concept discussed in the paper. Case in bold represents the full pricing policy currently being implemented in the Marketplaces.
Table A4.
Equilibrium Prices, Sorting, and Welfare with Uniform Pricing (20% Private Info)
| No Reinsurance | |||||
| Avg Price Diff | Avg Bronze Price | Avg Platinum Price | % in Platinum | Change in Welfare | |
|
| |||||
| No Risk Adjustment | n.a. | $1,969 | n.a. | 0.0% | $0 |
| Age/sex Risk Adjustment | n.a. | $1,969 | n.a. | 0.0% | $0 |
| HHS Risk Adjustment | n.a. | $1,969 | n.a. | 0.0% | $0 |
|
| |||||
| Reinsurance | |||||
| Avg Price Diff | Avg Bronze Price | Avg Platinum Price | % in Platinum | Change in Welfare | |
|
| |||||
| No Risk Adjustment | n.a. | $1,969 | n.a. | 0.0% | |
| Age/sex Risk Adjustment | n.a. | $1,969 | n.a. | 0.0% | $0 |
| HHS Risk Adjustment | $985 | $2,526 | $3,511 | 82.3% | $724 |
Notes: Table shows equilibrium price differential (price of Platinum – price of Bronze), prices, proportion enrolled in Platinum plan, and change in welfare from no risk adjustment case to case with indicated type of risk adjustment. All simulations use choice model parameters and expected out-of-pocket cost distributions with 20% private information about future health care costs. Bottom panel adds reinsurance where reinsurance reimburses 85% of an individual’s plan costs above $60,000 and is funded with an actuarially fair per capita premium. In all cases, prices vary by age according to the HHS age curve. Equilibrium found using algorithm described in the text. If there is no interior equilibrium, there is no price differential, and only the price of the plan in which the entire market enrolls is shown. Types of risk adjustment include age/sex which uses only demographic variables to predict costs and HHS which is a concurrent model that uses a different set of diagnosis groups and allows for higher risk scores for Platinum enrollees and a penalty factor for the Platinum plan. Welfare calculated by the certainty equivalent concept discussed in the paper. Case in bold represents the full pricing policy currently being implemented in the Marketplaces.
Table A5.
Equilibrium Prices, Sorting, and Welfare with Age-based Pricing
| No Reinsurance | |||||
| Avg Price Diff | Avg Bronze Price | Avg Platinum Price | % in Platinum | Change in Welfare | |
|
| |||||
| No Risk Adjustment | n.a. | $1,969 | n.a. | 0% | n.a. |
| Age/sex Risk Adjustment | n.a. | $1,969 | n.a. | 0% | $0 |
| HHS Risk Adjustment | $2,027 | $1,850 | $3,873 | 56% | $551 |
|
| |||||
| Reinsurance | |||||
| Avg Price Diff | Avg Bronze Price | Avg Platinum Price | % in Platinum | Change in Welfare | |
|
| |||||
| No Risk Adjustment | n.a. | $1,969 | n.a. | 0% | n.a. |
| Age/sex Risk Adjustment | n.a. | $1,969 | n.a. | 0% | $0 |
| HHS Risk Adjustment | $1,030 | $2,424 | $3,456 | 81.9% | $769 |
Notes: Table shows equilibrium price differential (price of Platinum – price of Bronze), prices, proportion enrolled in Platinum plan, and change in welfare from no risk adjustment case to case with indicated type of risk adjustment. All simulations use choice model parameters and expected out-of-pocket cost distributions with 20% private information about future health care costs. Bottom panel adds reinsurance where reinsurance reimburses 85% of an individual’s plan costs above $60,000 and is funded with an actuarially fair per capita premium. In all cases, prices vary by age according to the HHS age curve. Equilibrium found using algorithm described in the text. If there is no interior equilibrium, there is no price differential, and only the price of the plan in which the entire market enrolls is shown. Types of risk adjustment include age/sex which uses only demographic variables to predict costs, and HHS which is a concurrent model that uses a different set of diagnosis groups and allows for higher risk scores for Platinum enrollees and a penalty factor for the Platinum plan. Welfare calculated by the certainty equivalent concept discussed in the paper. Case in bold represents the full pricing policy currently being implemented in the Marketplaces.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
In the US, risk adjustment is used in some form in Medicare Advantage, Medicare Part D, the new state Health Insurance Marketplaces, and many state Medicaid Managed Care programs. Risk adjustment is also used in some form in the health insurance markets of the Netherlands, Switzerland, Germany, Israel, and Belgium.
See Layton, Ellis, McGuire, and van Kleef (2017) in this issue for a recent review of this literature.
Such a setting is not just a theoretical possibility. Cabral, Geruso, and Mahoney (2014) provide evidence that while on the margin Medicare Advantage is advantageously selected on total costs, it is adversely selected on the demographic risk scores used during the time period of their study. This implies that during their study period, risk adjustment may have implicitly transferred money to rather than from Medicare Advantage plans and further distorted sorting between Traditional Medicare and Medicare Advantage rather than correcting distortions due to adverse selection.
Other papers have considered imperfect risk adjustment when studying adverse selection (Handel, Kolstad, and Spinnewijn 2015; Mahoney and Weyl 2014), but they have assumed that the imperfections are equal across individuals and services, effectively eliminating the interaction between preference heterogeneity and risk adjustment imperfections that generates the result I highlight in this paper that risk adjustment can result in transfers from the adversely selected plan and to the advantageously selected plan.
In the Marketplaces, plans are divided into tiers based on their actuarial value. The tiers are called (from least to most comprehensive) Bronze, Silver, Gold, and Platinum. A Bronze plan has an actuarial value of 60% and a Platinum plan has an actuarial value of 90%.
This is a huge welfare improvement. It is worth noting that it is especially large compared to the calculations of welfare loss from adverse selection found elsewhere in the literature (Cutler and Reber 1998; Einav, Finkelstein, and Cullen 2010; Geruso 2016). It is important to note, however, that in all of these other settings, the plans consumers were choosing between were quite similar in terms of cost sharing. Here, the plans have large differences in cost sharing, reflecting the large differences in cost sharing found across tiers in the Marketplaces. Simulations with plan options that are more similar to the options available in the settings studied in other papers produced welfare results similar to the results from those papers, suggesting that if the estimated structural demand and cost parameters from those papers were used to study the Bronze-Platinum setting studied here, the results would be similarly large.
Other recent papers that have made important advances in the literature on the economics of adverse selection in health insurance markets include Veiga and Weyl (2016) and Azevedo and Gottlieb (2017) who study the more complex but also more interesting setting where insurance contracts are endogenous. Niether paper considers risk adjustment, however.
Handel, Hendel, and Whinston (2015) also show that risk adjustment is necessary for the market to function efficiently, though they simulate only a “perfect” risk adjustment policy based on ex-post spending rather than the imperfect diagnosis-based risk adjustment policy I study here.
This formulation assumes additive separability of premiums and willingness-to-pay in the utility function. This assumption is common in the adverse selection literature (see Einav, Finkelstein, and Cullen (2010) and Bundorf, Levin, and Mahoney (2012)).
This simultaneously assumes perfect competition and assumes away any administrative costs. Because sorting depends only on the difference between the average costs in the two plans, an equivalent assumption would be that administrative costs in E and B are the same at all levels of enrollment.
It is possible that a set of premiums resulting in positive enrollment in plans E and B will not exist. In this case, as shown in Handel, Hendel, and Whinston (2015) in equilibrium all individuals will enroll in Plan B if ΔAC(P) is always greater than Δν(θi, εi) − P for all values of P and in Plan E if ΔAC(P) is always less than Δν(θi, εi) − P for all values of P. In these cases P* is undefined, but the sorting of consumers across plans can still be determined.
If the assumption that both contracts offer identical benefits were relaxed, the black horizontal line in the left panel connecting the left-most point on Plan E's average cost curve and the right-most point on Plan B's average cost curve would have a non-zero slope equal to the average difference in Plan E costs and Plan B costs. This would cause a vertical shift in the incremental average cost curve in the right panel, but all intuition drawn from these figures would remain unchanged.
Generally, the slope and intercept of ΔAC(P) illustrate adverse selection. Both are functions of the joint distribution of health risk, θi, and preferences, εi, in the population. This is an important difference from the figures in Einav, Finkelstein, and Cullen (2010) and Einav and Finkelstein (2011) where consumers choose between insurance and uninsurance. In their setting, adverse selection reveals itself only through the slope of the IAC. For an example of a case where adverse selection presents itself in the intercept of the IAC, consider a setting where health risk is distributed uniformly and preferences are constant across individuals. In such a setting ACE and ACB will be parallel but downward sloping, producing a flat IAC even when there is substantial adverse selection. In this case, adverse selection is illustrated by the intercept of the IAC, rather than the slope. Other distributions will result in non-parallel average cost curves (producing an IAC with either a positive or a negative slope, depending on whether selection gets stronger or weaker as the price increases) and different intercepts.
In the Marketplaces, risk adjustment is implemented using plan, rather than individual, transfers. However, the plan transfers are equivalent to individual transfers aggregated to the plan level. Additionally, the Marketplace transfer formula is more complex. Throughout the theoretical framework, I omit the complexities for simplicity. In the empirical simulations, I use the transfer formula used in the Marketplaces.
Here, I assume that a consumer's adjusted costs do not depend on the plan the consumer enrolls in. In many settings this is likely to be true. However, in the Marketplaces, while consumers' risk scores are the same in different plans in the same metal tier, they vary across tiers. I account for this in the empirical section but abstract from it here for simplicity. This assumption would also break down if plans vary in the coding of diagnoses on which ri is based (Geruso and Layton 2015).
A detailed explanation of the demographic- and diagnosis-based risk adjustment models, including the method of calculating the weights, can be found in Appendix A.1.
For recent work on the endogenous contracts setting, see Azevedo and Gottlieb (2017) and Veiga and Weyl (2016).
While these assumptions are made here only to illustrate the full set of potential outcomes of risk adjustment, there is some evidence that demand for insurance may be negatively correlated with risky behaviors, such as drinking or not wearing a seat belt, that may increase an individual's propensity to incur accident-induced medical spending (Cutler, Finkelstein, and McGarry 2008). The intuition for this correlation is that consumers with relatively low levels of risk aversion will have relatively high demand for risky behaviors and relatively low demand for insurance.
In addition to making it unclear how risk adjustment will affect sorting, the potential for preference heterogeneity also makes it unclear ex-ante what optimal sorting looks like (Bundorf, Levin, and Mahoney 2012). However, a treatment of this issue is beyond the scope of the paper. Instead, I just suggest that the effect of risk adjustment on welfare is unclear ex-ante. A thorough study of risk adjustment in such an environment is a promising and interesting direction for future research.
Note that in the case where there is preference heterogeneity, in the figure IMC(P) would represent the average value of Δc(θi) for individuals with willingness-to-pay for E equal to P. In this case, the shaded areas do not represent the full welfare loss due to inefficient sorting. They do, however represent differences in welfare loss across the various risk adjustment regimes. See Geruso (2016) and Layton, Ellis, and McGuire (2015) for a full treatment of this issue.
This is the same employer used by Geruso (2016).
All of these parameters apply only to providers in the plan’s network. Claims from out-of-network providers are covered much less generously. However, because PPO networks are generally relatively broad, there are very few of these claims, and they are not consistently and clearly identified, so I ignore them here.
As discussed below, in order to estimate switching costs, I require the presence of new enrollees who were not previously enrolled in a plan. For these new enrollees, I require no enrollment in 2006 and continuous enrollment throughout 2007.
The definition of adjusted costs used in the simulations (and in the Marketplaces) differs slightly from the definition described in Section 2.2. In the simulations, adjusted costs are defined as being equal to the normalized risk score multiplied by the (enrollment-weighted) average premium in the market rather than the average cost: . In a perfectly competitive setting, these two definitions are equivalent.
This assumption would be violated if plans respond to risk adjustment by altering coding practices (“upcoding”) or by increasing utilization in order to increase the number of diagnoses and thus extract a larger risk adjustment transfer (see Geruso and Layton (2015) and Geruso and McGuire (2016) for treatments of these two issues). While this type of behavior is likely to occur, it is unlikely that it would dramatically alter individuals' risk scores. Additionally, if plans are identical and all individuals are equally “upcode-able,” upcoding will result in the market average risk score increasing in tandem with the plan average risks scores. Because risk adjustment transfers are based on normalized risk scores, this would result in precisely the same normalized risk scores as the setting with no upcoding.
The assumption of CARA utility makes Wi irrelevant, implying no income effects.
See Handel (2014) for a thorough discussion of potential sources of inertia.
I note that I sort individuals into cells based only on predictions of medical cost risk and not predictions of prescription drug cost risk because the plans offered by this employer do not vary with respect to cost-sharing for prescription drugs, making those costs irrelevant to the employee's choice. I do, however, incorporate predictions of prescription drug costs in the counterfactual simulations below where I assume that insurers cover both medical and prescription drug costs, as they do in the Marketplaces.
As mentioned above, there is no cost-sharing for ER and preventive visits. Because the prediction software predicts total medical risk, rather than medical risk other than ER and preventive visits, I cannot separately predict an employee's use of these services. Instead, I ignore the fact that they are priced differently and combine them with other medical spending. In practice, these services make up a relatively small portion of spending and have a small impact on inferences about the distribution of Fij(OOP).
Multiple risk scores are included in the model to allow for maximum flexibility of the relationship between preferences and adjusted costs and to allow for the simulation of multiple counterfactual risk adjustment policies.
This is the calculator that all insurers are required to use to ensure that their plans meet the actuarial value requirements of the ACA. The calculator can be found at http://www.cms.gov/CCIIO/Resources/Regulations-and-Guidance/Downloads/av-calculator-final.xlsm
In practice, most consumers will choose between 4 tiers of plans with varying levels of comprehensiveness. However, the competitive equilibrium in this environment would be quite complex and extremely difficult to model while not providing much additional intuition about the consequences of risk adjustment for sorting and welfare.
In practice, prescription drugs are included by first assigning each individual in the cost model sample (described in Appendix A.2) a new value for λ, λ̃, using a different predictive model that incorporates drug spending. Next, individuals in the cost model sample were divided into 500 cells based on λ̃, and a random sample of 1,000 individuals was taken for each cell. For each cell, a lognormal distribution was then fit to the realized spending of the individuals in the cell, allowing the distribution parameters to vary by age and sex. These parameters describe the version Fij(OOP) of used in the counterfactual simulations.
Note that in the simulations consumers are assumed to pay the full incremental cost of enrolling in the Platinum plan, as they would in the Marketpalces, rather than the estimated employee contribution used in the choice model. The estimated employee contribution was used to estimate the choice model because it is likely to correspond closely with the price the employees of the firm actually faced. The full incremental cost is used in the simulations because this is the price that will be faced by individuals purchasing coverage through the Marketplaces. This is true even for individuals receiving subsidies, as the subsidies are pegged to the price of the silver (here, bronze) plan, implying that they will not affect the incremental cost.
In future years, the Marketplaces will include a new (less generous) version of reinsurance that is embedded in the risk adjustment system as described in Layton and McGuire (2017).
This differs from the Marketplace policy which was funded partially by fees to Marketplace plans but also partially by fees to employer-sponsored plans.
It is interesting that for the diagnosis-based risk adjustment policy, Figure 9 indicates that after a certain point ΔACRA(P) begins to fall. There are two potential reasons for this. First, the risk adjustment model does not take reinsurance into account, so the plan is effectively being reimbursed twice for the highest cost individuals. Second, at the far right side of the figure, there are only a few individuals left in the Bronze plan, making ΔACRA(P) quite sensitive to the random component of costs.
This cost model sample also includes all individuals in the firm sample used for estimation of the choice model.
This is different from the age-based pricing studied by Shi (2014). HHS forces insurers to use their age curve rather than allowing insurers to set their own age-based prices according to age-specific expected costs. I choose to use the fixed age-curve approach because this is the approach used in the Marketplaces in every state. While the alternative approach is interesting, and was used in Massachusetts prior to the ACA, the concept of equilibrium is much more complex due to multiple age-based risk pools and is beyond the scope of this paper and not currently relevant in “realworld” settings.
References
- Abaluck Jason, Gruber Jonathan. Choice inconsistencies among the elderly: Evidence from plan choice in the Medicare Part D program. American Economic Review. 2011;101(4):1180–1210. doi: 10.1257/aer.101.4.1180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akerlof George. The market for “lemons”: Quality uncertainty and the market mechanism. Quarterly Journal of Economics. 1970;84:488–500. [Google Scholar]
- Azevdo Eduardo, Gottleb Daniel. Perfect Competition in Markets with Adverse Selection. Econometrica. 2017;85(1):67–105. 2017. [Google Scholar]
- Breyer Friedrich, Bundorf Kate, Pauly Mark. Health care spending risk, health insurance, and payment to health plans. In: Pauly M, McGuire T, Barros P, editors. The Handbook of Health Economics. Vol. 2. Elsevier; 2012. [Google Scholar]
- Brown Jason, Duggan Mark, Kuziemko Ilyana, Woolston William. How does risk selection respond to risk adjustment? Evidence from the Medicare Advantage program. American Economic Review. 2014;104(10):3335–3364. doi: 10.1257/aer.104.10.3335. [DOI] [PubMed] [Google Scholar]
- Bundorf Kate, Levin Jonathan, Mahoney Neale. Pricing and welfare in health plan choice. American Economic Review. 2012;97(3):745–788. doi: 10.1257/aer.102.7.3214. [DOI] [PubMed] [Google Scholar]
- Cabral Marika, Geruso Michael, Mahoney Neale. Does privatized health insurance benefit patients or producers? Evidence from Medicare Advantage. 2014 NBER Working Paper 20470. [PMC free article] [PubMed] [Google Scholar]
- Cohen Alma, Einav Liran. Estimating risk preferences from deductible choice. American Economic Review. 2007;97:745–788. [Google Scholar]
- Cutler David, Finkelstein Amy, McGarry Kathleen. Preference heterogeneity and insurance markets: Explaining a puzzle of insurance. American Economic Review. 2008;98(2):157–162. doi: 10.1257/aer.98.2.157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cutler David, Reber Sarah. Paying for health insurance: The trade-off between competition and adverse selection. Quarterly Journal of Economics. 1998;113(2):433–466. [Google Scholar]
- Einav Liran, Finkelstein Amy. Selection in Insurance Markets: Theory and Empirics in Pictures. Journal of Economic Perspectives. 2011;25(1):115–38. doi: 10.1257/jep.25.1.115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Einav Liran, Finkelstein Amy, Cullen Mark. Estimating welfare in insurance markets using variation in prices. Quarterly Journal of Economics. 2010;125(3):877–921. doi: 10.1162/qjec.2010.125.3.877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finkelstein Amy, McGarry Kathleen. Multiple dimensions of private information: Evidence from the long-term care insurance market. American Economic Review. 2006;96(4):938–958. [PubMed] [Google Scholar]
- Geruso Michael. Demand Heterogeneity in Insurance Markets: Implications for Equity and Efficiency. Quantitative Economics. 2016 forthcoming. [Google Scholar]
- Geruso Michael, Layton Timothy. Upcoding or selection? Evidence from Medicare on Squishy Risk Adjustment. 2015 doi: 10.1086/704756. NBER Working Paper 21222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geruso Michael, McGuire Thomas. Tradeoffs in the design of health plan payment systems: Fit, power, and balance. Journal of Health Economics. 2016 doi: 10.1016/j.jhealeco.2016.01.007. forthcoming. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glazer Jacob, McGuire Thomas. Optimal risk adjustment in markets with adverse selection: An application to managed care. American Economic Review. 2000;90(4):1055–1071. [Google Scholar]
- Glazer Jacob, McGuire Thomas, Shi Julie. Risk adjustment of health plan payment to correct inefficient plan choice from adverse selection. 2014 NBER Working Paper 19998. [Google Scholar]
- Hackmann Martin B, Kolstad Jonathan T, Kowalski Amanda E. Adverse Selection and an Individual Mandate: When Theory Meets Practice. American Economic Review. 2015;105(3):1030–66. doi: 10.1257/aer.20130758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handel Benjamin. Adverse selection and inertia in health insurance markets: When nudging hurts. American Economic Review. 2013;103(7):2643–2682. doi: 10.1257/aer.103.7.2643. [DOI] [PubMed] [Google Scholar]
- Handel Benjamin, Hendel Igal, Whinston Michael. Equilibria in health insurance exchanges: Adverse selection vs. reclassification risk. Econometrica. 2015;83(4):1261–1313. [Google Scholar]
- Handel Benjami, Kolstad Johnathon, Spinnewijn Johannes. Information Frictions and Adverse Selection: Policy Interventions in Health Insurance Markets. 2015 NBER Working Paper 21759. [Google Scholar]
- Handel Benjamin, Kolstad Jonathan. Health insurance for 'humans': Information frictions, plan choice, and consumer welfare. American Economic Review. 2015;105(8):2449–2500. doi: 10.1257/aer.20131126. [DOI] [PubMed] [Google Scholar]
- Kaiser Family Foundation. Employer Health Benefits Survey. 2013 Access at http://kaiserfamilyfoundation.files.wordpress.com/2013/08/8465-employer-health-benefits-20132.pdf.
- Kowalski Amanda. Estimating the tradeoff between risk protection and moral hazard with a nonlinear budget set model of health insurance. International Journal of Industrial Organization. 2015;43:122–135. doi: 10.1016/j.ijindorg.2015.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Layton Timothy, Ellis Randall, McGuire Thomas. Assessing incentives for adverse selection in health plan payment systems. 2015 NBER Working Paper 21531. [Google Scholar]
- Layton Timothy, McGuire Thomas. Marketplace Plan Payment Options for Dealing with High-Cost Enrollees. American Journal of Health Economics. 2017 forthcoming. [Google Scholar]
- Layton Timothy, Ellis Randal, McGuire Thomas, Van Kleef Richard. Measuring efficiency of health plan payment systems in managed competition health insurance markets. Journal of Health Economics. 2017 doi: 10.1016/j.jhealeco.2017.05.004. forthcoming. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newhouse Joseph, Price Mary, Hsu John, Michael McWilliams J, McGuire Thomas. How much favorable selection is left in Medicare Advantage? American Journal of Health Economics. 2015;1(1):1–26. doi: 10.1162/AJHE_a_00001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahoney Neale, Glen Weyl E. Imperfect competition in selection markets. 2014 NBER Working Paper 20411. [Google Scholar]
- Polyakova Maria. Regulation of insurance with adverse selection and switching costs: Evidence from Medicare Part D. American Economic Journal: Applied Economics. 2015 forthcoming. [Google Scholar]
- Rothschild Michael, Stiglitz Joseph. Equilibrium in competitive insurance markets: An essay on the economics of imperfect information. Quarterly Journal of Economics. 1976;90:629–649. [Google Scholar]
- Shi Julie. Efficiency in plan choice with risk adjustment and premium discrimination in health insurance exchanges. mimeo, Harvard University; 2014. [Google Scholar]
- Shepard Mark. Hospital network competition and adverse selection: Evidence from the Massachusetts Health Insurance Exchange. mimeo, Harvard university; 2016. [Google Scholar]
- Sinaiko Anna, Hirth Richard. Consumers, health insurance, and dominated choice. Journal of Health Economics. 2011;30(2):450–457. doi: 10.1016/j.jhealeco.2010.12.008. [DOI] [PubMed] [Google Scholar]
- Spinnewijn Johannes. Heterogeneity, Demand for Insurance, and Adverse Selection. American Economic Journal: Economic Policy. 2017;9(1):308–43. [Google Scholar]
- Train Kenneth. Discrete Choice Methods with Simulation. New York, NY: Cambridge University Press; 2009. [Google Scholar]
- Van de Ven Wynand, Ellis Randall. Risk adjustment in competitive health plan markets. In: Culyer AJ, Newhouse JP, editors. Handbook of Health Economics. Amsterdam, Elsevier: 2000. [Google Scholar]
- Veiga Andre, Glen Weyl E. Product design in selection markets. Quarterly Journal of Economics. 2016;131(2):1007–1056. [Google Scholar]
- Zhu Jane, Layton Timothy, Sinaiko Anna, McGuire Thomas. The power of reinsurance in health insurance exchanges to improve the fit of the payment system and reduce incentives for adverse selection. Inquiry. 2013;50(4):255–274. doi: 10.1177/0046958014538913. [DOI] [PubMed] [Google Scholar]