T7 RNA polymerase translocation is facilitated by a helix opening on the fingers domain that may also prevent backtracking

Abstract

Here, we studied the complete process of a viral T7 RNA polymerase (RNAP) translocation on DNA during transcription elongation by implementing extensive all-atom molecular dynamics (MD) simulations to construct a Markov state model (MSM). Our studies show that translocation proceeds in a Brownian motion, and the RNAP thermally transits among multiple metastable states. We observed non-synchronized backbone movements of the nucleic acid (NA) chains with the RNA translocation accomplished first, while the template DNA lagged. Notably, both the O-helix and Y-helix on the fingers domain play key roles in facilitating NA translocation through the helix opening. The helix opening allows a key residue Tyr639 to become inserted into the active site, which pushes the RNA–DNA hybrid forward. Another key residue, Phe644, coordinates the downstream template DNA motions by stacking and un-stacking with a transition nucleotide (TN) and its adjacent nucleotide. Moreover, the O-helix opening at pre-translocation (pre-trans) likely resists backtracking. To test this hypothesis, we computationally designed mutants of T7 RNAP by replacing the amino acids on the O-helix with counterpart residues from a mitochondrial RNAP that is capable of backtracking. The current experimental results support the hypothesis.

INTRODUCTION

The RNA polymerase (RNAP) that transcribes genes from DNA to RNA has been suggested to function like a Brownian ratchet moving along a template DNA strand (1–4). At the end of each transcription elongation cycle, the RNAP translocates forward to vacate the active site and allow for the incorporation of the next nucleoside triphosphate (NTP). The translocation presumably oscillates back-and-forth via Brownian motion between the pre-translocation (pre-trans) and post-translocation (post-trans) states until an incoming NTP stably binds to the active site, which prevents the backward movement (see Figure 1A).

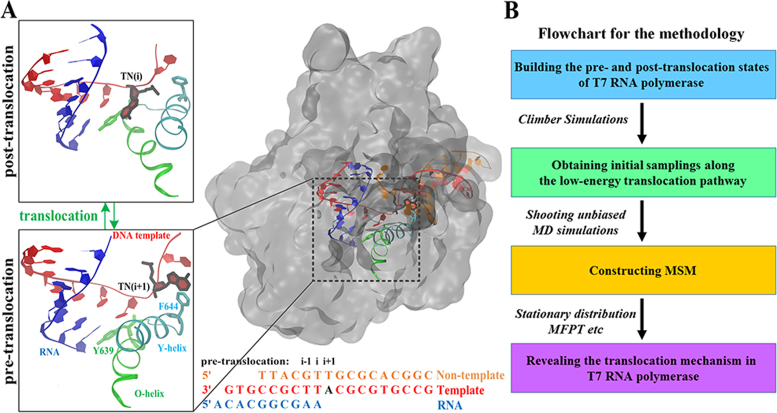
Figure 1.

Illustration of T7 RNAP translocation during transcription elongation and procedures used to construct a MSM from MD simulations. (A) T7 RNAP is represented in the transparent surface on the right panel with zoomed-in views around the active site for the modeled pre- and the post-trans states shown on the left panel. The essential structural components are shown in different colors (RNA in blue, non-template DNA in orange, and template DNA in red; TN in dark highlight; O-helix and Tyr639 in green; and the Y-helix and Phe644 in cyan). The DNA and RNA sequences used in this work are provided. (B) Computational procedures used for MSM constructions from MD simulations.

The viral RNAP from bacteriophage T7 is a prototypical single-subunit polymerase with a hand-like structure (see Figure 1A) (5,6) that has been characterized dynamically in experiments from transcription initiation to elongation and termination (7–10). A fingers domain on the T7 RNAP, which comprises a five-helix subdomain that includes an O-helix and a Y-helix, appears to be quite flexible and is able to open for NTP recruitment and close for catalysis in each transcription elongation cycle (11,12). Studies investigating high-resolution structures of T7 RNAP suggested that the translocation is mediated by a power stroke mechanism rather than a Brownian ratchet mechanism as follows: the product PPi release couples with the O-helix opening or the opening in the fingers domain, which directly drives the translocation (12). However, in our recent computational study on the PPi release of T7 RNAP, the PPi release did not couple tightly with the O-helix opening in the molecular dynamics (MD) simulation (13,14). In addition, the PPi release appears to be thermally activated but not energetically favored in the release channel. Hence, the PPi release is unlikely to directly drive or power the translocation.

Indeed, single molecule force measurements in T7 RNAP indicated that only a very small free energy bias (1–2k_BT) exists toward the post-trans state (9), thus supporting the Brownian ratchet mechanism. Accordingly, a structure-based kinetic model of T7 RNAP elongation was constructed (15). In addition to the Brownian ratchet scenario, the small post-trans free energy bias could help stabilize Tyr639 in the active site for an initial NPT screening or fidelity control. This hypothesis was then substantiated in another study exploring the Tyr639 selectivity upon an NTP pre-insertion (16). However, even though T7 RNAP showed equilibrium motions in the pre- and post-trans states in a previous MD study (17), the atomistic-level mechanism of the complete translocation process of T7 RNAP has not been elucidated.

Atomistic MD simulations of yeast RNAP II translocation revealed the Brownian nature of the translocation in multi-subunit RNAPs (18). The translocation is facilitated by bridge helix (BH) bending, which accelerates the movements of the upstream DNA/RNA hybrid chains via the key residue Tyr836 that stacks and un-stacks along with the transition nucleotide (TN) on the template DNA. The counterpart residue of Tyr836 in T7 RNAP is Phe644, which is located on the Y-helix and can form a direct contact with the TN during the pre-trans state (see Figure 1A). Moreover, in yeast RNAP II, an essential trigger loop (TL) opens and closes, which is analogous to the fingers domain opening and closing in T7 RNAP. Notably, the TL was set to open for the yeast RNAP II in the previous MD simulations (18) because it was determined that the translocation is viable only when the TL opens (13,19–21). It is then desirable to comparatively study the single-subunit T7 RNAP translocation to discern the Brownian or power stroke types of motion and determine whether and how the fingers helix subdomain motions are coupled with the translocation.

Additionally, backtracking has commonly been found in multi-subunit RNAPs. Backtracking plays a critical role in fidelity control, i.e. proofreading, and coordination with other physiological processes, such as mRNA folding and co-transcriptional translation (22–25). Backtracking also initiates from the pre-trans RNAP state from which the polymerase moves backward and opposite to the translocation direction. Nevertheless, in T7 RNAP, backtracking has not been detected to date, and it is highly likely that T7 RNAP does not backtrack. In contrast, the single-subunit mitochondrial RNAP (mt-RNAP), which is structurally similar to T7 RNAP, has been found to have pausing and backtracking activities (26). Hence, it would be highly interesting to probe the mechanisms leading to or preventing backtracking, particularly for the single-subunit RNAPs.

Here, by implementing extensive all-atom MD simulations and computational designing for mutagenesis experimental tests, we investigated the structural dynamic details of the T7 RNAP translocation and explored for potential of backtracking. The previous MD study in this system only revealed the nanosecond structural dynamics of the respective pre- and post-trans structures, which maintained the fingers domain in either the closed or open states but did not explore the transition from the pre-trans state to the post-trans state (17). In the current work, we launched several equilibrium MD simulations for a total of ten microseconds, covering a wide range of phase spaces where the complete translocation occurs. The RNAP complex was relaxed freely in the MD simulations to monitor the dynamics of the fingers domain involving the helix opening or closing motions. Finally, we collected many MD snapshots and established a Markov state model (MSM) using a time-structure independent component analysis (tICA) (27–30). The tICA can capture the principal dynamics of the conformational changes in a high-dimension configuration space (31–34). Our MSM revealed the key intermediate states, rate-limiting step(s) and dominant pathways during the translocation process. Moreover, we examined the mechanism of the coupling of the O-helix and Y-helix opening to the translocation, and based on these observations, we generated a hypothesis regarding the response of the O-helix to the RNAP backtracking. The hypothesis was tested both computationally and experimentally by mutating certain residues on the O-helix subdomain of the T7 RNAP to possibly design a mutant capable of backtracking.

MATERIALS AND METHODS

Based on the modeled pre- and post-trans states of the T7 RNAP elongation complexes (ECs), we first performed a Climber simulation (35) to obtain an initial low-energy translocation pathway. The conformations generated by the above-mentioned Climber simulation were then used as the initial seeds for the subsequent two rounds of equilibrium MD simulations. Finally, we used the dataset from the second round of MD simulations to construct the MSM and reveal the key intermediate states involved in the translocation process along with the associated thermodynamic and kinetic properties. The main procedures are summarized in Figure 1B. We additionally employed an isomap analysis (36) to determine whether the initial pathway dictates the actual translocation captured by the MSM.

Modeling the pre- and post-trans ECs of T7 RNAP

Crystallization studies have obtained the high-resolution structures of the T7 RNAP ECs during transcription elongation in the following different states: post-trans, pre-insertion, substrate or insertion, and the product (PPi)-bound state (PDB IDs: 1MSW, 1S0V, 1S76, and 1S77, respectively) (11,12,37). To study the translocation process, we established the pre- and post-trans states based on the crystal structures of the PPi-bound (PDB ID: 1S77) (12) and post-trans ECs (PDB ID: 1MSW) (37), respectively. In our modeled pre-trans state (see Figure 1A, left panel), the RNA nascent chain contains ten nucleotides (3΄-AAGCGGCACA-5΄), the DNA template strand is 19-mers (3΄- GTGCCGCTTACGCGTGCCG-5΄), and the non-template strand is 16-mers (3΄-CGGCACGCGTTGCATT-5΄). The missing residues were added based on the pre-insertion structure of T7 RNAP (PDB ID: 1S0V) (11). In the post-trans EC, we modified the original DNA/RNA sequences to be consistent with those used in the above-mentioned modeled pre-trans structure and shifted the DNA/RNA chains by one base step forward accordingly (see Figure 1A, left panel). In both the pre- and post-trans EC simulations, we placed one PPi group at the end of its releasing pathway at the interface between the protein and the bulk water because our previous study (14) revealed that the PPi release occurs prior to substantial conformational changes involved in the translocation.

Building an initial low-energy translocation pathway

Based on the modeled pre- and post-trans structures, we first obtained an initial low-energy translocation pathway using a modified version of the Climber algorithm (35). We selected the fingers domain (residues from 554 to 812) and all DNA/RNA chains as the morphed regions since these regions undergo substantial conformational changes before and after the translocation as observed from the crystal structures (12,37). During the Climber simulation, the external forces were applied only to the atoms in the morphed region, whereas the remainder of the system could respond to the structural changes in the morphed region during each morphing cycle. The target number of morphing cycles was set to 1200, and each morphing cycle consisted of 100 iterations of morphing with 10 steps of conjugate gradient-energy minimization for each 10 morphing iterations. The minimum distance (root mean square deviation, RMSD = 0.5 Å) to the target structure was reached after 600 morphing cycles. Finally, to generate the starting conformations for the subsequent MD simulations, we chose 20 representative structures from the above-mentioned Climber simulation using the k-centers clustering algorithm implemented in the MSMbuilder software (38–40). The chosen distance metric consisted of the RMSD values of the heavy atoms of the TN and the two adjacent nucleotides (nts), the heavy atoms of the RNA 3΄-end nt, and the Cα atoms of 64 residues in the fingers domain (residues 627–690). Then, we chose a central conformation for each cluster as the representative structure.

Seeding unbiased MD simulations

We performed two rounds of MD simulations. The first round of MD simulations was initiated from the 20 representative conformations obtained from the Climbing simulation (20 × 20 ns NPT simulations at 1 bar, 310 K). To eliminate the biases introduced by the Climber simulations, we selected 100 representative conformations from the first round of MD simulations (see upper right in Supplementary Figure S1). To ensure that we included enough transitions between the different states, we randomly selected 30 additional conformations from the first round of MD simulations (see upper right in Supplementary Figure S1). We then used these 130 conformations as the starting structures for the second round of MD simulations (NPT simulations at 1 bar, 310 K). Finally, we only used the dataset from the second round of simulations to construct the MSM. However, one particular trajectory generated from one of the 30 additional MD conformations had no direct transitions to other MD trajectories, which prohibited the construction of a connected transition network. Thus, we removed this particular trajectory from our model construction. Therefore, in total, we used 129 MD trajectories (129 × 80 ns ∼10.3 μs) for the MSM construction.

All MD simulations were performed using the GROMACS-5.1 software package (41–43). The AMBER99sb force field with PARMBSC0 nucleic acid parameters (44–47) was used to describe the system. The glycosidic angles of most of the RNA nucleotides adopted an anti-form in the simulation (48), except for the unstably paired i-site nucleotide, which demonstrated that the PARMBSC0 force field can describe the DNA/RNA hybrid system well. The whole cubic simulation box contained 29,300 Tip3p water molecules. To neutralize the electrostatic charges of the system and maintain the ionic concentration at 0.15 M, 139 Na⁺ ions and 94 Cl^– ions were added. The final system contained a total of 103,146 atoms. The cut-off values for the van der Waals (vdW) and short-range electrostatic interactions were set to 10 Å. Long-range electrostatic interactions were treated using the Particle-Mesh Ewald method (49). The neighbor list was updated after every five steps, and the time step was 2 fs.

For the first round of MD simulations, we adopted the following procedure for each of the 20 starting conformations: (i) 2000 steps of energy minimization using the steepest descent algorithm; (ii) 500 ps of NPT equilibration by position restraining the heavy atoms of the system with a force constant of 1000 kJ mol⁻¹ nm². The temperature was maintained at 310 K using a velocity rescaling thermostat (50) with a coupling constant of 0.1 ps⁻¹; and (iii) production runs of 20-ns NPT MD simulations were conducted at 310 K and 1 atm using the velocity rescaling thermostat and the Parrinello-Rahman Barostat (51,52), respectively.

We then applied the k-centers clustering algorithm to cluster the MD conformations obtained during the first round of MD simulations into 100 groups. Before the clustering, the first 5-ns simulation data of each 20-ns MD trajectory were discarded to eliminate the bias from the Climber simulation. We then chose the central conformation of each of the 100 clusters as the representative conformation and added another 29 conformations to increase the transition counts between certain regions. Finally, these 129 conformations were used to perform the second round of MD simulations. The MD setup was the same as that used during the first round, and the production runs were set to 80 ns each.

Finally, we performed an isomap analysis by projecting the representative conformations obtained by the Climber simulation and those obtained by the unbiased MD simulations onto the three top isomap vectors (36). The MD conformations substantially deviated from the initial translocation pathway obtained by the Climber simulation, and the 2D isomap projections for the five sub-datasets obtained by the MD simulations became similar (see Supplementary Figure S2). Thus, the analysis indicated that our samplings reached convergence reasonably well, and the unbiased MD simulations had successively eliminated the bias introduced by the Climber simulation.

Construction and validation of the MSM

The MSM has been used to investigate the dynamics of biomolecular systems (32–34,53–57) by discretizing both the conformational space and time; therefore, the transitions between different metastable states can be described by a Markovian process under a certain lag time (Δt) using the following master equation:

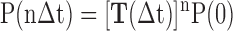(1)

where P(nΔt) represents the state distribution at time nΔt, and T represents the transition probability matrix that is built under a certain lag time Δt. The MSM partitions the high-dimensional conformational space into hundreds of discrete metastable states such that within each state, the transitions between different conformations are relatively fast compared with the inter-state transitions. To avoid the intra-state barriers, the chosen lag time (or Markovian time), Δt, should be sufficiently larger than the slowest timescales that take place within any state. Thus, the transition probability from any state i to another state j (T_ij) after a certain lag time Δt is dependent only on the current state i but not on the states it had previously visited. The transition probability matrix T can be constructed by performing extensive short-time MD simulations within the phase space. Then, by propagating Equation (1) to a given time of interest, we can simulate the stochastic transitions of the systems among the different metastable states.

Here, we first discretized the conformational space by projecting the high-dimensional conformations onto a low-dimensional space using tICA (27,28). We then grouped the projected conformations into various numbers of microstates by applying the k-centers clustering algorithm. Then, we generated implied timescale plots to choose the appropriate Markovian time for the MSM construction. After the model construction, we also performed a Chapman–Kolmogorov test to validate the model (58). The detailed procedures of the MSM construction and validation were as follows.

Clustering the MD conformations into microstates

tICA, which is a dimension-reduction technique, can successively be used to detect the slowest and de-correlated dynamics in a system by calculating the time-lag correlation matrix (27,28). A similar method, principle component analysis (PCA), however, cannot guarantee that the slowest event is constantly top-ranked in its ordered eigen-functions. Therefore, the tICA is an appealing tool for reducing a high-dimensional dataset to low dimensions when constructing an MSM (29,30). To apply the tICA in our study, we chose a total of 2394 distances between the following atom pairs as the input dataset for the dimension reduction because these parts are closely coupled with the overall translocation process (see Supplementary Figure S3):

Heavy atoms of the TN —— CA atom of three helices in the fingers domain (residues 627–688).

Heavy atoms of the TN —— Heavy atoms of the ±1 surrounding nts of the TN.

Heavy atoms of the TN —— Heavy atoms of the side chain of Y639.

Heavy atoms of the TN —— Heavy atoms of the side chain of F644.

We then projected the MD conformations (∼900,000) onto the four slowest tICA components based on the above-mentioned distance metrics. As shown in Supplementary Figure S1 (upper panel), the MD conformations were projected onto the two slowest tICs. The free energy landscape plot clearly shows that the first tIC dictates the transition between the pre-trans and post-trans states, i.e. the overall translocation process. In particular, the largest correlation component with the first tIC contributes to the distance between the TN (N6) and its upstream adjacent DNA nucleotide (O4) (see Supplementary Figure S4). Similarly, we determined that the largest anti-correlation component with the second tIC (see Supplementary Figure S4) corresponds to the distance between the TN (O4΄) and the Y-helix residue Gly645 (C_α), which likely reflects the coupling motions between the TN and the Y-helix.

Finally, we grouped the projected conformations onto different numbers of microstates using the k-centers clustering algorithm.

Validation of the MSM

To evaluate the discretization effects on the kinetic properties and the robustness of the MSM, we performed tICA at three different correlation lag times (10 ns, 20 ns and 30 ns). For each lag time, we constructed four MSMs using the following different microstate numbers: 500, 600, 700 and 800. We finally calculated the implied timescale plot for each of the MSM (see Supplementary Figure S5) using the following equation:

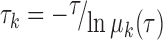(2)

where μ_k is the kth eigenvalue of the transition probability matrix T with lag time τ. Each implied timescale curve represents the average transition time between two sets of states. Therefore, the slowest dynamics in the conformational changes correspond to the largest τ_k. All implied timescale curves leveled off after a lag time of 10 ns regardless of the microstate number, and the slowest transition converged to a timescale of ∼10 μs, suggesting that the model is robust regardless of the numbers of the microstates (see Supplementary Figure S5). Furthermore, we performed a Chapman–Kolmogorov test (58) to validate our model. The test showed that the evolution of the residence probability of several of the most-populated microstates observed from the raw MD simulations data matched very well with the values predicted by the MSM (see Supplementary Figure S6).

Finally, to visualize the intermediate states during the translocation, we chose the 500-state model to lump the microstates into six macro-states using the PCCA+ method (59).

Calculating the mean first passage time (MFPT), stationary distributions and forward translocation flux

We calculated the MFPT between each pair of metastable states and the stationary distributions in each state by first generating a long 10-ms Monte-Carlo (MC) trajectory based on a transition probability matrix constructed using the 500-state MSM under the lag time of 10 ns. The MC trajectory is sufficiently long to be considered well equilibrated. Consequently, the MFPT and the equilibrated populations can be derived from the long MC simulation. Notably, we refined our MFPT calculation by first collecting all MFPT values from the MC trajectory for a certain transition and then truncating the very small and very large MFPT values according to the histogram distributions. Thus, we avoided the non-Markovian issue in the macro-state construction and obtained a high-quality linear regression according to the Poisson distribution as conducted in our previous work (13,14). To estimate the statistical errors of the above-mentioned properties, we adopted the ‘bootstrapping’ approach to re-sample the trajectory list 100 times. For each bootstrapping, we randomly chose 129 trajectories from the original trajectory list (with replacement), and then, based on the new trajectory list, we re-calculated the MFPT and the equilibrated populations by creating a new 10-ms MC trajectory. Finally, the mean values of the MFPT and the populations were calculated by averaging the 100 sampled datasets, and the corresponding standard errors were also obtained.

In addition, we calculated the forward translocation flux in the macro-state transition network (58) based on the transition path theory (60,61). The translocation flux was attributed to the fraction of the transitions that started from the pre-trans state and ended at the post-trans state without any detouring. The dominant pathway could then be determined by ranking the relative probabilities of all possible translocation pathways based on the calculated fluxes.

Convergence of MD simulation data for the MSM construction

To verify that our datasets were sufficient for constructing a reliable MSM, we performed a convergence test by projecting the conformations onto the two slowest tICs using datasets with aggregated simulation times of 5.2, 6.5, 7.7, 9.0 and 10.3 μs. As shown in Supplementary Figure S1 (lower panel), we observed that the projection of the free energy landscape achieved a reasonable convergence without additional metastable regions emerging from the increasing datasets. Then, to evaluate the stability of the model, we constructed MSMs for each of the abovementioned sub-datasets. As shown in Supplementary Figure S5 (lower panel), the implied timescale plots for the different models were consistent, and all indicated that the slowest transition occurs at a timescale of approximately tens of microseconds.

Performing steered MD (SMD) simulations to generate a frayed state of the RNA 3΄-end nucleotide in T7 RNAP EC

Recent structural and computational studies revealed a ‘frayed’ state (not yet backtracked) during the RNAP II backtracking process (62,63). In this frayed state, the RNA 3΄-end nt flipped from the active site, which was considered a metastable state before the backtracking completed. To understand why T7 RNAP does not backtrack, we generated a frayed 3΄-end RNA nt by performing SMD simulations (64). First, the pre-trans state of T7 RNAP was modeled based on the product state crystal structure (PDB ID: 1S77) by removing the PPi group (5). Then, we applied SMD simulations to pull the RNA 3΄-end nt from the active site to obtain a frayed conformation An external force was applied to the center of the mass (COM) of the RNA 3΄-end nt toward the COM of two separated structural elements, including the Cα atoms of residues 482–486 and residues 627–633 (see Supplementary Figure S7), with a force constant of 10 kJ/mol/Ų and a pulling rate 0.001 Å/ps. During the SMD, 100 kJ/mol/Å force restraints in the x, y and z directions were imposed on the COM of the protein to stabilize the protein complex in a water box. To determine the responses of the system to the fraying of the RNA 3’-end, we then equilibrated the frayed state structure (without adding external forces) by performing 200-ns MD simulations.

MD simulation of several mutant T7 RNAP ECs with the RNA 3΄-end nucleotide in a frayed state

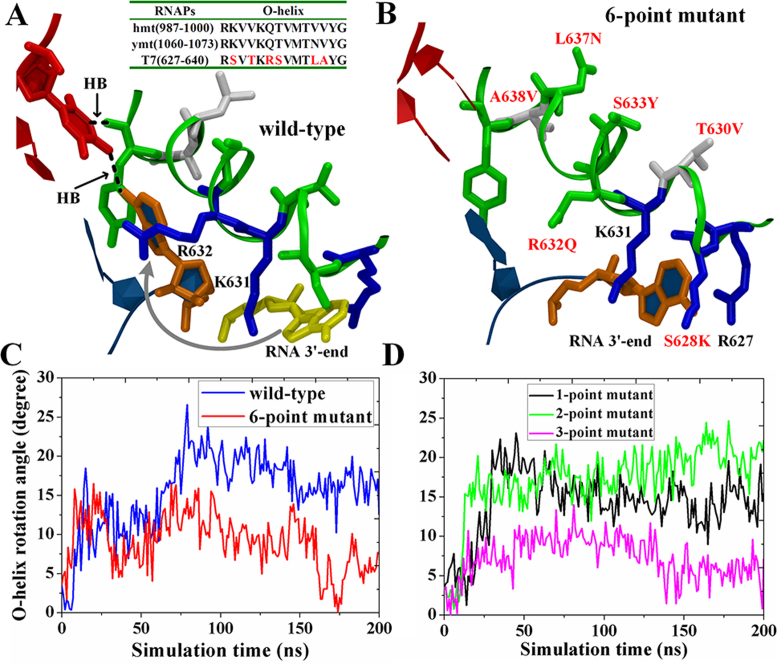
T7 RNAP shares structural similarities with mitochondrial RNAPs (mt-RNAPs) as shown in the structural alignment of the T7 RNAP and human mt-RNAP (see Supplementary Figure S8). Although it is unlikely that T7 RNAP backtracks, the yeast mt-RNAP was shown to backtrack by single molecule experiments (26). Sequence alignments revealed that T7 RNAP has six residues on the O-helix that are different from those of the yeast mt-RNAP (and only one residue is different between the human and yeast mt-RNAP). Therefore, we hypothesized that by mutating the six different residues in T7 RNAP into the corresponding ones in the mt-RNAP, the mutant T7 RNAP may show a tendency to backtrack. Several mutant T7 RNAP structures were thus constructed based on the abovementioned modeled frayed state, including a six-point mutant (S628K, T630V, R632G, S633T, L637N and A638V) and mutants with fewer mutations from one (S628K) to two (S628K and T630V) and three (S628K, T630V and R632G) point mutations because these mutations gradually move from the N-terminal end of the O-helix to the C-terminal end. The mutant protein structures were generated by changing the side chain of the amino acid residues using the Tleap method in Amber tools (65). Finally, for each mutant and wild-type (wt) frayed state, we performed three independent 200-ns MD simulations to investigate the dynamic properties.

T7 RNAP and mutant (6-point) purification

The T7 RNAP coding sequence was subcloned into the pET-28a vector (Novagen, USA), containing an N-terminal 6x-his tag, and the plasmid was transformed into E. coli strain BL21 (DE3) cells. For the protein purification, the cells were harvested from a 1-liter LB (Luria-Bertani) medium after an 18-h incubation (at 16°C) and re-suspended with the binding buffer (1 M NaCl and 25 mM Tris–HCl, pH 8.0). The re-suspended cells were sonicated in an ice box and then centrifuged at 20 000 rpm for an hour in a Beckman JA25.50 centrifuge rotor to separate the cell debris. T7 RNAP was first purified by HisTrapTM (GE, USA) with an elution buffer (1 M NaCl, 25 mM Tris–HCl, and 250 mM imidazole, pH 8.0). Then, the eluent was concentrated, loaded onto a Superdex 200TM (GE, USA) column, purified by gel filtration (see Supplementary Figure S9A) with a low salt buffer (500 mM NaCl and 25 mM Tris–HCl, pH 8.0) and then dialyzed against the storage buffer (66) (20 mM K₃PO₄, 100 mM NaCl, 10 mM DTT, 0.1 mM EDTA and 5% glycerol). The protein purity was verified by 8% SDS-PAGE (polyacrylamide gel electrophoresis) as shown in Supplementary Figure S9B.

In vitro transcription preliminary test

Transcription reactions were performed in a volume of 20 μl containing 1X RNApol reaction buffer (NEB); 1 mM GTP, CTP, UTP and ATP; 1 ng plasmid template; 15 μM SYTO RNA selected dye (Invitrogen); and 1 mg RNAP. The reactions were pre-warmed at 37°C for 2 min and initiated by the addition of RNAP. The fluorescence emission at 530 nm was recorded at 30 s intervals at least 30 times.

RESULTS

Below, we demonstrate the main simulation results according to the MSM construction, which revealed the dominant T7 RNAP translocation pathways, key intermediate states, and associated structural and kinetic features. Additionally, to investigate the mechanism preventing the backtracking of T7 RNAP, we explored O-helix responses to an enforced fraying of the RNA 3΄-end nt and describe the design of the mutant T7 RNAPs used to explore the backtracking tendency.

The MSM reveals Brownian translocation pathways

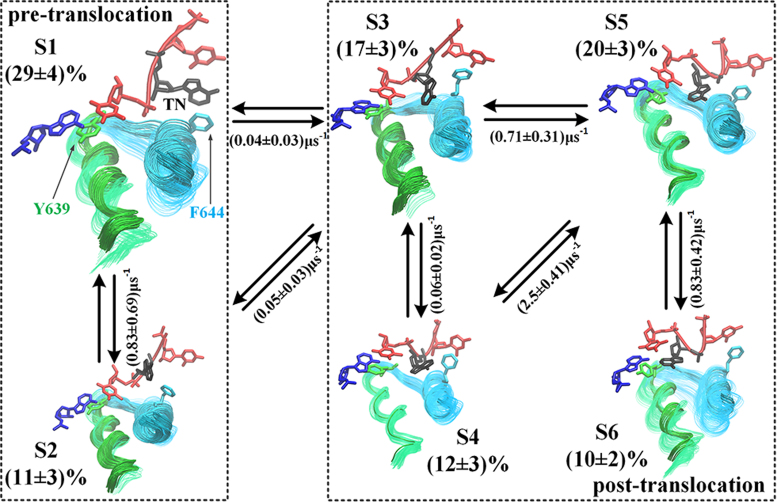
Using the tICA with the MSM construction, we built a six-state transition network to represent the T7 RNAP translocation (see Figure 2), which included the pre-trans state (S1, ∼29%) and a pre-alike intermediate (S2, ∼11%), a key translocation intermediate (S3, ∼17%), an off-path intermediate (S4, ∼12%), a post-alike intermediate (S5, ∼20%), and the post-trans state (S6, ∼10%). All state populations varied only by several fold within an order of magnitude, which indicated quasi-equal free energetics in the transition network. Additionally, based on the transition path theory (60,61), we calculated the forward translocation flux in the six-state transition network (58) and identified that the dominant translocation path follows S1↔S2↔S3↔S5↔S6 (44%; see SI Movie S1). In addition, two alternative paths, i.e. S1↔S3↔S5↔S6 and S1↔S3↔S4↔S5↔S6, were also identified (30% and 25%). On the dominant path, the transition between S2 and S3 is the rate-limiting step (∼20 μs) linking the pre- (S1 and S2) and post-trans configurations (S3 to S6). A further partition of the six states into the two groups (pre- and post-trans) was supported by measuring the distance between the TN and its adjacent nt upstream or between the TN and Tyr639, which is located around the active site (see Supplementary Figure S10A and B). Notably, the overall pre- and post-trans populations are approximately equal (∼40% and 60%), with only a slight bias toward the post-trans configurations.

Figure 2.

The T7 RNAP translocation pathways and representative structural intermediates obtained from the MSM. The six macro-states are shown from S1 (the pre-trans state) to S6 (the post-trans state), and the size of the conformation image is nearly proportional to the corresponding equilibrated populations. The populations and kinetic rates (approximated by the inverse of the MFPTs between the macro-states) calculated by the MSM are provided. The dominant translocation pathway identified was S1 ↔ S2 ↔ S3↔ S5 ↔ S6. The two rectangles in the dashed lines separate the overall pre-trans and post-trans alike configurations. In each structural snapshot, the O-helix is colored in green and the Y-helix is colored in cyan; the light and dark coloring represents the opened and closed conformations, respectively; the two critical amino acids Y639 and F644 are shown in green and cyan, respectively; the RNA 3΄-end nt is shown in blue, the template DNA is shown in red, and the TN on the template DNA is shown in black.

In particular, we found that in S1, the pre-trans state, the TN stacks well with Phe644 from the Y-helix; the O-helix along with the full fingers domain oscillates largely from the closed to the open configuration. In S2, the pre-alike state, however, the TN-Phe644 stacking is broken, and the fingers domain becomes largely closed. Notably, in S3, the key translocation intermediate state, the Y-helix opens significantly, whereas the O-helix remains closed, and the synthesizing RNA strand reaches the post-trans configuration (see next subsection). Throughout S3, the overall fingers domain opens substantially in the remaining states (S4 to S6). The template DNA strand moves to the post-trans configuration in S5, while the TN completes the translocation in S6.

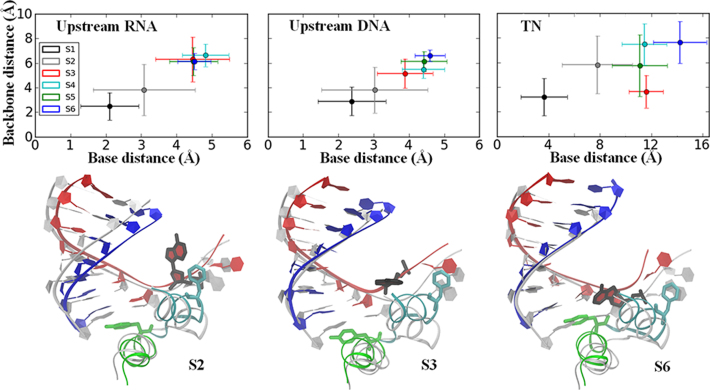
The RNA moves to the post-trans configuration first while the template DNA lags slightly behind

Interestingly, the movements of the RNA and DNA strands occur in a non-synchronized manner. The upstream RNA–DNA hybrid starts the translocation from S1 to S2 (see Figure 3) during which Phe644 un-stacks from the TN to allow for the translocation to occur (see Supplementary Figure S10C).

Figure 3.

Translocation of the upstream RNA/DNA strands occurs in a non-synchronized manner. The translocation distances on the upstream RNA/template DNA and the TN movements in each intermediate state are shown in the upper panel. The translocation distances were measured as the RMSDs to a pre-trans reference structure for the backbone P atom (backbone distance) and the heavy atoms of the nucleotide base (base distance) averaged within each macro-state (error bars represent the standard deviation). For the upstream RNA chain (upper left) and DNA chain (upper middle), the distances were the averages of seven upstream RNA and DNA nucleotides (from i to i – 6 sites, see Supplementary Figure S11). The translocation distance of the TN on the template DNA is shown in the upper right. Structural alignments of one representative conformation from S2, S3 and S6 with the pre-trans reference structure (gray) are shown in the lower panel. The color coding of the S2, S3 and S6 structures is the same as that shown in Figure 1. A different view of each representative conformation is also provided in Supplementary Figure S12.

Notably, the translocation of the RNA and the template DNA de-synchronizes in the rate-limiting transition from S2 to S3 (or directly from S1 to S3) as follows: the RNA strand moves completely to the post-trans configuration in S3, while the template DNA strand slightly lags (see Figure 3). The delayed movements of the upstream template DNA strand are mainly attributed to the nts near the active site (see Supplementary Figure S11B). In addition, the downstream template DNA, particularly the backbone of the TN, does not move significantly upon transition to S3. Further examination of S3 shows that Phe644 stacks with the downstream template DNA nt adjacent to the TN (see Figure 3 and Supplementary Figure S10D), which essentially hinders DNA movement in S3. Hence, the RNA translocation completes during the first stage, i.e., from S1 to S3, via S2 or directly (see Supplementary Figure S11A); the upstream DNA chain, however, is delayed. The unpacking of Phe644 from the TN allows for the RNA–DNA hybrid translocation to occur during this stage. During the second stage, further translocation of the template DNA from S3 to S5 is then enabled by the unpacking of Phe644 from the downstream nt of the TN. Finally, the relaxation of the template DNA chain and the TN concludes the translocation in S6 (see Figure 3). An additional view showing the non-synchronized motions of the RNA and template DNA strands is provided in Supplementary Figure S12.

The translocation is essentially supported by either the O-helix or Y-helix opening

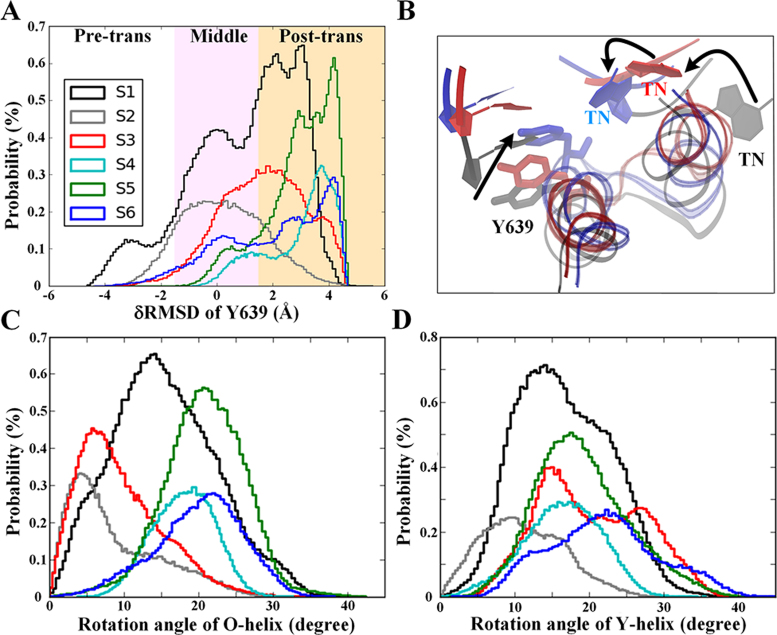
Finally, we focused on identifying the key structural components that support the translocation. As previously mentioned, the unpacking between Phe644 and the TN enables the first-stage translocation through the S1 → S2 transition. In S1, we unexpectedly found that the O-helix could transition from the closed to the open configuration (see Figure 4C), which coordinated very well with the oscillations of residue Tyr639, located on the C-terminus of the O-helix (see Figure 4A). Indeed, a robust correlation exists between the O-helix opening and the Tyr639 post-trans configuration in the S1 state (see Supplementary Figure S13A). However, in S1, the active site is still occupied by the 3΄-end RNA nt. Therefore, the oscillation of the Tyr639 side chain toward the post-trans configuration, which is facilitated by the O-helix opening motions, also helps push the upstream DNA/RNA chains forward for the initial translocation (see Figure 3).

Figure 4.

Opening motions of the O-helix or Y-helix facilitate the T7 RNAP translocation. Statistics of Tyr639 movements (A) along with a zoomed-in structural view (B) and rotational angles of the O-helix (C) and Y-helix (D) sampled along the translocation pathway from S1 to S6. The Y639 movements were monitored by the δRMSD between the pre- and post-trans configurations (A), i.e. δRMSD ≡ RMSD_conf-pre-RMSD_conf-post, where RMSD_conf-pre and RMSD_conf-post represent the RMSD of the current conformation of Y639 to that of the pre-trans and post-trans reference structure, respectively. In the zoomed-in structural view showing Tyr639, the O/Y-helix, and TN, the pre-trans structure is shown in grey, the post-trans structure is shown in blue, and the intermediate structure (S3) is shown in red.

In the transition from S2 → S3, we observed that the opening of the Y-helix, which is also accompanied by the pre- to post-trans of Tyr639, further promotes the upstream DNA/RNA movements, particularly for the RNA chain that largely reaches the post-trans configuration in S3 (see Figures 3 and 4). The pre- to post-trans movement of Tyr639 is correlated with the opening of the Y-helix in S3 (Supplementary Figure S13B). Notably, even though the O-helix remains fairly closed in both S2 and S3 (see Figure 4C), the pushing exerted by Tyr639 on the RNA/DNA translocation can still be supported by the Y-helix opening motions. A structural inspection shows that the loop region between Tyr639 and Phe644 indeed propagates the Y-helix opening motions toward Tyr639 to enable the coordination (see Figure 4B). Moreover, the opening of the Y-helix in the S3 state allows residue Phe644 to form hydrophobic packing interactions with the downstream template DNA nt adjacent to the TN, which leads to a delay in the upstream DNA translocation (see Figure 3).

Finally, for the transitions from S3 to S6, the substantial opening of the O-helix, which facilitates the insertion of Tyr639 into the active site, also allows the DNA chains to enter the post-trans configuration (see Figures 3 and 4A). Consistently, we found that residue Tyr639 adopts a post-trans configuration in the S4 to S6 states during which it can directly stack or push onto the base pair (bp) at the end of the RNA–DNA hybrid near the active center (see Figure 4A and Supplementary Figure S14), which is also observed in the post-trans crystal structure of T7 RNAP (PDB: 1MSW) (37).

Taken together, the opening of either the O-helix (i.e., from S1 → S2 and S3 → S6 transitions) or Y-helix (from S2 → S3 transition) can promote the translocation. During the translocation, two key residues, i.e., Phe644 on the Y-helix and Tyr639 on the O-helix, play essential roles in regulating the RNA/DNA movements by forming stacking interactions between their hydrophobic ring and the DNA or RNA bases.

The O-helix opening resists the fraying of the RNA 3΄-end nucleotide for backtracking

We noticed that the O-helix can frequently open and close in the pre-trans state S1. To determine the reactions of the O-helix to the potential backtracking of the polymerase, we conducted an SMD simulation of the pre-trans complex (in S1 with a closed O-helix) and pulled the 3΄-end of the RNA strand ‘backward’ along the product exit channel, roughly following the O-helix from its C-terminus toward the N-terminus. The procedure created a ‘frayed’ end in the RNA transcript, which was captured by the backtracking complex of yeast RNAP II (62) and was suggested to be an important intermediate state prior to complete backtracking (63). At the end of the pulling simulation, we allowed the system to relax and monitored the ensuing responses.

Interestingly, we noticed that the modeled frayed RNA 3΄-end nt quickly withdrew to the active site (see Figure 5A). This withdrawal was mainly due to the opening motion of the O-helix, which allowed residues K631 and R632 to rotate and paved the way for the 3΄-end nt to re-track. In addition, we also noticed that the re-tracked 3΄-end RNA base re-covered pairing or hydrogen bonding with the DNA template nt, while this DNA template nt formed another hydrogen bonding with the backbone oxygen of Tyr639 (see Figure 5A and Supplementary Figure S15). These features suggested that the wt T7 RNAP resists backtracking in the pre-trans state.

Figure 5.

An unbiased simulation of the ‘frayed’ state after an SMD simulation that pulled the RNA 3΄-end backward to mimic the onset of backtracking. (A and B) The molecular views of the active site region along with the O-helix (green ribbon) and the RNA–DNA hybrid end (RNA in blue with the 3΄-end nt in orange; DNA in red). For the wt T7 RNAP (A), the RNA 3΄-end nt quickly withdrew back to the active site as indicated by the arrow. A sequence alignment of T7 RNAP and the mtRNAPs is shown on the top. For the six-point mutant (B), the RNA 3΄-end nt was stable in the ‘frayed’ state. The O-helix residues are colored according to the polar/nonpolar (in green/while) and charged status (negative/positive in red/blue). (C and D) The O-helix opening angles observed in the unbiased simulations of the wt-T7 RNAP (blue), the six-point mutant (red), the one-point mutant (S628K, black), the two-point mutant (S628K and T630V, green) and the three-point mutant (S628K, T630V, and R632G, magenta).

The above-mentioned results demonstrate the importance of the O-helix in regulating the DNA backbone movements, i.e., facilitating the forward translocation while preventing backtracking. Since some other single-subunit RNAPs endowed with a fingers domain and an O-helix, e.g. the mt-RNAP, can backtrack (26), we speculated whether a mutant T7 RNAP could be designed that might also backtrack. Therefore, we created six-point mutations in the O-helix of T7 RNAP (in the modeled ‘frayed’ state) that are sequence-wise identical to the O-helix from the mt-RNAP (67). We then performed unbiased MD simulation as conducted for the wt-RNAP. Remarkably, we observed that the ‘frayed’ 3΄-end RNA nt was maintained stable by forming hydrophobic interactions with -CH2- groups of K631, K628 and R627 (see Figure 5B). Notably, unlike the wt-RNAP, the O-helix in the mutant RNAP maintained a stably closed form and could not open any further (see Figure 5C and Supplementary movies S2 and S3). In addition, the hydrogen bonding interaction between the template nt and the backbone oxygen of Tyr639 that appeared in the wt-RNAP was abolished (see Supplementary Figure S15). The results accordingly suggested that the resistance to backtracking was relieved in the six-point mutant of T7 RNAP. Notably, our current experimental tests showed that the six-point mutant of T7 RNAP would still actively transcribe (SI and Supplementary Figure S16), and the mutant transcription activity was slightly suppressed compared with that of the wt T7 RNAP.

To locate the critical point mutations responsible for the substantial changes, we also constructed mutants with a subset of mutations and compared these mutants with the above-mentioned six-point mutant. We found that when three point mutations were established in the N-terminal end of the O-helix (S628K, T630V and R632G), the mutant behaved similarly to the six-point mutant in the simulation as follows: the frayed 3΄-end of the RNA could be stabilized to the N-terminal O-helix, and the O-helix would not open. In contrast, the one or single-point mutant (S628K) and the two-point or double mutant (S628K and T630V) could not resist the O-helix opening, although they allowed the frayed RNA 3΄-end to remain in the N-term O-helix. Hence, it appears that at least three mutations are required in the O-helix for the mutant T7 RNAP to behave similarly to the six-point mutant or the mt-RNAP. We repeated these simulations three times each to simulate the systems of the wt-T7 RNAP and single, double, triple and the six-point mutants. All independent simulation runs showed consistent results (see Supplementary Figure S17).

DISCUSSION

Based on extensive all-atom MD simulations and the constructed MSM, we showed that the T7 RNAP translocation on DNA follows quasi-equal free energy pathways, supporting a Brownian ratchet scenario in which the movements are Brownian. The overall pre- and post-trans populations were approximately equal with a slight bias toward the post-trans configuration, which is consistent with previous experimental and modeling analyses (9,15). The rate-limiting transition from the pre- or the pre-alike configuration to the translocation intermediate occurred over tens of microseconds (∼20 μs).

In particular, the fingers domain oscillated between the closed and open conformations significantly in the pre-trans state, which was unexpected based on previous structural studies (5,12,37). In the high-resolution structure of the T7 RNAP EC at the product state prior to the translocation (12), the fingers domain, along with the O-helix, was captured in the closed conformation, while the open conformation was only captured in the post-trans complex (37). Our previous computational studies (14) showed that the PPi release from the product complex does not immediately trigger the O-helix opening as expected in a power stroke scenario (12). However, the release of PPi likely enhances the flexibility of the O-helix; therefore, both the closed and open forms of the O-helix/fingers domain were observed in the pre-trans EC in our simulations.

The translocation was then enabled by un-stacking the TN base from Phe644, which is located on the N-terminus of the Y-helix. The Y-helix appears to be a structural analog of a segment of the BH in the multi-subunit RNAP II, which was shown to facilitate the translocation by its continuous bending motions (18). The Y-helix in the single-subunit T7 RNAP, however, is much shorter than the full BH from RNAP II; therefore, it cannot bend as the BH does. Instead, the Y-helix can undergo substantial opening/closing motions that facilitate the upstream DNA/RNA translocation (i.e. for S2 → S3 transition). Moreover, Phe644 on the Y-helix appears to play a role to a certain extent that is similar to that played by Tyr836 on the BH as the side ring of this residue stacks with the TN and then un-stacks during the translocation. Nevertheless, the TN-Phe644 unpacking is not a rate-limiting step as is the Tyr836 unpacking transition in RNAP II (18), although it is indispensable for the translocation in T7 RNAP.

The essential structural dynamic component identified to facilitate the T7 RNAP translocation involved Tyr639 oscillation from the pre- to post-trans configuration (referred to as the side chain OUT to IN movement in (15)), which is supported by the helix opening on the fingers domain. Tyr639 is located on the C-terminus of the O-helix, and according to the crystal structures (5,12), the pre- and post-trans configurations of Tyr639 accompany the closed and open conformations of the O-helix or fingers domain, respectively. In the pre-trans configuration, Tyr639 stays slightly distant from the end bp of the DNA-RNA hybrid and away from the active site (OUT). In the post-trans configuration, in contrast, the Tyr639 side chain becomes inserted into the active site (IN) and likely stacks with the base of the RNA 3΄-end or, occasionally, the template DNA base. Hence, it is reasonable that Tyr639 can ‘push’ onto the RNA–DNA hybrid during the translocation as demonstrated in our simulations.

Interestingly, we noticed that the O-helix opening supports the Tyr639 switching from the pre- to the post-trans configuration, but the Y-helix opening also supported the Tyr639 switching even when the O-helix closed as occurs in the key translocation intermediate state (S3). The structural coordination originates from the loop region between the C-terminus of the O-helix and the N-terminus of the Y-helix, which links the two helices and propagates the rotational opening motions of the Y-helix to the Tyr639 side chain. Upon the Tyr639 stacking onto the end of the RNA–DNA hybrid, the translocation barrier lowers to facilitate the process. In addition, our results indicated that the pushing onto the RNA–DNA hybrid by the Tyr639 side chain during the translocation may help provide a slight free energy bias toward the post-trans state as previously suggested (15). Consequently, Tyr639 is stabilized in the active site at the post-trans to perform an initial screening for incoming NTP at the pre-insertion (16). The suggested function of Tyr639 in promoting the DNA/RNA motions is also consistent with the former mutagenesis results in which a substitution of Tyr639 by phenylalanine (Y639F) had nearly no impact on the transcription elongation rate, although this mutant could significantly eliminate the discrimination of RNA NTPs against DNA NTPs (68,69). Other mutant types, such as Y639D and Y639A, could significantly reduce transcription activities (69,70).

Notably, we found that the synthesizing RNA strand moves first toward the post-trans while the template DNA strand lags in the translocation. There are two stages in the translocation as follows: During the first stage, the RNA–DNA moves simultaneously upon the Phe644 unpacking from the TN; the RNA and template DNA then soon de-synchronize as they reach the key intermediate state, and the RNA strand completes the translocation. Meanwhile, the central and downstream part of the template DNA is stuck due to the re-stacking of Phe644 with the next nt downstream of the TN. Only after the un-stacking of Phe644 from this downstream DNA nt can the template DNA and the TN conclude the translocation. The asymmetrical translocation pattern between RNA and DNA has not been observed in the multi-subunit RNAP II in which the RNA–DNA hybrid moves in a fully synchronized manner (18). This difference is likely due to the fingers domain in T7 RNAP undergoing substantial conformational changes, particularly involving the opening motion of the Y-helix in the translocation intermediate state that leads to close packing from Phe644, which hinders the template DNA movements. In contrast, in the yeast RNAP II, no such significant structural changes are revealed other than the BH bending with limited impacts from Tyr836 on the DNA backbone movements. Interestingly, a translocation intermediate recently discovered in high-resolution structures of a single-subunit viral RNA-dependent RNAP (RdRP) featured the asymmetrical movements of the RNA and DNA strands (71). Hence, the asynchrony appearing in the translocation between the RNA and DNA can be a common feature in viral RNAP species with fairly compact protein structures.

Finally, we inferred a link between the flexible helix/domain rotational opening at the pre-trans state and the propensity of backtracking in T7 RNAP. To date, backtracking in T7 RNAP has not been observed, while the structurally similar mt-RNAP has been shown to backtrack or pause at the single molecule level (26). We hypothesized that the O-helix opening in the pre-trans state of the wt T7 RNAP helps prevent backtracking, which was then tested using our enforced simulation pulling the RNA 3΄-end backward to a frayed state as the onset of backtracking. The pulled RNA 3΄-end in the wt T7 RNAP withdrew during the followed unbiased simulation to resist the fraying or backtracking, while the O-helix opened simultaneously. In contrast, when we mutated the residues on the O-helix of T7 RNAP to mimic that on the mt-RNAP (67), the pulled RNA 3΄-end sustained in the frayed state, and the O-helix was less likely to open in the mutant T7 RNAP simulation. Based on the computational studies, we experimentally obtained a mutant T7 RNAP that has the potential to backtrack. Currently, our in vitro transcription assay shows a designed six-point mutant with a notable but slightly suppressed level of elongation activities compared with those of the wt T7 RNAP. Hence, it is plausible that the mutant T7 RNAP can pause and backtrack during transcription elongation. Substantial experimental proof regarding the backtracking of the candidate mutants is expected to come from single molecule measurements, which will be conducted next.

CONCLUSION

We studied the translocation of a single-subunit T7 RNAP during transcription elongation by implementing extensive atomistic MD simulations to construct a network of six macro-states from the pre- to the post-trans. The process follows a Brownian pathway with a slight population or free energy bias toward the post-trans state. The un-stacking of the TN from Phe644 on the Y-helix enables the first stage of the translocation, during which RNA moves to the post-trans first, while the template DNA slightly lags. The overall translocation of the RNA–DNA is facilitated by either the O-helix or the Y-helix opening, which allows Tyr639 to push onto the RNA–DNA end. The stacking and un-stacking of Phe644 with the adjacent nt downstream of the TN then coordinates the second stage translocation in which the template DNA along with the TN catches up. The second stage translocation is further supported by a substantial opening of the fingers domain and Tyr639 oscillation into the active site. Remarkably, the O-helix rotationally oscillates between the closed and open conformations even at the pre-trans state, which appears to prevent backtracking in T7 RNAP. In the current work, we computationally show that the O-helix resists fraying or backtracking of the RNA 3΄-end by opening at the pre-trans, while mutations in the O-helix residues to resemble mt-RNAP abolish the opening or resisting response. These studies, thus, not only reveal the detailed translocation mechanism but also provide a basis for the rational design of backtracking mutants in the single-subunit viral RNAP.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

This work was supported by National Natural Science Foundation of China [11275022, 31270803 and U1430237]. Funding for open access charge: National Natural Science Foundation of China.

Conflict of interest statement. None declared.