How to Measure Load-Dependent Kinetics of Individual Motor Molecules Without a Force-Clamp

Abstract

Single-molecule force spectroscopy techniques, including optical trapping, magnetic trapping, and atomic force microscopy, have provided unprecedented opportunities to understand biological processes at the smallest biological length scales. For example, they have been used to elucidate the molecular basis of muscle contraction and intracellular cargo transport along cytoskeletal filamentous proteins. Optical trapping is among the most sophisticated single-molecule techniques. With exceptionally high spatial and temporal resolutions, it has been extensively utilized to understand biological functions at the single molecule level, such as conformational changes and force-generation of individual motor proteins or force-dependent kinetics in molecular interactions. Here, we describe a new method, “Harmonic Force Spectroscopy (HFS).” With a conventional dual-beam optical trap and a simple harmonic oscillation of the sample stage, HFS can measure the load-dependent kinetics of transient molecular interactions, such as a human β-cardiac myosin II interacting with an actin filament. We demonstrate that the ADP release rate of an individual human β-cardiac myosin II molecule depends exponentially on the applied load, which provides a clue to understanding the molecular mechanism behind the force-velocity curve of a contracting cardiac muscle. The experimental protocol and the data analysis are simple, fast, and efficient. This chapter provides a practical guide to the method: basic concepts, experimental setup, step-by-step experimental protocol, theory, data analysis, and results.

1. INTRODUCTION

1.1 Single-Molecule Force Spectroscopy Techniques

During the past two decades, significant progress has been made in understanding the molecular basis of load-dependence, primarily due to developments of new methodologies that are capable of directly manipulating forces and characterizing force-dependent functional changes at the molecular level. In particular, various single-molecule force spectroscopy techniques, including optical trapping, magnetic trapping, and atomic force microscopy, have been developed and utilized in characterizing detailed mechanisms of load-dependence at the single-molecule level (Capitanio & Pavone, 2013; Greenleaf, Woodside, & Block, 2007; Neuman & Nagy, 2008). Optical trapping, in particular, is among the most sophisticated single-molecule force spectroscopy techniques with exceptionally high spatial (nanometers) and temporal (milliseconds) resolution, which can directly characterize conformational changes, binding/unbinding kinetics, and force-dependent enzyme kinetics (Capitanio & Pavone, 2013; Neuman & Block, 2004).

1.2 Force-Clamp Optical Trap

Force-clamp is one configuration of an optical trap that can directly measure force-dependent kinetics or conformational changes of proteins or nucleic acids via sophisticated active feedback control of the trap. For example, Veigel et al. showed that the lifetime of the bound crossbridge between a smooth-muscle myosin and an actin filament is modulated by an applied load, which provides a clue in explaining the “Fenn effect” in muscle contraction (Veigel, Molloy, Schmitz, & Kendrick-Jones, 2003). A conventional force-clamp is usually operated in the following steps: (1) detect the event, such as binding or conformational changes; (2) apply a constant force by an active feedback control of the trap setup; (3) measure the lifetime of the state at the applied constant force; and (4) repeat the previous steps to obtain enough data at the applied force. The measurement is performed multiple times at different forces to obtain the force-dependent kinetics of the molecule.

Success of a force-clamp experiment is mainly determined by (i) the speed and accuracy with which the true signal is detected in the presence of noise and (ii) the speed of the ensuing feedback response of the trap, working in a highly reliable manner. The noise consists of intrinsic Brownian noise and instrument noise. Speed and accuracy, however, compete with each other. For example, in order to improve accuracy, one needs more data, longer time series, before deciding about detection, which in turn delays the feedback response time. This can be especially problematic if the signal of interest, such as a binding lifetime or a conformational state, is transient and similar to or shorter than the time needed for reliable detection and feedback response. Instead, one can use shorter time series, less data in order to speed up the detection, but that inevitably increases the chance of errors, such as false-positive or false-negative events. Therefore, it has been the main focus in the field to develop improved feedback algorithms that work both quickly and accurately. One such example is the ultrafast force-clamp technique recently developed by Capitanio et al. (2012). Oscillating the trap in a triangular waveform and fast feedback control of the trap increased the detection sensitivity and the speed, achieving sub-ms temporal resolution.

A drawback of the active feedback methods is that they all require a complicated apparatus for fast and accurate on-line detection of the events, followed by careful control of the system for robust operation of the feedback setup, which is technically challenging. In addition, this complication for the operation makes data sampling less efficient and hence lowers throughput, making it difficult to collect enough data to assess the load-dependence of individual molecules. Thus, earlier methods (Greenberg, Shuman, & Ostap, 2014; Veigel et al., 2003) average over results from multiple molecules, though obtained individually, to characterize the force dependence, based on the assumption that the molecules all are identical, which may or may not be true.

1.3 Harmonic Force Spectroscopy

We recently developed an approach orthogonal to current force-clamp methods, a new method that we refer to as harmonic force spectroscopy (HFS) for reasons given later (Sung et al., 2015). HFS can detect and apply forces to weak and transient molecular interactions. Its experimental protocol and data analysis are simple, fast, and efficient. HFS runs automatically, without any feedback control, and applies a randomly chosen force to a single motor protein, practically without delay, after the motor protein has bound to its track. Moreover, the sampling efficiency is improved with HFS, so we could collect enough data from an individual molecule for a range of forces to get full load-dependent kinetics curves for individual molecules. In Sung et al. (2015), we demonstrated the power of HFS by directly measuring the force-dependent ADP release kinetics of human β-cardiac myosin II (Fig. 1), as an example of load-dependent transient molecular interactions. The method, however, is not limited to actin–myosin interactions, but can be modified and applied to other systems where force matters in molecular interactions, such as microtubule-associated proteins (MAPs including kinesin and dynein motors) interacting with a microtubule track, or DNA/RNA-binding proteins interacting with their filamentous track.

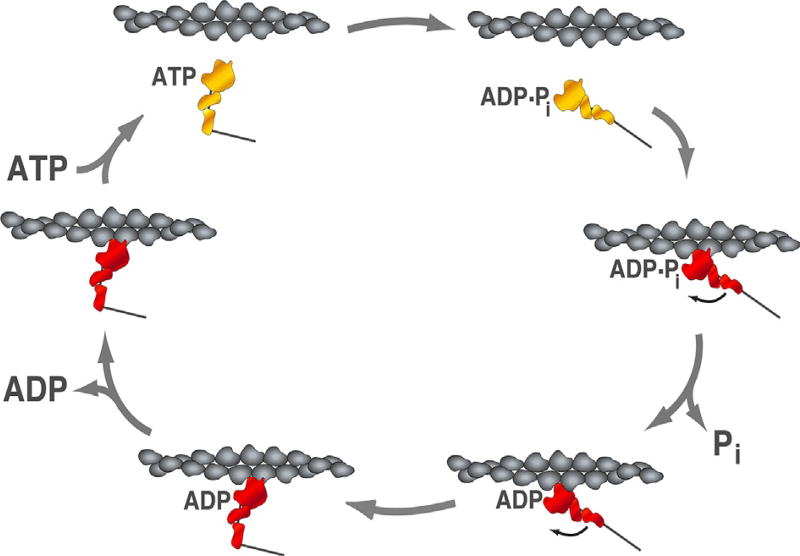
Fig. 1.

Actin-activated ATPase cycle of human β-cardiac S1. The actin-activated ATPase cycle of myosin illustrates the conformational states and the nucleotide states of the motor in association with an actin filament. The actin filament is shown in gray, myosin is shown in red in the strongly bound states, and in yellow in the weakly bound states. Arrows indicate the transition between the states. At saturating ATP concentration, the rate limiting step of the overall strongly bound states is the ADP release step, which takes ~10 ms with human β-cardiac S1. The time spent in the strongly bound state divided by the cycling time is the duty-ratio, which is ~10% with human β-cardiac S1.

In this chapter, we provide a practical guide to an experiment using HFS. We describe the basic concept of HFS, the experimental setup, preparations of samples and reagents, the step-by-step experimental protocol to obtain data, the theory and data analysis, and conclude with conclusion and outlook.

2. HFS: BASIC CONCEPT

Here, we briefly describe the basic concept of the method before we get into the details. The way it works is quite simple. We trap two beads using a dual-beam trap, and bridge them with an actin filament, called an actin dumbbell (details later). Motors are anchored to the surface, some of which are at the top of a platform-bead stuck to the surface. We move the dumbbell in proximity to the platform bead to let the surface-attached motor bind to the actin dumbbell (Fig. 2). The motor consequently undergoes a power-stroke immediately, which results in an abrupt displacement of the dumbbell. Binding of ATP to the motor terminates the myosin– actin bond, and the freed dumbbell goes back to its original position. This defines a single myosin–actin binding event, which repeats multiple times until the active motor becomes inactive.

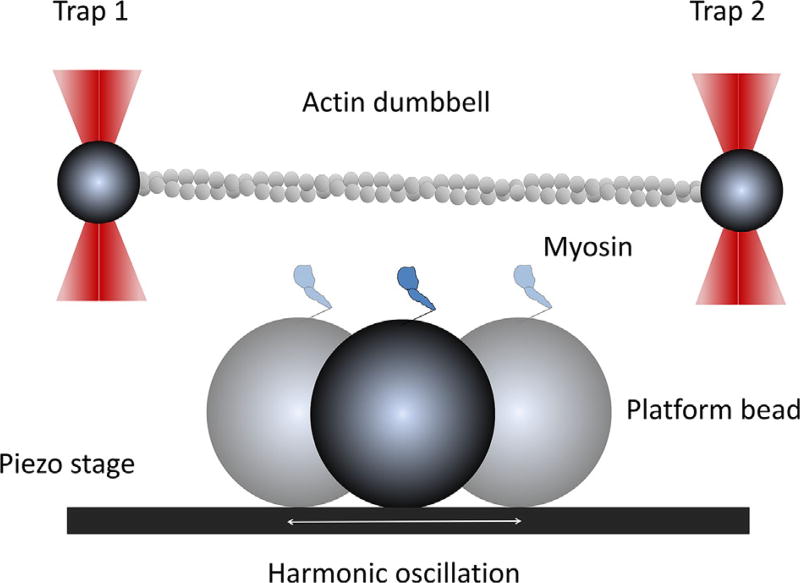
Fig. 2.

Illustration of the harmonic force spectroscopy experiment. Two trapped beads (dark gray) are bridged with an actin filament (light gray) and tightly stretched by dual-beam traps. Myosin is anchored on a platform bead and harmonically oscillated by a piezo-electric stage. The platform bead is positioned in the middle of the dumbbell, slightly below the actin filament. Lowering the dumbbell close to the platform bead will allow the motor to bind to actin and oscillate the trapped beads. Binding can take place anywhere in the oscillation cycle. This figure is not to scale.

So far, this description is just that of the conventional dual-beam three-bead assay for myosin, and we are now ready to start the HFS measurements. Now, we simply oscillate the sample sinusoidally, using a piezo-electric stage (PZT) (alternatively one may oscillate the dumbbell using an acousto-optic deflector (AOD) or acousto-optic modulator (AOM)), while the motor and the actin dumbbell undergo cycles of binding and unbinding (see Fig. 2 for a schematic illustration). When the motor binds and holds the dumbbell, the oscillatory translation of the motor with the stage is transferred to the position of the dumbbell, which results in harmonic oscillation of the dumbbell. This oscillation amplifies the binding signal and enables us to detect readily brief and weak binding events, which are difficult to detect without this or similar amplification. We continue the measurement to obtain multiple binding events from the same molecule until the motor becomes inactive. We then correlate the force applied to the motor and the time spent in the bound state. Since the binding occurs at different phases of the oscillation, a spectrum of different mean forces are applied, as the cycle-averaged force depends on where in the cycle binding took place. For example, the motor can bind when it is on the left side of the oscillation (Fig. 3A). In this case, the motor is under net negative (or backward) mean force. On the other hand, the binding site could be in the central region (Fig. 3B) or the right side of the oscillation (Fig. 3C), and different force will be applied accordingly. When we correlated the mean force and the dwell time, we observed that the human β-cardiac myosin S1 molecule displays highly asymmetric dwell time distribution, implying that the ADP release rate is force dependent. Note here that the experiment was done at saturating ATP concentration (2 mM). Unlike the case with a force-clamp, in HFS a motor experiences an oscillating force while bound. The quantitative description of this requires a little extra math, but it results in a force-dependent detachment rate that is identical to the one for constant force, except the mean force appears in the place of the constant force, and a “correction factor” appears, which describes the effect of force oscillations. Derived once and for all, we use this formula to obtain the force-dependent ADP release rate of individual human β-cardiac myosin S1 molecules under constant force. The rate we find fits well with the Bell-Evans model, describing bond rupture under force (Bell, 1978). HFS is so efficient that we could find the force-dependent ADP release rate of individual molecules. We did this for multiple molecules to test reproducibility and individuality of hypothetically identical molecules.

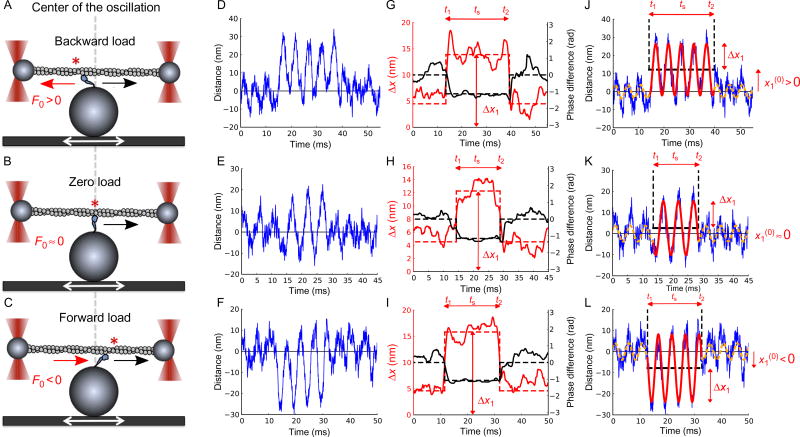
Fig. 3.

Myosin binding and unbinding under harmonic oscillation. Harmonic force spectroscopy with human β-cardiac S1. (A, B, C) An actin dumbbell held by two fixed optical traps interacts with a β-cardiac S1 molecule that is surface-attached to the top of a platform bead on a sinusoidally translating piezo-electric stage. Upon binding, the motor strokes toward the right (black arrows). Depending on whether the binding occurs left of the center (asterisk in (A)), at the center (asterisk on gray dashed line in (B)), or right of the center (asterisk in (C)), the motor experiences backward (A), near zero (B), or forward (C) mean load F₀. (D, E, F) Three examples of time traces of the displacement x₁ of a dumbbell bead in its trap. The other bead has coordinate x₂ (not shown). Large sinusoidal oscillations caused by being attached to the stage by a motor are observed in the middle portion of the traces. Small oscillations before and after attachments are caused by drag from buffer moving past the unattached dumbbell. (G, H, I) Change in phase shift φ₁(t) relative to the unbound state (black lines, dashed black lines showing its time average) and amplitude Δx₁(t) of oscillations (alternatively colored lines, dashed alternatively colored lines showing its time average obtained from longer stretches of unbound state times than shown) of bead positions in trap shown in (D, E, F) reveal binding and unbinding of motor. For each binding event, we determine the duration (t_s = t₂ – t₁) of the attached state, the mean load (F₀), and the amplitude of load oscillations (ΔF) (See Sung et al. (2015) for details). (J, K, I) Data in (D, E, F) fitted with two harmonic functions, full line for attached state, dashed lines for unattached. Figure and legend are adapted from Sung, J., Nag, S., Mortensen, K. I., Vestergaard, C. L, Sutton, S., Ruppel, K. M., … Spudich, J. A. (2015). Harmonic force spectroscopy measures load-dependent kinetics of individual human β-cardiac myosin molecules. Nature Communications, 6, 7931. http://dx.doi.org/10.1038/ncomms8931, with a Creative Commons license.

3. EXPERIMENTAL SETUP

The experimental setup required for HFS in this study is a conventional dual-beam optical trap setup (Finer, Simmons, & Spudich, 1994; Sung, Sivaramakrishnan, Dunn, & Spudich, 2010) with capability of harmonic oscillation of the sample chamber via a PZT with a well-defined oscillation amplitude and frequency. Unlike other force-clamp methods, no feedback control of the trap is required to measure the load-dependent lifetime or kinetics. The detailed protocol on how to set up the dual-beam optical trap instrument used in this study is described in Sung et al. (2010). The instrumentation used in this study is described in detail elsewhere (Sung et al., 2015).

Briefly, we used a 1064-nm fiber-coupled diode-pumped ND:YAG trapping laser beam (IPG Photonics, YLR-10–1064-LP), which was separated into two paths, one for each of the two traps, by a polarizing beam cube. An oil-immersion TIRF objective lens (Nikon, CFI Plan Apo 60 ×) with high NA (NA = 1.45) was used to tightly focus the trapping beams in the sample plane. Such beams can hold polystyrene beads near the focus with a Hookean spring-like force. We used an independent 845-nm fiber-coupled diode laser as detection beam (Lumics, LU0845) to measure the position of the beads via back-focal-plane (BFP) interferometry: a detection beam centered on a trapped bead produces an interference pattern at the BFP of the condenser. Each pattern is imaged on the sensor of a quadrant photodiode detector (QPD, Pacific Silicon Sensor, QP45-Q-HVSD). QPD outputs are in units of volt, which is why a calibration for volt-to-nm is required. The analog voltage signal was preamplified and antialiasing filtered (second order low-pass Butterworth) with a programmable filter (KROHN-HITE, 3944) with the cut-off frequency at the Nyquist frequency (20 kHz). The analog signal was digitized and sampled through a data acquisition card (National Instruments, PCIe-6363). Our normal sample rate of 40 kHz is sufficient to monitor fast dynamics and to perform trap calibration using power-spectral analysis. Bright-field illumination using a 740-nm LED (Mightex, LCS-0740-03–38) in conjunction with a CMOS camera (Thorlabs, DCC3240M) were used to image the beads in the sample chamber. Fluorescently labeled actin filaments were excited by a 532-nm diode laser and imaged with an EM-CCD camera (Andor, iXon Ultra 897). A high-accuracy, high-speed PZT (Physik Instrumente, P-545.3D7) was used to oscillate the sample chamber. We used a custom-built microscope body to mount the microscope components including the objective lens, condenser, PZT, LED, and QPD. Custom-written LabVIEW software was used to control most of the components and to display and record the data, including the positions of the beads and the stage. Schematics of the beam layouts and photos of the microscope are shown in Sung et al. (2010).

4. SAMPLE PREPARATIONS: PROTEINS, REAGENTS, AND BUFFERS

4.1 Human β-Cardiac Myosin S1

We expressed a short S1 construct (Sommese et al., 2013) of MYH7 (residues 1–808, truncated after the MYL3 binding site) followed by a 1 × GSG flexible linker and an enhanced green fluorescent protein (eGFP) tag, which was coexpressed with MYL3 (ventricular essential light chain) with a FLAG-tag for purification. Motors were further purified by a two-step purification procedure through actin sedimentation, the first with rigor attachment of motors to actin filaments without ATP and the second with inactive motors remaining bound to actin at high ATP concentration. Detailed protocols on cloning, virus production, and protein expression and purification are found elsewhere (Sommese et al., 2013; Sung et al., 2015).

4.2 Actin Filaments

Actin was purified from fresh chicken-breast skeletal muscle, as described previously (Pardee & Spudich, 1982; Sommese et al., 2013). Purified actin was biotinylated to attach to NeutrAvidin-coated beads, and actin filaments were fluorescently labeled to be imaged under a fluorescence microscope. Surface exposed Cys residues on F-actin were covalently conjugated with biotin-maleimide, and subsequently labeled with TMR-Phalloidin. The detailed protocol is found in Sommese et al. (2013) and Sung et al. (2015).

4.3 Anti-GFP Antibody

Anti-GFP antibody from Abcam (ab1218, 1 mg/mL or ~6 µM) was used to attach the myosin-GFP specifically to the surface with the motor’s head oriented toward the actin dumbbell. The stock was aliquoted (2 µL), snapfrozen, and kept at −80°C. When to be used, one aliquot was thawed and diluted 100-fold (0.01 mg/mL or ~60 nM) in assay buffer without BSA (see later), and was used directly for the trap experiments for a week or two without refreezing. We found that the binding specificity varies between different batches. We tested several different batches to find a satisfactory one and ordered from that (identified by its LOT number) from then on. Some batches showed a very high degree of nonspecific binding, which should be avoided.

4.4 Trapping Beads

NeutrAvidin-coated polystyrene beads (1 µm in diameter) were used to trap and attach the biotin-labeled F-actin to form a dumbbell. We use commercially available NeutrAvidin-coated microspheres (Life Technologies, F8777), which have proven to work well for our trapping assay. These easily bind to biotin F-actin and we seldom observed aggregated beads.

4.5 Nitrocellulose-Coated Coverslip

A glass coverslip was first spin-coated with 1.5-µm diameter silica beads (Polysciences, 24327–15) after dilution to proper concentration in 0.1% Triton X-100. One such bead was used as a platform to support the motor in the three-bead assay. After the beads were dried on the surface, the coverslip was subsequently spin-coated again with 20 µL of nitrocellulose (EMS, 0.1% Collodion in amyl acetate). The nitrocellulose-coated glass coverslip was used to nonspecifically attach anti-GFP antibody to the surface, and subsequently it was blocked by BSA.

4.6 Other Reagents

• Milli-Q water or equivalent that has ultra-purity with high resistance (>14.3 MΩ). This water was used for buffers and reagents throughout the experiment.

• BSA: 10 mg/mL in water (10 × stock).

• DTT: 1 M in water (100 × stock).

• Unlabeled phalloidin: 100 mM in water (100 × stock).

• ATP: 100 mM in water. pH was adjusted at (pH 7–7.5) using KOH.

• ATP regeneration system

  • ○Creatine phosphokinase (CPK): 10 mg/mL in AB with 50% glycerol (100 × stock).
  • ○Phosphocreatine (PCR): 100 mM (25 mg/mL) in AB (100 × stock).

• Oxygen-scavenging system

  • ○Glucose oxidase and catalase (GOC): 11 mg/mL glucose oxidase, and 1.8 mg/mL catalase in AB (100 × stock).
  • ○Glucose: 20% (v/v) in water (100 × stock).
  • ○Trolox: 25 mM in AB (20 × stock)
  • ○Note that other oxygen-scavenging systems (e.g., PCA/PCD) can be used instead.

4.7 Assay Buffer (AB)

Assay buffer (25 mM imidazole (pH 7.5), 25 mM KCl, 4 mM MgCl₂, 1 mM EGTA, and 10 mM dithiothreitol (DTT)) was used for all trap experiments. We made a 10 × AB stock without DTT and prepared fresh 1 × AB with DTT prior to the experiments.

4.8 AB with BSA (ABBSA)

AB with BSA (1 mg/mL) (ABBSA) is used to passivate the nitrocellulose surface after attaching the anti-GFP antibody to the surface. Surface blocking with BSA is to prevent any unwanted nonspecific attachment of other proteins including myosin and actin. We used a frozen aliquot of 10 × BSA stock (10 mg/mL in water) to prepare fresh ABBSA before use.

4.9 GO buffer

The final buffer for the trap experiments, termed GO buffer here, includes NeutrAvidin-coated polystyrene beads (10⁴-fold diluted from the stock), TMR-phalloidin labeled biotinylated actin filaments (1–2 nM), non-fluorescent phalloidin (1 mM), ATP (2 mM) and an ATP regeneration system (0.1 mg/mL CPK and 1 mM PCR), and an oxygen-scavenging system (0.2% glucose, 0.11 mg/mL glucose oxidase, and 0.018 mg/mL catalase) in ABBSA.

5. EXPERIMENTAL PROTOCOLS

The following procedures describe how to prepare and perform the experiment and collect data. For each step, we discuss important issues and how to trouble-shoot potential problems.

5.1 Preparation of Flow-Cell Sample Chamber

The following steps prepare the sample chamber containing all the sample/reagents:

1. Prepare buffers, samples, and reagents as described earlier.

2. Make a sample chamber with a glass slide and a nitrocellulose-coated coverslip attached with double-sided tape. The volume of the sample chamber is ~10–15 µL.

3. Inject anti-GFP antibody (0.01 mg/mL in AB), which nonspecifically binds to the nitrocellulose surface. Incubate for 2 min.

4. Wash with ABBSA (5 × volume) to passivate the sticky surface with BSA, which prevents nonspecific attachment of proteins except the preattached antibody. Incubate for 2 min.

5. Dilute the motor to an appropriate concentration. 100–500 nM (final concentration) is usually used for single molecule binding events.

6. Inject the motors through the chamber to let them bind to the antibody. Incubate for 2 min.

7. Wash with ABBSA (5 × volume).

8. Inject GO buffer.

9. Seal the ends of the chamber with vacuum grease to avoid buffer evaporation during the experiment.

10. Mount the sample chamber firmly on the sample stage.

11. Image beads, actin in solution, and surface.

    • Image the beads and the actin filaments in solution to check their concentrations. If too high, then the beads or actin floating in bulk solution can interfere with the experiment. If too low, it becomes difficult to form a dumbbell. As a rule of thumb, one should observe only a few beads and filaments in each field of view.

    • Check whether many filaments are stuck to the surface, as this may indicate the presence of inactive motors or nonspecific sticking to the anti-GFP antibody.

    • Check the density of platform beads on the surface. Fast spin coating helps to spread the beads uniformly and prevents bead aggregation as the solution dries out.

    • Surface passivation is a critical step and is context dependent. Surface and filament interaction depends on many factors, including the electrical charge, hydrophobicity, pH, and salt condition. Surface passivation with BSA has been commonly used in the field of actin-based myosin motility. Other surface passivation can be used alternatively, e.g. PEG, pluronic acid, or casein, depending on the types of protein and the filament. For example, casein has been commonly used in microtubule-based kinesin or dynein motility, and BSA does not work in this system (personal communication).

5.2 Formation of an Actin Dumbbell

The following steps lead to a dual-trap and a stable actin dumbbell for HFS. The experiment is described in the next subsection.

1. Trap two beads near the surface, one bead in each trap.

   • Adjust the power of the trapping beam. If too weak, it cannot trap a bead. If too strong, it can cause damage to the optics or electronics in the system. Higher power, though, increases stability. A typical range of trap power in our experiment was 100–200 mW when measured at a position right before the objective lens.

   • Trapping is possible only near the surface of the glass coverslip, within a few micrometer where aberration due to the index mismatch at the interface between glass and water is not significant for the employed oil-immersion objective lens. Since the HFS experiment is done near the surface, this is not a problem. A water immersion lens would allow trapping deep in solution.

   • It is only possible to trap beads below the focal plane since the radiation force pushes the beads in the direction of the beam propagation, which is upward in our inverted microscope system. In our imaging system, a bead below the image plane looks dark in the central area of its image, while beads above the plane look bright in the same central area.

   • If the beam alignment is done properly, then the focal plane of the trap and the detection beams are near the sample plane of the imaging system. The trapped bead should remain in focus. Otherwise, adjust the focal depth of the trap/detection beam and the imaging system.

2. Separate the beads by 3–5 µm, appropriate to form an actin dumbbell in the next step.

   • If too close, then the two trapped beads might interfere with each other as well as with the platform bead on the surface.

   • If too far apart, then it becomes difficult to find a long filament to bridge them and the compliance in the dumbbell becomes significant.

3. Position the detection beams to the center of the trapped beads.

   • Move the detection beam in (x, y) direction using the piezo mirror in the detection beam path and find the center of the detection signal.

   • When the trap and the detection beams are coaligned, choose a pair of trap and detection beams with orthogonal polarization (p or s) to minimize the risk of interference between the trap and the detection beams.

   • If the trap and the detection beam alignment is done properly and the trapped bead is spherically isotropic, then the (x, y) detection signal should show effectively a sinusoidal-like signal in the overall range and a linear signal near the center. If not, then release and trap another bead to check the possibility of a bead-specific problem (nonspherical bead or junk stuck to the bead), multiple beads trapped, or a bubble near the laser focus. If the problem is systematic, then realign the trap and the detection beam paths.

   • Detection beam power should be strong enough to get high-resolution and low-noise signals, without affecting the trapping and interfering with it.

   • Check the Brownian fluctuations of the trapped beads. If the signal looks noisy, especially in the low frequency range, junk might be stuck to the beads. Real-time display of the power spectrum helps to identify the noise level.

4. At this stage, we normally calibrate the force from each trap, due to variable bead properties. We usually do this calibration before taking data with myosin in case the beads are lost over the course of the experiment. The calibration protocol is described in the next section. After calibration, we form an actin dumbbell.

5. Move the sample stage to attach biotin-labeled actin diffusing in solution to the trapped NeutrAvidin-coated beads. Attach each end of the filament to each bead to form an actin dumbbell.

   • We do bright-field imaging of beads and surface via LED and a CMOS camera and fluorescence imaging of actin via a 532-nm diode laser and an EM-CCD camera. Visualize them together to check coordinated positions of beads and actin.

   • To form a dumbbell, first, find an actin filament with an appropriate length (3–5 µm). Place a bead near one end of the filament. Sometimes it is time consuming and difficult to make the attachment as the filament moves around and easily diffuses away from the focus. Be patient and move on to the next filament until catching one. If one end of a filament is attached, then move the stage in the opposite direction at a constant speed, such that the free end of the filament comes close to another bead. Once in a while move the stage in the orthogonal direction of the dumbbell to check the double attachment.

   • Sometimes, beads bind around the middle of the filament. In this case, it is difficult to form a dumbbell, and it is preferable to release the bead and trap a new one.

   • Be careful to avoid accidental trapping of additional free beads in solution. It causes release of the trapped bead or aggregation of the two beads.

   • Radiation pressure from the trap often pushes the actin filament into the solution, away from the trapped beads. If this continues, then temporarily reduce the trapping power until the actin filament is attached.

   • Moving deep in solution, a few micrometer further, increases the chance of finding more actin filaments. The trapping force, however, becomes weak due to aberrations. Be careful not to move too deep.

   • Abrupt and fast stage movement can cause escape of the beads from the trap due to the drag force from the fluid. Move beads at an appropriate speed and acceleration to avoid their accidental loss.

   • Sometimes actin does not stick to the beads. If biotin or NeutrAvidin is not fresh, then prepare fresh samples. Often, the biotin-labeling efficiency on actin is not high and there is not enough biotin on the filament. Prepare new biotin-actin with fresh biotin-maleimide. Test the biotin-labeling efficiency by attaching the filament to a StreptAvidin or NeutrAvidin-coated surface on the coverslip.

   • Check the time traces of bead positions and their power spectra. If the position signal is much noisier than previously, then a short filament or junk may have stuck to the bead. Trap new beads in this case.

   • Forming a dumbbell in a timely manner (ideally in 10–20 min) is critically important to increase the chance of success for collecting quality data. Human β-cardiac myosin stays active for an hour or two at room temperature. After that, a new sample should be prepared.

6. Make a tightly stretched dumbbell by separating the two beads.

   • To make a tight dumbbell, first, oscillate one of the beads (call it Bead 1) via the AOD. The amplitude of this oscillation should be two or three times the amplitude of the bead’s Brownian motion in the trap. If the dumbbell is not stretched, the other bead (Bead 2) does not oscillate in response. Second, in that case, use the piezo mirror to move Bead 1 slowly to increase the interbead distance. Third, move Detection Beam 1 to the center of Bead 1. Fourth, repeat the second and the third steps until Bead 2 oscillates when Bead 1 is oscillated. Finally, carefully move Bead 1 until the oscillation signals of the two beads are similar. In the ideal limit of a completely stretched dumbbell with no compliance, bead-to-bead correlation is complete.

   • Be very careful not to break the actin. Actin becomes fragile under strong tension when it is fully stretched. If this happens, trap new beads and make a new dumbbell.

   • Sometimes only one of the beads is lost while the actin dumbbell is still connected. This happens frequently when the stage suddenly moves while the dumbbell is fully stretched. Retrapping the straying bead is, however, not easy due to the radiation force pushing on it during attempts. If one dumbbell bead goes astray, first turn off the trapping beam of the lost bead. Then, reduce the distance between the two traps. Move the stage in the direction of the empty trap, such that the fluid drag force on the dumbbell drags it toward capture in both traps. Then, suddenly turn on the beam of the empty trap again. This will allow the retrapping of the lost bead while maintaining the dumbbell. Since the dumbbell is relaxed, it needs to be stretched again as described ealier.

5.3 HFS: Experiment

The HFS experiment roughly consists of three steps: searching for an active motor, executing HFS, and data collection.

1. Move the dumbbell close to a platform bead and find an active motor.

   • To find an active motor, first, slowly move the stage such that a platform bead is placed between the two trapped beads of the dumbbell. Second, lower the dumbbell close to the platform bead’s surface such that a motor attached to the platform bead can bind to the actin filament. Third, sinusoidally oscillate the PZT, which amplifies the binding signal to allow easy detection of the motor binding event. It is important to position the dumbbell at an appropriate height not too close to the surface, since that may cause signals from nonspecific sticking. If no binding is observed, stop the oscillation, move it to the next platform bead, and oscillate the PZT again. Repeat these steps until a binding event that appears to be from an active motor is observed. Finally, stop the oscillation and confirm that it is indeed from an active motor. The latter produces a unidirectional stroking signal, while nonspecific sticking does not. Once an active motor has been confirmed, one is ready to execute the experiment and collect data.

   • Be careful to avoid signals from nonspecific sticking since they contaminate the actual signal. A too-short distance between dumbbell and platform beads, an elevated amplitude of oscillation, and an elevated frequency of attachment all indicate nonspecific sticking. Certain batches of anti-GFP antibody seem to cause sticking with a higher probability, as does higher concentration of the anti-GFP antibody. We tried to avoid false-positive signals with these observations in mind.

   • Before doing the trapping experiment, we usually start with the motility assay (actin gliding driven by motors attached to the surface). Observation of smooth actin gliding in the motility assay is a prerequisite for the success of the single-molecule experiment, as our three-bead assay with a dual-beam actin dumbbell is simply a single-molecule version of the motility assay.

   • We do multiple control experiments to make sure that the signal is from an active motor. Parameters to control include motor and ATP concentrations. Start with high concentration of motor at low ATP concentration, since this shows more frequent and longer binding, easy to detect even without the PZT oscillation. Then, lower the motor concentration at low ATP concentration to find the optimal motor concentration. As a rule of thumb, one should find one motor binding among 10–20 platform beads. Finally, use the same condition and gradually increase the ATP concentration till saturated (2 mM), which results in short binding time.

2. Execute the HFS experiment with the single active motor.

   • Single-molecule HFS is simply a continuation of the myosin–actin binding events with PZT oscillation, performed in a more controlled manner. Once an active motor is confirmed, we repeat the sinusoidal oscillation of the PZT at an appropriate amplitude and frequency, and record data until the motor becomes inactive. We oscillated the PZT with an amplitude of 30–50 nm at a frequency of 100–200 Hz in our previous study. While strongly bound, myosin is under an oscillation force with a mean force that depends on where in the oscillation cycle the binding happened. This way, randomly selected mean forces are applied in every binding event. The amplified signal of the bead position with the harmonic oscillation of the PZT makes it easy to detect the binding and measure the dwell time accurately with an automatic binding detection algorithm (see next section).

   • It is important to maintain the dumbbell position at the appropriate position in 3D, where the single motor has binding access to the actin without spatial constraints. The dumbbell should not be too close to the platform bead: so close that the signal becomes noisier and nonspecific sticking might happen. At an appropriate distance and position, motor binding happens frequently, e.g., once every second on average. Optimal statistics are achieved with the highest frequency of true binding for which one can distinguish consecutive binding events.

   • Drift of the sample chamber can occur over the course of the data collection. If the binding frequency drops, then stop data collection, fine tune the position in 3D using the PZT, and recollect data, if the binding signal is recovered with the adjustment.

   • It is important to know the actual amplitude of the PZT oscillations. Our PZT has a resonance frequency at 500 Hz in (x, y) according to its specification, and its amplitude of oscillation is attenuated as the frequency of oscillation of the voltage driving the stage approaches the resonance frequency. This is due to a built-in low-pass filter, a safeguard against potential damage to the PZT. Consequently, the amplitude specified for a given voltage may differ in a frequency-dependent manner from the actual amplitude achieved. Please note that the resonance frequency value depends on the load applied to the PZT, so the information in the specification might be different from the actual value. Our PZT outputs a sensor signal in volt as a read-out of the position of the PZT. The volt-to-nm conversion factor of the sensor signal was precalibrated by the manufacturer (Physik Instrumente) and we confirmed it, using a calibration bar. We then characterized the frequency-dependent amplitude changes in our system. For example, when we oscillated the PZT at 200 Hz with amplitude 50 nm, the actual oscillation amplitude was around 35 nm. We used the latter value in our study.

   • It is also important to carry out the experiment at different oscillation amplitudes and frequencies to find a regime in which it works. For example, if the amplitude of oscillations is too large, then the force applied to the motor exceeds the motor’s stall force, which can result in premature detachment from the actin. Also, our theory assumes that the motor is in a quasi-steady state under the applied oscillations at frequencies of 100–200 Hz, which means that the motor continuously is in a configuration adapted to the instantaneous load. This proved to be true in our experiment. However, this assumption might not be satisfied at much higher frequencies.

   • We used a PZT to apply a harmonic oscillation, but one could use other methods. In fact, an AOD or AOM can also be used to oscillate the dumbbell directly with increased oscillation frequency and temporal resolution, which would be useful to measure the load-dependence of even shorter and weaker events.

6. TRAP CALIBRATION

We recorded data from the detector in volts, which needs to be converted to nanometers. Each trap beam pulls a bead similarly to a Hookean spring, so one needs to determine the spring constant. Calibration of the trap is critical in order to obtain accurate information of the force in pico-newtons (pN) and displacement in nanometers (nm). We obtain two pieces of information from the following calibration procedure, one is the volt-to-nm conversion factor for the detector (QPD) and the other is the trap stiffness (or spring constant) in pN/nm.

1. After trapping a bead in each trap, we move it close to the surface where the HFS experiment is usually carried out. Both the trap stiffness and the volt-to-nm conversion factor are functions of distance from the surface, so it is important to calibrate at the right height. For example, the trap stiffness grows weaker with distance from the surface due to aberrations in our microscope system.

2. We calibrate the QPD by raster scanning of each bead in 2D using the AOD (or AOM), e.g., we displace the beads by 60-nm steps over an area of 600 × 600 nm. Meanwhile, we simultaneously record both the QPD output signal (x and y in volt) and the bright-field images of the beads (in pixels). Centroid tracking of the bead displacement (in pixels) and imaging a calibration bar (pixels to nanometers) allowed us to convert the bead displacement from pixels to nanometers. We then correlated the linear relationship between the QPD signal (in volt) and the bead displacement (in nanometers) to obtain the volt-to-nm conversion factor.

3. We estimate the trap stiffness by maximum-likelihood fitting of the theoretical power spectrum to the measured power spectrum of the recorded thermal motion of the beads in the traps (Nørrelykke & Flyvbjerg, 2010; Tolić-Nørrelykke et al., 2006). We used the QPDs record the positions of the beads for ~25 s (10⁶ data points at 40 kHz sampling frequency) and calculated the power spectra of the recorded time series using windowing (4000 data points in each window) as described in Section 12.7 of Press, Teukolsky, Vetterling, and Flannery (1986). We fitted each power spectrum with a sum of two Lorentzians while taking into account low-pass filtering by our antialiasing filter and aliasing of the filtered signal (Berg-Sørensen & Flyvbjerg, 2004). One Lorentzian models low frequency noise in the setup due to air fluctuation and vibration. The other Lorentzian extracts the trap stiffness and the bead’s drag coefficient near the surface (Schäffer, Nørrelykke, & Howard, 2007; Tolić-Nørrelykke et al., 2006).

7. HFS: THEORY AND DATA ANALYSIS

The next step is to extract the force-dependent kinetic information from the recorded data. The original data are time traces of the trapped beads’ positions in volts. With the calibration information, we can convert the bead positions to nanometers by multiplication with the QPD factor in nm/V, and also measure the force applied to the motor in pico-newtons by multiplication of the trap stiffness in pN/nm. The time trace displays multiple independent myosin binding events with large amplitude harmonic oscillations, separated by unbound states with smaller oscillation amplitude and different phase in response to the drag force from the buffer’s oscillatory motion with the sample chamber (Fig. 3D–F). Force–kinetics relationships can be investigated by plotting the bound time (inverse kinetic rate) vs the mean force applied during that time. To that end, we need good statistics, i.e., we need to detect a large number of binding events effectively and accurately.

7.1 Automatic Binding Detection

We detect events of myosin binding to the actin dumbbell by monitoring the displacements of the individual bead in its optical trap (Fig. 3D–F). When the myosin is not bound to the dumbbell, the dumbbell oscillates due to drag from the fluid in the sample chamber (Fig. 3D–F, left and right portions of the traces), which follows the stage motion. In this oscillation, the dumbbell position follows the fluid velocity closely and is therefore ahead of the stage position by almost π/2, see Eq. (7) in Tolić-Nørrelykke et al., 2006. When the myosin is bound to the actin dumbbell, the oscillation of the PZT is transferred to the trapped beads, and the positions of the beads are now almost in phase with the oscillating position of the stage (Fig. 3D–F, center portions of the traces)—compliance of the dumbbell allows the beads to get a little ahead of the stage position, dragged by the fluid in the sample chamber, but the net effects of binding are oscillations of the dumbbell with much larger amplitude, typically around a different mean position, and a phase shift by almost −π/2 relative to the phase of oscillations in the unbound state (Fig. 3G–I, black traces). Thus, we have two criteria for selection of binding events: changes in phase (Fig. 3G–I, black traces) and changes in amplitude (Fig. 3G–I, alternatively colored traces), like the signals of AM and FM radio, respectively, except we “listen” to both simultaneously.

We developed an automatic binding detection algorithm that finds true motor binding events in the presence of noise from full time traces. This method is superior to manual selection since it is more objective, efficient, and accurate. The software that executes this algorithm is freely available via http://www.nanotech.dtu.dk/Research-mega/Forskningsgrupper/SSS. Details about its signal processing are given in the methods section of Sung et al. (2015).

7.2 Force-Dependent Kinetics Under Harmonic Force

HFS hinges on two points: (i) Because of the vast separation of scales between the myosin molecule and the microscope stage, our harmonic motion of the stage is extremely slow as experienced by the motor. So while we vary the force exerted on the motor harmonically, the motor experiences a quasi-stationary situation. The force appears as if clamped on the motor’s time scale—for long enough, anyways, for the motor to be in equilibrium with the instantaneous force at every instant. Consequently, the rate of detachment of the motor from actin is, at each instant, the rate we would observe, if the force were clamped with the value it has at that instant. This is an assumption, but a plausible one, as just argued, and it is tested experimentally when we use it. (ii) This assumption makes force-clamping superfluous. It is replaced with a little bookkeeping of rates that vary with varying loads. This goes on continuously in time, so a differential equation appears. Our second point is that we can handle this, and we do so in the next subsection. Force-clamping reduces this bit of math to elementary arithmetic. But one should not complicate experimental design just to simplify the math of one’s data analysis, because math is pure logic. It processes data without adding noise, which makes it better than most experimental tools.

Moreover, in the specific case at hand, the assumed quasi-stationarity simplifies kinetics to such an extent that the release rate for actin from myosin when experiencing a harmonic load is the same function as for a constant load, except the mean load replaces the constant load, and an overall correction factor describes the increase in release rate resulting from harmonic oscillations in load; see next subsection.

7.3 Mathematical Model and Theory

The mean value F₀ of the oscillating load on the myosin depends on where in the cycle of the periodic motion of the stage the myosin happens to attach to the dumbbell. F₀ equals minus the sum of the mean forces from the two traps on the dumbbell, which we measure. Thus, we measure the lifetime of the attached state of myosin for a range of measured F₀-values. Fig. 4A shows a scatter plot of this F₀ vs lifetime. It is interpreted as follows: Let k(F) denote the load-dependent rate of unbinding of myosin from actin. Let F be a function of time t. Then the “survival function” P(t₁, t₂) of the attached state— i.e., the probability of remaining attached from time t₁ of binding till a later time t₂—evolves in time according to the quasi-stationary dynamics

$$\frac{d}{\mathit{\text{dt}}}P(t_1,t)=-k(F(t))P(t_1,t).$$ (1)

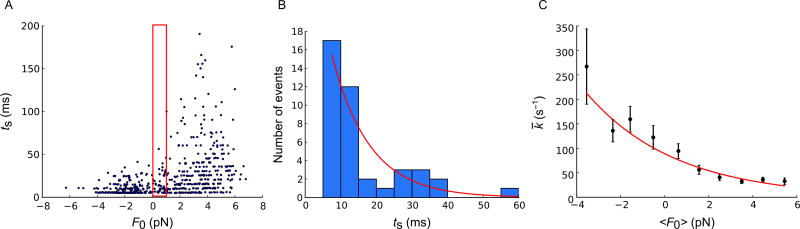
Fig. 4.

Load-dependent ADP release rate measured with 200-Hz stage oscillation. (A) Scatter plot of duration of binding (t_s) vs load (F₀) (N = 388). (B) Histogram of durations t_s in the narrow range of loads in the red box in panel (A) (N = 41). Histogram bins are 5 ms wide, i.e., one period of the stage motion. The histogram is fitted by Eq. (4) using maximum-likelihood estimation (MLE) to obtain k̄ = k(〈F₀〉, ΔF).The histogram is consistent with an exponential distribution (full line). The characteristic time of this exponential is the inverse of the ADP release rate under the average load in the red box in panel (A), k̄ = k(〈F₀〉, ΔF). (C) ADP release rates depend exponentially on applied load. Black data points show ADP release rates k̄ = k(〈F₀〉),ΔF) against mean load 〈F₀〉 for each of 10 consecutive 1-pN bins. The individual error bars are calculated from the variance of the MLE in (B) as the inverse Fisher information for the parameter (Sung et al., 2015). The full curve is the fit of Eq. (8) to the rates, yielding k₀ = 71 ± 4s⁻¹, δ = 1.01 ±0.09nm, corresponding to k(0, ΔF) = 89s⁻¹ on the full curve. Figure and legend are adapted from Sung, J., Nag, S., Mortensen, K. I., Vestergaard, C. L, Sutton, S., Ruppel, K. M., … Spudich, J. A. (2015). Harmonic force spectroscopy measures load-dependent kinetics of individual human β-cardiac myosin molecules. Nature Communications, 6, 7931. http://dx.doi.org/10.1038/ncomms8931, with a Creative Commons license.

This differential equation is solved by

$$P(t_1,t_2)=\text{exp}(-{\int }_{t_1}^{t_2}k(F(t))\mathit{\text{dt}}).$$ (2)

The probability density function (pdf) on the time axis for unbinding at a time t, given binding took place at time t₁, is equal to minus the right-hand side in Eq. (1). At constant load F, as in force-clamp spectroscopy, this pdf is a simple exponential function of the difference t₂ – t₁. For time-dependent F, this pdf is the function that results from inserting Eq. (2) in the right-hand side of Eq. (1). If F is a periodic function of t, and t₂ – t₁ = nt_drive is an integer number of periods t_drive of F, then

$$P(t_1,t_2)=e^{-\overline{k}{\mathit{\text{ n t}}}_{\text{drive}}}=e^{-\overline{k}(t_2-t_1)},$$ (3)

where k̄ denotes the time average of k(F(t)) over a period. This is a simple exponential function of n. In our data analysis, we use the probability of unbinding in the period following n periods in the bound state, which is

$$P(t_1,t_2)-P(t_1,t_2+t_{\text{drive}})=C{e}^{-\overline{k}{\mathit{\text{nt}}}_{\text{drive}}},$$ (4)

where C = 1—e^−k̄t_drive. This also is a simple exponential function of n, known as the geometric distribution. It shows that “periodic force spectroscopy,” as we call it, in its data analysis is as simple as force-clamp spectroscopy. Its use only requires that the period, t_drive, is shorter than the timescales one wishes to resolve.

We achieve further simplifications by using a periodic load that is harmonic, in what we call “Harmonic Force Spectroscopy,”

$$F(t)=F_0+\mathrm{\Delta }F\text{ sin}(2\pi f_{\text{drive}}(t-t_{\mathrm{M}})).$$ (5)

It has f_drive = 1/t_drive and t_M denoting the arbitrary phase of the oscillating stage. As ΔF differs little between binding events, F₀ is the only quantity in this expression that really differs between binding events. Eq. (4) therefore predicts that binding events which have (nearly) the same mean load F₀, have attachment times that are exponentially distributed in time, when binned on the time axis in bins that last an integer number of periods of the stage motion, e.g., one period. Fig. 4B shows that this is, indeed, the case. In this manner, we determine k̄ experimentally for a range of values for F₀. Fig. 4C shows a plot of these values. This plot describes a load-dependent ADP release rate that is convincingly described by an exponential dependence on the load F₀. This observation points toward Arrhenius’ equation,

$$k=A\text{ exp }(-\frac{E_{\mathrm{a}}}{k_{\mathrm{B}}T})$$ (6)

and transition state theory. In Eq. (6), E_a is the activation energy, the energy difference between the bound state and the transition state for detachment. If a constant external load F opposes the transition, E_a is increased by the amount of work done by the myosin against that load. With δ denoting the distance between the bound state and the transition state, as measured along the reaction pathway, the height of the energy barrier toward unbinding is increased from E_a to E_a + Fδ. Consequently,

$$k(F)=k_0\text{ exp }(-\frac{F\delta }{k_{\mathrm{B}}T})$$ (7)

where k₀ is the rate at zero load, and hence, with our harmonic force in Eq. (5),

$$\overline{k}=k(F_0,\mathrm{\Delta }F)=k_0\cdot I_0\left(\frac{\mathrm{\Delta }F\delta }{k_{\mathrm{B}}T}\right)\text{ exp }(-\frac{F_0\delta }{k_{\mathrm{B}}T})$$ (8)

where I₀ is the zeroth-order modified Bessel function of the first kind. Thus, we see that Arrhenius’ equation explains the observed exponential dependence of k̄ on the mean load F₀. Since k_B T and ΔF are known, a fit of Eq. (8) to data, using k₀ and δ as fitting parameters, determines these two parameters of the load-dependent ADP release rate; see Fig. 4C.

8. RESULTS AND DISCUSSION

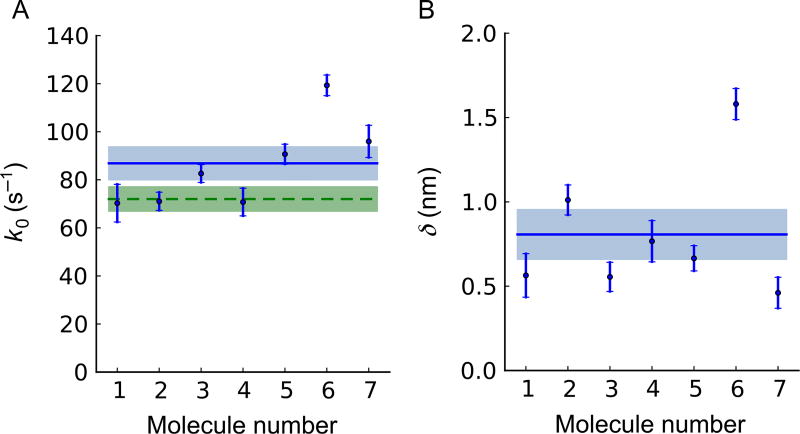
We found that the force-dependent ADP release rate of human β-cardiac S1 fits well to a single exponential function (Fig. 4C), consistent with the transition state theory and the Bell–Evans model for bond rupture. A fit of Eq. (8) to the data yielded k₀ = 71 ± 4s⁻¹ and δ = 1.01 ± 0.09nm (Fig. 4C). We obtained the fitting results from seven independent measurements with six different molecules (Fig. 5A and B). They average to k₀ = 87 ±7s⁻¹ (Fig. 5A, blue) and δ = 0.8 ± 0.1nm (Fig. 5B) (mean ± s.e.m., N = 7). The unloaded ADP release rate also agrees with our stopped-flow experiment, done in solution and hence unloaded (Fig. 5A). Our protocol enabled recording of a sufficient number of attachment events for individual molecules—between 138 and 950—to allow this statistical analysis for individual molecules. This is an essential improvement of a single-molecule experiment: this step from ensemble results to single-molecule results allows us to inspect the performance of individuals in an ensemble before we average experimental results over the ensemble to improve statistics. By doing that, statistical outliers can be eliminated from the ensemble before averaging, which may improve accuracy and precision of ensemble-averaged results dramatically, depending on the frequency and extremity of outliers. Molecule #6 in Fig. 5 provides an example: its elimination as an outlier shifts the ensemble-averaged value for k₀ by one standard error.

Fig. 5.

Individual parameter values for seven independent measurements with six myosin molecules. Each molecule is analyzed as in Fig. 4. The stage is oscillated at 200 Hz except for #1 (100 Hz). The number of attachment events for each molecule are, respectively, N = 138, 388, 569, 174, 539, 950, and 229. Figs. 3 and 4 use data for Molecule #2. Points with error bars denote single-molecule results. The error bars are obtained from the theoretical covariance matrix (=inverse Fisher information matrix) of the single-molecule estimates for k₀ and δ (Sung et al., 2015). (A) The load-free ADP release rates k₀, corrected by I₀(ΔFδ/k_BT) to adjust for oscillation effects. Their weighted mean value, k₀ = 87 ± 7s⁻¹, is shown as a horizontal full line with s.e.m. shown as a shaded area. If Molecule #6 is treated as an outlier and dropped from our statistics, we find k₀ = 80 ± 7s⁻¹. The unloaded ADP release rate measured in stopped-flow experiments, k₀ = 72 ± 5s⁻¹, is shown as a horizontal dashed line with s.e.m. shown as a shaded area. (B) The distance δ from the strongly bound state of each myosin to its transition state toward ADP release, measured along the reaction path. Their weighted mean value, δ = 0.8 ± 0.1 nm, is shown as a horizontal full line with s.e.m. shown as a shaded area. If Molecule #6 is treated as an outlier and dropped from our statistics, we find δ = 0.7 ± 0.1 nm. Figure and legend adapted from Sung, J., Nag, S., Mortensen, K. I., Vestergaard, C. L, Sutton, S., Ruppel, K. M., … Spudich, J. A. (2015). Harmonic force spectroscopy measures load-dependent kinetics of individual human β-cardiac myosin molecules. Nature Communications, 6, 7931. http://dx.doi.org/10.1038/ncomms8931, with a Creative Commons license.

9. CONCLUSION AND OUTLOOK

HFS has proven to be useful for obtaining the load-dependent rate at the single-molecule level in an easy, fast, and efficient way. The method was applied to demonstrate the load-dependent ADP release rate of human β-cardiac S1. The exponential change of rate provides a clue to the molecular basis of the force–velocity curve and the Fenn effect of contracting muscle. In a translational point-of-view, the method can be applied to human β-cardiac S1 bearing hypertrophic cardiomyopathy (HCM)-causing single-point mutations to understand the devastating heart disease at the single-molecule level (Spudich, 2014; Spudich et al., 2016). This method is not limited to our myosin study but can be further extended into other systems, with some modification and optimization. In this method chapter, we aimed to provide a detailed protocol for how to carry out the experiment. We hope that this is useful to others who want to apply HFS to their own experimental system.