Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2018 Apr 1.
Published in final edited form as: Biomed Phys Eng Express. 2017 Mar 9;3(2):027001. doi: 10.1088/2057-1976/aa6228

Effect of slice excitation profile on ungated steady state cardiac perfusion imaging

Haonan Wang 1, Edward VR DiBella 2, Ganesh Adluru 2, Daniel J Park 1, Meredith I Taylor 1, Neal K Bangerter 1,2
PMCID: PMC5738031  NIHMSID: NIHMS923591  PMID: 29276628

Abstract

In cardiac perfusion imaging, choice of flip angle is an important factor for steady state acquisition. This work focuses on presenting an analytical framework for understanding how non-ideal slice excitation profiles affect contrast in ungated 2D steady state cardiac perfusion studies, and to study a technique for estimating flip angle that maximizes enhanced/unenhanced myocardial contrast-to-noise ratio (CNR) in single slice and multi-slice acquisitions. A numerical simulation of ungated 2D golden ratio radial spoiled gradient echo (SPGR) was created that takes into consideration the actual (Bloch simulated) slice excitation profile. The effect of slice excitation profile on myocardial CNR as a function of flip angle was assessed in phantoms and in-vivo. For fast RF pulses, the flip angle that yields maximum CNR (considering the actual slice excitation profile) was considerably higher than expected, assuming an ideal excitation. The simulation framework presented accurately predicts the flip angle yielding maximum CNR when the actual slice excitation profile is taken into consideration. The prescribed flip angle for optimal contrast in ungated 2D steady-state SPGR cardiac perfusion studies can vary significantly from that calculated when an ideal slice excitation profile is assumed. Consideration of the actual slice excitation can yield a more optimal flip angle estimate in both the single slice and multi-slice cases.

Keywords: 2D cardiac perfusion, saturation preparation, multi-slice, slice profile

1. INTRODUCTION

First-pass myocardial perfusion MRI with ECG-gated saturation recovery acquisition is useful for the detection of ischemic heart disease (Atkinson et al., 1990; Klassen et al., 2006; Schwitter et al., 2001; Wieben et al., 2008; Ishida et al., 2009). However, some patients do not provide an ECG signal of sufficient quality for accurate gating. These poor or inconsistent ECG signals can have adverse effects on image quality and cause loss of important diagnostic information.

A new acquisition technique with no need for a saturation pulse or for ECG triggers has been proposed for cardiac perfusion (DiBella et al., 2012; Sharif et al., 2015; Sharif et al., 2014; Wang et al., 2014). The sequence eliminates the saturation preparation and has sufficiently rapid acquisition speed to eliminate the need for cardiac gating. A spoiled gradient echo (SPGR) sequence is used to drive the acquisition into steady state. It has been implemented in both 3D (DiBella et al., 2012) and 2D. The 2D versions have been implemented in both a single slice (Sharif et al., 2014) and a three interleaved slice mode (Sharif et al., 2015; Wang et al., 2014). The interleaved mode acquires a specific k-space line for all the three slices during one TR. In these ungated cardiac perfusion techniques (with no saturation pulse), the prescribed flip angle is typically determined by calculating the single flip angle that maximizes contrast between enhanced and unenhanced myocardium. This calculation normally assumes an ideal slice excitation profile (i.e., that the flip angle is constant across the entire slice), which implies an ideal slice steady-state signal profile. While this assumption can be reasonably accurate for longer RF pulses with close to ideal slice excitation profiles, it breaks down for short RF pulses where the slice excitation profile can deviate significantly from the ideal. Hanicke et al. (Hänicke et al., 1988) demonstrated that the prescribed flip angle that achieves maximum signal from a slice can be significantly higher than the computed Ernst angle when the RF slice excitation profile is poor. They demonstrated that at high prescribed flip angles or low TR/T1 ratios, a severely distorted slice steady-state signal profile can be observed due to the non-uniform distribution of the flip angle across the slice (Hänicke et al., 1988).

Before continuing, it is useful to carefully define several terms. We will use “slice excitation profile” or “slice flip angle profile” to describe the spatial variations in flip angle in the slice direction across a slice. These variations in flip angle across a slice lead to variations in both the initial and steady-state signals emanating from various positions across the slice. We describe the spatial variations in the steady-state signal (as opposed to the flip angle) across a slice as the “slice steady-state signal profile”, and the spatial variations in initial signal (defined as the signal after a single RF excitation pulse) across a slice as the “slice initial signal profile”.

More recently, Sharif et al. used phantom studies to determine empirically an optimal flip angle for multi-slice interleaved ungated perfusion sequences (Sharif et al., 2015). The work here extends this effort by explicitly modeling RF excitation pulses like those used in myocardial perfusion sequences, demonstrating how the slice excitation profiles of these short RF pulses can lead to a significant underestimation of the prescribed flip angle, and then formulating the flip angle that will maximize contrast between enhanced and unenhanced myocardium in both the single slice and multi-slice cases. In addition, interactions between slices (due to non-ideal slice excitation profiles) will be studied for multi-slice acquisitions.

2. METHODS

2.1 Pulse Sequence

We modified a cardiac pulse sequence to enable a golden ratio radial k-space trajectory for continuous (no saturation pulse) ungated myocardial perfusion data acquisition (SPGR). The sequence was implemented on a 3T Siemens whole-body scanner with 45mT/m gradient strength (Trio, Siemens Medical Systems, Erlangen, Germany). 144 readout samples on each of 24 radial lines were acquired for each slice. The sequence employed both RF and gradient spoiling. Both a single slice and three interleaved slice mode were implemented. Note that operating the sequence in three interleaved slice mode gives three times the TR than when the sequence is operated in single slice mode. In both modes, a FOV of 280 – 300mm2 was used, yielding an in-plane resolution of 1.9–2.1mm. Readout bandwidth was 1389 Hz/pixel. The TR, TE, RF pulse characteristics, slice thickness, and slice distance were varied for the different study cases discussed below.

2.2 Numerical Simulation

We performed a numerical Bloch simulation of the sequence accounting for the RF slice excitation profile to estimate the actual steady state signal level from the slice. The simulation was applied in both single-slice mode and multi-slice mode, and takes the RF pulse profile exported from the Siemens sequence simulator (IDEA VB17) as an input in order to mirror the actual RF pulse used during acquisition. The excited region was divided into 300 sub-slices, with each sub-slice receiving a different effective flip angle based on its location. The signal contributions were summed across all of the sub-slices, and the overall signal from the actually excited slice volume was then used for signal and contrast optimization. Alternately, the signal at each sub-slice was plotted to show the signal profile. The simulation models all of the RF excitations, to account for the effect of crosstalk between slices (which were acquired interleaved in the simulation and actual acquisition as the current radial line for every slice was acquired prior to the next radial line).

For a given parameter set, the simulation performed 500 excitations to reach steady state (more than enough to ensure steady state was reached). The simulation takes as inputs the T1 and T2 of the tissue being studied, the TR and TE of the SPGR sequence, the prescribed flip angle, the RF excitation pulse characteristics, the prescribed slice width, the slice selection gradient characteristics, the RF center frequency, and the inter-slice gap (in the multi-slice case only).

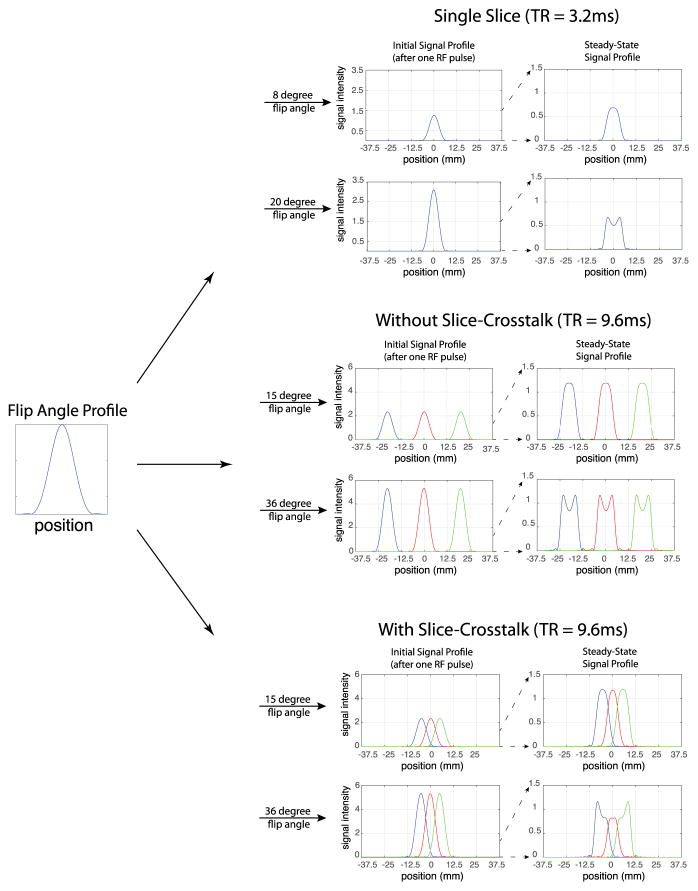
To help elucidate the differences between the initial signal profile and the steady-state signal profile, the simulation was used to generate plots of each for the single slice case (Case 1 described below) and the three interleaved slice case with large and zero inter-slice distance (Case 2 and Case 3 described below). The simulation was performed for a low flip angle close to the ideal slice-profile maximum-contrast angle (8 degrees and 15 degrees respectively for the single slice and three interleaved slice cases) and at a larger flip angle (20 degrees and 36 degrees respectively for the single slice and three interleaved slice cases) closer to the true maximum-contrast angle.

2.3 Phantom Experiments with Comparison to Numerical Simulation

To validate the accuracy of the numerical simulation, three different phantom imaging cases were investigated. We imaged two uniform phantoms with measured T1 values of ~300ms and ~1000ms. For all of the phantom studies, 150 time frames were acquired with 3600 radial lines for each slice. The body coil was used for both RF transmit and signal reception in all phantom experiments, because it provided both excellent transmit and receive RF homogeneity (removing coil inhomogeneity effects from the evaluation). Average signal intensities were measured across each vial, and the contrast calculated as the difference in the average signal intensities. The comparison details are listed in the table 1

Table 1.

The parameters of three phantom and simulation cases.

Case 1: Single slice
RF pulse (duration/TBW) effective TR/TE slice thickness /slice gap (edge to edge) flip angle
truncated sinc
1000μs
TBW = 2		 3.2/1.5ms 5mm
single slice		 8 to 50 degrees in 2 degree increments
Case 2: Three interleaved slices with large inter-slice distance
RF pulse (duration/TBW) effective TR/TE slice thickness /slice gap (edge to edge) flip angle
truncated sinc
1000μs
TBW = 2		 9.6/1.5ms 5mm /15mm 8 to 50 degrees in 2 degree increments
Case 3: Three interleaved slices with large inter-slice distance
RF pulse (duration/TBW) effective TR/TE slice thickness /slice gap (edge to edge) flip angle
truncated sinc
1000μs
TBW = 2		 9.6/1.5ms 5mm /0mm 8 to 50 degrees in 2 degree increments
Open in a new tab

For each case, the simulation was performed by using the same parameter settings with both the real RF pulse and ideal RF pulse (perfect rectangular). Overall signal scaling from the phantom scans was normalized to the simulation signal levels. A single normalization constant was determined for each tissue and applied across all flip angles.

In addition, the phantom experiment outlined in Case 1 was repeated using three additional RF pulses, one with a short duration that duplicated the RF pulse for the in-vivo studies, and the other two with a longer duration than the pulse studied in Case 1 but with the same spectral bandwidth. The RF pulse studied in Case 1 was a truncated sinc with duration of 1000μs and time bandwidth product (TBW) of 2. The three additional RF pulses studied were truncated sincs with duration 600μs, 4000μs and 8000μs and time bandwidth products of 1.6, 8 and 16 respectively. In order to accommodate the longer RF pulse durations, we use TR/TE = 16/9 ms for each of the four different RF pulses studied. The same phantom was imaged with flip angles ranging from 12 to 60 degrees in 4 degree increments. Normalized contrast vs. flip angle curves were generated from each of these two phantom experiments.

2.4 In Vivo Experiments

A comparison experiment was performed. The three interleaved slice sequence was tested in vivo on a human subject using a 32-channel surface coil. This test was approved by the University of Utah Institutional Review Board (IRB), and informed consent was obtained from the subject. The in-vivo test employed a truncated sinc RF pulse of 600μs duration and time/bandwidth product =1.6, TR/TE = 8.34/1.3ms, 8mm slice thickness and a 2.4mm inter-slice gap.

The subject was imaged using the sequence mentioned above with three different flip angles (22, 30, and 36 degrees) at both pre-contrast and approximately 2 minutes post-contrast. Although the post-stage is not close to the peak enhancement, it is at a relatively stable contrast level. A set of 50 temporal frames (10 seconds) was acquired at each flip angle at both time points.

Image orientation in was chosen to yield a short-axis stack of slices. Subject were instructed to hold their breath as long as possible during the acquisition. Image reconstruction was performed using the spatiotemporal constrained reconstruction described below.

2.5 Image Reconstruction

Since the golden ratio radial trajectory was used and no motion is anticipated, a sliding window reconstruction algorithm was expected to perform well and was adopted for the experiments outlined above (Winkelmann et al., 2007). A total of 2400 radial lines (from the last 100 frames when the signal is expected to be in steady state) were regrouped to form a single frame, and a nonuniform FFT routine was used to generate the images (Fessler, 2007).

For the in-vivo data set, the reconstruction was performed independently for each slice using SENSE-based spatiotemporal constraints with 3 dimensional total variation (2 spatial dimensions and the temporal dimension) as the constraints (Adluru et al., 2009; Feng et al., 2014).

Before reconstruction, the in-vivo data from the 32-channel multi-coil was combined to 8 virtual coils via coil PCA to speed up the computation process (Buehrer et al., 2007; Adluru and DiBella, 2012). An eigenvector estimation method was employed for coil sensitivity maps (Walsh et al., 2000). To keep the total variation (TV) weight factor consistent, the maximum value of each data set was normalized to 1. The temporal weight factor was chosen as 3e-4, which was 10 times higher than the spatial TV weight factor, set at 3e-5. A total of 250 iterations of the reconstruction were performed for each slice. All images were reconstructed off-line using MATLAB (Mathworks, Natick, MA) on a 16-core Linux workstation with 64 GB of RAM.

3. Results

3.1 Numerical Simulation

The results of the numerical simulation illustrating differences between the shape of the slice excitation profile, the steady-state signal profile, and the initial signal profile (the signal level after a single RF excitation) are shown in Figure 1. The top row of the figure illustrates the single slice case, at a low flip angle (8 degrees, close to the Ernst angle if an ideal slice excitation profile is assumed) and a larger flip angle (20 degrees, close to the optimized flip angle if the actual excitation profile is considered). As illustrated, the signal evolves over time at larger flip angles to yield a steady-state signal profile that is very different in shape from both the slice excitation profile and the initial signal profile. A concave shape signal profile is observed in steady state at the higher flip angle.

Figure 1.

Figure 1

Open in a new tab

Simulation of the slice initial signal profile and steady state signal profile for the RF pulse with slice excitation profile shown. Three different cases are demonstrated: the single slice acquisition case, a three slice multi-slice acquisition with large interslice gap (no slice crosstalk), and a three slice mutli-slice acquisition with zero interslice gap (showing slice crosstalk). The top row of each case uses a low flip angle that is close to the ideal maximum contrast flip angle (when an ideal slice excitation profile is assumed). The bottom row of each case utilizes a higher flip angle that is close to the actual maximum contrast flip angle.

The middle and bottom rows of Figure 1 illustrate the three interleaved slice case with a large inter-slice gap (middle row) and no inter-slice gap (bottom row). Note that a TR three times as long as the TR of the single slice case is used due to the multi-slice interleaving. As would be expected, when a large inter-slice gap is used there is very little cross talk between the slices, and the signal profile evolves in much the same way as the single slice signal profile for each slice. However, when the inter-slice gap is eliminated, crosstalk becomes significant. Mutual influences between the slices cause the slice profiles to differ from the non-crosstalk case by spreading the concave shape of the profile across the three slices. Consequently, the outer slices have peaks, while the center slice is more flat. In this case, contrast may vary for the middle slice versus the edge slices, and it may not be possible to maximize enhanced/unenhanced myocardium contrast simultaneously for both the middle and edge slices.

3.2 Phantom Experiments with Comparison to Numerical Simulation

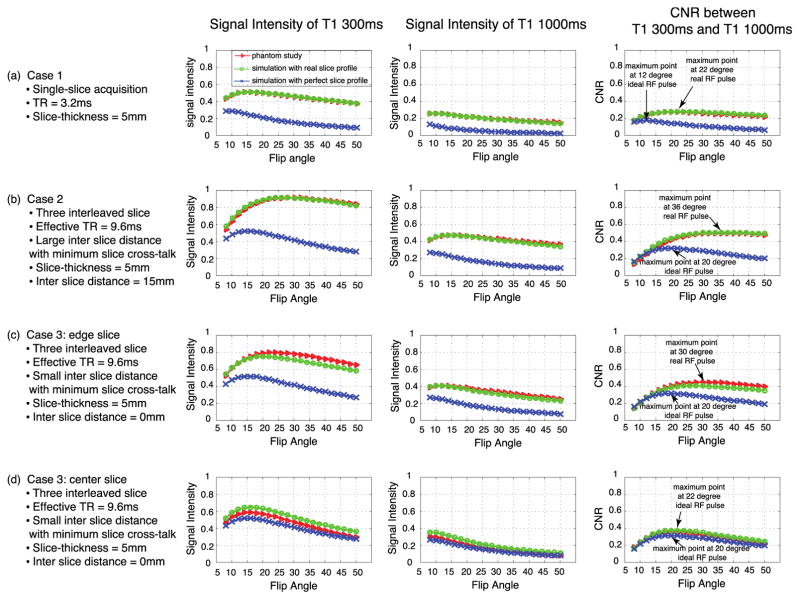
Figure 2 illustrates the signal levels as a function of flip angle of enhanced (T1 = 300ms, left column) and unenhanced (T1 = 1000ms, middle column) myocardium, as well as the contrast-to-noise ratio (CNR, calculated in this case as the signal differences) between the two (right column). The blue trace on each graph denotes the simulated signal levels assuming an ideal slice excitation profile. The green trace illustrates the simulated signal levels when the actual slice excitation profile is taken into consideration. Finally, the red trace shows the result of the phantom experiment, where vials with known T1 values of ~300ms and ~1000m were scanned across a range of flip angles.

Figure 2.

Figure 2

Open in a new tab

Variations in signal intensity and CNR as a function of flip angle for both single slice and three slice multi-slice acquisitions. Phantom results are shown in red, and are compared to simulation results assuming an ideal slice excitation profile (blue) and those incorporating the actual slice excitation profile (green). (a) Single slice case: the theoretical optimized flip angle for CNR is ~12 degrees, while the phantom study and simulation using the actual slice profile shows an optimal flip angle of ~22 degrees. (b) 3 slices with large inter-slice gap: the CNR was maximized at ~20 degrees with an assumed ideal slice profile, but at ~36 degrees when the actual slice excitation profile was considered. (c) Edge slice results for the 3 slice multi-slice case with no inter-slice gap. (d) Center slice results for the 3 slice multi-slice case with no inter-slice gap.

In all cases, the actual phantom experiment results are in much better agreement with the simulation results that take into consideration the actual slice excitation profile.

The top row (Figure 2a) illustrates the single slice case (Case 1), and the second row (Figure 2b) illustrates the three interleaved slice case with an inter-slice gap equal to three times the prescribed slice thickness of 15mm (Case 2). The third and fourth rows illustrate the three interleaved slice case with no inter-slice gap for the edge slices (Figure 2c) and the middle slice (Figure 2d). It is interesting to note that the differences between the middle and edge slices in the three interleaved slice case are clearly evident in the phantom experiments, validating our model of excitation crosstalk between the slices.

In all cases, the phantom experiments are in excellent agreement with the numerical simulation when the actual slice excitation profile is taken into consideration. It is also evident in all cases that the flip angle that maximizes contrast between enhanced and unenhanced myocardium is significantly different than would be expected given an ideal slice excitation profile. Assumption of an ideal slice excitation profile results in all cases in a significant underestimation of the flip angle that will actually yield maximized contrast. For the RF excitation profile and parameters used in these experiments, the maximum-contrast flip angle increased from 12 degrees (assuming an ideal slice excitation profile) to 20 degrees when the actual profile was taken into consideration. Similar results are seen in Cases 2 and 3 illustrated.

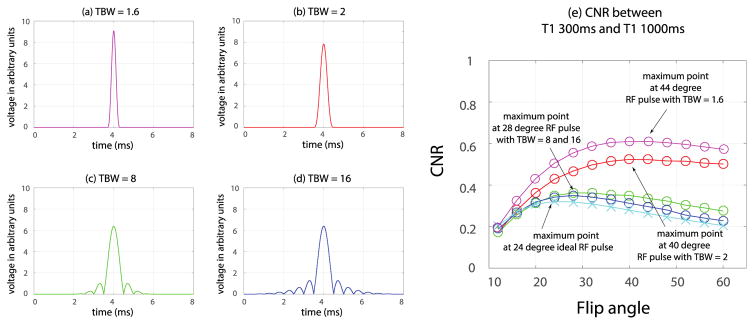
Figure 3 illustrates how the contrast vs. flip angle results vary (in numerical simulation) when RF pulses with short duration and RF pulses with longer duration (and the same spectral bandwidth as the pulse studied in Case 1) are used. The RF envelope with a short duration (with time-bandwidth product of 1.6) that was used for the in-vivo studies is shown in Figure 3a. The RF pulse of the original pulse used in Case 1 (with time-bandwidth product of 2) is shown in Figure 3b, and those of the two additional pulses that were simulated are shown in Figures 3c and 3d (with time-bandwidth products of 8 and 16 respectively). These longer RF pulses progressively get closer to an ideal slice excitation profile. Enhanced/unenhanced myocardial contrast vs. flip angle is shown in Figure 3e for each of the three RF pulses. The curve assuming an ideal excitation profile is also shown for comparison. As expected, the longer RF pulses provide a more ideal slice excitation profile, pushing the expected maximum-contrast flip angle closer to that of the ideal case.

Figure 3.

Figure 3

Open in a new tab

Four different RF pulses were tested with fixed TR/TE=16/9ms in a single slice. The RF excitation envelopes for each pulse are shown in (a)-(d). In (e), phantom results for each RF pulse (denoted with the symbol “o” on the graph) are compared with the simulation result assuming an ideal slice excitation profile (denoted with the symbol “x” on the graph). As can be seen, the phantom results approach the simulated (ideal slice excitation) results as a longer duration (larger time bandwidth product (TBW)) RF pulse is used.

3.3 In Vivo Experiments

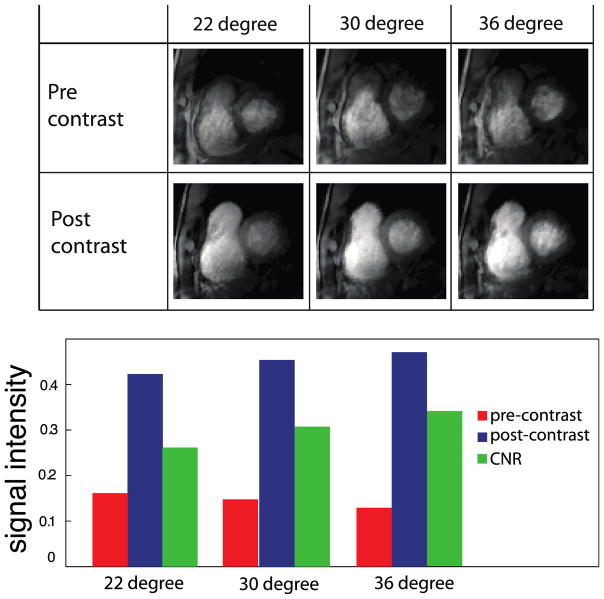
Figure 4 demonstrates the CNR achieved at different flip angles in a human subject. The CNR is calculated from the difference between averaged post-contrast and pre-contrast signal intensity. The pre contrast and post contrast signal intensity is achieved from manually segmented ROIs in the myocardial wall region. The highest CNR between enhanced and unenhanced myocardial tissue was observed at a flip angle of 36 degrees rather than the 22 degree flip angle that was close to the flip angle predicted by a theoretical optimization that assumed an ideal slice profile.

Figure 4.

Figure 4

Open in a new tab

In-vivo results showing signal intensity variations at different flip angles both pre-contrast and post-contrast. The highest CNR between enhanced and unenhanced myocardial tissue was observed at a flip angle of 36 degrees, significantly higher than the 22 degree flip angle predicted by a theoretical optimization that assumed an ideal slice profile.

4. Discussion

While numerous studies have addressed the effect of slice profiles on SPGR imaging, this study investigates in depth this effect on a new method for acquiring cardiac perfusion data. For the three-slice interleaved acquisition, we predicted the best flip angle to be 30 ~ 36 degrees depending on the slice gap. This extends the empirical findings from (Sharif et al., 2015), where an RF pulse with 600μs duration and 10mm slice thickness was used, and a flip angle of ~30 degrees gave maximal CNR. Our analysis gives a similar result and also reports optimal flip angles for other pulses and for situations with slice cross-talk.

The non-ideal slice profile leads to flip angle variation across the slice. This causes the edge area to experience a lower flip angle that is closer to the Ernst angle, and therefore produces higher signal intensity than the center area. Since the total signal from a given slice is an integral of the signal across the slice, it is important to take into account these actual slice signal profiles when determining the flip angle that will yield the highest contrast between enhanced and unenhanced myocardium.

When acquiring adjacent or nearby slices, the cross-talk between slices is important to consider. In general, the cross-talk effects generated by non-ideal slice excitation profiles cannot be avoided. However, if the slice profile can be estimated, the effects of cross-talk can be minimized. For example, the cross-talk effects lead to different optimal flip angles for different slices. Future studies could estimate the different flip angles needed at each slice to optimize slice CNR, and flip angle could be varied for each slice individually based on the results.

Our work did not take into consideration additional variations in the spatial excitation profile resulting from RF transmit coil characteristics and tissue properties. While many excitation systems do a very good job at delivering homogenous flip angles over the field of view, this assumption of B1 transmit homogeneity is not strictly valid. Others have studied these effects in different contexts (e.g., for DCE MRI of the breast (Cron et al., 1999)). Other issues, such as the efficacy of the RF and gradient spoiling, were not considered here. Our analyses also used relatively simple sinc pulses; the RF pulse design could be tailored to improve slice profiles even for relatively fast excitations.

The slice profile issues described here are also important for other sequences commonly used in cardiac imaging, such as balanced SSFP and saturation recovery with turboFLASH or SSFP readouts. Balanced SSFP has a similar slice profile issue as SPGR (Deppe et al., 2010; Coolen et al., 2009). The ECG-gated saturation recovery sequence, which is much more widely used in cardiac perfusion imaging than ungated SPGR, employs a non-selective saturation pulse, typically with a rapid gradient echo (SPGR) readout (Fenchel et al., 2004). Depending on T1 and sequence parameters, the readouts may reach steady state rapidly. Regardless, the repeated application of short RF pulses with poor slice profiles leads to the same type of effects that were quantified here, although further work is needed to better quantify the effects and the improvements possible with new RF pulses.

5. Conclusion

Ungated SPGR acquisition was shown to be a feasible method for cardiac perfusion studies. Since the choice of flip angle is an essential factor in obtaining optimal CNR, the true slice profile needs to be considered when determining what flip angle to use. The optimal flip angle was found to vary by more than 40% depending on the slice profile. This work provided a framework to optimize the flip angle choice using different RF pulse profiles combined with slice cross-talk effects.

Acknowledgments

This work was supported by R01HL113224.

References

  1. Adluru G, DiBella EVR. Compression2: compressed sensing withcompressed coil arrays. Proceedings of the 15th Annual Meeting SCMR; Orlando, FL, USA. 2012. p. 242. [Google Scholar]
  2. Adluru G, McGann C, Speier P, Kholmovski EG, Shaaban A, Dibella EV. Acquisition and reconstruction of undersampled radial data for myocardial perfusion magnetic resonance imaging. J Magn Reson Imaging. 2009;29:466–73. doi: 10.1002/jmri.21585. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Atkinson DJ, Burstein D, Edelman RR. First-pass cardiac perfusion: evaluation with ultrafast MR imaging. Radiology. 1990;174:757–62. doi: 10.1148/radiology.174.3.2305058. [DOI] [PubMed] [Google Scholar]
  4. Buehrer M, Pruessmann KP, Boesiger P, Kozerke S. Array compression for MRI with large coil arrays. Magn Reson Med. 2007;57:1131–9. doi: 10.1002/mrm.21237. [DOI] [PubMed] [Google Scholar]
  5. Coolen BF, Heijman E, Nicolay K, Strijkers GJ. On the use of steady-state signal equations for 2D TrueFISP imaging. Magnetic Resonance Imaging. 2009;27:815–22. doi: 10.1016/j.mri.2008.12.001. [DOI] [PubMed] [Google Scholar]
  6. Cron GO, Santyr G, Kelcz F. Accurate and rapid quantitative dynamic contrast-enhanced breast MR imaging using spoiled gradient-recalled echoes and bookend T-1 measurements. Magnetic Resonance in Medicine. 1999;42:746–53. doi: 10.1002/(sici)1522-2594(199910)42:4<746::aid-mrm17>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]
  7. Deppe MH, Teh K, Parra-Robles J, Lee KJ, Wild JM. Slice profile effects in 2D slice-selective MRI of hyperpolarized nuclei. J Magn Reson. 2010;202:180–9. doi: 10.1016/j.jmr.2009.11.003. [DOI] [PubMed] [Google Scholar]
  8. DiBella EV, Chen L, Schabel MC, Adluru G, McGann CJ. Myocardial perfusion acquisition without magnetization preparation or gating. Magn Reson Med. 2012;67:609–13. doi: 10.1002/mrm.23318. [DOI] [PubMed] [Google Scholar]
  9. Fenchel M, Helber U, Simonetti OP, Stauder NI, Kramer U, Nguyen CN, Finn JP, Claussen CD, Miller S. Multislice first-pass myocardial perfusion imaging: Comparison of saturation recovery (SR)-TrueFISP-two-dimensional (2D) and SR-TurboFLASH-2D pulse sequences. J Magn Reson Imaging. 2004;19:555–63. doi: 10.1002/jmri.20050. [DOI] [PubMed] [Google Scholar]
  10. Feng L, Grimm R, Block KT, Chandarana H, Kim S, Xu J, Axel L, Sodickson DK, Otazo R. Golden-angle radial sparse parallel MRI: combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magn Reson Med. 2014;72:707–17. doi: 10.1002/mrm.24980. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Fessler JA. On NUFFT-based gridding for non-Cartesian MRI. J Magn Reson. 2007;188:191–5. doi: 10.1016/j.jmr.2007.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hänicke W, Merboldt K-D, Frahm J. Slice selection and T1 contrast in FLASH NMR imaging. Journal of Magnetic Resonance (1969) 1988;77:64–74. [Google Scholar]
  13. Ishida M, Kato S, Sakuma H. Cardiac MRI in ischemic heart disease. Circ J. 2009;73:1577–88. doi: 10.1253/circj.cj-09-0524. [DOI] [PubMed] [Google Scholar]
  14. Klassen C, Nguyen M, Siuciak A, Wilke NM. Magnetic resonance first pass perfusion imaging for detecting coronary artery disease. Eur J Radiol. 2006;57:412–6. doi: 10.1016/j.ejrad.2005.12.029. [DOI] [PubMed] [Google Scholar]
  15. Schwitter J, Nanz D, Kneifel S, Bertschinger K, Buchi M, Knusel PR, Marincek B, Luscher TF, von Schulthess GK. Assessment of myocardial perfusion in coronary artery disease by magnetic resonance: a comparison with positron emission tomography and coronary angiography. Circulation. 2001;103:2230–5. doi: 10.1161/01.cir.103.18.2230. [DOI] [PubMed] [Google Scholar]
  16. Sharif B, Arsanjani R, Dharmakumar R, Bairey Merz CN, Berman DS, Li D. All-systolic non-ECG-gated myocardial perfusion MRI: Feasibility of multi-slice continuous first-pass imaging. Magn Reson Med. 2015;74:1661–74. doi: 10.1002/mrm.25752. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Sharif B, Dharmakumar R, Arsanjani R, Thomson L, Bairey Merz CN, Berman DS, Li D. Non-ECG-gated myocardial perfusion MRI using continuous magnetization-driven radial sampling. Magn Reson Med. 2014;72:1620–8. doi: 10.1002/mrm.25074. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magn Reson Med. 2000;43:682–90. doi: 10.1002/(sici)1522-2594(200005)43:5<682::aid-mrm10>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
  19. Wang H, Bangerter N, Adluru G, Taylor M, DiBella E. Myocardial perfusion imaging with an interleaved multi-slice acquisition for steady-state readout without saturation preparation or gating. Proceedings of the 22nd Annual Meeting of ISMRM; Milan, Italy. 2014. [Google Scholar]
  20. Wieben O, Francois C, Reeder SB. Cardiac MRI of ischemic heart disease at 3 T: potential and challenges. Eur J Radiol. 2008;65:15–28. doi: 10.1016/j.ejrad.2007.10.022. [DOI] [PubMed] [Google Scholar]
  21. Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An optimal radial profile order based on the Golden Ratio for time-resolved MRI. IEEE Trans Med Imaging. 2007;26:68–76. doi: 10.1109/TMI.2006.885337. [DOI] [PubMed] [Google Scholar]

RESOURCES