Enhancing the Sensitivity of Multidimensional NMR Experiments by using Triply-Compensated π Pulses

Abstract

In multidimensional solution NMR experiments, π pulses are used extensively for inversion and refocusing operations on ¹H, ¹³C and ¹⁵N nuclei. Pulse miscalibration, off-resonance effects, and J-coupling evolution during π pulse execution result in severe signal losses that are exacerbated at high magnetic fields. Here, we report the implementation of a universal, triply-compensated π pulse (G5) optimized for both inversion and refocusing in widely used 2- and 3-dimensional experiments. By replacing most of the hard π pulses, adiabatic or composite pulses on the ¹H, ¹³C and ¹⁵N channels with G5 pulses, we obtained signal enhancements ranging from 80 to 240%. We anticipate that triply-compensated pulses will be crucial for improving the performance of multidimensional and multinuclear pulse sequences at ultra-high fields.

Introduction

In pulsed Fourier Transform NMR (FTNMR), off-resonance effects, pulse miscalibrations, and J-coupling evolution (i.e., ‘zz’ evolution) cause differential responses of nuclear spins to the applied radio frequency (RF) pulses, resulting in substantial signal losses¹. In triple-resonance experiments performed at high magnetic fields on biological macromolecules, these effects are more severe because of high-salt concentrations typically required for sample stability. High salt concentration increases the duration of the RF pulses used for excitation (π/2), inversion, and refocusing (π) operations.

Due to their longer duration, π pulses are the most error-prone elements in a pulse sequence (Fig. S1). Increasing the RF power would, in principle, achieve nearly perfect inversion or refocusing operations and mitigate off-resonance effects on π pulses. However, power handling for current probeheads puts strict limits on the shortest achievable pulse width. These limitations become even more stringent for cryogenically-cooled probes. Composite pulses^2–10 or shaped π pulses^11–18, designed for either inversion or refocusing, represent alternative solutions. Nevertheless, these pulses are relatively long and during their execution the nuclear magnetization may undergo J-coupling evolution or relaxation, resulting in spectral artifacts and signal loss. As a result, most of the INEPT–based heteronuclear multidimensional NMR experiments¹⁹ still adopt hard pulses for both through-bond magnetization transfer and heteronuclear decoupling. Even simple 2D pulse sequences such as the ¹H-¹⁵N HSQC^20,21 and the ¹H-¹³C HSQC²² experiments contain several hard π pulses (Figs. S2 and S3), and signal losses are exacerbated in through-bond^23–25 and through-space^22,26 triple-resonance experiments.

Recently, using a genetic algorithm (GA) optimization, we designed a triply-compensated pulse (G5), with simultaneous compensation for off-resonance effects, RF inhomogeneity/miscalibrations, and J-coupling evolution²⁷. According to the nomenclature of Levitt⁴, the G5 pulse is a ‘type A composite pulse’, which can be used for both inversion and refocusing. The total nutation angle of the G5 pulse is 5π and its duration is five times that of a single π pulse.²⁷ Compared to G3 and Q3 pulses^13,14, the G5 pulse has three major advantages: i) it exhibits wider inversion and refocusing bandwidths for ¹H, ¹³C, and ¹⁵N nuclei, ii) it has a significantly shorter duration, and iii) it requires substantially lower RF power.

Here, we show that by replacing ¹H, ¹³C and ¹⁵N hard π pulses and selected ¹³C shaped π pulses with the G5 pulse, it is possible to enhance the sensitivity of resonances at the edge of the effective bandwidths of widely used 2D ¹H-¹⁵N and ¹H-¹³C HSQC as well as 3D TROSY-HNCA and ¹³C-edited NOESY-HSQC experiments. We anticipate that the sensitivity gain obtained with triply-compensated pulses will be even more significant for experiments carried out at ultra-high magnetic fields.

Material and Methods

The 2D ¹H-¹⁵N HSQC spectrum and the first 2D ¹H-¹³C plane of 3D TROSY-HNCA were acquired at 298 K on a Bruker 900 MHz spectrometer equipped with a 5 mm TCI CryoProbe. A U-[²H, ¹⁵N,¹³C]-labeled 25 kDa human heat shock protein 90 N-domain (Hsp90N) sample in 20 mM phosphate buffer at pH 7.0, 100 mM KCl, and 5 mM β-mercaptoethanol (BME) was used as a benchmark for the experiments. The standard Bruker pulse sequences hsqcetfpf3gpsi2 (Fig. S2), trhncagp2h3d2 (Fig. S4) and their G5-replaced versions (described below) were used. The 2D ¹H-¹³C HSQC spectra and the first 2D ¹H-¹H plane of ¹³C-edited 3D NOESY-HSQC were acquired at 298 K with a Bruker 850 MHz spectrometer equipped with a 5 mm TCI CryoProbe. A sample of 0.3 mM U-[¹⁵N,¹³C]-labeled 21 kDa Abelson kinase 1b regulatory module (Abl-1b RM) in 25 mM phosphate buffer, 100 mM NaCl at pH 6.5 was used to test these two types of experiments. The standard Bruker pulse sequences hsqcetgpsisp2.2 (Fig. S3A), noesyhsqcetgpsi3d (Fig. S5) and their G5-replaced versions were used. Acquisition and processing parameters were kept constant for each experiment type. Relevant acquisition parameters are detailed in the figure captions. U-[¹³C¹⁵N]-labeled 42 kDa maltose binding protein (MBP) sample (1.0 mM), prepared in 20 mM of phosphate buffer, 100 mM NaCl, 2 mM DTT, 0.1 mM NaN₃ at pH 7.5, was used to perform carbon HSQCs shown in Fig. S9.

Results and Discussion

Pulse miscalibration, RF inhomogeneity, offset effects as well as J coupling evolution can cause significant reductions in the sensitivity of multidimensional NMR experiments. The major sources of errors and sensitivity losses are due to the presence of multiple π pulse, which are essential for heteronuclear decoupling and refocusing operations. To quantify these sensitivity losses, we systematically study different cases where of π pulses are used for heteronuclear decoupling, chemical shift refocusing, and simultaneous refocusing pulse in INEPT (Figs. 1A–D and Supplementary Material). The ¹H_A/¹H_B and ¹H_N decoupling scheme (Fig. 1A) is typically used for 3D TROSY triple-resonance experiments (e.g., TROSY-HNCACB²⁸). In these experiments, and when partially deuterated proteins are studied, a π pulse on ¹H channel is necessary to decouple ¹H_A/¹H_B from ¹³CA/¹³CB during ¹³C evolution. In this case, imperfect π pulses reduce the magnetization transferred by a factor – cosα (Supplementary Material).

Fig. 1.

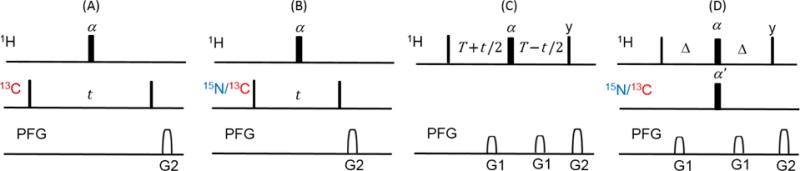
Four common placement of hard π pulses in multidimensional NMR. Imperfect pulse with flip angle α or α′ ≤ 180° for ¹H_A/¹H_B and ¹H_N decoupling (A), ¹H_N decoupling (B), chemical shift refocusing (C), and both refocusing and decoupling in INEPT (D). Narrow bars represent 90° pulses, and the flip angles of wide pulses are α and α′ as indicated on the plot. The default pulse phase is +x. Delay Δ is 1/(4J), and J is the scalar coupling between ¹H and ¹⁵N. T is a delay. PFG G1 = (1 ms, 10%), G2 = (1 ms, 20%).

For both ¹H_N decoupling sequence (Fig. 1B) and chemical shift refocusing scheme (Fig. 1C), used in the ¹H-¹⁵N HSQC experiments and constant-time evolution, respectively, the magnetization is scaled by (1 − cosα)/2. Finally, for two simultaneous refocusing π pulses in the INEPT building block (Fig. 1D), the scaling factor becomes −(cos α + cos α′)/2. We can combine these scaling factors in an overall semi-quantitative expression: ${(-\mathit{cos}\mathrm{\alpha })}^{n1}\frac{{(1-\mathit{cos}\alpha )}^{n2+n3}}{2^{n2+n3}}\frac{{(-\mathit{cos}\alpha -\mathit{cos}\alpha \prime )}^{n4}}{2^{n4}}$, where n1, n2, n3 and n4 represent the occurrences of each scheme in a given pulse experiment. In the case of perfect flip angles both α and α′ are 180° and the effective scaling factor is 1. However, even small deviations from ideality in the flip angles result in a significant signal loss.

Here we show that pulse-dependent errors can be remedied by substituting the inversions or refocusing π pulses with our G5 pulse. The G5 pulse has a built-in simultaneous compensation for RF inhomogeneity, offset, and heteronuclear J-coupling/dipolar coupling. The G5 pulse was designed using a Genetic Algorithm (GA) and was described in our earlier work²⁷. IBriefly, GA defines a pulse as an array of phase values (i.e., individual). The amplitude of each pulse is usually kept constant (not shaped), i.e., not included in the optimization protocol. Starting from a random population, GA evolves each individual to maximize the imposed features such as offset, RF compensation, and J-coupling/dipolar coupling. The evolution of phase arrays continues until GA finds an optimal bandwidth. Of all GA optimized pulses, here we selected the G5 pulse, which has the shortest duration and is most suitable for solution NMR spectroscopy. G5’s operational bandwidth is reported in Figure S1. Based on the fidelity plot at 99% efficiency (i.e., 99% fidelity rectangle)²⁷, the RF compensation for the G5 pulse is greater than 10% and the zz - coupling compensation bandwidth in relative coupling strength D/B₁ is greater than 1, where D is the coupling strength in Hz and B₁ is the RF amplitude in Hz. Experimentally, one should calibrate the RF amplitude by evaluating the pulse length of a π/2 pulse. For this RF amplitude, the tolerance limit of the G5 pulse is ±10%. In our experiments, the duration of the G5 π pulse is 144 μs. In contrast to the ¹H hard π pulse, the G5 pulse displays much more uniform inversion and refocusing profiles over a range (or width) of approximately 20 kHz (23.5 ppm in the ¹H chemical shift scale). The inversion profiles of G5 pulse for typical experimental RF amplitudes in ¹H, ¹⁵N and ¹³C channels are shown in Fig. 1. The observed bandwidths are 23.5 ppm, 105 ppm and 116 ppm for ¹H, ¹⁵N and ¹³C, respectively. A detailed simulation of the G5 pulse with x phase on z magnetization is shown in Fig. S1. A perfect inversion is achieved for both z and y magnetization as in the case of the ideal hard π pulse.

In the following sections, we apply and discuss the G5 pulse for the most representative experiments used for protein resonance assignments.

2D ¹H-¹⁵N HSQC

For the 2D ¹H-¹⁵N HSQC pulse sequence, we first replaced all five ¹H hard π pulses with the G5 pulse (Fig. S2). As expected, signal enhancements are resonance offset-dependent (Fig. 2A and 2B), with significant enhancements for the most downfield peaks in the ¹H dimension. Compared to the reference spectrum, we obtained signal enhancement ranging from 30–60% (Fig. 3B). Subsequently, we also replaced four ¹⁵N hard π pulses with G5. In this latter case, we achieved signal enhancement from 50–80% (Fig. 3C), with significant signal increase for the Nε resonances of the arginine residues.

Fig. 2.

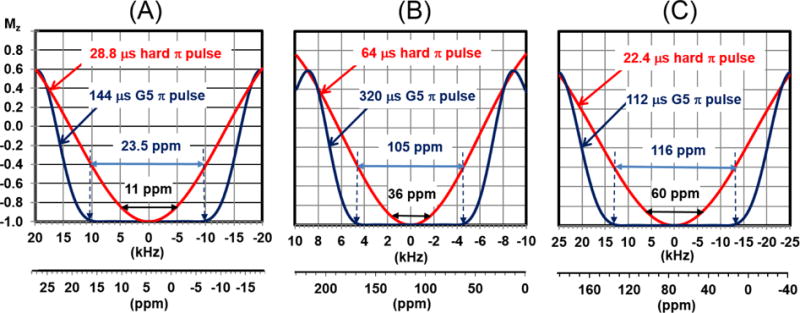
Simulated inversion profiles of a hard and G5 π pulses for ¹H (A), ¹⁵N (B), and ¹³C (C) on an 850 MHz spectrometer. The simulated curves were obtained using the ‘shapetool’ in the Bruker software. The durations of G5 pulse is ten times longer than a hard π/2 pulses (Note that the durations of hard π/2 pulses for the ¹H, ¹⁵N and ¹³C are 14.4, 32.0 and 11.2 μs, respectively). The spectral widths indicated in the axis are those commonly used for biomacromolecules (11, 36, and 60 ppm for ¹H, ¹⁵N and ¹³C dimensions). Note that the G5 pulse uniformly excites 23.5, 105, and 116 ppm for ¹H, ¹⁵N and ¹³C, respectively.

Fig. 3.

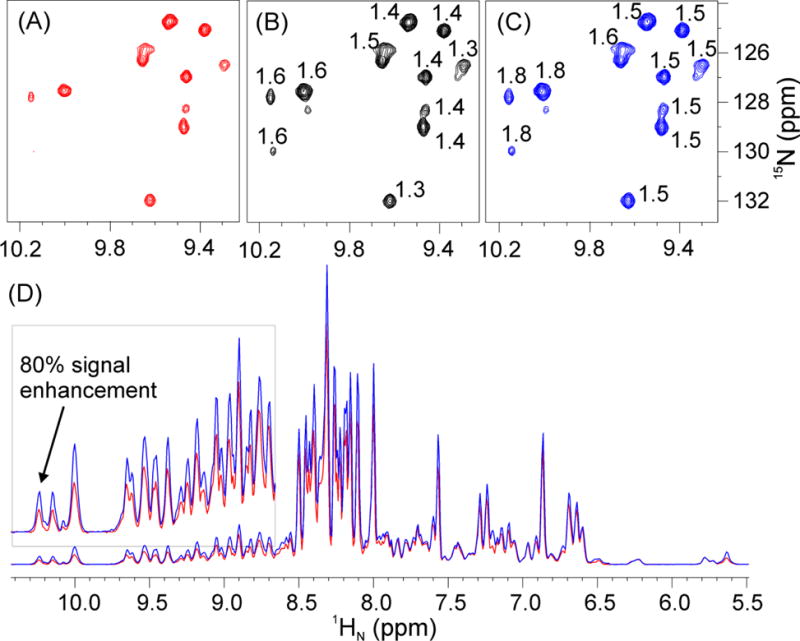
2D ¹H-¹⁵N HSQC spectra of U-²H,¹⁵N,¹³C labeled Hsp90N acquired on a 900 MHz spectrometer using: (A) the original Bruker pulse sequence (hsqcetfpf3gpsi2, Fig. S2); (B) replacing all ¹H hard π pulses with G5; (C) replacing all ¹H and ¹⁵N hard π pulses with G5. (D) Overlay of 1D projections of the spectra in (A) and (C). The low field region is shown in the inset with ×5 magnification. Acquisition parameters: d1 = 1 sec, ns = 8 (number of scans), TD = 2k×128, p1 = 14.4 μs (length of ¹H π/2 hard pulse), p21 = 32 μs (length of ¹⁵N π/2 hard pulse), the offsets of ¹H and ¹⁵N are 4.7 and 118 ppm, respectively. The pulse widths of the ¹H and ¹⁵N G5 are 144 and 320 μs, respectively. The numbers indicated on the resonances for the spectra in panels (B) and (C) represent the ratios of signal intensities of (B) and (A), and (C) and (A), respectively.

2D ¹H-¹³C HSQC

For the broadband 2D ¹H-¹³C HSQC experiment (Fig. S3A), we replaced all ¹H hard π pulses with the G5 pulse. In this case, the signal enhancement ranges from 20–90% with respect to the reference spectrum (Figs. 4A and 4B). In particular, the 1D projections of the two 2D spectra show dramatic signal enhancement for the methyl resonances (Fig. S6). Additionally, the 2D ¹H-¹³C HSQC pulse sequence includes two shaped π pulses (Crp80,0.5,20.1) of 0.5 ms for the inversion of the ¹³C longitudinal magnetization, and two shaped π pulses (Crp80comp.4) of 2.0 ms for refocusing the ¹³C transverse magnetization. These two types of pulses should cover 50 kHz bandwidth, corresponding to 234 ppm at 850 MHz and, in principle, should be able to perform both inversion and refocusing operations efficiently. Notably, after replacing both Crp80,0.5,20.1 and Crp80comp.4 with the G5 pulse, we observed 60–130% signal enhancement for the methyl resonances and 240% for aromatic groups. This is probably due to a combination of the significantly longer pulse duration for Crp80,0.5,20.1 and Crp80comp.4, the longer interpulse delays, and inefficient J-coupling evolution during the Crp80comp.4 shaped pulse. We attempted adiabatic pulse optimization by changing the ¹J_NH-dependent delay (cnst2 in Bruker naming) and the delay compensation of Crp80comp.4 pulse (cnst17) values. We found that the J-evolution is optimal with default values (cnst2 = 145, cnst17 = −0.5) in the pulse sequence. However, the total duration of the two Crp80comp.4 pulses is 4 ms, which affects the decay of ¹³C transverse magnetization. In contrast to these shaped pulses, the duration of the G5 pulse is only 112 μs. In addition, the pulse sequence includes a delay (Δ2) of 2.36 ms (Fig. S3A). With the implementation of the G5 pulse, this delay is set to 1/(8×¹J_CH), corresponding to 0.86 ms for ¹J_CH = 145 Hz, which reduces the duration from 4.7 ms to 1.7 ms (2×Δ2). In terms of overall duration of the pulse sequence, the implementation of the G5 pulse in the 2D ¹H-¹³C HSQC pulse sequence decreased the experiment length by a total of 7 ms, with a substantial boost in signal-to-noise ratio.

Fig. 4.

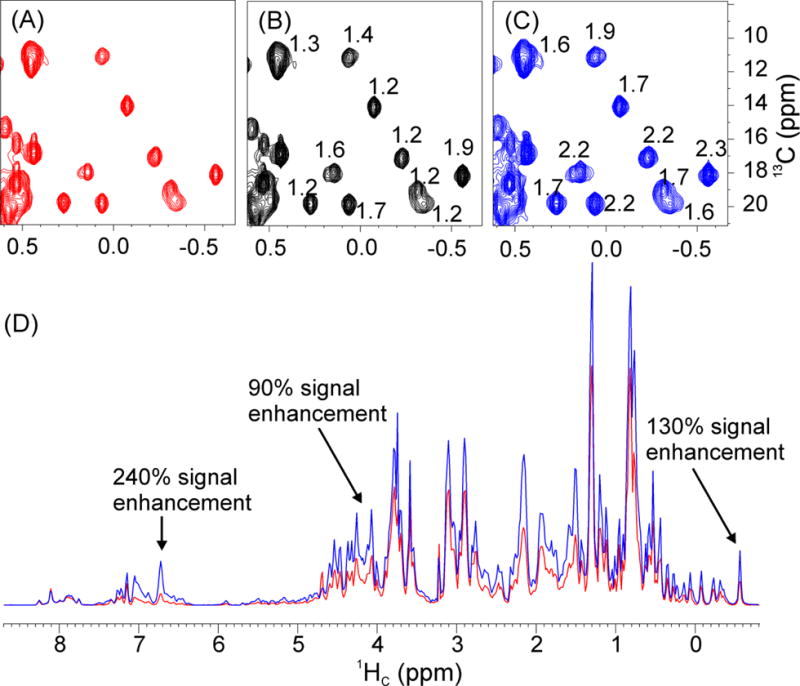
2D ¹H-¹³C HSQC spectra of the U-¹⁵N,¹³C-labeled Abl1b RM acquired on an 850 MHz spectrometer. (A) original Bruker pulse sequence (hsqcetgpsisp2.2, Fig. S3A); (B) replacing all ¹H hard π pulses with G5; (C) replacing all ¹H and ¹³C hard pulses with G5. (D) Overlay of 1D projections of (A) and (C). The numbers in (B) and (C) represent the ratios of the signal intensities of (B) and (A), and (C) and (A), respectively. Acquisition parameters: d1 = 1 sec, ns = 16 (number of scans), TD = 2k×256, p1 = 11.3 μs (length of ¹H π/2 hard pulse), p3 = 11.2 μs (length of ¹³C π/2 hard pulse), the offsets of ¹H and ¹³C are 4.7 and 75.0 ppm, respectively. The spectral width of the ¹³C dimension was 165 ppm.

Remarkably, the signal enhancement for the aromatic peaks was more than 2-fold higher than for aliphatic peaks. To understand the nature of this difference in signal enhancements, we ran 2D ¹H-¹³C HSQC experiments (Fig. S3B), modified from original Varian Chsqc pulse sequence. Since the pulse sequence uses States-TPPI for phase sensitive detection (Fig. S3B), it is significantly shorter than the corresponding Echo-antiecho (or Rance-Kay) by ~ 8 ms (Fig. S3A), we observed 120% and 40–60% signal enhancement for the aromatic and aliphatic regions, respectively. In fact, the aromatic signals benefit from the shorter pulse sequence more than the aliphatic CH_n (n=1, 2, or 3) counterparts due to chemical shift anisotropy (CSA) and other factors that contribute to faster transverse (T₂) relaxation²⁹. After replacing the ¹H hard π pulses and ¹³C CHIRP pulses in the Chsqc (Fig. S3B) with the G5 pulse, the pulse sequence becomes 1.9 ms shorter. Note that the solvent suppression of the States-TPPI 2D ¹H-¹³C HSQC is not as good as that of Echo-Antiecho as the latter sequence uses PFG for coherence selection²¹. Finally, we tested the effects of the ¹³C offset values (39, 75, and 125 ppm) on the original and G5-modified 2D ¹H-¹³C HSQC. For this test, we used a sample of U-[¹³C-¹⁵N] maltose binding protein. As shown in Fig. S9, the most uniform irradiation for both aliphatic and aromatic signals is obtained with the G5-modified pulse sequence setting the ¹³C transmitter offset at 75 ppm.

3D TROSY-HNCA

To demonstrate the effects of the new pulse in deuterium decoupled triple resonance experiments, we selected the 3D TROSY-HNCA experiment and utilized a U-[²H,¹⁵N,¹³C] labeled Hsp90N sample (Fig. 5). By replacing five ¹H hard π pulses with G5 pulses, we observed ~60% signal enhancement for ¹H resonances in the downfield region (~8 to 11 ppm) of the spectrum. Subsequently, we replaced the six ¹⁵N hard π pulses, resulting in an additional 20% increase of signal intensities for ¹⁵N resonances both in the downfield and upfield regions. Therefore, the effective enhancement for resonances in the ¹H downfield region and ¹⁵N downfield and upfield regions was up to 70% (Fig. 5). All other pulse sequences (HSQC-based or TROSY-based) for protein backbone chemical shift assignments have similar numbers of ¹H and ¹⁵N hard π pulses; therefore, we anticipate similar signal enhancement after replacing the ¹H and ¹⁵N hard π pulses with the G5 pulses.

Fig. 5.

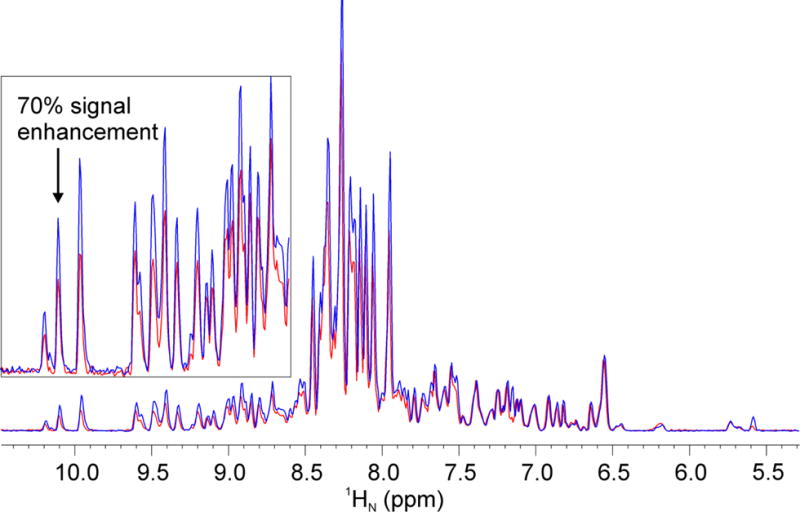
1D projections of 2D ¹H-¹³C planes of the 3D TROSY-HNCA spectrum of U-²H,¹⁵N,¹³C labeled Hsp90N acquired on a 900 MHz spectrometer with original Bruker pulse sequence (trhncagp2h3d2, Fig. S4) (red spectrum) and replacing ¹H and ¹⁵N hard π pulses with the G5 (blue spectrum). The inset indicates the lower field region with ×6 magnification. Acquisition parameters: d1 = 2 sec, ns = 64 (number of scans), TD = 2k×128, p1 = 14.4 μs (the length of ¹H π/2 hard pulse), p3 = 11.8 μs (the length of ¹³C π/2 hard pulse), p21 = 32 μs (the length of ¹⁵N π/2 hard pulse), the pulse widths of ¹H and ¹⁵N G5 are 144 and 320 μs, respectively. The offsets of ¹H and ¹⁵N are 4.7 and 118 ppm, respectively.

3D ¹³C-edited NOESY-HSQC

We tested the performance of the G5 pulse on the 3D ¹³C-edited NOESY-HSQC experiment (Fig. S5) in which the HSQC block differs slightly from that of the 2D ¹H-¹³C HSQC. In this experiment, two ¹³C hard π pulses are used instead of the composite smoothed CHIRP pulses (Crp80comp.4) to refocus the ¹³C transverse magnetization. By removing the CHIRP delay compensation, these two ¹³C hard π pulses shorten the pulse sequence by 3 ms; however, they cause significant off-resonance effects. As with the previous pulse sequences, we replaced six ¹H hard π pulses (Fig. S5), two ¹³C hard π pulses, and two ¹³C shaped π pulses with the G5 pulse. Note that the first ¹³C shaped π pulse to refocus all aliphatic and carbonyl carbons was not replaced. Fig. 6 shows a comparison of the 1D spectra of the first point increment of the two 3D experiments. As expected, the signal intensities of aliphatic CH groups are near to a maximum as the inversion operations are close to be perfect for ¹H and ¹³C transmitter offsets when set to 4.7 and 75.0 ppm. In contrast, the downfield resonances of aromatic residues and upfield resonances of methyl groups display 100% and 200% signal enhancement, respectively.

Fig. 6.

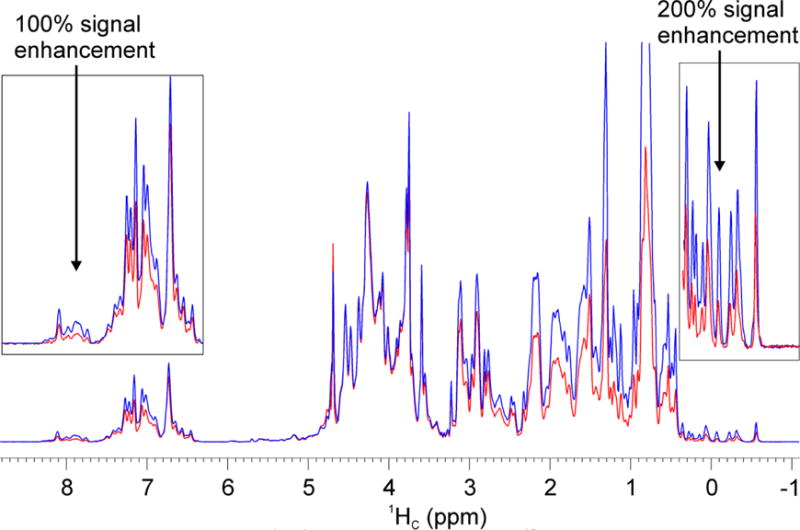
1D projections of 2D ¹H-¹H planes from the 3D ¹³C-edited NOESY-HSQC spectra of U-¹⁵N,¹³C-labeled Abl1b RM acquired on an 850 MHz spectrometer with the original Bruker pulse sequence (red spectrum) (noesyhsqcetgpsi3d, Fig. S5); replacing ¹H and ¹³C hard and shaped π pulses with G5 (blue spectrum). The inset shows both the lower and high field regions of the spectrum. Acquisition parameters: d1 = 1 sec, d8 = 0.15 sec (mixing time), ns = 64 (number of scans), TD = 2k×256, p1 = 11.3 μs (the length of ¹H π/2 hard pulse), p3 = 11.2 μs (the length of ¹³C π/2 hard pulse), the offsets of ¹H and ¹³C are 4.7 and 75 ppm, respectively.

In general, shaped π pulses represent a suitable alternative to a hard pulse for removing off-resonance effects^8,17. For instance, IBURP and smoothed CHIRP (Crp80,0.5,20.1 with total 80 kHz sweep-width, 0.5 ms pulse length, 20% to be smoothed, and sweep from high to low field) can be used to invert the longitudinal z-component of magnetization¹⁶. Also, composite pulses such as CHIRP (Crp80comp.4)¹⁷ and REBURP¹⁵ can be used to refocus transverse x and y components of the magnetization. However, these four shaped π pulses cannot be used for both inversion and refocusing operations. In contrast, the G5 is relatively short (¹H π pulse of 144 μs) and is applied at the same power level as a hard π/2 pulse, which is sufficiently short to avoid signal losses due to transverse relaxation. Importantly, the G5 pulse was developed via GA optimization^30,31 and is designed to operate on both inversion of longitudinal magnetization and refocusing of transverse magnetization²⁷. Although the Gaussian cascade pulse (Q3) is also able to operate on both longitudinal and transverse magnetization, the bandwidth of the G5 pulse is 20% wider while using ~75% of the maximum RF amplitude necessary for the Q3 π pulses¹⁴. A comparison of the Q3 and G5 pulses using 100 μs pulse width is included in Fig. S7A. To achieve the maximum RF amplitude of 25 kHz, the duration of G5 and Q3 pulses needs to be 100 and 132 μs, respectively, for a full inversion (Fig. S7B). Under these conditions, the bandwidth of G5 is ~60% wider than the Q3 pulse. Note that the G5 shaped π pulse can replace all hard π pulses and some ¹³C shaped π pulses, with the exception of the Q3 pulses in the 3D HNCACB-type experiments^23,24 (such as HNCACB, HN(CO)CACB, HNCA, HN(CO)CA). In that experiment, the Q3 pulse is used to invert CO or CA/CB magnetization while leaving the other ¹³C resonances unaffected. The G5 pulse has been designed to carry out inversion and refocusing only within the given bandwidth and does not perform well outside of this range (Fig. S8). Our future goal is to design an improved pulse for Q3-type operations in the HNCACB-type experiments.

Based on the above examples, it is clear that the implementation of the G5 pulse is generally beneficial in a variety of multidimensional NMR experiments. Since no J-coupling evolution occurs during the execution of the G5 pulse²⁷, the delays used for shaped pulses can be removed, making these pulse sequences much shorter. For instance, in an INEPT where two simultaneous G5 pulses are applied at the center of a J evolution period, the pulse program only needs to include a delay between pulses equal to 1/(4J), without the correction for J-evolution during the G5 pulse. As a result, a significant advantage of the G5 pulse is the easy implementation into complex pulse sequences.

Conclusions

In sum, we introduced the use of a triply-compensated π pulse for solution-state NMR spectroscopy that drastically reduces off-resonance effects, pulse miscalibration, as well as J-evolution. By replacing the ¹H, ¹⁵N and ¹³C hard π pulses with the G5 pulse in multidimensional experiments such as 2D ¹H-¹⁵N, ¹H-¹³C HSQC, 3D TROSY-HNCA, and 3D ¹³C-edited NOESY-HSQC we achieved ~80% signal enhancement. Furthermore, by replacing the ¹³C shaped π pulses in the 2D ¹H-¹³C HSQC and 3D ¹³C-edited NOESY-HSQC, we achieved up to 200% signal enhancement. We anticipate that this new generation of triply-compensated pulses²⁷ will dramatically improve the performance of multidimensional NMR experiments at ultra-high fields.