A Simple and Powerful Analysis of Lateral Subdiffusion Using Single Particle Tracking

Abstract

In biological membranes, many factors such as cytoskeleton, lipid composition, crowding, and molecular interactions deviate lateral diffusion from the expected random walks. These factors have different effects on diffusion but act simultaneously, so the observed diffusion is a complex mixture of diffusive behaviors (directed, Brownian, anomalous, or confined). Therefore, commonly used approaches to quantify diffusion based on averaging of the displacements such as the mean square displacement, are not adapted to the analysis of this heterogeneity. We introduce a parameter—the packing coefficient Pc, which gives an estimate of the degree of free movement that a molecule displays in a period of time independently of its global diffusivity. Applying this approach to two different situations (diffusion of a lipid probe and trapping of receptors at synapses), we show that Pc detected and localized temporary changes of diffusive behavior both in time and in space. More importantly, it allowed the detection of periods with very high confinement as well as their frequency and duration, and thus it can be used to calculate the effective k_on and k_off of scaffolding interactions such as those that immobilize receptors at synapses.

Introduction

In cell membranes, molecules exhibit complex diffusive behaviors that reflect local heterogeneity of the membrane and/or interactions established with other molecules. Many factors such as the cytoskeleton, the lipid composition, crowding, and molecular interactions affect diffusion simultaneously (1). The analysis of the transitions between different diffusive behaviors can provide hints about the organization of the membrane and the interactions that a given molecule is undergoing. Single-particle tracking (SPT) fits well with this approach because it enables the localization of an individual molecule with nanometer precision, yielding detailed information on its motion (reviewed in (2)). However, the detection of transient changes in diffusive behavior along a trajectory is a long-standing problem for SPT techniques. Classical analyses based on the mean square displacement (MSD) and the calculation of the diffusion coefficient D are not appropriate due to the averaging intrinsic to their calculation (3, 4).

We introduce a parameter, the packing coefficient Pc, which provides an estimate of the degree of free movement that a molecule displays in a period of time independently of MSD and D calculations. Pc scales with the size of the confinement area; thus, it is possible to identify periods of confinement by setting a threshold corresponding to a given confinement area size. Then it is possible to calculate the frequency and duration of confinement periods and to localize them in space.

An important type of interaction that membrane molecules may establish are scaffolding interactions, which are responsible for the accumulation of specific molecules in membrane domains. Scaffolding interactions immobilize, for example, receptors for neurotransmitters on the postsynaptic side of neuronal synapses (5). Due to the limited localization accuracy in SPT, immobilization is translated into confinement in an area whose size is the localization accuracy. In this way, the Pc analysis is able to identify periods of transient immobilization. Assuming that these periods arise from a scaffolding interaction, the effective k_on and k_off of this interaction can be extracted from the frequency and the duration of immobilizations, respectively ((6) and references therein). This is particularly important as the understanding of molecular interactions under physiological conditions (in cellulo) is not straightforward. Classical bulk biochemistry used to identify interactions and to quantify molecular affinities favor the detection of strong molecular interactions. In addition, in these experiments molecules interact in an environment and under conditions that can be very different from the real situation in cells. This is particularly true in the case of reactions occurring in cell membranes. By providing access to kinetic parameters of molecular interactions in cellulo, Pc analysis can help understand the formation and dynamics of specialized membrane domains such as neuronal synapses within a living cell.

Materials and Methods

Cell culture and transfections

All animal procedures were carried out according to the European Community Council directive of 24 November 1986 (86/609/EEC), the guidelines of the French Ministry of Agriculture and the Direction Départementale des Services Vétérinaires de Paris (Ecole Normale Supérieure, Animalerie des Rongeurs, license B 75-05-20), and were approved by the Comité d’Ethique pour l’Expérimentation Animale Charles Darwin (license Ce5/2012/018). All efforts were made to minimize animal suffering and to reduce the number of animals used. Primary cultures of rat hippocampal neurons were prepared as reported (7). For GFP-GPI experiments, neurons were transfected at 9 days in vitro (DIV) using Lipofectamine2000 (Invitrogen, Cergy Pontoise, France) following the manufacturer’s instructions. GFP-GPI plasmid was described elsewhere (7). SPT experiments were performed at 21–24 DIV. Neurons were transfected with SEP-γ2 (8) chimera at DIV 13–15 using Transfectin (Bio-Rad, Schiltigheim, France) according to the manufacturer’s instructions. Universal-point-accumulation-for-imaging-in-nanoscale-topography (uPAINT) experiments were performed 1 week after transfection.

Drug treatment

Actin filaments were depolymerized with latrunculin A (3 μM; Sigma-Aldrich, Lyon, France) solubilized in DMSO (Sigma-Aldrich). Cells were preincubated for 30 min with latrunculin or the control solution (0.002% DMSO), and used for SPT (performed in presence of the drugs). For the induction of chemical long-term potentiation (cLTP), neurons were treated with glycine (200 μM) for 3 min in a bathing solution of osmolarity between 325 and 335 mOsmol, containing 140 mM NaCl, 1.3 mM CaCl₂, 5.0 mM KCl, 25 mM HEPES, 33 mM glucose, 0.0005 mM TTX, 0.001 mM strychnine, and 0.02 mM bicuculline methiodide (pH 7.4) (9) (all chemicals from Sigma-Aldrich). Cells were then rinsed and left in the bathing solution without glycine for SPT experiments. NMDA was applied for 3 min at 20 μM (10) (Tocris Bioscience, Bristol, United Kingdom).

Single particle imaging with quantum dots

To track membrane protein diffusion, quantum dots (QDs) were precoupled to the corresponding primary antibodies, as reported previously (7). Briefly, goat anti-rabbit F(ab′)2-tagged QDs emitting at 655 nm (Q11422MP; Invitrogen) were incubated first with polyclonal rabbit anti-GFP antibody (cat. No. 132002; Synaptic Systems, Göttingen, Germany) or anti-GluA1 (AGC-004; Alomone Labs, Israel) for 30 min in PBS, and then blocked for 15 min with casein in a final volume of 10 μL. Neurons were incubated with the precoupled QDs (1:6000–1:10,000 final QD dilution) for 5 min at 37°C.

All incubation steps and washes were performed at 37°C in MEM recording medium (MEMr: phenol red-free MEM, 33 mM glucose, 20 mM HEPES, 2 mM glutamine, 1 mM Na-pyruvate, and 1×B27). Cells were imaged within 30 min after QD staining. Neurons were imaged in MEMr at 37°C in an open chamber mounted on an IX70 inverted microscope (Olympus France, Rungis, France) equipped with a 60× objective (NA 1.45; Olympus France). Fluorescence was detected using a Xenon lamp, appropriate filters (QD: FF01-460/60-25, FF510-DiO × 36, and FF01-655/15-25, from Semrock, Rochester, NY; GFP: HQ500/20, HQ535/30m and FM4-64: D535/×, E590lpv2 from Chroma Technology, Bellows Falls, VT), and a charge-coupled device camera (Cascade 512BFT; Roper Scientific SARL, Lisses, France). QDs were recorded during 1000 consecutive frames (time points) at a frequency of 33 Hz (GFP-GPI) or 20 Hz (AMPA receptors, AMPARs).

Single particle imaging with uPAINT

Neurons transfected with SEP-γ2 were imaged in MEMr at 37°C in an open chamber mounted on a N-STORM Eclipse Ti microscope (Nikon, Tokyo, Japan) equipped with a 100× oil-immersion objective (N.A. 1.49). Receptors were labeled with anti-GFP ATTO647N-coupled nanobodies (GFP-Booster; ChromoTek, Planegg/Martinsried, Germany). Nanobodies are small Camelidae antibody fragments (∼15 kDa) consisting of a single monomeric variable antibody domain that allows specific labeling while introducing minimal linkage-error (11). After adding the solution of nanobodies to the medium (1:400 in PBS), cells were illuminated (622 nm) with a laser (Genesis MXSLM; Coherent, Les Ulis, France). Oblique illumination of the sample allowed us to image nanobodies bound to their ligands in the cell surface without illuminating the molecules in the solution above (12). Fluorescence was detected using a C-NSTORM QUAD filter cube (Nikon) and an iXon Ultra EMCCD camera (pixel size, 160 nm; Andor Technology, Windsor, CT). SEP fluorescence was detected using an Intensilight lamp (Nikon) and appropriate filters (GFP Cube, Nikon; excitation 472/30 nm, DM495, emission 520/35). Nanobodies were recorded during 10,000–20,000 consecutive frames (time points) at a frequency of 33 Hz. The z position was maintained during acquisition using the Perfect Focus System (Nikon). Mechanical x-y drift was corrected by adding individual fluorescent beads adsorbed on the glass coverslips, used as immobile references.

Tracking and analysis of diffusion

Tracking was performed with homemade software (SPTrack_v4) in MATLAB (The MathWorks, Natick, MA). The center of the spot fluorescence was determined by 2D-Gaussian fit. Spatial resolution was ∼10–20 nm for QDs and ∼30 nm for nanobodies. The spots in a given frame (time point) were associated with the maximum likely trajectories estimated on previous frames of the image sequence. In uPAINT experiments, unbound fluorescent molecules freely diffusing in solution were discarded; their fast 3D diffusion avoided their detection in more than three images (trajectories of <10 points were discarded). Trajectories were defined as “synaptic” if they colocalized with a synaptic cluster. The MSD was calculated using

$$MSD\left(ndt\right)={\left(N-n\right)}^{-1}\sum _{i=1}^{N-n}\left[{(x_{i+n}-x_i)}^2+{(y_{i+n}-y_i)}^2\right],$$

where xi and yi are the coordinates of an object on frame i, N is the total number of steps in the trajectory, dt is the time interval between two successive frames, n is the number of frames, and ndt is the time interval over which displacement is averaged. The diffusion coefficient D was calculated by fitting the first 2–5 points of the MSD plot versus time (13) with the equation

$$MSD\left(t\right)=4D_{2-5}t+4{\sigma }_x^2,$$

with σ_x as the spot localization accuracy (positional accuracy (2)) in one direction.

Packing coefficient

The packing coefficient (Pc) at each time point i was calculated as

$$P{c}_i=\sum _i^{i+n-1}\frac{{\left(x_{i+1}-x_i\right)}^2+{\left(y_{i+1}-y_i\right)}^2}{S_i^2},$$

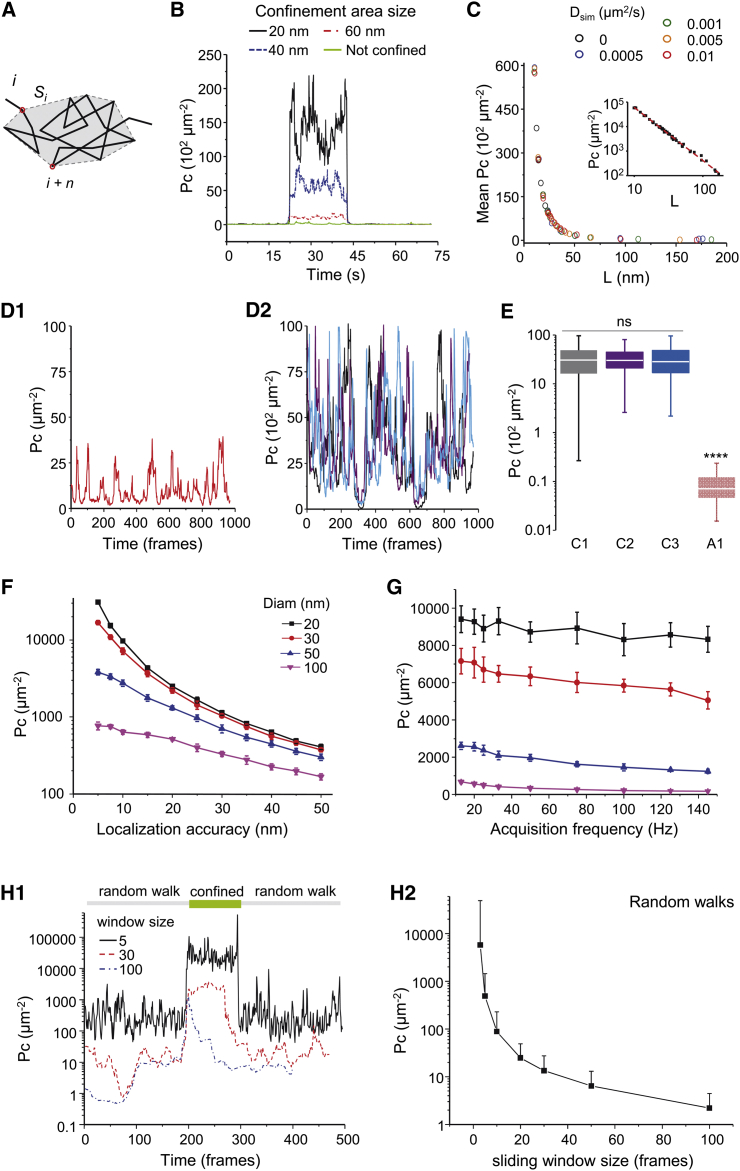
where x_i, y_i are the coordinates at time i; x_i+1, y_i+1 are the coordinates at time i+1; n is the length of the time window (when using QDs, n = 30 time points, but in uPAINT experiments, n = 10 time points); and S_i is the surface area of the convex hull of the trajectory segment between time points i and i+n. The value S_i was calculated using the convhull function in MATLAB (The MathWorks) (Fig. 2 A). The validity of the packing coefficient to detect transient stabilization periods was checked on Monte Carlo simulations of Brownian or confined trajectories.

Figure 2.

Detection of transient confinement using the packing coefficient (Pc). (A) A scheme representing the calculation of Pc at time point i. S_i is the convex hull of the trajectory segment i−i+n. The sum of the square displacements between successive time points of the trajectory stretch spanning from i to i+n is divided by S_i². (B) Pc values of examples of 75 s-long simulated trajectories are given that were fully Brownian (green) or that have a period of confinement in areas of the indicated sizes. (C) The mean Pc versus the diameter of the confinement area L on simulated trajectories constructed with the indicated D_sim. (Inset) The same plot in log-log axis (D) Pc values of the simulated trajectories A1 (D1, always Brownian) and C1–C3 (D2, with immobilization periods; C1 in black, C2 in purple, C3 in blue) of Fig. 1. (E) Pc values for the trajectories in (D) (median, 25–75% interquartile range (IQR)), Kruskal–Wallis test with Dunn multiple comparisons; ns, not significant, ^∗∗∗∗p < 0.0001). (F) The mean values of Pc during confinement periods of the indicated sizes, obtained on trajectories simulated with different localization accuracies (mean ± SE, n = 1000; note the semilog scale). (G) Values of Pc are given during confinement periods of the indicated sizes, obtained on trajectories simulated with a localization accuracy of 10 nm and an interval of time between trajectory points that matched the desired acquisition frequencies (see Materials and Methods). (H) The effect of the size of the sliding window. (H1) Pc values of simulated trajectory with a confinement period of 100 time points. Pc was calculated using different sliding window sizes. The largest windows (100 time points) could not detect properly the confinement period. The shortest window (five time points) accurately detected this period, but the fluctuations were significantly higher than for longer sliding windows (note the semilog scale). (H2) Pc values (mean ± SE, n = 1000) were obtained on Brownian simulated trajectories using different sliding window sizes. The statistical uncertainty increases in shorter windows. To see this figure in color, go online.

Monte Carlo simulations

The program was written in MATLAB (The MathWorks, Natick, MA) and run on a personal computer (Precision T1700; Dell, Round Rock, TX). Trajectories were simulated as in Renner et al. (14), with some modifications. The x and y components of the ith displacement step in the trajectory were randomly selected from two independent normal distributions with the mean of zero and the variance equal to 2D_sim Δt, using different Δt and D_sim as indicated (Fig. 2 C). The noise introduced in SPT trajectories by the limited accuracy of localization was simulated by adding a distance to x and y, distance chosen from an independent normal distribution with the mean of zero, and a given variance that corresponds to the desired localization accuracy. This distance was calculated independently for x and y at each time point. Typically, trajectories had one or more periods of confinement, in which the positions were forced to stay in within a circle of the selected diameter L and reflecting border. Periods of confinement were imposed by inserting a boundary at a given time during the run, and removing it at a later prescribed time. To analyze the effect of acquisition frequency, trajectories were simulated with a Δt that matched the chosen acquisition frequencies.

Statistical analyses

Statistical analyses were performed using two-tailed Student’s t-test, Mann–Whitney test, one-way ANOVA, or Kruskal–Wallis with Dunn multiple comparison test using GraphPad Prism (GraphPad Software, La Jolla, CA). Images were prepared using Photoshop (Adobe Systems, Mountain View, CA).

Results and Discussion

The averaging effect of MSD calculation overlooks transient confinement periods

The MSD provides the simplest type of classification of the diffusion behavior. Brownian motion yields a MSD = 4Dτ (in two dimensions) where D is the diffusion coefficient and τ is the time interval. In contrast, anomalous diffusion is characterized by a nonlinear MSD = 4Dτ^α with α < 1. When diffusion is confined, the MSD asymptotically approaches a value related to the size of the confinement area (15, 16). Unfortunately, the information obtained from MSD analysis is limited and, in practice, different situations of non-Brownian diffusion can produce the same MSD. This is due to the fact that the MSD is calculated by averaging all the displacements within the trajectory that correspond to a given time interval (see Materials and Methods). Thus, if the molecule switches between different diffusive behaviors, the final MSD depends not only on the difference in diffusivity but also on the duration of each behavioral (Brownian/anomalous/confined) period.

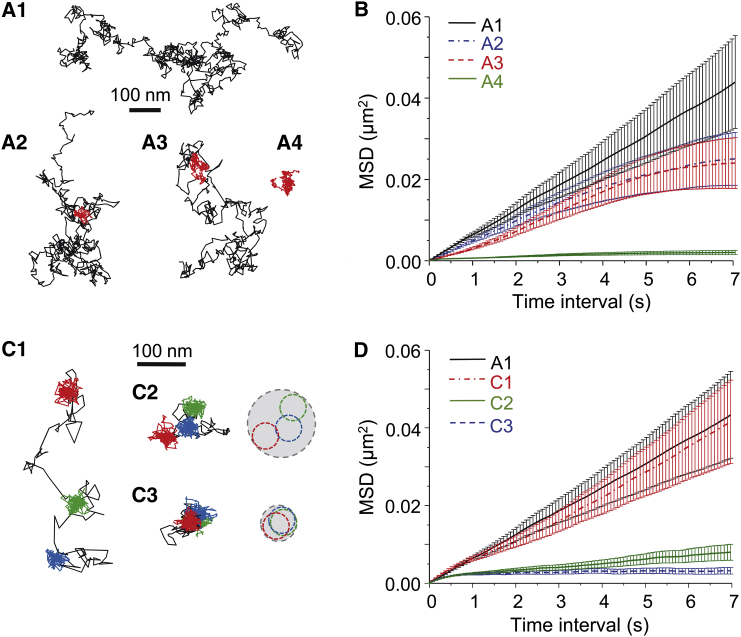
Fig. 1 illustrates some of the caveats of MSD analysis. We simulated random walk trajectories (10 s-long with Δt = 10 ms; see Materials and Methods) without (A1) or with a period of confinement that lasted 3 s in an area of 50 nm in diameter (A2) or that lasted 5 s in an area of 100 nm in diameter (A3). A fourth trajectory (A4) was always confined in an area of 100 nm in diameter. The MSD (Fig. 1 B) of the trajectory A4 shows its confinement. In the case of trajectories A2 and A3, the MSD plot (Fig. 1 B) displayed the expected shape of confined diffusion; however, it should be noted that both trajectories had the same MSD despite their different confinement (3 s in a compartment of 50 nm in diameter for A2, 5 s in a compartment of 100 nm in diameter for A3; Fig. 1 B). Next, we simulated trajectories that switched between periods of free diffusion (D_sim = 0.02 μm²/s during 3.75 s) and strong confinement (corralled in a 30-nm-diameter area during 22.5 s) (Fig. 1 C). We chose three examples with confinement periods that were distanced (C1), apposed (C2), or colocalized (C3). The calculation of MSD on these three trajectories (Fig. 1 D) allowed us to detect the confinement of trajectory C3 and the hopping behavior of trajectory C2. However, the trajectory in C1 produced a value of MSD similar to that of a trajectory that displayed slower free random movement (A1). Thus, the MSD hid the confinement of trajectory C1.

Figure 1.

The averaging effect of MSD calculation within the trajectory overlooks transient confinement periods. (A) Brownian simulated trajectories without (A1), with one period of confinement (in red) of 3 s in a confinement area of 50 nm in diameter (A2), with one period of confinement of 5 s in a confinement area of 100 nm in diameter (A3) or always confined in an area of 100 nm in diameter (A4). (B) MSD values of the simulated trajectories in (A) (mean ± SE). (C) Brownian simulated trajectories with three periods of confinement (in color) in 30-nm-diameter areas that were distanced (C1), apposed (C2), or colocalized (C3). (On the right) Minimum circles containing each confinement period (in colors) or the whole trajectory (gray). (D) MSD values of the simulated trajectories in (C) and of trajectory A1 for comparison (mean ± SE). To see this figure in color, go online.

To identify and quantify transient changes between free and confined diffusion, we set the packing coefficient (Pc). Pc quantifies the degree of compaction of a trajectory by comparing the length of the trajectory in a short time window and the surface area that it occupies (both to the square):

$$P{c}_i=\sum _i^{i+n-1}\frac{{\left(x_{i+1}-x_i\right)}^2+{\left(y_{i+1}-y_i\right)}^2}{S_i^2},$$ (1)

where x_i, y_i are the coordinates at time i; x_i+1, y_i+1 are the coordinates at time i+1; n is the length of the time window; and S_i is the surface area of the convex hull of the trajectory segment between time points i and i+n (Fig. 2 A; see Materials and Methods). Unless indicated, we set n = 30 time points (see below).

To evaluate the capacity of Pc to detect transient confinement periods, we first simulated trajectories undergoing simple Brownian diffusion with or without a transient confined period in areas of variable sizes (Fig. 2, B and C). Pc values were higher when the confinement area was smaller (Fig. 2 B). Importantly, when simulations were done also varying the global D (D_sim) of the trajectories, Pc scaled inversely to the size of the confinement area L independently of D_sim (Fig. 2 C).

Theoretically, Pc tends to infinite when L tends to zero. However, in the case of trajectories obtained experimentally, the localization accuracy imposes a limit to the minimum L that can be observed. Thus, we simulated trajectories taking into account the localization accuracy (Materials and Methods). Under these conditions, the relationship between Pc and L followed the expected power law (inset, Fig. 2 C), with

$$\log L\cong 3.2-0.46\log Pc.$$ (2)

As shown in Fig. 2, D1 and D2, Pc versus time for trajectories of Fig. 1 C (that underwent analogous confinement periods) were similar for the three trajectories (Fig. 1, C1–C3) but different from that of the trajectory A1 (free diffusion) (Fig. 2 E). Thus, Pc correctly detected and quantified the temporary changes in diffusion behavior in these trajectories.

As expected, localization accuracy affected the capacity of Pc to evaluate the confinement. The relative differences in Pc due to different sizes of confinement were smaller when the localization accuracy decreased (Fig. 2 F). Pc values also varied with the acquisition frequency, but this did not preclude the detection of confinement. Confinements in circles of 20–100 nm in diameter were distinguishable, with sampling frequencies between 13 and 145 Hz (Fig. 2 G), and the relationship between Pc and L (Eq. 2) was conserved. Finally, the length of the sliding window had to be short enough to optimize the ability to detect short stabilization events (Fig. 2 H1) but long enough to sense the confinement and to decrease statistical uncertainty (Fig. 2 H2). Given our acquisition frequency, we set this value to 30 time points.

Many methods have been described to characterize various diffusion behaviors, each one fitting well with a particular experimental situation (for a review of analytical approaches, see (17)). The Pc analysis presents some advantages with respect to other strategies, particularly in the case of populations of molecules diffusing slowly and displaying multiple periods of confinement. The method proposed by Simson et al. (18), developed initially to study the effect of lipid rafts on lateral diffusion, is commonly used to detect confinement by calculating a confinement probability level comparing local and global diffusivity. This method allows the identification of periods in which the molecule remains in a region for a longer duration than predicted by a Brownian motion model. This is done by using a sliding time window to calculate the local maximum displacement and comparing it to the global D (D calculated over the entire trajectory). However, this method has two drawbacks: 1) random walks can be discriminated from confinement periods only if the presence of confinement does not affect global D, and if the difference between the diffusivity of the random and confined trajectories is large enough (Fig. S1); and 2) to access to short-lived changes in diffusion, the calculation of D has to be performed on short trajectory segments that render the calculation of D less reliable (3, 4, 19). An alternative and derived approach compares D to the variance of displacement steps (20). However, this strategy can only be successfully applied, once more, if the difference in the diffusivity between random and confinement states is large. The gyration quantification method (21) determines the area a given molecule explores by computing the radius of gyration. It is an efficient approach, but only if the trajectories have enough steps to define the motion (∼50 steps). Furthermore, the fast and slow diffusion coefficients should differ by at least a factor of 5 (21). In contrast, in our experiments we found that Pc is independent from the global diffusivity, and it efficiently discriminated confinement from slow Brownian movement (Fig. S1).

Other proposed approaches analyze, e.g., the autocorrelation function of squared displacements (22) or the first passage time variance (23). Yet, in these two cases the temporal and spatial positions of the confinement periods are not provided. In contrast, the analyze of Pc versus time allowed the localization of the confinement periods that could then be correlated to a specific membrane region such as neuronal synapses (see below).

The Pc analysis as well as other confinement analyses face a major problem: Brownian diffusion trajectories can temporarily mimic confinement due to random fluctuations of the length of the displacements. However, the amplitudes and durations of these fluctuations are most of the time smaller and shorter than the ones associated with real non-Brownian transient motion (18). Therefore, the use of a threshold value of Pc (Pc_thresh) and of a minimal duration above this threshold (t_thresh) can suppress the detection of apparent nonrandom behaviors without excluding the detection of real confinement. P_thresh can be set to the P95 or P99 percentile of Pc distribution of simulated random walks that are matched to the experimental data in acquisition frequency, localization accuracy, and length of trajectories. The duration time threshold t_thresh can then be chosen by applying P_thresh to random walk trajectories and extracting the P95 or P99 of the distribution of durations. Thus, true confinement corresponds to a period with Pc being above P_thresh that lasts more than t_thresh. For example, when Pc was calculated over a window of 30 time points on random walks, P95 was equal to 67 μm⁻² (Fig. S2). Using this value as Pc_thresh, we found t_thresh = 0.81 s (P99 of the distribution of durations). Alternatively, the definition of a threshold that corresponds to a given confinement area size L_thresh allows the localization of the trajectory sequences in time and space confined in areas of size ≤ L_thresh. In this case, t_thresh will depend on the acquisition frequency and the characteristic time of confinement.

Detection of diffusive behavior transitions on GFP-GPI trajectories

Membrane proteins and some lipids may undergo hop diffusion, being temporarily confined in 30 to 700-nm-diameter compartments and displaying frequent jumps between adjacent compartments (24). In cultured CHO cells, GPI-anchored GFP (GFPGPI) molecules display hop diffusion between compartments of ∼40 nm in diameter, the size of which depend on F-actin integrity (24, 25).

We first tested the Pc analysis on SPT trajectories analyzing the diffusion of GFP-GPI on cultured hippocampal neurons. GFP-GPI molecules were labeled with QDs coupled to an anti-GFP antibody (QD-GFPGPI). QD-GFPGPI were detected with a localization accuracy of 20–30 nm and tracked at 33 Hz. QDs blink; thus, to avoid introducing unwanted uncertainty, Pc was calculated only if the dark state within the sliding window was <5-time-points long.

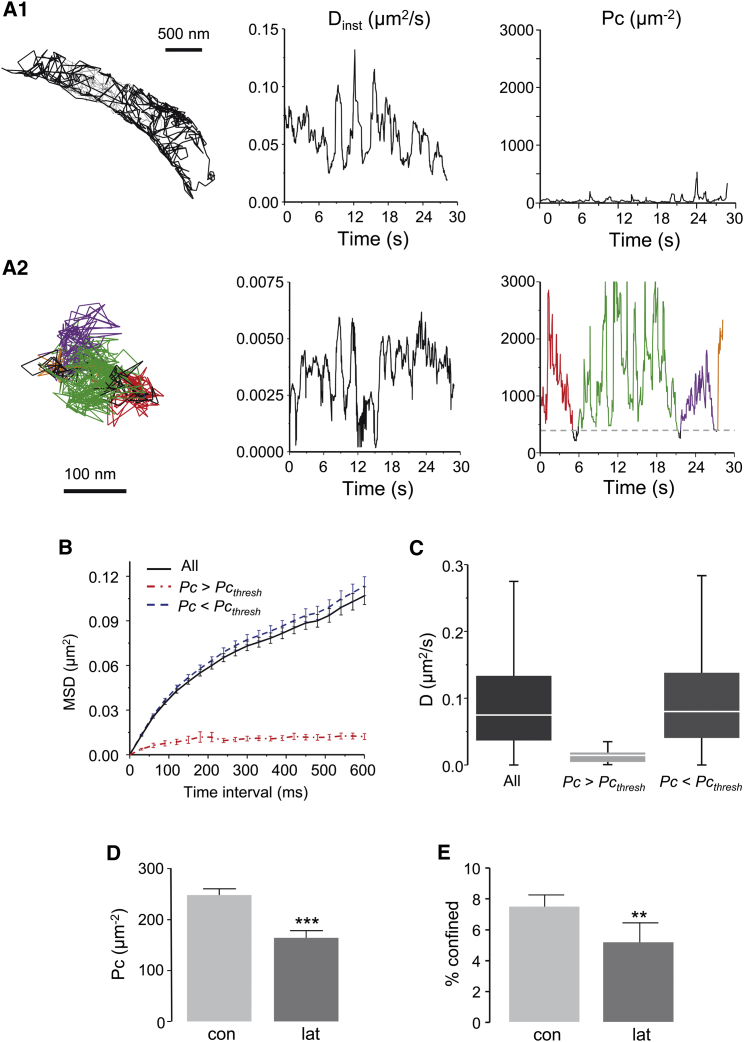
As exemplified in Fig. 3, A1 and A2, Pc values versus time for each trajectory revealed various patterns. Most trajectories had low Pc values characterizing free diffusion (Fig. 3 A1), whereas some displayed high Pc values suggesting constrained (not free) diffusion (Fig. 3 A2).

Figure 3.

Lateral diffusion of GFP GPI on neurites, effect of F-actin depolymerization. (A) Examples of QD-GFPGPI trajectories (left) are given, with the corresponding instantaneous D (D_inst, center) and Pc (right) plots. D_inst and Pc were calculated on the same sliding window (30 time points). (A1) Trajectory without confinement. (A2) Trajectory with multiple periods of confinement in areas ≤100 nm (Pc_thresh= 406 μm⁻²). The detected periods are shown in color. (B) An average MSD plot of all QD-GFPGPI trajectories (black), portions of trajectories with Pc below (Pc ≤ Pc_thresh, blue), or above (Pc >Pc_thresh, red) threshold (n = 275–926 trajectories). (C) Distribution of D (median, box: 25–75% IQR, whiskers: 5–95%) for the trajectories in (B). (D) Mean Pc values of trajectories in control condition (con) or after latrunculin treatment (lat) (mean ± SE, Mann–Whitney test ^∗∗∗p < 0.001, n = 40–70). (E) The percentage of confined trajectories (C1), in control conditions (con) and after latrunculin application (lat) (mean ± SE, t-test ^∗∗p < 0.01, n = 40–70). To see this figure in color, go online.

To quantify the diffusive behaviors of QD-GFPGPI, we set an initial Pc_thresh of 406 μm⁻², which corresponds to a confinement area size of 100 nm. In Fig. 3 A2, the portions of trajectories for which Pc values are above Pc_thresh (thus confined) appear in different colors. The mean Pc value during these periods was 2120 ± 125 μm⁻², which corresponds to a confinement area size of 44.87 ± 3.31 nm in diameter. Interestingly, this value is close to the proposed size of hopping confinement areas described by Umemura et al. (24) for GFPGPI (40 nm). However, in our experiments, using a much lower acquisition frequency (33 Hz) than the one used by Umemura et al. (24) (50 kHz), only 7.50 ± 0.75% of the trajectories displayed this behavior. Thus, in our recordings, we detected the corralled molecules that remained a sufficiently long time in a hopping compartment to be detected at 33 Hz of sampling frequency.

We then sorted portions of QD-GFPGPI trajectories in two groups: those with Pc > 406 μm⁻² (confined) and those with Pc < = 406 μm⁻² (free). In each case, we analyzed their diffusion comparing their MSD and D (Fig. 3, B and C). Further, we compared the results obtained with the intact trajectories (whole) with those obtained on free and confined sections of trajectories. The MSD and D values of the whole trajectories were close to that of the free-group, overlooking the presence of confined events (Fig. 3, B and C).

The disruption of the actin cytoskeleton using latrunculin increases the mobility of GFPGPI (24). This effect was attributed to a reduction in the amount of F-actin bound pickets that act as obstacles to diffusion and ultimately define the hopping compartments (26). We then checked if the confinement highlighted by Pc could be modified by F-actin depolymerization. As expected, the Pc values were significantly lower under the latrunculin condition (Fig. 3 D) and the percentage of confined trajectories decreased by 30% (control: 7.50 ± 0.75%; latrunculin: 5.20 ± 1.25%; Mann-Whitney test p = 0.008; Fig. 3 E). The confinement area diameter was larger under latrunculin (44.87 ± 3.31 vs. 50.72 ± 1.15 nm, t-test p = 0.008), which corresponds to an increase of ∼30% of the surface area. Therefore, despite a low frequency of acquisition, Pc analysis detected both the typical size of hopping compartments reported for GPI molecules and the enlargement of the confinement area size due to F-actin depolymerization.

Using Pc to detect transient immobilizations

The number of receptors for neurotransmitters accumulated at the synapse is an important parameter setting the strength of the response and thus plays a key role in regulating neuronal function. The number of receptors depends upon the interactions that immobilize them by binding to specific scaffolding molecules. Actually, this immobilization is transient and receptors diffuse in and out of the synaptic area at unexpectedly high rates (reviewed in (27, 28)). This suggests that the receptor-scaffold interactions are short-lasting, i.e., in the range of seconds.

The main ionotropic receptors at excitatory synapses are AMPA- and NMDA-type glutamatergic receptors. The number of AMPARs fluctuates rapidly with receptors swapping between extra- and intrasynaptic areas and this dynamic accounts for the construction and plasticity of excitatory synapses (reviewed in (27, 28)). AMPARs have a preponderant role in the expression of synaptic plasticity, therefore an important question is that of their stabilization by synaptic activity. Actually, global modifications of network activity tune the mobility of AMPARs (reviewed in (27, 28)).

Here, we compared the diffusion of AMPARs (GluA1 subunit with QDs-bound antibodies; QD-GluA1) in control conditions and after inducing synaptic plasticity. QD-GluA1s were detected with a localization accuracy of 20–30 nm and tracked at 20 Hz. The trajectories were then chopped and sorted into extrasynaptic and synaptic ones as described (29).

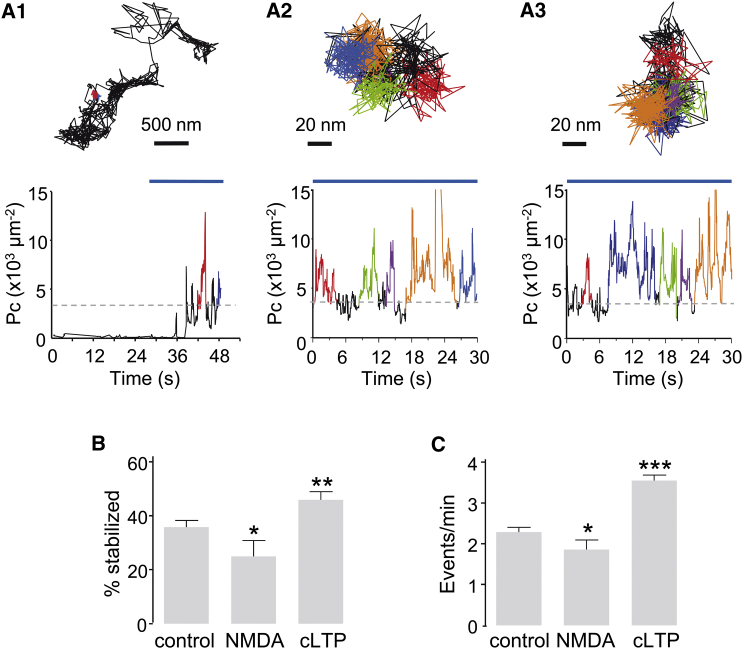
The stabilization periods (immobility) were identified by a highly confined diffusion in a small area whose size was of the order of the localization accuracy. To detect these events and given the localization accuracy, we set a threshold of Pc_thresh = 3300 μm⁻² (corresponding to a confinement area size with a diameter of ∼35 nm) and time threshold of 0.375 s (five time points at 20 Hz). During the recording session, Pc values varied displaying no, one, or more stabilization events in synapses (exemplified in Fig. 4 A) and 35.83 ± 2.44% of synaptic QD-GluA1 had at least one stabilization event (Fig. 4 B).

Figure 4.

Stabilization of AMPAR analyzed by Pc analysis. (A) Examples of Pc values upon time for QD-GluA1. The detected periods of stabilization are shown in color. (Top) Examples of trajectories in a dendritic spine (A1) or in synapses (A2 and A3). (Bottom) The corresponding plots of Pc versus time for each trajectory are given. The horizontal blue line shows the synaptic localization in time. The horizontal discontinuous line shows P_thresh. (B) The percentage of stabilized trajectories of QD-GluA1 in the indicated conditions (mean ± SE, n = 16–48 recordings, t-test ^∗p < 0.05, ^∗∗p < 0.01). (C) The frequency of stabilization events (number of events per min) (mean ± SE, n = 331–1440 trajectories, t-test ^∗p < 0.05, ^∗∗∗p < 0.001). To see this figure in color, go online.

Assuming that the stabilization results from the first-order reaction,

$$R+S\begin{array}{c}\begin{array}{c}{k}_{\text{on}}\\ \to \end{array}\\ \begin{array}{c}\leftarrow \\ k_{\text{off}}\end{array}\end{array}RS$$

where R represents the receptors and S the scaffolding molecules, we can define an effective forward binding rate k_on that corresponds to the frequency of the binding events and an effective backward binding rate k_off that is the reciprocal of the mean duration of the stabilization periods ((6) and references therein).

Synaptic QD-GluA1 underwent 2.29 ± 0.11 stabilization events per minute (Fig. 4 C), thus indicating an effective k_on = 3.81 ± 0.18 × 10⁻² s⁻¹. The duration of the stabilization events was variable (spanning between 0.375 and 50 s; the limit of our recording session), with a mean of 8.49 ± 0.32 s that corresponds to a k_off of 0.11 s⁻¹. In some cases, events lasted the whole recording session (50 s), leading to a bias in the measurements of k_off; however, these long stalling periods were scarce. Despite this limitation, our effective k_off was similar to the one obtained by Czöndör et al. (30) by combining fluorescence recovery after photobleaching and SPT data with simulations (0.1 s⁻¹).

On the other hand, the effective k_on obtained here was lower than the value obtained by Czöndör et al. (30) (1.5 s⁻¹), who calculated k_on by fitting the reduction of global diffusion of AMPARs along the maturation of synapses. However, the k_on calculated in this way reflects the random walk of receptors outside synapses and their probability to find synapses. Our effective k_on was calculated only for receptors that are already in synapses and thus corresponds to the probability to find and bind to a scaffolding site.

The low value of k_on suggests that these sites were not readily accessible and/or that the affinity of receptors for their scaffolding molecules was low. In agreement with this, synaptic QD-GluA1s were immobilized only during 11.50 ± 0.66% of the whole time that they spent in synapses. However, AMPARs often displayed more than one stabilization event (Fig. 4, A2 and A3); therefore, they were likely to undergo multiple short-lasting binding-unbinding events. The molecular crowding at the postsynaptic membrane may contribute to the successive trapping events by reducing the escape of receptors off synapses (7, 31, 32). Our results suggest that the proportion of receptors considered as immobile by MSD and D analysis, or the stable fraction obtained by fluorescence recovery after photobleaching (∼50% (33, 34)) are receptors that do not exit the synapse during the recording time although they are not necessarily immobilized during the whole recording period. P_c analysis revealed that immobilization events could be multiple and short-lasting, which could help the synapse to rapidly exchange receptors with the extrasynaptic area, i.e., to replace desensitized receptors by naïve ones (34, 35).

Synaptic plasticity mechanisms rely on changes in the number of AMPARs, which is increased or decreased during LTP and long-term depression, respectively (reviewed in (36)). The accumulation of synaptic AMPAR is decreased by NMDA application (referred to as a model for chemical long-term depression (9)), whereas cLTP protocols induce the enrichment of GluA1-containing AMPARs (10).

Neuronal cultures were challenged with a cLTP protocol or NMDA application to modify the stabilization of QD-GluA1 at synapses. As expected, both treatments had opposite effects on the stabilization of receptors, affecting the percentage of stabilized QD-GluA1 (control = 35.83 ± 2.44%, NMDA = 24.94 ± 5.88%, Mann-Whitney test p = 0.041, cLTP = 45.95 ± 2.97%, Mann-Whitney test p = 0.007; Fig. 4 B) and the number of immobilization sequences per minute (control = 2.29 ± 0.11 events/min, NMDA = 1.85 ± 0.23, Mann-Whitney test p = 0.025, cLTP = 3.55 ± 0.13, Mann-Whitney test p < 0.0001, Fig. 4 C). Thus, in agreement with the reported reduction of AMPAR amount in synapses (10), NMDA application decreased their trapping probability. Conversely, cLTP protocol increased their trapping probability, which is consistent with the increased number of receptors in excitatory synapses induced by this treatment (9).

Overall, the Pc approach presented here allowed the identification of transiently stabilized trajectories, thus providing a better and to our knowledge, new characterization for the subsynaptic diffusion of receptors and the computation of effective kinetic parameters of scaffolding interactions. Furthermore, the Pc analysis provided the spatial localization of the stabilization events. This approach could then be combined with superresolution microscopy of postsynaptic scaffold molecules to investigate fluctuations of the trapping of receptors (37) with respect to the nanoorganization of the postsynaptic scaffold (38).

Application of Pc analysis to short trajectories

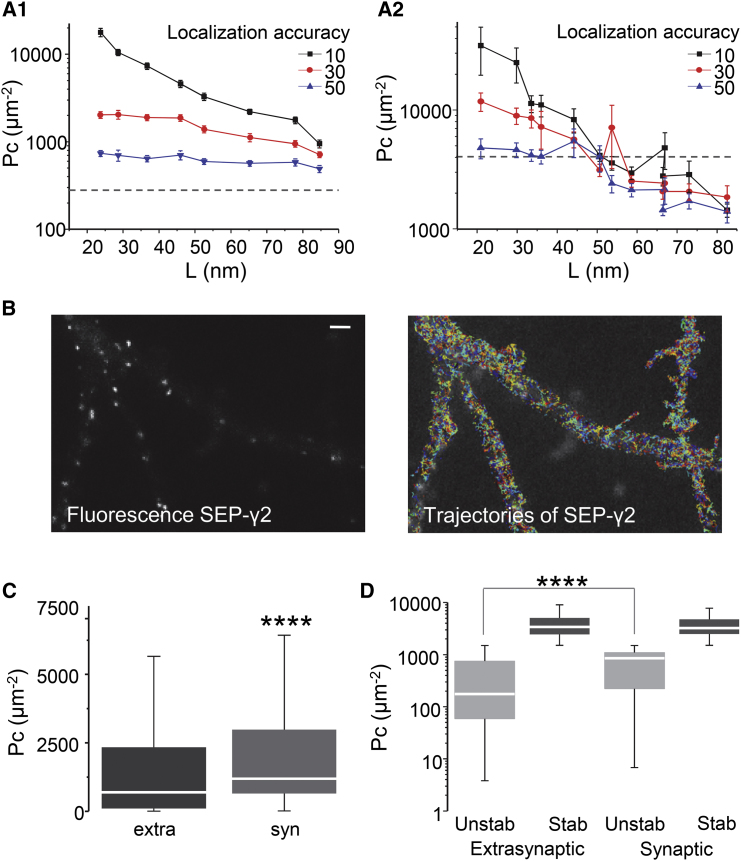
Until recently, single-molecule studies were restricted to only a few spatially isolated molecules sparsely labeled on living cells. A number of approaches have emerged that generate reconstructed images of single-molecule localizations at high density, such as sptPALM or uPAINT (12)). The drawback of these techniques is that the resulting trajectories are short due to the rapid photobleaching of fluorophores. Indeed, short trajectories constrain the time window used to calculate Pc, thus lowering its statistical power. In addition, short trajectories do not display a confined behavior if they are not long enough to sense the limits of the confined area. Moreover, the relatively poor signal-to-noise ratio of available fluorophores introduces extra noise, reducing the localization accuracy. Therefore, we questioned if Pc analysis could be used in the case of short trajectories. Thus, we simulated trajectories with lengths of 5 or 10 time points, being confined or not in areas of different sizes. We took into account localization accuracies related to common fluorophores (Fig. 5, A1 and A2). Pc revealed confinement at different levels in the longer trajectories (Fig. 5 A1). As expected, the localization accuracy had an important effect on Pc values. As a rule of thumb, the minimum size of confinement that could be detected was twice the localization accuracy. In the case of shorter trajectories, Pc values were highly scattered (Fig. 5 A2). Thus, if the localization accuracy is good enough (30 nm or less), the Pc analysis on trajectories of <10 points could be used only to detect immobility (L < 60 nm in this case).

Figure 5.

Pc analysis applied to short trajectories. (A) Mean Pc values 10 time-points long (A1) or five time-points long (A2) shown for simulated trajectories confined in areas of the indicated sizes (L) (mean ± SE, n = 100 trajectories in each case). Simulations took into account different localization accuracies. (Horizontal broken line) The P95 value of Pc distribution of random walk trajectories. (B) The fluorescent image of SEP-γ2 displaying synaptic puncta (right) overlaid with trajectories (each trajectory in a different color) of nanobodies-labeled SEP-γ2 (left). Bar: 1 μm. (C) Distribution of Pc (median, box: 25–75% IQR, whiskers: 5–95%) given for SEP-γ2 trajectories inside (syn) and outside (extra) synapses. Mann–Whitney test ^∗∗∗∗p < 0.0001, n synaptic = 427, n extrasynaptic = 4319. (D) Distribution of Pc (median, box: 25–75% IQR, whiskers: 5–95%) values given for trajectories in (C), after sorting into stabilized (Stab, P_c >1241 μm⁻²) and unstabilized (Unstab) (Mann–Whitney test ^∗∗∗∗p < 0.0001, n = 199–2838).

To test the suitability of Pc for experimental data, we performed uPAINT acquisitions to analyze the diffusion of GABA receptors on the surface of hippocampal neurons (Fig. 5 B). uPAINT consists of recording single-molecule trajectories that appear sequentially on the cell surface upon the continuous labeling of the molecules of interest (12). Membrane molecules are labeled with fluorescent ligands that are diluted in the cell medium to the adequate concentration, to obtain a sparse labeling at each time point. Only ligands bound to membrane molecules are considered, by excluding fluorescent molecules freely diffusing in solution (see Materials and Methods). uPAINT provides massive amounts of trajectories that can be used to create maps of the diffusive state of membrane molecules. Neurons were transfected with SEP-tagged γ2 subunit of GABA_A receptors (SEP-γ2 (8, 29),) which could be tracked using extracellular labeling with ATTO647N-coupled nanobodies against GFP. Actually, GABA_A receptors are pentamers of at least three different subunit isoforms, being immobilized or not at synapses depending on their subunit composition ((39) and references therein). Most γ2-subunit-containing receptors are accumulated in synapses, but γ2-GABA_AR that include also the α5 subunit are not stabilized by the synaptic scaffold ((29) and references therein). In fact, α5-containing GABA_AR are trapped outside synapses by interactions with radixin (40), thus some SEP-γ2 labels receptors can be stabilized either inside or outside synapses. Fluorescent images (10,000–20,000 consecutive frames) were recorded at 33 Hz with a localization accuracy of ∼30 nm. The obtained trajectories had a median length of 12 time points (first and third quartile 8 and 19, respectively). We kept only trajectories with at least 10 time points, calculating Pc on a sliding window of 10 points. Only one Pc value was extracted for each trajectory: for trajectories longer than 10 points, Pc was averaged among all the calculated values.

Synapses were identified by the fluorescent spots of SEP-γ2 (Fig. 5 B), and trajectories were sorted into extrasynaptic and synaptic as done previously (29). As expected from the enrichment of GABA_AR in synapses, the Pc values distributed around higher values for synaptic SEP-γ2 than for extrasynaptic ones (Fig. 5 C). To sort stabilized and unstabilized trajectories, given our localization accuracy, we set Pc_thresh to 1241 μm⁻² (corresponding to a confinement area size with a diameter of ∼60 nm) and t_thresh to 0.33 s (10 time points at 30 Hz). With these settings, the proportion of stabilized trajectories was higher in synapses (46.60%) than at extrasynaptic locations (34.29%). In agreement with the increased confinement of diffusion in synapses reported previously (29), synaptic unstabilized trajectories displayed higher confinement than unstabilized extrasynaptic ones (Fig. 5 D). Even if trajectories obtained with uPAINT were indeed too short to detect transitions between different diffusive states, Pc analysis successfully detected different levels of confinement and stabilization of SEP-γ2 GABA_AR in and out of synapses.

Conclusion

The Pc parameter defined here allows the detection and quantification of transient confinement sequences. The main advantages of this analysis approach are: 1) simple implementation and rapid calculation; 2) calculation from a sliding window, allowing the detection of transient changes and their localization; and 3) independency from MSD and D calculation, thus it can be used to compare molecules or situations with different global diffusivity (i.e., comparison of confinement between molecules with different mobility, or analysis of diffusion-trapping in crowded environments such as synapses).

Above all, the Pc analysis allows the detection of stabilization events along trajectories, thanks to their sensitivity to confinement within small (<50 nm) areas. It is then possible to derive the effective kinetic constants of the molecular interactions implicated in the stabilization even if interactions are weak and transient. This type of short-lived interaction is difficult to grasp with classical bulk methods (such as coimmunoprecipitation, mass spectrometry, or isotitration calorimetry (37)), although it can be an important parameter being regulated during cellular processes such as synaptic plasticity.

Author Contributions

M.R. designed research, performed research, contributed analytic tools, analyzed data, and wrote the manuscript. L.W. performed research. L.H. performed research and analyzed data. S.L. contributed with materials and equipment. A.T. designed research and wrote the manuscript.

Editor: Valentin Nagerl.