Ultrahigh-Resolution Optical Coherence Elastography Images Cellular-Scale Stiffness of Mouse Aorta

Abstract

Cellular-scale imaging of the mechanical properties of tissue has helped to reveal the origins of disease; however, cellular-scale resolution is not readily achievable in intact tissue volumes. Here, we demonstrate volumetric imaging of Young’s modulus using ultrahigh-resolution optical coherence elastography, and apply it to characterizing the stiffness of mouse aortas. We achieve isotropic resolution of better than 15 μm over a 1-mm lateral field of view through the entire depth of an intact aortic wall. We employ a method of quasi-static compression elastography that measures volumetric axial strain and uses a compliant, transparent layer to measure surface axial stress. This combination is used to estimate Young’s modulus throughout the volume. We demonstrate differentiation by stiffness of individual elastic lamellae and vascular smooth muscle. We observe stiffening of the aorta in regulator of G protein signaling 5-deficient mice, a model that is linked to vascular remodeling and fibrosis. We observe increased stiffness with proximity to the heart, as well as regions with micro-structural and micro-mechanical signatures characteristic of fibrous and lipid-rich tissue. High-resolution imaging of Young’s modulus with optical coherence elastography may become an important tool in vascular biology and in other fields concerned with understanding the role of mechanics within the complex three-dimensional architecture of tissue.

Introduction

Arterial wall stiffness is a key determinant of vessel compliance and recoil, and is important in cardiovascular function (1, 2, 3). To maintain local and systemic blood pressure, arterial blood vessels remodel in response to changes in multiaxial mechanical loading (4). Arterial stiffening due to dysfunction in vascular remodeling processes has been implicated in cardiovascular-related diseases such as hypertension, heart failure, and stroke (4, 5). Furthermore, increased arterial stiffness is an independent predictor of mortality (6, 7), and age-related stiffening has been linked to the higher prevalence of cardiovascular diseases in the older population (8, 9).

Animal in vitro and in vivo studies have been informative in mapping the relationships between genetics, pathology, and cardiovascular mechanics; however, the mechanisms of vascular stiffening are still poorly understood (8). These studies typically rely on whole-vessel measurement techniques, such as pressure myography or pulse wave velocity, which are limited to providing either single-point measurements or, at best, a macroscopic view of regional stiffness. However, blood vessels are structurally complex and their function relies on the assembly, structural composition, and individual mechanics of their constituents, including vascular smooth muscle cells, collagen, and elastic lamellae (3, 5, 8, 10, 11, 12). It is the local changes and remodeling of these elements—including the migration and proliferation of smooth muscle, fenestration (opening of holes) of the lamellae, cell hypertrophy, calcification, and degradation of extracellular structural fibers—that are thought to give rise to local mechanical dysfunction (13, 14, 15). Although the morphology of these changes has been documented (3, 8), the cellular-scale measurement of arterial mechanical properties has been limited, for example, to thin (5–30 μm) tissue sections with surface acoustic microscopy (8) and Brillouin microscopy (16), and to isolated cell or tissue surfaces with atomic force microscopy (5, 17, 18).

Elastography, the use of imaging to map the local mechanical properties of tissue (19, 20), may provide a new avenue for discovery in cardiovascular mechanics. Elastography is typically performed in three steps: 1) the tissue is mechanically loaded; 2) its deformation is captured by an imaging system; and 3) input into a mechanical model to estimate a mechanical property or parameter (20). The most prominent imaging modalities used to perform elastography have originally been ultrasound imaging, magnetic resonance imaging, and, latterly, optical coherence tomography (OCT) (21, 22). OCT employs low-coherence interferometry to capture volumetric images of tissue microstructure, typically at resolutions of 5–15 μm, over 5–15 mm lateral fields of view, and 0.5–3 mm in depth, depending on the scattering and absorption properties of the sample. Over the past 20 years, a variety of optical coherence elastography (OCE) methods have been proposed (21, 22, 23, 24, 25), with the most prominent being based on quasi-static compression or shear wave imaging. A number of application areas have been explored, most notably in oncology (26, 27) and ophthalmology (28, 29). In cardiology, there have also been several preliminary demonstrations (30, 31, 32); however, a clear picture of arterial micro-structure and micro-mechanics elucidated from OCE has yet to emerge.

Recently, we have demonstrated elastography based on ultrahigh-resolution OCT, a variant of OCT that achieves sub-2-μm isotropic resolution (33). Our method, which we refer to as ultrahigh-resolution OCE (34), achieves cellular-scale resolution over a three-dimensional (3D) volume of intact tissue, with a lateral field of view of 1 mm and a 94-μm illumination depth of focus, and has achieved the highest resolution to date with elastography based on OCT (34). We have employed quasi-static compression loading over the full sample field of view to capture images of local axial strain (35, 36), a relative measure of tissue mechanics. However, quantification of an intrinsic mechanical property, such as Young’s modulus, is preferred as it allows for system-independent intersample and longitudinal comparisons. To achieve this, we have developed a method to estimate Young’s modulus (which, to be consistent with previous literature in vascular mechanics, we also refer to as stiffness (37)) by performing compression elastography through a compliant, transparent layer (38). The axial deformation (change in thickness) of the layer is used to estimate the axial stress applied to the tissue surface, which, coupled with local axial strain, is used to estimate the tangent modulus (equivalent to Young’s modulus in linear-elastic material) throughout the volume.

In this article, we adapt our method of compression elastography using a compliant layer to ultrahigh-resolution volumetric imaging of stiffness. We demonstrate the technique on the aortas from mice that have had the regulator of G-protein signaling 5 (RGS5) gene deleted and wild-type (wt) controls. G-protein signaling is an important process in cardiovascular function (39, 40, 41, 42). RGS5 protein is predominantly expressed in arterial vascular smooth muscle cells (43, 44) and has recently emerged as a critical regulator of cardiovascular remodeling processes (39, 45, 46). With elastography, we observe the cellular-scale organization of the aorta and, in some cases, the individual mechanics of elastic lamellae and vascular smooth muscle. We measure vascular stiffening associated with RGS5 deficiency and, further, discern regional changes along the length of the aorta. We also observe local micro-mechanical features that correlate with observed vessel wall micro-structure. The technique is capable of achieving a sub-2-μm structural resolution and an isotropic mechanical resolution of as high as 15 μm, maintained over a 1-mm lateral field of view and across the entire depth of the intact mouse aortal wall; to the best of our knowledge, the highest resolution of tissue mechanical properties achieved with OCE to date. Such information is typically not available from current mechanical characterization methods, suggesting that ultrahigh-resolution OCE could contribute to the better understanding of the role that cardiovascular micro-mechanics plays in cardiovascular disease and therapeutic interventions.

Materials and Methods

Extended-focus optical coherence microscopy

The variant of ultrahigh-resolution OCT (often referred to as optical coherence microscopy (OCM)) employed here is described in (34), and briefly here. Fig. S1 shows the optical setup of the system. We implement extended depth-of-field (DOF) Fourier-domain OCM with a supercontinuum optical source (SuperK Extreme EXR-1, NKT Photonics, Denmark), spectrally shaped to produce a central wavelength of 785 nm and a 3-dB bandwidth of 200 nm, and combined it with a spectrometer operating at 70 kHz and utilizing 2048 pixels of the line-scan camera (spL4096-140 km; Basler, Ahrensburg, Germany). The acquisition rate of each spectrum was 20 kHz (50-μs period), with a pixel exposure time of 30 μs. Typically, Fourier-domain (and full-field) OCM requires the beam focus to be scanned in z to form volumetric images, which is necessitated by the limited DOF of high-numerical aperture microscopes (33, 47, 48, 49). In our implementation, we employ Bessel beam illumination with effective numerical aperture of 0.27 and Fresnel number N = 10.5 generated by a spatial light modulator (Pluto NIR II-HR, HOLOEYE Photonics AG, Berlin, Germany) and propagated in free space, achieving an illumination DOF of 94 μm; well beyond the typical 7 μm in Gaussian illumination (for an equivalent resolution), which enables one-shot depth imaging of small tissue volumes (one depth image (1D) per one spectral acquisition). A lower numerical aperture (0.16) Gaussian mode detection is used for the apodisation of the Bessel beam side lobes and as a more energy efficient mode of detection to improve sensitivity (50); however, this is at a slight cost of transverse resolution and the combined DOF of the system (34). The combined DOF of the system is nontrivial to calculate; however, in practice it proved sufficient to provide reliable OCE measurements from ∼100 μm of tissue (Fig. 2, e and f), which were used to generate the mean aorta stiffness results. The maximum sensitivity of the system was measured to be 96 dB at 12-μs exposure time, and the sensitivity roll off was 17 dB at 1 mm imaging depth. The axial and lateral OCM resolutions were measured to be 1.5 and 1.6 μm, respectively (34). The transverse field of view is ∼1.5 mm.

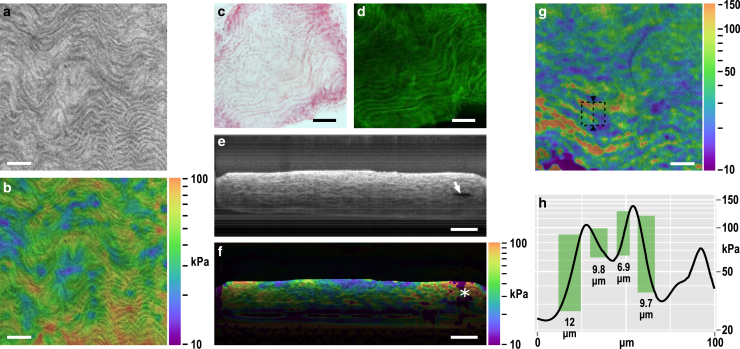
Figure 2.

(a) En face (x,y) structural image of an aorta virtually sliced 20 μm past the adventitia; and (b) corresponding stiffness elastogram on a log₁₀ scale overlaid on the structural image. Representative longitudinal, histological aortic sections: (c) hematoxylin and eosin and (d) autofluorescence, showing similar micro-structure to that seen in (a). (e) B-scan (x,z) structural image with the compliant layer above the collapsed aorta (scanning from the top down); arrow shows a small gap in the lumen; and (f) corresponding stiffness elastogram overlaid on the structural image (compliant layer masked out in black). The asterisk shows a stiffness artifact from the gap in the lumen. In (e and f), depth is scaled by refractive index of 1.4. (g) En face (x,y) elastogram virtually sliced 50 μm below the adventitia, corresponding to the tunica media. The dashed square denotes the region displayed in Fig. 3. (h) Line plot of stiffness along the triangle-marked dashed line in (g). The 10–90% rise distance is shown by the green boxes and quantified. The scale bars represent 100 μm. To see this figure in color, go online.

Compression elastography with a compliant layer

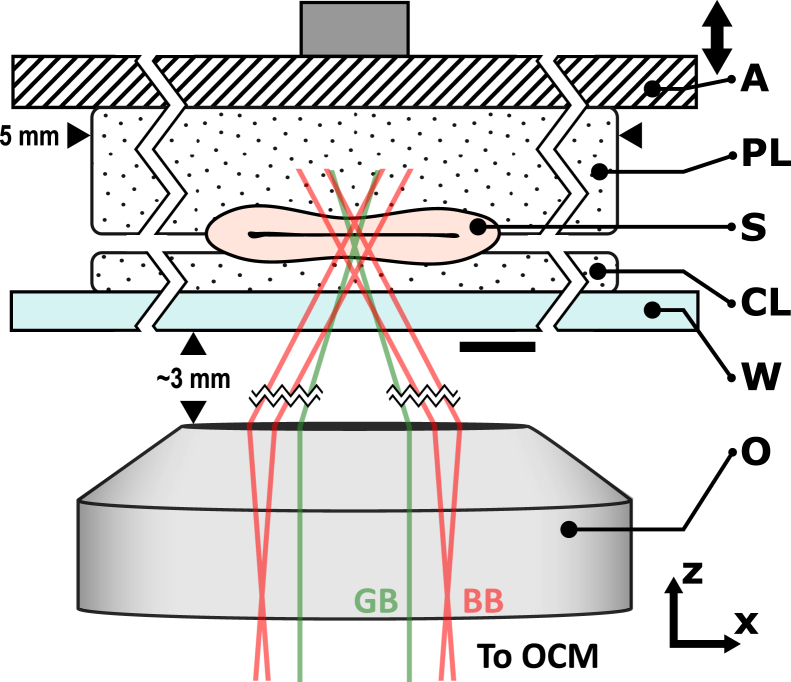
Fig. 1 shows the imaging setup of our system. To measure the stiffness of the aorta samples, we perform compression elastography through a compliant layer, a method previously demonstrated by our group (38) and modified here to adapt to the higher spatial resolution. The measured change in thickness of the compliant layer is used to estimate the axial component of stress at the sample surface, which, coupled with local axial strain captured by compression elastography in each voxel of the tissue, enables the estimation of stiffness. To obtain an accurate estimation, the method requires the stress in the compliant layer and in the tissue to be close to uniform and uniaxial (51). To account for the uneven geometry of the aorta sample (S), it is placed between a compliant layer (CL) and a thicker padding layer to more evenly distribute the compressive load. Both layers are fabricated from room temperature-vulcanizing silicone rubber (Elastosil P7676; Wacker, Munich, Germany), with the compound and cross-linker mixed at a 1:1 ratio. The use of this silicone in tissue-simulating phantoms has been reviewed previously (52). The CL was fabricated to a thickness of 150 μm by curing it between two glass microscope slides, with the separation adjusted with the aid of monitoring with OCT, where the refractive index of silicone was assumed to be 1.4 (52). The padding layer was fabricated to a thickness of 500 μm in a glass petri dish. Both layers were cut to 5-mm width.

Figure 1.

Imaging setup of the elastography system. The aorta sample (S) is placed between a compliant layer (CL), which is used to measure stress, and a padding layer (PL), which is used to more evenly distribute the compressive load applied to the sample. The sample layer assembly is preloaded against a rigid glass window (W) by translating a piezoelectric actuator (A), which is also used to apply step-wise micro-scale compressive loading during imaging. The objective (O) is used to focus the Bessel beam (BB) into the sample and collect the Gaussian component of the backscattered beam (GB) from the sample. The scale bar represents 300 μm. To see this figure in color, go online.

Before imaging, the S and layer assembly were placed on a rigid glass window and were preloaded against it, in the axial (z-) direction, by a flat plate attached to a piezoelectric actuator. The applied preload bulk compression of the tissue was 5–10%, which ensured that S (an intact tube segment roughly 500 μm in diameter and 5 mm in length in an unloaded state) was collapsed with no gap inside the lumen. The S was lubricated with physiological saline, and the layer surfaces in contact with the window and the actuator were lubricated with polydimethylsiloxane oil (AK50; Wacker) to minimize friction, since the presence of friction reduces the accuracy of stiffness assessment (51).

During imaging, the piezoelectric actuator provided step-wise loading and unloading via displacements in the range of 1–2 μm, whereas the window remained static, establishing a displacement gradient in the sample and the layers. The imaging beam was scanned in the x- and y-directions, capturing depth scans (A-scans) at each location. Scanning was synchronized with loading such that colocated cross-sectional images (B-scans) were captured sequentially at each loaded and unloaded state. This procedure was repeated at each y location to ultimately capture volumetric data. The loading rate was 5 Hz and the A-scan sampling density was 0.5 μm in the lateral directions, resulting in volumes (loaded and unloaded) with 2000 samples in x and y within a 1-mm field of view, captured in under 7 min.

Inverse Fourier transformation of the recorded A-scan produces the complex back-scattered signal versus depth. Using the principles of phase-sensitive detection (53), local axial displacement $\left(u_z\right)$ of the sample and the layer, in response to the micro-scale compression, can be extracted as $u_z=\mathit{\Delta }\varphi {\lambda }_0/4\pi n$, where $\mathit{\Delta }\varphi$ is the difference in phase between the colocated scans in the loaded and unloaded state, ${\lambda }_0$ is the central wavelength of the light source (785 nm), and $n$ is the refractive index in tissue. Calculation of stiffness is independent of refractive index (38); the refractive index of tissue was assumed to be 1.4 and also used to scale all images in depth to represent their physical size. Local axial strain, i.e., the gradient of the local displacement with respect to depth $\left({\epsilon }_z={\nabla }_z{u}_z\right)$, is estimated using a weighted least-squares linear regression (35) with an axial fitting range with a full width at half maximum (FWHM) of ∼15 μm, resulting in a resolution of the estimated local axial strain of ∼2 × 2 × 15 μm (x,y,z) (34). However, the inversion process to determine Young’s modulus, described below, is sensitive to noise; therefore, the strain is further spatially filtered in x and y by a Gaussian kernel with a FWHM of 15 μm, producing strain with an expected isotropic resolution of ∼15 μm.

Determining Young’s modulus from Hooke’s Law requires a measurement of local stress and local strain in the tissue. Local stress is approximated with the aid of the CL (36). The intrinsic nonlinear properties (stress-strain curve) of the CL are well characterized (repeatability ± 0.25%) independently using standard compression testing (Instron 5848; Norwood, MA). Given that we know the strain in the CL from elastography data, we can estimate the stress at the CL-S interface by using the stress-strain curve as a look-up table. The procedure is detailed in (38); briefly, Canny edge-detection is used to evaluate the preloaded CL thickness in x and y. The difference between the preloaded thickness and the unloaded thickness is used to estimate the preload strain in the CL. Axial strain from micro-scale actuation is evaluated as the displacement of the CL-S interface over the preloaded CL thickness. The local gradient of the stress-strain curve at the preload strain is the local tangent modulus $\left(E_T\right)$, which relates local stress $\left(\sigma \right)$ to local strain as $\sigma =E_T{\epsilon }_z$. This is done for every point in x and y to estimate the local axial stress imparted across the CL-S interface. The stress is assumed to be uniform in z through the tissue volume, which is a necessary assumption to enable a rapid approximation of stiffness that is robust to noise (51, 54). Fig. S2 shows an example of these intermediate outputs, including the preload CL thickness, and the CL stress and sample strain from micro-scale actuation. Finally, the local Young’s modulus is estimated as the local axial stress over the local axial strain; in an ideal case, producing an isotropic stiffness map, i.e., an elastogram, with an expected resolution of 15 μm. Tissue is usually nonlinear elastic; and as we image at a given preload, the estimated tangent modulus at the particular preload (and here referred to as stiffness) is equal to or greater than the Young’s modulus.

Animal preparation and imaging protocol

All experimental protocols involving mice were approved by the Animal Ethics Committee of The University of Western Australia. Arteries were isolated from 10–14-week-old male wt C57BL/6J mice and RGS5 gene knockout (ko) mice on a C57BL/6J background (n = 5 each) (55). After intraperitoneal injection with urethane, arterial blood was removed by perfusion with ice-cold physiological saline via cardiac puncture. The arch, thoracic, and abdominal regions of the aorta and proximal conduit arteries (i.e., left subclavian, brachiocephalic, and left and right common carotid arteries) were isolated and cleaned of perivascular fat and connective tissues. Arteries were incubated in ice-cold physiological saline until stiffness measurements were made (<4 h). Low-resolution scanning (n = 2) was performed on the whole aorta and proximal conduit arteries using a wide-field OCT system described elsewhere (56). High-resolution scanning (n = 30 scans) was performed on the aorta (n = 10 samples) segmented into three equidistant sections labeled as proximal, medial, and distal relative to the heart. After stiffness was measured, arteries were embedded in Tissue-Tek O.C.T. Compound (ProSciTech Pty Ltd, Australia), sectioned longitudinally in 7 μm-thick sections mounted on 1% gelatin-coated glass slides, and stained with hematoxylin and eosin ready for bright-field and autofluorescence microscopy using a Nikon Eclipse Ti-E microscope (Nikon Instruments, Inc.). Microscopy image analysis was performed using NIS software modules (Nikon, version 4). Elastography acquisition and processing to stiffness images were performed as a blind study. All statistical analyses were performed using the R statistical package (version 3.3.2).

Results

Ultrahigh-resolution OCE

Our technique provides volumetric images of both the structure and stiffness of tissue. In this article, we present two-dimensional images as either “en face” in the xy plane, which are taken from 20 μm (unless otherwise specified) in depth (z) above the interface between the compliant layer and the aorta (anatomically, the edge roughly corresponds to the adventitia); or, as B-scans, which are cross sections in the xz plane. Structural images are averaged (Gaussian, 10-μm FWHM) in the z direction for en face and y direction for B-scans, to more closely correspond to the z-resolution of the estimated stiffness. Presented stiffness elastograms are overlaid (multiplicatively) on grayscale structural images to provide morphological context to the observed mechanics. Overlays have been used previously in parametric OCT techniques to enhance the interpretability of images (57, 58).

Fig. 2, a and b show, respectively, a representative en face structural image and a stiffness elastogram. A wavy appearance is evident, which corresponds to features seen in representative histological sections: hematoxylin and eosin and autofluorescence, Fig. 2, c and d, respectively. The morphology and autofluorescence signals suggest that the higher intensity (brighter) wavy micro-structure is likely to be the elastin as part of the elastic lamellae. The size and appearance of these structures also correspond well with previous histological and SEM studies (8, 59). The individual lamellae can be seen to overlay each other as the averaged structural images (Fig. 2 a) and histological images (Fig. 2, c and d) section multiple elastic lamellae in depth.

Fig. 2, e and f show B-scans of structure and stiffness. The imaging beam is incident from the top of the images (inverted relative to Fig. 1), thus, the compliant layer corresponds to the region of low intensity above the aorta. The preloaded aorta is largely collapsed with good contact between the inner surfaces of the lumen, which provides mechanical continuity, i.e., an even transfer of load from one side of the aorta to the other. Due to the geometry (a tight radius bend), the far left and right regions of the compressed aorta in Fig. 2 e are under a high internal preload. A small gap in the lumen can be seen on the right side due to the latent stress in the folded aorta (arrow), generating an artifact in measured stiffness (asterisk); further, the high preload increases the effective local stiffness observed near the edges. Thus, mean stiffness values are taken 150 μm away from the lateral edges of the aorta and away from potential artifacts. The focus is set roughly 40 μm into the aorta as a trade-off to provide sufficient signal in the compliant layer (required for stiffness calculation), although ensuring that the majority of the focus is within the tissue. Beyond the extent of the DOF, the OCM signal is observed to reduce in sensitivity and resolution, reducing the quality of stiffness data, as seen in Fig. 2 f. Fig. 2, e and f demonstrate the effective imaging range of OCM and stiffness, which is sufficient to capture an entire wall of the aorta (100–150-μm thick).

The spacing between the elastic lamellae and the vascular smooth muscle cells varies across different depth sections. The B-scan in Fig. 2 e shows this change in morphology. In certain sections, the spacing is sufficiently large to enable our method to distinguish the individual micro-mechanics of the elastic lamellae and vascular smooth muscle cells (Fig. 2 g). Fig. 2 h shows a line plot of stiffness across a 100-μm region marked in Fig. 2 g by a triangle-marked dashed line. The plot demonstrates the presence of three elastic lamellae (higher local stiffness). By characterizing feature sharpness as the 10–90% rise distance (Fig. 2 h), which is 1.08 $\times$ FWHM assuming a Gaussian response, we confirm that we achieve sub-15-μm feature resolution in a practical tissue measurement. Resolution is further discussed in the Discussion.

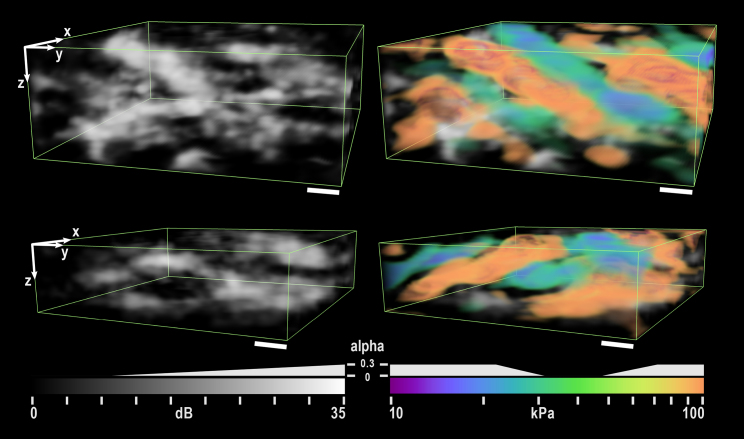
Fig. 3 shows a 3D rendering of two local 100-μm (x,y) regions in an aorta. The top rendering corresponds to the dashed region outlined in Fig. 2 g. The micro-mechanical signature of the interleaved hard and soft regions is evident. Their thickness (10–20 μm), morphology, and correspondence to the micro-structure suggests that the hard regions delineate the elastic lamellae and the soft regions delineate the vascular smooth muscle cells. Rendering was performed with ParaView (Kitware, Inc., Clifton Park, NY) (60).

Figure 3.

Three-dimensional rendering of two local 100-μm (x,y) regions in an aorta. Structure (left) is rendered with linear transparency. Stiffness is overlaid (right) with only the particularly hard and soft regions given opacity. The upper rendering is taken from the region outlined by the box in Fig. 2g. The rendering clearly delineates interleaved hard and soft regions, which are presumed to represent the elastic lamellae (hard) and smooth muscle (soft). α indicates the transparency value for each color and greyscale value. Depth is scaled by refractive index of 1.4. The scale bars represent 10 μm. To see this figure in color, go online.

Aortic stiffening in RGS5 deficient mice

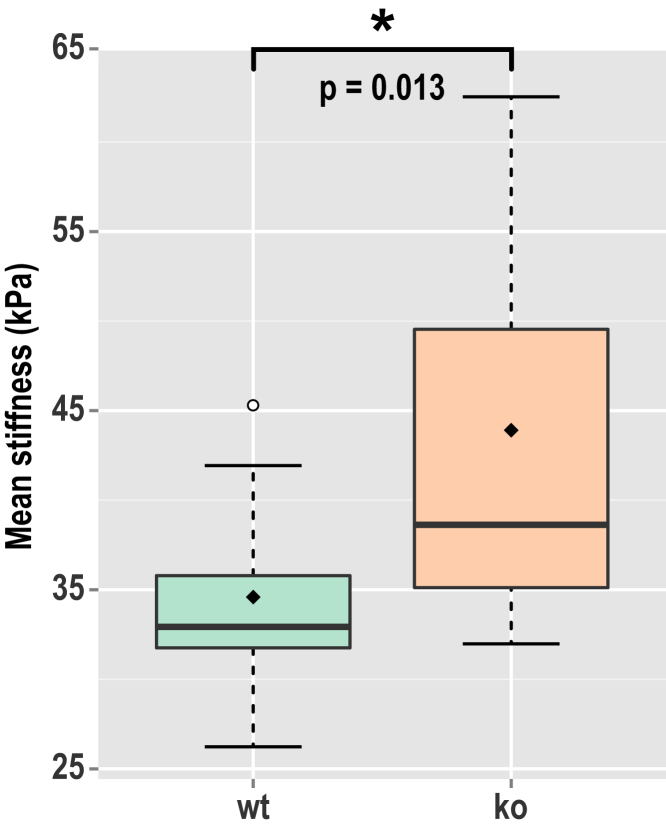
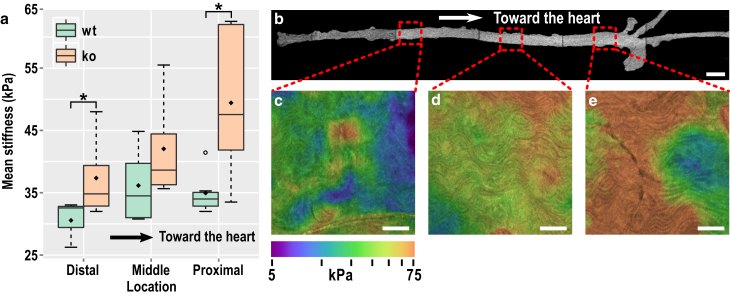
Fig. 4 shows the mean stiffness of the aorta walls from wt and RGS5 ko mice. Of the 30 measurements taken from 10 animals, two measurements were excluded (under blind conditions) due to the presence of excessive adipose tissue. The averages were taken from the central 700-μm long region and over the range 5–100 μm in depth to avoid influences from tissue boundaries. A significant increase in stiffness in the aorta of RGS5 ko mice compared to wt controls (n = 29; p = 0.013; Welch’s t-test) is observed. The measured mean stiffness was 34 and 43 kPa in the wt and ko mice, respectively. The measured stiffness is within the expected range observed in wt mice using pressure myography characterized by a constitutive model (61) or estimated as stress divided by strain (62, 63).

Figure 4.

Mean stiffness of the wild-type (wt) and knockout (ko) mouse aortas represented as box plots. The whiskers represent the range of measurements within the 1.5× interquartile range. The hollow circle represents an outlier. The diamond is the overall mean of stiffness. To see this figure in color, go online.

Although mean stiffness may be assessed by myography, and indirectly by pulse wave velocity, measuring the spatial variation in stiffness along the length of the aorta is challenging. Observation of local changes in stiffness may be important in understanding the formation of local pathologies (e.g., plaque) and cardiac events (e.g., stroke). Fig. 5 a shows the mean of the measured stiffness along the aorta in locations distal, medial, and proximal in relation to the heart. The averages were taken in the same regions as the results for Fig. 4. A wide-field OCT en face image of a whole aorta (Fig. 5 b) delineates the anatomical regions (the system used to capture the image is described elsewhere (56)).

Figure 5.

(a) Mean stiffness in various locations along the wild-type (wt) and knock-out (ko) mouse aorta, showing stiffening with proximity to the heart, and the enhanced stiffening in ko mice (^∗p < 0.05). The whiskers represent the range of measurements within the 1.5× interquartile range. The hollow circle represents an outlier. The diamond is the overall mean of stiffness. (b) Wide-field en face OCT image of a whole mouse aorta, showing representative locations of elastography imaging. (c–e) Mean stiffness elastograms (averaged from 5 to 100 μm in depth) on a log₁₀ scale overlaid on structural images virtually sliced 20 μm past the adventitia, showing an overall stiffening of the aorta toward the heart. The scale bars represent 1 mm in (b) and 200 μm in (c)–(e). To see this figure in color, go online.

Specific locations along the aorta were compared between ko and wt mice. In both proximal and distal locations, the aortas of ko mice were significantly stiffer (p < 0.05); however, stiffness at the middle location does not reach significance. Further, locations were grouped, to permit a more powerful analysis to that in Fig. 4, similarly showing greater stiffness in ko mice (n = 5; p = 0.010; ANOVA one-way). Furthermore, Fig. 5 a shows a significant increase in the stiffness of ko aortas versus proximity to the heart (n = 5; p = 0.039; ANOVA 1-way) (visualized in Fig. 5, c–e). This increase in stiffness is not as pronounced in wt mice (n = 5; p = 0.37). However, ko aortas display a significant stiffness gradient when compared to wt data, and there is insufficient power to confirm that the aortas of ko mice exhibit a proportionally higher increase in stiffness with proximity to the heart than the wt mice (n = 5; p = 0.072; Welch’s t-test). These data, together with the finding that RGS5 levels vary between different vascular beds (44), support the hypothesis that RGS5 may have a role in regulating vascular smooth muscle phenotype and stiffness along the aorta, which is considered further in the Discussion.

Micro-mechanical features

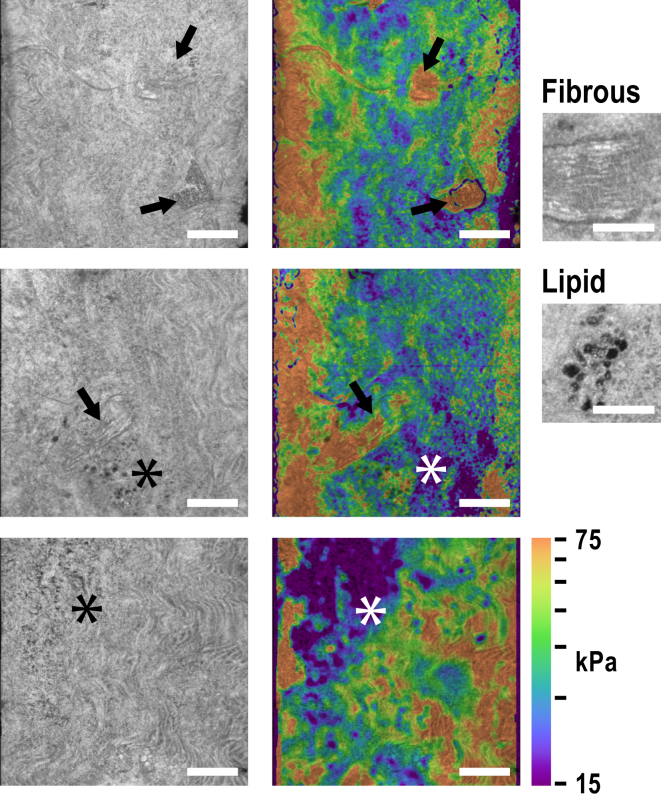
Local mean stiffness can be obtained through careful excision and standard mechanical testing, such as biaxial tensile testing (37, 64). However, the distinct advantage of ultrahigh-resolution OCE is the ability to measure local micro-mechanics within a volume, along with co-located images of tissue micro-structure. Notably, we observed the presence of eight local fibrous regions, of which six were in the RGS5-deficient mice. Further, the fibrous regions were observed from only 3 of the 10 mice (2 ko and 1 wt). All fibrous regions were significantly stiffer, in the range 70–150 kPa. Fig. 6 shows selected examples of structural images and stiffness elastograms.

Figure 6.

Micro-structure and micro-mechanics of the aorta. Structural images on the left show the presence of local fibrous nodules (arrows) and lipid (asterisk). Stiffness elastograms (right) on a log₁₀ scale overlaid on the structural images show the localized stiffening in fibrous regions and softening in lipid-rich regions. Magnified insets at far right illustrate the characteristic signature of fibrous tissue and lipid in OCM (taken from aorta images not shown here). All images are from knockout mice. The scale bars represent 200 μm, and 100 μm in the insets. To see this figure in color, go online.

Regions of small lipid vesicles (∼5–20 μm in diameter) were revealed in the tunica media by the structural images. Fig. 6 shows the characteristic signature of lipid as sub-30 μm diameter spherical cells of low intensity (65). These lipid features were found in both wt and ko mice. The majority of lipid regions, such as in the bottom panels of Fig. 6, were observed to be softer (7 out of 9), in the range 5–20 kPa. However, two regions (including the middle panel of Fig. 6) showed no significant change or an unexpected slight increase in stiffness. The morphology of these lipid-rich regions does not correspond to developed lipid-rich plaque, as seen in previous studies of atherosclerosis (49); by contrast, they present as distinct lipid deposits. SEM studies of the aortal ultrastructure have revealed lipid deposits on a sub-μm scale (66, 67); in early fibro-lipid lesion formation, extra- and particularly intracellular lipid deposits were seen to grow in size and quantity (68). The lipid-rich regions seen in our study may be early signs of plaque formation; however, an atherosclerotic mouse model and further data, including collocated ultrastructure, is needed to confirm this.

Discussion

Ultrahigh-resolution OCE through a compliant layer provides simultaneous volumetric imaging of tissue micro-structure and micro-mechanics at sub-2-μm structural resolution (demonstrated previously (34)) and nominally 15-μm isotropic resolution of Young’s modulus preserved over a 1-mm lateral field of view through the entire depth of an intact aortic wall, enabling the observation of mechanical contrast down to the individual elastic lamellae and vascular smooth muscle cells in select regions of the aorta. To the best of our knowledge, this is the highest quantitative mechanical resolution demonstrated with OCE to date. Further, our technique does not require labeling, fixation, or tissue sectioning, and can be performed in under 7 min. Fig. 2 h demonstrates a resolution exceeding 15 μm. As discussed in the Materials and Methods, spatial filtering is performed on the strain, which sets its minimum resolution; however, upon division of stress by strain, in regions of high mechanical contrast (such as between the lamellae and vascular smooth muscle cells), the observed resolution of stiffness may be higher because the averaging no longer follows a Gaussian response. The lateral spatial resolution of the stress measurement is close to the lateral resolution of OCM, assuming that the stress is uniaxial; however, in heterogeneous tissue, the resolution is degraded (51). In aorta, the estimated surface axial stress was largely uniform, thus, its contribution to the resolution of mechanical features was small; however, heterogeneity of tissue and effects of friction are likely to introduce systematic errors affecting the accuracy of stiffness assessment due to nonuniform stress in the volume. The dependence of the spatial resolution of stiffness elastograms on the tissue mechanical properties, and the link between resolution and accuracy, has been discussed previously, and is nontrivial to estimate for a general case (51, 54).

Ultrahigh-resolution OCT is termed as such because it approaches the practical resolution limit of OCT (33, 69). Higher axial resolution can be achieved by using a shorter wavelength and wider bandwidth light source; however, there are a number of practical limitations on the achievable resolution. It is a technical challenge to propagate such a wide bandwidth through all elements of the optical system without loss. Even if this can be done, wavelength-dependent sample absorption and dispersion limit the effective resolution to ∼1–1.5 μm (69). Lateral resolution is dependent on the numerical aperture, and to achieve extended-DOF performance over most of the depth range requires the use of extended-focus beams (such as Bessel beams), with sensitivity reduced through optical power present in side lobes. However, the capacity to improve mechanical resolution lies not only in improving the resolution of the underlying optical system, but also on the sensitivity of its displacement measurements. The fitting range used in estimating strain has a greater contribution to the mechanical resolution than the optical resolution of the system. Improvements in displacement sensitivity, through the implementation of more stable optical sources and components, and through different acquisition and processing strategies, will reduce the requirement for spatial averaging and increase the attainable resolution of mechanical properties.

Measurement of micro-mechanical properties has increased in importance in recent years, with the recognition of their contribution to mechanisms of disease and their utility in clinical diagnosis (23). We demonstrate the potential of elastography in aiding cardiology; however, high-resolution elasticity imaging underpins the field of mechanobiology (70, 71, 72) and is also being pursued for applications in cancer (26, 27), muscular dystrophy (73), and eye disease (74). We anticipate that OCE will become an important tool in observing and characterizing mechanical properties of tissue in three dimensions, particularly, in studying the role of mechanics and remodeling processes within the complex 3D hierarchical architecture of tissues. Ultrahigh-resolution OCE may, further, bridge the gap between subcellular mechanical measurement techniques, such as atomic force (75) and traction force microscopy (76), and macro-scale techniques, such as magnetic resonance imaging and ultrasound elastography (20).

High-resolution mechanical imaging is not exclusive to the technique presented here; other loading methods and optical imaging systems have been proposed. For example, dynamic loading methods have been prominent in OCE. Measurement of wave propagation, vibration, harmonic frequencies, or wave dispersion in tissue in response to pulsed or continuous wave loading provides alternate approaches for characterization of local mechanical properties (21, 22, 25). Dynamic methods may enable noncontact tissue loading, particularly advantageous for delicate tissues, or the translation of OCE toward in vivo use. However, dynamic methods reported to date demonstrate poorer resolution of mechanical properties (from the fitting of a dynamic mechanical model to measured data) and require a greater volume of data to be acquired. Young’s modulus imaging using dynamic methods has not been demonstrated with OCM systems to date; however, dynamic contrast in cellular spheroids has been measured using a closely related full-field version of OCT (77). Very recently, OCM has been advanced as a means of performing 3D traction force microscopy (78), which, with further development, has the potential to map cellular forces. Another promising technique is Brillouin microscopy (23), which estimates the longitudinal modulus from the Brillouin frequency shift arising from the interaction of light with Gigahertz-frequency acoustic waves (phonons) (79). Brillouin microscopy is able to achieve a high spatial resolution (equivalent to confocal microscopy) and is distinguished from other elastography methods in that tissue loading is not required, enabling noncontact and minimally invasive imaging. Brillouin microscopy has already been demonstrated in measuring plaque stiffness in serial sections of vessel tissue (16). Further, subcellular-scale resolution has been demonstrated in imaging single cells (80). However, Brillouin microscopy is limited in its imaging speed, as it requires confocal scanning and long acquisition times to capture the weak Brillouin spectrum. Further, it is not yet clear how the estimated high-frequency longitudinal modulus, which is heavily influenced by tissue incompressibility and viscoelasticity, is related to the more familiar Young’s modulus or shear modulus in the more physiologically relevant lower frequency range.

Compression elastography techniques face their own challenges. In the aorta, a relatively large preload was necessary to ensure complete contact of the sample with the loading mechanism. Tissue is typically nonlinear elastic, thus, a preload imparts an offset along its nonlinear stress-strain curve, which makes the tissue appear stiffer than it is under relaxed conditions. Further, regions of tissue may be under different preloads, potentially creating false contrast, especially if the tissue has an uneven surface topography. The variation in total preload between measurements may also introduce a bias to the stiffness, which may challenge any comparison of measurements between different systems or measurement methods. Discontinuities or gaps in the tissue, such as the artifact observed at the edge of the compressed aorta (Fig. 2 f), can further confound the estimated stiffness. There are a number of avenues to address these challenges. Localized loading, such as indentation, may be used to selectively compress only a part of the aorta at a time. Although leading to a smaller required preload, and a smaller contribution from surface topography, the field of view is limited. Thus, to access the entire aorta, loading would have to be repeated in multiple positions, for instance, as the aorta is rotated. Alternatively, loading could be applied radially from the luminal side (e.g., in vivo using intrinsic pulse pressure), uniformly distributing stress across the aortic wall. In general, the loading approach will be tailored to each tissue and application.

The mechanical model employed is a further important consideration. The model employed here assumes that the stress field is uniaxial. Such an assumption holds true if the sample is mechanically and structurally uniform, and if there is minimal friction along its boundaries. The accuracy of the estimated Young’s modulus is progressively degraded with increasing nonuniformity of the sample, or by increasing friction (51). These effects are particularly evident at the boundaries of the aorta (Fig. 2 f). The error can be minimized by employing computational approaches to solve the forward elasticity problem in the compliant layer or by solving the inverse elasticity problem in its entirety, directions we are actively pursuing (51, 54). Solutions to the inverse elasticity problem through an iterative approach, for instance, are able to recover the mechanical properties of the sample without the assumption of uniaxial and uniform stress, leading to a more accurate characterization. Their use has been limited due to their significant computational load; however, computationally efficient approaches are emerging (54).

A remaining challenge in this technique is validation of the accuracy of the measured local micro-mechanical properties. On a whole-organ scale, the measurements of stiffness in the aorta are similar to those of established methods, such as myography. However, on the micro-scale, direct comparison is challenging. Techniques such as atomic force microscopy, which probe the mechanical properties in two dimensions, do so on a different length scale and with significant influence from tissue boundaries. Direct comparison would require the same tissue to be profiled with tight control of the loading parameters; such a study would be very informative. Alternatively, accuracy may be assessed by using tissue-simulating phantoms with well characterized mechanical properties. The accuracy of compression OCE was measured to be 8% (SE) at a lower resolution than here (38); however, similar analysis would require the fabrication of features in the order of a few 10 μm, which will require the development of new phantom fabrication methods.

We have demonstrated an ability to characterize stiffness in wt and RGS5 ko mouse aortas and observed that RGS5 deficiency leads to an overall stiffening of the aorta, further supporting its role in regulating vascular remodeling (45, 46). Importantly, we have observed a location-dependent local stiffening of the aorta with proximity to the heart. Interestingly, RGS5 expression in vivo is under epigenetic control (44), and regional differences may manifest in phenotypic differences in vascular smooth muscle cells with far reaching consequences for vessel stiffness and hemodynamics. The ratio of elastin to vascular smooth muscle has been noted to decrease in proportion to distance away from the heart (81); in contrast, age-related stiffening is observed to increase with distance away from the heart, and young aortas seem to possess less stiffness heterogeneity (37). These results imply that RGS5 has disparate roles in regulating vascular smooth muscle phenotype and stiffness along the aorta.

We have also observed the presence of fibrous and lipid-rich regions with distinct optical and mechanical characteristics. Such observations are difficult to make using the current conventional methods of mechanical characterization, such as pulse wave velocity and myography, and are unattainable deep within an intact 3D architecture of tissue. These micro-mechanical signatures cannot be easily obtained with elastography systems of 5–10 times lower resolution than reported here and, further, the small size of the S presents an additional complication when compressed by the typical wider-field loading of lower resolution compression elastography. Localized measurement of mechanical properties can enable a closer link between the composition of the vessel architecture, its genetic profile, and mechanical function (37). Future therapeutic intervention strategies based on RGS5, or perhaps other regulators of vascular stiffness and remodeling processes (3), would benefit from local mechanical characterization. Further, cardiovascular pathogenesis in plaque and aneurism formation, development, and rupture is often driven by the local vessel wall composition, mechanics, and the introduced turbulence in blood flow (82, 83). Our observations suggest many future directions, but further experimentation is required to elucidate with certainty their biological origins.

Our technique can be improved to facilitate its introduction into biological applications. More rapid acquisition may be enabled by increasing the OCM line rate, either by trading off the sensitivity of the OCM signal, or by increasing the power of the optical source. Different acquisition (84) and loading (85) strategies may be used to further trade-off the acquisition rate and the sensitivity of the estimated Young’s modulus, tailored to the application. In vivo applications may be supported by the technique if the imaged tissue is superficial, such as the skin. However, the use of a compliant layer introduces a challenge for in vivo imaging. Its placement must be controlled, and the phase-sensitive measurement used to assess displacement is sensitive to motion. A possibly useful strategy is to cure the layer to the interface of the imaging probe. Although this will introduce significant friction, it may be compensated for computationally (51). The optical beam may be further relayed via a rigid endoscope, similar in principle to those developed for microscopy (86), to enable in vivo measurement in deep tissues, an avenue we are actively pursuing.

Conclusions

We have combined ultrahigh-resolution OCE with a compliant layer to enable high-resolution imaging of stiffness. We have demonstrated that the technique can capture local stiffness changes, detecting features related to systemic remodeling as well as to local micro-structure. We achieve approximately a 15-μm resolution in stiffness over the entire wall of the mouse aorta and a 1-mm lateral field of view, which is, to the best of our knowledge, the highest achieved performance in OCE to date. We exploit such resolution to observe the stiffness of individual lamellae and vascular smooth muscle layers, and micro-mechanical signatures corresponding to fibrous and lipid-rich regions. We anticipate that ultrahigh-resolution OCE will become an important tool in cellular-scale characterization of vascular mechanics, with potential for translation to other fields in which mechanical properties within the complex 3D architecture of tissue, and their modification by disease, are of primary importance, such as mechanobiology and oncology.

Author Contributions

P.W., A.C., D.D.S., and B.F.K. designed and developed the imaging method. P.W., N.J., R.G., and B.F.K. designed the tissue experiments. P.W., N.J., and A.C. performed the experiments. N.J. performed animal preparation and histology. P.W., N.J., D.D.S., R.G., and B.F.K. analyzed the data. P.W. wrote the article. All authors edited and reviewed the article.

Editor: Catherine Galbraith.