Characteristics of School Districts That Participate in Rigorous National Educational Evaluations

Abstract

Given increasing interest in evidence-based policy, there is growing attention to how well the results from rigorous program evaluations may inform policy decisions. However, little attention has been paid to documenting the characteristics of schools or districts that participate in rigorous educational evaluations, and how they compare to potential target populations for the interventions that were evaluated. Utilizing a list of the actual districts that participated in 11 large-scale rigorous educational evaluations, we compare those districts to several different target populations of districts that could potentially be affected by policy decisions regarding the interventions under study. We find that school districts that participated in the 11 rigorous educational evaluations differ from the interventions’ target populations in several ways, including size, student performance on state assessments, and location (urban/rural). These findings raise questions about whether, as currently implemented, the results from rigorous impact studies in education are likely to generalize to the larger set of school districts—and thus schools and students—of potential interest to policymakers, and how we can improve our study designs to retain strong internal validity while also enhancing external validity.

1. Background and Overview

Evaluations of educational programs or interventions typically begin by recruiting a sample of schools, districts, or other providers of educational services to participate in the study. The evaluation team first must decide where they would like to conduct the study and recruit sites that they would like to include. Then, in most evaluations for which participation is voluntary, the sites must decide whether to participate. This process determines which districts, schools, teachers, and students are represented in the study sample.

The recruitment process plays out differently in different types of evaluations in education—but, at least anecdotally, they generally favor certain types of schools and districts over others. For example, many education studies exploit State Longitudinal Data Systems and longitudinal analysis methods to estimate the effects of a range of interventions, such as charter schools or alternative certification programs for teachers (e.g., Bifulco and Ladd, 2006; Booker et al., 2007; Clark et al., 2013). These researchers have tended to conduct their studies in states with well-developed, high-quality data systems, such as North Carolina and Florida. Other education studies are small-scale randomized trials of researcher-developed educational interventions, including many studies supported by education research grants issued by the Institute of Education Sciences (IES). Since these studies are typically proposed by university professors, it is not surprising that the participating schools and districts are often in close proximity to their universities. IES also sponsors large-scale evaluations through contracts to major research firms (e.g., Abt Associates, Mathematica Policy Research, MDRC). These evaluations usually select a sample designed to cover all regions of the country, but sites are selected purposively to reduce costs and sometimes with other objectives in mind (e.g., to test the intervention in sites where it will produce the greatest “contrast” between the treatment and control conditions, suggesting that it may have the greatest impact); they are rarely selected randomly to be formally representative of any broader population of potential interest to policymakers (Olsen et al., 2013).

While the limitations of conducting impact studies in non-random samples may be widely understood, they are not uniformly acknowledged in the reports on the findings from these studies. In a review of 19 National Center for Education Evaluation (NCEE) funded studies (see details below and Appendix Table 1), we found that 6 studies did not discuss the idea of having an explicit target population, and 8 of them did not discuss generalizability or external validity. Of the 13 studies that identified one or more target populations, 4 did not present any evidence on the differences between participating districts or schools and the target population specified. Thus, although the majority of studies at least acknowledged the potential for lack of generalizability, many did not explicitly specify a target population. And even among those that did specify a target population, not all presented evidence that could help readers assess the generalizability of study findings to that population.

It is an open question whether non-random site selection typically has a substantial influence on findings from evaluations of educational interventions. But some initial evidence suggests that purposive site selection can yield impact estimates that are biased for the populations of interest to policy makers. Bell et al. (2016) used data from a rigorous evaluation of Reading First —a Federal education program— to compare the impact in a population of school districts to the impacts in 11 purposive samples of districts that participated in rigorous evaluations of other interventions. The goal of that study was to estimate how much bias would have resulted from evaluating Reading First in a purposive sample of sites. Their estimates suggest that the impact estimates would have been biased downward by 0.10 standard deviations. This suggests that non-random site selection can have a substantial influence on evaluation findings and produce results that are misleading for the intervention’s target population.

Given how schools and districts are selected for educational evaluations, it is reasonable to ask how broadly the evaluation results generalize to other schools and districts. For example, given that charter school laws vary by state, findings from studies in Florida may not be predictive of charter school effects in Michigan. Research conducted in schools or districts near a major research university may or may not be predictive of an intervention’s effects when implemented elsewhere. And large-scale “national” studies conducted in a range of non-randomly selected schools and districts across the country may or may not provide valid national estimates of the average effects of the intervention.

As shown in earlier work (Olsen et al., 2013), external validity bias may arise if the characteristics of sites included in an evaluation differ from those in the population of interest in a way that correlates with impact magnitude—i.e., if site-specific impacts vary with those same characteristics. Although there is growing research investigating the extent of treatment effect heterogeneity (e.g., Schochet, Puma, & Deke, 2014; Weiss, Bloom, & Brock, 2014) there is very little evidence regarding variation in impacts between the types of districts that do and do not participate in educational evaluations. This paper provides some of the first evidence of how districts that participate in evaluations differ from those that do not on the background characteristics of their students, schools and communities. Bell et al. (2016), cited above, provides indirect evidence on how these characteristics may translate into differences in impacts and lead to external validity bias.

Despite the uncertainty about whether findings from studies conducted in selected places generalize to other places, to our knowledge no research has been conducted on whether—and if so, how—schools and districts that participate in RCTs of educational interventions differ from the broader set of schools and districts that could adopt these interventions. This paper begins to close that gap. In the remainder of this section, we state the question addressed by this paper, consider the policy decisions that educational evaluations are designed to inform, and define the target populations for different policy decisions.

1.1 Question Addressed by this Paper

This paper addresses the research question: How do the districts included in large-scale educational evaluations differ from the broader populations of potential interest to policymakers or local education decision-makers? The answer to this question will help to assess whether study findings are likely to generalize to the broader population of sites that could be affected by the policy decisions that motivate the study. Policymakers can make more informed policy decisions if they have evidence on the effects of the programs and interventions for the population potentially affected by these policy decisions. The answer to this question could also inform site selection in future studies if the goal is to produce evidence that is generalizable to a broader set of school districts than have typically been included in prior studies.

1.2 Populations of Interest to Policymakers

In this paper, we compare school districts that have participated in 11 federally-funded evaluations of educational programs or interventions to three potential populations of interest to policymakers. Each of these populations consists of students that are potentially affected by a policy decision that the evaluation is intended to inform.

In our assessment, federally-funded evaluations in education are designed to inform three types of policy decisions:

1. Federal decisions on whether to continue or cancel a federal program. To inform these types of decisions, studies are designed to estimate the effects of the program relative to its absence. Examples include completed evaluations of Upward Bound (Seftor, Mamun, and Schirm, 2009), Head Start (Puma et al., 2010), and Reading First (Gamse et al., 2008).

2. Decisions on whether incorporating a particular intervention within a federal program will improve that program. To inform these types of decisions, studies are designed to estimate the effects of an innovation that could be implemented within a federal program or adopted by local grantees funded through the program. Examples include completed evaluations of interventions tested within the Smaller Learning Communities Program (Somers et al., 2010) and 21st Century Community Learning Centers (Black et al., 2009).

3. Local decisions on whether to adopt a particular intervention. Many federally funded education studies are not explicitly designed to inform federal policy decisions. Rather, they are designed to help schools and districts decide which interventions to adopt. Examples include completed evaluations of teacher induction programs (Glazerman et al., 2008; Isenberg et al., 2009; Glazerman et al., 2010) and education technology products (Dynarski et al., 2007; Campuzano et al., 2009).

For all three types of studies, we define the population of policy interest to include all districts across the country that would be affected by the related policy decision. For studies that estimate the effect of continuing or cancelling a federal program or the effect of incorporating a new intervention within a federal program ((1) and (2) above), we define this population to include the districts that receive (or could receive) federal funding to operate that program. We term this the “population of interest for the program funder”.

The third type of policy decision noted above – decisions by local school districts to adopt an intervention – could be made by virtually any school district for which the intervention is appropriate. We term this population the “population of potential implementation” and include in it all school districts in the country where the intervention could be implemented – e.g., for a variant on a third-grade reading curriculum, we might include all school districts that include third-grade classrooms; for interventions related to special education, we might include all districts with special education classes. In some cases interest may also be in a particular subset of this broad population of potential implementation. For example, education policymakers’ concerns are often particularly focused on disadvantaged or low-performing students and districts and thus many of the interventions under study are targeted towards those groups. Below we discuss how we operationalize this to compare participating districts to the national population of potential implementation as well as to a subset of those districts defined by a level of disadvantage, labeled the “population of disadvantaged districts.”

There are multiple ways of defining these populations more precisely. For example, the national population of potential implementation could be defined broadly to include all districts in which it would be feasible to implement the intervention (e.g., districts with some minimal number of English Language Learners, for an intervention targeted to them) or more narrowly to include districts in which it might be particularly likely the intervention would be implemented (e.g., districts with a large share of English Language Learners). Similarly, the population of disadvantaged districts could be defined more broadly to include all districts with some minimum number of disadvantaged students or more narrowly to include only the most disadvantaged districts nationwide. Finally, the population of policy interest for the program funder could be defined to include only those districts that currently receive funding from the program, or it could be defined more broadly to also include districts that may receive program funding in the future if the program were to continue (e.g., those districts nationwide that would meet some eligibility criterion for the program, such as having a high proportion of low-income students). Of course, it may be possible to define some of these populations in theory but not possible to identify them in practice. The approach we take in this paper to defining these populations is described in Section 2.

We recognize that, from a policy perspective, populations of interest should be defined in terms of students who are potentially affected by policy decisions because policy interest in education is focused on students and their outcomes. At the same time, educational evaluations typically select samples of students in a multi-stage process that involves selecting districts, then selecting teachers or schools within districts, and finally selecting students that are served by those teachers or schools. This paper focuses on the types of districts that participate in rigorous evaluations of educational interventions for both pragmatic and principled reasons. The pragmatic reason for this focus is that identifying the schools, teachers, or students that participated in evaluations sponsored by IES is not permitted under existing IES data release agreements (per the IES statute). The more principled reasons are that (1) district characteristics may moderate the effects of educational interventions and (2) the selection of particular districts can substantially influence the types of students that participate in the evaluation—and thus the populations of students to which evaluation results can be generalized. Therefore, for this paper, we define populations of interest in terms of the districts that include students who could potentially be affected by the policy decision that the evaluation is intended to inform.

We also recognize that a single study can inform multiple policy decisions; therefore, there are typically multiple populations of interest for each study. We reflect this in the current study by comparing the same samples to multiple populations of interest.

1.3 Overview of the Paper

In this paper, we compare the school districts included in 11 large-scale education evaluations with multiple populations of policy interest. These evaluations include all of the large-scale impact studies conducted by the National Center for Education Evaluation and Regional Assistance (NCEE) at the Institute of Education Sciences (IES) that had selected school districts by 2011 and for which we were able to identify the participating districts. We focused on NCEE-funded impact evaluations because NCEE has played a prominent role in the growth of education impact evaluations that have high internal validity (e.g., random assignment or regression discontinuity). However, like most other rigorous impact studies, NCEE-funded impact evaluations have typically been conducted in a sample of sites that were not selected randomly—or even nonrandomly—to be representative of a broader population on key characteristics. Each of the 11 studies is either a randomized control trial (RCTs) or used a regression discontinuity design (RDD). We begin with simple univariate comparisons of district characteristics between study samples and populations of policy interest, using data drawn from the Common Core of Data and other sources, with each district weighted equally in each study and each study weighted equally in an overall average. We then show similar comparisons for the individual studies. Finally, we compare the prevalence of certain profiles of school districts in the United States with the proportion of those types of districts actually participating in the 11 evaluations.

We find that the districts that participate in the 11 large-scale evaluations differ from those in the target populations in a number of ways; most notably, they are much larger and much more urban. These results hold for both the 11 studies taken as a group and for individual studies. Of course these findings may not generalize to all evaluations, but provide among the first formal comparisons of districts that participate in rigorous educational evaluations and potential target populations of interest.

Section 2 describes our data sources. Sections 3 and 4 describe the statistical methods and results of the analyses, respectively. The final section discusses the results.

2. Data Sources and Analysis Plan

In this section we describe our data sources and the analysis methods used to quantify differences between the districts that participate in educational evaluations and the potential target populations of the interventions under study.

2.1 Districts Included in the Study

We use the Common Core of Data (CCD) as a source of information on all public school districts nationwide to define the populations of interest. The CCD, maintained by the U.S. Department of Education’s National Center for Education Statistics, provides annual fiscal and non-fiscal data about all public schools, public school districts and state education agencies in the United States (http://nces.ed.gov/ccd/). The CCD district/agency and school universe surveys—incorporated into the national database each year—are the primary data sources for the variables used in this paper. In addition to the district-level CCD file, we also use the school-level CCD file to create some district averages.

As a first step, we narrowed attention to all US districts in the CCD that were in operation during the 2004–2005 school year. The 2004–2005 school year was used because that was the time period during which many of the 11 studies utilized were recruiting districts to participate in their evaluations. Figure 1 details the process by which districts and schools are excluded and the number excluded at each stage. (Note that although the file is a district-level file, individual schools not in operation during the 2004–2005 school year are also excluded and aggregate district-level variables recalculated without them). The following types of districts were excluded from the analysis:

• -Districts and schools located outside of the 50 U.S. states.
• -Districts and schools that were non-operational in 2004–2005.
• -“Non-regular” schools, including special education, vocational, and other types of alternative schools that are not typically relevant for the interventions under study.
• -“Non-regular” districts. These include regional administrative service centers without students, special needs agencies, districts with no school counts or no pupil expenditures or teachers, and districts composed of only non-regular schools or schools with more than 50% of students classified as non-regular.

Figure 1.

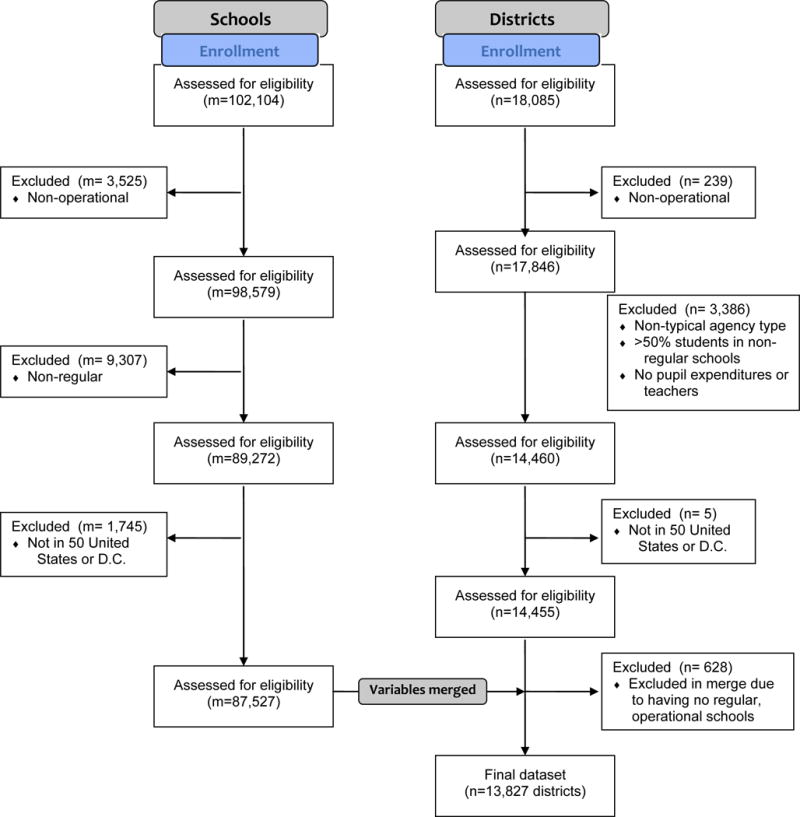
Flow chart of school and district inclusion

2.2 Characteristics of Districts

The primary variables of interest are district characteristics from the CCD, which we supplement with additional variables, as detailed below. Broadly, variables are selected because they are hypothesized to be related to whether or not districts are included in rigorous evaluations and because they may—in some studies—be related to the impact of the intervention. In the text below, we present the justification for inclusion of each of these variables. Details of how measures are created or obtained are in the Appendix.

In particular, we select measures of:

• ■District size. Larger districts may be included in impact evaluations more often than smaller districts because they offer more schools and students that can be included in the sample, thereby making it easier to achieve any given target sample. Measures of district size in our analysis include the number of schools, teachers, and students in the district.
• ■District resources. School districts with more resources may be better able to support evaluations. On the other hand, they may be less in need of the interventions that some evaluations offer to participating schools. Measures of district resources in our analysis include the student-to-teacher ratio and per pupil expenditures.
• ■Student achievement and demographics. Many interventions target disadvantaged and low-performing students. Evaluations of these interventions may target districts with a large share of disadvantaged and low-performing students to maximize the size of the potential student sample. Measures of student disadvantage in our analysis include the percent of students who are English Language Learners, eligible for Free or Reduced Price Lunch, or non-white; and the percent of schools that are eligible to receive Title I funding, are designated School-wide Title I schools, and/or fail to make Adequate Yearly Progress. Finally, they also include average NAEP scores for students in the state.
• ■Location. Districts in urban areas and districts that are located close to major evaluators of educational programs may be attractive to evaluators in recruiting schools to participate in an evaluation. Urban schools frequently combine unusually large schools with a high concentration of disadvantaged students and, in many cases, limited resources. Measures of location in our analysis include urbanicity and distance to cities that include major education evaluation firms (these firms are concentrated in eastern seaboard cities and San Francisco).
• ■Political leaning. Given that most of the studies examined were conducted during the George W. Bush Administration, it is possible that districts from Republican districts would be more amenable to cooperating with federal evaluations than Democratic districts. Alternatively, Republican districts may be generally less inclined to cooperate with the federal government, regardless of the party affiliation of the current president. We include a single measure of political leaning: the percentage of the two-party vote that voted Republication in the 2000 and 2004 Presidential elections in the county in which the district is located.
• ■Access to student-level administrative data. Evaluators may prefer to include districts from states that have well-developed and accessible administrative data systems on students and their scores on standardized tests. Measures of access to student-level administrative data, which are obtained from the Data Quality Campaign, include whether the state has (1) a purposeful research agenda and collaboration with universities, researchers, or intermediary groups to explore the data for useful information, (2) a unique statewide student identifier that connects student data across key databases, and (3) the ability to match individual students’ test records from year to year.

2.3 Impact Studies Used to Identify Purposive Samples

To compare samples of school districts included in rigorous impact studies with the populations of interest for these studies, we identified a set of studies that were each conducted in a purposive sample of districts. For this sample, we relied on federal studies conducted by the National Center for Education Evaluation and Regional Assistance (NCEE) in the Institute of Education Sciences (IES). The founding of the IES led to a boom in federal education studies that used random assignment or regression discontinuity designs—designs that provide rigorous causal evidence on the effects of educational interventions but typically rely on purposive samples.

To identify this set of studies, we first identified the 19 NCEE-sponsored impact studies of K-12 educational interventions that had either been completed or were ongoing and had identified participating schools and districts as of the point in 2011 when the list of studies was compiled. For our purposes, it is critical to note that all of these studies selected a purposive sample of sites: none of them selected a representative sample of school districts for inclusion in the study.¹ For a list of these studies along with citations to the final reports, see Appendix Table 1. For a description of these studies, as well as studies initiated by the NCEE since 2011, see http://ies.ed.gov/ncee/projects/evaluation/index.asp.

Consistent with NCEE policy, the published reports from these studies do not identify the participating school districts. To identify the districts that participated in each of these studies, we contacted each study’s Project Director and requested this information. For 11 of these studies, we were able to obtain lists of the school districts that participated in the studies.² The Project Directors for the other 8 studies were unable to provide the list of participating school districts because their agreements with school districts prevented doing so or because identifying a school district would effectively identify the schools that participated in the study (which would be a violation of the federal law under which the Institute of Education Sciences was established).³ The 11 studies included were either randomized control trials or used regression discontinuity designs; they were carried out by five different research organizations. We note that these studies may not be representative of all educational evaluations.

2.4 Populations of Interest for these Impact Studies

As described in Section 1, the population of interest depends on the policy action that the study could inform. Since all of these studies could influence decisions about whether to adopt an intervention locally, we first define the national population of potential implementation related to a given study broadly, to include all school districts that during the 2004–2005 school year served students at the grade levels studied in that evaluation. The focus on grade level, without additional criteria, is motivated by our assessment that most educational programs or interventions are generally feasible to implement in any district or school that serves students at the right grade levels. Grade level information for each school district was obtained from the Common Core of Data. We label these the “national populations of potential implementation” (plural “populations” because the population of interest is defined separately for each study).

We then define the populations of disadvantaged districts based on a standard measure of disadvantage—whether students were eligible for free or reduced price lunches (FRPL). In particular, we define this population to be those districts within each study’s population of potential implementation that lie in the quartile with the highest percentage of students eligible for FRPL nationwide. We focus on this relatively narrow group of the most disadvantaged districts to see if we can—to preview our results—reduce the differences observed between the purposive samples and the broad, national populations of potential implementation.

In addition, for seven studies that tested the effects of a federal program—or an intervention within a federal program—we also identify the populations of policy interest for the program funder. In particular, we identified the school districts that received funding from the relevant federal program at approximately the time the study would have selected school districts to participate in the research. This set of districts could reasonably be argued to be the primary population of policy interest to the U.S. Department of Education (which funded all of these studies) at that time, and these are the districts that would likely be most immediately affected by the federal policy decisions that these studies inform. To identify the school districts that received federal funding, we use publicly-reported information, most often from the websites associated with the federal programs involved. One challenge in identifying both the purposive samples and the populations of policy interest is that the “sites” that receive federal funding and implement educational programs are not always school districts; sometimes they are entities such as non-profit organizations. To address this challenge, we matched non-district entities to one or more school districts with which they are likely to partner in delivering services based on their location (see Appendix B for details). Across the 7 studies that we could associate with a federal program, the proportion of the national population of potential implementation that is in the population of policy interest to the program funder varies considerably, with an average of 30% but a range from 1% to 87%. Note again that the population of policy interest to the program funder is defined separately for each study.

2.5 Statistical Analysis

The primary analysis of interest is a comparison of the districts that participate in the 11 large-scale educational evaluations in our sample with the potential target populations. Results are combined across studies as described below. To do this comparison we used permutation-based analyses that compare the mean of each characteristic observed in each study with the distribution of the mean that would be obtained if in fact each study selected districts randomly from its target population. This comparison allows us to directly test the hypothesis of interest and combine information across studies without making parametric modeling assumptions such as normality or assumptions about asymptotics.⁴

To be more specific, for a given district characteristic X the test statistic examined is the average of the difference in means between each study’s mean ( ${\overline{x}}_i$; studies indexed by i) and the mean of X in that study’s population of interest ( ${\mu }_i$), with each study weighted equally:

$$\mathrm{\Delta }=\frac{1}{11}{\displaystyle \sum }_{i=1}^{11}({\overline{x}}_i-{\mu }_i).$$ (1)

To test the significance of the observed test statistic as compared to a random selection of districts, we randomly selected districts for each study, using the number of districts actually included in each study. For each draw we thus had 11 study samples generated by random sampling, from which we calculated the statistic Δ in Equation (1). We then repeated this 30,000 times and compared our observed test statistic (from the actual 11 studies) with the distribution of test statistics obtained by random selection. We computed a p-value as the percentage of random draws in which the absolute value of the test statistic was larger than that observed in our data. In other words, the p-value reflects the answer to the question, “If in fact each of the studies selected districts randomly from their target populations, how likely would we be to observe a value as large or larger (in absolute value) than the value we observe?” This analysis was repeated three times, once for each of the populations of interest (the population of potential implementation, the disadvantaged population, and the population of policy interest). Thirty thousand draws was determined to be sufficient to obtain stable results.

Because these comparisons average across studies for each characteristic, they may mask important variability among the studies. For example, if some studies systematically “undersample” districts with a particular characteristic while other studies systematically “oversample” these districts, the positive and negative differences may cancel out across studies even if there are large differences in each study. We thus provide two additional comparisons. First, for each of the three populations of interest we repeat the permutation test described above, but replace the difference in means between the study and the population with the absolute value of that difference. Second, we present forest plots that show, for selected characteristics (and the full set of characteristics in Appendix Figure 1), the results from the permutation test described above, but separately for each study. To illustrate statistical significance graphically, rather than with p-values, the forest plots show for each study the 95% confidence interval calculated from 10,000 random samples along with the observed difference between the study mean and the mean in its corresponding national population of potential implementation. We then show, for each variable, the number of studies with an observed mean that lies below the confidence interval obtained from random sampling, the number of studies with an observed mean that lies within the confidence interval, and the number of studies with an observed mean that lies above the confidence interval. This allows us to quickly see whether the studies appear to have differences from their populations in the same directions or if some have positive differences while others have negative differences. These forest plots are presented just for the national population of potential implementation.

To look at how combinations of factors may impact district inclusion we also present descriptive statistics that summarize how likely different “profiles” of districts are to be included in rigorous evaluations. For districts defined by size, location, and performance, we compare the proportion of districts of each type in the US population with the proportion of that type of district in the 11 studies.

3. Results

This section presents results comparing the districts that participated in 11 large-scale IES-funded evaluations to the three populations of policy interest defined earlier.

3.1 Comparison with national populations of potential implementation and the national populations of highly disadvantaged districts

Table 1 presents the average characteristics of the districts participating in the large-scale rigorous IES-funded evaluations in our sample compared to the population of potential implementation for the intervention being evaluated (roughly, districts across the United States that cover the grades for which each intervention is relevant) and, separately, to the subpopulation of highly disadvantaged districts, based on percent of students eligible for free or reduced price lunch (FRPL). We discuss each in turn. In general, it appears that the 11 IES-funded evaluations tended to focus on large, urban districts with relatively low-performing students.

Table 1.

Comparisons of districts participating in rigorous educational evaluations with the national population of potential implementation and a subpopulation of the most disadvantaged districts (N=11 studies)

District Characteristic	Sample Mean or Percentage (average across 11 study samples)	National Population of Potential Implementation	National Population Std. Mean Diff1,2	Disadvantaged Districts	Disadvantaged Population Std. Mean Diff1,2
District Size
Number of schools	127	6	6.96***	8	6.89***
Number of teachers	5,308	213	7.08***	248	7.03***
Number of students	98,747	3,503	6.67***	4,077	6.63***
District resources
Per pupil expenditures	$10,681	$10,895	−0.04	$10,532	0.03
Number of students per teacher	16.47	14.50	0.44***	14.39	0.46**
Student demographics
% of students who are non-white	64	22	1.64***	46	0.71***
% of students who are English language learners	11	4	0.69***	10	0.15
% of students eligible for free or reduced price lunch	55	38	0.74***	68	−0.59***
% of schools eligible for Title I	63	64	−0.01	81	−0.54***
% of schools with school-wide Title I	52	26	0.70***	61	−0.25**
Student achievement
State grade 4 NAEP math scores	237.50	238.38	−0.17*	235.69	0.35***
State grade 8 NAEP math scores	277.23	279.52	−0.36***	275.63	0.25**
State grade 4 NAEP reading scores	217.74	219.21	−0.25***	215.82	0.33***
State grade 8 NAEP reading scores	260.08	262.96	−0.49***	259.38	0.12
% of schools not meeting adequate yearly progress ‘04–‘05	39	16	0.86***	27	0.44***
District location
Miles to San Francisco	1,839	1,685	0.22**	1,459	0.54***
Miles to the Northeast	1,019	1,049	−0.04	1,336	−0.44***
City (%)	60	5	2.47***	8	2.34***
Suburb (%)	33	26	0.16*	15	0.40***
Town (%)	4	12	−0.26***	15	−0.35***
Rural (%)	4	57	−1.07***	62	−1.16***
Political leaning
County average % Republican of two-party vote (2000, 2004)	46	57	−0.84***	57	−0.89***
Data access measures
In states implementing DQC Action 83 in 2009 (%)	27	32	−0.11	34	−0.16*
In states with DQC essential element 14 in 2005 (%)	61	61	0.00	71	−0.20**
In states with DQC essential element 35 in 2005	60	53	0.14	67	−0.14

¹Standardized Mean Difference, defined as the difference in means divided by the standard deviation of the variation in the population

²Asterisks denote significance levels for comparison of average differences (proportion of 30,000 random samples with larger mean differences than those observed);

^*for 0.05 <= p < 0.10,

^**for 0.01 <= p < 0.05,

^***for p <= 0.01.

All p-values are for two-sided tests.

³DQC Action 8 is defined as: “Develop a purposeful research agenda and collaborate with universities, researchers, or intermediary groups to explore the data for useful information.” (www.dataqualitycampaign.org)

⁴DQC essential element 1 is defined as: “A unique statewide student identifier that connects student data across key databases across years”

⁵DQC essential element 3 is defined as: “The ability to match individual students’ test records from year to year”

The districts included in the 11 evaluations are much larger on average than those in the national populations of potential implementation (see columns 1 and 2 in Table 1): 127 schools per district compared to only 6 schools per district in the populations (p<0.001). As might be expected, the number of students per district differs in a similar way, with approximately 100,000 students per district in the average participating district and approximately 3,500 students in the average district in the national populations (p<0.001).

The findings for district resources are mixed. Total expenditures per pupil were quite similar between participating districts and districts in the national populations of potential implementation ($10,681 vs. $10,895; p=0.63). However, the student-to-teacher ratio was higher for participating districts than for districts in these populations (16.47 vs. 14.50; p<0.001).

The types of students in the participating districts also differ from students in the national populations. Higher percentages of students in the participating districts are non-white (64% vs. 22%; p<0.001), English Language Learners (11% vs. 4%; p<0.001), and eligible for free or reduced price lunch (55% vs. 38%; p<0.001). In addition—reflective of their more disadvantaged students—a larger share of the schools in participating districts have school-wide Title I (52% vs. 26%; p<0.001) than the national populations of potential implementation.

Compared to the national populations of potential implementation, participating districts come from states with lower than average student achievement, based on measures from the National Assessment of Educational Progression (NAEP). However, despite being statistically significantly different, the differences themselves are not very large, on the order of 1–3 test score points. There is a larger difference between participating districts and the populations in the percentage of schools in a district making adequate yearly progress (AYP); in 2004–2005 39% of schools in participating districts did not make AYP, as compared to 16% of schools in the populations of potential implementation (p<0.001).

There are also differences in the locations of participating districts compared to the average district in the national populations of potential implementation. In particular, participating districts are much more likely to be located in a city (60% vs. 5%; p<0.001), somewhat more likely to be in a suburb (33% vs. 26%; p=0.08), and much less likely to be in a rural area (4% vs. 57%; p<0.001).

There are also differences in the political environments of the counties in which participating districts are located, as compared to the national populations of potential implementation: people in participating districts were much less likely to vote for the Republican candidate in the 2000 and 2004 Presidential elections than were people in the national populations of potential implementation (46% vs. 57%; p<0.001).

Interestingly, we do not see evidence that state-level data quality differs between participating districts and districts in the national populations of potential implementation. Participating districts are not, on average, more likely to come from states with either established research collaborations or unique statewide student identifiers. This indicates that evaluators of these NCEE-sponsored impact evaluations apparently were not selecting districts based on ease of access to data from state data systems.

Table 1 also compares the average characteristics of the districts participating in these studies to subpopulations of disadvantaged districts—those in the top quartile nationwide on the percentage of students eligible for FRPL. The finding that participating districts tend to be more disadvantaged than the national populations of potential implementation reinforces the argument for considering this subpopulation.

Almost by construction, focusing on this subpopulation substantially reverses the earlier finding that participating districts have a higher share of students eligible for FRPL than districts in the national populations: this percentage is lower for participating districts than for the subpopulation of disadvantaged districts (55% vs. 68%; p<0.001). Focusing on this subpopulation also closes the gap in the percentage of students who are English language learners (11% vs. 10%; p=0.15). Finally, focusing on this subpopulation reduces but does not close the gap in the percentage of schools in the district that do not make adequate yearly progress (39% vs. 27%; p<0.001).

However, just as striking are the findings that do not change when we focus on the subpopulation of disadvantaged districts. In particular, we still find that participating districts are much larger on average (e.g., for number of students, 98,747 vs. 4,077; p<0.001) and much more likely to come from urban areas (60% vs. 8%; p<0.001) than districts in the populations. We also find that participating districts have higher student-to-teacher ratios, are more white, and lean more to the Democratic Party—just as we found in the comparison to the full national populations of potential implementation (see Table 1 for the full set of results).

3.2 Comparison with the population of policy interest to the program funder

Table 2 compares the districts that participate in a given evaluation with the population of districts most likely to be affected by a policy decision made by the program funder: those districts currently receiving funding for that program from the federal government. (This analysis is restricted to the seven studies of interventions tested in the context of programs administered by the federal government). We might expect the sample to be more similar to the population of policy interest to the program funder than to the population of potential implementation if the goals of the program funder influence the selection of schools and districts for the evaluation.

Table 2.

Comparisons of districts participating in rigorous educational evaluations of programs funded by federal grant programs with the population of policy interest of the program funder (N=7 studies)

Characteristics	Sample Mean or Percentage (average across 7 study samples)	Population of Policy Interest	Std. Mean Diff.1,2
District Size
Number of schools	89	22	3.90***
Number of teachers	3,696	857	3.95***
Number of students	67,122	15,188	3.64***
District resources
Per pupil expenditures	$10,864	$10,329	0.10
Number of students per teacher	16.16	16.45	−0.07
Student demographics
% of students who are non-white	58	40	0.69***
% of students who are English language learners	8	10	−0.20
% of students eligible for free or reduced price lunch	51	44	0.30***
% of schools eligible for Title I	63	65	−0.06
% of schools with school-wide Title I	48	37	0.30***
Student achievement
State grade 4 NAEP math scores	238.22	237.00	0.24**
State grade 8 NAEP math scores	277.70	277.76	−0.01
State grade 4 NAEP reading scores	218.76	216.87	0.32***
State grade 8 NAEP reading scores	260.94	260.24	0.12
% of schools not meeting adequate yearly progress ‘04–‘05	36	23	0.48***
District location
Miles to San Francisco	1,920	1,465	0.65***
Miles to the Northeast	942	1,316	−0.53***
City (%)	48	24	1.07***
Suburb (%)	41	34	0.17
Town (%)	6	9	−0.10
Rural (%)	5	33	−0.56***
Political leaning
County average % Republican of two-party vote (2000, 2004)	48	54	−0.44***
Data access measures
In states implementing DQC Action 83 in 2009 (%)	23	32	−0.22**
In states with DQC essential element 14 in 2005 (%)	64	62	0.04
In states with DQC essential element 35 in 2005	62	58	0.08

¹Standardized Mean Difference, defined as the difference in means divided by the standard deviation of the variation in the population

²Asterisks denote significance levels for comparison of average differences (proportion of 30,000 random samples with larger mean differences than those observed);

^*for 0.05 <= p < 0.10,

^**for 0.01 <= p < 0.05,

^***for p <= 0.01.

All p-values are for two-sided tests.

³DQC Action 8 is defined as: “Develop a purposeful research agenda and collaborate with universities, researchers, or intermediary groups to explore the data for useful information.” (www.dataqualitycampaign.org)

⁴DQC essential element 1 is defined as: “A unique statewide student identifier that connects student data across key databases across years”

⁵DQC essential element 3 is defined as: “The ability to match individual students’ test records from year to year”

Table 2 shows many of the same patterns as seen in Table 1 for the national populations of potential implementation, with somewhat less extreme differences. For example, while Table 1 showed that the average participating district had 20 times as many schools as the average district in the national populations of potential implementation, Table 2 shows a four-fold difference (89 schools vs. 22 schools; p<0.001) between participating districts and the populations of policy interest to the funder. Differences between participating districts and the populations of policy interest remain statistically significant for the percentage of non-white students and for the percentage of students eligible for free or reduced price lunch but are smaller in absolute value. However, there is no longer a significant difference in the percentage of students who are English language learners.

Fewer differences also arise with respect to academic performance when comparing participating districts to the populations of policy interest to the funder rather than the national populations of potential implementation. Participating districts are in states that have slightly higher Grade 4 test scores than districts in the populations of policy interest, rather than lower, while Grade 8 NAEP test scores are no longer significantly different.

Table 2 shows differences in the locations of participating districts, compared with the populations of policy interest to the funder. In terms of urbanicity, the differences again are less stark than when comparing to the populations of potential implementation. For example, 48% of participating districts are in urban areas compared with 24% of districts in the population of policy interest (p<0.001). Finally, as in Table 1 we do not see, on average, differences in measures of data quality or availability between participating districts and the populations of policy interest to the funder.

3.3 Magnitude of the differences between Samples and their Populations

Average differences in characteristics between participating districts and the target populations in Tables 1 and 2 may be muted by offsetting contributions from the multiple studies included in the averages if positive and negative differences cancel each other out. To counter this tendency, we also performed tests of statistical significance using permutation tests based on the average of the absolute value of the difference between a particular evaluation sample and the population mean. In these tests, positive and negative differences compound rather than cancel. The results of these tests are shown in Appendix Tables 2–3.

We generally see similar patterns of results when considering absolute differences, primarily because most of the studies differ from the reference population in the same direction for a given characteristic. Thus, taking the absolute value of the difference before averaging makes for very little change in the magnitude of the average (see details below and the forest plots in Appendix Figure 1). The exceptions are for some of the locational measures and the data access measures for which no difference was seen based on the simple average but for which significant differences emerge using the average of absolute differences. In particular, distance from the northeastern United States and percent suburban become significant for some population comparisons while percent of students living in towns loses significance in the comparison with the populations of potential implementation. Also, almost all data access measures show significant absolute differences between the evaluation districts and the two populations whereas before almost none did.

It is also informative to examine the 11 studies individually compared to their national populations of potential implementation. Figure 2 provides forest plots on individual studies for the difference between the study sample’s districts and the national populations of potential implementation. Four illustrative characteristics are presented in Figure 2: those with the largest, median, and two smallest p-values from the mean difference p-value column in Table 1 (DQC element 1; grade 8 math scores; number of teachers per district and proportion of schools with school-wide Title 1). For these characteristics, very rarely do we see positive and negative differences for individual studies “canceling out” in the arithmetic average across studies to create small or null differences overall. Similar forest plots for all of the variables are shown in Appendix Figure 1.

Figure 2.

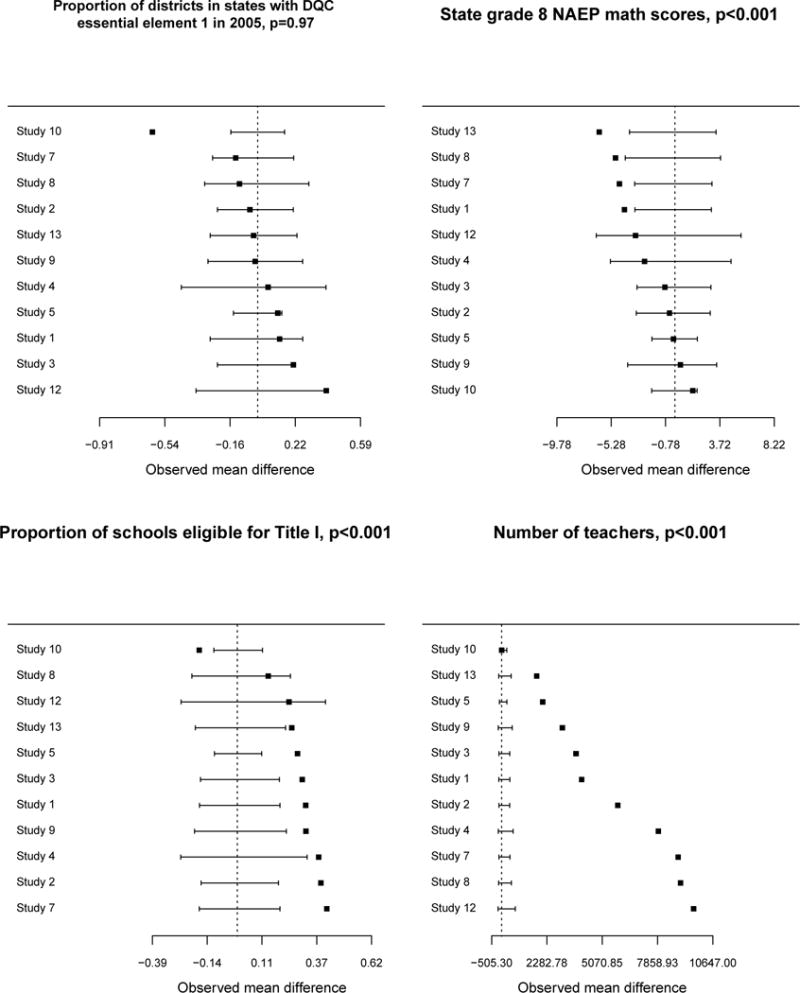
Forest plots of characteristics of participating districts compared with random samples from national populations of potential implementation. Four variables chosen to reflect range of p-values from Table 1: Two with smallest p-values (number of teachers, proportion school-wide Title 1), one with the largest p-value (% of districts in states with state-wide student identifiers), and one with the median p-value (grade 8 math test scores).

Table 3 summarizes the information in the forest plots by showing, for each characteristic, the number of studies for which the observed sample mean was less than the 95-percent confidence interval that would be obtained if districts were selected randomly from their national populations of potential implementation, within the confidence interval, or above the confidence interval. For example, when looking at district size, 91% (10 of 11) studies included districts whose average size (in terms of number of students, number of schools, or number of teachers) was significantly larger than districts in the populations of potential implementation; i.e., the study mean fell above the 95% interval that would be obtained had districts been selected randomly. As would be expected, for characteristics for which minimal differences were found in Table 1, the studies spread across the three columns of Table 3 or concentrate primarily in the middle column, where study means fall within the confidence interval generated by random sampling. For example, 91% of studies had average percentage suburban districts within the confidence interval obtained by random sampling, and for statewide Grade 8 NAEP reading scores, 45% of studies had a mean below the confidence interval, 45% in the confidence interval, and 9% above the confidence interval.

Table 3.

Summary of distribution of test statistics for individual studies, in comparison to samples selected randomly from the national population of potential implementation.

Characteristics	% studies < 95% CI	% studies in 95% CI	% studies > 95% CI
District size
Number of schools	0	9	91
Number of teachers	0	9	91
Number of students	0	9	91
District resources
Per pupil expenditures	0	100	0
Number of students per teacher	0	45	55
Student demographics
% of students who are non-white	0	9	91
% of students who are English language learners	9	45	45
% of students eligible for free or reduced price lunch	9	27	64
% of schools eligible for Title I	0	100	0
% of schools with school-wide title I	9	18	73
Student achievement
State grade 4 NAEP math scores	18	73	9
State grade 8 NAEP math scores	36	64	0
State grade 4 NAEP reading scores	27	64	9
State grade 8 NAEP reading scores	45	45	9
% of schools not meeting adequate yearly progress ‘04–‘05	0	18	82
District location
Miles to San Francisco	0	73	27
Miles to the Northeast	9	82	9
City (%)	0	9	91
Suburb (%)	0	91	9
Town (%)	9	91	0
Rural (%)	91	9	0
Political leaning
County average % Republican of two-party vote (2000, 2004)	64	36	0
Data access measures
In states implementing DQC Action 81 in 2009 (%)	9	91	0
In states with DQC essential element 12 in 2005 (%)	9	91	0
In states with DQC essential element 33 in 2005	9	73	18

¹DQC Action 8 is defined as: “Develop a purposeful research agenda and collaborate with universities, researchers, or intermediary groups to explore the data for useful information.” (www.dataqualitycampaign.org)

²DQC essential element 1 is defined as: “A unique statewide student identifier that connects student data across key databases across years”

³DQC essential element 3 is defined as: “The ability to match individual students’ test records from year to year”

3.4 Comparisons of district profiles between study samples and the US population of districts

To provide a broader view of how the districts in the 11 studies differed from those of a particular target population in a more holistic way, we combine information across three measures to form profiles based on district size (number of students), performance (percentage of schools not meeting Adequate Yearly Progress in 2004–2005), and location (urbanicity). We compare the districts that participated in at least one of the 11 evaluations with 1) districts across the US, and 2) districts in the top quartile of the percentage of students eligible for free or reduced price nationwide. For these comparisons we use the US population of districts as the target population for every study. This is done because the calculations are not straightforward if each study has its own population; in addition, the national populations of potential implementation generally overlap approximately 95% with the population of districts across the US.⁵ For the various combinations of characteristics that appear in the national population, Table 4 summarizes the US national population of districts and the US population of disadvantaged districts compared to districts in the 11 impact studies. The significance levels for differences in proportions having particular profiles are calculated using the permutation-based test procedure described earlier.

Table 4.

Population prevalence of district profiles compared with percentage in 11 impact studies¹

Type	National Population %	Sample %	Disadvantaged Population %
Urban
Small and Medium, Low Performing	0.05*	0.00	0.12*
Small and Medium, Mid Performing	0.01	0.00	0.00
Small and Medium, High Performing	0.25*	0.00	0.26*
Large, Low Performing	1.94*	24.74	4.37*
Large, Mid Performing	2.10*	22.63	3.01*
Large, High Performing	0.77	2.11	0.43
Suburban
Small and Medium, Low Performing	1.69	3.16	2.78
Small and Medium, Mid Performing	1.04*	0.00	1.04*
Small, High Performing	1.61*	0.00	0.81*
Medium, High Performing	5.39	4.74	1.27*
Large, Low Performing	3.87*	12.11	5.81*
Large, Mid Performing	5.89	8.95	2.63*
Large, High Performing	6.65	10.53	0.95*
Town
Small and Medium, Low Performing	1.19*	0.00	2.00*
Small and Medium, Mid Performing	1.20*	0.00	1.56*
Small and Medium, High Performing	4.51*	0.00	3.88*
Large, Low Performing	1.33	2.11	2.66
Large, Mid Performing	2.04	2.63	2.92
Large, High Performing	1.80*	0.00	1.88*
Rural
Small, Low Performing	3.20*	0.00	6.8*
Small, Mid Performing	1.15*	0.00	1.71*
Small, High Performing	26.25*	1.05	28.84*
Medium, Low Performing	3.20	1.05	5.67*
Medium, Mid Performing	2.85*	0.00	3.3*
Medium, High Performing	13.08*	0.53	7.12*
Large, Low Performing	1.69	1.05	2.95
Large, Mid Performing	2.81	2.11	3.5
Large, High Performing	2.42	0.53	1.74

¹Significance (denoted by *) is defined as being outside the 95% confidence interval of proportions generated from 10,000 random draws. District size (small, medium, and large) is categorized by tertiles of the student enrollment distribution. District performance is defined as high if all schools in the district made AYP in 2004–2005, mid if the percentage of schools not making AYP is below the median of the distribution of districts with schools not making AYP, and low if it is above the median. Low and mid-performing categories were combined if either was less than 1% in the national population.

The results in Table 4 are striking. Large, urban, low- or mid-performing districts make up only approximately 4% of districts in the US and 7% of disadvantaged districts, but constitute nearly 50% of districts included in the 11 impact studies. On the other hand, small, rural, high-performing districts make up 26% of districts in the US and 29% of disadvantaged districts but only 1% of districts in the 11 impact studies. Other notable but much smaller discrepancies from the national population follow similar lines: high sample prevalence of large, suburban, low-performing districts compared to the national population (12% vs. 4%) and low study sample prevalence of medium-sized, rural, high-performing districts compared to the population (1% versus 13%). Patterns are generally similar when comparing with disadvantaged districts, but with more sample and population differences seen among suburban districts. For example, the samples included more large mid- or high-performing suburban districts than are seen in the population of disadvantaged districts (9% vs. 3% for mid performing; 10.5% vs. 1% for high performing); no significant differences were observed for these profiles when comparing with the national population.

4. Discussion and Implications

There is increasing interest in assessing the external validity, “generalizability,” or “transportability” of rigorous evaluations in education research and other fields (Cook, 2014; Stuart, Bradshaw, & Leaf, 2015; Tipton, 2014). As the internal validity of evaluations has improved, researchers and policy-makers have begun thinking more seriously about how to make sure those evaluations—while retaining their high internal validity—are as relevant as possible for policymaking in a broader arena.

For education evaluations, until now there has been almost no evidence on the characteristics of the “typical” studied district and how it differs from districts in the target populations of interest for policy making. This paper provides the first systematic empirical evidence regarding how districts included in rigorous educational evaluations differ from the larger universe of districts of policy importance. We show that there are large differences between the types of districts that participate in rigorous educational evaluations and the average district in two salient populations: all districts in which it is feasible to implement the studied intervention and all districts of interest in the policy agendas of the evaluation funder. We found somewhat more muted, but still statistically significant, differences between participating sites and a third population of policy importance – districts with high proportions of students eligible for free and reduced price lunch.

In particular, we found that participating districts tend to be larger and from more urban areas than districts in the populations of potential implementation, and that the participating districts tend to consist of students who are more disadvantaged than those in the average district in that population (e.g., higher percentages are eligible for free or reduced price lunch, more schools have school-wide Title 1). The differences between the typical study district and the typical district in the population of funder policy interest (for evaluations of federally administered programs) are less extreme, but still substantial.

It is important to recognize some limitations of the results presented here. In particular, we have worked from lists of participating districts in just 11 of the 19 studies conducted by IES during the study period, so, ironically, the results obtained may not generalize to all evaluations. Although we would have preferred to have lists of participating districts from more evaluations, such lists proved difficult to obtain given concerns about confidentiality and district identification. In addition, because we have no data on which districts were recruited but not included in any given study, we cannot distinguish between the differences attributable to non-random selection of districts by evaluators and the differences attributable to non-random opt-out of districts among those selected by evaluators. Further research should be undertaken to investigate those two processes, and how each might be modified to help improve the representativeness of districts included in future evaluations—and hence their value for policy guidance.

In this paper we also investigate only district participation, and do not consider which schools within those districts participate. That is in part due to difficulties in getting information on participating schools, as described above. However, focusing on district participation gets at something that matters, given that school districts generally serve as the first “gate-keeper” for any school participation in a given evaluation. In addition, most interventions require district support, even if the intervention is implemented in schools, so district characteristics may influence an intervention’s effectiveness. A final limitation is that we can only investigate differences in observed characteristics across districts; there may be additional unobserved characteristics that differ between participating and non-participating districts, some of them related to the impact of the intervention being evaluated.

Another crucial point is that any discussion of generalizability of course presumes an identified population of interest. We investigate three such populations here: the population of districts that could conceivably implement the interventions under study, the population of disadvantaged school districts, and the districts relevant for federal policy decisions regarding programs administered through federal grants. For any particular evaluation there may be multiple populations of interest, depending on the policy decisions under consideration. For this reason, we encourage researchers and policy makers to be thoughtful and strategic about defining the populations to which they seek to have their evaluation findings generalize, and about designing studies to come as close as possible to this goal. Parallel work is investigating strategies for district recruitment to move participating samples closer to being population representative (Olsen & Orr, 2015). Tipton et al. (2014) proposes a sample selection procedure intended to ensure representativeness among the included schools or districts.

Of critical importance is whether the differences reported here lead to biased impact estimates. Olsen et al. (2013) demonstrate that the external validity bias from nonrandom site selection depends on the correlation between the probability of site inclusion and site-level impacts. Therefore, any factors that are associated with both the probability of inclusion and site-level impacts will generate impact estimates that are biased for the population of interest. This paper identifies several district-level factors that were clearly associated with the probability of inclusion for the 11 studies, given the differences reported between the 11 study samples and the populations of policy interest. The big question is whether those factors are also associated with site-level impacts, meaning that these factors “moderate” the impacts of the intervention: if so, the differences reported here would in general yield biased impact estimates for the population.⁶

Unfortunately, we cannot directly test whether the characteristics with observed differences moderate the impacts of the interventions tested in the 11 studies because we are unable (and not permitted) to link the data on district characteristics to the data that can be used to estimate impacts separately by district. Therefore, to explore the possible moderating effects of the differences we reported, we reviewed the publications from the pool of all NCEE studies from which the 11 studies were selected. None of these studies test for the moderating effects of district characteristics (as opposed to school or student characteristics).⁷ This finding is consistent with our impressions of the literature more generally: that very few education studies conduct subgroup analyses for different types of districts (perhaps because the statistical power of these comparisons would be so low).

However, there is some indirect evidence that conducting impact evaluations in samples of districts like those included in the 11 studies can yield biased impact estimates. Bell et al. (2016) report evidence that the impacts of a particular educational intervention, Reading First, differs substantially between the districts included in 13 purposive samples—which include the 11 samples analyzed for this paper—and the population of potential policy interest. This evidence suggests that some combination of the observed district-level differences reported in this paper and unobserved district-level differences on other factors can yield biased impact estimates.

Another key question is whether the findings reported here warrant substantial changes in how we conduct impact studies in education. For example, should we select districts randomly for RCTs, or should we make sure our samples include a substantial number of the types of districts that have historically be excluded from RCTs in education? Without more direct evidence that the differences reported in this paper yield biased impact estimates, large and costly changes to evaluation practice would be premature. An obvious strategy would be to select sites randomly. Olsen and Orr (2015) describe how to select a probability sample of sites, where the probabilities can vary across sites. However, since districts may refuse to participate, the resulting sample is not likely to be fully representative of the target population. Future research should explore the costs and benefits of different site-selection strategies with an eye toward reducing the external validity bias from unrepresentative samples.

In the short run, researchers could take a few modest steps to improve their studies and contribute to the evidence base about the consequences of nonrandom site selection. In particular, researchers should specify the population of interest for the evaluation. They should also (1) hypothesize the district factors that may moderate impacts for the tested intervention, (2) measure these factors, (3) account for these factors when selecting sites for the study (e.g., ensuring that the study sample includes some smaller districts), and (4) test for and report whether these factor moderate the intervention’s impacts. The results from these tests could be used to identify factors that can lead to externally biased impact estimates. In the longer run, researchers should consider whether standard approaches to site selection and recruitment are yielding the best possible evidence on the effects of educational interventions. If we find that that factors associated with site inclusion do in fact moderate the impacts of the these interventions, we should explore different ways of reducing the external validity bias through better sample design and analysis methods.

Appendix

A. Definition of Measures

Many of the district variables of interest were obtained or calculated directly from the district CCD. These include the district location (e.g., urban/rural), English language learner percentage, per-pupil expenditure, and distance variables.

Additionally, aggregation from the school CCD to district level was possible, and sometimes needed (e.g., to decrease the incidence of missing observations). For example, for some districts the district teacher totals are missing in the district dataset but can be obtained by aggregating the school-level teacher totals across the district. For variables that could be obtained either directly at the district level or by aggregating from schools (e.g., teacher counts from the district dataset versus teacher counts aggregated per district from the school dataset), considerations and analyses were done to choose the method that resulted in more complete and accurate data for each variable. Since some specific schools were excluded within some districts, when possible and for relevant variables, totals were aggregated across the non-excluded schools for each district and then merged with the district dataset. Despite the school-level exclusions, correlations remained high (>0.99) between the aggregated variables and those from the district-level CCD. The variables aggregated from the school-level CCD include school, teacher, and student counts, the free and reduced price lunch percentage, non-white percentage, Title 1 eligible percentage, and school-wide Title 1 eligible percentage variables. Full details are provided below.

In addition to the variables obtained from the district and school CCD surveys described above, state test scores from the National Assessment of Education Progress (NAEP), three elements of the Data Quality Campaign (DQC), publically available election data, and adequate yearly progress (AYP) variables were obtained and included in the analyses. The NAEP state test scores included grade 8 and grade 4 math and reading composite scores from 2005 and are available from the National Center for Education Statistics website (http://nces.ed.gov/nationsreportcard/naepdata/dataset.aspx). The three elements from the DQC include DQC essential elements 1 and 3 reflecting 2005 status, and DQC action 8 from 2009. Elements 1 and 3 correspond to data collection and tracking elements, specifically state-wide student identifiers and longitudinal student-level test data respectively. Action 8 indicates that states have developed an agenda to work with outside individuals and institutions to leverage their expertise in analyzing the collected data. All of the DQC data were obtained through contacts at the DQC. The election data were taken from the 2000 and 2004 general presidential elections and were downloaded from www.uselectionatlas.org. The AYP data reflect the 2004–2005 school year, and are available from www.air.org/project/national-ayp-and-identification-database.

Full details for the construction of each variable are provided here:

• Number of schools: Count per district from the school CCD of schools defined as regular and operational. The school CCD was used to calculate the total counts instead of the district CCD in order to obtain a more accurate count since individual schools within districts were excluded by our exclusion criteria, as well as to decrease the amount of missingness due to missing data in the district CCD. Correlations between the totaled school CCD counts and given district CCD counts remained high, above 0.99.

• Number of teachers: Total count per district of full-time teachers in regular, operational schools. As with the number of schools, the school CCD was used to calculate the total counts per district.

• Number of students: Total count per district of students in regular, operational schools. As with the number of schools, the school CCD was used to calculate the total counts per district.

• Students per teacher: Number of students divided by number of teachers.

• English language learner %: The number of English language learners was only available from the district CCD, so this variable was calculated by dividing that count by the total number of students in the district as given by the district-level CCD.

• Free and reduced price lunch %: Total count per district of free and reduced price lunch eligible students divided by the number of students. As with the school, teacher, and student counts above, this was calculated using the school CCD.

• Non-white %: Total count per district of minority students divided by the number of students. As with the school, teacher, and student counts above, this was calculated using the school CCD.

• Title I %: Total number of Title 1 eligible schools per district divided by the number of schools. The school CCD was used to calculate this.

• School-wide Title I %: Total number of school-wide Title 1 eligible schools per district divided by the number of schools. The school CCD was used to calculate this.

• Per pupil expenditures: District total expenditures less payments to private and non-district charter schools divided by the number of students. Source is the CCD district finance survey and since totals are per district, the number of students is as given in the district CCD.

• State Grade 4 NAEP math scores: State test scores from the National Assessment of Education Progress (NAEP). All NAEP test scores were obtained from the National Center for Education Statistics website (http://nces.ed.gov/nationsreportcard/naepdata/dataset.aspx).

• State Grade 8 NAEP math scores: State test scores from the National Assessment of Education Progress (NAEP).

• State Grade 4 NAEP reading scores: State test scores from the National Assessment of Education Progress (NAEP).

• State Grade 8 NAEP reading scores: State test scores from the National Assessment of Education Progress (NAEP).

• Average % of schools per district not passing adequate yearly progress in 2004–2005: School-level average yearly progress (AYP) status in 2004–2005 was obtained from the National AYP database (www.air.org/project/national-ayp-and-identification-database). The number of schools per district not making AYP was summed and divided by the district’s total number of schools, as calculated with the school CCD.

• % of districts in states implementing DQC Action 8 in 2009: Binary variable indicating if district is located in a state implementing the Data Quality Campaign (DQC) Action 8 in 2009, which is defined as, “Develop a purposeful research agenda and collaborate with universities, researchers, or intermediary groups to explore the data for useful information.” (www.dataqualitycampaign.org) This and the other two DQC variables were obtained through personal contacts at the DQC.

• % of districts in states with DQC essential element 1 in 2005: Binary variable indicating if district is located in a state with the DQC essential element 1 in 2005, which is defined as, “A unique statewide student identifier that connects student data across key databases across years”.

• % of districts in states with DQC essential element 3 in 2005: Binary variable indicating if district is located in a state with the DQC essential element 3 in 2005, which is defined as, “The ability to match individual students’ test records from year to year”.

• County average % Republican of two-party vote (2000,2004): Publically-available election data (www.uselectionatlas.org) from the 2000 and 2004 general elections was used to calculate the average per-county republican share of the two-party (Democrat, Republican) vote.

• Distance to San Francisco: “Great circle” distance with ellipsoid effects between district and San Francisco, in miles.

• Average distance to the Northeast: “Great circle” distance with ellipsoid effects between district and Boston, New York City and Washington D.C., averaged in miles.

• Locale indicators: Binary variables indicating if district is located in a city, suburb, town, or rural area. This variable was constructed with the district CCD “LOCALE” variable and defined as in the majority of evaluation reports. “LOCALE” levels “1” and “2” correspond to the city indicator, “3” and “4” to the suburban indicator, “5” and “6” to the town indicator, and “7” and “8” to the rural indicator.

B. Matching Non-District Entities to School Districts

One challenge in identifying both the purposive samples and the populations of policy interest results from the fact that the “sites” were not always school districts. Non-district entities (e.g., non-profit organizations) can receive federal funding to operate federal programs. Furthermore, researchers often have to obtain the cooperation of non-district entities to include particular schools or districts in impact studies because these entities often partner with school districts to deliver services. Even when non-district entities receive federal funding and serve as the “gate keeper” to obtaining cooperation on federal studies, the characteristics of partner school districts may still be important moderators of the effects of the interventions because they influence the context in which educational programs or interventions are implemented.

Since data on partnerships between district and non-district entities is not consistently available, we developed an algorithm for matching non-district entities to one or more school districts with which they likely to partner. In particular, we matched each non-district entity to school districts by location. More specifically, we matched a non-district entity to a school district if the city and state of the non-district entity matched the city and state of either (1) the district office’s mailing address or physical address or (2) at least one school in the district. Supplemental analyses conducted but not reported here suggest that the rate of mismatching is nontrivial, but these mismatches are not likely to substantially influence the results of the analysis.⁸

Appendix Figure 1.

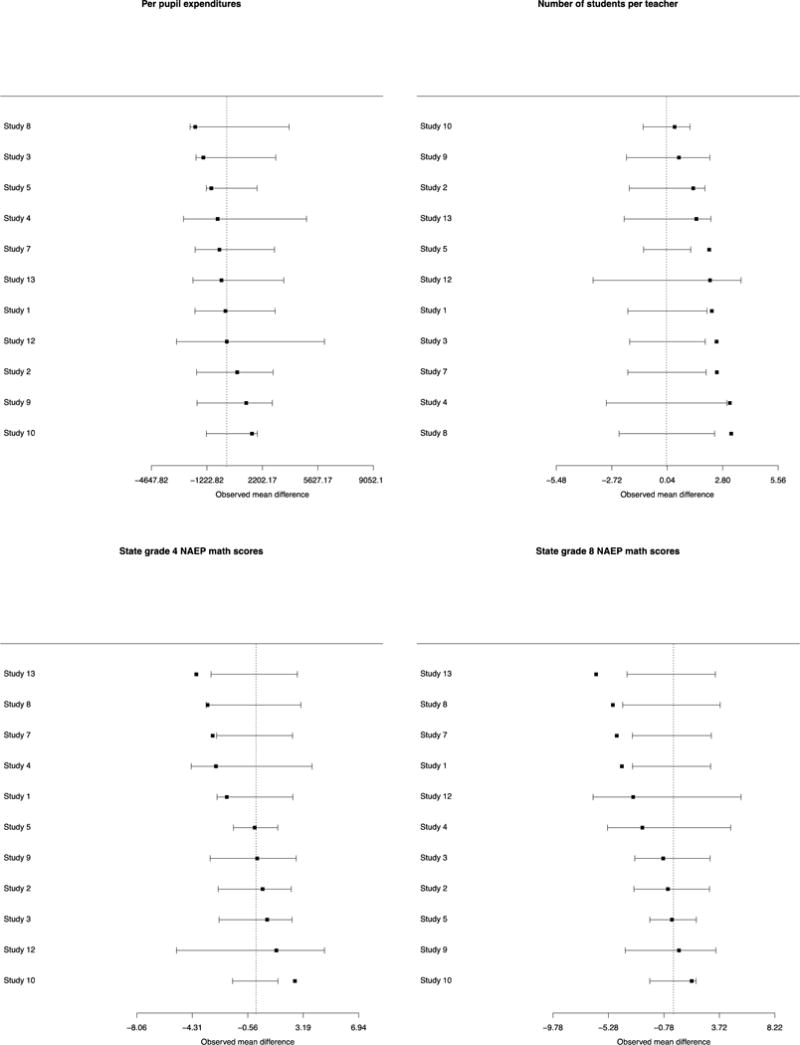
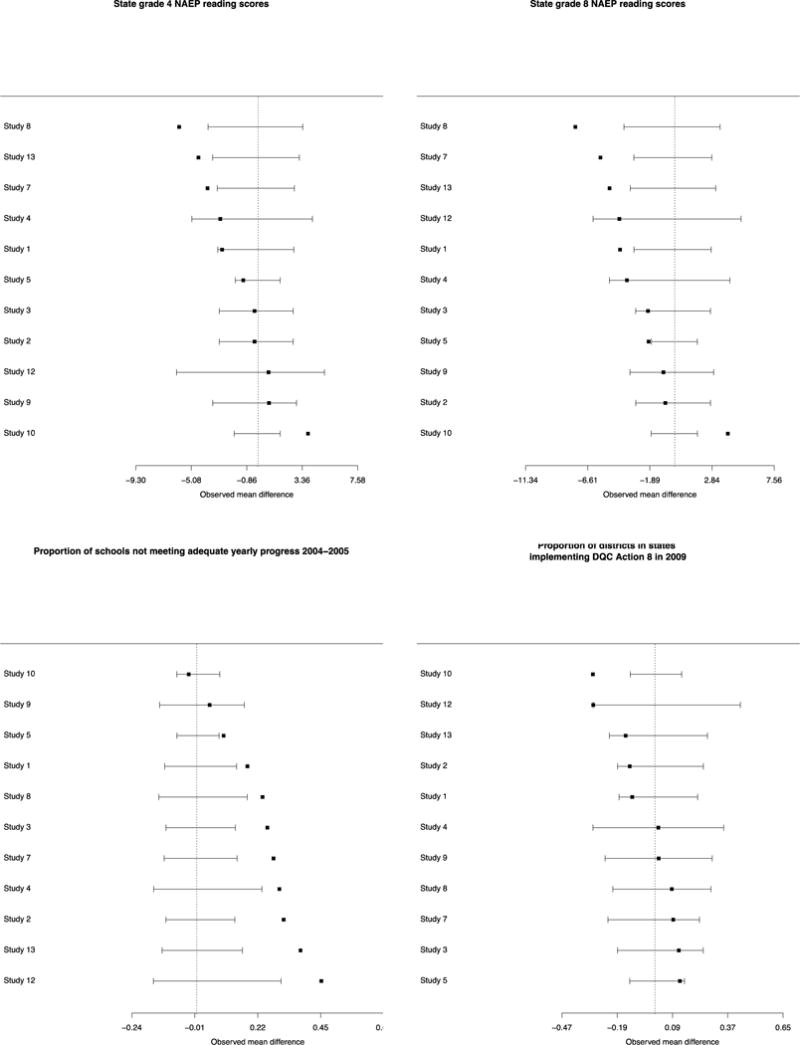
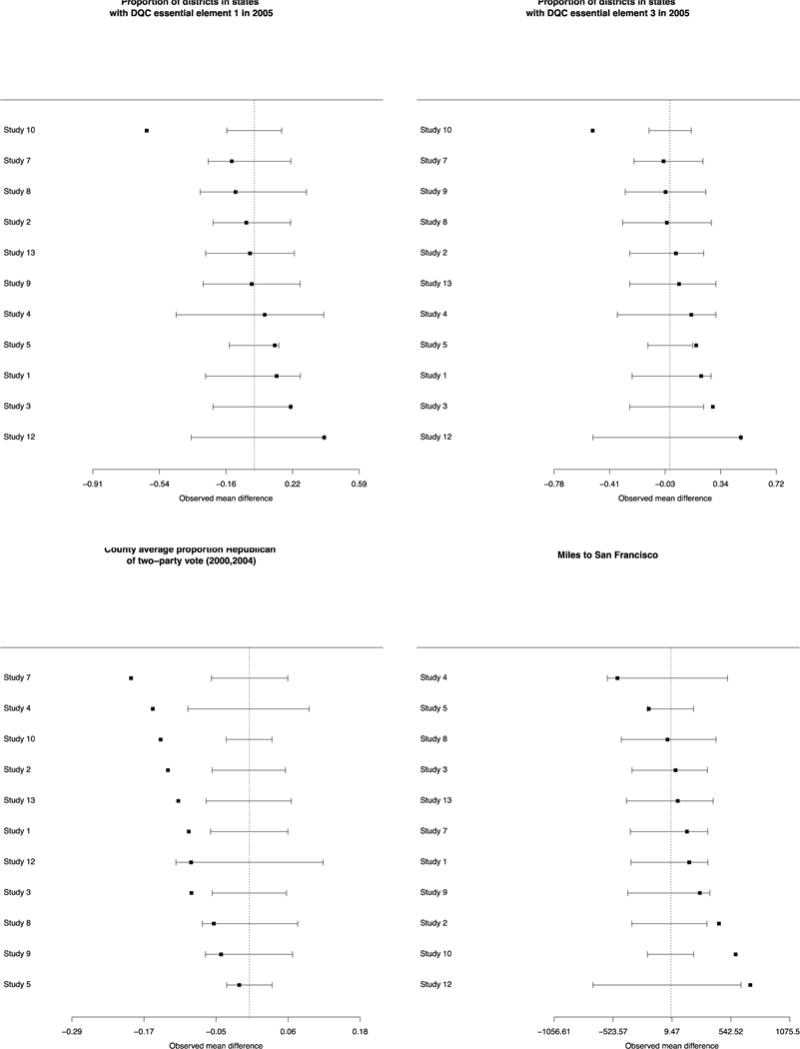
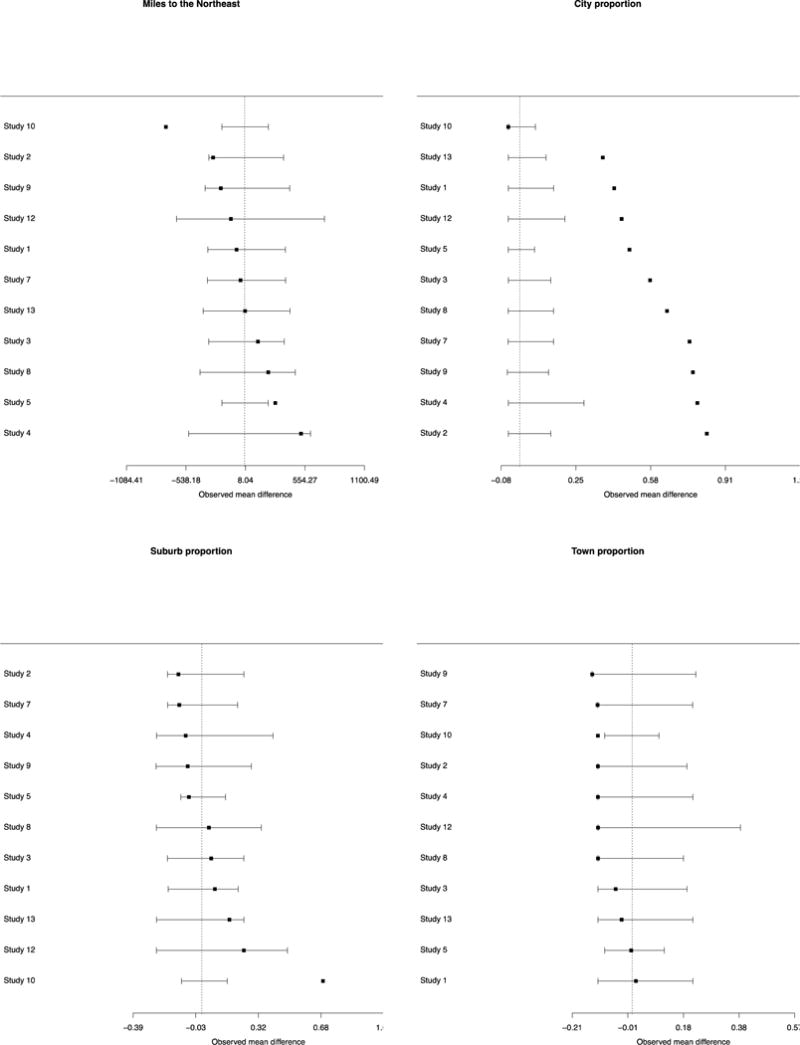
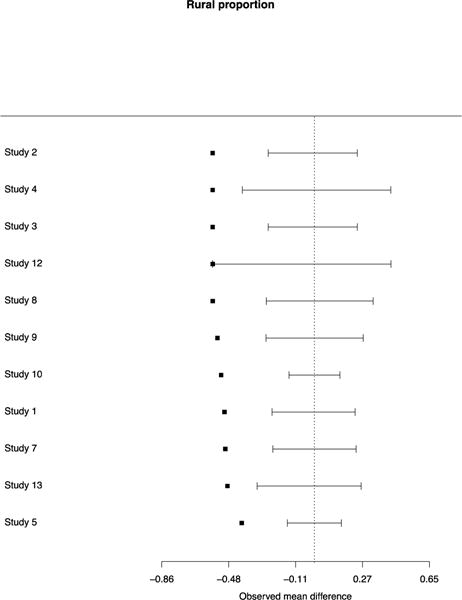
Forest plots of characteristics of participating districts compared with random samples from population of potential implementation. One forest plot shown for each characteristic.

Appendix Table 1.

NCEE-Funded Impact Evaluations in K-12 Education, 2001 – 2011

Study Name	Final Report
An Evaluation of Teachers Trained Through Different Routes to Certification N=20 districts	Constantine, J., Player, D., Silva, T., Hallgren, K., Grider, M., and Deke, J. (2009). An Evaluation of Teachers Trained Through Different Routes to Certification, Final Report (NCEE 2009-4043).
An Evaluation of the Impact of Mandatory Random Student Drug Testing N=7 districts	James-Burdumy, S., Goesling, B., Deke, J., and Einspruch, E. (2010). The Effectiveness of Mandatory-Random Student Drug Testing (NCEE 2010-4025).
An Evaluation of the Impact of Supplemental Literacy Interventions in Freshman Academies N=10 districts	Somers, M.-A., Corrin, W., Sepanik, S., Salinger T., Levin, J., and Zmach, C. (2010). The Enhanced Reading Opportunities Study Final Report: The Impact of Supplemental Literacy Courses for Struggling Ninth-Grade Readers (NCEE 2010-4021).
An Evaluation of the Impact on Secondary Student Math Achievement of Two Highly Selective Routes to Alternative Certification N=15 districts	Clark, M.A., Chiang, H.S., Silva, T., McConnell, S., Sonnenfeld, K., Erbe, A., and Puma, M. (2013). The Effectiveness of Secondary Math Teachers from Teach For America and the Teaching Fellows Programs (NCEE 2013-4015).
Closing the Reading Gap N=27 districts	Torgesen, J., Schirm, A., Castner, L., Vartivarian, S., Mansfield, W., Myers, D., Stancavage, F., Durno, D., Javorsky, R., and Haan, C. (2007). National Assessment of Title I, Final Report: Volume II: Closing the Reading Gap, Findings from a Randomized Trial of Four Reading Interventions for Striving Readers (NCEE 2008-4013).
Evaluation of Conversion Magnet Schools N=11 districts	Betts, J., Kitmitto, S., Levin, J., Bos, J., & Eaton, M. (2015). What Happens When Schools Become Magnet Schools? (ED-04-CO-0025/0013)
Evaluation of Early Elementary Math Curricula N=12 districts	Agodini, R., Harris, B., Thomas, M., Murphy, R., and Gallagher, L. (2010). Achievement Effects of Four Early Elementary School Math Curricula: Findings for First and Second Graders (NCEE 2011-4001).
Evaluation of Reading Comprehension Programs N=10 districts	James-Burdumy, S., Deke, J., Lugo-Gil, J., Carey, N., Hershey, A., Gersten, R., Newman-Gonchar, R., Dimino, J., Haymond, K., and Faddis, B. (2010). Effectiveness of Selected Supplemental Reading Comprehension Interventions: Findings from Two Student Cohorts (NCEE 2010-4015).
Evaluation of the Effectiveness of Educational Technology Interventions N=33 districts	Campuzano, L., Dynarski, M., Agodini, R., and Rall, K. (2009). Effectiveness of Reading and Mathematics Software Products: Findings from Two Student Cohorts (NCEE 2009-4041).
Evaluation of the Impact of Charter School Strategies N=29 districts1	Gleason, P., Clark, M., Tuttle, C. C., and Dwoyer, E. (2010). The Evaluation of Charter School Impacts: Final Report (NCEE 2010-4029).
Evaluation of the Impact of the DC Choice Program N=1 district	Wolf, P., Gutmann, B., Puma, M., Kisida, B., Rizzo, L., Eissa, N., and Carr, M. Evaluation of the DC Opportunity Scholarship Program: Final Report (NCEE 2010-4018).
Impact Evaluation of a School-Based Violence Prevention Program N=13 districts	Silvia, S., Blitstein, J., Williams, J., Ringwalt, C., Dusenbury, L., and Hansen, W. (2011). Impacts of a Violence Prevention Program for Middle Schools: Findings after 3 Years of Implementation (NCEE 2011-4017).
Impact Evaluation of Academic Instruction for After-School Programs N=7 districts	Black, A. R., Somers, M.-A., Doolittle, F., Unterman, R., and Grossman, J. B. (2009). The Evaluation of Enhanced Academic Instruction in After-School Programs: Final Report (NCEE 2009-4077).
Impact Evaluation of Moving High-Performing Teachers to Low-Performing Schools N=10 districts	Glazerman, S., Protik, A., Teh, B., Bruch, J., and Max, J. (2013). Transfer Incentives for High-Performing Teachers: Final Results from a Multisite Experiment (NCEE 2014-4003).
Impact Evaluation of Teacher Induction Programs N=17 districts	Glazerman, S., Isenberg, E., Dolfin, S., Bleeker, M., Johnson, A., Grider, M., and Jacobus, M. (2010). Impacts of Comprehensive Teacher Induction: Final Results from a Randomized Controlled Study (NCEE 2010-4027).
Impact Evaluation of the US Department of Education’s Student Mentoring Program N=11 districts	Bernstein, L., Dun Rappaport, C., Olsho, L., Hunt, D., and Levin, M. (2009). Impact Evaluation of the U.S. Department of Education’s Student Mentoring Program (NCEE 2009-4047).
Impact Evaluation of Title I Supplemental Educational Services N=8 districts	Deke, J., Dragoset, L., Bogen, K., and Gill, B. (2012). Impacts of Title I Supplemental Educational Services on Student Achievement (NCEE 2012-4053).
National Evaluation of the 21st Century Community Learning Centers N=12 districts	Dynarski, M., James-Burdumy, S., Moore, M., Rosenberg, L., Deke, J., and Mansfield, W. (2004). When Schools Stay Open Late: The National Evaluation of the 21st Century Community Learning Centers Program: New Findings. (ED-99-CO-0134)
Reading First Impact Study N=17 districts	Gamse, B. C., Jacob, R. T., Horst, M., Boulay, B., and Unlu, F. (2008). Reading First Impact Study Final Report (NCEE 2009-4038).

¹The exact number of districts was not reported, but the study included 29 clusters with one or two charter schools and several public schools within the same school district—or, for independent charter schools that are not a part of the public school district—within the same geographic area.

Appendix Table 2.

Comparisons of districts participating in rigorous educational evaluations with the national population of potential implementation and a subpopulation of the most disadvantaged districts. Mean differences calculated using absolute values.

District Characteristic	Sample Mean or Percentage (average across 11 study samples)	National Population of Potential Implementation	National Population Std. Mean Diff1,2	Disadvantaged Districts	Disadvantaged Population Std. Mean Diff1,2
District Size
Number of schools	127	6	6.96ˆˆˆ	8	6.89ˆˆˆ
Number of teachers	5,308	213	7.08ˆˆˆ	248	7.03ˆˆˆ
Number of students	98,747	3,503	6.67ˆˆˆ	4,077	6.63ˆˆˆ
District resources
Per pupil expenditures	$10,681	$10,895	−0.04	$10,532	0.03
Number of students per teacher	16.47	14.50	0.44ˆˆ	14.39	0.46ˆˆ
Student demographics
% of students who are non-white	64	22	1.64ˆˆˆ	46	0.71ˆˆˆ
% of students who are English language learners	11	4	0.69ˆˆˆ	10	0.15
% of students eligible for free or reduced price lunch	55	38	0.74ˆˆˆ	68	−0.59ˆˆˆ
% of schools eligible for Title I	63	64	−0.01	81	−0.54ˆˆˆ
% of schools with school-wide Title I	52	26	0.70ˆˆˆ	61	−0.25
Student achievement
State grade 4 NAEP math scores	237.50	238.38	−0.17ˆˆ	235.69	0.35ˆˆˆ
State grade 8 NAEP math scores	277.23	279.52	−0.36ˆˆˆ	275.63	0.25ˆˆ
State grade 4 NAEP reading scores	217.74	219.21	−0.25ˆˆˆ	215.82	0.33ˆˆˆ
State grade 8 NAEP reading scores	260.08	262.96	−0.49ˆˆˆ	259.38	0.12ˆˆ
% of schools not meeting adequate yearly progress ‘04–‘05	39	16	0.86ˆˆˆ	27	0.44ˆˆˆ
District location
Miles to San Francisco	1,839	1,685	0.22ˆˆˆ	1,459	0.54ˆˆˆ
Miles to the Northeast	1,019	1,049	−0.04ˆˆ	1,336	−0.44ˆˆˆ
City (%)	60	5	2.47ˆˆˆ	8	2.34ˆˆˆ
Suburb (%)	33	26	0.16ˆˆ	15	0.40ˆˆˆ
Town (%)	4	12	−0.26	15	−0.35ˆ
Rural (%)	4	57	−1.07ˆˆˆ	62	−1.16ˆˆˆ
Political leaning
County average % Republican of two-party vote (2000,2004)	46	57	−0.84ˆˆˆ	57	−0.89ˆˆˆ
Data access measures
In states implementing DQC Action 83 in 2009 (%)	27	32	−0.11	34	−0.16
In states with DQC essential element 14 in 2005 (%)	61	61	0.00ˆˆ	71	−0.20ˆˆˆ
In states with DQC essential element 35 in 2005	60	53	0.14ˆˆ	67	−0.14ˆˆ

¹Standardized Mean Difference, defined as the difference in means divided by the standard deviation of the variation in the population

²Carets denote significance levels for comparisons of absolute differences (proportion of 30,000 random samples with larger absolute mean differences than those observed):

^ˆfor 0.05 <= p < 0.10,

^ˆˆfor 0.01 <= p < 0.05,

^ˆˆˆfor p <= 0.01.

All p-values are for two-sided tests.

³DQC Action 8 is defined as: “Develop a purposeful research agenda and collaborate with universities, researchers, or intermediary groups to explore the data for useful information.” (www.dataqualitycampaign.org)

⁴DQC essential element 1 is defined as: “A unique statewide student identifier that connects student data across key databases across years”

⁵DQC essential element 3 is defined as: “The ability to match individual students’ test records from year to year”

Appendix Table 3.

Comparisons of districts participating in rigorous educational evaluations of programs funded by federal grant programs with the population of policy interest of the program funder (N=7 studies). Mean differences calculated using absolute values.

Characteristics	Sample Mean or Percentage (average across 7 study samples)	Population of Policy Interest	Std. Mean Diff.1,2
District Size
Number of schools	89	22	3.90ˆˆˆ
Number of teachers	3,696	857	3.95ˆˆˆ
Number of students	67,122	15,188	3.64ˆˆˆ
District resources
Per pupil expenditures	$10,864	$10,329	0.10
Number of students per teacher	16.16	16.45	−0.07
Student demographics
% of students who are non-white	58	40	0.69ˆˆˆ
% of students who are English language learners	8	10	−0.20
% of students eligible for free or reduced price lunch	51	44	0.30ˆˆˆ
% of schools eligible for Title I	63	65	−0.06
% of schools with school-wide Title I	48	37	0.30ˆˆˆ
Student achievement
State grade 4 NAEP math scores	238.22	237.00	0.24ˆˆ
State grade 8 NAEP math scores	277.70	277.76	−0.01ˆˆ
State grade 4 NAEP reading scores	218.76	216.87	0.32ˆˆ
State grade 8 NAEP reading scores	260.94	260.24	0.12ˆˆˆ
% of schools not meeting adequate yearly progress ‘04–‘05	36	23	0.48ˆˆˆ
District location
Miles to San Francisco	1,920	1,465	0.65ˆˆˆ
Miles to the Northeast	942	1,316	−0.53ˆˆˆ
City (%)	48	24	1.07ˆˆˆ
Suburb (%)	41	34	0.17ˆˆˆ
Town (%)	6	9	−0.10
Rural (%)	5	33	−0.56ˆˆˆ
Political leaning
County average % Republican of two-party vote (2000,2004)	48	54	−0.44ˆˆˆ
Data access measures
In states implementing DQC Action 83 in 2009 (%)	23	32	−0.22ˆˆˆ
In states with DQC essential element 14 in 2005 (%)	64	62	0.04ˆˆˆ
In states with DQC essential element 35 in 2005	62	58	0.08ˆˆˆ

¹Standardized Mean Difference, defined as the difference in means divided by the standard deviation of the variation in the population

²Carets denote significance levels for comparisons of absolute differences (proportion of 30,000 random samples with larger absolute mean differences than those observed):

^ˆfor 0.05 <= p < 0.10,

^ˆˆfor 0.01 <= p < 0.05,

^ˆˆˆfor p <= 0.01.

All p-values are for two-sided tests.

³DQC Action 8 is defined as: “Develop a purposeful research agenda and collaborate with universities, researchers, or intermediary groups to explore the data for useful information.” (www.dataqualitycampaign.org)

⁴DQC essential element 1 is defined as: “A unique statewide student identifier that connects student data across key databases across years”

⁵DQC essential element 3 is defined as: “The ability to match individual students’ test records from year to year”