Improved spatial regression analysis of diffusion tensor imaging for lesion detection during longitudinal progression of multiple sclerosis in individual subjects

Abstract

Subject-specific longitudinal DTI study is vital for investigation of pathological changes of lesions and disease evolution. Spatial Regression Analysis of Diffusion tensor imaging (SPREAD) is a non-parametric permutation-based statistical framework that combines spatial regression and resampling techniques to achieve effective detection of localized longitudinal diffusion changes within the whole brain at individual level without a priori hypotheses. However, boundary blurring and dislocation limit its sensitivity, especially towards detecting lesions of irregular shapes. In the present study, we propose an improved SPREAD (dubbed improved SPREAD, or iSPREAD) method by incorporating a three-dimensional (3D) nonlinear anisotropic diffusion filtering method, which provides edge-preserving image smoothing through a nonlinear scale space approach. The statistical inference based on iSPREAD was evaluated and compared with the original SPREAD method using both simulated and in vivo human brain data. Results demonstrated that the sensitivity and accuracy of the SPREAD method has been improved substantially by adapting nonlinear anisotropic filtering. iSPREAD identifies subject-specific longitudinal changes in the brain with improved sensitivity, accuracy, and enhanced statistical power, especially when the spatial correlation is heterogeneous among neighboring image pixels in DTI.

1. Introduction

Diffusion tensor imaging (DTI) enables description of the degree and direction of water movement in biological tissues, which in turn provides information about white matter (WM) microstructure (Basser et al 1994). It has been widely used in neuroscience and medicine to investigate brain development, to identify subtle changes in white matter, and to monitor pathologic severity of lesions and disease evolution (Werring et al 1999). Group-level analysis, which includes both ROI-based (Douaud et al 2006) and voxel-based (Ashburner and Friston 2000, Smith et al 2006) statistical tests, are often used for statistical comparisons in longitudinal study of DTI-derived parameters, such as mean diffusivity (MD) and fractional anisotropy (FA). However, group-level analysis is most suitable when pathological changes are located in similar anatomical regions among subjects. It often fails when the longitudinal changes/effects are diverse and highly specific for individual subjects, where the inter-subject variations (within-group) exceed the between-group variations. More recent works have focused on individual-level longitudinal analysis with DTI measurements (Chung et al 2008, Zhu et al 2013).

Both parametric (Friston et al 1994) and non-parametric statistical methods (Chung et al 2006, Holmes et al 1996) have been used for subject-specific longitudinal studies. Since non-normally distributed residuals of DTI parameters make statistical inferences with a parametric approach problematic (Jones et al 2005), nonparametric resampling methods such as bootstrap and permutation have gained much favor in recent years. Compared to the parametric methods (Friston et al 1994), nonparametric methods, which include both descriptive and inferential statistics, have the advantage of being able to achieving sufficient statistical power with minimal assumptions about the data being investigated. Bootstrap (Heim et al 2004, Chung et al 2006, Zhu et al 2008) has been used to quantify uncertainties of DTI-derived parameters through both simulation and real human DTI data. However, these methods rely on bootstrapping the signs or labels of residuals from regression analysis, which do not necessarily share the same distribution even under the null hypothesis. Furthermore, while bootstrap tests are known to be asymptotically consistent, the p-values they generate are only approximations for finite sample (Efron 1979). The permutation test, first introduced to image analysis by Holmes et al (Holmes et al 1996), is able to devise a data-driven null distribution of data with only minimum assumptions and produce exact or almost exact p-values (Nichols and Holmes 2002). This method provides more freedom in terms of selecting suitable summary statistics and has been widely used in the field of functional MRI (fMRI). In recent years, several permutation-based methods such as PERVADE (Chung et al 2008) and SPREAD have been developed for voxel-wise whole brain longitudinal studies of local DTI changes or lesion evolution.

The SPREAD (Zhu et al 2013) relies on permuting time and scan labels and spatial kernel regression. It makes use of intrinsic correlation between neighboring image voxels and overcomes major limitations of existing non-parametric statistical methods in DTI analysis, most of which depend largely on the same DTI protocol at different time points and the achievable p-value is often limited by the availability of existing diffusion-weighting directions. SPREAD requires as little as only one scan per time point for a valid hypothesis test, which greatly reduces the granularity of permutation and has proved to be an effective method for monitoring lesion progression. Results from Monte Carlo simulation show that SPREAD consistently outperforms voxel-based morphometry (VBM) approach when the number of repeated scans per subject is small (n < 5). However, the Gaussian kernel used for spatial regression blurs and dislocates important image features such as edges, common drawbacks of non-adaptive linear filtering. These intrinsic limitations could introduce partial volume or voxel-averaging artifacts and consequently affect the accuracy of interpretation of the orientation of neuron fiber structures (Van Hecke et al 2010).

In this work, we improved the sensitivity and accuracy of SPREAD by incorporating nonlinear anisotropic filtering. This new method is dubbed improved SPREAD or iSPREAD. The nonlinear adaptive filtering, based on the nonlinear partial differential equation proposed by Perona and Malik (Perona and Malik 1990), prefers intra-region smoothing over inter-region smoothing, which leads to nonlinear scale in image space. The method has been applied for image enhancement (Sun et al 2007), edge detection (Catte et al 1992), and image segmentation (Holmes et al 1996, Ardizzone et al 2003) to preserve regional boundaries as well as for noise reductions (Gerig et al 1992, Saha and Udupa 2001). The goal of the current work is to demonstrate that the detection sensitivity of SPREAD can be improved substantially by adapting nonlinear anisotropic filtering when monitoring subject-specific longitudinal DTI changes. Our results suggest the method preserves the heterogeneous spatial correlation between neighboring voxels, which allows identifying local voxel-wise changes in the brain in single subject longitudinal studies.

2. Methods

2.1. Overview of iSPREAD

In SPREAD (Zhu et al 2013), the longitudinal tensor-derived parameter D_nsti, which is the nth subject's sth scan at time t measured for the ith voxel (n = 1, 2, …, N, s = 1, 2, …, S, i = 1, 2, …, I, t = t₁, t₂, …, t_T), is modeled as a continuous spatial function Φ_n(z_i), where z_i is the 3D spatial coordinate at the ith voxel, superimposed with measurement errors ε_nsti. The disease effect is modeled as the longitudinal DTI change with rate β(z_i) at the ith voxel (equation (1)).

$$D_{\mathit{\text{nsti}}}={\mathrm{\Phi }}_n(z_i)+\beta (z_i)\diamond f(z_i,t-t_1)+{\epsilon }_{\mathit{\text{nsti}}},$$ (1)

where ◊ is the Hadamard product, f(z_i, t′) is a continuous tensor-valued function of z_i and t′ with f(z_i, 0) = 0. β(z_i) is a continuous, tensor-valued spatial function. The statistical theory behind SPREAD is that both the scan (s in equation (1)) and the time (t in equation (1)) are interchangeable without affecting the distribution functions of D_nsti under the following null hypothesis:

$$H_{i0}:\beta (z_i)=0$$ (2)

Given the exchangeability, the scan/time labels for the DTI-derived parameters such as FA or MD maps from each subject are randomly permuted at each voxel for N = 1000 times to generate a permutation distribution under the null hypothesis for each voxel. The original FA/MD images, together with the permutated images are smoothed in iSPREAD using the nonlinear anisotropic instead of Gaussian filtering for edge-preserving image enhancement as well as for maintaining spatial correlation between neighboring voxels, which will be discussed in detail in the next section. In the third step, a repeated measures comparison is performed for each subject between the baseline scan and scans at other time points after permutation and image smoothing to test whether there are subject-specific longitudinal changes of DTI-derived parameters between any two time points. The following voxel-wise test statistic was chosen to illustrate the temporal changes in FA at each voxel.

$$\mathrm{\Delta }{\mathit{\text{FA}}}_i=\frac{1}{\sqrt{2}}\sum _{n=1}^N|{\overline{\mathit{\text{FA}}}}_{n\cdot 1i}-{\overline{\mathit{\text{FA}}}}_{n\cdot 2i}|,$$ (3)

where ${\overline{\mathit{\text{FA}}}}_{n\cdot ti}=\frac{1}{s}{\sum }_{s=1}^S{\mathit{\text{FA}}}_{\text{nsti}}$ is the scan average and ${\overline{\mathit{\text{FA}}}}_{n\cdot \cdot i}=\frac{1}{T}{\sum }_{s=1}^S{\mathit{\text{FA}}}_{n\cdot ti}$ is the scan and time average for each subject. The Westfall-Young multiple testing procedure (Nichols and Hayasaka 2003) is used to control the familywise error rate (FWER) in the last step. Voxels are identified as significantly changing voxels (e.g. lesion area) if the adjusted p-value is less than a predefined threshold (e.g. 0.05). A similar procedure can also be applied to the MD map. The flowchart of the method iSPREAD is shown in figure 1.

Figure 1.

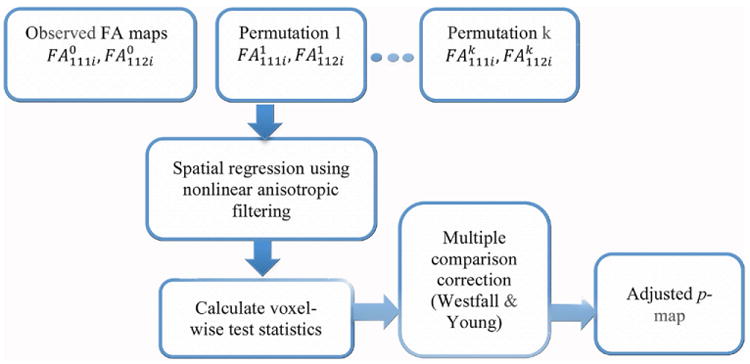
Flow diagram of iSPREAD.

2.1.1. Justification of permutation invariance

Statistical inference of iSPREAD depends on permuting time/scan labels, so it is important to show that the likelihood function of the permuted scans are the same as the original ones under the null hypothesis. According to equations (1) and (2), D_nsti = Φ_n(z_i) + ε_nsti under the null hypothesis, we denote the totality of D_nsti, for all s,t,i, as D_n. Although the nonlinear anisotropic filtering used in iSPREAD is a complex procedure, it can be abstracted as a nonlinear function of D_n. In other words, D̂_n = G(D_n), where D̂_n is the collection of filtered diffusion tensors of the n-th subject and G is the nonlinear transformation defined by the filtering procedure. Let π be a permutation of t and π the induced transformation of D_n, we only need to show that the joint-density function of G(π(D_n)) is the same as that of G(D_n). Obviously, this reduces to showing the joint-density function of ε, the totality of random errors of subject n, is invariant under time-permutation because the true signal, Φ_n(z_i), is a constant for all time points/scans under the null hypothesis. The exchangeability is guaranteed if we assume D_nsti follows a typical random effects model under the null hypothesis:

$$D_{\mathit{\text{nsti}}}={\mu }_i+{\epsilon }_{\mathit{\text{nsti}}}={\mu }_i+{\alpha }_n+{\gamma }_{\mathit{\text{nst}}}+{\xi }_{\mathit{\text{nsti}}},$$ (4)

where μ_i represents the mean of D_nsti and ε_nsti is partitioned into three independent components of random effects: the subject-specific variation α_n, the scan-specific variation γ_nst and the per-measurement error ξ_nsti. More discussions can be found in section 2.2. in Zhu et al (2013).

2.2. Overview of anisotropic diffusion (AD) filter

Nonlinear anisotropic diffusion filtering is a general scale-space approach for edge-preserving piecewise smoothing of the original image. Note that diffusion in this content refers to a diffusion process that creates a nonlinear scale space, which is different from physical process of molecular diffusion measurement in DTI. In the scale-space, an image is seen as one sample from a continuous range of scaled images with the level zero representing the original image. The linear scale-space filtering technique, first introduced by Witkin (1984), involves convolving the original image with Gaussian kernels with different bandwidths to generate gradually smoother versions of the original image. This technique demonstrates the natural way of quantitatively presenting image ambiguity at different scales. However, the isotropic filtering method with a Gaussian kernel has the disadvantage of blurring object boundaries and of the suppression of fine structures at a large scale (Perona and Malik 1990). The nonlinear scale space generated by nonlinear diffusion filtering, which is proposed from an analogy to thermal equations describing the diffusion process, provides an alternative way to maintain the primary properties of a scale space. The equation for the process was first presented by Perona and Malik (1990), and is referred to as the Perona–Malik (PM) equation as shown in equation (5).

$${\partial }_{t}I(z,\stackrel{\sim }{t})=\text{div}(g(z,\stackrel{\sim }{t})\cdot \nabla I(z,\stackrel{\sim }{t})).$$ (5)

where function I(z, t̃) is taken as the image intensity (e.g. FA or MD map in our study), t̃ is the processing ordering, referred to as iteration steps in discrete case. The conductance function g(z, t̃) controls the diffusion strength, which is usually taken as a parametric function of image local gradient (|∇I(z, t̃)|) given by equation (7). The original image I(z, 0) is regarded as the initial state of the diffusion process. The filtered versions are from its temporal evolution, evolving toward equilibrium. The entire diffusive process prefers intra-region smoothing over inter-region smoothing with proper spatial diffusion strengths g(z, t̃) selected. Adiabatic boundary condition is often used to guarantee the consistency of the average grey value of the image during the filtering process (Weickert 1997). However, the fixed boundary condition (also called the first boundary condition) was also used and proved to have superior deblurring effects and inner edge enhancement compared with adiabatic boundary condition (Sun et al 2007), and therefore was used in our study.

For each iteration step, the image intensity change is defined as the flow contributions from 26 neighboring pixel intensities within a 3 × 3 × 3 neighborhood, and the contribution of each neighboring voxel is inversely proportional to the distance between the centroid and the corresponding neighboring voxels. The stability of the iterated processing scheme is obtained by properly adjusting the integration constant Δt according to the 3 × 3 × 3 neighborhood structure and is given in Gerig et al (1992) by Gerig et al as in equation (6):

$$\mathrm{\Delta }t\le \frac{1}{1+\sum _{i=1}^N\frac{1}{{(\mathrm{\Delta }{d}_i)}^2}},$$ (6)

where N is the number of nearest neighbors (N = 26 in a 3D case), and Δd_i is the distance between the centroid and its neighboring voxels. The proper selection of the integration constant guarantees a stable evolution of the PM equation.

Conductance function g has been well studied and can take many forms, but the following function was chosen in our study because it is considered to provide better balance between smoothing-efficiency and edge preserving and have more stable performance (Voci et al 2004, Tsiotsios and Petrou 2013).

$$g=\frac{1}{1+{(\frac{|\nabla I(\overline{x},t)|}{\kappa })}^2},$$ (7)

where |∇I| is taken as rough edge detector and κ is the diffusion contrast parameter. The ratio $\frac{|\nabla I(\overline{x},t)|}{\kappa }$ controls the flow strength. The maximum flow, ∂_tI(z, t), is obtained when gradient |∇I| = κ, which represents inhomogeneous regions, and reduces to 0 when |∇I| ≫ κ or |∇I| ≪ κ, which represents either potential edges or homogeneous regions. For each iteration, the gradient map was first calculated to identify the conductance function (equation (7)) and those calculated parameters were used for image smoothing. The gradient threshold κ was estimated according to the following p-norm method proposed by Voci et al (2004):

$$\kappa (m\mathrm{\Delta }t)=\frac{\lambda \sigma \cdot {\Vert I(m\mathrm{\Delta }t)\Vert }_p}{N_{\text{column}}\times N_{\text{row}}},$$ (8)

where the constant σ is proportional to the image average intensity and λ is a trade-off parameter and was set to be 0.5 in this study (Tian et al 2011). ‖I(mΔt)‖_p represents the p-norm of image I at time step mΔt, usually p = 2. The columns and rows of the image is N_column and N_row respectively. The p-norm method was chosen here because it is a close estimation with a simple calculation.

2.3. Monte Carlo simulations

Monte Carlo simulations were performed to conduct repeated measurements comparisons of the same subject with a predefined area of simulated pathology; the effectiveness and statistical power of iSPREAD and SPREAD were evaluated and compared. For Monte Carlo simulations, synthetic DW data were generated using a DTI dataset of the brain from a healthy volunteer. The original DTI dataset was used as the template for the first group (DTI_pre), which represented the baseline scan when no disease effect was presented. The template for the second group (DTI_post) was generated by defining a ‘diseased’ region in the first group with different effect sizes (es) of the largest eigenvalue (λ₁) added in each voxel. Two shapes of disease areas were considered: a 5 × 5 × 3 cubic region and a 3 × 10 × 3 cuboid region located at the center of the splenium of the corpus callosum were simulated to mimic real brain abnormality. In this study, es took values from 10 to 50%. Repeated measurements of the same subject were simulated by adding Gaussian-distributed noise to both DTI_pre and DTI_post templates to obtain SNR ≈ 50 in non-diffusion weighted images. The effect of thermal noise was first generated using complex random numbers with their real and imaginary parts sampled independently from a Gaussian distribution function with a zero mean and a standard deviation determined by the desired SNR level (Gudbjartsson and Patz 1995, Andersen 1996); the real parts of the complex noise signals were then added to the noise-free baseline signal S₀ and DW signals S_i. The magnitude of the final complex data was then used to synthesize the noisy DTI datasets that were further used for calculations of the noisy tensors. The magnitude of DTI_pre and DTI_post templetes were then calculated from the envelope of the complex signals. For each group, n (n = 2 – 5) repeated measurements of the same subject were simulated. A total of 100 simulations were generated for each combination of es and n.

Repeated measures comparisons were conducted using both SPREAD and iSPREAD. For each subject, the scan and time label were randomly permuted for N = 1000 times to derive a distribution of p-values for each voxel under the null hypothesis. True Positive Runs (TP_Runs) and false positive runs (FP_Runs), which are defined as the total number of simulations within which at least one voxel was correctly detected in the disease area or incorrectly detected in the non-disease area in those 100 simulation data, respectively, were calculated. Sensitivity and Specificity values are defined as follows:

$$\begin{array}{c}\text{Sensitivity}=\frac{\text{TP}\_\text{Runs}}{\text{Total}\_\text{Simulation}\_\text{Runs}}\\ \text{Specificity}=1-\frac{\text{FP}\_\text{Runs}}{\text{Total}\_\text{Simulation}\_\text{Runs}},\end{array}$$ (9)

ROC curves were drawn by selecting the per-voxel p-value from 0.01 to 0.3 with an increment of 0.01.

2.4. In vivo human brain data

2.4.1. Subjects and Image acquisition

Our method was first validated on the simulated data and then applied to repeated measures comparisons of in vivo human brain data. Five healthy volunteers and seven multiple sclerosis (MS) patients were included in this study. All participants were given written informed consent and datasets were acquired using protocols approved by the local institutional review board.

Five healthy volunteers were chosen to compare the ability for false positive control of both SPREAD and iSPREAD, when no biological changes over time were assumed. For five healthy volunteers (2 male and 3 female, mean age 22 ± 8 years, right-handed), data were scanned twice within one week using a 3T Siemens TIM Trio scanner (Erlangen, Germany). The standard protocol included a 3D axially acquired high-resolution T1-weighted MP-RAGE sequence (1 × 1 × 1 mm³), and a DTI scan. DTI data were acquired using a single-shot echo-planar (SS-EPI) sequence with a voxel resolution of 2 × 2 × 2 mm³ voxel, TR/TE = 9100/89 ms, 60 non-coplanar diffusion-encoding directions at b = 1200 s mm⁻² as well as 10 non-diffusion weighted images with a minimum b value of 0 s mm⁻².

Seven Relapsing-Remitting MS (RRMS) patients (5 male and 2 female, mean age 40 ± 8) from an ongoing longitudinal MS study were selected retrospectively to test the statistical power of both the SPREAD and iSPREAD methods to monitor the disease progression. RRMS is characterized by relapses when clearly defined symptoms of attacks occur, followed by the remission of symptoms. For each patient, there were at least two scans with an enhanced lesion visible on T1 enhanced scans. MS patients were scanned 2–4 times within a 2 year period on a GE HDX 3T scanner (Milwaukee, WI, USA). The typical MRI protocol consisted of a T2 FLAIR scan, a T1 contrast enhanced scan, a high resolution T1 SPGR scan, and a DTI scan. The SS-EPI DTI images were acquired with TR/TE = 10500/82 ms, FOV = 240 × 240 mm², acquisition matrix = 128 × 128 zero-filled to matrix size = 256 × 256; slice thickness 3mm with no gap; 24 DWIs with b = 1000 s mm⁻² and 4 b₀ s with minimum b value. Both the axial T2 FLAIR and the T1 contrast enhanced scans with resolution 2 × 2 × 3 mm³ were used as image guidance for manual drawing of lesion masks used as the gold standard for evaluating automatic lesion detection by SPREAD and iSPREAD.

2.4.2. Steps of analysis

Data analysis was performed using MATLAB (MATLAB 2013b, The Mathworks, Natick, MA, USA) and FSL (FSL5.0.4, FMRIB Analysis Group, Oxford University, Oxford, UK). The analysis of in vivo human data consisted of the following five steps:

Step 1: Data preprocessing

The eddy_correct Tool of FSL package was first applied to DTI data to correct eddy current and motion-induced artifacts. Non-brain tissues were removed using the Brain Extraction Tool in FSL. FA and MD maps were then generated using the DTIFIT tool of FSL.

Step 2: Image registration between different time points

For healthy volunteers, the registration was performed between two time points. In the first step, linear registrations were performed between FA/MD images at different time points using the FLIRT tool of FSL (degree of freedom = 12). The resultant transformation matrix was saved and split into one forward and one backward half transformation. Next, one of the FA/MD maps (either pre or post) was transformed to the ‘halfway’ using the halfway transform matrix and used as the reference image for nonlinear registration. This guarantees the equivalent interpolation bias to both time points (Smith et al 2002). In the final step, the nonlinear registration tool of FSL (FNIRT) was used to perform the nonlinear registration.

For each MS patient, the baseline FA/MD maps were used as the reference image, and FA/MD maps at later time points were co-registered to this reference image using the FNIRT tool of FSL. The co-registered FA/MD maps were used for iSPREAD/SPREAD analyses.

Step 3: Permutation testing

For each subject, the scan and time labels were randomly permuted at each and every voxel for N = 1000 times to generate the permutation distribution under the null hypothesis.

Step 4: Spatial regression

For iSPREAD, nonlinear anisotropic filtering was applied to the co-registered FA/MD maps combined with the first boundary condition, where the original FA/MD maps were used as the initial condition. The tradeoff parameter λ in equation (8) was chosen to be 0.5 and time step Δt was calculated based on spatial configuration of the 3 × 3 × 3 neighborhood of each FA/MD map according to equation (6). In order to ensure stable evolution while save computational cost, the time step Δt was set to the largest value possible according to equation (6). Number of iterations was fixed to 4 in all simulations. A Gaussian kernel with fixed FWHM = 2 × 2 × 2 voxels was used for SPREAD.

Step 5: Statistical analysis for healthy volunteers and MS patients

The total number of false positive voxels were counted in healthy volunteers and compared between SPREAD and iSPREAD in terms of the false positive control when no biological changes were presumed. For MS patient data, to quantitatively compare both methods in their power for detecting lesion progression, lesion masks were drawn manually based on T1 enhanced images (transformed to baseline DTI space) by an experienced radiologist and served as the gold standard. We calculated True Positive Ratio in lesions (TPR_L) and false positive ratios in non-lesion white matter (FPR_NLWM) for each subject and compared them between SPREAD and iSPREAD. The Westfall-Young method (22) was used to control the FWER.

$$\begin{array}{c}{\text{TPR}}_{\mathrm{L}}=\frac{\text{Significant}\_\text{Voxel}\_\text{Number}\_\text{in}\_\text{Lesion}\_\text{Mask}}{\text{Total}\_\text{Voxe}\_\text{Number}\_\text{in}\_\text{Lesion}\_\text{Mask}}\times 100\%\\ {\text{FPR}}_{\text{NLWM}}=\frac{\text{Significant}\_\text{Voxel}\_\text{Number}\_\text{in}\_\text{NonLesion}\_\text{WM}}{\text{Total}\_\text{Voxe}\_\text{Number}\_\text{in}\_\text{nonLesion}\_\text{WM}}\times 100\%,\end{array}$$ (10)

3. Results

3.1. Monte Carlo simulations

ROC analyses for the repeated measures comparisons showed that the iSPREAD method outperformed the original SPREAD method consistently; the differences became more obvious when effect size es and group size was small, while reduced with the increasing effect size or increasing sample size. The results were also affected by the different shapes of the disease area. The iSPREAD showed much better performance and the differences between the two methods became larger when the disease area was cuboid-shaped, which further proved that nonlinear anisotropic filtering has better performance in the presence of lesions of irregular shape. Similar results were also observed for the MD analysis.

3.2. Healthy volunteers

On average, each DTI scan collected from five healthy volunteers consists of 75 000 WM/GM voxels. The average false positive voxels for FA and MD analysis in five healthy volunteers were 11 ± 4 and 10 ± 12 voxels for iSPREAD, compared to 44 ± 30 and 74 ± 74 voxels for SPREAD. While both methods were shown to control the FP voxels at a reasonable rate, iSPREAD is better at controlling FPR with fewer FP voxels for both FA and MD. Careful examinations of the location of those false positive voxels indicated that most of them appeared at brain boundaries, mainly due to brain extraction residuals or mis-registration.

3.3. MS patients

Seven patients with RRMS were selected for the investigation of effectiveness of iSPREAD, as well as the comparison between iSPREAD and SPREAD. The patient characteristics, findings and clinical diagnoses are summarized in table 1.

Table 1.

Patient clinical characteristics and diagnoses.

Patient	Age	Gender	Number of scans	Location of T1 post contrast enhancement lesions
Patient 1	37	Female	4	Active lesion around the atrium of the left lateral ventricle at 6-month follow-up
Patient 2	39	Female	2	Periventricular white matter lesion near the right temporal parietal area, 24 months after the baseline
Patient 3	34	Female	2	Incomplete ring enhancing lesion in left frontal subcortical white matter area at baseline. The enhancing lesion resolved after 6 months
Patient 4	41	Female	4	Lesion in the posterior limb of the right internal capsule at baseline and resolved in the follow-up scan 3 months later
Patient 5	29	Male	3	Two enhancing lesions located in the right temporal subcortical white matter near the right occipital horn of the right lateral ventricle which resolved in the follow-up 3 month scan
Patient 6	44	Female	2	Lesion in right corona radiata at baseline, which resolved at one month follow-up scan
Patient 7	53	Male	2	Incomplete ring enhancing lesion in the right corona radiate, 7.5 months after the baseline

The results of the iSPREAD versus SPREAD on seven MS patients are listed in table 1. Detailed results on the first three patients are shown in figures 4–6. The pairwise comparisons were conducted between the baseline scan and its first follow-up scan. The representative FA results are reported in table 2.

Figure 4.

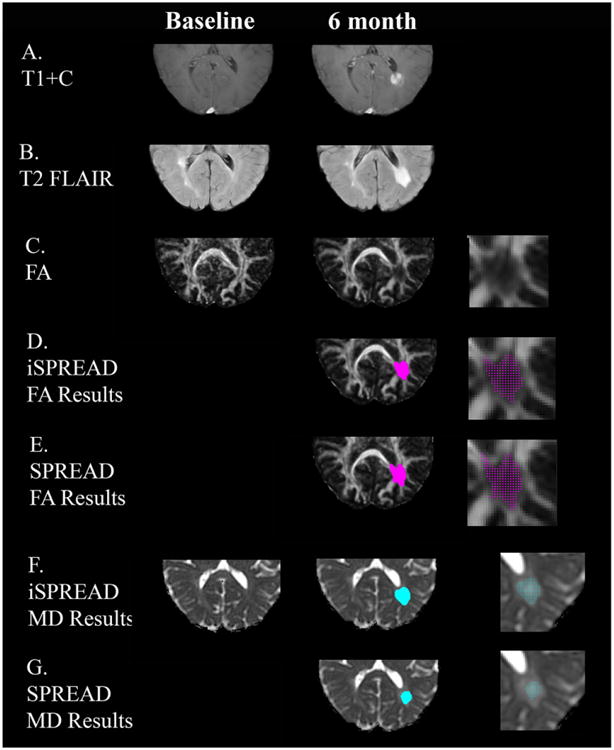
Comparison of significant voxels detected for FA (marked by magenta dots) and MD (marked by cyan dots) using SPREAD (Row E and G) and iSPREAD (Row D and F) analysis of longitudinal data in monitoring disease progression for patient 1. This patient had an active lesion around the atrium of the left lateral ventricle visible on the post contrast T1 images at 6 month (Row A) after baseline, which shows as hyperintensity on FLAIR image (Row B). The images are magnified in the disease area showing the detected significant voxels on the right column.

Figure 6.

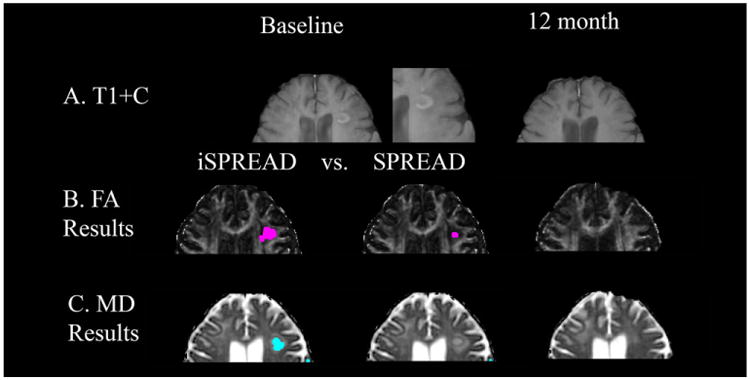
Comparison of significant voxels detected for FA (marked by magenta dots) and MD (marked by cyan dots) using iSPREAD (Row B & C. First column) and SPREAD (Row B & C. Second column) analysis of longitudinal data in monitoring disease progression for patient 3. This patient had a lesion shown as a ring-enhancing lesion on T1-weighted post contrast image at baseline (Row A).

Table 2.

FA results for iSPREAD versus SPREAD.

FA results	iSPREAD		SPREAD
	TPRL (%)	FPRNLWM (%)	TPRL (%)	FPRNLWM (%)
Patient 1	94.68	1.88	85.99	1.6
Patient 2	81.50	0.89	49.71	0.43
Patient 3	73.38	0.31	16.55	0.2
Patient 4	85	0.2	75	0.14
Patient 5	62.11	0.86	11.58	0.47
Patient 6	58.97	1.8	17.95	0.8
Patient 7	62.2	0.8	54.05	0.62

TPR_L: true positive ratio in lesions.

FPR_NLWM: false positive ratios in non-lesion white matter.

3.3.1. MS patient 1

This patient had an active lesion around the atrium of the left lateral ventricle, visible on T1 enhanced images 6 months after the baseline. Voxels with significant longitudinal FA/MD changes between the baseline and 6 month are shown in figure 4. Based on the gold standard lesion mask, TPR_L values were 94.68% for FA and 90.48% for MD with iSPREAD, compared to the TPR_L values of 85.99% (FA) and 69% (MD) for SPREAD. FPR_NLWM values were 1.88% (FA) and 0.96% (MD) with iSPREAD in the non-lesion WM area, compared to the FPR_NLWM values of 1.6% (FA) and 0.8% (MD) for SPREAD. While the location of the lesion was precisely detected by both iSPREAD and SPREAD, it is clear that iSPREAD outperformed SPREAD in terms of detection sensitivity. It is worth noting that the FPR_NLWM for iSPREAD is slightly higher than that of the SPREAD method. Further investigation showed that false positive voxels occurred mainly at the brain boundaries due to FSL brain extraction tool (BET) residuals or tissue/lesion boundaries caused by partial volume effect or atrophic changes. Since iSPREAD is more sensitive to longitudinal changes in FA/MD images, it is also prone to more FP voxels caused by image co-registration errors. This is not obvious with the healthy volunteers because the two scans were taken within one week using exact same imaging protocols, the atrophic changes were negligible and the co-registration errors were minor in such case. With the zoomed images showing the detected significant voxels in the lesion area on the right column of figure 4, it is clear that the disease area was better defined with nonlinear anisotropic filtering, with clearer boundaries and fewer FP voxels around the lesion.

3.3.2. MS patient 2

This patient developed a new lesion in the periventricular white matter near the temporal parietal area 24 months after the baseline. Permutation testing was conducted from the FA/MD image at baseline versus 24 months. TPR_L values were 81.50% (FA) and 71.68% (MD) for iSPREAD, compared to the 49.71% (FA) and 27.17% (MD) for SPREAD. The FPR_NLWM values were 0.89% (FA) and 0.22% (MD) for iSPREAD, compared to 0.43% (FA) and 0.05% (MD) for SPREAD. iSPREAD outperformed SPREAD in terms of lesion detection sensitivity while controlling FPR_NLWM at a relatively low rate.

3.3.3. MS patient 3

This patient had a lesion shown as a ring-enhancing lesion on T1-weighted post contrast image at baseline, which resolved 12 months after the baseline. Based on the gold standard lesion mask, TPR_L values were 73.38% (FA) and 53.24% (MD) for iSPREAD, compared to the 16.55% and 0 for SPREAD. The FPR_NLWM values were 0.31% (FA) 0.28 %(MD) for iSPREAD, compared to 0.2% (FA) and 0.1% (MD). It is clear that iSPREAD was more sensitive to longitudinal changes and could identify subtle changes not detectable by SPREAD. Although the FPR_NLWM was slightly higher for iSPREAD compared to SPREAD, it was still reasonable compared to the large voxel numbers in a whole image volume.

4. Discussion

In this paper, we proposed a method dubbed iSPREAD, designed to address potential pitfalls caused by the Gaussian kernel used in the SPREAD method. It is a non-parametric permutation-based statistical framework that combines spatial regression and resampling methods, and provides effective detection of subject-specific, localized longitudinal changes of DTI parameters within the whole brain without a priori hypotheses. The improvements in lesion detection sensitivity introduced by anisotropic filtering were clearly demonstrated by both Monte Carlo simulations and applications of clinical brain DTI data. The results show that the nonlinear anisotropic filtering provides better spatial regression analysis when the spatial correlation is heterogeneous among neighboring pixels. The proposed method provides an effective tool for individual-level automatic lesion detections or for quantify progression of brain abnormalities through longitudinal DTI studies, which can assist physicians in their prognoses of various diseases.

The adaptive filtering method allows for the improvement of spatial resolution thus enhanced lesion detection power. From our study, two improvements are shown in iSPREAD compared to the original SPREAD: (1) the nonlinear anisotropic filtering process provides piecewise smoothing while preserving important structures such as edges. The tissue boundaries in the filtered image are better determined, leading to better results in differentiating tissue types as well as the lesion areas; (2) As an iterative process, the heterogeneous structure between neighboring voxels are preserved at each iteration, which yields much better image enhancement results than the traditional Gaussian filtering.

The results from both simulated data and human in vivo brain data showed the improvement in sensitivity introduced by the nonlinear anisotropic filtering. Differences between iSPREAD and SPREAD were most significant when the effect size and sample size were small. The improvement in statistical power for iSPREAD was further validated by the results form MS patients for monitoring lesion progression. The FA results for iSPREAD versus SPREAD are shown in table 2, iSPREAD was able to detect longitudinal changes in FA maps with an average TPR_L of 73.98%, compared to 44.40% for SPREAD for the seven selected MS patients. Given the high sensitivity of iSPREAD in detecting brain abnormalities, it is possible for iSPREAD to detect brain abnormalities even at an early stage of the disease, which merits further investigation.

There are also some limitations for the iSPREAD method. First and foremost, the errors caused by image preprocessing steps, namely the BET residuals and registration errors, remain a major challenge, which is also common to all voxel-based analyses of DTI data(Smith et al 2006). Registration errors occur mostly at boundaries between different tissue types or lesion/normal tissue boundaries. Although the nonlinear anisotropic filtering method and nonlinear registrations with high degrees of freedom (DOF) were applied during the image preprocessing stage to better preserve tissue boundaries and to minimize errors from registration, mis-registration was still inevitable because of effects such as atrophic changes and lesion evolution. This is more severe for longitudinal studies that last for a long period of time. Those effects can bring uncertainties to image alignments which are driven by different tissue contrasts. It is worth noting that the FPR_NLWM of iSPREAD (0.96% for FA) was slightly higher than that of SPREAD (0.61% for FA) in MS patients. Further investigation showed that most of the FPs stemmed from misregistration and BET residuals. Since iSPREAD is more sensitive to longitudinal changes, it is more sensitive to those registration errors as well. These FP voxels will also cause problems when detecting very small lesions. In this case, small lesions (true positive voxels) are easily ‘submerged’ into the FP voxels that makes them difficult to be identified. More in-depth investigation of the lesion evolution over time and devising the test statistic accordingly will bring more insight into the statistical framework and will work towards removing registration errors. Second limitation related to this study is that the parameters chosen for the anisotropic filtering were based on tests from both the simulation and clinical data and, therefore, more empirical than theoretical. As an iterative process, the number of iterations is very crucial to the result of the filtering and should be chosen based on the needs of different applications. A large number of iterations mean a strong smoothing effect, and the level of smoothing in the case of image enhancement should be used with more constraints than in the case of image segmentation (Voci et al 2004). 3–4 times of iteration have been used for image smoothing and enhancement (Tian et al 2011), and a larger number of iterations have been used for image segmentation (Li et al 2004, Petrovic et al 2004). Given the fact that iSPREAD is a permutation-based method, a large number of iterations for AD filtering will certainly increase the computational burden. Our experiments show that satisfactory results can be obtained with around 4 iterations and iSPREAD took about 2 – 3 times of computation time of the original SPREAD method. Since the anisotropic filtering was implemented using MATLAB in the current study, a much faster performance can be expected when using C/C++.

The present work can be extended in at least two directions. First, only the scalar images (e.g. FA/MD map) were considered and the diffusivity was designed as a spatial varying scalar in the current study. However, when vector- or tensor-valued images are considered, it is more desirable to rotate the flux towards the orientation of interesting features, such as the tangential direction of structure boundaries (Weickert 1997). In such a case, a 3 × 3 adapted diffusion tensor can be used instead of the scalar diffusivity, in which the smoothing effect along the edges is more preferred than perpendicular to it. Such a filtering technique has been proposed and tested in Ding et al (2005), which proved to be more suitable for the smoothing of bundle-like structures. With the more advanced filtering design, similar analyses can be carried out on other quantities such as fiber tracts or displacement from q-space imaging to help identify differences in generalized FA (GFA) or peaks of diffusion orientation distribution function (ODF). Secondly, longitudinal comparisons between scans at two different time points were considered and discussed for the statistical inference test in this study. Although such repeated measures analyses would give potentially the exact disease progression information at each time point, it is very time consuming for longitudinal studies comprised of multiple time points. In such cases, a voxel-wise statistical inferential test for a serial DTI (with more than two time points) that provides general disease progression information would be preferred. Moreover, it would be a natural extension of this work to carry other summary statistics for investigating disease evolution and performing statistical inferential tests based on the prior information about disease progression models.

5. Conclusion

A 3D nonlinear anisotropic filter was integrated into the iSPREAD method to eliminate the potential shortcomings caused by the Gaussian kernel used in the SPREAD method. The improvements in sensitivity and accuracy in lesion detection introduced by anisotropic filtering were clearly demonstrated by both Monte Carlo simulation and in vivo human brain data. The nonlinear anisotropic filtering allows for noise reduction and reduces grey scale inhomogeneity as well as preserving important image detail, resulting in a better lesion detection when the spatial correlation is heterogeneous among neighboring pixels. As a result, iSPREAD is an effective voxel-wise nonparametric method for detecting local changes in whole brain, subject-specific longitudinal DTI studies.

Figure 2.

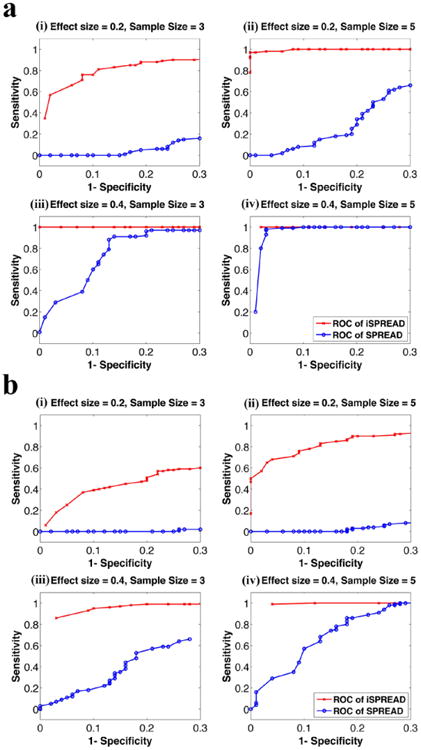
ROC analyses for the two-group comparisons using iSPREAD (red crosses) and SPREAD (blue dots) from Monte Carlo simulated data under different combinations of effect size (es = 0.2, 0.4) and sample size (n = 3, 5) of each group. The disease area was simulated as either a 5 × 5 × 3 cubic region (figure 2(a)) or a 3 × 10 × 3 cuboid region (figure 2(b)). Sensitivity and Specificity were calculated using equation (9). Results for FA analysis are shown here as an example. The nonlinear anisotropic diffusion filtering was used for data smoothing in the iSPREAD method and a Gaussian kernel of fixed FWHM = 2 × 2 × 2 voxels were applied for estimation of spatial regression for SPREAD.

Figure 3.

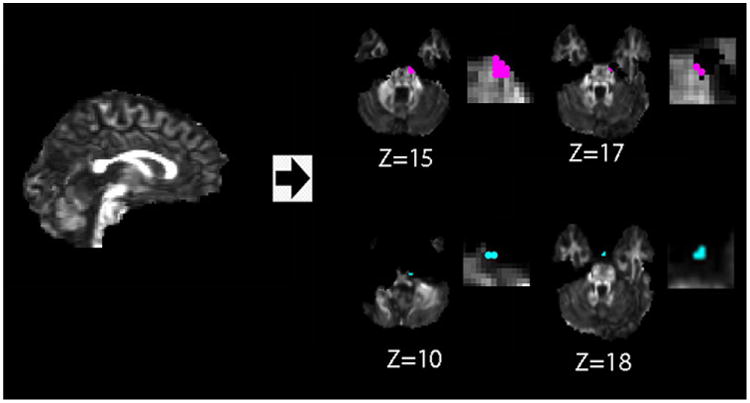
Location of false positive voxels detected (with zoom in images on the right) using iSPREAD analysis in longitudinal DTI data of one healthy volunteer. False positive of FA (red dots) and MD (blue dots) for iSPREAD are mostly occurred due to image misregistration error or BET residuals, either at tissue boundaries or brain boundaries. Figures are displayed according to radiological convention.

Figure 5.

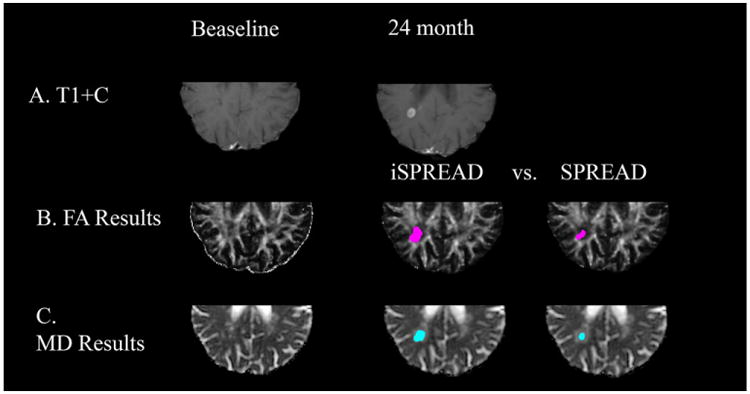
Comparison of significant voxels detected for FA (marked by magenta dots) and MD (marked by cyan dots) using iSPREAD (Row B & C. Second column) and SPREAD (Row B & C. Third volume) analysis of longitudinal data during disease progression for patient 2. This patient had a lesion in the periventricular white matter near the temporal parietal area, which shows enhancement on the post contrast T1 image (Row A) 24 months after the baseline.