B₀ Concomitant Field Compensation for MRI Systems Employing Asymmetric Transverse Gradient Coils

Abstract

Purpose

Imaging gradients result in the generation of concomitant fields, or Maxwell fields, which are of increasing importance at higher gradient amplitudes. These time-varying fields cause additional phase accumulation, which must be compensated for to avoid image artifacts. In the case of gradient systems employing symmetric design, the concomitant fields are well described with second-order spatial variation. Gradient systems employing asymmetric design additionally generate concomitant fields with global (zeroth-order or B₀) and linear (first-order) spatial dependence.

Methods

This work demonstrates a general solution to eliminate the zeroth-order concomitant field by applying the correct B₀ frequency shift in real time to counteract the concomitant fields. Results are demonstrated for phase contrast, spiral, echo-planar imaging (EPI), and fast spin-echo imaging.

Results

A global phase offset is reduced in the phase-contrast exam, and blurring is virtually eliminated in spiral images. The bulk image shift in the phase-encode direction is compensated for in EPI, whereas signal loss, ghosting, and blurring are corrected in the fast-spin echo images.

Conclusion

A user-transparent method to compensate the zeroth-order concomitant field term by center frequency shifting is proposed and implemented. This solution allows all the existing pulse sequences—both product and research—to be retained without any modifications.

INTRODUCTION

MRI ideally utilizes linearly varying magnetic fields to encode position over the imaging field of view (FOV). This linear assumption violates a principle of the magnetic field described by Maxwell’s equations, namely that its divergence is zero, or $\nabla ·\overrightarrow{B}=0$. This deviation from the linear assumption, known analytically and well described for variety of situations, is commonly termed the Maxwell field or concomitant field (1). Note that concomitant fields are created simultaneously with the spatial encoding gradient fields, which differs from eddy currents generated in response to such fields and have associated delay time constants (2,3). The presence of the concomitant fields causes undesired phase to accumulate within the measured k-space data. If not properly accounted for during image reconstruction or pulse sequence design, this results in image blurring and spatial shifts in a variety of applications, including but not limited to phase-contrast (1), spiral (4), fast spin-echo (5), and echo-planar imaging (EPI) (6–8).

For standard, whole-body MR systems, all three cylindrical gradient coils are typically symmetric, that is, the gradient isocenter coincides with the geometrical center of the gradient coil. Due to this symmetry, the leading terms of the concomitant field have second-order spatial dependence. These terms add significant phase contributions to the measured data (1,9); compensation for these effects has been well studied and typically already has been implemented with software modifications on the MR scanners (1,4,5,8). For phase-contrast and EPI applications, a joint pulse sequence and reconstruction correction based on tracking the applied gradient waveform and applying exactly the inverse concomitant fields phase term to the image resulted in almost complete elimination of this artifact (7,8). For spiral imaging, a similar technique, which compensates for the known frequency shift associated with gradient activities during the reconstruction, usually is performed (4).

Previously, head-only or compact gradient systems with asymmetry in the transverse (i.e., physical x and y) gradient axes have been described (10–14). With these gradient coils, the gradient isocenter is shifted along the longitudinal axis toward the patient-entry side of the magnet bore, typically by approximately 10 cm. The reduced size of these gradient coils enables greatly reduced peripheral nerve stimulation compared to whole-body coils (15) and lower self-inductance (16). These in turn permit increased slew rate capability (17), lending themselves to pulse sequences with high-performance gradient requirements such as EPI. Asymmetric gradient coils, however, produce additional concomitant fields with zeroth and first-order spatial dependence, which require additional compensation (18,19).

The first-order concomitant gradient terms result in blurring in spiral, shifting that depends on z-axis slice location in axial EPI, and spatially dependent phase accumulation in a phase-contrast type sequence. A partial correction was proposed in (18) for several imaging sequences. Later, a pre-emphasis method (20) fully compensated for the linear concomitant field without the need for any pulse sequence modification.

The zeroth-order terms manifest as global phase offsets in phase-contrast type imaging, shifts along the phase-encoding direction in axial EPI acquisition, and again as blurring similar to off-resonance in spiral imaging. Previous work (18) suggested protocol changes and gradient lobe reordering to mitigate the concomitant field-induced artifacts and demonstrated the effectiveness of B₀ concomitant field correction with one example; however, it did not describe the specific implementation. The work described in this paper exploits the real-time hardware frequency shift capability for B₀ eddy current correction (2) to fully compensate for the global off-resonance without any pulse sequence or protocol modification. The proposed method is experimentally demonstrated in phantom and volunteer datasets with Cartesian and non-Cartesian acquisitions, including phase-contrast, fast spin echo (FSE), spiral, and EPI.

THEORY

To describe the physical effect, we denote the static main magnetic field as B₀ and by convention denote its direction as z. If we denote the spatiotemporally varying 3D fields inside a MRI scanner as B(x, y, z, t) = [B_x(x, y, z, t), B_y(x, y, z, t), B_z(x, y, z, t)], the B_x and B_y components ideally would be zero, and the longitudinal component satisfies B_z(x, y, z, t) – B₀ = G_x(t)x + G_y(t)y + G_z(t)z. However, the physical constraints asserted by Maxwell’s equation dictate that the ideal linear gradient fields G_x, G_y, and G_z bring along with them well-described B_x and B_y components. The mathematical description of Maxwell fields can be described by looking at the power series expansion of the overall magnetic field experienced by the sample. The overall magnetic field can be expressed as

$$|\mathit{B}(x,y,z,t)|=\sqrt{B_x^2(x,y,z,t)+B_y^2(x,y,z,t)+B_z^2(x,y,z,t)}\approx B_0+G_x(t)x+G_y(t)y+G_z(t)z+B_c(x,y,z,t)$$ [1]

where the first two orders (zeroth- and first-order) represent the spatially invariant magnetic field and the applied linear gradients, and the last term is the concomitant field at time t. Expanded out,

$$B_c(x,y,z,t)=\frac{1}{2B_0}\left[{\left(G_x(t)(z+z_{0x})-\mathrm{\alpha }{G}_z(t)(x+x_0)\right)}^2+{\left(G_y(t)(z+z_{0y})-(1-\mathrm{\alpha })G_z(t)(y+y_0)\right)}^2\right]$$ [2]

where α represents the relative strength of B_x and B_y induced by the G_z field. Variables appearing in Equation [2] are as follows: z_0x and z_0y represent the z-axis offset of the x and y gradient coils, respectively, from isocenter. The terms x₀ and y₀ represent the offset of the z gradient coil in the x and y direction. Equation [2] can be expanded to the first three significant orders, which are the zeroth-, first-, and second-order components, as follows:

$$B_c(x,y,z,t)=B_{c,0th}(t)+B_{c,1st}(x,y,z,t)+B_{c,2nd}(x,y,z,t).$$ [3]

For a symmetric gradient coil system, Equation [3] has a leading order term that is quadratic in the spatial coordinates. For a more comprehensive treatment leading to Equations [1] and [2], we would direct the reader to (1) for the general case and to (18) for a more specific treatment specific to asymmetric gradient systems. Previous works have demonstrated that the second-order terms can be compensated for with pulse sequence modification and reconstruction methods (1,4,5,8). The first-order terms for asymmetric systems are described and compensated for partially in (18) and fully in (20). For asymmetric gradient systems, this leaves the spatially invariant, but time-varying, zeroth-order term described by

$$B_{c,0th}(t)=\frac{G_x^2(t)z_{0x}^2}{2B_0}+\frac{G_y^2(t)z_{0y}^2}{2B_0}+\frac{{\mathrm{\alpha }}^2{G}_z^2(t)x_0^2}{2B_0}+\frac{{(1-\mathrm{\alpha })}^2{G}_z^2(t)y_0^2}{2B_0}-\frac{{\mathrm{\alpha }\mathrm{G}}_x(t)G_z(t)x_0{z}_{0x}}{B_0}-\frac{(1-\mathrm{\alpha })G_y(t)G_z(t)y_0{z}_{0y}}{B_0}$$ [4]

as derived in (18,20). Assuming the typical case of the z-gradient coil being centered along the x and y axes yields x₀ = y₀ = 0. The construction (15) of the x- and y-gradient coils typically is equivalent, thus we can further assume z_0x = z_0y = z₀. Hence, the B_c,0th term simplifies to

$$B_{c,0th}(t)=\frac{z_0^2\left(G_x^2(t)+G_y^2(t)\right)}{2B_0}$$ [5]

The center frequency of demodulation typically is assigned as $f(t)=\frac{\mathrm{\gamma }}{2\mathrm{\pi }}{B}_0$, where $\frac{\mathrm{\gamma }}{2\mathrm{\pi }}$ is the gyromagnetic ratio. The B_c,0th term only affects the temporal shift of the static main magnetic field. By varying the center frequency in time based on the expected effects from the zeroth-order concomitant field (i.e., by introducing a frequency variation by Δf_c,0th(t)), the latter also can be addressed. Specifically, the new demodulation frequency can be expressed as

$$f_{\mathit{new}}(t)=f_0+\mathrm{\Delta }{f}_{c,0th}(t)=\frac{\mathrm{\gamma }}{2\mathrm{\pi }}{B}_0+\frac{\mathrm{\gamma }}{2\mathrm{\pi }}\left(G_x^2(t)+G_y^2(t)\right)z_0^2/2B_0$$ [6]

METHODS

Because the B₀ concomitant field is spatially invariant, adjusting the transmit/receive frequency in real time can be performed, analogous to the method for B₀ eddy current mitigation (2). That strategy was implemented on the scanner hardware in this work.

The correction technique was evaluated with four different acquisition pulse sequences on a lightweight, low-cryogen prototype compact MRI system (GE Global Research, Niskayuna, New York, USA) employing asymmetric gradients with a 37-cm bore diameter and capable of 80 mT per meter (mT/m) sustained gradient amplitude and 700 Tesla per meter per second (T/m/s) slew rate (15). The analytic formula (Eq. [6]) for the frequency offset was implemented on the subsystem responsible for the B₀ eddy current correction, with z₀ = 12 cm and B₀ = 3.0T. With this implementation, the transmit/receive center frequency is updated every 16 μs based on the current gradient amplitudes on the three axes. Note that for all experiments described here, the linear concomitant field preemphasis method described by Tao et al. (20) is enabled, effectively eliminating any phase error arising from the first-order terms.

An axial first-moment-nulled gradient echo sequence with phase difference reconstruction (21) was acquired at isocenter on the American College of Radiology (ACR) quality-control (QC) phantom (22). One of the two acquisitions used for the phase difference reconstruction employed a three-lobed $1\overline{2}1$ (zeroth and first moment nulled) sensitizing waveforms. The first-order moment nulling for the $1\overline{2}1$ waveform minimized any residual flow artifacts from this liquid-filled phantom present after 10 minutes of settling time. The peak gradient amplitude of the phase-contrast pulses of 20 mT/m was chosen to minimize phase wrap; and a 3D spoiled gradient echo sequence was acquired with 128 readout points, ± 15.63 kHz readout bandwidth, and 22 cm FOV. In addition to the $1\overline{2}1$ sequence, a second scan with identical acquisition parameters, but without the phase sensitizing lobes, was acquired to serve as a subtraction reference to exclude phase accrual from off-resonance or other effects such that the effects of zeroth-order concomitant field can be isolated and observed. The phase difference maps with and without the proposed concomitant field compensation were then reconstructed using phase-difference reconstruction algorithm with integrated gradient nonlinearity correction (23).

Scans with the phase sensitizing lobes, as prescribed, also were performed using a software concomitant field correction as a comparison to the hardware compensation. In this software correction, the spurious phase accumulation explicitly is calculated based on the imaging gradient waveforms using Equation [5]. This spatially invariant phase is then subtracted from the reconstructed phase image. In all cases, the second-order concomitant fields also were retrospectively corrected using previously established methods (1).

Next, an axial 2D Archimedean spiral scan with 4,096 readout points and 16 interleaves at a 12-cm FOV was acquired at isocenter on a small ACR phantom for musculoskeletal QC (24). Separate 2D B₀ map sequences also were acquired, which consisted of a two-shot gradient echo with 1 ms echo spacing and matched FOV to the spiral scans, with a 256 × 256 matrix size, ± 15.63 kHz readout bandwidth, repetition time (TR) = 50 ms, and echo time (TE) = 7 ms. The spiral scan data acquired with and without the proposed zeroth-order concomitant field compensation were reconstructed using a noniterative type-III nonuniform fast Fourier transform (NUFFT)–based reconstruction framework, which simultaneously accounts for the off-resonance and gradient nonlinearity correction effects (25). The image matrix size was 256 × 256 for all cases. The NUFFT operators were implemented with a (width 5) Kaiser-Bessel kernel and an (1.25×) oversampled FFT operator (26,27). Off-resonance effect was corrected using time segmentation with 32 segments and Hann window apodization (28). The B₀ field map for off-resonance correction was estimated based on the regularized regression model described by Funai et al. (29), which was solved via a graph cut-based α-expansion procedure (30).

For comparison, the gradient trajectory for the spiral scan also was retained to enable a retrospective, software-based, zeroth-order concomitant field correction to validate the proposed hardware correction. The software correction here takes into account the accumulated phase at each acquired time point based on the history of gradient activity. Removing the spurious phase from the raw signal during reconstruction then eliminated the blurring experienced in an uncorrected spiral image. For all the spiral examples shown here, the effects of the second-order concomitant fields were removed using the previously established method (4).

A 2D axial EPI acquisition with and without the proposed hardware correction was acquired with informed consent on a healthy volunteer under an institutional review board (IRB)-approved protocol. EPI acquisition parameters were as follows: 4-mm slice thickness, 128 × 128 acquired matrix, frequency encoding in the left/right direction, and 22 cm FOV in both x and y directions. Ramp sampling was enabled for these acquisitions, implying the readout bandwidth was set to the system maximum of ±250 kHz.

Finally, a T2-weighted axial fast spin-echo acquisition of the wrist was performed with and without the B₀ concomitant field-correction enabled under an IRB-approved protocol. The acquisition was identical, except for application of the B₀ concomitant field correction, and used the following parameters: axial acquisition; frequency encoding in the left/right direction; 384 × 256 matrix; two averages; 32 2-mm thick slices with 0-mm gap; 10-cm frequency FOV and 7-cm phase FOV; ± 41.7 kHz readout bandwidth; TR of 4,000 ms; effective TE of 52.8 ms; and an echo train length of 8. A single-channel, 10-cm diameter transmit/receive coil was used (BC-10, Medspira, Minneapolis, Minnesota, USA) for all wrist studies.

RESULTS

The phase difference data were analyzed with a region-of-interest (ROI) measurement over the homogenous portion of the phantom. Because the gradient pulse is zeroth- and first-moment-nulled, any deviation from zero phase on the image primarily should be the result of an uncompensated concomitant field and/or eddy currents. Figure 1 shows the phantom image and ROI results, with the uncorrected acquisition showing 0.36 ± 0.18 radians of residual phase. Both the hardware and software corrected results show very small amounts of residual phase accrual, 0.058 ± 0.18 and 0.075 ± 0.18 radians, respectively. These remaining phase accrual results and their spatial deviations likely are due to residual eddy current effects. The substantial reduction in phase accrual after applying the zeroth-order concomitant field correction indicates that, for the phase error in the phase difference, data is dominated by concomitant fields rather than eddy currents.

FIG. 1.

Phase contrast sequence with before correction, after hardware (proposed) and software corrected off-resonance. Phase contrast lobes are zeroth and first moment nulled; therefore, any additional global phase accumulation should be due to the off-resonance induced by the zeroth-order concomitant field. Note that the hardware and software correction results are near zero compared to the precorrection average. ROI, region of interest.

Spiral imaging results are shown in Figure 2. The spiral images were inspected for blurring reduction, and a line profile demonstrates the edge sharpening with the proposed correction. Note that the results without compensating for the zeroth-order concomitant field exhibit substantial blurring, and the line profile is wider compared to those corrected with either the software or hardware correction.

FIG. 2.

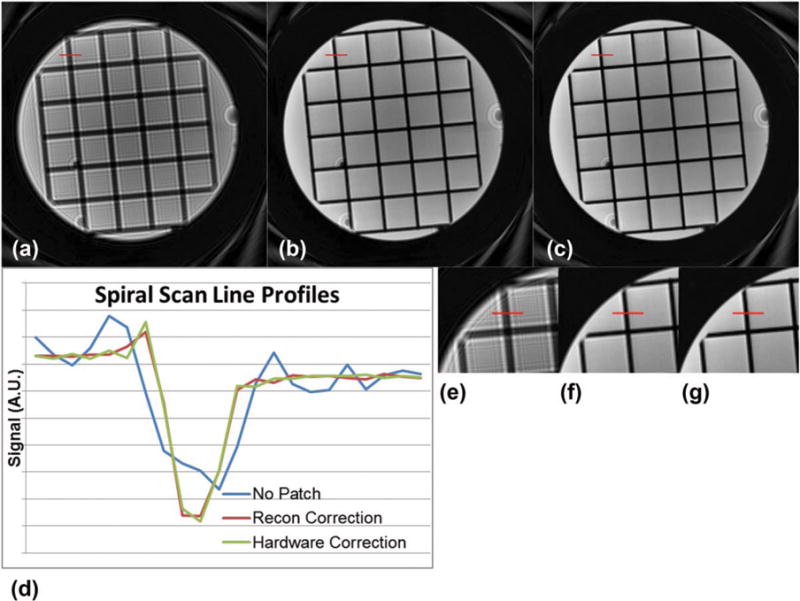
A spiral scan of a small phantom for MSK quality control. (a) is the uncorrected image; (b) is the image with a software correction applied; and (c) is the image with the hardware off-resonance correction. (d) shows line profiles indicated in (e–g) with the same ordering. A.U., arbitrary unit, recon, reconstruction.

The in vivo EPI data are shown in Figure 3, with a reference line drawn across the bottom of the axial head images to show the position shift effect of the zeroth-order concomitant field. Unlike in linear- (20) or second- (8) order concomitant field correction, this is a global shift that does not manifest as local warping, shearing, or blurring. A byproduct of shifting the image toward its true position is that the gradient nonlinearity compensation is applied more accurately. There is some increased geometric distortion evident in the frontal lobes in the uncorrected image in Figure 3, which is reduced in the corrected image.

FIG. 3.

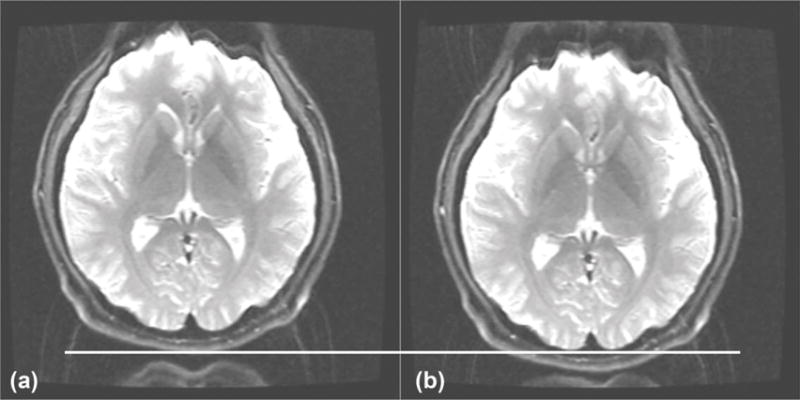
An EPI image of a human brain showing before (a) and after (b) the real-time off-resonance correction. Note the spatial shift as indicated by the line, and also that the shift allows the gradient nonlinearity correction to be more effective given the object is at the expected spatial position. This sequence was set up to illustrate the position shift with EPI and was not optimized for EPI image quality. EPI, echo-planar imaging.

A comparison of the axial T2-weighted wrist image is shown in Figure 4. Aside from a general decrease in signal amplitude, there is a substantial blurring associated with the phase inconsistency from the uncompensated B₀ term (Fig. 4a). In particular, definition of the right edge of the wrist is lost, as well as the boundaries between nerve bundles in the central portion of the image. The high-signal intensity fluid also is smeared out significantly, resulting in a loss of distinction between simple joint fluid, synovium, and cartilage—and vessel wall boundaries are less well resolved. Figures 5a,b illustrate (arrow) the inability to differentiate between joint fluid, synovium, and cartilage, as well as definition (c,d) of the scapholunate and lunatotriquetral ligaments. In each case, the B₀ concomitant field correction (b,d) is required for adequate visualization of the anatomy.

FIG. 4.

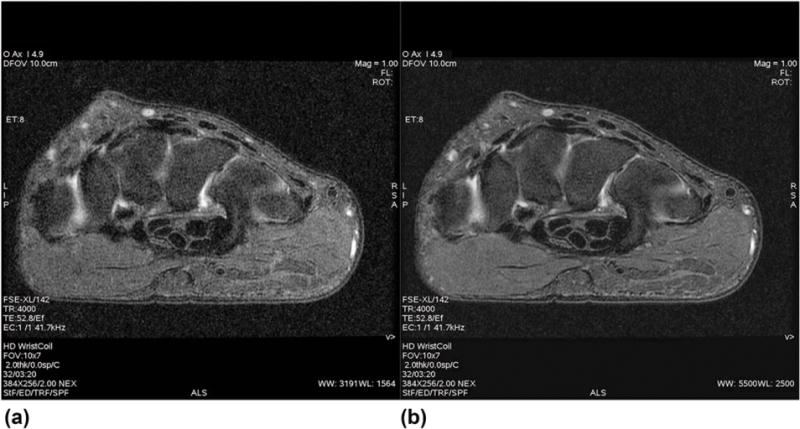
Comparison wrist images without (a) and with (b) the B₀ concomitant field correction. Note the general decrease in signal, as well as overall blurring associated with imaging without compensation for the B₀ concomitant field. FSE, fast spin echo; TE, echo time; TR, repetition time.

FIG. 5.

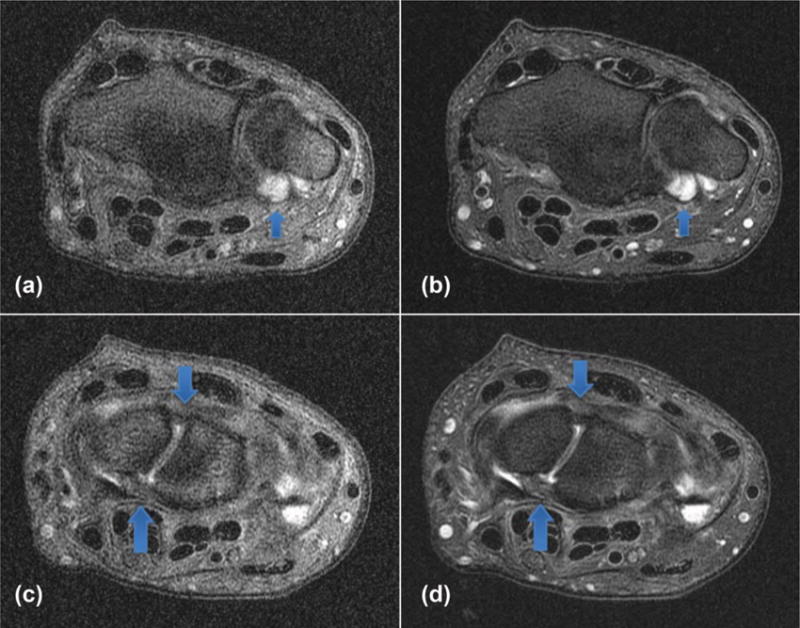
Comparison wrist images without (a,c) and with (b,d) the B₀ concomitant field correction. Note the inability to differentiate between joint fluid and synovial thickening without compensation for the B₀ concomitant field. Also note the general decreased definition and conspicuity of the volar and dorsal components of the scapholunate ligament without compensation (c) for the B₀ concomitant field.

DISCUSSION

A solution to various artifacts due to the zeroth-order concomitant field present with asymmetric gradient systems has been proposed and implemented. Feasibility has been demonstrated across several pulse sequences in phantom and human imaging examples. The method uses the real-time frequency offset subsystem available on the standard MR scanners to correct for B₀ eddy currents. When implemented in conjunction with gradient preemphasis to compensate for the linear concomitant field (20), this work differs from previous efforts (18) in that it does not require any specific protocol or pulse sequence changes to mitigate the artifact. However, the method of frequency shifting to compensate for spatially independent terms is not new, being utilized in (2) and mentioned explicitly in (18,19). This work builds on the prior literature by providing a detailed description of methods to compensate the spatially independent concomitant field, and by presenting imaging experimental results that demonstrate the effective correction of substantial artifacts.

These effects, if uncorrected, could manifest as flow-quantification errors in phase-contrast applications and subpar image quality in spiral, EPI, and FSE acquisitions. Note that with the bulk shift experienced in EPI, interaction with the gradient nonlinearity correction would further distort peripheral regions of the FOV away from isocenter. Another advantage of this real-time hardware compensation is that commonly deployed reference “prescan” (31) eddy current-correction techniques no longer can be confounded by the B₀ concomitant field-induced phase. This can improve the EPI phase correction and reduce Nyquist ghosting in the final EPI images, as compared to adjusting the center frequency manually solely to correct the global position shift. We note that, although many of these effects alternatively could be compensated for during reconstruction, and indeed as demonstrated in Figures 1 and 2, it entails a considerable amount of work. For this solution, the correction for the B₀ shift must be tailored for each individual acquisition. The proposed hardware real-time compensation also will allow for correction of the off-resonance effects in any type of selective excitation, which would not be possible with a retrospective correction. Figure 4 illustrates a substantial effect for a clinical fast spin-echo imaging situation in which the small-FOV wrist imaging aggravates these effects due to the high gradient amplitude demanded by the small FOV and high resolution. Note that the signal loss observed in these FSE examples is due to the incoherent phase accumulation caused by concomitant field, which leads to cancellation of echo signal from the different echo pathways (32). This effect can be compensated using the proposed hardware method but cannot be readily accounted for retrospectively. Additionally, Supporting Figure S1 shows an example of a shift in slice position solely due to the B₀ concomitant field effect during selective slice excitation.

An inability to differentiate between joint fluid, synovium, and cartilage (Figs. 5a,b) introduces the potential for diagnostic error with attendant implications for treatment, including potentially inappropriate therapy. For example, synovitis often is encountered in the clinical setting of inflammatory arthritis and treated with antiinflammatory agents, including disease-modifying antirheumatic drugs, some of which have significant associated side effects. Simple joint fluid may require no subsequent evaluation or treatment, whereas cartilage defects may require surgical repair, particularly in young patients or elite athletes. Artifact-free, high-resolution images are of paramount importance when assessing the intrinsic ligaments of the wrist, such as the scapholunate and lunatotriquetral ligaments in patients with suspected carpal instability (Figs. 5c,d). Similarly, artifact-free fluid-sensitive sequences, typically fat-suppressed proton density or T2-weighted images, can play a critical role in the detection of radiographically occult, nondisplaced stress fractures, particularly of the scaphoid bone. Missed, nondisplaced fractures of the scaphoid waist may go on to complete fractures with associated potential for complications in an individual not receiving appropriate wrist immobilization and protection.

CONCLUSION

In summary, a method for the correction of global frequency shift induced by zeroth-order concomitant field in asymmetric gradient systems is demonstrated with phantom and in vivo experiments. This method does not require any specific pulse sequence or reconstruction modification for an arbitrary imaging protocol, and hence is an ideal solution with the use of asymmetric gradient designs.

Supplementary Material

Figure S1

Fig. S1. Here a very thin slice (0.3 mm) is acquired to emphasize the effect of the 0th order concomitant field in excitation. The thin slice requires a high gradient amplitude in the slice direction. The 0th order concomitant field generated by this high gradient amplitude slice select gradient caused a shift of slice position as emphasized by the red lines. The readout portion of the sequence should cause negligible concomitant field effect due to low bandwidth and small gradient amplitude. (Acquisition Detail: Spin Echo Sagittal FOV = 16 cm × 16 cm; Matrix = 128 × 128; slice thickness = 0.3 mm; TR/TE = 433 ms/11 ms; BW = ±15.6 kHz; Receiver coil = 32-channel Nova, NEX = 2, Phantom = ACR MSK phantom)