Simulating a virtual population's sensitivity to salt and uninephrectomy

Abstract

Salt sensitivity, with or without concomitant hypertension, is associated with increased mortality. Reduced functional renal mass plays an important role in causing salt-sensitive hypertension for many individuals. Factors that are important in the condition of decreased renal mass and how they affect blood pressure (BP) or salt sensitivity are unclear. We used HumMod, an integrative mathematical model of human physiology, to create a heterogeneous population of 1000 virtual patients by randomly varying physiological parameters. We examined potential physiological mechanisms responsible for the change in BP in response to high-salt diet (8× change in salt intake for three weeks) with full kidney mass and again after the removal of one kidney in the same group of virtual patients. We used topological data analysis (TDA), a clustering algorithm tool, to analyse the large dataset and separate patient subpopulations. TDA distinguished five unique clusters of salt-sensitive individuals (more than 15 mmHg change in BP with increased salt). While these clusters had similar BP responses to salt, different collections of variables were responsible for their salt sensitivity, e.g. greater reductions in glomerular filtration rate (GFR) or impairments in the renin–angiotensin system. After simulating uninephrectomy in these virtual patients, the three most salt-sensitive clusters were associated with a blunted increase in renal blood flow (RBF) and higher increase in loop and distal sodium reabsorption when compared with the salt-resistant population. These data suggest that the suppression of sodium reabsorption and renin–angiotensin system is key for salt resistance, and RBF in addition to GFR may be an important factor when considering criteria for kidney donors. Here, we show that in our model of human physiology, different derangements result in the same phenotype. While these concepts are known in the experimental community, they were derived here by considering only the data obtained from our virtual experiments. These methodologies could potentially be used to discover patterns in patient sensitivity to dietary change or interventions and could be a revolutionary tool in personalizing medicine.

1. Introduction

Salt sensitivity is a global health problem and occurs when there is a greater than normal increase in long-term blood pressure (BP) during a sustained increase in salt intake. Approximately half of all hypertensive and one-fourth of normotensive individuals are salt sensitive [1,2]. Salt sensitivity, even without hypertension, is associated with increased mortality [3]. While it is known that early treatment of salt-sensitive hypertension is advantageous, individuals who would benefit the most from salt reduction remain unidentified.

Reduced functional renal mass has been shown to play an important role in causing salt-sensitive hypertension for many individuals including the elderly (the number of functional glomeruli declines 10% per decade even without renal disease [4]), adults who were born with low birth weight [5], and individuals with chronic kidney disease. Certain subpopulations with risk factors (such as age, sex and race) have long-term risk for end-stage renal disease and/or hypertension after donating a kidney, despite being healthy at the time of transplantation [6]. However, factors that are important during decreased renal mass and how they affect the sensitivity to long-term salt intake are unclear.

Salt-sensitive hypertension results from one or more disturbed mechanisms in the renal handling of sodium. Ostensibly, different derangements can manifest similarly, resulting in the same phenotype. Mathematical modelling provides the means to analyse complex relationships and potentially uncover mechanisms that are not feasible experimentally. Physiological models have been previously used for in silico testing through the generation of virtual patients to give insight into pathophysiological function [7]. Recently, topological data analysis (TDA) has been used to separate out subgroups within diseases such as fibromyalgia [8], lung cancer [9] and asthma [10]. Using physiological models with TDA could shed light on important mechanisms that play a role in patient-specific responses to changes in dietary salt and provide clues into which patients benefit the most from reduction of salt intake.

In the present study, we use HumMod, a mathematical model of human physiology that integrates a large number of hormonal, neural and physical factors that influence the salt sensitivity of BP. HumMod was developed by Thomas Coleman and described by Hester et al. [11] as an expansion of the cardiovascular model initially created by Guyton et al. [12]. HumMod contains over 8000 independent variables that interact to regulate multiple physiological systems, including the cardiovascular, renal, endocrine, metabolic and sympathetic nervous systems. This model was not fabricated specifically to simulate salt sensitivity or uninephrectomy, but rather to reflect multiple physiological conditions by incorporating experimental data and fundamental physiological principles. By varying key physiological variables and relationships, we created a diverse population with 1000 virtual individuals. We simulated the population's response to salt loading before and after the removal of the left kidney. We then used TDA in an attempt to separate out different mechanisms responsible for salt sensitivity.

2. Material and methods

2.1. Physiological model

In this study, a patient population was created using HumMod, a large physiological model composed of mathematical relationships based upon well-known principles of cell, tissue and organ physiology. Details of the entire model structure are beyond the scope of this study. How to interact with the graphical user interface and use the model has been previously described [11] and earlier versions of the model are described elsewhere [13–15]. However, a summary of the current model's elements of sodium and volume regulation, renal physiology and other relationships that are relevant to this study and the link to download the entire model and structure code are provided.

In HumMod, the body is divided into intracellular, interstitial and intravascular fluid spaces. Water and electrolyte transport occurs between the interstitial and intravascular compartments through capillary filtration, capillary reabsorption and lymph transport. Lymph flow is influenced by an increase in interstitial pressure, while capillary fluid filtration and reabsorption are determined by Starling forces (hydrostatic and colloid osmotic pressure gradients) across the capillaries and by the various capillary filtration coefficients (appendix A table 2).

The kidney in the model contains both vascular and tubular components, with its total function determined by the functioning nephron number and by various local and neurohormonal factors. Blood flow through the afferent arteriole, glomerulus and efferent arteriole is determined by the pressure gradients and resistances and influenced by local and neurohormonal controls (appendix A, table 3). These factors regulate renal blood flow (RBF) and glomerular filtration rate (GFR), as well as influence peritubular capillary and renal tubular reabsorption. Renal tubular reabsorption is presented as absolute (total) sodium reabsorption rate (mmol min⁻¹) which is not to be confused with fractional reabsorption of sodium (%).

The nephron tubule is divided into proximal tubule, loop of Henle, macula densa, distal tubule and collecting duct (CD). Reabsorption of sodium and water in these segments is influenced by physical factors, sympathetic nervous system and various hormones, including angiotensin II (Ang II) and aldosterone (appendix A, table 4). Reabsorption of sodium and water occurs in the renal tubules, into an interstitial compartment, and ultimately back in the circulation. Additional components of the model that are important for the present study include kidney renin secretion and Ang II formation, aldosterone secretion by the adrenal cortex and atrial natriuretic peptide (ANP) secretion from the heart. Details of the factors that regulate these systems in the model are included in appendix A, table 5.

HumMod's entire code, user interface and supplementary material are available for academic download as a single ZIP file at http://hummod.org/VPH_Clemmer.zip. Currently, HumMod can only be run on computers with a Windows operating system.

2.2. Sensitivity analysis

Using a variant of the Morris method, a previous study varied parameters in the Guyton physiology model and tested changes in model dynamics and model outputs when parameters were deflected from their baseline characterizations [7]. Similarly, we used a sensitivity analysis to observe interactions between parameters and select the important ones that influenced the salt sensitivity of BP in the model. For this analysis, a preliminary simulation was run on 500 virtual individuals where all parameters were randomly varied simultaneously by 5% and subjected to the same salt-loading protocol.

We computed a generalized first-order sensitivity analysis. We write for the model loaded with parameter vector , representing a unique virtual patient, and subjected it to the salt-loading protocol. Ordinary first-order sensitivity to the ith parameter is proportional to the ratio of the variance of the expected value of y for all models that had the best-fit value of p_i, divided by the variance of models where the ith parameter varied freely. Because all parameters were varied continuously, no models could be assured to use the best-fit value of a given parameter. Instead, we compared the variance of the expected value of y when the ith parameter was constrained to lie δ-near its best value to the variance when the ith parameter was constrained to lie more than δ units from its best fit. Early experimentation showed that the ratios were dependent on the δ used and varied between parameters. For this reason, we computed generalized first-order sensitivity at six different levels (), with the unit being standard deviations from best fit. This generated a distribution of ratios with mean μ and σ. We took all parameters that generated at least one ratio that was greater than μ + σ, which yielded 39 parameters (supplementary material). The parameters and variables with the highest degrees of influence on the sensitivity of BP during changes in salt intake were chosen as important variables and included in the parameter set that was varied in the total virtual population.

2.3. Patient population and protocols

Virtual patients (n = 1000) were created by randomly varying (by 5%) renal and cardiovascular parameters. Parameters were chosen based on a sensitivity analysis as described above. In our model, there were significant model effects (the ability of parameters to synergistically affect model outputs).

A uniform distribution was centred on each influential parameter value, with a radius of 5% of the parameter's original value. All 39 variables were varied simultaneously in each of the 1000 virtual patients and the sampled values replaced the original values in HumMod. Two copies of the virtual cohort were made: one with full renal mass and the other with renal mass reduced by 50% by removing the left kidney to simulate unilateral nephrectomy. These patients at full kidney mass were subjected to low, normal and high salt intake (90, 180 and 720 mmol d⁻¹, respectively) for three weeks at each salt level. Patients were defined as either salt sensitive (more than 15 mmHg change in mean arterial pressure (MAP) from low to high salt) or salt resistant (SR) (less than 15 mmHg change in MAP). Unilateral nephrectomy was then simulated by removing the left kidney in the same patients and running the simulation for two weeks to steady state. These virtual patients were then subjected to the same salt-loading protocol. Because all reduced renal mass patients were salt sensitive at the 15 mmHg threshold, we revised the threshold to 20 mmHg in this arm of the study (redefining salt sensitivity as more than 20 mmHg MAP change).

2.4. Topological data analysis

TDA is a collection of techniques that allow the user to view a complex data space as an integrated whole. Other techniques such as cluster analysis or principal component analysis fail at distinguishing local structure in high-feature spaces; TDA is designed to address this problem. We analysed the large dataset from the virtual patients with normal kidney mass using TDA and based on the 20 physiological variables listed in table 1 to create clusters of different subpopulations.

Table 1.

HumMod variables used in the TDA. The changes in each variable from low to high salt intake were used for the clustering.

systolic blood pressure	glomerular filtration rate	distal tubule sodium reabsorption	plasma atrial natriuretic peptide
mean arterial pressure	renal blood flow	collecting duct sodium reabsorption	plasma volume
cardiac output	proximal tubule sodium reabsorption	plasma renin activity	kidney conductance
total peripheral resistance	loop sodium reabsorption	plasma angiotensin II	efferent arteriolar resistance
left atrial pressure	macula densa sodium delivery	plasma aldosterone	afferent arteriolar resistance

Although all 20 variables were used for the analysis, we selected two filters through which all of the data were binned. In this work, we used left atrial pressure and total peripheral resistance (TPR) to bin the data. Bins are overlapping intervals in the plane formed by these two variables, where the number of intervals (k) and the overlap are defined by the user. In the present analysis, we chose k = 42 and an overlap of 20%. In each bin, the data are clustered by an aggregative method. Given a choice of a distance function d and number , data X₁ and X₂ are in the same node provided there exists a sequence

where the Y_i is datum in the bin for . Stated concisely, two data are in the same cluster provided there is a chain of points connecting the two, and the distance between successive points is less than . From this definition, it follows that each datum is in exactly one node (as they appear in figure 5) per bin. Because bins overlap, it is possible for an individual to be in multiple nodes, one for each bin in which it lies. From this, we construct a graph, that is, a collection of nodes and edges linking those vertices. An edge connects two vertices provided they share a datum in common. In this analysis, our aim was to adjust the clustering, filters, intervals and overlap to reach adequate resolution and separation in order to distinguish neighbourhoods of nodes (or clusters).

Figure 5.

Clustering of the 1000 virtual patients with full kidney mass using TDA. Salt-sensitive clusters are designated with darker blue/purple colouring and labelled 1–5. The colour legend indicates the change in blood pressure (BP) from 90 to 720 mmol d⁻¹.

2.5. Statistical analysis

Data in figures 1–4 are presented as mean ± standard deviation, whereas figures 6–9 are presented as mean ± standard error. Differences between kidney masses as well as the difference between each cluster with the SR population were compared using an unequal variance t-test. There were significant differences (p < 1 × 10⁻¹⁰) between kidney masses at every data point in figures 1–4, but statistical markers were not used for user readability. For comparisons between clusters, probability of p < 0.05 was accepted as statistically significant.

Figure 1.

Mean arterial pressure (MAP), cardiac output (CO) and total peripheral resistance (TPR) during chronic changes in salt intake (90–720 mmol d⁻¹). (a) MAP, (b) CO and (c) TPR for normal (100% kidney mass) are denoted by solid lines and by dotted lines for the nephrectomy simulation (50% kidney mass).

Figure 4.

Reabsorption of sodium (Na⁺) at different nephron segments at different salt intakes. (a) Proximal tubular (PT), (b) loop, (c) distal tubular (DT) and (d) collecting duct (CD) Na⁺ reabsorption in mmol min⁻¹ for the entire population at two kidney masses.

Figure 6.

Absolute changes from low to high salt in (a) mean arterial pressure (MAP) and (b) total peripheral resistance (TPR) of the salt resistant (SR) and salt-sensitive clusters (1–5) in the full kidney mass population.

Figure 9.

Absolute changes in (a) mean arterial pressure (MAP), (b) plasma angiotensin II (Ang II) concentration, (c) renal blood flow (RBF), (d) glomerular filtration rate (GFR), (e) afferent arteriolar resistance and (f) loop sodium (Na⁺) reabsorption from low to high salt for the original salt resistant (SR) and salt-sensitive clusters (1–5) at 50% kidney mass.

3. Results

3.1. Whole population physiology before and after nephrectomy

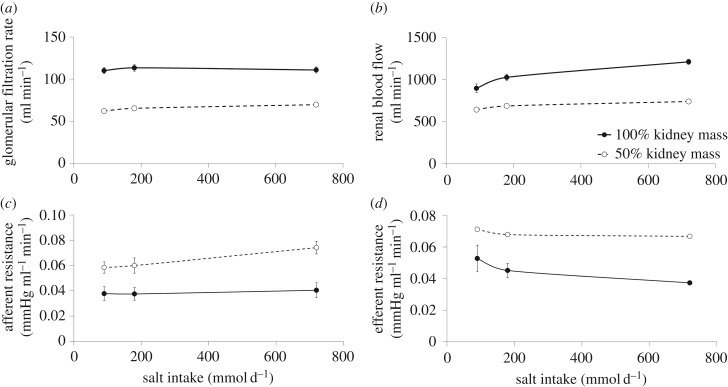
After increasing salt intake from 90 to 720 mmol d⁻¹ (for three weeks at each intake), the full population had a BP increase of 15 ± 1 mmHg before uninephrectomy and an increase of 22 ± 2 mmHg after the kidney removal (figure 1a). There was an increase in cardiac output (CO) with salt loading in both the full and 50% kidney mass populations, but the full kidney mass population had significantly higher CO (figure 1b). Similarly, both populations were associated with an increase in TPR with high salt intake; however, the uninephrectomized population had greater increase in TPR (0.0024 mmHg ml⁻¹ min⁻¹) when compared with before the kidney removal (0.001 mmHg ml⁻¹ min⁻¹) (figure 1c).

There were no robust changes in GFR with increasing salt intake; and as expected, GFR was reduced (−41 ± 0.02%) after uninephrectomy (figure 2a). The uninephrectomy population had significantly greater changes in GFR with salt (7.6 ± 1 ml min⁻¹) when compared with normal (1 ± 4 ml min⁻¹) (figure 2a). The increase in RBF from low to high salt intake, however, was significantly greater in the normal population (315 ± 45 ml min⁻¹) when compared with after nephrectomy (97 ± 8 ml min⁻¹) (figure 2b). The afferent and efferent arteriolar resistances were greater in the uninephrectomy population (figure 2c,d, respectively), while plasma Ang II was higher in the normal population at every salt intake (figure 3a). There was a decrease in plasma aldosterone (figure 3b) with increasing salt intake with minor differences between the two groups. Plasma ANP was slightly but significantly decreased with uninephrectomy (figure 3c). ANP increased as salt intake increased and was correlated with sodium and volume retention (not shown).

Figure 2.

Renal haemodynamics and renal resistance during changes in salt intake. (a) Glomerular filtration rate, (b) renal blood flow, (c) afferent arteriolar resistance and (d) efferent arteriolar resistance during changes in salt intake from 90 to 720 mmol d⁻¹ in the virtual population before and after kidney removal.

Figure 3.

Plasma angiotensin II (Ang II), aldosterone and atrial natriuretic peptide (ANP) in response to chronic changes in salt intake. Changes in (a) Ang II, (b) plasma aldosterone and (c) ANP from low to high salt intake.

Proximal tubular (PT) sodium reabsorption (figure 4a) decreased with higher salt intake at both kidney masses, while loop, distal tubule and CD were associated with increasing sodium reabsorptions as salt intake increased (figure 4b–d, respectively). As expected, at every tubular segment, uninephrectomy significantly decreased total sodium reabsorption at each salt intake (figure 4).

3.2. Clustering with topological data analysis

TDA on the full kidney mass population revealed a complex structure which is separated by 20 physiological variables (table 1) and coloured with the change in BP from low to high salt intake (figure 5). There were five distinct spars of individuals that deviated from the main structure; these spars were labelled Clusters 1 to 5, left to right (figure 5). There were also unconnected patient clusters that are displayed in the lower part of the figure.

The five clusters of salt-sensitive individuals had similar BP responses to salt (figure 6a), but significantly different underlying physiological responses. For example, when compared with the SR population, Clusters 1 and 2 had a blunted increase in TPR during high salt intake, whereas Clusters 3, 4 and 5 had a greater increase in TPR (figure 6b). Additionally, Clusters 1 and 2 had a fall in GFR during high salt intake, while SR and the other salt-sensitive clusters had an increase in GFR (figure 7a). During high salt intake, Cluster 5 was associated with a greater increase in GFR when compared with the SR population (figure 7a). Clusters 1 and 2 also had a greater increase in RBF when compared with the SR population, whereas Clusters 4 and 5 and a blunted increase in RBF (figure 7b). The increase in afferent arteriolar resistance was greater in Clusters 4 and 5 and compared to the SR population (figure 7c), whereas the efferent arteriolar vasodilation was greatest in Clusters 1 and 2 in response to high salt intake (figure 7d).

Figure 7.

Absolute changes from low to high salt in (a) glomerular filtration rate (GFR), (b) renal blood flow (RBF) and renal (c) afferent and (d) efferent arteriolar resistances for the salt resistant (SR) and salt-sensitive clusters (1–5) in the full kidney mass population.

When compared with the SR population, Clusters 1 and 2 had significantly greater suppression of the renin–angiotensin system, whereas Clusters 4 and 5 had an impaired suppression of plasma Ang II (figure 8a). This was associated with similar patterns in the change in PT sodium reabsorption (figure 8b). In response to increasing salt intake, Clusters 1, 2 and 3 had greater increase in loop and distal sodium reabsorption, whereas Cluster 5 had a blunted increase when compared with the SR population (figure 8c,d, respectively).

Figure 8.

Absolute changes from low to high salt in (a) plasma angiotensin II (Ang II) concentration, (b) proximal tubular (PT) sodium (Na⁺) reabsorption, (c) loop Na⁺ reabsorption and (d) distal tubular (DT) Na⁺ reabsorption for the salt resistant (SR) and salt-sensitive clusters (1–5) in the full kidney mass population.

The clusters that were salt sensitive at full kidney mass were also salt sensitive after uninephrectomy when compared with the SR population (figure 9a). Although the five salt-sensitive clusters had similar BP responses to salt with full kidney mass, after uninephrectomy these patient subpopulations had different magnitudes of salt sensitivity when moving from Cluster 1 to Cluster 5 in an increasing manner (figure 9a) (although the increase in BP in Clusters 4 and 5 was not statistically different, not shown). Interestingly, the most SR cluster after uninephrectomy (Cluster 1) was associated with greater suppression of Ang II (figure 9b), similar increase in RBF (figure 9c) and similar increase in loop sodium reabsorption (figure 9f) when compared with the SR population. Conversely, the most salt-sensitive clusters' uninephrectomy (Cluster 4 and 5) was associated with an impaired suppression of Ang II, blunted increase in RBF, greater increase in afferent arteriolar resistance, and greater increase in loop sodium reabsorption when compared with the SR population (figure 9). GFR increased in all individuals with one kidney, with salt sensitivity associated with a slightly lower increase in GFR when compared with the SR population (figure 9d).

4. Discussion

TDA separated out five different salt-sensitive clusters with different physiological responses and underlying mechanisms. Our results suggest that individuals with a similar magnitude of salt sensitivity can have different underlying physiology and different responses to reductions in kidney mass, and thus potentially differing in risks and optimal treatment modalities.

HumMod is a mathematical model of integrated physiology that demonstrates complex physiological interrelationships. The model has been developed over 45 years with it currently containing over 8000 variables and approximately 2000 nonlinear, physiological relationships derived from experimental data reported in the literature [12,16]. It should be re-emphasized that HumMod was not constructed specifically to simulate salt sensitivity, but it is the result of incorporating physiological principles to simulate multiple physiological conditions. Important findings from our simulations and analysis include: (i) HumMod can successfully create a heterogeneous population with responses and response variability similar to human responses to high salt intake and/or kidney mass reduction and (ii) TDA revealed multiple mechanisms of salt sensitivity in the virtual population.

4.1. Salt sensitivity in the total population with full kidney mass

HumMod created a population that is comparable, but slightly more salt sensitive than what would be expected for ‘normal’. At normal kidney mass, the population's response to high-salt diet was associated with a moderate increase in BP. This BP change (approx. 0.05 mmHg mmol⁻¹ of salt) is similar to human responses to salt. Bray et al. demonstrated a small increase in BP (approx. 0.03 mmHg mmol⁻¹ of salt) in a healthy control population (n = 121) [17]. The population was also characterized by an increase in GFR, increase in RBF and a significant decrease in plasma Ang II, which is similar to responses in humans and animals [18]. All segments were associated with a decreased fractional reabsorption of sodium (not shown). Conversely, besides PT sodium reabsorption, all tubular segments in the model increased absolute sodium reabsorption in response to high-salt diet (figure 4), which was associated with increased delivery of sodium in these segments (not shown). Renal tubular responses to changes in sodium intake have not been well characterized in humans. Some studies, however, have estimated proximal and distal sodium reabsorption using lithium clearance. For example, in men with normal BP, a high-salt diet significantly increased distal tubular (DT) sodium reabsorption, while there was a decreased trend in PT reabsorption [19]. These clinical and experimental data suggest that HumMod created a valid and realistic human population response to changes in salt intake.

4.2. Responses to uninephrectomy

Live kidney donation in the USA has risen over the past three decades to approximately 6000 yr⁻¹ due to the increased need for kidney transplants, the increased shortage of cadaveric kidneys, the superior outcome of live renal transplants and the expanded/relaxed criteria for a donor [20,21]. While some studies have shown that kidney donors have no long-term increase in BP [22–24], this has not been a universal finding [25,26]. However, it is well known that a decreasing kidney mass or GFR increase salt sensitivity [27–29] and poses a risk for higher BP in our high-salt-consuming culture. Unfortunately, the average salt intake for Americans greatly exceeds their physiological need. The ideal treatment for patients with salt sensitivity would be decreasing salt intake, but this remains an inefficient solution due to patient non-compliance and reluctance to change lifestyles and habits [30].

The increase in salt sensitivity after uninephrectomy was associated with blunted increase in RBF and greater increase in afferent arteriolar resistance (figure 2). Experimentally, salt-sensitive patients have been shown to have smaller increase in RBF in response to high-salt diets when compared with SR patients [18,31,32]. Additionally, the ability to suppress Ang II was also impaired in this population (figure 3a) which has also been shown to be associated with salt sensitivity [33]. These data suggest that the nephrectomy simulation is similar to the actual salt sensitivity seen in humans with lower kidney mass.

4.3. Topological data analysis and mechanisms of salt sensitivity

Investigators have used TDA to examine highly complex datasets and to separate out noise to identify important subgroups of patients [8–10]. For example, examining 1500 tumour genes from breast cancer patients with TDA produced unique subgroups, while standard techniques did not. Interestingly, TDA revealed a small group of patients who were expected to respond poorly to chemotherapy using a common heuristic, but actually survived [34]. This subpopulation was confirmed in another dataset of different patients, a difficult feat to perform with classical statistical tools alone. In the current study, TDA on the full kidney mass population revealed five different subpopulations of salt-sensitive individuals. Interestingly, these clusters were different in their salt sensitivities with lower kidney mass, suggesting TDA classified unique physiological subtypes of salt sensitivity with a single kidney in the model. Our results suggest that individuals with a similar magnitude of salt sensitivity can have different underlying physiology and different responses to reductions in kidney mass, and thus potentially differing in risks and optimal treatment modalities.

A single disease or disorder, such as salt-sensitive hypertension, is commonly treated as a single physiological derangement where clinicians treat every individual person similarly. However, the results from TDA on a virtual patient population suggest that some individuals might be at greater risk for salt-sensitive hypertension after reductions in kidney mass than others and that these individuals may require treatment modalities that differ from the normal presentation of a disorder. For example, African-Americans are more salt sensitive [17] and have been associated with blunted increase in RBF and increase in renal resistance in response to high salt intake [35]. This mechanism of salt sensitivity (blunted ΔRBF and increased Δ renal resistance) resembles Clusters 4 and 5 (figure 7). Another mechanism of salt sensitivity is resembled by Clusters 1 and 2, which had greater suppression of the renin–angiotensin system and greater decrease in PT sodium reabsorption during high salt intake (figure 8). This would imply that an angiotensin converting enzyme (ACE) inhibitor or Ang II receptor blocker (ARB) in this scenario may be less effective at lowering BP. However, these patient clusters were also associated with greater increase in loop and DT sodium reabsorption (figure 8), suggesting a loop diuretic and/or thiazide treatment would be ideal for this patient population. Finally, at higher salt intakes (or poor patient compliance), ACE inhibitors or ARBs, calcium channel blockers and loop diuretics, or a combination of these might be the most effective hypertensive treatment in a patient population with low renal mass, similar to Clusters 4 and 5 after uninephrectomy. However, during an increased salt intake with full kidney mass, these clusters had similar increase in loop sodium reabsorption when compared with the SR population. This suggests a loop diuretic in patients similar to these clusters may be especially effective if there is low kidney mass. Similarly, in patients who have low kidney function or chronic renal insufficiency, clinical studies demonstrate that loop diuretics are typically the drug of choice [36]. These results suggest that our virtual population created from our physiological model, paired with an advanced analysis technique, separated out known human pathophysiology and possibly physiological mechanisms that are not currently recognized.

5. Conclusion

These data are both a proof of concept of established physiology and a tool to generate new hypotheses and insights for patient-specific medicine. Using physiological modelling with TDA allows insight into important mechanisms involving patient-specific responses to changes in dietary salt. These data also suggest that certain pharmacological treatments may provide more appropriate care for patients with compromised renal mass.

Appendix A

Table 2.

Volume and water transport regulation. Total body water is calculated by the sum of three regions (torso compartments), each of which is divided into intracellular and interstitial spaces. Important calculation, variables, parameters are listed. Also included is a diagram of the water flux between the total intracellular, interstitial, and plasma fluid spaces with approximate volumes.

Table 3.

Control of renal vascular resistance and GFR. The dependent variables are displayed in the left column while factors and effects that impact the dependent variables are listed in the middle column, along with their effect range and input variable that determines the effect.

Tubuloglomerular feedback, TGF; atrial natiuretic peptide, ANP; filtration fraction, FF; single nephron glomerular filtration rate, SNGFR; proximal tubule, PT; capillary hydrostatic pressure, P_C; Bowman's Capsule hydrostatic pressure, P_BC; capillary colloid osmostic pressure, P_osm.

^*Indicates a negative relationship.

Table 4.

Control of sodium reabsorption in the nephron. The dependent variables are displayed in the left column while factors and effects that impact the dependent variables are listed in the middle column, along with their effect range and input variable that determines the effect.

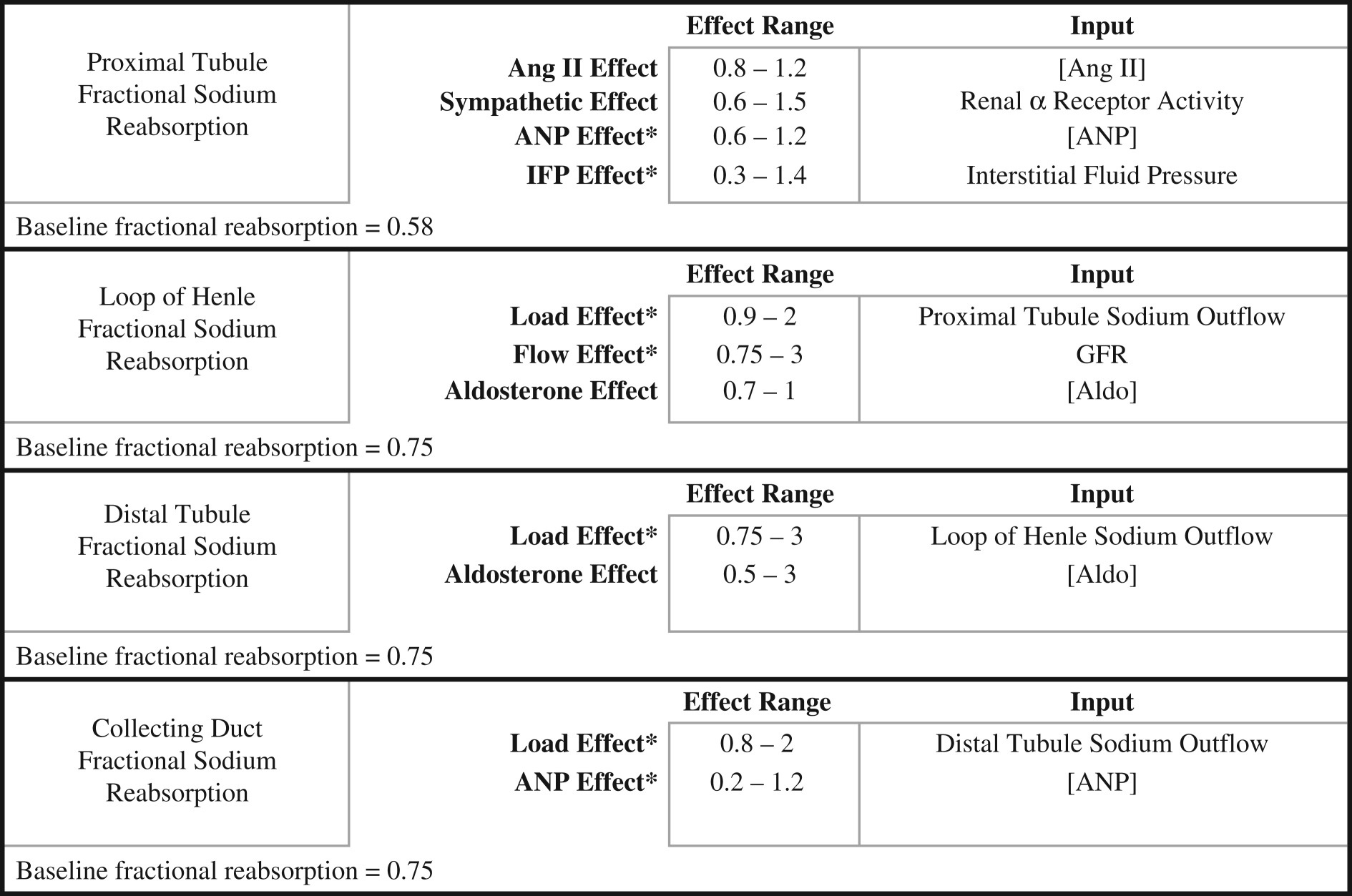Angiotensin II, Ang II; atrial natiuretic peptide, ANP; renal interstitial fluid pressure, IFP; glomerular filtration rate, GFR; aldosterone, Aldo.

^*Indicates a negative relationship.

Table 5.

Regulation of TGF and hormones. The dependent variables are displayed in the left column while factors and effects that impact the dependent variables are listed in the middle column, along with their effect range and input variable that determines the effect. Calculations are provided for some variables where indicated.

Atrial natiuretic peptide, ANP; angiotensin II, Ang II; Goldblatt Units, GU; volume of distribution, VD; angiotensin converting enzyme activity, ACE_Activity; plasma renin activity, PRA; extracellular fluid volume, ECFV; potassium concentration, [K+]; adrenocorticotropic hormone, ACTH; gram of tissue, G; aldosterone, Aldo; total body water, TBW; right atrial pressure, RAP; left atrial pressure, LAP.

^*Indicates a negative relationship.

Data accessibility

This article has no additional data.

Authors' contributions

J.S.C., W.A.P. and R.L.H. developed the concept and design of the research, interpreted results, edited and revised the manuscript and approved the final version of manuscript; J.S.C. performed experiments, analysed data, prepared figures and drafted the manuscript.

Competing interests

No conflicts of interest, financial or otherwise, are declared by the authors.

Funding

Our research was supported by grants from the American Heart Association (AHA 17POST33661071), the National Heart, Lung and Blood Institute (PO1 HL51971), the National Institute of General Medical Sciences (P20 GM104357) and the National Science Foundation (NSF EPS 0903787).