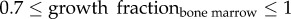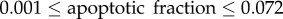A study on the predictability of acute lymphoblastic leukaemia response to treatment using a hybrid oncosimulator

Abstract

Efficient use of Virtual Physiological Human (VPH)-type models for personalized treatment response prediction purposes requires a precise model parameterization. In the case where the available personalized data are not sufficient to fully determine the parameter values, an appropriate prediction task may be followed. This study, a hybrid combination of computational optimization and machine learning methods with an already developed mechanistic model called the acute lymphoblastic leukaemia (ALL) Oncosimulator which simulates ALL progression and treatment response is presented. These methods are used in order for the parameters of the model to be estimated for retrospective cases and to be predicted for prospective ones. The parameter value prediction is based on a regression model trained on retrospective cases. The proposed Hybrid ALL Oncosimulator system has been evaluated when predicting the pre-phase treatment outcome in ALL. This has been correctly achieved for a significant percentage of patient cases tested (approx. 70% of patients). Moreover, the system is capable of denying the classification of cases for which the results are not trustworthy enough. In that case, potentially misleading predictions for a number of patients are avoided, while the classification accuracy for the remaining patient cases further increases. The results obtained are particularly encouraging regarding the soundness of the proposed methodologies and their relevance to the process of achieving clinical applicability of the proposed Hybrid ALL Oncosimulator system and VPH models in general.

1. Introduction

The shared long-term objective and vision of the emerging interdisciplinary fields of in silico oncology, in silico medicine [1,2] and the Virtual Physiological Human (VPH) Initiative (http://www.vph-institute.org/) [3] is the development of computational models that contribute to the personalization of disease treatment, primarily through their potential predictive capabilities. Among several significant contributions reported in the domain so far, a VPH-type multiscale model, with the aim of simulating acute lymphoblastic leukaemia (ALL) progression and response to treatment, has been developed, clinically adapted and evaluated. The latter took place in the context of the European Commission-funded p-medicine project (‘p-medicine—from data sharing and integration via VPH models to personalized medicine’, http://www.p-medicine.eu/). The aforementioned model, called the ‘ALL Oncosimulator’, was originally presented at the VPH2014 conference [4]. In this paper, a set of additional methodologies based on computational optimization and machine learning (ML) approaches, with the aim of expanding its predictive capabilities and supporting their evaluation, are presented.

ALL is the most common neoplastic malignancy in children, with thousands of young patients diagnosed every year and a significant percentage of them being recruited in ALL-BFM clinical trial series (http://www.bfm-international.org/). In the majority of treatment schemes, including those proposed by the ALL-BFM trials, a pre-phase treatment, primarily referring to the administration of glucocorticoids [5], is initially followed. In the context of the ALL-BFM clinical trial series, from which the data used in the present study originate, the pre-phase treatment lasts 7 days and involves the administration of daily doses of prednisone (glucocorticoid) and one dose of methotrexate. The response to this treatment cycle (usually reported as prednisone response) is assessed by observing the peripheral blood blast cell count on day 8 of treatment. This result is a strong prognostic factor for the stratification of patients into risk groups [5,6]. Patients showing lower than 1000 lymphoblasts per microlitre are characterized as good responders, while patients with more lymphoblasts are characterized as poor responders. In the context of the present study, we have focused on this treatment phase so that the development of the ALL Oncosimulator and the supporting methodologies, as well as the investigation of their performance, could be based on real and well-defined clinical scenarios and questions.

The ALL Oncosimulator, as with any model of its kind, should be parameterized as precisely as possible in order for its simulation results to approach clinical reality and gain descriptive and potentially predictive value. The latter is dictated by properties such as the sensitivity observed in its response regarding the choice of parameter values [7,8]. Referring to retrospective patient cases, for which both the pre- and post-treatment data are available, the estimation of the model parameter values can be achieved using adaptation/parameter estimation methods. For a newly introduced case, however, an alternative approach should be followed. This is due to the availability of only pre-treatment information, medical examination results or any other types of data. Therefore, the necessity for the addition of extra components to the ALL Oncosimulator clearly emerges. First, these components should be able to identify the correct parameter set input of the ALL Oncosimulator for the retrospective patient cases (i.e. to optimize the input parameter set so as the output of the model adequately matches a patient's post-treatment disease state). Second, they should be able to predict as accurately as possible the parameter input sets that would lead to a sound prediction of the treatment outcome for a newly arrived patient before this treatment is administered. Therefore, on the one hand, computational optimization methods should be exploited for the adaptation/parameter estimation of the ALL Oncosimulator input for retrospective patient cases. On the other hand, ML methods that would try to learn the relationship between personalized patients' data and the best possible oncosimulator parameterization for each patient case should be developed. The combination of these methods with the Oncosimulator leads to the formulation of a hybrid computational model consisting of a mechanistic part and several computational optimization and ML-based components.

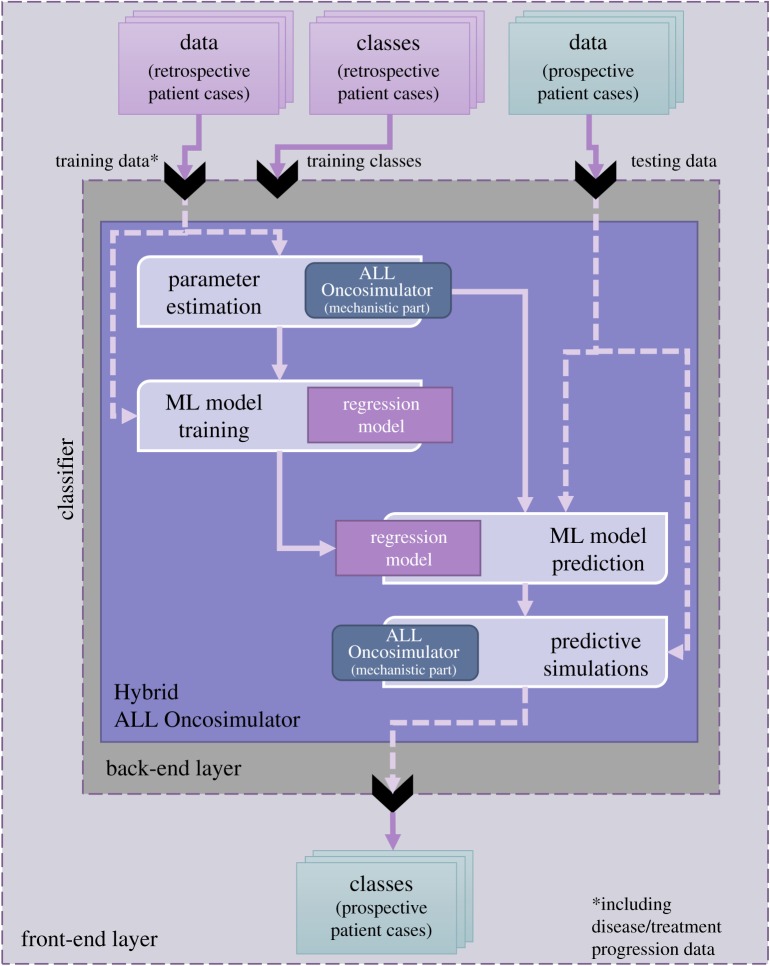
In this context, an adaptation methodology of the ALL Oncosimulator on retrospective patient cases and regression models with the aim of predicting a personalized value for the chemosensitivity-related parameter of the ALL Oncosimulator for prednisone have been presented and evaluated in [4]. Training of the regression models was based on pathway-aggregated [9] gene expression profiles. Moreover, the first results of an extended, fully automated and complete workflow for estimating and predicting the parameter values of the ALL Oncosimulator were presented at the VPH2016 conference [10]. Based on the previous efforts, a detailed presentation and a more thorough study of the Hybrid ALL Oncosimulator is provided in this paper. Despite the complexity of the assembled system, the end user may interact with the latter at the front end as if they interacted with any classifier. This is illustrated in figure 1.

Figure 1.

The Hybrid ALL Oncosimulator abstract structure and front-end and back-end layers. At the front-end, the user interacts with the system as with a classifier. At the back-end, the data provided for the retrospective cases (which should include disease/treatment progression data) are used for the estimation of the ALL Oncosimulator parameters and for the training of a regression model that is subsequently used for parameter value prediction for the prospective cases. The predicted values are passed to the ALL Oncosimulator resulting in the final classification via multiple simulations.

In the context of the present study, the model is used in order to predict the pre-phase therapy effect in childhood ALL patients. The basic evaluation criterion has been the accuracy in classifying a patient in either of the two prednisone response groups. This has been assessed in a cross-validation manner, explained in detail in the text. Taking into account the prognostic value of this classification in clinical practice and setting, the correct prediction of the prednisone response before the initiation of the treatment may facilitate the optimal treatment decision to be taken by the clinician at an earlier stage. Ideally, the validity and the added value of this prediction should be additionally assessed in the context of a prospective trial, a concept that is further discussed in subsequent parts of the paper.

2. Models and data

2.1. Available data

The data used in the present work originate from a cohort of 191 patients enrolled in the ALL-BFM 2000 clinical trial. For this specific group of patients, in addition to a set of commonly collected clinical variables and disease progression data (leukaemic blast counts), whole-genome expression measurements were made available. This molecular part of the dataset consists of log₂ R/G normalized ratio (mean) measurements for 39 778 probes (annotated as IMAGE CloneIDs). Details on the gene expression data accumulation procedure are given in [11]. Both clinical and gene expression data have been provided in an anonymized form within the framework of the p-medicine EU-funded project (FP7-ICT-2009-6-270089). All patients had received a pre-phase treatment, i.e. 7-day prednisone monotherapy with 60 mg m⁻² per day and one dose of intrathecal methotrexate on day 1 [12]. The eligibility criteria for the present study, except for the provision of whole-genome expression data, have been the availability of leukaemic blast counts before the initiation of treatment and at day 8 of treatment (immediately after the completion of the pre-phase treatment). Moreover, as suggested in [11], patients presenting BCR-ABL, MLL-AF4 or TEL-AML1 rearrangements, together with patients with DNA index measurement different from 1, were also excluded from the subsequent steps of the analysis, resulting in the inclusion of 87 patient cases in the study cohort. Table 1 presents several statistical properties of the available exploitable data.

Table 1.

Statistical properties of the available exploitable data.

factor
age	<10 yr (0.54%)	>10 yr (0.46%)
gender	female (41%)	male (59%)
white blood cell count at diagnosis (lymphoblasts per µl)	<50.000 (41%)	>50.000 (59%)
prednisone response	good (44%)	poor (56%)
immunophenotype	B-lineage ALL (78%)	T-lineage ALL (22%)

2.2. The acute lymphoblastic leukaemia Oncosimulator: the mechanistic part of the model

A mechanistic model called the ALL Oncosimulator simulating ALL progression and response to pre-phase treatment, as is followed in ALL-BFM clinical trial series, has been developed in the context of the European Commission-funded p-medicine project (http://www.p-medicine.eu/). The model was originally presented in [4]. The latter constitutes an extensive modification of algorithms and models (oncosimulators) previously proposed by the In Silico Oncology and In Silico Medicine Group (http://in-silico-oncology.iccs.ntua.gr/) for example [1,7,13–16]. Changes have been dictated by the special nature of ALL (non-solid tumour). It is noted that the terms Oncosimulator, ALL Oncosimulator and mechanistic part of the ALL Oncosimulator are used interchangeably throughout the text.

The core algorithmic formulation of the aforementioned Oncosimulators, including the ALL Oncosimulator, is based on the extensive use of cellular automata. The new feature of the ALL-specific model is the consideration of more compartments for proliferating and dormant cells. In classical oncosimulators [1,7,13–16], cycling cancerous cells are distributed over four-cell classes corresponding to the four phases of the active cell cycle (G1, S, G2 and M), whereas resting G0 cells constitute a single-cell class.

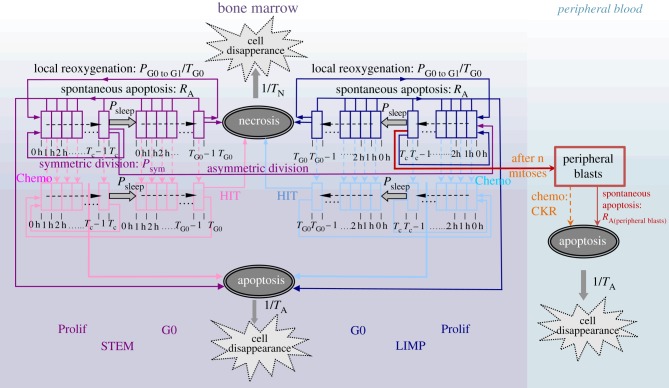
The ALL-specific model considers a number of cell classes for the proliferating or resting G0 cells, equal to the discrete duration of the active cell cycle or the resting phase, respectively, expressed in hours. More specifically, each cell class corresponds to a time interval equal to 1 h within the corresponding cell cycle phase (figure 2). The ALL cell multiplication rules of the model are based on the well-documented hypothesis of cancer stem cell theory [17–19]. Two major cancer cell compartments are distinguished: the bone marrow (BM) and the peripheral blood. The model assumes that leukaemic cancer stem cells are located in the BM and have the ability of unlimited self-renewal and differentiation. For this compartment, three additional leukaemic cell categories are considered: limited mitotic potential (LIMP) or restricted/committed progenitor cells, apoptotic cells and necrotic cells. Stem and LIMP cells can be either proliferating or resting, distributed over the cell classes previously described. The peripheral blood, in which peripheral leukaemic blasts are circulating, serves as the second cellular compartment of the model. As a first approximation, peripheral blasts are considered quiescent.

Figure 2.

ALL Oncosimulator generic cytokinetic model of bone marrow and peripheral blood cell compartments (cell category/phase transition diagram) for cancer response to chemotherapy. STEM, stem cell; LIMP, limited mitotic potential cancer cell (also called committed or restricted progenitor cell). Prolif, proliferating cell; G0, dormant cell; Chemo, chemotherapeutic treatment; HIT, lethally hit cells by the drug.

The model simulates a plethora of cellular and super-cellular bio-mechanisms, which are: (a) progression of proliferating cells through the active cell cycle, the ‘exit’ of proliferating cells to the resting G0 phase and the cell cycle re-entering of G0 cells, (b) symmetric and asymmetric divisions of stem cells, the former giving rise to daughter cells with stem-like cell fate and the latter giving rise to two distinct daughter cells, one with a stem-like and one with a LIMP-like cell fate (c) maturation arrest of LIMP cells after performing a limited number of divisions and entrance to circulation (i.e. to the peripheral blood compartment) through the mitosis phase and (d) cell loss primarily via apoptosis (either spontaneous or treatment-induced) in both BM and peripheral blood compartments. The rules governing the transition between the various cell compartments are depicted in figure 2. Additionally, the set of parameters related to these processes are listed and described in table 2.

Table 2.

ALL Oncosimulator (mechanistic part) input parameters and their ranges.

parameter	description	range set during parameter estimation	references
Tc	cell cycle duration	24–200 h	[20–23]
TG0	duration of dormant (G0) phase	0–120 h	(estimated)b
TN	time needed for both necrosis to be completed and its lysis products to be removed from bone marrow	100–140 h	[24], (estimated)b
TA	time needed for both apoptosis to be completed and its products to be removed	6 h	[25]
NLIMP	number of mitoses performed by LIMPa cells before they are arrested	7	(assumed)c
RA	apoptosis rate of living stem and LIMPa cancer cells in bone marrow(fraction of cells dying through apoptosis per hour)	0.0001–0.1 h−1	(estimated)b
RA(peripheral blasts)	apoptosis rate of peripheral blasts (fraction of cell number per hour)	set equal to RA
PG0 to G1	fraction of dormant (stem and LIMPa) cells that have just left dormant phase and re-enter cell cycle	0.005–0.9	(estimated)b
Psleep	fraction of cells that enter the G0 phase following mitosis	0.001–0.3	(estimated)b
Psym	fraction of stem cells that perform symmetric division	0.2–0.8	(estimated)b
CKRPRED	cell kill rate of prednisone	0–0.8	(estimated)b
CKRMTX	cell kill rate of methotrexate	0.2	(assumed)c

^aA LIMP cancer cell denotes a limited mitotic potential cancer cell (also referred to as LIMP or committed progenitor cancer cell).

^bThe value of the parameter was estimated during the parameter estimation process.

^cAn assumption was made for the value of the parameter.

Regarding the simulation of ALL treatment, cells of the BM lethally hit by a drug enter a rudimentary cell cycle that leads to apoptotic death via a specific phase. Drug hitting is applied to a proportion of tumour cells, determined by the sensitivity of cells to the drug administered. A specific parameter of the ALL Oncosimulator, called cell kill rate (CKR), is defined for each drug administered. In the context of the present study, two parameters of this kind are defined, one for the drug prednisone (CKR_PRED) and one for the drug methotrexate (CKR_MTX). The exact phase through which the cells enter the apoptotic process is dictated by the action mechanism of the drug considered. Methotrexate, a folate analogue showing activity in the S phase [26], is assumed to be absorbed at cycling phases only, whereas apoptotic death of treatment hit cells takes place in the S phase. Prednisone, a cell cycle non-specific drug, is assumed to affect cells at G0 and cycling phases, whereas apoptotic death of hit cells takes place at the end of the G1 phase [27]. Only prednisone is assumed to have a direct cytotoxic effect on peripheral blast cells.

The mechanistic part of the ALL Oncosimulator has been implemented using the C++ programming language. For the needs of the present study, the model has been used both as an executable (.exe) and as a dynamic-link library (.dll). The .dll form was specifically chosen for the efficient integration of the model into the environment of the R language [28] in which the development of the Hybrid ALL Oncosimulator has been done. For the needs of this integration, the .C Interface function of the R language has been used.

2.3. Machine learning-based aspects of the Hybrid Oncosimulator

As already discussed in the Introduction, the ability of the mechanistic part of the ALL Oncosimulator to accurately simulate or to predict disease progression and treatment outcome for a specific patient's case is significantly determined by the choice of its parameter values. Therefore, a combination of optimization and ML methods with the mechanistic part of the ALL Oncosimulator so as to form the Hybrid ALL Oncosimulator is proposed and evaluated. The abstract structural form of this combination has been depicted in figure 1. These extra components serve the need for: (i) automated and accurate parameter estimation for a set of retrospective patient cases and (ii) the tailoring of a procedure that would predict the most appropriate parameter values for prospective patient cases, based on the knowledge obtained from retrospective cases. The more precise this parameter prediction is, the more exact would the final prediction of the treatment outcome be (e.g. prednisone response category) based on ALL Oncosimulator simulation(s). In the following subsections, the detailed choices for the implementation of these components are presented.

2.3.1. Mechanistic model parameter estimation

As can be inferred from the presentation of the ALL Oncosimulator (§2.2), two basic sets of parameters have to be estimated [4]. The first one includes the parameters referring to the tumour growth properties (parameters T_c to P_sym in table 2), whereas the second one includes the chemosensitivity-related parameters (CKRs).

In general, the objective of the parameter estimation procedures is the minimization of the difference between the simulated tumour evolution (in the absence or presence of treatment) and the clinically observed disease progression for the retrospective patient cases. However, for the free tumour growth-related parameters, their direct estimation from the data is usually not practical. This is because the available clinical datasets do not usually include patient-specific proliferation indices or multiple tumour size measurements (in leukaemia, lymphoblasts measurements) for an adequate period of time before treatment. In that case, tumour growth descriptive characteristics reported in the literature may be used in order to estimate the parameter sets that lead to the simulation of tumour with specific properties [4]. For example, the doubling time (T_d) and the growth, apoptotic and necrotic fractions (or indexes), etc., of the inspected tumour may be exploited. This is also the case in the available dataset of the present study. Therefore, plausible parameter sets leading to six different realistic values for the doubling time (T_d) of ALL (7–42 days) [25,29,30] were estimated by minimizing the following objective function:

where 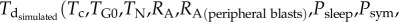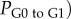is the doubling time of the leukaemic tumour as estimated by the ALL Oncosimulator for given specific values of the parameters and  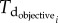is the doubling time set as the objective (7, 14, 21, 28, 35, 42 days, respectively). The selection of the above-presented objective function is dictated by the need for acquiring a parameterization that would lead to a simulated tumour with doubling time as close as possible to the target one. Moreover, the straightforwardness of the comparison between simulated and target doubling times renders the simple absolute difference, commonly chosen in similar parameter estimation tasks, adequate for the optimization algorithm to converge. The optimization procedure is also subjected to specific constraints: first, a criterion for self-sustained untreated tumour [7]—already implemented in the mechanistic part of the Oncosimulator—and second, specific constraints for tumour dynamics and constitution characteristics as given in table 3.

Table 3.

Constraints set on ALL growth properties during the parameter estimation process.

constraint	references/justification
	[31]
	[21]
necrotic fraction ≤ 0.02	a relatively small percentage of necrotic cells is allowed

The implementation of the optimization procedure has been done by estimating plausible sets of parameter values of the ALL Oncosimulator (in free tumour growth mode) through the use of the global stochastic differential evolution algorithm [32] implemented in the DEoptim R Package [33]. The tuned parameters and the ranges set for them during the parameter estimation process are included in table 2.

Subsequently, the related CKR values for each patient included in the available dataset and for each T_d value have to be estimated. This would be achieved by minimizing the difference between the value predicted by the Oncosimulator for the leukaemic cells in peripheral blood on day 8 and the real value observed in the dataset. In the context of the present study, the CKR value for the drug methotrexate (CKR_MTX) is arbitrarily assumed to take the value 0.2 as in [4], and therefore the CKR_PRED is box-constrained inside the range [0−0.8]. The estimation of the personalized CKR_PRED for each T_d has been done using the optimize function of the stats package [28] in R by minimizing the following objective function:

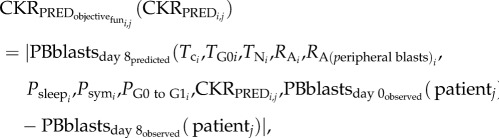where i = 1, 2, … , 6 (the parameter sets for the different doubling times), j = 1, 2, … , 87 (the different patients considered).

The reasons dictating the specific choice of the objective function are similar to those referring to the doubling time-related parameter estimation. Finally, it should be mentioned that the process described above is executed for each patient independently. Therefore, no interpatient correlations in CKR_PRED exist.

2.3.2. Treatment outcome prediction workflow

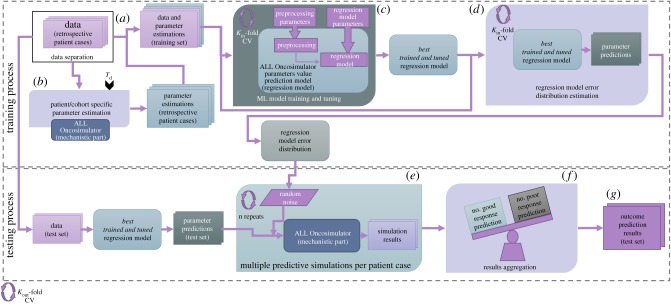
Following the presentation of the processes for adapting the mechanistic part of the model to the available retrospective data, the parts of the Hybrid Oncosimulator leading to a treatment outcome prediction for a prospective patient case are defined. The overall workflow is divided into seven basic sets of steps, shown in figure 3, including those that enable its cross-validation-based evaluation. The workflow has been implemented using the R language (v. 3.2.1–3.3.1) and several additional packages, mentioned in detail throughout the text of the present subsection. The whole workflow may be executed either once or many times (in an external CV manner) in order for the mean prediction accuracy to be estimated. In this study, five external CVs (k_out-CV in figure 3) were realized.

Figure 3.

Detailed structure of the Hybrid ALL Oncosimulator and cross-validation-based performance evaluation steps (see text for details).

In step (a), the dataset is randomly divided into Train and Test sets for the needs of the external CV. This is a necessary step in the case where an evaluation of the workflow without available prospective data (as is the case of the present study) needs to be done. Otherwise, the step can be omitted and the retrospective dataset can be provided directly to the prediction-related steps of the workflow. This separation approach is commonly followed in the literature for a classifier evaluation. In the present study, this step has been implemented using the createDataPartition function (specifically its createFolds functionality) of the caret package in R. The function splits the available dataset into non-overlapping parts, the Train and the Test sets. The separation is balanced based on the observed classes of the patients included in the dataset, in this work the binary prednisone response category (i.e. the proportions of the classes are preserved in Train and Test sets). For the needs of the present evaluation of the Hybrid ALL Oncosimulator, five folds of the exploitable part of the dataset have been created. In more detail, the dataset is split into five balanced parts and each part is used as the Test set for each execution of the workflow (external cross-validation), while the remaining four parts, combined, constitute the Train set.

This step is followed by the parameter estimation process (step (b)) for the Train set, as described in the previous sub-section. Before this step is executed, the clinical data and the T_d scenario choice should be provided. This refers to the selection of the doubling time(s) that the simulated tumours will exhibit. In the case where a choice from a pre-defined set of doubling time scenarios (as those discussed in §2.3.1) is made, the mechanistic part of the model is parameterized in a straightforward way. For these scenarios, the tumour growth-related Oncosimulator parameters have already been estimated (see §2.3.1). Otherwise, the parameters leading to the chosen doubling time (as well as the corresponding CKRs) should be first estimated, as presented in §2.3.1.

In step (c), a model intended to predict ALL Oncosimulator parameters values (regression model) is trained for the Train set. Its parameters are optimized by an internal k-fold cross-validation procedure (k_in-CV in figure 3) again using the caret package [34] in R. Based on the previous experience [4,10], the random forests algorithm [35] has been selected for assessment. Moreover, the Weighted k-nearest neighbours (k-NN) [36] algorithm was also evaluated. Both algorithms are provided by the caret package (and randomForest [37] and kknn packages [38]).

In the present study, the data types used as features in order for the regression models to be trained include the whole-genome expression data (the details of which have been presented in §2.1) and the initial peripheral blood blast count (day 0) for each patient. In the present approach, the CKR_PRED parameter has been selected as the one to be predicted (response variable). Therefore, the estimated values of CKR_PRED for the patients included in the Train set have been provided to the regression model. For each external-CV fold, the CKR_PRED was not estimated (or was estimated, but hidden from the rest of the workflow) for the cases included in the Test set.

Additionally, each time the training or the predicting procedures of the regression model algorithm are called, a sequence of data pre-processing steps is executed.

First, the gene expression dataset provided consists of measurements for different probes, although many of them may refer to the same gene. Therefore, in order to render the dataset compatible with pathway-based analysis, to strengthen its biological interpretability and to render the subsequent steps of analysis platform-independent as suggested in [39], the dataset should be transformed (collapsed) from the probe level (in our dataset IMAGE CloneIDs) to the gene level (e.g. EntrezIDs). In order for this step to be executed, the collapseRows function [39] of WGCNA R package [40] has been used. Among the different choices for the calculation of the expression at the gene level, the Average probes expression has been chosen. The latter implies calculating the average intensities of the probes among those referring to the same gene. For the implementation of the collapsing procedure, a mapping between CloneIDs accession numbers and EntrezIDs should be provided in the CollapseRows function. This mapping file has been created using the online conversion platform SOURCE, originally developed by The Genetics Department of Stanford University (http://source-search.princeton.edu/cgi-bin/source/sourceBatchSearch).

Subsequently, a procedure of gene filtering by the percentage of missing values is executed. Similar to the majority of the gene expression datasets in general, the available dataset has some missing values in the measurements of probes/genes. Although the step of collapsing probes to genes may lower the number of missing expression values in the datasets (the collapseRows function ignores probes that show missing values in higher than the 90% of cases provided), a significant number of these types of values may still exist. Thus, the genes that still show a high frequency of missing values (greater than 20%) across the dataset have been filtered out. Those genes may be thought to have been inadequately measured. The filtering step has been implemented using the goodGenes function of the WGCNA package [40] in R by selecting the minimum fraction of non-missing samples for a gene to be considered ‘good’ to be 80%.

The remaining unsuccessfully measured values of gene expression were filled by imputation. This step is believed to be preferable to the exclusion of all genes that show missing values, because the experience accumulated in the literature [41–45] has shown that an improper handling of missing data may hinder an effective downstream analysis. An exception has been made in the previously presented filtering step for the genes with high missing value frequency because the performance of the imputation algorithms in terms of accuracy has been found to drop significantly for these cases [42,45]. Therefore, these genes were filtered out. The algorithm selected for the imputation process has been the nearest neighbours algorithm (knn imputation) [46], recognized as the most widely and frequently used imputation algorithm. The knn imputation has been implemented using the Impute package in Bioconductor-R (http://www.bioconductor.org/) and by choosing the parameter k (the neighbours that are used in order for a missing value to be imputed) to be 20. The latter is one of the most commonly chosen values for this parameter in the missing values imputation context [42].

Subsequently, in order to conduct a pathway-based gene expression analysis, an aggregation of gene expression values to KEGG pathways activation has been implemented. As stated in the literature [47–49], the transformation of the gene expression data from the gene space to the pathway space is expected to lead to increased robustness of the results of the downstream analysis of molecular data. This is in contrast to the case of gene signatures that are commonly found to be unstable. Moreover, the aggregation of gene expression to another commonly shared space, i.e. the space of pathways, is thought to reduce the intrinsic technological and biological variances across samples. The method selected to be used has been gene set variation analysis (GSVA) [9] implemented in the synonymous Bioconductor-R package. The gene sets chosen in order to aggregate the gene expression values have been those referring to genes constituting the KEGG pathways (http://www.genome.jp/kegg/pathway.html) which at the time of the present analysis are 186 in number. They have been downloaded from the Broad Institute MsigDB (http://www.broadinstitute.org/gsea/msigdb) as a .gmt file (CP:KEGG: KEGG gene sets) and have been introduced into R using the getGmt function of the GSEABase package [50]. Following the application of the GSVA method, the molecular part of the dataset now consists of 186 pathway activation-related features (i.e. enrichment score for KEGG pathways) for each patient.

With the dataset in its finalized form, two additional pre-processing steps are executed. First, the values of the features are mean centred. Second, a step for reducing the level of correlation between the predictors has been followed by removing highly correlated features using the findCorrelation function of caret package.

Regarding the above-presented pre-processing steps, special versions of gene filtering, imputation, centring and features correlation reduction have been implemented for the prediction step of the regression model algorithm. The latter aims to base the pre-processing of the Test set data on the pre-processing results (e.g. filtered genes) and the data (e.g. for imputation) of the training set.

During the above-described training and tuning process, a number of parameters of both the pre-processing procedure and the regression model were optimized. These parameters, their description and the values tested are listed in table 4. The set of best parameters is chosen based on the root mean square error (RMSE) performance on predicting the CKR_PRED value.

Table 4.

Parameters of the pre-processing procedure and the regression model algorithms tuned by internal cross-validation on retrospective cases.

parameter name	description	tuning values
pre-processing parameters
collapse method	method used to collapse gene expression values from probes to genes level	average
good genes minimum fraction	minimum fraction of non-missing samples for a gene to be considered good and to be kept for further analysis	0.8
imputation knn k	number of neighbours to be used in the imputation	20
correlation cut-off	a value for the pair-wise (between feature variables) absolute correlation cut-off	0.5, 0.7, 0.9, 1.0
random forest parameters
mtry	number of feature variables randomly sampled as candidates at each split	five different mtry values were tested, produced by the var_seq function of caret package [34] in R. These values depend on the number of features of the finally preprocessed dataset, which in turn depends on the correlation cut-off parameter.
weighted nearest neighbours parameters
k	number of neighbours considered	5, 7, 9
distance	parameter of Minkowski distance	0.5, 1.0, 2.0, 3.0
kernel	kernel function used in order to weight the neighbours according to their distances	optimal

Referring back to the workflow presentation, in step (d) a new series of cross-validated regression model training, further splitting the Train set created for the external cross-validation, is followed in order to analyse the behaviour of the finally trained and tuned regression model error. Moreover, an estimate of the distribution of the expected error based on the model prediction residuals is acquired. For each external cross-validation fold, an additional fivefold cross-validation-like procedure is executed for the Train set. First, the Train set is further split into an error distribution Train set and an error distribution Test set. Second, the regression model using the best-tuned parameter values identified in step (b) is trained. Subsequently, the response values (CKR_PRED) for the error distribution Test set are predicted by the regression model. Finally, the residuals (errors) between these predicted CKR_PRED values and those already estimated by the parameter estimation procedure (i.e. the real CKR_PRED values) are calculated for each case included in the error distribution Test set. The residuals of all folds are combined and used, in three possible ways, in order to estimate the distribution of the error of the regression model. The first one consists of calculating the histogram of the residuals (and saving the midpoints and their probabilities) using the hist base function in R. The second one refers to the fitting of a normal distribution on the residuals (using the fitdist function of fitdistplus package [51]). The third one resorts to the computing of kernel density estimates (using the density base function in R, with default parameters). The way that this distribution is used in the next steps of the workflow and the effect of the choice of the method on the final results are discussed later.

Thereafter, in step (e), the finally trained and tuned regression model is used to produce predictions for the CKR_PRED value of the patient cases included in the Test set or prospective cases in general. The extracted predictions are used in order for a number of simulations of the mechanistic part of ALL Oncosimulator (n repeats in figure 3, 500 repeats here) for each patient to be realized. In each simulation, a different value of additive noise, sampled from the aforementioned error distribution, is added to the predicted CKR_PRED value. With this parameter value as part of the input, a prediction of the number of lymphoblasts in the peripheral blood at day 8 is returned by the Oncosimulator. After the execution of the simulations, in step (f), each patient is finally classified into the prednisone response group that most frequently was predicted (based on the 1000 lymphoblasts per microlitre threshold). In the extreme case where a patient is equally frequently classified into the two groups, a last run is executed and the result of this simulation is considered the final prediction. The execution of multiple simulations is viewed as essential because it is known a priori that the CKR_PRED would be predicted with an error. Therefore, instead of unconditionally adopting the predicted CKR_PRED and use it to produce the patient category prediction, a number of simulations with slightly changed parameter input are expected to be able to show possible trends in the response categorization of the patient. Moreover, a quantification of the confidence for the resultant classification is produced based on the rate by which this classification result is returned from the multiple simulations for each patient. Such a feature is considered essential for any system claiming future clinical application, such as the Hybrid Oncosimulator. The latter is expected to offer its user the opportunity to decide whether or not the final prediction should be adopted as a means supporting clinical decisions.

Finally, in step (g) the classification results for each external fold and for the overall procedure are accumulated.

3. Results and discussion

3.1. Parameter estimation results

Regarding the estimation of free tumour growth-related parameters for the six T_d scenarios, the latter was achieved with objective function values (targeted T_d minus simulated by the Oncosimulator T_d) ranging from 0.00018 to 0.00626 days. This shows an almost completely successful estimation of the parameters. The resulting parameter values are shown in table 5. The results of the overall model adaptation procedure are summarized in the mean CKR_PRED estimation values given in figure 4. For each patient, six different CKR_PRED values were estimated, one for each T_d case. It should be noted that for a number of patients, not all T_d scenarios lead to the estimation of a valid CKR_PRED value. These patients were characterized by a higher, instead of lower, blast cell count on day 8 of treatment compared to day 1. This behaviour can be explained by very rapid growth rates and/or low chemo-sensitivities. Low growth rates, reflected in scenarios with high doubling times, were unable to catch the observed behaviour; particularly, the simulated final blast count was always lower than the observed one, even in the absence of therapy. Such patients were excluded from further analysis.

Table 5.

Estimation procedure results for the tumour growth-related parameters of the mechanistic part of the ALL Oncosimulator for six different doubling time (T_d) scenarios.

	estimated values
parameter name	Td = 7 d	Td = 14 d	Td = 21 d	Td = 28 d	Td = 35 d	Td = 42 d
Tc	82 h	99 h	109 h	135 h	158 h	182 h
TG0	82 h	82 h	80 h	78 h	108 h	97 h
TN	106 h	119 h	126 h	113 h	133 h	120 h
RA = RA(peripheral blasts)	0.001508683 h−1	0.001280446 h−1	0.0005444389 h−1	0.0008812038 h−1	0.0006393167 h−1	0.000464761 h−1
Psleep	0.09283396	0.1712635	0.1044412	0.1523759	0.0735677	0.1194185
Psym	0.6881355	0.4957694	0.2705583	0.3605559	0.3041863	0.3208003
PG0 to G1	0.5676784	0.7851885	0.8349451	0.7924908	0.6382258	0.4995043

Figure 4.

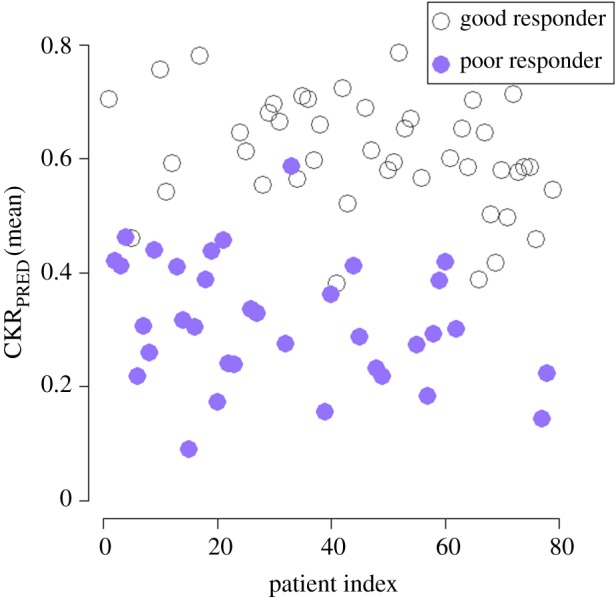
Scatter plot of mean CKR_PRED estimated value (six different doubling time scenarios) for the patients included in the study. Prednisone poor responders tend to have lower chemosensitivity parameter values compared with prednisone good responders. (Online version in colour.)

For each patient, and for the range of values of model parameters and the T_d scenarios considered, the variance in the CKR_PRED value for the six T_d scenarios was not found to be significant (mean CKR_PRED variance: 1.5036 × 10⁻⁴). This behaviour can be explained by the fact that the 7 days duration of the pre-phase treatment is probably too short for the effect of the different doubling times to the treatment simulation to be evident. Therefore, in the context of the present study, only the T_d scenario of 7 days was chosen for the further analysis steps.

As can be seen in figure 4 and in agreement with [4,10], prednisone good responders tend to have higher mean CKR_PRED values compared to prednisone poor responders. This finding further supports the validity of the parameter estimation/adaptation procedure and of the ALL Oncosimulator model as a whole. However, for a range of CKR_PRED values approximately [0.4–0.6] an overlapping of the two categories is observed. For these cases, the prediction of the outcome is expected to be a more difficult task. It should be noted, however, that the observed overlap regarding this feature is expected not to undermine the ability of the proposed methodology to classify the patients to poor or good responders. This is because except for the prediction of the CKR values, the methodology also relies on the initial blast cell count and the biological rules coded through the mechanistic model. These two sources of information are expected to significantly contribute to the successful separation of patients.

3.2. Cross-validation results regarding prednisone response category prediction

The overall results of the execution of the workflow are presented in table 6. For each regression algorithm and regression model error distribution estimation method, five external cross-validation procedures were followed. The resulting mean performance measurements are presented. As can be seen, the classification accuracy evaluated in the whole Test set (16 patients for every external CV fold) ranges in the interval [0.62–0.68] for the weighted k-NN algorithm and in the interval [0.55–0.65] for the random forests algorithm. This means that for a newly arrived patient, the fully tuned system (after choosing the best regression model and the best regression model error distribution estimation method) is expected to correctly classify approximately 70% of patients. The execution of the fivefold external cross-validation of the whole system (including data pre-processing, regression model training and tuning, error distribution estimation and prednisone response category prediction by multiple ALL Oncosimulator simulations) required 189 min on a personal desktop computer equipped with a CPU with four cores synchronized at 3.50 GHz and 16 GB of RAM. Although the training of the system may require several minutes, the process of predicting the response category of a single new patient (which includes the steps of pre-processing the personalized data, predicting the CKR_PRED value, executing 500 ALL Oncosimulator simulations and aggregating the results in a final response classification decision) lasts less than 1 min. It should be noted, however, that these durations, and especially the duration of the cross-validation process, may be significantly increased if a larger dataset (in terms of patient cases) is provided in the future. Nevertheless, both the external cross-validation repetitions and the multiple ALL Oncosimulator simulations may be easily executed in parallel because there are no dependencies between the different execution loops. Such a parallelization step may significantly lower the execution time of both processes. Presently, the Hybrid ALL Oncosimulator system is executed through the R language environment. Therefore, any computational infrastructure that supports this environment, including personal computers, virtual machines at the cloud and servers (e.g. an R server) could be used for the execution of the workflow. Regarding the underlying mechanistic model, which is developed in C++, the inherent capabilities of all the widely used operating systems (either Windows or Unix based) are adequate to support its execution either as an executable or as a dynamic library.

Table 6.

Results of the evaluation of the Hybrid ALL Oncosimulator by external cross-validation (CV) in classifying patients in either prednisone good or poor responders groups. The values in italics are those that provide the key results of the study (classification accuracy for all patient cases).

regression model error distribution estimation method	confidence cut-off threshold	classification accuracy (sensitivity, specificity)a,c,b [0–1]	no. test-set patients classified with confidenceb	confidence for correctly classified casesb [0–1]	confidence for wrongly classified casesb [0–1]	CKR RMSE on internal-CVb	CKR R2 on internal-CVb
weighted k nearest neighbours
kernel density estimation	—	0.682 (0.67, 0.695)	all	0.759	0.703	0.143	0.295
	0.7	0.709 (0.646, 0.753)	9.8
	0.75	0.749 (0.716, 0.768)	7.6
	0.8	0.736 (0.634, 0.753)	5.6
	0.9	0.95 (0.6, 0.933)	2.2
histogram	—	0.623 (0.58, 0.65)	all	0.778	0.745
	0.7	0.694 (0.607, 0.724)	10.2
	0.75	0.742 (0.598, 0.805)	8.4
	0.8	0.753 (0.45, 0.766)	5.2
	0.9	0.533 (0.6, 0.933)	3.6
normal distribution fitting	—	0.622 (0.558, 0.686)	all	0.754	0.649
	0.7	0.747 (0.633, 0.696)	7.6
	0.75	0.779 (0.7, 0.712)	7
	0.8	0.893 (0.8, 0.81)	5.2
	0.9	0.76 (0.6, 0.55)	2
random forests
kernel density estimation	—	0.558 (0.508, 0.609)	all	0.681	0.631	0.154	0.193
	0.7	0.648 (0.582, 0.62)	5.4
	0.75	0.703 (0.533, 0.6)	3.8
	0.8	0.667 (0.2, 0.566)	2
	0.9	0.5 (−c, 0.5)	1.2
histogram	—	0.597 (0.52, 0.694)	all	0.662	0.647
	0.7	0.5667 (0.285, 0.5)	5
	0.75	0.58 (0.333, 0.5)	4
	0.8	0.587 (0.3, 0.52)	3
	0.9	0.32 (−c, 0.5)	1.8
normal distribution fitting	—	0.658 (0.625, 0.683)	all	0.689	0.679
	0.7	0.7405 (0.733, 0.786)	5.6
	0.75	0.7843 (0.73, 0.82)	4.2
	0.8	0.75 (0.6, 0.85)	3.4
	0.9	0.5667 (−c, 0.66)	1.4

^aPrednisone poor response has been selected as the ‘positive’ class.

^bMean fivefold external cross-validation value.

^cFor some confidence thresholds, the ‘positive’ class was absent from the remaining patient cases. Therefore, the sensitivity metrics are not applicable.

Moreover, for the majority of method combinations, the system has been found to respond with higher confidence when its classification decision is correct. Therefore, the following hypothesis can be formulated: if only the patient cases included in the test set for which the Hybrid ALL Oncosimulator responds with relatively high confidence are taken into account, the classification accuracy can be increased and eventual misleading predictions could be avoided. The hypothesis has been tested, by setting four different confidence thresholds and re-calculating the accuracy only for the cases for which their classification was predicted with higher than the threshold confidence. As shown in table 6, by setting the confidence threshold to 0.9, the accuracy of the system may reach the 0.95 performance value when the weighted k-NN and the kernel density estimation methods are used. However, this accuracy is achieved by paying the price of denying the classification for the vast majority of the patient cases (only 2.2 out of 16 patients on average are classified). For lower values of the threshold, ‘trustworthy’ classification results are returned for a higher number of patients, generally with higher accuracy, compared to the unthresholded case, especially when the weighted k-NN algorithm is used. It is noted that the architecture of the Hybrid ALL Oncosimulator constitutes a proposal on the way through which a VPH model would become able to predict the treatment outcome of a real clinical scenario. Such a feature could allow the user (probably a clinician) to decide on the level of confidence through which he or she may trust the predictions of a system of this kind. Such a strategy could considerably support treatment-related decisions based on the model predictions.

The central property of the workflow that allows such a guidance is its ability to execute multiple simulations via the ALL Oncosimulator. In order to illustrate the way through which these simulations are exploited in order for the final classification decision to be made, the histograms of the peripheral blasts at the end of the pre-phase treatment (at a logarithmic scale) predicted by the ALL Oncosimulator for two indicative patient cases are given in figure 5. Both cases were correctly classified using the weighted k-NN algorithm and the kernel density estimation method. The first case depicted in figure 5a is a prednisone good responder, while the second case depicted in figure 5b is a prednisone poor responder. In both panels, the 1000 lymphoblasts per microlitre threshold is indicated with a red line, while the real number of peripheral blasts at the end of the treatment for the specific patients is indicated with a purple one. As can be seen, the vast majority of simulations for the good responder case conclude in a prediction for peripheral blood blast number, lower than the aforementioned threshold, while the opposite is true for the poor responder case.

Figure 5.

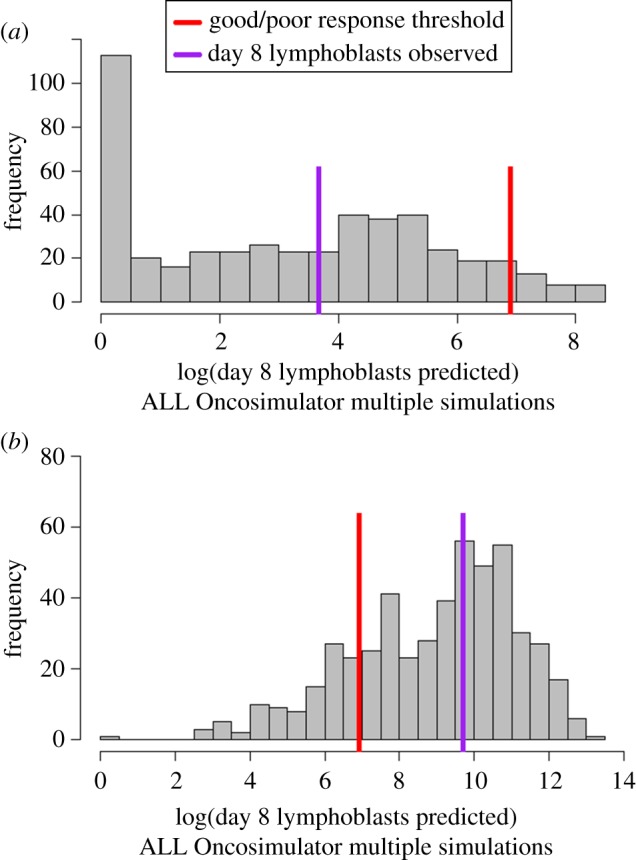
Histograms of multiple ALL Oncosimulator simulations for two representative patient cases. Both cases were correctly classified by the Hybrid ALL Oncosimulator system. Good/poor response threshold is indicated by a red line, while lymphoblasts actually observed on day 8 of treatment for the specific patients are indicated by a purple line. (a) The majority of simulations end up to day 8 lymphoblast number predictions lower than the good to poor response threshold for a prednisone good responder. (b) Simulation results more frequently return predictions higher than the threshold for a prednisone poor responder.

Regarding the comparison between the two regression algorithms tested, the weighted k-NN has proved to achieve better results compared with the random forests algorithm. The latter applies not only in classification accuracy terms but also in the number of patient cases for which a classification result with high probability of correctness is returned when a confidence threshold is set. This could be explained not only by the higher accuracy in predicting the value of CKR_PRED, as shown in table 6 but also by the significantly elevated R² performance (proportion of the variance in the response variable that is predictable from the feature variables) compared with those achieved by the random forests algorithm.

The results presented appear promising regarding the soundness of the proposed combination of methods as a workflow (Hybrid ALL Oncosimulator). Moreover, the approach's eventual contribution to the formulation of foundational guidelines for the clinical application of VPH models through predictive tasks appears a realistic endeavour.

4. Conclusion

In the present paper, a combination of a mechanistic VPH-type model, simulating ALL progression and treatment, called the ALL Oncosimulator [4], with computational optimization and ML methods, has been presented and their performance has been studied. The former methods have been used for parameter value estimation purposes, while the latter for parameter value prediction. The formulated system, entitled the Hybrid ALL Oncosimulator, has been exploited in order for the prednisone response category of a newly arrived ALL patient to be predicted. The cross-validation results have shown that the proposed system is expected to correctly classify approximately 70% of patients. Moreover, the accuracy may be elevated up to 95%, when the precision of the classification task via multiple simulations of the mechanistic model is requested to be high (classification confidence threshold set to 0.9) in order for only trustworthy classification decisions to be returned and eventual misleading predictions to be rejected. The adoption of already established clinical classification/stratification criteria is thought to be preferable in comparison with the adoption of a non-confident prediction by the system. Therefore, the confidence thresholding feature is considered crucial if the ambition for future clinical application and effective medical decision support of this type of system is taken into consideration. In the present study, the increase in classification accuracy and confidence has, however, been found to be coupled with a significant reduction in the number of patients for which an acceptable classification has been returned (only 2.2 out of 16 patients per each cross-validation fold have been finally classified with the classification confidence threshold set to 0.9). Among other possible reasons probably related to the system design (discussed in detail below), the lack of a sufficiently large set of admissible patient cases for the conduction of the present analysis may be responsible for the significant reduction in the cell occupancy of different prednisone response classes. Therefore, more comprehensive and standardized larger scale datasets would be required in the future to underpin this area of cross-disciplinary research.

Viewing the relative success of the proposed Hybrid ALL Oncosimulator system in predicting the outcome of the pre-phase treatment in ALL as a proof of concept, the fundamental steps formulated in the present study can be considered a good base for future advances of the system. Such envisaged advances could include the following: first, the predictive accuracy and the robustness of the proposed workflow should be increased as much as possible. In future efforts, further exploitation of regression methods, data pre-processing methodologies and exploitation of more data types (e.g. additional types of -omics) might increase the performance of the system. Additionally, potential alternative ways to exploit the ability of the system to execute multiple simulations should be studied in terms of final classification decision and the related classification confidence calculation.

The cross-validation-based evaluation of classifiers frequently appears in the ML-related literature. Nevertheless, a predictive system, as the one proposed (together with any eventual future improvements), should be thoroughly validated regarding its ability to predict the response of really prospective patient cases (independent validation set). Moreover, specifically for the pre-phase treatment-related Hybrid ALL Oncosimulator, the real benefits of predicting the prednisone response group for prospective patients, regarding the effective modification of their treatment, should be confirmed. Both these crucial steps would be integrated in a prospective clinical trial including two additional distinct phases. During the first phase, the Hybrid ALL Oncosimulator, which has already been tested using retrospective data, should prove its ability to predict the patient response group. Following this confirmation, in the second phase, an initial set of patients would be treated as suggested by the established clinical protocol, including the prednisone response evaluation through the pre-phase treatment. For another set, the prednisone response group would be predicted by the Hybrid ALL Oncosimulator and influenced by this stratification therapy, decisions would be taken immediately. After completing treatment, the potential benefits of accelerating the treatment would be extracted by comparing disease control success between the two sets.

Following such a future extensive validation, a natural next step would be to study the ability of a similar system to predict the outcome of a longer and more complex treatment or of a combination of treatment phases. For example, minimal residual disease (MRD) detection is of crucial importance for treatment response evaluation and the further stratification of patients into risk groups [52–54]. Such a step would require, on the one hand, the modelling of the administration of additional drugs using the mechanistic part of the model. On the other hand, this would require the prediction of more than one parameter by the ML methodologies. Such parameters would be chemosensitivity related (similar to the CKR_PRED predicted in this paper) as well as tumour growth related. Tumour growth-related parameter value estimation is thought essential because the doubling time of the simulated tumour may affect the simulation results of an extended treatment phase. The prediction of more than one parameter would require either multiple regression models or a single regression model with multiple responses. However, this process may be assisted by the addition of further mechanistic models focusing on specific ALL-related phenomena (e.g. [55–57]).

The results presented in this paper further support the idea that an effective combination of several heterogeneous models (in terms of biocomplexity scales and modelling principles) could lead to the emergence of systems able to assist treatment-related clinical decisions. It is envisaged that the healthcare personnel would easily interact with the underlying complex system using a clinical decision support (CDS) system, as proposed in [58]. Both the fields of effective model combination (hypermodelling) and integration of models into a CDS system have been central research fields of the CHIC and the p-medicine VPH projects, respectively. Their mid- and long-term goal is obviously to translate multiscale VPH models to clinical reality for the benefit of the patient.

Ethics

All pertinent ethical guidelines and directives have been observed within the framework of the European Commission-funded p-medicine project (no. 270089 ‘p-medicine’ (http://p-medicine.eu/).

Data accessibility

Part of the whole-genome expression dataset used in this study is publicly available in Gene Expression Omnibus and ArrayExpress databases with accession numbers GSE4057 and (E-GEOD-4057, E-SMDB-2922), respectively.

Authors' contributions

E.O., E.K. and G.S.S. conceived the experiment. E.O. conceived, designed and implemented the ML-based workflow and Hybrid ALL Oncosimulator integration, and carried out experiments and evaluation. E.K. and G.S.S. conceived the mechanistic part of the ALL Oncosimulator. E.K. implemented the mechanistic part of the ALL Oncosimulator and provided input during the Hybrid ALL Oncosimulator development and experiments. G.S.S. coordinated the theoretical study. M.S. provided the clinical data and contributed to the overall analysis. E.O. and E.K. wrote the initial draft of the manuscript. G.S.S. revised the manuscript. All authors read and approved the final manuscript.

Competing interests

We declare we have no competing interests.

Funding

The research leading to these results has received funding from the European Union's Seventh Framework Programme (FP7/2007–2013) under grant agreements no. 270089 ‘p-medicine’ (http://p-medicine.eu/) and 600841 ‘CHIC’ (http://www.chic-vph.eu/).