Meeting the multiscale challenge: representing physiology processes over ApiNATOMY circuits using bond graphs

Abstract

We introduce, and provide examples of, the application of the bond graph formalism to explicitly represent biophysical processes between and within modular biological compartments in ApiNATOMY. In particular, we focus on modelling scenarios from acid–base physiology to link distinct process modalities as bond graphs over an ApiNATOMY circuit of multiscale compartments. The embedding of bond graphs onto ApiNATOMY compartments provides a semantically and mathematically explicit basis for the coherent representation, integration and visualisation of multiscale physiology processes together with the compartmental topology of those biological structures that convey these processes.

1. Introduction

Two significant challenges for the VPH and Physiome projects are (i) to build better tools for combining biophysically based models involving multiple types of biological process (e.g. cell signalling, ion channel electrophysiology, metabolism and soft tissue mechanics) and (ii) to find ways of linking the biophysical models with the anatomical context in which they are applied. In this paper, we propose a new framework that addresses both of these issues.

1.1. Background

The VPH community¹ and the IUPS Physiome² community [1] are together developing the standards, tools and databases required to support quantitative multiscale modelling of the human body for a wide range of pharmaceutical and clinical applications. The primary goal is to link molecular level information with cell, tissue, organ and whole body models that are based on anatomical data and biophysical principles. Such an approach is needed (e.g. for medical diagnostics) if we are to exploit combined measurements in one individual of molecular biomarkers, physiological measurements and clinical imaging.

At the centre of this, effort is a set of markup language standards for encoding models and data. CellML [2] is used for encoding models based on ordinary differential and algebraic equations; FieldML [3] is used for models with spatially varying fields (typically governed by partial differential equations); SED-ML [4] codes the simulation protocol (including, for example, the numerical algorithms for solving the models and the display formats for specified outputs from solution of the models) and BiosignalML [5] is a data standard for encoding the input and output time varying signals.

A range of open source desktop and web-browser tools have been developed for building and solving Physiome models, including, for example, OpenCOR [6]. This tool provides a desktop environment for creating or reading CellML and SED-ML files, displaying and changing model and solution parameters, solving the models, graphing the output variables and uploading the models back into the user's workspace on PMR.

A database of models, the Physiome Model Repository [7], has also been developed. It currently contains about 600 exposures (models, based on peer-reviewed publications, that have been exposed for public access) and another 400 collaborative workspaces, used for models currently under development and therefore with restricted access.

1.2. Challenge

The current challenge for the VPH/Physiome community is to leverage representational standards in engineering and biology to improve the interoperability (and therefore the re-usability) and to clarify the meaning and readability (and therefore the verifiability) of biophysically based models. This representational challenge has to be met at two levels, namely (i) at a purely process level, to encapsulate biophysical processes and (ii) at a location level in which the anatomical, cellular, subcellular and molecular structures that participate in, or convey, a process are described. Furthermore, overcoming this challenge entails the coherent combination of process and location representation in describing the physiological meaning, or semantics, of a model.

In this paper, we introduce a solution that combines the standardised representation of process and location. In particular, we propose a new framework for developing multiscale biophysical models in physiology by combining (i) ApiNATOMY, a representation of functional anatomy, with (ii) bond graphs, an engineering methodology that represents mass and energy-conserving processes consistently and powerfully. We also demonstrate the application of bond graphs in ApiNATOMY by generating and linking three biophysical scenarios from different scales, namely:

• A. the fluid mechanics of blood and urine flow in the kidney;

• B. the biochemical and diffusive processes between blood and urine of the proximal tubule of the nephron and

• C. the multistate dynamics of a membrane transporter in the renal tubular epithelium.

2. Methods and results

2.1. Process knowledge: bond graphs

The theory of bond graphs was developed by Paynter [8] for electro-mechanical systems, with the theory of network thermodynamics, developed by Katchalsky and co-workers [9], providing additional thermodynamic concepts. The application of bond graphs to biological systems has been the focus of a number of studies (e.g. [10–17]).

Bond graphs provide a systematic way of constructing models of processes that obey mass conservation and energy conservation. (N.B. For readers not familiar with bond graphs, we provide a tutorial at this link: https://doi.org/10.17608/k6.auckland.5425879.v1.) The starting point is that power (or energy) is the common currency across all physical systems, and that power is always the product of a driving potential (μ), expressed as energy (in joules) per unit of some quantity and a flow (q), expressed as that quantity per second. For example, in electrical systems, the quantity being conveyed is charge in coulombs (C) and electrical power is J C⁻¹ × C s⁻¹. (expressing J C⁻¹ as ‘volts’ and C s⁻¹ as ‘amps’ unnecessarily hides the underlying concepts of energy and power.) Similarly, J m⁻¹ (rather than newtons) and m s⁻¹, or J m⁻³ (rather than pascals) and m s⁻³, express the equivalent concepts for mechanics. For biochemical reactions, the flow of a substance expressed in mol s⁻¹ is driven by a chemical potential expressed as J mol⁻¹. (N.B. The seven units of the SI system under the newly proposed definitions (http://www.bipm.org/en/measurement-units/rev-si/) are now based on constants that are consistent with the use of joules and seconds (together covering energy and power), metres, moles, entropy, coulombs and candela.) These seven units cover all of continuum physics (table 1).

Table 1.

The units used in formulating the bond graph equations. Everything is expressed in terms of the seven base units, which include two for energy and power (joules and seconds) and five (coulombs, metres, moles, entropy and candela) for the quantities conveyed in the various physical systems.

			mechanics
		electrical network	solid	fluid	biochemical reactions	heat flow	electro-magnetic	diffusion
potential	μ (u)	J C−1 (V)	J m−1 (N)	J m−3 (Pa)	J mol−1 (G)	J e−1 (K)	J cd−1	J m3 mol−1
quantity	q (q)	C	M	m3	mol	E	cd	mol m−3
flow		C s−1	m s−1	m3 s−1	mol s−1	e s−1	cd s−1	mol m−3 s−1
rate of flow		C s−2	m s−2	m3 s−2	mol s−2	e s−2	cd s−2	mol m−3 s−2
elastance	E ()	J C−2	J m−2	J m−6	J mol−2	J e−2	J cd−2	J mol−2 m6
resistance	R ()	J s C−2	J s m−2	J s m−6	J s mol−2	J s e−2	J s cd−2	J s mol−2 m6
inductance	L ()	J s2 C−2	J s2 m−2	J s2 m−6	J s2 mol−2	J s2 e−2	J s2 cd−2	J s2 mol−2 m6

Another key feature of bond graphs is the clear separation of processes that transmit energy (conveyed by a bond with its associated pair of variables potential and flow) from processes that store energy (either statically like a capacitor or spring or dynamically like an inductor or inertial mass) or dissipate energy (like a resistor or viscous damper). A bond graph depicts the flow of energy around a system with the topology of that system giving rise to the conservation of mass and conservation of energy, but with the constitutive laws (table 2) defined empirically for the storage and dissipative mechanisms.

Table 2.

Examples of constitutive laws for various physical systems.

		constitutive relations
		static storage (elastance)		dissipation
physics		BG expression	mechanism	BG expression	mechanism
electrical			electrical capacitor		resistor (Ohm's law)
heat transfer			heat capacity		entropy↑ (Fourier's law)
mechanisms	solids		elastic spring (Hooke's law)		viscous damper
	fluids		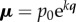fluid compressibility (vessel distensibility)		fluid viscosity
biochemical	biochemical		Boltzmann's formula		biochemical reaction
	diffusion		solute concentration		entropy↑ (Fick's law)
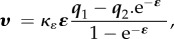
	ion channel		thermodynamic relation		Goldman–Hodgkin–Katz (GHK)

The key elements of the bond graph approach are shown in figure 1. The black arrows are bonds that carry a potential μ_i and a flow υ_i. The central row in figure 1a illustrates the topology of a simple system (e.g. an electrical network of capacitors, resistors and inductors; a mechanical system of springs, dashpots and masses or a biochemical system of solute concentrations and membrane-bound reactions). A junction or node, where bonds meet, is labelled with either a potential μ_i or a flow υ_i, and every bond impinging on that node has the value of the potential or flow at that node. The flows in the bonds at a potential node (also called a 0-node) sum to zero (mass conservation) and the potentials in the bonds at a flow node (also called a 1-node) sum to zero (energy conservation). In both cases, transmission of power through nodes is conserved () because with μ constant for 0-nodes and with υ constant for 1-nodes. (Note that labelling a 0-node with μ_i and a 1-node with υ_i, and the convention that the bonds impinging on the node adopt the value at that node, is a convenient shorthand—the full bond graph diagram is shown in figure 1b where every bond has been annotated with its potential-flow conjugate pair.)

Figure 1.

An illustration of network topology captured in bond graph form, with the associated conservation equations and constitutive relations. The potential nodes and flow nodes shown as 0-nodes and 1-nodes (this is the convention used in the engineering bond graph literature). Note that the use of colours (red for potentials and green for flows) is not standard in the engineering literature, but we think helps distinguish the driving potentials or forces from the kinematic quantities. (Online version in colour.)

The top band of figure 1a shows the constitutive relations for the three types of mechanism—static energy storage (a capacitor for which potential μ is a function of q, the integral of flow υ), energy dissipation (a resistance for which flow υ is a function of potential μ) and dynamic energy storage (an inductor for which μ is a function of a, the derivative of flow υ). The equivalent quantities for a range of physical systems are shown in table 2. The conservation equations generated by the bond graph topology are shown in the lower band of figure 1a. For the potential nodes, these equations are (i.e. conservation of current for an electrical system or mass for a mechanical or biochemical system), and for the flow node, the equation is (representing voltage drops around an electrical circuit, or force balance for a mechanical system, or the stoichiometry of a chemical reaction for a biochemical system). Also, shown below the conservation equations at the two potential nodes are the differential equations that express q (the stored charge in an electrical capacitor, displacement of a mechanical spring or solute amount dissolved in a solvent) or a (the rate of change of current in an electrical system, or acceleration in a mechanical system) with the flow υ.

In summary, bond graphs provide a graphical notation for the set of linear constraint equations (the conservation laws), but note that constitutive laws can be nonlinear (and usually are in biological systems).

2.2. Location knowledge: ApiNATOMY

The management of structural knowledge of (i) the scales at which compartments are defined as well as (ii) the parthood and connectivity relationships between compartments are key to provide a mechanistic explanation to a correlation between biophysical measurements (or model variables) from two distinct compartments. The consistent management of such knowledge provides the means to determine the anatomical route by which physical influence (that mechanistically accounts for the correlation) is transferred from one body region to another (also discussed further in [18]).

Given the above knowledge management goals, a methodology such as ApiNATOMY³ [19] is required to provide formal knowledge articulation for multiscale compartments and, in particular, to articulate topological information about key anatomical structures and processes of physiological relevance (figure 2) such as

• a. Conduits. geometric layered compartments from any scale, representing conduits that convey the movement of solutes. Conduits fall exclusively into one of three topological categories of tube, bag or cyst. Tubes, bags and cysts are all conduits of a kind that are topologically distinguished as follows:

  • i. a tube is a conduit with both terminal borders open;
  • ii. a bag is a conduit that has one open and one closed terminal border and
  • iii. a cyst is a conduit that has both terminal borders closed.

Figure 2.

(a) A 2D and corresponding 3D depiction of the three core topological classes of conduits in ApiNATOMY—note that the axis of rotation depicted as a dark hatched line at the base of each 2D-layered conduit schematic; (b) a graphical plot of an epithelial arborisation in ApiNATOMY, representing the urinary tree from the bladder root on the left to the Bowman's capsule leaf on the right—each node in this tree can be parametrised with branching probabilities, and each conduit associated with an edge represents a level in the tree and can be associated with distributions of length and thickness. (c) A radial coalescence operation in ApiNATOMY involving two side-by-side three-layered conduits each sharing outermost layer ‘C’ to create a five-layered coalescent structure. (d) Examples of housed assemblies in ApiNATOMY: (right) a ‘Bag’-type conduit, representing a kidney lobus, houses urinary and cardiovascular conduits—this schematic is elaborated in figure 4; (left) a detail encased with a dotted red line shows a coalescent assembly in which the epithelial layer houses an assembly of bags and tubes to represent the membrane channel machinery of renal epithelial cells. (Online version in colour.)

These geometric material objects are dependent upon a variety of features, in particular

• — the dimensional scales of their thickness and length;

• — a layered structure; and

• — an intrinsic polarity to support the relative orientation of geometric material objects within other geometric material objects.

• b. Trees. the longitudinal linkage of contiguous conduits of different scales to create canonical arborisation models of mesothelial, endothelial, neural and epithelial trees. A tree is an important kind of material object in the ApiNATOMY model, because many circuits of conduits have tree-like structures or tree-like parts. Furthermore, the number of levels in trees can quickly become very high and a discrete reconstruction of tree structures from simpler segmental objects becomes impractical. Thus, the category of tree as a material object in its own right is necessary for any practical treatment of the topology of physiological circuitry. Trees are characterised by the following features:

  • i. a number of levels,
  • ii. the degree of branching between consecutive levels,
  • iii. an association with a conduit type for each level,
  • iv. a distribution of the length for the conduit associated with each level and
  • v. a distribution of the thickness for the conduit associated with each level.

• c. Coalescences. the radial linkage of conduits that overlap over their outermost layer—a coalescence between two conduits occurs side to side, such that the outermost layer of the conduits is shared;

• d. Housed multiscale assemblies. the embedding of assemblies of conduits, trees and coalescences within layers of a housing conduit of a scale that is larger than that of the assembled constituent components.

• e. Bond graphs. the application of the bond graph formalism to formally represent the transfer of energy or mass along and across conduits in terms of physical laws.

The ApiNATOMY method thus outlined takes into account the above requirements to manage topological knowledge about key anatomical structures.

2.3. Multiscale scenarios: combining knowledge about process and location

In the examples below, we show how equations generated by the bond graph approach can be expressed in CellML and solved with OpenCOR. We also show how the quantities and processes defined by the bond graph model can be expressed within the anatomical framework established by ApiNATOMY.

2.3.1. Long-range advection scenario: renal blood supply

Here, we focus on the flow of blood over renal arterial, capillary and venous systems. The key anatomical components of this system are depicted in ApiNATOMY in figure 4.

Figure 4.

An ApiNATOMY-based representation of renal vascular and epithelial topological anatomy. In ApiNATOMY terms: (i) the kidney per se is represented as a bag conduit (orange) consisting of a ‘hilum’ innermost layer, a ‘parenchyma’ middle layer and a ‘capsule’ outermost layer (the orange hatched line depicts the axis of rotation of the bag unit). (ii) The kidney lobus (green) is also represented as a bag conduit, with an innermost ‘medulla’ and outermost ‘cortex’ layer (the green hatched line depicts the axis of rotation of the bag unit). (iii) The epithelial arborisation of urinary vessels is modelled as a single tree with the bladder tube segment (#1) as the root stem, and the visceral aspect of the Bowman's capsule bag (#17) as the terminal leaf segment. (iv) The cortical cardiovascular circuit consists of a (red) arterial tree (root tube segment is aorta, A, and leaf tube segment is afferent artery, G) and a (blue) venous tree (root tube segment is inferior vena cava, Q, and leaf tube segment is stellate vein, K), bridged by a (pink) exchange segment (H–J). (Online version in colour.)

We give an example in figure 3 of the bond graph formulation of blood flow over three modules of branching blood vessels: arterial (figure 4, tube segments B–G), capillaries (figure 4, tube segments H–J) and venous (figure 4, tube segments K–P).

Figure 3.

A bond graph model of blood flow through a branching vascular system over three main segments—arterial, capillary and venous. The equations for each segment and for the junctions are shown below the segments. (Online version in colour.)

Arterial vasculature is represented by a single module that includes a compliance represented by the parameter E₁, two viscous resistance terms R₁ and R₂, and two inertial terms I₁ and I₂.

Elastance is a function of the arterial wall, while the viscous and inertial terms are a function of the material properties of blood (viscosity and density, respectively) and the dimensions (radius and length) of the blood vessels.

Viscous resistance R can be evaluated from Poiseuille's equation, which describes the relation between pressure drop and steady blood flow through a uniform vessel:

where μ is blood viscosity, l is the length of the vessel and r is the radius of the vessel.

Vessel elastance, E, can be calculated from blood vessel properties:

where h and E_m are the thickness and elasticity of the vessel wall, respectively.

The inertial term I can be obtained numerically using the blood vessel properties:

where ρ is blood density.

The capillary bed module contains n₂ identical capillaries. Blood in these vessels flows into a single representative module for the venous side. Both the capillary module and the venous module contain compliant, inertial and resistive components similar to the arterial one, but with different parameter values.

Compared to figure 3, a more granular depiction of bond graph modules (corresponding to the anatomical segments in figure 4) is shown in figure 5. This depiction sets the stage to locate a bond graph module onto a two-layer ApiNATOMY tube segment representing a cardiovascular conduit. The details of this overlay are elaborated in figure 6.

Figure 5.

(a) A bond graph model of blood flow through the renal vascular system. The top line shows the arterial segments, starting with the renal artery, and feeds into the middle line for the capillary beds at the glomerulus and cortical peritubular capillary plexus (CPCP). The output then feeds into the venous circulation, ending with the renal vein. The equations for each segment and junction are also shown. These segments are mapped into the ApiNATOMY diagram shown in figure 4. A CellML implementation of the model summarised by the bond graphs in (a) is run over a 10-s span, giving rise to (b) flow and (c) pressure plots corresponding to the anatomical segments in (a). (Online version in colour.)

Figure 6.

Overlaying bond graph representations of resistive (R), inertial (L) and elastance (E) features of blood flow through a prototypical blood vessel segment. This segment is depicted as a two-layered tube conduit in ApiNATOMY: innermost layer represents ‘blood’ and the outermost layer represents ‘wall’. In particular, (a) a detailed bond graph view over a prototypical segment [i] is shown in this view, with resistive and inertial variables located in the blood compartmental layer (shown as rectangular nodes), while the elastance component is anchored in the wall compartment. ‘0’ nodes are circular and marked with a ‘0’. ‘1’ nodes are diamond-shaped. (b) Here, we show the above information in an ‘outline’ ApiNATOMY view, which hides most of the bond graph detail, but highlights key constitutive relationships between variables and their compartmental location. In addition, the dependency relationship between these variables and compartmental features, such as dimensional size and material constitution, is also highlighted. A depiction of the canonical tree model, which affects the degree of branching ‘n’ originating from the segment, is shown on the top right of the figure. (Online version in colour.)

To illustrate how the pressure in one vascular segment can influence the wall elastance and hence resistance to flow of another vessel, we include the bond graph representation of the vasa vasorum for the renal artery in figure 7. The elastance of the renal artery wall (represented by E₁) is a function of renal artery pressure μ₁. The elastance of the vasa vasorum, which is embedded in the renal artery wall, is represented by E_v, and this can be described empirically as a function of μ₁.

Figure 7.

A bond graph model of blood flow through the vasa vasorum supplying blood to the renal artery. The elastance of the vasa vasorum vessels is influenced by the changing elastance of the renal artery wall. (Online version in colour.)

2.3.2. Subcellular transepithelial transport scenario

reabsorption is one of the main cellular mechanisms in the kidney. filtered by the glomerulus is combined with H⁺ excreted from the epithelial cell (via an ATP-ase proton-pump and the passive sodium–hydrogen exchanger 3 (NHE3) transporter) to form CO₂ and water (via the carbonic anhydrase reaction in the tubule). Then, CO₂ returns into the epithelial cell (via the diffusion channel in the brush border) to regenerate in the epithelial cell (via the carbonic anhydrase reaction in the epithelial cell). Finally, diffuses into the blood through leak channels in the basolateral membrane of the epithelial cell.

Figure 8 gives the bond graph corresponding to the reabsorption model in the kidney. We assume that every that is transported out of the epithelial cell to the blood is immediately replaced with a H⁺ from the hydration reaction. We are also assuming the cell to be a well-mixed system. In this diagram, symbols representing ionic concentration measurements are located in the precise ApiNATOMY layer representing the corresponding anatomical compartment from where such measurements were taken.

Figure 8.

Bond graph model of acid–base-related ionic exchanges between blood and urine laid out over an ApiNATOMY coalescence model. This diagram zooms in on a detail of this coalescence model (fully featured in figure 2c,d) to show three of the five-layered coalescence at the level of the proximal convoluted tubule, namely urinary fluid, epithelium and basement membrane. The epithelial layer features a cyst-type assembly representing the epithelial cell apical and basolateral plasma membranes (abbreviated as ‘P.M.’) and intervening cytosol. (Online version in colour.)

The six reactions are modelled by the six Re components. The reactions for this model are (c, cytosol; b, basolateral extracellular; a, apical extracellular) as follows:

The state derivatives are as follows:

and the reaction flows are as follows:

2.3.3. Sodium–hydrogen exchanger 3 transporter mechanism scenario

The NHE3 (also known as the 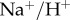antiporter) was studied experimentally and explained by a biophysical model by Aronson [20]; further experiments and modelling were conducted by Weinstein [21]. Chang & Fujita [22] examined the kinetics of the model and calculated the kinetic rates. This section looks at the bond graph-based model of NHE3 based on the model of Chang & Fujita [22].

The model illustrated in figure 9 is based on the eight-state biomolecular cycle presented in the Chang & Fujita model. This figure shows an electroneutral antiporter in which a single transporter site, E, may be oriented towards the outside, E_o, or internal, E_i, membrane face. It also includes three solute species: Na⁺, H⁺ and . This transporter mediates the 1 : 1 exchange of Na⁺ for H⁺ with competitive binding and transport of .

Figure 9.

Schematic representation of the NHE3 mechanistic model. (Online version in colour.)

The nine reactions are modelled by the nine Re components, and there is no slippage reaction component which the enzyme undergoes conformational changes without transporting species:

The nine sets of reaction kinetic parameters are given in the Chang & Fujita model and listed in the first two columns of table 3, and the third column gives the corresponding equilibrium constants.

Table 3.

Reaction parameters for acid–base transport model.

reactions
Re 1	100 000	3 270 000	0.0306	513 598
Re 2	3 270 000	100 000	32.7	513 598
Re 3	100 000	3.52	28 409.1	411 592
Re 4	3.52	100 000	0.0000352	411 592
Re 5	100 000	713 000	0.14025	713 000
Re 6	713 000	100 000	7.13	713 000
Re 7	2.41	2.41	1	0.378523
Re 8	0.48	0.48	1	56.126
Re 9	2.41	2.41	1	2.41

The vector of nine equilibrium constants is converted into the vector of 10 thermodynamic constants K of table 4 using the formula of [11].

Table 4.

Species parameters for acid–base transport model.

species

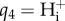The corresponding rated constants are then computed as discussed by Gawthrop et al. [11] and listed in the final column of table 3.

The eight states of the transporter form a conserved moiety:

where is the total number of transporters corresponding to the experimental situation. Here, a normalised model was used where, in effect, a value of was used. The corresponding membrane current can then be scaled accordingly using the physiological value of .

The biomolecular system of the is described in stoichiometric form as follows:

where is the system state, is the stoichiometric matrix and is the vector of reaction flows. In the case of the , state derivatives are as follows:

and the reaction flows are as follows

The bond graph model of is implemented in CellML, simulated using OpenCOR and illustrated an ApiNATOMY context using bond graphs in figure 10.

Figure 10.

The NHE3 mechanistic model. (a) A detail from the ApiNATOMY layers discussed in figure 8, showing a horizontal two-layered tube conduit representing the NHE3 protein wall and pore. This compartmental representation serves as a backdrop to house the nine reaction nodes from the bond graph model shown in (b) below and to link the concentration variables located in the appropriate anatomical compartments (i.e. urinary layer and cytosol). (b) This diagram gives a succinct version of a bond graph corresponding to the model. The eight states of the complex are represented by the eight C components , ,, , , , and , the outside and inside by and , the outside and inside by and , and the outside and inside by and . When operating normally, is transported from the outside to the inside of the membrane, while or is transported from the inside to the outside of the membrane. (Online version in colour.)

3. Discussion

Bond graphs provide a highly modular and systematic way of expressing the topology of a process network in graphical form. This topological structure is amenable to express both (i) the equations governing conservation of mass and conservation of energy for the network and (ii) the constitutive relations that capture the empirically determined properties of the components of the network. These two sets of equations map precisely to a declarative framework such as CellML and can be solved with freely available open source software such as OpenCOR. Furthermore, because biophysical models are generated from an underlying physics framework and are given a biological context through the embedding with ApiNATOMY, annotations needed to describe both the physical and biological meaning of the model parameters and variables are automatically available as CellML metadata.

From the perspective of knowledge management about biological structure and location, ApiNATOMY provides a flexible modularisation of compartments that correspond to the field of ‘0’ nodes in bond graphs. Specifically, based on our experience with the above three biophysical scenarios, an ApiNATOMY compartment is semantically equivalent to a well-mixed, equipotential field tracked by a variable associated with a 0-node in a bond graph. In the case of a chemical reaction, this 0-node corresponds to the chemical potential of a single chemical species in a well-mixed compartment.

The explicit mapping of bond graph nodes to ApiNATOMY compartmental location sets the stage to coherently link bond graphs for the (i) NHE3 mechanism, (ii) subcellular transepithelial transport and (iii) long-range renal advection. In particular, such linkage would require (i) the bond graph and compartments of the NHE3 mechanism in figure 10 to plug into the Re4 component of the model in figure 8, and the resulting solution to be plugged into (ii) the compartmental coalescence of the peritubular capillary (figure 4, J) and proximal convoluted tubule (figure 4, 15) to bridge to the higher-scale bond graph model of long-range advective flow of blood and urine. To this end, future work in support for this strategy in multiscale model integration includes the following:

• a) developing new interfaces in OpenCOR to create models based on bond graphs and to associate the parameters, variables and compartments of the CellML model with the corresponding components in ApiNATOMY. These interfaces will be tailored to the context appropriate for the model or part of the model (e.g. electrophysiology, metabolism, signalling pathways and mechanics).

• b) building a modular catalogue of multiscale compartments in ApiNATOMY to create a canonical map of anatomical components across scales (see mockup of this map in figure 11).

• c) generating a catalogue of structure–function modules combining ApiNATOMY compartments and associated bond graphs for repeating canonical units in physiology such as vessel segments, primary functional tissue units [23] and membrane transporters.

Figure 11.

ApiNATOMY mock-up of modular tissue and cellular compartments (rectangles), as well as processes (lines) representing long-range and local physiological interactions relevant to acid–base regulation. The process lines provide a visual summary of an underlying bond graph representation of the physical interactions taking place between anatomical locations across scales. (Online version in colour.)

4. Conclusion

Bond graphs support cross-talk between processes from different domains of physics and encourage unit harmonisation across physical domains. The power of the bond graph approach is particularly relevant when different physical mechanisms interact with one another. In such integrative scenarios, the 1-node concept, in particular, is a powerful mechanism for ensuring consistency between, for example, molar flow rates, associated charge transfer and metabolic energy considerations. Conversely, the 0-node concept is essential to match an equipotential field with anatomical location—a key feature that informs the interoperation between bond graphs and ApiNATOMY.

Implementing a combination between ApiNATOMY and bond graphs is anticipated to foster significant knowledge modularisation in physiology by

• i. encouraging the communal development of catalogues of modular structure–function units at different scales;

• ii. supporting the coherent visualisation and curation of multiscale physiology knowledge by clinicians, physiologists, systems biologists and modellers and

• iii. enhancing publication services in physiology model building, sharing and verifiability, such as the upcoming Physiome journal that is to be launched by the IUPS and VPH communities to support reproducible, reusable biophysically based modelling, and associated biomedical knowledge management frameworks.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

We received no funding for this study.