Delayed behavioural shifts undermine the sustainability of social–ecological systems

Abstract

Natural habitat destruction and fragmentation generate a time-delayed loss of species and associated ecosystem services. As social–ecological systems (SESs) depend on a range of ecosystem services, lagged ecological dynamics may affect their long-term sustainability. Here, we investigate the role of consumption changes for sustainability, under a time-delayed ecological feedback on agricultural production. We use a stylized model that couples the dynamics of biodiversity, technology, human demography and compliance with a social norm prescribing sustainable consumption. Compliance with the sustainable norm reduces both the consumption footprint and the vulnerability of SESs to transient overshoot-and-collapse population crises. We show that the timing and interaction between social, demographic and ecological feedbacks govern the transient and long-term dynamics of the system. A sufficient level of social pressure (e.g. disapproval) applied on the unsustainable consumers leads to the stable coexistence of unsustainable and sustainable or mixed equilibria, where both defectors and conformers coexist. Under bistability conditions, increasing extinction debts reduces the resilience of the system, thus favouring abrupt regime shifts towards unsustainable pathways. Given recent evidence of large extinction debts, such results call for farsightedness and a better understanding of time delays when studying the sustainability of coupled SESs.

1. Introduction

Early research on the interaction between human populations and their environment emphasized the need for government control in order to prevent the overexploitation of common pool natural resources [1]. However, subsequent research has shown that local communities can achieve sustainable resource use through cooperative self-governance [2]. Successful communities often establish social norms (i.e. rules of shared behaviour) that protect common natural resources [3]. Such regulatory mechanisms are ‘bottom-up’ processes, as opposed to classical ‘top-down’ government control. Both types of regulation involve, however, sanctioning mechanisms that seek to internalize the externalities of human activities, be they moral incentives (e.g. social exclusion) in the first case, or economic instruments (e.g. taxes, subsidies) and regulatory policies in the second [4].

Human behavioural change can significantly affect the dynamics of social–ecological systems (SESs), and is a central aspect of their adaptability and resilience [5]. The evolution of social norms affects feedbacks and drivers of SESs, potentially leading to large-scale behavioural shifts [6]. Such shifts may allow escape from social-ecological traps (i.e. persistent mismatches between the responses of people and their ecological conditions) that are undesirable from a sustainability perspective [7].

The establishment of sustainable social norms strongly hinges on the ecological characteristics of SESs. Previous experimental and theoretical studies have emphasized the role of resource productivity and mobility as well as temporal variability [8,9] on the robustness of cooperation. Evidence from the literature on natural resource management shows that the interaction between fast and slow ecosystem processes affects the optimal management strategy [10], while inappropriate management may reinforce undesirable feedbacks and push the SESs into a social–ecological trap [11]. However, the consequences of mismatches between slow and fast social–ecological processes on the robustness of cooperation remain an open question.

Extinction debts (i.e. time-delayed loss of species following habitat destruction) can emerge from the spatial dynamics of SESs [12]. Indeed, land conversion and fragmentation alter spatial ecological processes and the rate of relaxation of natural communities (i.e. the rate of change of species richness in response to habitat destruction) [13]. Recent evidence suggests increasing ecological relaxation rates, generating large extinction debts [14]. As an example, 80% of the species extinctions in the Amazon are estimated to be pending [15], which may increase the number of twentieth-century extinctions in bird, mammal and amphibian forest-specific species by 120% [16]. In European landscapes, studies find that extinctions lag well behind contemporary levels of socio-economic pressures, the current number of threatened species being better explained by socio-economic indicators from the early or mid-twentieth century [17].

The accumulation of these extinction debts generates functioning debts [18] that postpone the negative effect of biodiversity loss on ecosystem processes. As many of the ecosystem services that play a direct or indirect role in agricultural production depend on biodiversity [19], current species extinction rates [20] not only threaten the long-term provisioning [21] and stability of ecosystem processes [19,22], but also generate a time-delayed feedback loop between humans and nature [23]. In the long run, such time-delayed biodiversity feedbacks may result in large environmental crises (i.e. overshoot-and-collapse population cycles [23]), similar to the famine cycles that have been observed in extinct societies [24].

Characteristics common to the majority of modern agricultural systems were found to increase the vulnerability of SESs to such crises [23]. Among these characteristics are a high production efficiency and a low labour share per unit of agricultural good, due to the substitution of technology (e.g. machines, fertilizers and pesticides) for human labour and ecosystem services. Recent evidence suggests that land use efficiency has been rising at the global scale [25]. However, it is not clear whether these efficiency gains will help save natural habitats and biodiversity in the long run, due to economic rebound effects (i.e. when lower prices stimulate demand and higher yields raise profits, encouraging further agricultural expansion) [26]. Such a decoupling between human population growth and ecological dynamics can thus reinforce unsustainable feedbacks [27]. Shifting consumption has, however, been identified as a major strategy that could allow doubling food production while greatly reducing the environmental impacts of agriculture [28]. Norm-driven consumption changes towards more environmentally friendly agricultural goods, whose production relies more on ecosystem services and labour than on technology, may thus play a key role in ensuring the long-term sustainability of SESs at large scales. However, the magnitude of time-delayed ecological feedbacks may postpone the required behavioural changes, and push (or keep) the global SESs into a social–ecological trap [27].

The aim of this article is to investigate the effects of time-delayed biodiversity loss on the establishment of sustainable social norms. To this end, we develop a dynamical system model of an endogenously growing human population divided into norm-following and norm-violating consumers that share a common stock of land and associated biodiversity. Rising consumption demand of the human population drives production supply and natural habitat conversion through market constraints. The model thus differs from related common-pool resource systems that only consider a constant population of harvesters and a single resource [8]. The present model builds upon previous work [23], where the growth rate of the human population depends on the consumptions of industrial and agricultural goods, as well as on the strength of the demographic transition governed by technological change. The time-delayed loss of biodiversity-dependent ecosystem services then acts as a lagged feedback on agricultural productivity that can push the system into an overshoot-and-collapse crisis [24]. In the following, we present the model structure and show that allowing for consumers' behavioural change generates bistability between sustainable and unsustainable equilibria, and thus the potential for regime shifts. We then explore different scenarios of social pressure and extinction debts, and conclude with a discussion of our results.

2. Model description

(a). Coupling human demography, biodiversity and social dynamics

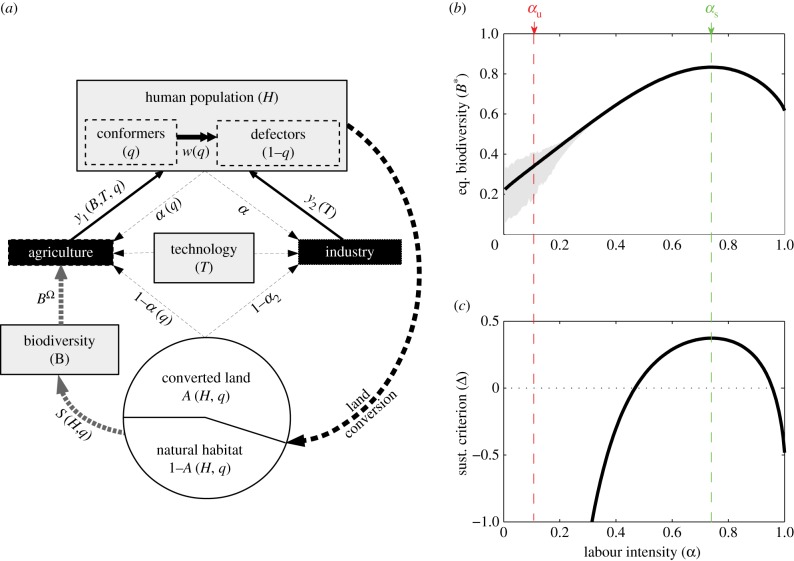
We model a population of consumers, whose demand for agricultural and industrial goods requires the conversion of their common natural habitat. Our SES model describes the long-term interaction between four dynamical variables (figure 1): the human population (H), technological efficiency (T), biodiversity (B) and the proportion of sustainable consumers, hereafter ‘conformers’ (q). Conformers, by complying with a sustainable norm prescribing the consumption of environmentally friendly agricultural goods, reduce their footprint in terms of natural habitat destruction and long-term biodiversity loss. Total habitat is gradually converted towards agricultural and industrial lands. The remaining natural habitat supports a community of species (biodiversity) that provides a range of ecosystem services to agricultural production [19]. Loss of natural habitat leads to time-delayed species extinctions, thus reducing both the common-pool biodiversity and long-term agricultural productivity [29]. Such a lagged feedback on agricultural production can result in long-term environmental crises characterized by overshoot-and-collapse population cycles (figure 4c). These crises transiently reduce human well-being [23], thus threatening intergenerational equity and sustainability [30]. As the vulnerability of SESs to lag effects increases with natural habitat destruction and biodiversity loss [23], a sufficient proportion of conformers reducing their consumption footprint may help limit land conversion while preserving the long-term sustainability of the SES. The following sections present the main features of our dynamical system. Further details about the economic derivations can be found in Lafuite & Loreau [23], from which the model is extended.

Figure 1.

Coupling between human, social and ecological dynamics, and definition of the sustainable and unsustainable consumption norms. (a) Model summary. Black boxes: production sectors; grey boxes: dynamical variables; dashed lines: production inputs (labour, land and technology), with α(q) being the share of labour compared to land to produce one unit of agricultural good; solid lines: per capita consumptions of agricultural and industrial goods, y₁(B, T, q) and y₂(T); grey dotted lines: ecological feedback; double arrow: social sanctioning (e.g. ostracism); circle: total land divided into converted land A(H, q) and natural habitat, which supports a long-term species richness S(H, q). All functions are explicitly defined in the main text and in electronic supplementary material, table S2. (b) Effect of labour elasticity on equilibrium biodiversity. Grey areas represent the amplitude of the transient environmental crises. (c) Effect of labour elasticity on sustainability. The sustainability criterion Δ is derived in [37]. Δ > 0 stands for sustainable transient trajectories (i.e. no environmental crises). The sustainability-optimal agricultural labour elasticity α_s maximizes both Δ and the biodiversity at equilibrium, B*. The unsustainable labour elasticity α_u is chosen so that α_u > α_s and Δ(α_u) < 0.

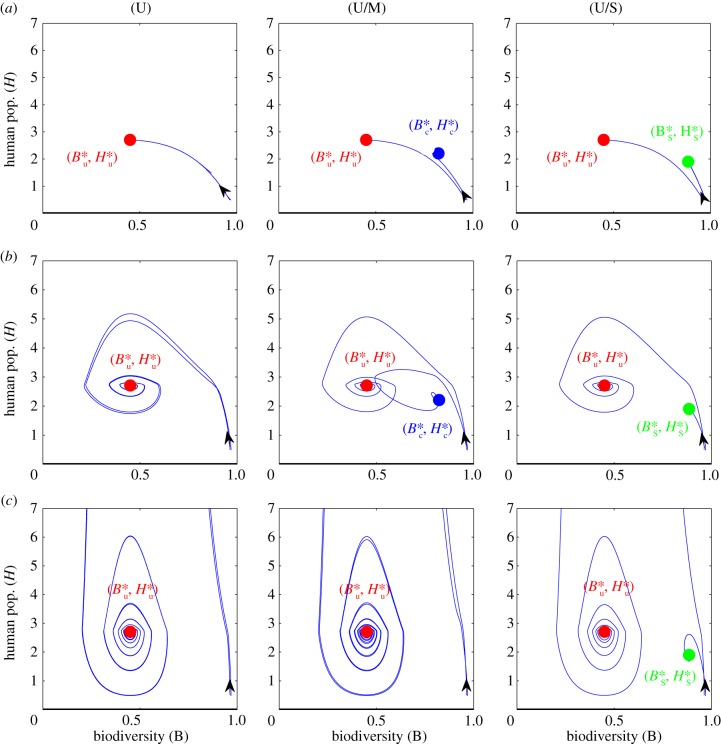
Figure 4.

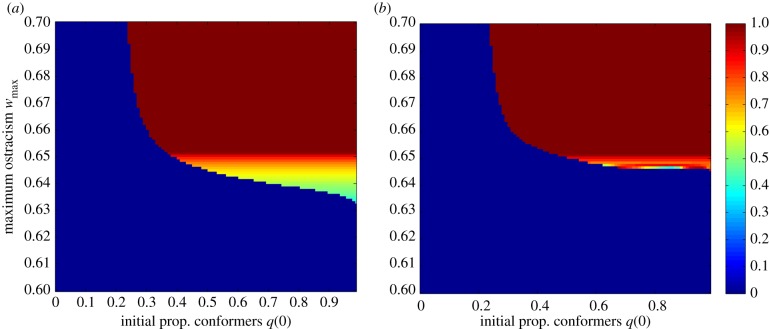
Effect of varying extinction debts ε and ostracism strengths w_max on transient dynamics and stability, for two initial proportions of conformers q(0). Cases (U), (U/M) and (U/S) correspond to the ostracism functions defined in figure 2a, with similar initial conditions, namely H(0) = 0.5, B(0) = (1 − H(0)/ϕ(q))^z and q(0) = 0.2 or q(0) = 0.6. (a) low extinction debt (ε = 0.1); (b) intermediate extinction debt (ε = 0.0025); (c) large extinction debt (ε = 0.0005); green dot: (stable) sustainable equilibrium; red dot: (stable) unsustainable equilibrium; blue dot: (stable) mixed equilibrium; transient trajectories are represented by the blue curves. See electronic supplementary material, table S1 for other parameter values.

(b). Human consumption and technological change

Human consumption is related to the production of agricultural and industrial goods through an auxiliary economic model, which is assumed to be at a moving market equilibrium. Following previous work [23], the effects of both biodiversity and technology on agricultural (j = 1) and industrial (j = 2) productions (e.g. ecosystem services, chemicals and machines) are captured by the total factor productivity (TFP) term of Cobb–Douglas production functions, with labour L_j and land A_j as inputs (equation (2.1)).

2.1

where α and α₂ are the labour elasticities of the agricultural and industrial sectors, respectively. The relationship between biodiversity and ecosystem services [19] is captured by a concave-down function of biodiversity, B^Ω, with Ω < 1 [31], and the feedback of ecosystem services on industrial production is neglected. For simplicity's sake, technology is taken as exogenous, i.e. independent from the human and ecological dynamics, and technological efficiency is assumed to follow a logistic growth at a rate σ towards a maximum efficiency, T_m (equation (2.2)). Such a logistic growth allows reproducing the past rise and current stagnation of the agricultural TFP [32]. Other forms of technological change (e.g. exponential or endogenous) do not qualitatively affect the dynamics of the model [23].

2.2

Solving for the market equilibrium (i.e. when supply equals demand) gives the per capita industrial and agricultural consumptions as functions of biodiversity and technological efficiency. Industrial consumption, y₂ = γ₂T/T_m, varies with technological efficiency only, while agricultural consumption y_1i = γ_1iB^ΩT/T_m of conformers (i = s) and defectors (i = u) also depends on biodiversity-dependent ecosystem services. Both industrial and agricultural consumptions increase with technological efficiency, T. By increasing production efficiency (equation (2.2)), technological change helps in counterbalancing the feedback of biodiversity loss on agricultural productivity in the short term, thus ensuring that the consumption utility of consumers does not decrease with time [23]. By γ_1i and γ₂ are denoted functions of socio-economic parameters that capture the characteristics of agricultural and industrial productions (electronic supplementary material, table S1). Using these parameters, a norm of sustainable agricultural practices γ_1s is defined in the next section.

(c). A norm of sustainable consumption

The footprint of agricultural goods can be related to the parameters of their production function, and especially to the output elasticity of labour, hereafter denoted as α, and the output elasticity of land, which equals 1 − α (equation (2.1)). In economics, output elasticity captures the per cent change in production resulting from a 1% change in an input, and is a proxy for the relative share of inputs used in production. Thus, the higher the α, the higher is the labour force per unit of land used in agricultural production. Agricultural labour forces have been globally declining with the substitution of machines, fertilizers and pesticides for labour and ecosystem services, and the consequent rise in production efficiency [33] and economies of scale [34]. Conventional industrialized agricultural systems thus have lower labour elasticities α than environmentally friendly systems, such as small-scale organic farming, where the substitution of labour and ecosystem services for technology is lower.

In previous work, labour elasticity has been related to the sustainability of SESs, in terms of their vulnerability to overshoot-and-collapse crises [23]. To do so, we have captured the transient dynamics of our SES by a sustainability criterion, Δ. This criterion captures the relative rate of change of biodiversity compared to the human population, because it is the difference between the ecological relaxation rate, ε, and the maximum growth rate of the human population, μ, as Δ = ε − θμ. The respective roles of these parameters are detailed in the following sections. By θ we denote a function of assessable ecological and economic parameters of the SES (electronic supplementary material, table S1), and ε captures the rate of change of species richness in response to land conversion [13,15]. Δ > 0 means that the ecological dynamics is fast enough compared to the human dynamics (ε > θμ), thus preventing transient overshoot-and-collapse crises. However, Δ < 0 means that the ecological dynamics is much slower than the human dynamics (ε < θμ), so that there is a high probability of experiencing transient crises. Using this criterion, we show in [23] that a low labour elasticity (i.e. a low share of labour in production) or, equivalently, a high substitution of human capital for technology, increases the vulnerability of SESs to lag effects, while there exists an intermediate sustainability-optimal labour elasticity that maximizes both long-term biodiversity (figure 1a) and sustainability (figure 1b).

Let us define as α_s the sustainability-optimal labour elasticity, and α_u < α_s an unsustainable labour elasticity chosen such that Δ(α_u) < 0 (figure 1a). The expected agricultural labour elasticity then varies with the proportion of conformers as α(q) = qα_s + (1 − q)α_u. Through means of eco-labelling, consumers can either buy sustainable agricultural products (y_1s), or follow their unsustainable consumption habits and buy unsustainable agricultural products (y_1u). As economic dynamics are much faster than ecological and demographic dynamics, we assume that agricultural and industrial production instantaneously follows consumers’ demand. Such a shift in agricultural production may not be met instantaneously due to inertia and production barriers [35], and farmers' adaptability may have to be supported through adequate policy changes [36]. However, given the large time scales considered here, it seems reasonable to neglect such time delays with respect to the extent of extinction debts. Thus, in our system, a consumption shift towards sustainable goods, which, in turn, drives a shift towards more environmentally friendly agricultural practices, may prevent environmental crises.

(d). Human demography

The growth rate of human populations can be related to consumption levels by capturing basic linkages between technology and human demography [37]. Following previous studies, we assume that the human growth rate endogenously varies with the mean agricultural and industrial consumptions, so as to increase with agricultural consumption, and decrease with industrial consumption, capturing the effect of the demographic transition.

2.3

where μ is the maximum growth rate, y^min₁ is the minimum consumption threshold, 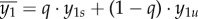is the average agricultural consumption and b₂ is the demographic sensitivity to industrial consumption. The strength of the demographic transition thus gradually increases with industrial consumption and limits human population growth [37].

Dependence of the human growth rate on consumption levels also allows coupling human demography with social changes regarding consumption choices. Indeed, conformers do not only have a lower consumption footprint than defectors, it can be shown that they also have a lower agricultural consumption level (i.e. y_1s < y_1u). As a result, conformers also have a lower reproduction rate compared to defectors. This can be interpreted as a quantity–quality trade-off in both consumption choices and the number of children, a mechanism which has been shown to partly explain the fertility reductions observed during the demographic transition [38]. Under our assumptions, shifting behaviours towards sustainable consumption habits thus reduces the growth rate of the human population, therefore increasing the sustainability of the SES.

(e). Land conversion and biodiversity dynamics

The rate of land conversion is also derived at market equilibrium, as a function of the dynamical variables of our system under sustainable and unsustainable labour elasticities, α_u and α_s (see [23] for more details about the economic derivations). For a given proportion of conformers q and human population H, converted area is written as 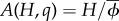, where 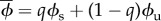is the mean population density on converted land, and ϕ_u and ϕ_s are explicitly defined as functions of the economic parameters of the SES in electronic supplementary material, table S1.

Natural habitat conversion results in time-delayed changes in species richness, so that the long-term species richness may be reached only after decades [15]. These extinction debts [12] are a result of many mechanisms which lower the relaxation rates of communities [13]. We use a power-law species–area relationship to capture the dependence of long-term species richness on the remaining area of natural habitat [39]. As A(H, q) ∈ [0; 1], we allow the long-term species richness to vary between 1 (no habitat conversion) and 0 (all habitat is converted) by writing S(H, q) = (1 − A(H, q))^z, where the slope z ∈ [0; 1] ensures that the function is concave-down [31]. Following experimental and theoretical results [13,15,40], we then assume that the rate of community relaxation is proportional to the difference between current biodiversity B and long-term species richness S(H, q).

2.4

where ε measures the relaxation rate of the community of species. The inverse of the relaxation coefficient ε measures the time it takes to lose approximately 63% of the species that are doomed to extinction [13].

(f). Social dynamics

Let us assume that the human population has identified the sustainability-optimal agricultural labour elasticity, α_s (figure 1b,c). Restricting one's consumption to sustainable agricultural goods has become a social norm, i.e. a shared rule of behaviour. Recent studies demonstrate the importance of social norms on eating behaviours and their role in shifting preferences towards healthy food [41]. The importance of dietary social norms is especially important in young adults, whose eating patterns typically become lifelong habits [42]. Perception of others’ pro-environmental behaviour was identified as the first step towards environmentally friendly behavioural change [43].

Deviance from a social norm can lead to direct or indirect sanctioning from other members of the SES, be they important others or strangers [44]. Ostracism can result in social exclusion or poor reputation [45], thus decreasing the well-being of individuals. As a consequence, social pressure can reduce the well-being of defectors to the point where it becomes more profitable for them to shift behaviour in order to conform to the sustainable norm. A common way to approximate the well-being of consumers is through their consumption utility, which is a function of their per capita agricultural and industrial consumptions, and thus varies with the dynamical variables of the system. Let us denote the utility of a consumer of type i (i = {u, s}) as U_i = y^η_1i y^1−η₂, where η is the preference for agricultural goods. Under our assumption that α_s > α_u, it can be shown that the consumption utility of defectors in the absence of social pressure, U_u, is always higher than the consumption utility of conformers, U_s. Therefore, in the absence of social pressure, defectors have no incentive to shift their habits.

Following previous studies [8,9], we assume that social pressure decreases the utility of defectors, U_d = U_u − w(q) · δ_u, so that it may become more profitable for defectors to shift their consumption and comply with the sustainable norm. The severity of the ostracism function, 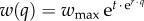, increases with the proportion of conformers in the population, q, and depends on the maximum sanctioning w_max, the sanctioning effectiveness threshold t and the growth rate of the function, r. In addition to depending on the number of conformers in the community, graduated sanctioning and equity considerations lead conformers to act more strongly against defectors, whose consumption is the most unsustainable [3]. Thus, the lower the α_u and the larger the difference in consumption utilities between conformers and defectors, δ_u = (U_u − U_s)/U_u, the stronger will be the social pressure.

The proportion of conformers then follows a replicator dynamics [8,9] (i.e. varies both with the proportion of conformers, q, and the difference between the sustainable consumption utility, U_s, and the average consumption utility, 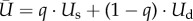, itself varying with the other dynamical variables of the system through the consumption of agricultural and industrial goods, y_1i and y₂).

2.5

As U_u > U_s in our model, a global dietary shift towards sustainable consumption (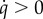) is only possible if the severity of the social pressure is higher than the utility of defectors in the absence of social pressure (i.e. w(q) > U_u; equation (2.5)).

In the following, our focus is on the potential of consumers’ behavioural change in preventing unsustainable trajectories (i.e. overshoot-and-collapse population crises leading to biodiversity-poor equilibria in the long run [23]). We first analyse the dynamical system of equations (2.2)–(2.5), with a negligible ecological relaxation rate (ε = 0.1). The consequences of lag effects are explored in §3d.

3. Results

(a). Social–ecological equilibria

Our SES can have two types of equilibria (H*, B*, T_m, q*), hereafter denoted as viable (H* > 0 and B* < 1) or unviable (H* = 0 and B* = 1), when the economic parameters do not allow the human population to maintain itself in the environment [23]. Let us denote the viable equilibria as (H*_i, B*_i, T_m, q*_i), with i = {u, s, c}. Among the viable equilibria, one is unsustainable (i = u), i.e. only defectors persist (q*_u = 0) and the transient dynamics includes overshoot-and-collapse population cycles under large extinction debts (figure 4c). The other two types of viable equilibria are either fully sustainable (i = s) when only conformers persist (q*_s = 1), or partially sustainable (i = c) when both conformers and defectors coexist (q*_c ∈ ]0; 1[). The coexistence equilibrium satisfies w(q*_c) = U*_u(B*_c), for which there is no analytical solution.

A general analytical solution for the unsustainable and fully sustainable equilibria is given in equation (3.1), where the population density ϕ_i and γ_1i (i = {u, s}) are explicitly defined as functions of the parameters of the SES in electronic supplementary material, table S1.

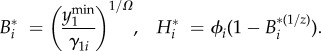3.1

Under our assumption that α_s > α_u, it can be shown that γ_1s < γ_1u, so that biodiversity at the sustainable equilibrium is higher than that at the unsustainable equilibrium, i.e B*_s > B*_u. However, population density is also higher at the sustainable equilibrium, i.e. ϕ_s > ϕ_u, so that the human population size at equilibrium does not necessarily decrease with the proportion of conformers. Compliance with the sustainable consumption norm thus helps in preserving biodiversity while not necessarily reducing the size of the human population.

(b). Alternative stable states

A stability analysis of our SES model shows that two of the viable equilibria can be both stable at the same time, depending on the severity of the ostracism function compared to the consumption utility at equilibrium (electronic supplementary material, §3). The per capita consumption utilities at the sustainable, unsustainable and coexistence equilibria are equal to U* = (y^min₁)^ηγ^1−η₂. Compliance with the sustainable consumption norm thus does not reduce the long-term consumption utility.

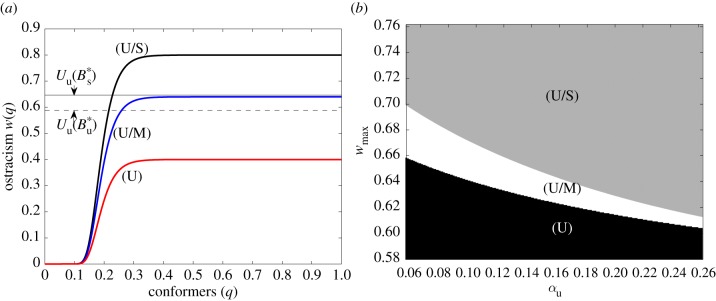
The sustainable equilibrium is stable if the maximum ostracism w(1) is higher than the consumption utility that the defectors would have at the sustainable equilibrium (i.e. w(1) > U_u(B*_s), where U_u(B*_s) = (γ_1u/γ_1s)^ηU*). Conversely, the unsustainable equilibrium is stable if the minimum ostracism w(0) is lower than the consumption utility at the unsustainable equilibrium (i.e. w(0) < U_u(B*_u) where U_u(B*_u) = U*; figure 2a). Therefore, for intermediate consumption utilities, w(0) < U_u(B*_u) < U_u(B*_s) < w(1), both the unsustainable and sustainable equilibria are stable ((U/S) region in figure 2b). For high consumption utilities, w(0) < U* and w(1) < U_u(B*_s), ostracism is too weak to allow norm-driven behavioural change, and the unsustainable equilibrium is the only stable equilibrium that the SES can reach ((U) region in figure 2b), or both the unsustainable and mixed equilibria are stable ((U/M) region in figure 2b). As there is no analytical expression for the mixed equilibrium, we are not able to derive any stability condition for this bistability region. However, figure 2b shows that the shift between the two bistable regions (U/M) and (U/S) depends on the footprint α_u of unsustainable consumption. The larger the footprint of defectors compared to conformers (α_u≪α_s), the larger is the bistability region (U/M) between the mixed and unsustainable equilibria and the smaller the bistability region (U/S). Thus, the larger the required behavioural change to shift from unsustainable habits (α_u) towards sustainable habits (α_s), the more difficult it is to reach sustainability.

Figure 2.

Combined effect of the ostracism parameters and the difference between sustainable and unsustainable norms on the stability of the equilibria. (a) Shape of the ostracism function for varying maximum ostracism w_max. (U) Weak sanctioning (w_max = 0.4) and stability of the unsustainable equilibrium only, such that w(0) < w(1) < U_u(B*_u) < U_u(B*_s); (U/M) intermediate sanctioning (w_max = 0.64) and bistability of the unsustainable and the mixed equilibria; (U/S) strong sanctioning (w_max = 0.8) and bistability of the unsustainable and the sustainable equilibria, such that w(1) > U_u(B*_s) and w(0) > U_u(B*_u). See electronic supplementary material, table S1 for other parameter values. (b) Stable equilibria with varying maximum ostracism w_max and unsustainable labour elasticity α_u. Regions (U), (U/M) and (U/S) correspond to the red, blue and black curves in (a), respectively.

(c). Impact of the initial state of the social–ecological system

Depending on the parameters of the SES, the size of the human population at the sustainable equilibrium can be either higher (e.g. for T_m = 2) or lower (e.g. for T_m = 1.8) than at the unsustainable equilibrium. Let us now consider a situation where the human population size at the sustainable equilibrium is lower than that at the unsustainable equilibrium.

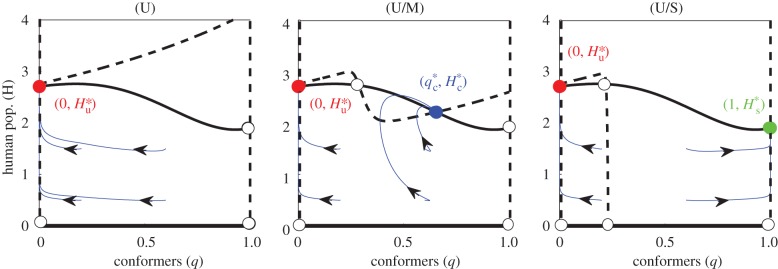
Figure 3 shows that when there is bistability ((U/M) and (U/S) panels), the sustainable and mixed equilibria are only reached in the long run when the initial proportion of conformers is high enough. The stronger the ostracism, the lower is the minimum proportion of conformers required for sustainability (i.e. the larger the sustainable basin of attraction). Gradually changing social parameters may thus push an initially unsustainable SES ((U) panel in figure 3) towards a sustainable path ((U/S) panel in figure 3), provided that the initial social capital is large enough.

Figure 3.

Effect of the initial conditions on the long-term equilibria, for various ostracism strengths w_max. Cases (U), (U/M) and (U/S) correspond to the ostracism functions defined in figure 2a. Black curve: isocline 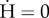; dashed curve: isocline 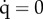; white dots: unstable equilibria; green dot: (stable) sustainable equilibrium, (H*_s, B*_s, 1); red dot: (stable) unsustainable equilibrium, (H*_u, B*_u, 0); blue dot: (stable) coexistence equilibrium, (H*_c, B*_c, q*_c ); transient trajectories are represented by the blue curves. See electronic supplementary material, table S1 for parameter values.

Under conditions of bistability, the type of equilibrium that will be reached in the long run thus depends on the rate of social change. In the following, we show that the rate of social change also depends on human perception of environmental changes and, in our case, extinction debts.

(d). Impact of extinction debts on the effectiveness of ostracism

We now explore the transient behaviour of the SES with varying ecological relaxation rates, ε, for two of the initial conditions used in figure 3, corresponding to two initial proportions of conformers q(0) = 0.2 and q(0) = 0.6, with the same human population size H(0) = 0.5. To better visualize transient environmental crises, we plot the null-clines and transient trajectories in the human-biodiversity phase plane (figure 4a). Ecological relaxation rates slow down the social dynamics by postponing the utility reduction of defectors, U_u, and therefore, their consumption shift towards sustainable habits (equation (2.5)). When the extinction debt is moderate, transient dynamics towards the unsustainable and mixed equilibria show environmental crises, the amplitude of which is lower for the mixed equilibrium (figure 4b). The sustainable trajectories do not experience any overshoot-and-collapse behaviour, even for high extinction debts ((U/S) panel in figure 4c), which confirms the relevance of our sustainability criterion. A high extinction debt leads to very large environmental crises over the unsustainable trajectories (figure 4c). Moreover, in the case of bistability between the unsustainable and mixed equilibria, all trajectories now reach the unsustainable equilibrium ((U/M) panel in figure 4c). Large ecological relaxation rates thus result in the loss of stability of the mixed equilibrium in favour of the unsustainable equilibrium. This result suggests a shift in the dominant social-ecological feedback for increasing relaxation rates. At low relaxation rates, the ecological dynamics is fast enough for the negative effect of environmental degradation on human well-being to result in fast enough social changes, thus reinforcing sustainable feedbacks through an efficient social ostracism. However, large extinction debts slow down the ecological dynamics and postpone the negative ecological feedback on human well-being. This reduces the efficiency of social ostracism and results in a shift of the dominant feedback towards unsustainable feedbacks (i.e. increasing consumptions and decreasing labour intensities).

Figure 5 shows the combined impact of lag effects and social ostracism on the basins of attraction of the sustainable, mixed and unsustainable equilibria. Increasing both the initial proportion of conformers and the strength of the ostracism can push an initially unsustainable SES into the basin of attraction of the sustainable or mixed equilibria (figure 5a). However, decreasing the ecological relaxation rate ε reduces the basin of attraction of the mixed equilibrium in favour of the unsustainable equilibrium (figure 5b). The stability of the mixed equilibrium appears to be much more sensitive to ecological time lags than that of the sustainable equilibrium. Thus, moderate behavioural changes leading to a mixed equilibrium may not be robust enough to ecological lag effects. These results suggest that only important behavioural changes allowing to reach the fully sustainable equilibrium may be able to counteract the destabilizing effect of ecological time lags. The extinction debt, by postponing the consequences of environmental degradation on human well-being, thus reduces the robustness of social change and norm-driven sustainability.

Figure 5.

Proportion of conformers at equilibrium (q*) under the combined effects of the initial proportion of conformers q(0) and maximum ostracism w_max, for an increasing extinction debt. Other initial conditions: H(0) = 0.5, and B(0) = (1 − H(0)/ϕ(q(0)))^z. See electronic supplementary material, table S1 for other parameter values. (a) low extinction debt (ε = 0.2); (b) high extinction debt (ε = 0.0005). Blue represents a population of defectors (q* = 0), red represents a population of conformers (q* = 1) and intermediate colours represent a coexistence of conformers and defectors (q* ∈ [0, 1]).

4. Discussion and conclusions

We investigate the robustness of norm-driven sustainability, as measured by a shift towards low-footprint consumption habits. Specifically, we focus on the robustness of SESs to time-delayed biodiversity losses caused by human-driven natural habitat destruction. Time-delayed ecological feedbacks are known to reinforce negative management feedbacks and potentially push SESs into social-ecological traps [10]. However, little research so far has investigated the long-term impacts of extinction debts on the sustainability of coupled SESs. Ecological studies of the anthropogenic impacts on resources or ecosystems often neglect changes in the size and behaviour of the human population. Additionally, natural resources are often managed as decoupled from the ecosystems they are part of, and most socio-economic studies overlook the finiteness and physical limits of natural systems. Modelling sustainability requires accounting for the bidirectional coupling between human and natural systems [46], and especially the feedback loop between human population growth and environmental degradation [23].

In our model, this feedback loop is mediated through biodiversity-dependent ecosystem services to agricultural production. A human population exploits a shared land resource divided into natural habitat and converted agricultural and industrial lands. Natural habitat supports a community of species and provides a range of biodiversity-dependent regulatory services to agricultural production, which can itself be seen as a provisioning service. A norm of sustainable consumption is maintained through social sanctioning of unsustainable consumers. Increasing demand for sustainable consumption translates into more sustainable agricultural practices, which involve the use of a larger proportion of labour compared to land. Finally, human population growth is driven by the interaction between available agricultural resources, and technological and social changes, thus adding to the growing literature modelling the interaction between human populations and their environments [24].

Our approach thus differs from the classical economic literature related to the internalization of intertemporal externalities of agricultural production [4]. Though we also consider the pressure of a group over another as a driver of sustainable change, the penalties involved are not chosen optimally. This would require that each of the conformers had access to perfect information regarding the social damage associated with the unsustainable consumption of defectors, as well as the optimal social pressure to apply. The point of this article was not to derive an optimal regulation strategy, but to illustrate the potential of bottom-up consumption changes in driving sustainable shifts in production practices, given the long-term ecological dynamics of the SES.

The sustainable consumption norm is identified following Lafuite & Loreau's [23] sustainability criterion, which characterizes the vulnerability of an SES to transient ‘overshoot-and-collapse’ population crises. This criterion captures the difference between the rates of ecological relaxation and human population growth, so that sustainable SESs have high enough ecological relaxation rates compared to the growth rate of their human populations. We verify here the validity of this sustainability criterion, showing that a shift towards more environmentally friendly agricultural practices (i.e. characterized by a lower substitution of ecosystem services and labour for technology) decreases the vulnerability of SESs to transient crises. Such a global shift towards sustainable agricultural practices would require reversing current trends of land-intensive and highly mechanized agricultural production towards more labour-intensive productions (e.g. small-scale agro-ecological farms). Growing evidence suggests that diverse small-scale agro-ecological farms increase carbon sequestration, support biodiversity, rebuild soil fertility and sustain yields over time, thus securing farm livelihoods, while competing with industrial agriculture in terms of total outputs, especially under environmental stress [47].

Under a negligible ecological time delay between natural habitat loss and biodiversity erosion, full sustainability is ensured when both social sanctioning and the proportion of conformers are large enough, and when the required behavioural change to shift from unsustainable to sustainable habits is not too large. Otherwise, a minority of defectors coexists with a majority of conformers at the mixed equilibrium. When social sanctioning and/or the proportion of conformers is too low, only defectors persist at equilibrium. This unsustainable equilibrium is always stable, so that there is bistability between the unsustainable and sustainable or mixed equilibria, when these are stable. These findings echo those of Tavoni et al. [8], who used a similar non-costly social sanctioning to study cooperation in the management of a single natural resource under variable environmental conditions. However, time delays have an opposite effect to resource variability, because temporal variability tends to decrease the mean resource level, thus increasing the probability of a behavioural shift towards norm compliance. Our model differs from Tavoni et al. [8] in many aspects; first, here we focus on the interaction between various ecosystem services, especially provisioning and regulatory services, instead of a single natural resource; second, these services feed back on the dynamics of the human population that uses these services, so that the human population varies endogenously with the state of the environment; lastly, social sanctioning affects consumers' behaviour, instead of producers'. The latter feature allows us to focus on the potential of consumers' behavioural changes in establishing sustainability in coupled SESs. We could also have a modelled a reciprocal pressure between conformers and defectors, in which case our result would also depend on the relative strength of these pressures.

Our study provides insights into the consequences of lag effects for norm-driven sustainability. Biodiversity loss acts as a negative feedback on human well-being, through the loss of biodiversity-dependent regulatory services to agricultural production. A time-delayed biodiversity feedback thus maintains a high utility of defectors for a longer period of time. This time lag decreases the efficiency of social ostracism, thus delaying behavioural shift. Postponing the behavioural shift of defectors towards sustainable consumption for too long can make the mixed equilibrium totally unreachable, meaning that a tipping point has been crossed in terms of human population size and habitat destruction. The lower stability of the mixed equilibrium and its propensity to regime shifts was already observed by Lade et al. [48]. Thus, under large time delays, the only way to reach sustainability is to reach the full-sustainability equilibrium, which requires much larger behavioural changes. However, given the widely observed coexistence of both conformers and defectors in small groups [49], such behavioural changes seem rather unlikely.

Moreover, theory suggests that relaxation rates are not constant, but increase with the extent of habitat destruction and fragmentation, thus further delaying the feedback of biodiversity-dependent ecosystem services on human societies [18]. In situations where habitat destruction leads to a strong increase in ecological relaxation rates, we would expect a decrease in sustainability, or a shift towards unsustainable development paths. An interesting extension to our work would thus be to use a spatially explicit ecological model, in order to gain more realism regarding the temporal dynamics of ecological relaxation rates under habitat destruction, and study social-ecological regime shifts from a spatial perspective.

The emergence of tipping points and regime shifts in coupled SESs [48] is gaining increasing interest, with many implications for the adaptive management of SESs [50]. Regime shifts can lead to social–ecological traps, where unsustainable feedbacks reinforce each other and push the SES into an undesirable state [7]. Some authors suggest that humanity may be locked in a technological innovation pathway that reinforces such unsustainable feedbacks [27].

Our results highlight the importance of accounting for the feedback loop between human demography, environmental degradation and behavioural changes when studying the long-term sustainability of coupled SESs. Especially, the temporal dynamics of coupled social–ecological processes matter, because time-delayed ecological feedbacks alter the human perception of environmental degradation and the rapidity of behavioural changes. Policies that enhance the adaptive capacity of SESs may thus benefit from taking both social norms and time delays into account [6]. These insights also point to future research needs regarding the interplay of social, demographic and ecological long-term dynamics.

Data accessibility

This article has no additional data.

Author's contributions

A.-S.L., C.d.M. and M.L. jointly designed the study, developed the model, and analysed and interpreted the model results. A.-S.L. drafted the manuscript; M.L. and C.d.M. revised it critically. All the authors gave their final approval for publication.

Competing interests

We have no competing interests.

Funding

This work was supported by the TULIP Laboratory of Excellence (ANR-10-LABX-41) and the Midi-Pyrénées Region.