Selection bias in studies of human reproduction-longevity trade-offs

Abstract

A shorter lifespan as a potential cost of high reproductive effort in humans has intrigued researchers for more than a century. However, the results have been inconclusive so far and despite strong theoretical expectations we do not currently have compelling evidence for the longevity costs of reproduction. Using Monte Carlo simulation, it is shown here that a common practice in human reproduction-longevity studies using historical data (the most relevant data sources for this question), the omission of women who died prior to menopausal age from the analysis, results in severe underestimation of the potential underlying trade-off between reproduction and lifespan. In other words, assuming that such a trade-off is expressed also during reproductive years, the strength of the trade-off between reproduction and lifespan is progressively weakened when women dying during reproductive ages are sequentially and non-randomly excluded from the analysis. In cases of small sample sizes (e.g. few hundreds of observations), this selection bias by reducing statistical power may even partly explain the null results commonly found in this field. Future studies in this field should thus apply statistical approaches that account for or avoid selection bias in order to recover reliable effect size estimates between reproduction and longevity.

1. Introduction

One of the most enduring questions in studies of human life-history evolution has been whether women, who invest more direct energetic resources in reproduction than men, sacrifice their longevity for higher reproductive success. These studies are often grounded on the evolutionary theories of senescence that predict reduced old-age somatic maintenance and survival resulting from higher lifetime reproductive effort at early ages [1,2]. Despite over a century-long research effort, starting from Beeton et al. [3], evidence for the survival costs of reproduction at the phenotypic level is still surprisingly scarce in humans (reviewed in [4–8]). The reasons why we do not generally see such costs in most of the human populations studied are not well understood, but methodological discrepancies and issues concerning data quality may be likely candidates for the mixed results [5,7].

The most relevant sources of human reproduction-longevity associations come from historical parish records. In historical populations, natural fertility was high owing to negligible birth control, mortality rates were high in the absence of modern medical care and the full length of lifespan of individuals can be tracked from these records [5,7]. A common practice in these studies has been to restrict the analysis to those women only who survived beyond the expected age of natural menopause, often defined as the age of 45–55 years [4–8]. The obvious inferential reason for this has been to maintain the ‘causal’ interpretation of the regression estimate of lifespan on reproduction. That is, by including also women who died before reaching menopausal age might confound the regression estimate because longer lived women not dying from reproduction-related causes also had more time to produce many offspring during their lifetime, resulting in a positive association between reproduction and lifespan. More often, stated reason for considering post-menopausal women only has, however, been the interest to focus on women's post-reproductive or -menopausal survival. In addition to that, this latter argument may be a natural consequence of the former argument, it is unlikely that reproductive costs in human females are manifested only during post-menopausal lifespan and not also during reproductive years [9,10]. A most obvious example against this argument being maternal death at childbirth. But what is important here is that restricting the analysis to post-menopausal women has a major statistical drawback: the fraction of women excluded by this procedure based on how long they lived does not represent a random draw from the available sample and, thus, it distorts the results of the analysis owing to selection bias (e.g. [11,12]). In missing data literature, this phenomenon is termed as non-ignorable missingness, meaning that the data are missing not at random but depending on its own values [13,14]. Inconsistency of estimated regression coefficients owing to the omission of observations of the dependent variable based on its values seems somewhat recognized among human evolutionary demographers, but despite the very few exceptions [9,15], researchers interested in human reproduction-longevity associations seem to largely discard potential selection bias. This may partly owe to the fact that the magnitude of this problem has not been explicitly demonstrated in this field and, hence, its severity may not be yet fully acknowledged.

To fill this gap, this article provides an explicit demonstration of the adverse consequences of selection bias on drawing biological conclusions from the data in the context of human reproduction-longevity trade-offs. This is done using Monte Carlo simulation, where the influence of non-random selection of observations of the dependent variable into the analysis (i.e. selection of women based on the length of their lifespan) on the consistency of regression estimate is investigated. In order to also assess the influence of selection bias on the statistical power of the regression estimate of interest, the simulation is run using three different sample sizes (n = 200, 500 and 1000) commonly encountered in these kinds of studies. Furthermore, a dataset from preindustrial northern Finland [16] is examined by first performing an analysis only for post-menopausal women and then by correcting for the non-random omission of pre-menopausal women from the analysis.

2. Methods

Monte Carlo methods rely on repeated random sampling from probability distributions to obtain numerical results [17]. Such simulations are a convenient way to examine experimentally how the violations of the particular assumptions of statistical models influence the robustness of statistics of interest. These simulations involve the generation of numerous sample datasets based on a true population model, which are then examined using a misspecified analysis model that differs in its data-generating assumptions [18]. After this, the results are aggregated and the researcher can evaluate the impact of model misspecification, for example, on parameter estimates and their standard errors.

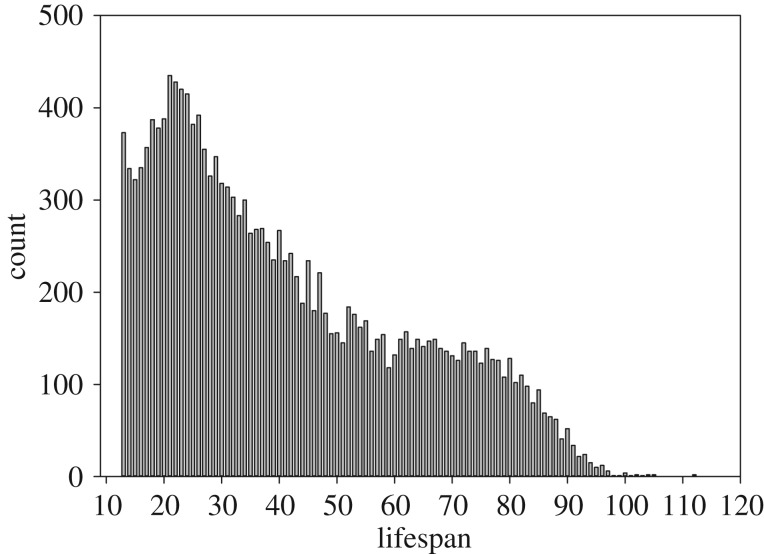
The simulation started by the generation of two continuous and normally distributed random variables, both having a mean of zero and unit variance (i.e. the variables were standardized by standard deviation). Here, the dependent variable represents simulated lifespan and the independent variable represents simulated reproductive effort (e.g. the lifetime number of offspring born). Note that real-life distribution of lifespans in historical populations unlikely conformed smoothly to a normal distribution. For example, as seen in the data of reproductive aged women (i.e. over the age of 13 years in these data) from historical northern Sweden [19], the distribution of lifespans is rather highly skewed to the right (i.e. positive skew) (figure 1). The consequences of sample selection in the presence of strong positive skew should, however, become evident faster than in distributions with zero skew (i.e. symmetric normal distribution), because the mass of the distribution in positively skewed distributions is concentrated on earlier deaths, hence the median shifting to the left from the mean (being equal in a zero-skew distribution). Moreover, as selection bias is inherently a problem arising from non-ignorable missing data [12,13], regression models based on different outcome distributions should be equally vulnerable to selection bias (excluding logistic regression, see [20]). In addition, the distribution of reproductive effort is irrelevant here, because the marginal distribution of independent variables is not part of the regression models [12].

Figure 1.

The frequency distribution of lifespans of reproductive age women in five historical parishes (Karesuando, Jukkasjärvi, Jokkmokk, Vilhelmina and Gällivare) from northern Sweden (n = 16 621).

In the data-generating model, a regression coefficient between these two variables was set to three different values: −0.1, −0.3 and −0.5. These values are commonly considered as small, medium and large effect sizes in the statistical literature [20]. These negative correlations illustrate the different magnitudes of the trade-off between reproduction and lifespan. A total of 10 000 replications were drawn. Since studies of human reproduction-longevity trade-offs usually vary in their sample size, ranging approximately from less than 100 women to some thousands of women, the simulations were run with the samples sizes of 200, 500 and 1000 observations (sample sizes exceeding n = 1000 had trivial influences on the results; see the electronic supplementary material, table S1). All replications converged normally.

In order to demonstrate the effects of non-random selection of women based on their lifespan on the expected trade-off between reproduction and longevity, the data were analysed using the same model, but sequentially deleting the observations by every 10th percentile of the simulated lifespan and then re-running the model. The exact values for the percentiles used as cut-off values for the simulated lifespan distribution were obtained by running one replication with a very large sample size (n = 10 000) (see the electronic supplementary material, figure S1). To evaluate the stability of the simulations conducted, the seed value was changed once in order to confirm the results of the simulations.

The inconsistency introduced to the regression estimate by the per-10th-percentile deletion of simulated lifespans was estimated using the mean relative percentage of parameter and standard error bias [18]. A bias more than 10% and 5% in the point estimate and in its standard error, respectively, is considered as unacceptable [21]. Monte Carlo simulations can also be used to simultaneously estimate the statistical power of the estimates of interest [21]. Hence, the 95% coverage of the regression estimate and its power were determined. The 95% coverage represents the proportion of replications for which the 95% confidence interval (CI) contains the population value of the parameter, while statistical power (for those population parameters that differ from zero by design) means the probability of rejecting the null hypothesis when it is false. For the 95% coverage, values between 0.91 and 0.98 are desired [21], whereas the critical value for adequate statistical power is usually considered to be 0.8 [22].

As a simple solution to this selection bias problem, censored-normal (Tobit) regression modelling [23] is introduced. In this approach, instead of treating the women dying prior to menopause as missing data, all women dying before, e.g. age of 50 years were scored as having died exactly at the age of 50 years (i.e. they are considered as left- or below-censored). The censored regression approach was then applied to the Monte Carlo simulated datasets with the medium effect size (β = −0.3) in the same manner as above. In addition, a previously published dataset from preindustrial northern Finland examining how women's lifetime reproductive effort, measured as the number of offspring surviving to adulthood, was related to their post-menopausal lifespan [16] is re-analysed using censored-normal regression approach. Because the whole dataset has been re-collected since the publication of Helle et al. [16], the results are not expected to replicate perfectly. Furthermore, the model used here controlled for mothers' ages at first and last reproduction, ethnicity (indigenous Sami or settled Finn), the main livelihood of their family (traditional Sami livelihood or animal husbandry of Finns), study parish and study period, of which all were not included in the original analysis [16]. First, the analysis was restricted only to women who survived to age 50 or above (n = 503) using regular regression approach with robust maximum-likelihood estimation. The model was then re-run with scoring all those women who died prior to age 50 as having died at the age 50 of years (n = 689) and using censored-normal regression approach with robust maximum-likelihood estimation. In this sample, 27% of women were thus excluded non-randomly from the analysis if only post-menopausal mortality is considered. The simulations and the re-analysis of human dataset were conducted with Mplus v. 8 [24]. Mplus code used in simulations is given in the electronic supplementary material.

3. Results

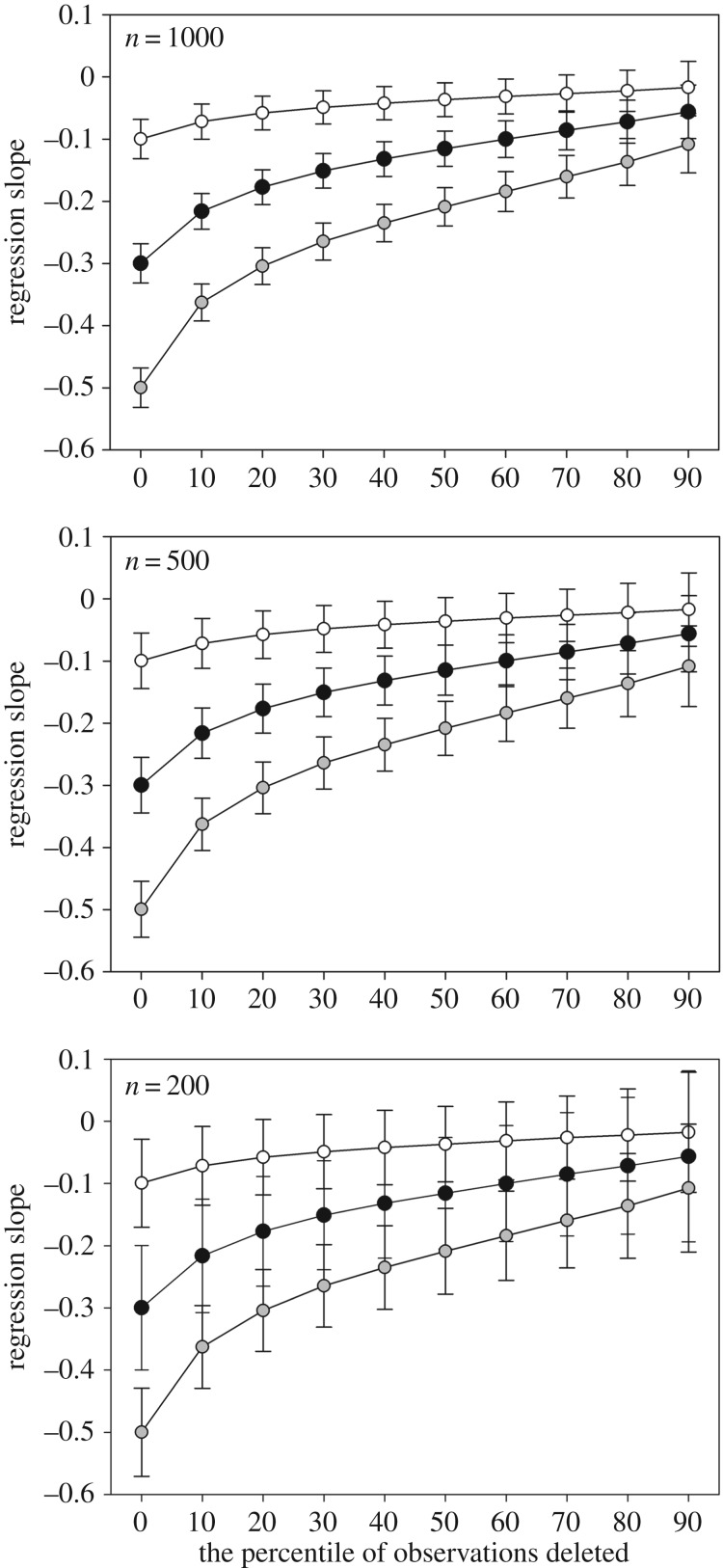
Irrespective of the sample and effect size used in the simulations, non-random deletion of the observations of simulated lifespan based on their face value had a clear attenuating effect on the regression estimate: the more low-value observations of the dependent variable were omitted from the analysis, the more the regression estimate was biased towards zero (figure 2; electronic supplementary material, table S2). In other words, the underlying trade-off between reproduction and longevity was greatly underestimated when women dying at younger ages were left out of the analysis. The relative bias of regression slope in all the sample sizes considered greatly exceeds the recommended cut-off value of 10% when just 10% of observations from the lower bound of the distribution were deleted (electronic supplementary material, table S2). The non-random deletion of observations of the dependent variable seems to affect the relative bias of standard errors less dramatically compared with their point estimates, although the recommended cut-off value of 5% is also clearly exceeded when just 10% of the observations were deleted from the analyses, irrespective of effect and sample sizes (electronic supplementary material, table S2). In addition, the 95% coverage of CIs dropped immediately below the recommended threshold (i.e. below 0.91), meaning that even excluding only the 10% of the lower-bound observations will produce incorrect results in terms of true effect size. A slight exception to this was seen in the case of small effect and sample sizes, where 95% coverage dropped below the threshold when 20% of the lower-bound observations were deleted (electronic supplementary material, table S2).

Figure 2.

The behaviour of average regression slopes and their average standard errors across 10 000 replications in response to selecting sample observations based on their values, by the every 10th percentile. From the top to the bottom, the Monte Carlo simulation was run using large (n = 1000), medium (n = 500) and small (n = 200) sample sizes using three effect sizes: −0.1 (white dots), −0.3 (black dots) and −0.5 (grey dots).

Monte Carlo determined estimates of statistical power showed that if the effect size is small (i.e. −0.1) and sample selection is present, there is not enough power to detect a trade-off between reproduction and longevity in sample sizes below 1000 observations (electronic supplementary material, table S2). When the effect size increases to −0.3, statistical power remained acceptable (i.e. greater than 0.8) until roughly the 70% and 60% of the lower bound observations were excluded from the analysis in sample sizes of 1000 and 500 observations, respectively (electronic supplementary material, table S2). In effect size of −0.3 and small sample size of just 200 observations, even excluding the observations below the 20th percentile was enough to drop the probability to correctly reject the null hypothesis below the generally accepted value of 0.8 (electronic supplementary material, table S2). In the case of a large effect size (i.e. −0.5), sufficient power was obtained until 90%, 80% and 20% of the lower bound observations were excluded from the analysis in sample sizes of 1000, 500 and 200 observations, respectively (electronic supplementary material, table S2).

When applied to the same Monte Carlo simulation scenario as used above, the approach based on censored-normal regression successfully produced consistent regression estimates, attained good coverage of those estimates and preserved high statistical power (see the electronic supplementary material, table S3).

Re-analysis of the association between reproductive effort and longevity in preindustrial northern Finland showed that when the analysis was restricted to women living to age 50 or above, the regression estimate of lifespan on reproductive effort was 0.25 (95% CIs = −0.45, 0.95). By contrast, the inclusion of women who died prior to age 50 into the analysis and scoring them as having died at the age of 50 years, the censored-normal regression reported a regression estimate of 0.58 (95% CIs = −0.25, 1.41). That is, accounting for selection bias more than doubled the effect size estimate in this sample.

4. Discussion

The Monte Carlo simulation study and empirical example from preindustrial northern Finland clearly showed that regression estimates are strongly biased towards zero when observations of the dependent variable are deleted from the analysis based on their scores (i.e. non-randomly). Such an attenuation of regression estimates is because of the resulting correlation between the independent variable and the model error term, thereby violating one of the key assumptions of any regression analysis [25]. This is not a new result and the adverse consequences of non-random sampling are well known in the statistical literature (see, e.g. [11–13]). But despite its detrimental effects on the interpretation of the data, it seems that the severity of selection bias is not yet fully appreciated in the field of human evolutionary demography (but see [9,15]), because there are recent studies that did not consider potential selection bias in their data analysis although it was probably working (e.g. [26–28]).

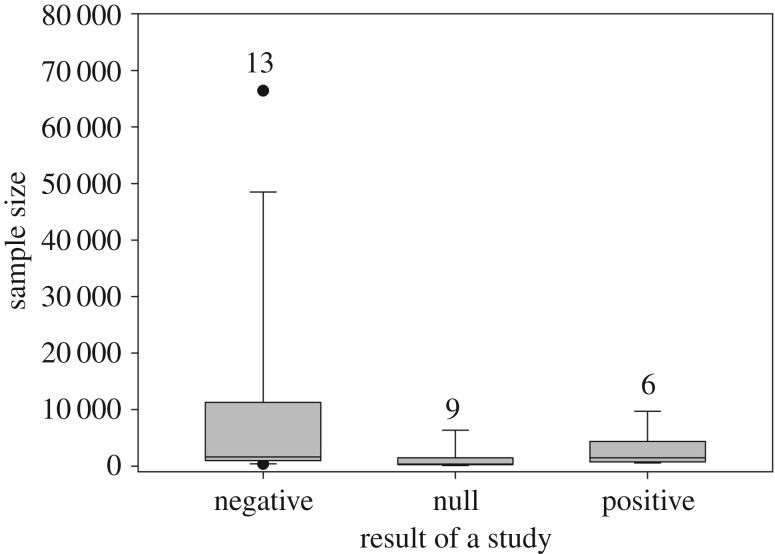
It is worrisome that excluding merely 10% of the women who died at the youngest ages, the probability to detect the true parameter value dropped well below the acceptable level and the results were biased accordingly. This means that despite the high statistical power to detect statistically significant effects differing from zero (unless the sample size was small, here n = 200), the regression analysis failed to recover the true magnitude of the underlying assumed trade-off between reproduction and lifespan. This suggests that studies with adequate sample size and statistical power finding evidence for the predicted trade-off between reproduction and longevity, but suffering from selection bias, have probably underestimated the effect size of the trade-off. On the other hand, studies based on small sample sizes (i.e. on few hundreds of cases), suffering from selection bias and finding no statistical evidence for the trade-off might have been underpowered to detect small-sized trade-offs (please note that we do not know the true biological effect sizes in these studies). This is not surprising because it is well known that small statistically significant associations are harder to find in small samples owing to larger sampling error. This can be seen also in the current literature: when plotting the results from those previous studies that have examined reproduction-longevity trade-off in historical data by including only post-menopausal women, it is obvious that null results (and positive associations) are related to small sample size in this field (figure 3; electronic supplementary material, table S4). For example, the median sample size of studies finding a statistically significant negative association between reproductive effort and longevity is 3666 women, whereas for those studies reporting a null finding it is just 386 women (note that variability in the inclusion of confounding factors among studies is also likely to, at least partly, explain the mixed results).

Figure 3.

Box plot of statistical associations found in the previous studies using individual-level data from historical databases to examine reproduction-longevity trade-off in post-menopausal women. Numbers above the bars represent the number of studies in each category.

The current simulation assumed that the two variables modelled were negatively associated regardless of the values of the dependent variable. In terms of life-history trade-offs, this means that the simulation did not assume that reproductive costs were manifested only during post-menopausal period, as assumed by the most (reviewed in [4–8]) but not by all previous studies [9,10]. Obviously, if the reproductive costs are truly delayed and manifested solely during post-menopausal period, then the approach restricting analysis to post-menopausal women and discarding selection bias would be fully appropriate. This is, however, unlikely because it ignores the historically relevant direct cost of reproduction, maternal death at childbirth. It also overlooks the fact that proportionally considerably fewer women survived beyond menopausal age in historical populations, for which we can determine their full length of lifespan and hence appropriately assess the costs of reproduction [6]. In addition, from an evolutionary perspective, reproductive costs should be examined in terms of their fitness consequences to the individual, and thus it can be argued that the potential costs are more important during reproductive than post-reproductive years [29]. As a matter of fact, in a long-lived species like humans, reproductive costs are predicted to involve mostly future reproduction and not future survival [29]. It should also be acknowledged that mammalian studies of longevity costs of reproduction do not make respective assumption that such costs would be confined to individuals of the oldest age-class only [29,30].

These results were also based on a simple bivariate simulation. However, because the selection bias results from the non-random selection of dependent, not of independent variables [12], these results should be transferrable to situations with multiple independent variables. This is because the selection of observations based on the scores of independent variables has no similar consequences on statistical inference based on unstandardized estimates because the marginal distribution of independent variables is not part of the regression models [12]. In addition, the current simulation used effect sizes considered typical for small, medium and large effect sizes in the statistical literature [21]. Because there has not been much discussion in the literature on the expected effect size with respect to reproduction-longevity trade-offs in humans, it is not straightforward to say whether the effect sizes used here were realistic or not.

It goes without saying that selection bias is particularly problematic in populations with marked mortality during reproductive years [8], concerning not only women but also their spouses as women need to have a living partner to produce offspring. If we, for instance, consider reproductive aged women from the preindustrial (1750–1900) northern Sweden [18], 68.9% of the women died before their 50th birthday (figure 1). Note that such mortality may have been mainly caused by extrinsic factors (diseases, food deprivation, etc.) and not directly by maternal deaths at or soon after childbirth as discussed in the previous paragraph. Therefore, selection bias is an issue predominantly in studies using historical populations that lived prior to modern medical care, which has greatly improved women's survival prospects in modern societies. However, the most relevant studies in this field examining the known lifespan of women (i.e. not using mortality data where part of the women analysed were still alive) rely on historical datasets where pre-menopausal mortality was high [6].

When examining populations where pre-menopausal mortality cannot be ignored, methods to adjust for non-random sampling need to be applied if the researcher is determined to use post-menopausal sample only. Statistical methods developed to incorporate the selection or missing data processes into the modelling exercise include Heckman's two-stage modelling [11] and several of its newer variants [12,31–33]. However, these models are sensitive to whether the mechanism of missing data has been adequately modelled and thus great care should be taken when applying these models [13,32,33]. Moreover, one can use censored-normal (Tobit) regression modelling [23], which when applied to the same Monte Carlo simulation scenario successfully produced consistent regression estimates, attained good coverage of those estimates and preserved high statistical power. Traditionally, censored regression approach is used in situations where the values below or above certain thresholds are real but unobserved in the current study, and thus they are scored at to those boundary values [12]. The trick here is to regard the women dying prior to menopause as such unobserved cases and not as missing values. Note that possible reversed causality between reproduction and survival among mothers dying during the reproductive years is not a concern when the observations are censored from below (or left), because the effect size between reproduction and lifespan is dominated by the data points above the given censoring point. Below-censoring is also possible in survival analysis framework and e.g. accelerated failure time models can be applied in the same way as censored regression models [34], and skewed response distributions can be accommodated [35].

There is also a simpler and more straightforward way to circumvent the need to apply the above-mentioned selection modelling. That is by directly modelling the length of post-reproductive (not post-menopausal as the women's age of natural menopause is not known from demographic records) lifespan instead of total lifespan while controlling for the age when women ceased reproduction, which obviously also affected how long women lived after their last childbirth. This approach avoids the need to apply any threshold age for women entering post-reproductive period, the need to correct for sample selection, and retains the full sample size and the direction-of-causality problem of including also pre-menopausal women owing to the proper time-ordering of the events studied [10]. Such approach to model a time-to-event variable is commonplace in survival analysis [34].

This simulation should not be seen as an attempt to model the intricacies of trade-offs between lifetime reproductive effort and survival in humans. Instead, the aim here was simply to demonstrate the harmful consequences of a common statistical practice in the field of human evolutionary demography using historical data, i.e. the non-random selection of post-menopausal women only into the analysis. It is important to acknowledge that the simulations conducted here implicitly assumed that trade-off between reproduction and longevity existed. In contrast with these simulations, the real-life example from preindustrial northern Finland showed that the effect size estimate between lifetime reproductive effort and lifespan was positive and increased in size when accounting for below-censoring. There is naturally no conflict between this empirical result and simulations because both demonstrate the attenuation of regression estimate towards zero when there is non-ignorable missing data in the response variable. In this empirical example, we just do not know the true effect size between reproductive effort and longevity. That is, despite the inclusion of several covariates, we might have missed important confounders from the model, or simply the trade-off is missing at the phenotypic level in this sample. Censored regression approach will not alleviate the need to account for other threats that prevent us from discovering true effect sizes common to all regression modelling.

It has long been known among evolutionary biologists that revealing underlying life-history trade-offs using correlative data is very challenging, particularly at the phenotypic level [36,37]. Although there have been recent efforts to examine the costs of reproduction at the genetic level also in humans [38–40], and presumably such studies are likely to increase owing to greater data availability, our current knowledge in this area rests heavily on phenotypic associations found in historical data that are particularly vulnerable to methodological problems. Omitted variable bias is known to be a more serious obstacle in this respect than selection bias, because its role blurring the trade-offs cannot be tested and because there are potentially numerous omitted causes that may be responsible for the observed associations between reproductive traits and individual's health and survival in correlative data. Nevertheless, a worthwhile service to the field would be to re-analyse those historical datasets by accounting for the likely selection bias or by avoiding it using the length of post-reproductive lifespan instead of the total length of lifespan, and to conduct a meta-analysis based on those re-analyses. Before that, it may be premature to make general conclusions on how expensive reproduction really is to human longevity.

Data accessibility

The data used in this article can be obtained from the electronic supplementary material.

Competing interests

I declare I have no competing interests.

Funding

This study was funded by Kone Foundation (grant nos. 086809 and 088423).