Assessing Noninferiority in Treatment Trials for Severe Infectious Diseases: an Extension to the Entire Follow-Up Period Using a Cure-Death Multistate Model

ABSTRACT

In current and former clinical trials for the development of antibacterial drugs, various primary endpoints have been used, and treatment effects are evaluated mostly in noninferiority analyses at the end of follow-up, which varies between studies. A more convincing and highly patient-relevant statement would be a noninferiority assessment over the entire follow-up period with cure and death as coprimary endpoints, while preserving the desired alpha level for statistical testing. To account for the time-dynamic pattern of cure and death, we apply a cure-death multistate model. The endpoint of interest is “get cured and stay alive over time.” Noninferiority between treatments over the entire follow-up period is studied by means of one-sided confidence bands provided by a flexible resampling technique. We illustrate the technique by applying it to a recently published study and establish noninferiority in being cured and alive over a time frame of interest for the entire population, patients with hospital-acquired pneumonia, but not for the subset of patients with ventilator-associated pneumonia. Our analysis improves the original results in the sense that our endpoint is more patient benefiting, a stronger noninferiority statement is demonstrated, and the time dependency of cure and death, competing events, and different follow-up times is captured. Multistate methodology combined with confidence bands adds a valuable statistical tool for clinical trials in the context of infection control. The framework is not restricted to the cure-death model but can be adapted to more complex multistate endpoints and equivalence or superiority analyses.

INTRODUCTION

Severe bacterial diseases arising in hospitalized patients include, for example, hospital-acquired pneumonia (HAP) and ventilator-associated pneumonia (VAP). The economic impact of HAP and VAP is an immense burden on health care resources (1). In current and former clinical trials, a variety of primary endpoints have been used (2–4)—even recommendations given by existing guidelines are not consistent. The European Medicines Agency (EMA) (5) proposes clinical cure, the clinical outcome of a test-of-cure (TOC) visit, as an acceptable primary endpoint. In contrast, the Food and Drug Administration (FDA) (6) recommends considering 28-day mortality as the primary endpoint. The drawback of the former endpoint is that cure is a sojourn state (patients may still die after cure), while the latter does not account for cure status. Below, we will account for both cure and vital status.

Especially in an intensive care unit with severely ill patients, a high mortality rate can be assumed within the first days after infection, and thus, death may preclude the TOC as a so-called “competing event” (7). Also, death following shortly after cure should be considered, since cure then does not benefit the patient. Recently, Doshi pointed to a situation where patients were considered cured but died on the same day (8). The joint analysis of nonmortal endpoints like cure and the competing endpoint, death over time, can be captured by the flexible multistate framework (9, 10), which found its way into applied infection control literature (11–18). For that purpose, it has recently been suggested to simultaneously study the two coprimary endpoints, cure and death (2, 19), in order to understand how the new treatment influences the whole etiological cure process, even beyond the TOC. This is achieved by a multistate “cure-death” model (19), which accounts for the time dependency of cure and death, the presence of competing risks, and various follow-up times. The patient-relevant outcome of interest is to be cured and alive over time. In terms of studying the efficacy of a novel treatment, such an outcome as the probability to be cured and alive is sometimes used in the context of bone marrow transplant studies (20), in a similar way, when estimating current leukemia-free survival (21) or for the estimation of being alive without relapse and immunosuppression for graft-versus-host disease in a population of patients with acute lymphoblastic leukemia (22). The purpose of such an outcome is to synthesize the different summary statistics commonly used, the proportion of patients who respond, and the average duration of response (here defined as the proportion of cured patients and the average duration of cure). Our approach can distinguish between a treatment producing a high cure rate but generally short-lived cure cases and another treatment with a low cure rate but longer cure durations. This is highly relevant from the patients' perspective and provides a complete summary and an attractive visual display of the given data.

Further, the benefit of newly developed treatments over existing treatments in terms of efficacy is often only marginal, but these new treatments might be rather advantageous in reducing costs or having fewer adverse effects. Thus, noninferiority analyses are indispensable (23). For serious infections such as HAP and VAP, the EMA as well as the FDA recommended that it is possible to set up a reliable and consistent estimate of the efficacy of active treatment relative to a comparator, which can serve as the basis for defining a new inferiority margin for an active-controlled noninferiority trial (5, 6). The traditional noninferiority procedure for a treatment comparison is to examine the difference in cure proportions with corresponding confidence intervals at a prespecified time point, most often the end of follow-up. However, both from the patients' and from a biological perspective, a much more convincing statement than merely demonstrating noninferiority at a single point in time is how the active treatment performs over the complete cure process (24, 25) and, simultaneously, if the treatment is also beneficial in terms of mortality. A time-simultaneous analysis also allows to put results from former trials with possibly different times of follow-up into perspective. This requires more advanced statistical methodology and has not been evaluated so far for clinical cure. To assess noninferiority over the entire follow-up period, a so-called “confidence band” is required, in which the difference in probabilities of being cured and alive for active treatment A minus control B over a relevant time interval (and not just at a single time point, possibly differing between studies and also within studies, where such time points may differ between patients), lies within a probability of, e.g., 95%. Such a confidence band generalizes the concept of a confidence interval to an entire time interval of interest. Treatment A can be deemed noninferior to B if the confidence band for the difference of the treatment-specific probability curves lies above the protocol-defined noninferiority margin over the whole time period. Finally, and to demonstrate direct implications to trial results, we applied this procedure to actual antimicrobial trial data.

In this article, the application of the cure-death model to a recently published ceftobiprole trial (26) is given in Results. In this trial, described in Materials and Methods, the new regimen of ceftobiprole was compared to the two-drug regimen of ceftazidime plus linezolid for the treatment of patients with HAP and VAP. We introduce the concept of the cure-death multistate model (Fig. 1) and describe how to assess noninferiority over an interval of interest. The application of the cure-death model to the ceftobiprole trial is shown to yield a much stronger noninferiority statement, both from the patients' and from a biological perspective, than that published previously, without changing the noninferiority margin. We describe the benefits and limitations of the proposed methodology in Discussion. Details and an illustrative implementation example are provided in the Supplemental text.

FIG 1.

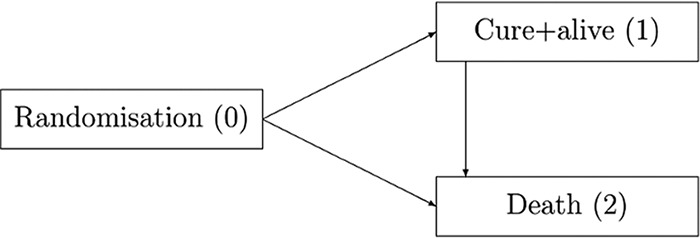
The cure-death model for comparing two antimicrobial therapies with an initial infection/randomization state, a cured and alive state, and a death state. The direction of arrows illustrates the potential transitions between the states determined by transition hazards. They can be interpreted as the momentary forces that pull a subject out of one state into another.

RESULTS

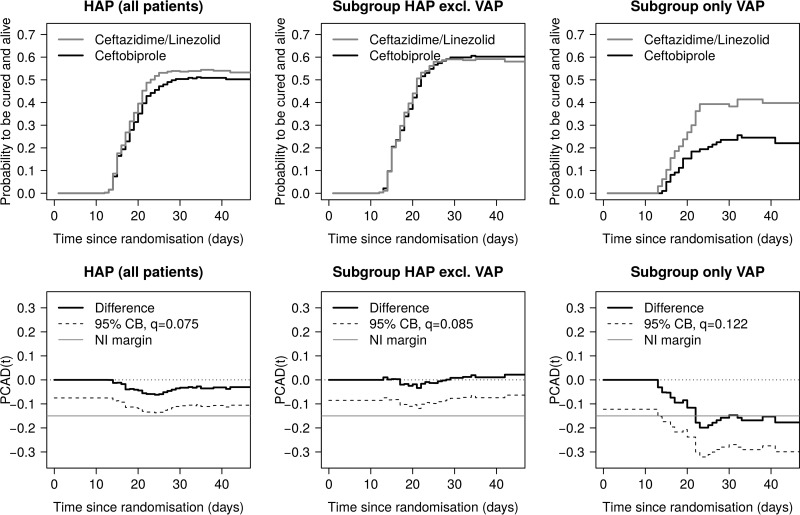
The Aalen-Johansen estimator of the probability to be cured and alive over the whole time frame of interest is displayed in the upper panels of Fig. 2. For the entire sample (781 patients) and the HAP-excluding-VAP group (571 patients), the probability curves show a similar course across treatment groups. In the VAP-only group (210 patients), there is a clear distinction between treatments, favoring ceftazidime plus linezolid. The lower panels of Fig. 2 illustrate the probability of being cured and alive difference at time t [PCAD(t)] (solid black line) together with the 95% one-sided simultaneous confidence band (dashed black line) on the time interval of interest [0, 47] (in days). The interval is chosen such that all observed transition times are covered. The boundary values (q) for the construction of the respective confidence band are also displayed [see Materials and Methods for details on PCAD(t) and q]. It can be seen that for both the entire sample and the HAP-excluding-VAP group, the confidence band lies above the noninferiority margin of −15% (solid gray line) for the entire interval [0, 47], but this is not true for the group of VAP patients. Hence, for the entire sample and the HAP-excluding-VAP group, noninferiority concerning “cured and alive” over the time period of interest is shown. All results do support the original analysis (26), which showed noninferiority of overall cure proportions for both the entire sample (cure risk difference ceftobiprole minus ceftazidime/linezolid of −2.9 [−10.0, 4.1]) and the HAP-excluding-VAP group (cure risk difference ceftobiprole minus ceftazidime/linezolid of 0.8 [−7.3, 8.8]) at the end of follow-up.

FIG 2.

Transition probabilities and differences in probabilities derived from the Aalen-Johansen estimator for subgroups in the ceftobiprole trial (26). (Top) Probability to be cured and alive. (Bottom) Estimated difference of probabilities, PCAD, with the 95% one-sided simultaneous confidence band (CB), the corresponding boundary value, q, and the protocol-defined noninferiority (NI) margin of −15% on the time interval [0, 47].

DISCUSSION

Our analysis not only confirms the noninferiority of ceftobiprole as found by Awad et al. (26) but also provides a stronger and more patient-benefiting noninferiority result. First, the endpoint “get cured and stay alive over time” is a highly relevant outcome in the context of antimicrobial trial data, because patients benefit from cure only when staying alive for a certain time. Second, we demonstrate noninferiority of being cured and alive over the complete treatment process and not only at the end of follow-up as intended in the original analysis. To include all time points simultaneously avoids having to decide for a single time point, especially when there is no agreement of the adequate time point for the TOC (4) or when a patient's status may be highly time dependent on a daily basis. Third, in contrast to the traditional proportion comparisons, the comprehensive cure-death multistate model captures the complex timing of cure and death and competing events and also allows for different follow-up times due to death or right-censoring.

We emphasize that a multistate analysis may offer a more detailed insight into how treatment influences the cure and death process in other situations. For instance, even though noninferior cure and (30-day) all-cause mortality proportions for the treatment group may be observed at some prespecified time point, the probability of being cured and alive as a function in time may be substantially higher for the control group during some stages of follow-up, i.e., noninferiority cannot be established for some points in time. However, such time-dynamic patterns are important from a patients' perspective, may have direct impact on patient care (see also references 27 and 28), and may provide additional biological insight. Depending on the disease and the medical indication, these additional clinical data can point out, e.g., that additional clinical action may be required. But this is not the case in the present study example; thus, continual noninferiority is demonstrated. Further, in a recent article (19), we examined several simulation scenarios in which a treatment might be beneficial by the end of follow-up but not over the entire treatment process. Such time-varying treatment effects might be detected by the approach suggested in the present paper but not by a conventional analysis.

In the aforementioned article (19), we used innovative regression methods for a risk ratio of being cured and alive and a restricted log rank-based test for a formal treatment comparison. However, the approach in reference 19 does not immediately lend itself to comparing absolute differences between the outcome probabilities and a subsequent noninferiority analysis.

The applied cure-death multistate model requires a time-inhomogeneous Markov assumption (9), which is tantamount to assuming that the 1→2 hazard depends only on the time since randomization and not on the time since cure. According to the approach described by Beyersmann et al. (10), we assumed the Markov assumption to be reasonable in the present situation. If the Markov assumption is violated, a time-simultaneous analysis is still feasible, but the technical details become more involved. To begin, the Aalen-Johansen estimation of state occupation probabilities as considered in this work will still apply (29). The technical requirements on the censoring mechanism will be stricter but likely be met in a situation such as ours. Confidence bands may again be constructed using resampling techniques, either sampling with replacement from the individual patients or using an approach as in the present paper, adapted to the method seen in reference 29. We also note that modeling is done within treatment strata.

Another point worth mentioning is that while this is a time-simultaneous approach, we do not extrapolate beyond follow-up. In other words, also the time-simultaneous approach is limited to the duration of follow-up within a study.

The proposed resampling procedure is not restricted to the cure-death model but can be applied to arbitrary multistate models with finite state spaces, which makes it attractive for various applications not restricted to the context of antimicrobial trial data. For instance, an illness-death model with recovery can be used to quantify alternative efficacy measures in clinical trials such as the probability to be alive and not under mechanical ventilation in patients with acute respiratory distress (30), the probability to be alive and not under immunosuppressive therapy in leukemia patients after stem cell transplantation (22, 31), or the probability to have a sustained cure (to be cured and free of recurrent infection) in patients with Clostridium difficile infection (27). Furthermore, it can easily be adapted to investigate the equivalence or superiority of a treatment A compared to a treatment B concerning an outcome transition probability over a time frame of interest, or it can be applied to more complex functionals incorporating the matrix of transition probabilities that quantify, e.g., length of stay (32).

A different question that can be posed is what if cure were assessed as a continuous variable and artificial dichotomization should be avoided. Then, one option would be a joint model (33) for the longitudinal continuous outcome, informatively censored by death. One might still envisage a comparison of cure curves in a such a case; however, how to define an endpoint that accounts for both vital and cure status is less clear.

In conclusion, we propose an approach that addresses three significant issues often arising in noninferiority clinical trials in the context of infection control, namely, the arbitrary nature of the timing of endpoint assessment within and not across the time interval of interest, the erosion of the 5% significance level over the entire endpoint interval due to multiple testing, and the lack of accounting for vital status after cure. Our approach optimizes use of the available data by assessing the endpoint “get cured and stay alive” over the entire time period of interest while calculating a confidence band over that period preserving the 5% confidence level. Most importantly, our proposal develops both a patient-centric and a biologically relevant approach and adds a valuable statistical tool for such analyses.

MATERIALS AND METHODS

Example study data.

Treatment with ceftobiprole was established to combat a wide range of Gram-positive bacteria, and this drug belongs to the class of β-lactam antibiotics. The noninferiority trial described here (26) compared the new regimen of ceftobiprole to the two-drug regimen of ceftazidime plus linezolid. It was a double-blind, randomized, multicenter comparison involving 781 patients with HAP, among them 210 with VAP.

Clinical cure diagnosed at the TOC visit, mostly held within a time frame of 7 to 14 days after the end of treatment, served as the primary endpoint, and all-cause mortality was the secondary endpoint. With the protocol-defined noninferiority margin of −15%, risk differences of proportions of cured patients at the TOC showed that ceftobiprole is noninferior to ceftazidime plus linezolid for the entire study population of patients with HAP (−2.9 [−10.0, 4.1]) and for the population of HAP patients excluding the VAP patients (0.8 [−7.3, 8.8]). But noninferiority was not demonstrated in VAP patients (−13.7 [−26.0, −1.5]). These results were given by Awad et al. (26) and refer to ceftobiprole versus ceftazidime/linezolid.

The cure-death model.

In order to suitably account for the time-dynamic pattern of cure and death after randomization, we focus on the “illness-death model without recovery” embedded in the flexible and powerful multistate model framework (9, 10). Since the context here is hospital-acquired infection, we call this model “cure-death model” (19) (Fig. 1), with state 0 defined as initial, state 1 as cured and alive, and state 2 as absorbing death. According to the study protocol, all patients start in state 0, which is randomization to treatment, immediately after infection. The time scale of interest is “time since randomization” in days. The outcome most relevant for patients is “being cured and alive” (state 1); however, all patients, whether cured or not, are permanently at risk for death (state 2) during the entire follow-up. If a patient is still alive at the end of follow-up, (s)he is right-censored. Note that we summarize the competing events “death from the condition treated” and “death from any cause” that can be analyzed separately if information is available; such a separation does not influence the present outcome of interest but may be interesting for a broader treatment comparison. The arrows in Fig. 1 illustrate the possible transitions within our multistate model determined by the so-called “transition hazards.” They can be interpreted as momentary forces that pull a subject out of one state into another.

However, a hazard-based analysis applying, for instance, the well-known Cox proportional hazards model does not allow direct statements regarding the probability of interest because the latter involves all hazards. Instead, the Aalen-Johansen estimator (9) is employed for nonparametric estimation of the probability of interest, which generalizes the well-known Kaplan-Meier estimator to multistate settings. Note that in the absence of right-censoring, the Aalen-Johansen estimator is identical to the relative proportion of patients being in a certain state at time t.

Assessing noninferiority over the entire follow-up period via confidence bands.

The target aim of our analysis is to establish noninferiority for the difference in probabilities of being cured and alive for patients of two treatment groups, A and B, on a relevant time interval of interest. In practice, the maximum of this interval can be, e.g., the largest observed cure or death time. Pointwise 95% confidence intervals can be constructed for the difference of these probabilities. Similar to risk differences, we consider the difference of the treatment-specific Aalen-Johansen estimates, P̂(cured and alive at t∣treatment group) function (PCAD, which stands for the “probability of being cured and alive difference”), calculated as follows: PCAD(t) = P̂(cured and alive at t∣A) − P̂(cured and alive at t∣B), in the comparison of treatments A and B.

But assessing noninferiority only pointwise separately for each time point t does not have an overall 5% significance level due to the problem of multiple testing (34). Instead, our aim is to construct a so-called (one-sided) confidence band over the time interval of interest. A confidence band is a region in which the entire true curve (here defined as the difference in probabilities over time) falls within a probability of 95%. Statistical inference is commonly based on approximate normality of the estimators. For the Aalen-Johansen estimator, this enables the construction of 95% confidence intervals via the usual “±1.96 × standard error” rule. However, a generalization to confidence bands requires some additional effort because analytical solutions for the calculation of such bands are available only for the standard survival setting and not for more complex multistate models as in the present data situation. As a solution, we suggest the use of a convenient and computationally attractive resampling procedure known as “wild bootstrap,” which was originally established for competing risks settings (35, 36).

The idea is to introduce computer-generated standard normal variates that are plugged into a transformation of the Aalen-Johansen estimator. Repeating this approach, say 1,000 times, allows deriving a quantile q. The one-sided 95% confidence band for the difference in probabilities is then given by its lower boundary, PCAD(t) − q.

Adapting the principles of confidence interval inclusion as discussed in reference 37 to simultaneous confidence bands, treatment A can be deemed noninferior to B if the 95% confidence band, i.e., PCAD(t) − q, lies above the protocol-defined noninferiority margin on the entire time interval of interest. This approach corresponds to a formal statistical noninferiority test at the 5% significance level.

The practical construction of the quantile q and an exemplary implementation of the procedure in the statistical software R (38) are given in the Supplemental text. Fast computation of the Aalen-Johansen estimators is provided by the etm function (39).