Bayesian Quantile Impairment Threshold Benchmark Dose Estimation for Continuous Endpoints

Abstract

Quantitative risk assessment often begins with an estimate of the exposure or dose associated with a particular risk level from which exposure levels posing low risk to populations can be extrapolated. For continuous exposures, this value, the benchmark dose, is often defined by a specified increase (or decrease) from the median or mean response at no exposure. This method of calculating the benchmark dose does not take into account the response distribution and, consequently, cannot be interpreted based upon probability statements of the target population. We investigate quantile regression as an alternative to the use of the median or mean regression. By defining the dose–response quantile relationship and an impairment threshold, we specify a benchmark dose as the dose associated with a specified probability that the population will have a response equal to or more extreme than the specified impairment threshold. In addition, in an effort to minimize model uncertainty, we use Bayesian monotonic semiparametric regression to define the exposure–response quantile relationship, which gives the model flexibility to estimate the quantal dose–response function. We describe this methodology and apply it to both epidemiology and toxicology data.

1. INTRODUCTION

To evaluate risk in an exposed population, quantitative risk assessment links exposure of a given chemical to a specified response through regression modeling. After an appropriate exposure–response relationship is found or assumed, the exposure associated with a specified level of risk is identified. For dichotomous outcomes (e.g. death or tumor incidence), this value, termed the benchmark dose (BMD) by Crump,⁽¹⁾ is defined to be the exposure or dose, or internal concentration, associated with increasing risk (here risk is the probability of an adverse response).

For continuous outcomes, the method of Crump cannot be defined without specifying a value such that responses more extreme are considered adverse as well as specifying a corresponding response distribution to estimate the probability of such a response. Here, an adverse response is frequently defined such that extreme values of the response are considered harmful, and the response distribution is chosen to describe the pattern of responses seen in the population. For example, liver weight is a continuous endpoint where a high liver weight is considered harmful and the data are modeled using a log-normal distribution. When such assumptions can be made, a continuous risk-based BMD definition^(2–4) exists. This is appealing as it is analogous to the standard BMD methodology for dichotomous responses, but dependent upon the calculation of the standard deviation of the controls.^(5,6) Further, this method is often not used in practice as software packages do not support its implementation. For example, the U.S. Environmental Protection Agency BMD software⁽⁷⁾ allows this approach to be used only when the response distribution is assumed to be normal with constant variance.

As this approach is difficult to implement in practice, alternative definitions of the BMD have been proposed. The approach of Slob⁽⁸⁾ defines the BMD as the dose, d, associated with a response equal to an effect threshold. The BMD is the exposure linking the median (in the case of Slob⁽⁵⁾) or mean (in the case of the BMDS software⁽⁴⁾) with a response that is “without an adverse biological consequence.” As the BMD is estimated from the central tendency of the exposure response, the approach does not control for the probability the exposed population will exhibit the adverse response if the response mean and variance changes with exposure.

Such an approach does not control for risk in the studied population, and leaves little guidance as to how one could extrapolate to levels of risk in target human populations. This makes it difficult to use such an approach to meet the National Research Council’s (NRC) Silver Book⁽⁹⁾ recommendation that risk assessments be based upon the probability of the adverse response to the target population. We develop a method similar in spirit to the methodology of Slob, which can also be used to set the probability the studied population exhibits the adverse response and, when modeling animal data with a suitable transformation to the target human population (which is beyond the scope of this article), may be able to be used to help meet the NRC’s recommendations given the ideas advanced in this article.

We take the approach of Slob and, building on to the methods of Wheeler et al.,⁽¹⁰⁾ use quantile regression⁽¹¹⁾ to define a BMD approach, which we term the “quantile impairment threshold benchmark dose” (QIT BMD) where we estimate the dose associated with an impairment threshold where responses that are equal to or more extreme than the threshold are considered adverse. Further, because we are using quantile regression, the methodology defines the probability of adverse response in the exposed population, which implies the BMD defines the risk to the exposed population.

To create a flexible approach, we define the quantile dose response using Bayesian monotone smoothing splines.⁽¹²⁾ Such splines define a monotone smoothing prior over the quantile dose–response curve, which is used to account for uncertainty in the dose response by assuming the quantile dose response can be represented by a large class of smooth continuous functions. In what follows, we use this approach for monotone increasing functions, although extensions to monotone decreasing functions are straightforward.

2. THE QUANTILE IMPAIRMENT THRESHOLD BMD

Slob⁽⁸⁾ defined the BMD using the median dose–response function, M(d), and the USEPA focused on the mean response, μ(d), in its software.⁽⁷⁾ From Slob’s definition, the BMD is the dose satisfying

$$M(\text{BMD})=x_0,$$ (1)

in the case of the median or, μ(BMD) = x₀, in the USEPA case of the mean where x₀ is the minimum response viewed as adverse. The value x₀ is an impairment threshold defining a biologically significant or possibly adverse impairment. If one assumes a monotone curve, x₀ can also be defined by some relative difference from background, i.e., if one defines the BMD using M (BMD) − M(0) = θ · M(0), then x₀ = (1 + θ) · M(0). In the first case, when x₀ is specified as a predefined value, this estimate is often called the point estimate of the BMD; in the other case, this is called the relative deviation definition of the BMD.

In our experience, this definition leads to confusion when understanding the risk estimate, and risk managers often interpret it as controlling for risk when it is not. For example, when calculating the BMD, the BMDS software labels θ as BMRF, which may be confused with the benchmark response (BMR), a value that defines a predetermined level of adverse risk in the exposed population in dichotomous BMD risk assessment. However, if the distributional assumptions are not met, which is any time the data are not normally distributed when using the BMDS software, the BMD does not give an indication of the probability a population will be under x₀. Even when one is using the median, 50% of the exposed population will have an adverse response at the estimated BMD, which is usually an unacceptable level of risk. Such issues may lead to misunderstandings as to the actual risk to an exposed population.

As an alternative to the mean or median response, we define an approach based on the quantiles distribution function ω_τ (d). This function is assumed to be a continuous monotone function of dose, d, where Pr[Y_d < ω_τ (d)] = τ, for 0 < τ <1, and τ is the probability the population will not have a response as extreme as the impairment threshold. As an example, suppose the data are normally distributed with mean function μ(d) = β₀ + β₁d and variance σ ². The quantile dose–response function for the 95th quantile is ω_τ (d) = β₀ + β₁d + 1.65σ. Similarly, the quantile dose–response function associated with τ = 97.5% is ω_τ (d) = β₀ + β₁d + 1.96σ.

Assuming that the quantile dose response is known and the impairment threshold x₀ is specified, the QIT BMD is the value, BMD, solving:

$${\omega }_{\tau }(\text{BMD})=x_0.$$ (2)

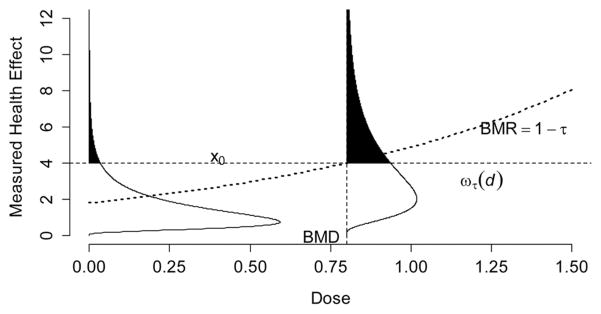
This formulation is identical to Equation (1) except the BMD is specified using a quantile of the response distribution. For monotone increasing responses, let τ = 1 − BMR, which defines the BMR as the probability a person will experience the adverse response. The relationship between the quantile dose–response function, the impairment threshold, and the BMD is described graphically in Fig. 1. The quantile dose–response function identifies the level of response that 100· (1−BMR)% of the population will be under for a given dose. In this figure, the BMD is the dose associated with the quantile response function intersecting the impairment threshold. For decreasing responses simply multiply all responses by −1 and continue with the above.

Fig. 1.

Graphical depiction of the impairment threshold benchmark dose. For a given dose, the quantile dose–response function, ω_τ (d), represents a response that 100•BMR% of the population will have responses more extreme than the given quantile; here the benchmark response (BMR) is set equal to 1 − τ. The impairment threshold x_0, is the level of response that is considered adverse, and the benchmark dose is computed as the dose where the critical effect meets the quantile dose–response function.

2.1. Defining the Impairment Threshold

We define the impairment threshold in two ways that are analogous to the point and relative definitions of the BMD. We call these the point impairment threshold and the relative impairment threshold. The point definition should be used when there is a biological understanding of the hazard and a threshold can be established from the available literature. For example, if one were considering blood pressure, a systolic blood pressure greater than 140 mm Hg is defined as hypertensive. If one sets the BMR = 10% and lets x₀ = 140 mm Hg, then the BMD is the level at which 90% of the exposed population would not be classified as hypertensive.

If there is no literature supporting a point impairment threshold value, then the relative definition impairment threshold BMD can be used. For example, if one is interested in the 90th quantile (i.e., BMR = 10%), then one may define the threshold x₀ as a 20% increase over ω₉₀(0). In this case, the BMD is the dose where 90% of the population has a response that is less than a value equal to 120% of ω₉₀(0). Continuing with the blood pressure example, if the baseline 90th quantile were 130, that is ω₉₀(0) = 130, then this approach would yield a threshold of 120% of 130 or 156 mm Hg. In general, this approach sets x₀ = ω_τ (0)(1 + θ), where θ > 0 is the relative change from background and specifies the percent increase deemed acceptable from the background response quantile.

Like the previous relative deviation approach defined above, the change from background value is subjective, and care must be taken in defining this value. If θ is large (e.g., 200%), the resultant BMD might be an exposure that is much greater than exposures where meaningful adverse biologic responses occur. If it is too small, the BMD might suggest exposures as adverse where the response is effectively not different from background. Unlike the relative deviation definition, the impairment threshold approach is no longer confounded with the BMR, allowing for more transparency in the analysis. As such, when the impairment threshold is based upon a percentage increase or decrease from background we recommend a full rationale of the choice as well as possibly including a sensitivity analysis of other choices that may be equally valid.

2.2. Bayesian Quantile Dose–Response Estimation

To estimate a smooth quantile dose–response function ω_τ (d), we use Bayesian quantile regression⁽¹³⁾ with a smoothing prior. Our approach is related to frequentist quantile regression where quantile estimates are found by minimizing the check loss function. In Bayesian quantile regression, the check loss function is used in the asymmetric Laplace distribution,⁽¹⁴⁾ which defines the likelihood for the data. To make the Bayesian case explicit, we introduce the check loss function and its relation to the asymmetric Laplace distribution.

The check loss function, ρ_τ (c), is defined as:

$${\rho }_{\tau }(c)=c[\tau -1(c<0)],$$

where 1(c < 0) is 1 if the argument is true, and is 0 otherwise. In the frequentist context, c = y − ω_τ (d), where Σρ_τ [y_i − ω_τ(d_i)] is the function minimized. Fig. 2 shows four different check loss functions centered on the origin. The first row of figures shows the function where the quantile of interest is 0.25 and 0.75, and shows how the loss function inverts by penalizing the left tail when τ = 0.25, which is the same as the right tail when τ = 0.75. The bottom-left panel shows how values in the distribution above the 0.95 quantile, which has less probability, are penalized greater than values below the quantile, and that this penalization increases further out in the tails of the distribution. Finally, the bottom-right picture gives the case of median regression. Here the curve is the same above and below the quantile of interest. In all cases, the estimate that satisfies the minimization criterion is unbiased for the quantile being estimated.

Fig. 2.

The check loss function for different values of τ, where the origin (i.e., x = 0) is the quantile of interest. The lower-right case where τ = 0.50 is proportional to the absolute value function and is used in median regression.

The Bayesian approach assumes that the observed data (y₁, … ,y_n) are independently and identically distributed asymmetric Laplace random variables, with density function:

$$f_{\tau }(y\mid d)=\tau (1-\tau )exp\{-{\rho }_{\tau }[y-{\omega }_{\tau }(d)]\}.$$

Although the asymmetric Laplace distribution is not an intuitive data generating mechanism, the use of this distribution is very similar to distributions where inference is based upon the mean. For example, when the data are distributed normally this is often expressed as:

$$y={\mu }_i+{\epsilon }_i,$$

where μ_i is the mean and ε_i is a zero-centered normal random variate with some constant variance. Here, even when the data are not distributed normally, such an estimate is the best unbiased linear estimate of the mean. Likewise, the above model centers the observed data on the quantile function of interest and assumes the stochastic component comes from a random variate with mean zero and heavy tails. As this definition is based upon the check loss function, the distribution has the same mode as the minimizer to the frequentist estimate.

Kozumi and Kobayashi⁽¹⁵⁾ proposed an efficient Gibbs sampler for the asymmetric Laplace distribution. We take advantage of this development to define a Bayesian smoothing prior over the quantile dose–response function. This is significant as this smoothing prior has properties that have been better studied than the smoothing method used in frequentist quantile regression, and may provide better estimates of the quantile of interest.

2.3. Smoothing Prior Over the Quantile Dose–Response Function

We use M-splines⁽¹²⁾ to model the quantal dose–response function. These splines are monotonic polynomial functions that go from 0 to 1, which when used as a linear combination, model the quantal dose–response function as:

$${\omega }_{\tau }(d)={\beta }_{\tau 0}+\sum _{j=1}^J{\beta }_{\tau j}{b}_j(d).$$ (3)

Here b_j (d) is an M-spline function, β_{τ 0} is the intercept, and β_τj is an unknown coefficient for each spline. In Equation (3), if β_τj > 0 for all j ≥ 1, then the function is monotone increasing.

Like more familiar spline bases, such as the natural cubic spline or the B-spline,⁽¹⁶⁾ the M-spline is specified on a knot sequence, which must be specified a priori. As the choice of the knot sequence defines flexibility of the spline construction in Equation (3), the number and placing of the knots is important. To model arbitrary smooth functions with a smoothing spline, as in the case below, it is often sufficient to have 20 to 30 knots evenly spaced across the domain. For the jth spline function b_j(d), define its knot sequence as κ_j1 ≤ κ_j2 ≤ … ≤ k_jk., with the spline function being 0 before κ_j1, and 1 after κ_jk. Fig. 3 shows quadratic M-splines (top) whose knots are chosen to be equally spaced, as well as a monotone increasing curve formed by making all of the splines’s β coefficients positive (bottom). Given enough splines, the model defined in Equation (3) provides a flexible method to model most smooth monotone functions.

Fig. 3.

Pictorial representation of M-splines (top), where the vertical dotted lines are the location of the knots, and corresponding monotone increasing curve using positive coefficients, i.e., βj > 0.

To enforce monotonicity, we place a prior over the β_τj coefficients that places zero prior probability on values less than 0. This prior is based upon the second-order random walk prior described in Lang and Brezger⁽¹⁷⁾ with additional positivity constraints. For the spline construction defined in Equation (3), given the vector β_τ = (β_{τ 1},· · ·,β_{τ J} )’ of spline coefficients, this prior is:

$${\mathbf{\beta }}_{\tau }\mid \lambda \propto exp\left\{-\frac{1}{2\lambda }{{\mathbf{\beta }}_{\tau }}^{\prime }{\mathrm{\sum }}^{-1}{\mathbf{\beta }}_{\tau }\right\}1\left({\mathbf{\beta }}_{\tau }>\left[\begin{array}{c}0\\ ⋮\\ 0\end{array}\right]\right),$$

where 1(·) is an indicator function taking 1 if the condition is satisfied, 0 otherwise, and λ is the smoothing parameter. We complete the prior over the spline coefficients by letting β _τ0 ~ N(0,1 × 10⁶).

The matrix Σ⁻¹ has a band diagonal structure that is derived from the second-order random walk, i.e., β_τ1 = ε_τj, β_τ2 = β_τ1 + ε_τ2, and β_τj = 2β_τj−1 − β_τj−2 + ε_j for j > 2 with ε_j ~ N(0, λ) for 1≤j ≤J. The priors can be equivalently defined conditionally by considering the left and right neighbors of a given parameter. As described in Fahrmeir and Lang,⁽¹⁸⁾ Σ⁻¹ can also be represented as a band matrix with a well-defined structure. For example, if there are six coefficients (J = 6) over the spline functions described in Equation (3), then one has the inverse variance–covariance matrix being

$${\mathrm{\sum }}^{-1}=\left(\begin{array}{cccccc}1& -2& 1& 0& 0& 0\\ -2& 5& -4& 1& 0& 0\\ 1& -4& 6& -4& 1& 0\\ 0& 1& -4& 6& -4& 1\\ 0& 0& 1& -4& 5& -2\\ 0& 0& 0& 1& -2& 1\end{array}\right).$$ (4)

This construction produces a matrix of rank (Σ⁻¹) = J − 2 and care must be taken to specify a prior over the smoothing hyper parameterλ. As recommended in Lang and Brezger, we use an inverse Gamma prior (IG) and let λ ~ IG(1,0.005), which gives a proper posterior when the model design matrix is of full rank. As shown in the examples, this prior performs well in practice, producing smooth curves.

As an aside, one could define the above prior for monotone decreasing curves by restricting the β parameters to be negative. However, this is not necessary; instead, we leave the prior unchanged and multiply the M-splines by −1. This forces the equivalent behavior without changing the prior. Though different priors might be used in practice, which may lead to issues of the sensitivity of the estimates with regard to the prior specification, the above prior is used because Bayesian P-splines have been shown to be robust when estimating the true underlying response.⁽¹⁹⁾

2.4. Benchmark Dose Estimation and Posterior Sampling

We sample the posterior distribution through Monte Carlo Markov chain (MCMC) using series of conditionally conjugate Gibbs sampling steps given the R programming language.⁽²⁰⁾ The posterior distribution for the BMD is estimated through this MCMC simulation and given the current parameters, the BMD is monitored at each iteration and sampled by solving Equation (2). For our purposes, the BMD point estimate is taken to be the mean of the posterior distribution, i.e., the arithmetic average of the posterior samples, and the 100(1 − α)% BMD lower confidence limit (BMDL) is estimated as the α lower quantile of the distribution of the posterior samples.

Convergence to the steady-state distribution is fast, taking about 100 iterations and, in the data examples, was monitored by evaluating the trace plots of three chains. For the simulations, to ensure the steady-state distribution has been reached, we take 10,000 samples disregarding the first 1,000 as burn in. All sampling algorithms were written in the R statistical programming language⁽²⁰⁾ with some extensions written in C++ using Rcpp.⁽²¹⁾

3. EXTENSIONS TO COVARIATES

In some contexts, there are additional covariates that are thought to affect the response of interest. For example, in epidemiology studies, age, race, and smoking status are often covariates that impact the probability of an adverse response. As long as there is no interaction between these covariates and the exposure variable (i.e., no effect modification), the BMD can be estimated for different values of the covariates, where the values serve to offset the intercept term. If there are interaction effects, the quantile response function is dependent on the given covariate and so is the BMD. We extend Equation (3) to include both cases.

For the case where a covariate has no interaction with the exposure, assume that h covariates are observed for each subject and define these covariates as c₁, … , c_h. Given that the quantile dose response is a function of the exposed dose d and the covariates, we represent this quantity by the additive model:

$${\omega }_{\tau }(d,c_1,\dots ,c_h)=f(d)+g(c_1,\dots ,c_h),$$ (5)

where f(d) is the monotone function defined in Equation (3) and g(c₁, … , c_h)is a function of the covariates. For this function, we assume no interaction between covariates and use a generalized additive model⁽²²⁾ letting

$$g(c_1,\dots ,c_h)=g_1(c_1)+\cdots +g_h(c_h).$$

To allow flexibility in the modeling response, g_h(c_h) is modeled using Bayesian P-splines,⁽¹⁷⁾ which are used over M-splines as there is no reason to assume monotonicity. These splines model the response as a linear combination of B-splines, that is $g_i(c)={\sum }_{l=1}^L{\xi }_l{B}_l(c)$, where B_l(c) is a B-spline,⁽¹⁶⁾ ξ_l is an unknown coefficient, and the prior on the coefficients is a second-order random walk. That is, if ξ = (ξ₁, … , ξ_L)’, then P-splines place a prior over the coefficient matrix that is proportional to $exp\{-\frac{1}{2\lambda }{\xi }^{\prime }{\mathrm{\sum }}^{-1}\xi \}$, where Σ⁻¹ is constructed as in Equation (4), and a prior is placed over λ as above. P-splines have a natural intercept and one must remove the first spline of the construction (i.e., B₁(c)) to make f(c)’s intercept term identifiable. Consequently, we complete the construction by removing the first spline basis from each g_h(c_h).

As the quantile dose–response function is independent of these covariates, BMD estimation proceeds as above using the covariates as an offset for the intercept. For example, if the only covariate is age, one may define a BMD for a 45-year-old and a BMD for a 35-year-old. This approach is only appropriate if it is reasonable to assume the dose response and the covariates have no interaction. If an interaction is present, this implies the quantile dose response changes over different values of the covariate. If this is not the case, one can extend the model to include categorical covariates and model a different quantile dose response for each category. In the case of a continuous covariate, if the response is expected to be similar across the range of the category, it may be reasonable to assume this variable can be categorized.

For a categorical covariate having M levels, Equation (5) can be extended to include this covariate as:

$${\omega }_{\tau }(d,c_1,\dots ,c_h)=g(c_1,\dots ,c_h)+\sum _{m=1}^M{f}_m(d),$$ (6)

where f_m(d)represents one of the M quantile dose–response functions that depend upon the given level of the covariate. When using model (6), the QIT BMD is estimated for each level of the covariate. Continuing the above example, suppose that the dose response is dependent on smoking status with age being a covariate that is independent of dose. The QIT BMD dose would be estimated separately for both 35- and 45-year-old smokers as well as nonsmokers.

This adds the difficulty that M separate BMDs are estimated, and the estimates may add additional complexity to the risk management decision because the calculated BMDs are estimates for specific subpopulations. In the data example below, the response is lung function given exposure to coal dust, and the quantile response curve is different for smokers and nonsmokers; consequently, the BMD for two subpopulations is considered. In this case, the BMD must be reported for each subpopulation, and, when a single value is needed the most susceptible subpopulation should be used, which is an issue that is not unique to the QIT BMD.

4. SIMULATION

To investigate the performance of our approach, we conduct a small simulation study. In this study, we investigate two dose–response curves using the point and relative definitions of the QIT BMD for the 75th and 90th quantiles of the distribution, that is, the BMR = 25% and 10%, respectively. The simulation is conducted assuming the following true dose–responses curves:

$$\begin{gathered} {\mu }_1(d)=E[lnY]=0.01d \\ {\mu }_2(d)=E[lnY]=\mathrm{\Phi }\left\{\raisebox{1ex}{$(x-7)$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\right\}, \end{gathered}$$

where Φ() is the cumulative distribution function for the standard normal distribution, which was chosen as it is a sigmoidal function that is not a standard parametric model for continuous data. For the simulation, the true underlying distribution was lognormal with variance proportional to the exposure, i.e., ln(Y) ~ N[μ(d), σ ²d] with σ = 0.112. For the relative deviation approach, we set θ = 600%; for the absolute cutoff, this value was set to x₀ = 5.

For each condition, a total of 1,000 simulations were performed. This was done for sample sizes of n = 50, 100, 200, where observations were taken evenly across the interval [0,20]. All BMDL calculations were done setting α = 0.05, and observed coverage as well as bias was investigated. For the specification of the spline, J = 20 knots were placed evenly across the interval. With the priors over the spline coefficients defined as above.

Table I shows the results of the simulation study. For smaller sample sizes, the method produced conservative coverage with some evidence of bias that often decreased as the sample size increased. The observed coverage, although still conservative, became closer to nominal. In addition, the estimates were more accurate for small sample sizes when estimating the 75th quantile as opposed to the 90th, and the bias was increased for the relative definition of the QIT BMD. This implies that more data are frequently needed to estimate quantiles that are further in the tails of the distribution, and this is especially true when a cutoff relative to background is chosen.

Table I.

Observed Coverage and Bias for a Small Simulation Study Investigating the Method’s Accuracy Computing the QIT BMD

	Quantile			Sample Size
				50	100	200
Function 1	75th	Relative	Bias	−1.5	−0.5	−0.1
			Coverage	100%	100%	100%
		Absolute	Bias	−0.21	−0.08	0.04
			Coverage	99.6%	97.9%	96.0%
	90th	Relative	Bias	−0.19	0.61	1.00
			Coverage	100%	100%	94.7%
		Absolute	Bias	−0.49	−0.19	0.0
			Coverage	99.9%	99.5%	98.3%
Function 2	75th	Relative	Bias	−5.2	−4.98	−3.20
			Coverage	100%	100%	100%
		Absolute	Bias	−0.12	0.00	−0.02
			Coverage	100%	99.3%	99.1%
	90th	Relative	Bias	−3.5	−2.99	−1.61
			Coverage	100%	100%	100%
		Absolute	Bias	−0.15	0.00	0.02
			Coverage	100%	100%	98.2%

5. TOXICOLOGICAL DOSE–RESPONSE DATA

The level of the alanine transaminase (ALT) enzyme found in the blood can be a sign of liver damage. We investigate the level of ALT (IU/L) in a short-term bioassay described by the National Toxicology Program.⁽²³⁾ From this study, we look at the 2-week exposure data of Fisher 344 rats exposed to differing levels of 4-chloronitrobenzene in the air, and it is of interest to look at the effects of exposure to the level of ALT found in the blood.

In this example, high levels of the ALT enzyme are biomarkers related to liver damage, and it is not clear how the impairment threshold should be set; consequently, a biologically meaningful impairment threshold is not available. Further, if one were to use a direct multiplier of the response (e.g., 200% of the background response quantile), there are similar problems with justification. We use both approaches and compare the results. First, as there is a natural variation in blood ALT levels, we choose the impairment threshold level to be 100(IU/L) as an adverse response level. With this same thought process in mind, we estimate the impairment threshold at 125%, 150%, and 200% of the background response quantile, where the different values are chosen to investigate the sensitivity of the choice. In addition, we compute the BMD and BMDL with the BMR = 10% and the BMDL is computed to be the lower 5% of the BMD distribution.

Fig. 4 shows the posterior estimated curve for the quantile dose–response curve (solid line) and corresponding 95% pointwise credible intervals for the quantile dose response (dashed line). The BMD and BMDL for the impairment threshold of x₀ = 100 (IU/L) is also shown. In this figure, the quantile dose–response curve includes approximately 10% of the observed data points above the curve, which is evidence it is providing a reasonable estimate of the 90th quantile dose–response function. The estimated BMD between the two methods is different. When x₀ is set to the response of 100 (IU/L), the estimated BMD is 10.9 with a BMDL of 10.6 (same as figure). When x₀ is defined as the point where the quantile dose–response curve is specified as a percent increase from background response the QIT BMD is 10.8, 8.4, and 6.4 for 100%, 50%, and 25% increases from the background (not illustrated). In addition, the BMDLs are computed to be 10.5, 8.0, and 5.6 for increases of 200%, 150%, and 125%, respectively.

Fig. 4.

The estimated 90th quantile dose response of the alanine trasnsaminase (IU\L) level for Fischer 344 rats exposed to 4-chloronitrobenzine with a corresponding 95% percent credible intervals (dotted line) around the central estimate. Here the impairment threshold is defined as alanine transaminase levels above 100 IU/L. In this example, the benchmark dose is estimated at 10.9 ppm with a 95% lower bound of 10.6 ppm.

In this analysis, it is not clear how x₀ should be set. The two methods produce QIT BMD estimates that are different. For the relative change approach, the differences in the estimate are approximately linear, indicating that the response is increasing with increasing exposure. This is not obvious looking at the raw data in Fig. 4, which suggest there may be no response initially; if this is assumed, it is very possible that the cutpoint of 100 (IU/L) may be too high even if a threshold were assumed. As above, when making a choice between the methods, we recommend that multiple values be reported to the risk manager.

6. EPIDEMIOLOGICAL DOSE–RESPONSE DATA

We investigate data from Round 1 of a cross-sectional survey from the NIOSH National Pneumoconiosis Program described previously.^(24,25) For this analysis, there are 8,146 complete observations in which we investigate differences in forced expiratory volume in one second (FEV₁) in relation to cumulative dust exposure. As age, height, ever-smoker, total pack-years, and race are possible determinants related to the response variable, these variables are included in the analysis. The covariates age, height, and total pack-years are included in the model as unconstrained P-splines. In addition, a race term (white/nonwhite) is included in the model; here, an intercept term for ethnicities other than Caucasian was included as well as interaction effects with age, height, and pack-years.

The categorical variable, ever-smoker, addresses the difference in respiratory status of people choosing to become smokers. As ever-smokers have a lower baseline FEV₁ caused by smoking, there is less of an effect for higher dust exposures for ever-smokers, and we separately model the effect of coal exposure for never-smokers as well as ever-smokers as in Equation (6). Although previous smoking status has an effect on the quantile dose–response function, there is little evidence to suggest a synergistic effect relating dust to the number of pack-years smoked, and the pack-years variable was included in the analysis independent of dust exposure.

For this analysis, all knots were chosen at locations that were located at equally spaced intervals on the quantiles of the covariate as well as the minimum and maximum of the covariate. For the continuous variable age, knots were placed at the minimum observed age and at the maximum observed age, as well as at the deciles of the age distribution. This decile spacing was done for all covariates except exposure. Here, more knots were used, with knots located at equally spaced 5% intervals starting at 5% and ending at 95% of the observed exposures.

To specify the impairment threshold, there is a literature on the distribution of FEV₁ values in healthy populations. We use equations defined as “the lower limit of normal” outlined in Hankinson et al.⁽²⁶⁾ to define the impairment threshold. The lower limit of normal estimates a value for healthy nonsmoking populations for the FEV₁ and allows one to base risk estimates on a large healthy non-smoking population. The lower limit of normal is given for a unique age and height, and we compute the impairment threshold for nine age and height combinations. Here ages 30, 45, and 60 are considered as well as heights of 68, 69, and 70 inches. In addition, for smokers we used 9.4, 17.4, and 22.1 as the value of pack-years for ages of 30, 45, and 60, which were based upon pack-year means in the population for the corresponding ages. In computing the BMD, a BMR representing the lower 10% and 20% of the exposed population’s FEV1 score is considered for all analyses. We report only the values for white miners as nonwhite miners represent only about 5% of the study and estimates were very similar to the white miners.

Table II gives a listing of BMD values for all age and height combinations for never-smokers and ever-smokers. The BMD values for ever-smokers are systematically lower than never-smokers, and in some cases orders of magnitude lower. This is different from the estimates provided by Noble et al.⁽²⁷⁾ on the same data set. In their analysis, estimates were based upon absolute decreases in the mean response, that is, they did not use a threshold lower limit of normal approach, and their estimates were often well beyond the maximum exposure of 347 mg/m³ and suggested that smokers had a lower risk of impaired lung function than nonsmokers, which may seem paradoxical given that smokers already have impaired lung function.

Table II.

A List of QIT BMD Estimates, and Corresponding Lower Limit Values, for Coal Dust Exposure (in Mg/M³) for Coal Miners for White Nonsmokers and Smokers for Benchmark Responses of 10% and 20%

	Quantile	Height	Age
			30	45	60
Nonsmokers		70	24.2 (3.61)	61.4 (27.3)	79.6 (49.9)
	10%	69	31.0 (6.04)	68.8 (39.0)	70.2 (37.1)
		68	30.9 (5.7)	68.8 (39.0)	50.6 (16.5)
		70	87.0 (54.9)	126.9 (88.9)	145.5 (102.8)
	20%	69	88.6 (57.2)	128.8 (90.7)	144.7 (101.9)
		68	88.2 (55.9)	128.4 (90.3)	144.3 (102.2)
Smokers		70	3.1 (0.0)	18.6 (0.8)	26.6 (2.2)
	10%	69	5.1 (0.0)	24.1 (2.2)	33.4 (2.9)
		68	5.1 (0.0)	23.7 (2.2)	33.1 (2.9)
		70	44.0 (7.4)	76.8 (38.2)	90.9 (52.8)
	20%	69	45.6 (9.0)	78.4 (39.4)	92.9 (53.9)
		68	45.3 (8.2)	78.2 (39.1)	92.5 (53.5)

Our result is in stark contrast to their estimates, as it suggests smokers are a susceptible subpopulation, which is the opposite conclusion of Noble et al. This is the case even though there is less of a decrease in lung function given dust exposure. Fig. 5 shows this relationship; here, as compared to the group’s baseline exposure, the never-smoking population (gray line) has a greater overall decrease in lung function than the ever-smoking population (black line) due to exposure, which is what Noble et al. described in their manuscript; however, this group’s lung function is already significantly less than the nonsmoking population, which places it much closer to the lower limit of normal impairment threshold value. This results in smokers being able to tolerate much less exposure to coal dust.

Fig. 5.

Comparison of the effect of dust exposure on FEV₁ between ever-smokers (black line) and nonsmokers (gray line). These estimates are estimated for the 10th quantile of the response distribution.

7. DISCUSSION

Like the other definitions of the BMD for continuous endpoints, the method still suffers from the difficulty in defining a threshold when a biologically acceptable value is not available. However, unlike previous definitions, the choice of the percent increase is not cofounded with the BMR (or the BMRF in the BMDS software), which may be misleading to some risk managers. We stress that the choice of the impairment threshold should be fully transparent and a sensitivity analysis should be performed on an array of possible choices with all choices given to the risk manager. In addition, if the location and number of knots are incorrectly chosen, the choice of knots in the smoothing spline may be an issue. When it is reasonable to assume the exposures are distributed uniformly over some interval, defining knots in equal spaced intervals is appropriate. However, as in the coal dust example, equal knot spacing is not appropriate when the covariates (including exposed dose) are not uniformly distributed; here knots should be placed equally across the quantiles of the variable, which may help prevent overfitting at the edge of the distribution.

There are further areas of research to explore that may allow the researcher to develop more parsimonious models. Specifically, the method flexibly included the covariates assuming that they did not interact, and there was no formal test designed to see if the covariates were needed in the model. From a Bayesian perspective, Bayes factors⁽²⁸⁾ could be constructed by modifying the above prior and monitoring the MCMC sample appropriately, and would allow researchers to estimate the posterior odds the covariate is important in the analysis. When computing the BMD, such an approach would be akin to Bayesian model averaging over the possible model forms with similar interpretation as in Noble et al.⁽²⁷⁾ Alternatively, model selection criteria such as the DIC⁽²⁹⁾ or the WAIC⁽³⁰⁾ may be preferred as Bayes factors are often very dependent on the prior.

The proposed quantile impairment threshold BMD methodology provides a way of estimating the BMD similar to the previously proposed methodologies based on the mean or median response, but adds the ability of the BMD to be computed based upon the probability of adverse effect to an exposed population. Such a definition may be preferable as it allows risk to be based upon both a probabilistic understanding as well as a biological understanding of the system of interest. Further, if research is done in developing suitable transformations of responses from the exposed population to the human population, then one could extend this definition to meet the recommendations of the NRC.