Patterns of coevolving amino acids unveil structural and dynamical domains

Significance

Patterns of pairwise correlations in sequence alignments can be used to reconstruct the network of residue-residue contacts and thus the three-dimensional structure of proteins. Less explored, and yet extremely intriguing, is the functional relevance of such coevolving networks: Do they encode for the collective motions occurring in proteins at thermal equilibrium? Here, by combining coevolutionary coupling analysis with a state-of-the-art dimensionality reduction approach, we show that the network of pairwise evolutionary couplings can be analyzed to reveal communities of amino acids, which we term “evolutionary domains,” that are in striking agreement with the quasi-rigid protein domains obtained from elastic network models and molecular dynamics simulations.

Abstract

Patterns of interacting amino acids are so preserved within protein families that the sole analysis of evolutionary comutations can identify pairs of contacting residues. It is also known that evolution conserves functional dynamics, i.e., the concerted motion or displacement of large protein regions or domains. Is it, therefore, possible to use a pure sequence-based analysis to identify these dynamical domains? To address this question, we introduce here a general coevolutionary coupling analysis strategy and apply it to a curated sequence database of hundreds of protein families. For most families, the sequence-based method partitions amino acids into a few clusters. When viewed in the context of the native structure, these clusters have the signature characteristics of viable protein domains: They are spatially separated but individually compact. They have a direct functional bearing too, as shown for various reference cases. We conclude that even large-scale structural and functionally related properties can be recovered from inference methods applied to evolutionary-related sequences. The method introduced here is available as a software package and web server (spectrus.sissa.it/spectrus-evo_webserver).

A powerful paradigm in molecular biology is the flow of information from the chemical composition of proteins to their biological function, which is typically viewed as a chain of implications: The protein sequence encodes for the structure, which, in turn, assists function (1, 2). Much attention has been—and still is—paid to the two key steps in this logical ladder, namely the sequence–structure and structure–function relationships. These, however, have been mostly considered separately, and addressed with distinct conceptual frameworks and tools.

For instance, a nowadays well-established mediator of structure and function for globular proteins is their internal dynamics. Single-molecule experiments, in fact, have provided vivid and quantitative descriptions of the dynamical basis of protein function (3–7). Computational and theoretical studies, from atomistic molecular dynamics (MD) simulations (8–10) to coarse-grained elastic networks (11–13), have also provided a detailed understanding of the strong ties between proteins’ structural architecture and internal dynamics. In particular, the secondary and higher-order structural organization of several proteins and enzymes are well suited to sustain collective conformational changes needed for function (3, 4, 14). These large-scale changes can therefore be efficiently excited by thermal fluctuations or triggered by the binding of ligands and effectors (15–31).

Efforts to clarify the sequence–structure relationship have also followed different routes: from the development of increasingly accurate force fields to be used in unbiased folding simulations (8, 9) to higher-level approaches where structural features are inferred from the sole physicochemical or statistical profiling of the primary sequence (32–36). Recent methodological breakthroughs for the latter contexts involve the application of statistical inference techniques to the analysis of multiple sequence alignments (MSAs). Correlated substitutions can help identify those sites that host coevolving mutations, and these, in turn, are an indicator of spatial proximity (37–46). The natural question posed by these parallel advances in the sequence–structure and structure–function relationships is whether or not it is at all feasible to establish a more direct connection between them (29, 47). In particular, one may ask if, going beyond the simple impact of function on sequence conservation, covariation between pairs of amino acids can be directly related to functional properties without relying on the prior knowledge of the structure. A positive answer to this question would have important practical implications. For instance, it could be used in contexts where structural information is covered more sparsely than at the sequence level. It could also clarify how local mutations in a given protein family are related to conserved global functional features, which is beyond the reach of structure-based approaches.

To our knowledge, this overarching question has been previously addressed only in specific, though important, contexts (29, 48–58), and hence a more comprehensive, general approach would be particularly valuable. Here, motivated by these studies and especially by the protein sector analysis of ref. 49, we carry out a systematic characterization of the sequence$\to$function relationship without harnessing the wealth of dynamical properties encoded in protein structures. We shall, in fact, only rely on sequence-based coevolutionary data and use it to infer dynamical/functional domains whose organization has been conserved by evolution. We term such fundamental units “evolutionary domains” (EDs).

The presentation of the strategy is articulated in the following way. First, we introduce and apply the method to a prototypical system, namely adenylate kinase, and show the consistency of the EDs with known structural and functional units for the enzyme. Next, for a database-wide survey, we apply the method to the previously annotated set of about 800 MSAs of ref. 42. The results show that the EDs, inferred from the sole sequence comutations analysis, are compact in space and well consistent with dynamical, or quasi-rigid domains established from structural fluctuations. They demonstrate also a strong robustness with respect to the number of sequences contained in the MSA and to the methods used in the inference of the coevolutionary coupling and are in good agreement with protein sector analysis (49), as discussed in detail in Results and Discussion and SI Appendix. Finally, for a more direct functional interpretation of the EDs, we consider various representatives of the ion channels superfamily (59). For such members, that have functionally diverged while retaining the same overall structural architecture, we show that our sequence-based partitioning highlights a diverse spatial organization of the domains, allowing for comparative functional analysis.

Results and Discussion

Our strategy is based on the analysis of comutating pairs of amino acids to identify groups of residues that have putatively evolved in a concerted manner. Revealing such coevolving groups is important because they would expectedly reflect the action of structural and functional constraints operating at a larger scale than the pairwise one, which can be elegantly and effectively probed by direct coupling analysis methods (39, 42, 60). Considering this expectedly extended organization of such coevolving clusters of amino acids, we shall refer to them as EDs. A detailed presentation of the ED search method is presented in Materials and Methods. For completeness, and to make this section self-cointained, we provide a brief summary of the method before discussing its applications.

Searching for EDs: Methodological Overview.

As summarized in Fig. 1A, the input of the ED search strategy for a given protein is the matrix of the statistical couplings between any two pairs of amino acid positions within the relative MSA encoding for its protein family. Our method of choice for the coupling analysis is the plmDCA approach described in ref. 60, but similar results can be obtained by other approaches, such as gplmDCA and plmDCA20 (42) (Materials and Methods and SI Appendix).

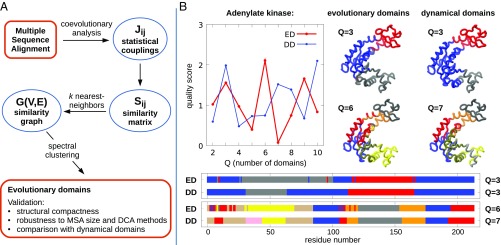
Fig. 1.

(A) Schematic illustration of the steps performed for identifying the groups of coevolving residues (EDs) from a protein MSA. (B) Application to adenylate kinase. The evolutionary partitioning is compared with the subdivisions into quasi-rigid, DDs obtained from the analysis of an MD simulation with the SPECTRUS webserver (61). The local maxima of the quality score guides the choice of the main sequence- and dynamics-based subdivisions, shown in two color-coded representations, both on the protein structure and on its sequence.

The evolutionary relatedness encoded by the statistical coupling is used to assign a similarity score (or evolutionary proximity) between pairs of amino acids. The subdivision of the whole sequence in multiple EDs is then the result of a clustering procedure, the spectral clustering (62), which returns an optimal set of densely connected groups. To ensure a robust domain subdivision, the similarity matrix is regularized into a $k$-nearest neighbors graph by retaining the top $k=7$ strongest evolutionary couplings of each amino acid, which have been found to maximize the clustering properties of the coupling network (as will be discussed in Dataset-Wide Survey). The $k$-nearest neighbors strategy has been chosen for its simplicity, but we note that the final outcomes are not significantly affected by the particular sparsification strategy used to regularize the similarity matrix (Materials and Methods and SI Appendix).

The number of evolutionary-based subdivisions is not specified a priori but is set by analyzing the profile of a quality score indicating the best protein decomposition as a function of the number of domains, providing thus a consistent description of the protein at both large and small scales, respectively, for low and high numbers of clusters. The clustering strategy is similar to that used by the SPECTRUS (spectral-based rigid units subdivision) algorithm (61) to determine dynamical, quasi-rigid domains in proteins or protein complexes.

A Test Case: Adenylate Kinase.

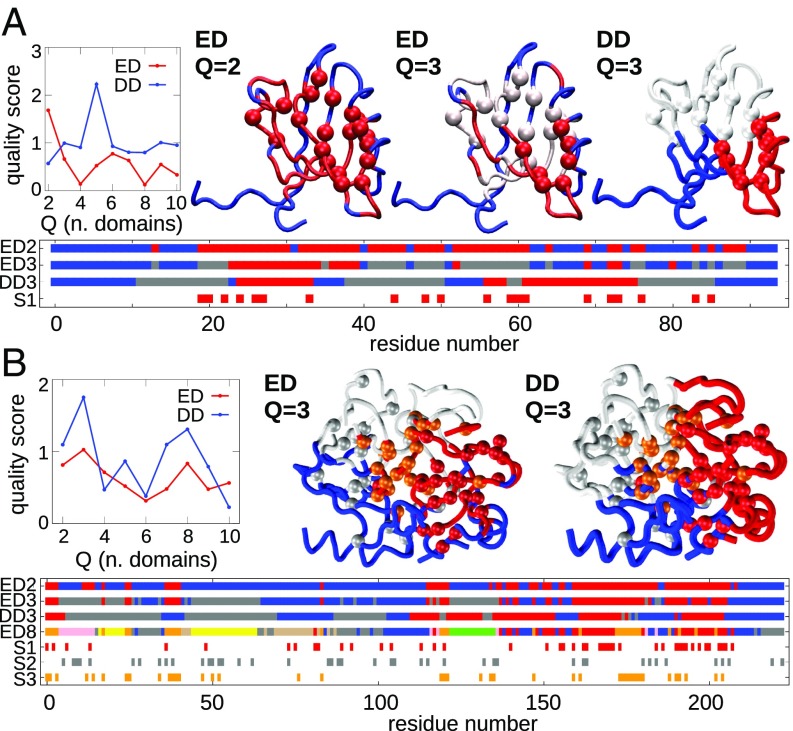
To illustrate and validate the sequence-based ED decomposition, we first apply it to Escherichia coli adenylate kinase [Protein Data Bank (PDB) ID 4AKE], a standard benchmark for domain partitioning methods. The results are given in Fig. 1B. The red curve in the upper left graph shows the quality score, $Q$, for subdivisions of the enzyme into an increasing number of EDs. The quality score reflects how sharply defined, according to the clustering metrics, is the returned optimal subdivision compared with random partitions. The highest scores for the sequence-based partitioning are found for $Q=3$, $6$, and $9$ EDs. The structural and sequence-wise representations of the partitions into Q = 3 and 6 domains are given in Fig. 1B. Note that EDs, which can span several intercalated stretches of the primary sequence, are nonetheless structurally compact. This is a noteworthy and intriguing result, since the evolutionary subdivisions are exclusively sequence-based, with no input about the actual structure of the protein.

As a matter of fact, the returned subdivisions are viable from the structural and functional point of view. This emerges from their comparison with quasi-rigid, dynamical domains (DDs). These were identified with the SPECTRUS web server (61) using as input the structural fluctuations observed in extensive MD simulations of adenylate kinase. As shown in Fig. 1B, the $Q=3$ and $Q=6$ evolutionary subdivisions are well consistent, both structurally and sequence-wise, with the high-scoring quasi-rigid partitionings into similar numbers of domains. In particular, for both cases, the $Q=3$ subdivision corresponds to the well-known partitioning into three main functional domains, namely the ATP-binding site, the AMP-binding site, and the core, shown respectively in red, gray, and blue. In addition, even the finest partitionings ($Q=9$ and $Q=10$; see SI Appendix, Fig. S1) provide consistent decompositions in the two cases and highlight structural elements that are arguably crucial for the protein functional dynamics.

The result is noteworthy because, although sequences code for both structural and functional properties, it would have been difficult to anticipate that the latter could be obtained directly from the primary sequence without additionally using a 3D conformation. In addition, although DCA is a very powerful means of extracting reliable indications of proteins’ folds, we are not aware of documented instances where DCA-derived structural information was used to infer functional movements. These considerations reinforce the significance of showing that functional and structural domains can be directly and confidently extracted from the coupling analysis of MSAs (see SI Appendix, Fig. S2).

Dataset-Wide Survey.

For a systematic characterization of the EDs, we then extended the analysis to a dataset of 813 MSAs compiled by Feinauer et al. (42). This was chosen for two main reasons. First, it gives a comprehensive coverage of several protein families, with various MSA sizes (from 16 to 65,000 entries) and protein lengths (from 30 to 500 amino acids). Second, a PDB entry is available for a representative protein of each family/MSA. This is a key element in this study because it allows us to assess the spatial compactness of ED decompositions, which are exclusively based on the sequences defining each MSA, and to compare them to the DDs subdivisions.

Evolutionary couplings: Clustering propensity and community structure.

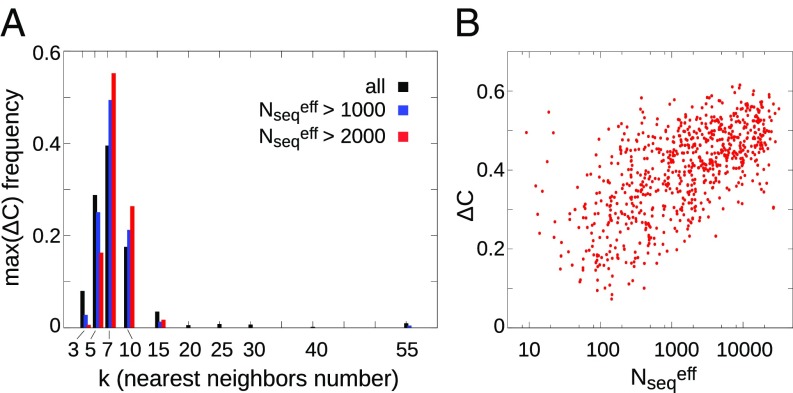
As a preliminary step toward identifying the EDs, we first investigated if the input networks of statistical couplings $J_{ij}$, obtained from coevolutionary analysis, exhibit an intrinsic propensity to be densely organized and, thus, to be clustered. As detailed in Materials and Methods, such propensity is conveniently captured by $\mathrm{\Delta }C=C-C_{\text{rand}}$, that is, the difference of the clustering coefficients of the $k$-nearest neighbors graph, $C$, and of a randomized, reshuffled version, $C_{\text{rand}}$ (63), measuring the probability that two neighbors of a vertex are also connected between themselves. As shown in Fig. 2A, this quantity also proves useful in choosing the optimal $k$, since the different graphs show usually a maximum for the clustering coefficient $\mathrm{\Delta }C$ at $k=7$, especially for MSA containing a large number of sequences (see also SI Appendix, Fig. S3 for the other inference methods). Importantly, the MSA size (calculated as effective number of sequences, $N_{seq}^{eff}$, i.e., the number of sequences in the set whose mutual identity is smaller than 90%) crucially affects the clustering propensity of the similarity graph, as clarified by the strong correlation between these two quantities shown in Fig. 2B (and SI Appendix, Fig. S4). Thus, when a large dataset is available and the reconstruction of the network of couplings is most reliable, the latter shows a high tendency to cluster and an unambiguous number of “relevant” neighbors ($k=7$), which is indicative of an inherent collective organization of the coevolution patterns. Strikingly, this number coincides with the average structural neighbors surrounding each residue in protein structures ($6.75\pm 0.04$, calculated on the PDB structures of this dataset using a C$\beta$–C$\beta$ distance threshold of 8.5 Å as in ref. 42). We also note that, for $k=7$, the percentage of true contacts (including along the sequence) is systematically larger than 50%, especially for larger MSA size (SI Appendix, Fig. S5 and Materials and Methods).

Fig. 2.

(A) Histograms of the maximum adjusted clustering coefficient $\mathrm{\Delta }C$ for plmDCA method, obtained by progressively excluding from the dataset the MSAs containing a low number of sequences. (B) Scatter plots of $\mathrm{\Delta }C$ as a function of the corresponding MSA size ($N_{seq}^{eff}$, effective number of sequences with sequence identity less than 90%).

Compactness of evolutionary domains.

We used the networks of evolutionary couplings, derived from each of the 813 MSAs, as input for the clustering algorithm. For an initial unsupervised overview of the EDs organization, we identified the subdivisions from $Q=2$ to $Q=10$ domains for each protein family. Next, we studied whether the sequence-based subdivisions corresponded to spatially compact domains once mapped on the available PDB structures of the MSAs’ representatives. The results are given in Fig. 3.

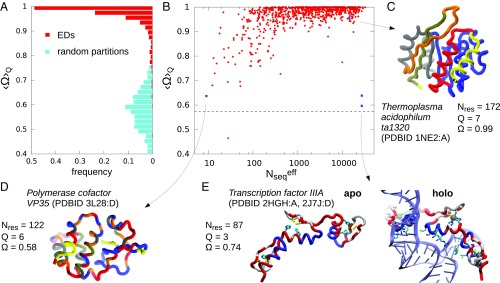
Fig. 3.

(A) Distribution of the average structural compactness ${⟨\mathrm{\Omega }⟩}_Q$ over the MSA dataset (in red), compared with the one computed for random partitionings of the same protein sequences (in cyan). (B) Scatter plot of the EDs structural compactness $\mathrm{\Omega }$, computed for each single MSA and averaged over the subdivisions into $Q=2,\mathrm{\dots },10$ domains, vs. the relative MSA size. The dashed line represents the average compactness for the set of random partitionings. (C–E) Structural representations of three notable examples of ED decompositions, marked by blue squares in B. (E) Views of the transcription factor IIIA, in the apo form and in complex with a 5S rRNA 55mer.

Fig. 3A presents the probability distribution of the compactness parameter, $\mathrm{\Omega }$, which measures the fraction of amino acids that are no further than 10 Å from most residues in their same domain (Materials and Methods). For clarity, the results are presented as aggregated over the considered values of $Q$; more detailed, nonaggregated representations, including those for the other inference methods, are given in SI Appendix, Figs. S7–S9. The $\mathrm{\Omega }$ distribution of genuine ED partitions in Fig. 3A is strongly skewed toward the $\mathrm{\Omega }=1$ limit. In fact, the median value is 0.98, indicating that, over all considered MSAs and partitioning levels $Q$, very few amino acids are isolated, or at a distance larger than 10 Å from the other members of their domains. By contrast, the compactness $\mathrm{\Omega }$ computed for random partitioning of the same entries, and into the same range of $Q$, follows a very different distribution that is so shifted toward lower $\mathrm{\Omega }$ values (the mean is about 0.57) that it has negligible overlap with the ED one. The scatter plot in Fig. 3B additionally reveals a strong correlation between the number of sequences in the MSAs and the observed compactness of the inferred EDs, similarly to what is observed for the clustering coefficient. In fact, one notes that values in the left tail of the $\mathrm{\Omega }$ distribution are typically found for MSAs featuring the smallest numbers of entries, 300 sequences or less. We interpret this result as an indirect indication that, when less than $\sim$300 sequences are used to infer the couplings, the network is less reliably reconstructed and consequently the ED subdivisions are less compact, although their compactness can still be significantly high compared with the random case. Analogous conclusions, but with even higher values of compactness $\mathrm{\Omega }$, can be drawn when repeating the analyses in Fig. 3 A and B for the optimal decompositions in $Q_{\text{opt}}$ domains, picked according to the quality score of the ED decomposition, demonstrating its relevance in the method (see SI Appendix, Fig. S10).

To illustrate the concepts discussed above within the context of selected protein structures, we show a few notable examples of ED subdivisions in Fig. 3 C and E. The entry in Fig. 3C corresponds to an MSA with a large pool of sequences (14,080) and an average compactness ${⟨\mathrm{\Omega }⟩}_Q=0.96$. The structure shown in figure is the representative PDB entry 1NE2, and the subdivision corresponds to the optimal partitioning ($Q=7$). Its high degree of compactness, $\mathrm{\Omega }=0.99$, is readily perceived by inspecting the subdivisions that, with the sole exception of a terminal residue, are visibly compact in space. The other two examples in Fig. 3 D and E, by contrast, pertain to proteins whose average ED compactness is about $0.62\pm 0.02$, i.e., on the low side of the distribution. The first instance is the Ebola viral protein 35, represented by PDB entry 3L28, which has the least numerous MSA in the dataset (nine sequences only). This entry presents a noticeable fragmentation of each of the $Q=6$ domains, and, indeed, its compactness value is not too dissimilar from the case of random partitions.

The second instance is a most interesting outlier, because it corresponds to one of the most numerous MSAs, specifically encoding the transcription factor IIIA (TFIIIA), a Cys2His2 (C2H2) zinc finger protein involved in nucleic acid recognition and regulation (64). The two structures in Fig. 3E represent the fingers 4 to 6, both in the free state (65) (PDB ID 2J7J), and bound to 5S rRNA 55mer (66) (PDB ID 2HGH). TFIIIA is particularly noteworthy because it contains nine C2H2 domains. As discussed by Espada et al. (67), in such cases, DCA signals can reflect correlations due to the common origin of the domains, as well as correlations due to genuine structural and functional couplings.

The optimal partitioning of TFIIIA, i.e., the one with the highest quality score, consists of $Q=3$ EDs. When the corresponding tripartite subdivision is superposed to the apo structure of the zinc finger, it yields spatially fragmented domains. However, differently from the previous instance in Fig. 3D, the residues in each domain are not scattered but rather are arranged in coherent structural patterns. In particular, the partitioning of a single zinc finger is consistently repeated across all three motifs. Indeed, when the same subdivision is superposed to the holo (RNA bound) form, the domains acquire a spatial organization that is functionally meaningful. Specifically, (i) the red domain outlines the binding site formed by two cysteines on the $\beta$-hairpin and two histidines in the helix (highlighted in the apo form in yellow and cyan, respectively) that coordinate the zinc ions crucial to stabilize the fold (66); (ii) the white domain sustains and locks the hairpin onto the helix (note the facing white residues, consistently present in all three helices); and, finally, (iii) the remaining blue part of the helix (referred to as “recognition helix”) contains residues forming sequence-specific contacts with the groove of the nucleic acid. Therefore, the seemingly fragmented nature of this outlier can be recapitulated in more coherent functional ways in the holo context. This suggests that, even in challenging cases where DCA reflects the presence of repeated domains, the ED analysis can still extract meaningful large-scale functional relationships.

Comparison with dynamical domains.

Motivated by these observations, we undertook a systematic comparison of the EDs and the quasi-rigid (or dynamical) domains (DDs) for each of the 813 MSAs. The DDs were obtained from the SPECTRUS decomposition tool (61), based on an elastic network model (ENM) analysis (68, 69) of the PDB structures of the MSA’s reference entries, as detailed in Materials and Methods. The structure- and dynamics-based character of the DD analysis is an apt complement of the sequence-based one of EDs. This duality makes the comparison particularly interesting and relevant for framing the sequence$\to$structure$\to$function relationship. The overlap of the two types of domain subdivisions was measured in terms of the adjusted mutual information (AMI), which allows for a straightforward assessment of the statistical significance of the subdivisions overlap, as described in SI Appendix, Supplementary Methods.

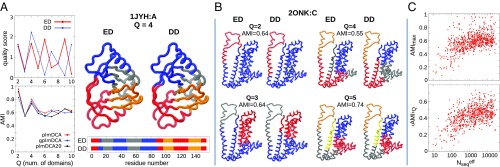
To better illustrate the correspondence of the EDs and DDs and to give an immediate meaning to the AMI value, we discuss here two examples. Fig. 4A shows the results for SbmC protein (PDB ID 1JYH, $N_{seq}^{eff}=3,707$) subdivided into $Q=4$ domains. This level of subdivision was considered because it provides the best quality score for dynamical domains. The consistency of the ED and DD subdivisions is very clearly conveyed by the structural and sequence-wise representations, which overlap almost perfectly. This consistency extends to both coarse and finer subdivisions, as highlighted by the AMI profile, which is particularly high ($>0.8$) for $Q=2$ and $Q=4$, and remains larger than 0.5 in all other cases as well. Likewise, for the example in Fig. 4B [ATP-binding cassette (ABC) transporter, PDB ID 2ONK, $N_{seq}^{eff}=17,503$], a consistent overlap between EDs and DDs is observed at various levels of subdivision. In particular, we note that even the lowest AMI value of 0.5, attained for $Q=4$, still corresponds to a clear and satisfactory consistency of the two types of subdivisions.

Fig. 4.

(A and B) ED and DD decompositions of an SbmC protein (PDB ID 1JYH:A) and an ABC transporter permease protein (PDB ID 2ONK:C). (C) Scatter plots of the maximum (Upper) and average (Lower) AMI, over the domain number $Q$, between the ED and DD decompositions, as a function of the effective MSA size.

To extend considerations to the entire dataset, we computed for each MSA the average and the largest AMI between EDs and DDs, for $Q$ in the range $[\mathrm{2,10}]$. The results are presented as a function of the number of MSA sequences in the scatter plots of Fig. 4C. Interestingly, we observe again a strong dependence on $N_{seq}^{eff}$: For MSAs with 500 sequences or more, the average values for ${\text{AMI}}_{\text{max}}$ and ${⟨\text{AMI}⟩}_Q$ are 0.62 and 0.47, compared with the corresponding values of 0.49 and 0.35, respectively, when $N_{seq}^{eff}<500$. Clearly, when $N_{seq}^{eff}$ tends to 0, the AMI vanishes, again consistent with a random partitioning of a sequence. Slightly higher values of AMI are observed, on average, when comparing domains at the optimal ED number $Q_{\text{opt}}$, as determined by the individual quality scores. However, such comparison is more delicate, because the respective $Q_{\text{opt}}$s for ED and DD decompositions do not generally coincide, making it advisable to consider the more stable average ${⟨\text{AMI}⟩}_Q$. For more details, see discussion in SI Appendix, Fig. S11.

The good overlap between EDs and DDs at all levels of subdivision suggests that our clustering approach captures all of the relevant topological features from the network of statistical couplings. It thus constitutes a powerful tool for inferring meaningful structural and functional relationships, as discussed in Case Study: Comparative Analysis Across the 6TM Family of Ion Channels.

Case Study: Comparative Analysis Across the 6TM Family of Ion Channels.

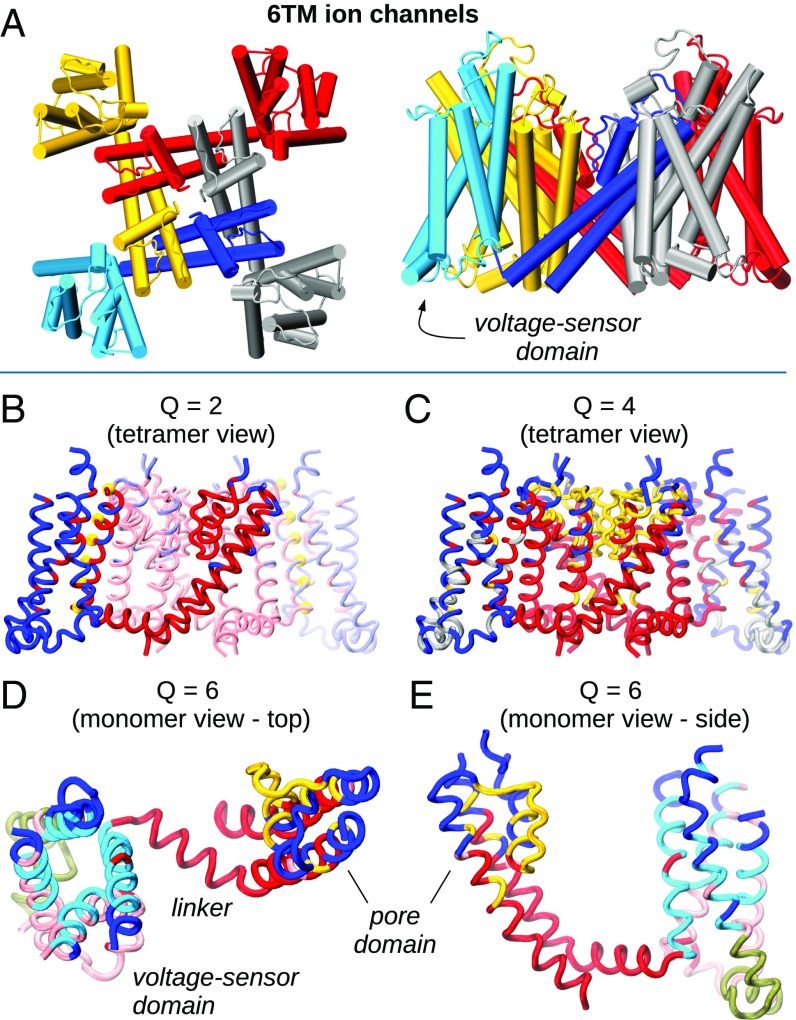
To further assess the capability of ED decompositions to outline important functional properties of a protein family, we conclude by applying the ED analysis in a comparative scenario to a specific class of ion channels, the six-transmembrane-helices (6TM) superfamily, for which the sequence–function relationship has been actively investigated in a number of seminal studies (70). This superfamily is characterized by a strictly conserved tetrameric architecture. The latter is shown in Fig. 5A where different colors are used to highlight the main functional domains, including the four-helix bundle voltage sensor domain (VSD) and the pore of the ion conduction pathway, which involves two transmembrane helices and the linking reentrant pore, containing the selectivity filter. This single structural template inherited from an ancestor gene has enabled, through differentiation, an explosion of functional variability. Channels in the 6TM class, in fact, are involved, for instance, in reporting noxious environmental conditions, in shaping the neuronal action potential, and in syncing the beating of the heart (59). Since all these channels share the same architecture, different decompositions in EDs in different phylogenetic groups likely reflect distinct functional rather than structural aspects (51, 52).

Fig. 5.

EDs for Kv channels. (A) Schematic representation of biological tetrameric assembly of 6TM channels, with each color representing a single monomeric subunit (top and lateral view). For the blue subunit, the VSD is highlighted in cyan. (B) Representation of the most significant monomeric subdivision, $Q=2$, shown in the context of the full tetramer; see SI Appendix, Fig. S13 for the quality score. Positively charged residues responsible for voltage sensing are shown as yellow spheres. (C–E) Finer subdivisions into four and six monomeric domains.

For definiteness, we focus on three different 6TM families: the voltage-gated potassium-selective channel [Kv, PDB ID 2R9R (71)], the bacterial voltage-gated sodium-selective channel [BacNav, PDB ID 4EKW (72)], and transient receptor potential [TRP, PDB ID 3J5P (73)] channels. We analyzed the MSAs for the three families based on a pool of $\sim 800$ sequences, each with 200 positions (74) from which we omitted the highly gapped regions of the alignments (typically occurring in loops between the six transmembrane helices). Although the 6TM dataset that we used is the most comprehensive available at the moment, its size is clearly limited by comparison with the much better populated cases discussed previously, showing a pretty low $\mathrm{\Delta }C$ (see SI Appendix, Fig. S12). To ensure a robust analysis, we decided to decompose the graph corresponding to the maximum $\mathrm{\Delta }C$ for each MSA.

In Fig. 5 B and E, we present various subdivisions for the Kv family for increasing numbers of domains (see SI Appendix, Fig. S13 for quality score). The subdivision for $Q=2$ is already unexpectedly informative, since the fourth helix of the VSD (called S4) and its facing residues are associated with the pore domain rather than the rest of the VSD. This is an intriguing result because the aforementioned classic subdivision into structural domains would have kept these elements apart. From a functional point of view, however, the sequence-based subdivision of the primary ($Q=2$) EDs is meaningful. In fact, it agrees with the strong mechanical coupling between the pore region and S4 (75–77). We recall that the latter contains the positive residues (yellow spheres in Fig. 5B) that sense transmembrane potential variations and determine the movement of this helix across the membrane; this movement is, in turn, transmitted to the pore domain for gating. The division into $Q=4$ EDs, in Fig. 5C, picks up further functional features. One domain largely corresponds to the selectivity region, formed by all of the residues lining the narrow and highly conductive ion pathway (in yellow), another is associated to the gating region (red), and the other two comprise, respectively, the internal and external residues of the VSD. It is notable that a different domain assignment is found for the two faces of the pore helix, with the upper one sustaining the selectivity filter and the lower one contacting the gating domain. This Kv example is also particularly instructive regarding the multilevel description that EDs can provide about the various protein features. Finer subdivisions ($Q=6$) mostly return the basic structural elements of the system. In this subdivision, the pore and the voltage sensor regions are mostly assigned to different EDs, with the exception of the extracellular portion of the channel (highlighted in blue in Fig. 5 D and E), which still bridges between the two. When viewed in the context of the channel tetramer, it appears natural to speculate that this region is instrumental for the signal propagation between the loops of the voltage-sensing and the pore domains, which can indeed be modulated by external stimuli, like ligand binding. We accordingly surmise that amino acids in this region are genuinely evolutionary-related for functional reasons.

Further elements regarding the functional role of EDs emerge from the comparisons of Kv, BacNav, and TRP subdivisions, which are given in Fig. 6 and are further detailed in SI Appendix, Fig. S13. The comparison between Kv and BacNav (another tetrameric voltage-gated family, selective for sodium) reflects how the functional constraints shaped these two families along evolution, in an almost superimposable way. In fact, the S4 helix segregates with the lower part of the pore, and, together, they form the “gating domain” (in red). Similarly, the reentrant pore helix is split into the upper and lower faces, sustaining the selectivity domain (in yellow), and the rest of VSD is grouped into internal and external residues. The organization of EDs for TRP channels is, instead, totally different. Indeed, this channel family, identified only in Eukaryota, has distinct characteristics with respect to the other ones. Specifically, it is a nonselective cation channel gated by a variety of stimuli, such as temperature, pH, and ligands binding (78–81). In particular, these channels have been shown to possess two different gating regions (73, 82), which are, indeed, well captured by the ED decomposition. The division of S4 is compelling in this respect, since it is consistent with the lack of the dynamical role that, instead, characterizes it in voltage-gated ion channels: Only the C-terminal residues are associated with the gating domain (in red). The upper part of S4 is, instead, longitudinally sectioned, with the internal residues all grouped with the upper part of the rest of the VSD. The external part of S4 belongs to the extended yellow domain: The latter represents effectively a second upper gating domain, as suggested in refs. 73 and 82. Remarkably, the yellow cavity determined by the two pore helices and the external part of S4 corresponds exactly to the location of the vannilloid pocket (82–86), which represents the main intracellular binding site for the activators of these channels.

Fig. 6.

Comparative analysis of the EDs for Kv, BacNav, and TRP channels, corresponding to subdivision Q = 4 (see quality scores in SI Appendix, Fig. S13). While Kv and BacNav show similar organization, coherent with their analogous functional requirements, TRP is characterized by a different domain pattern, consistent with its ligand-gated properties and loss of voltage-gated ones, specific to the other two channels.

The indication from the 6TM family is that EDs can single out domains that, owing to their specific functional character, are distinct from subdvisions made with static structural criteria.

Comparison with Protein Sectors Analysis.

Identifying groups of coevolving residues from patterns of correlated mutations is a long-standing issue (48) that has been tackled from various perspectives. Among the best-known and most elegant approaches are the protein sectors analysis (49) and CoeViz (87), which provides insight into the cooperative nature of residue coevolution. ED analysis is mostly complementary to these techniques, because of several methodological differences. For instance, protein sectors analysis returns a nonexhaustive coverage of the protein residues. In fact, it uses the top eigenvectors of a conservation-weighted covariance matrix built from an MSA, and typically only 20% of residues with the largest component on one eigenvector determines a sector, i.e., a group of residues evolving concertedly. By construction, the method prioritizes the most conserved residues (88). Importantly, this nonexhaustive assignment is nonexclusive too, meaning that one residue can be part of distinct sectors. By contrast, the ED decomposition uses the entire DCA-based similarity to ensure a residue assignment that is both exhaustive and exclusive. The latter feature, in particular, is instrumental to the specific goal pursued here of comparing EDs with DDs.

DCA and statistical coupling analysis share nevertheless important conceptual similarities (89, 90), and, therefore, similarities between EDs and sectors can be expected in specific contexts. We therefore compared the two types of subdivisions for several case studies. We first considered the two datasets of ref. 49, which consist of the PDZ domain and the S1A serine protease families. The former dataset has 240 sequences and features one sector. The quality score profile of the ED analysis in Fig. 7A has an overall decreasing trend, which is typical of datasets of this size, indicating meaningful division for $Q=\mathrm{2,3}$. The first subdivision features a domain that totally includes the aforementioned sector (red spheres). In the finer ED subdivisions, the protein sector is resolved into smaller and spatially coherent EDs (red and gray domains in the sequence diagram), allowing a further comparison with DDs for $Q=3$: the highlighted residues (and corresponding EDs) overlap with two distinct dynamical partitions of the protein. The second dataset, with a larger number of sequences (1,388), yields three sectors. The EDs quality score profile in Fig. 7B indicates that significant subdivisions are found for $Q=2,\mathrm{3,8}$ domains. Two of the three sectors (red and orange in the diagram) have a good correspondence with the EDs. They are compact and both contained in the red domain for $Q=2,3$, and then perfectly separated for $Q=8$. The other sector (in gray in Fig. 7B) instead comprises scattered residues. This is consistent with previous studies that showed that this sector is more related to thermal stability than structural properties (49). Interestingly, when S1A sectors and EDs differ from DDs (again for $Q=3$), they are still consistent with each other. In fact, one sees in Fig. 7 that the red ED includes the orange sector but both groups differ from the blue DD. Overall, the comparative analysis of these two families, whose MSAs contain homogeneous sets of sequences, shows that EDs and sectors have significant similarities.

Fig. 7.

Comparison of ED decomposition and protein sector analysis (49) for (A) the PDZ domain (PDB ID 1BE9) and (B) the S1A serine proteases family (PDB ID 3TGI), also with the corresponding division in DDs. The sectors are shown as spheres in the 3D representations, and EDs and DDs are shown as different colors also in the sequence diagram.

Remarkable differences, however, are observed in case of larger and more heterogeneous sets of sequences. In SI Appendix, Figs. S14–S16, we illustrate three examples discussed previously, namely SbmC gyrase inhibitory protein, adenylate kinase, and ABC transporter, whose MSAs have been built by including the largest number of sequences (42). While, for SbmC ($N_{seq}^{eff}$ = 3,714), some similarity is still noticeable between two sectors (cyan and orange in SI Appendix, Fig. S14) and the subdivisions in two DDs and EDs, for the other datasets (adenylate kinase and the ABC transporter), it is not possible to relate sectors to EDs or DDs: Protein sector analysis on these large datasets (more than 14,000 effective sequences) returns groups of residues distant in both primary and tertiary structure (see SI Appendix, Figs. S15 and S16). The fact that the differences between EDs and protein sectors are more pronounced for large datasets suggests that, when presented with highly heterogeneous sequence sets, these two algorithms highlight different aspects of residue–residue correlations. For instance, protein sectors analysis has been shown to effectively identify the groups of amino acids that experience the largest variations on passing from one phylogenetic group to another (91). On the other hand, DCA is seemingly less sensitive to the phylogenetic structure of the MSA analyzed (42). For this reason, we believe that the interpretation of EDs in terms of structural domains and DDs ought to be applicable in more general contexts, and particularly to large datasets.

Conclusions

Patterns of correlated mutations in an MSA can be used to reveal a set of pairwise statistical interactions that are often informative about the possible spatial proximity between the residues involved. Strikingly, we showed that this network of couplings has a peculiar structure with communities of residues that are more connected among themselves than with the rest of the sequence. Therefore, beyond compensatory mutations involving pairs of contacting residues, entire groups of residues appear to evolve in a concerted fashion. We characterized these communities, that we term EDs, by interpreting the statistical couplings as a measure of evolutionary proximity between residues. To this end, we used an efficient clustering framework, namely, the spectral clustering. When analyzed in the context of the protein structure, these couplings show an innate tendency to segregate into spatially localized and compact groups. We explored the possible biological meaning of these subdivisions, comparing EDs with the dynamical, quasi-rigid domains identified by a recently introduced approach (61). The sequence- and structure-based subdivisions were found to be very consistent across a diverse repertoire of protein families. This is noteworthy because sequence-based approaches could be expected to give a less direct, and hence noisier, route to domain decompositions than structural ones. As a matter of fact, the two subdivision approaches provide consistent results for both small and large number of domains, thus indicating the viability of ED decompositions at different “spatial resolutions.” These features ought to be particularly valuable in contexts where structural data are not available or are sparser than the sequence-based data.

In these cases, detecting the hierarchical organization in domains can represent a crucial initial step for any structural modeling with an atomistic level of detail. Even more interesting is the perspective of using this approach to engineer existing proteins: Transferring EDs across proteins sharing the same architecture might enable de novo design of protein chimeras with novel biological properties.

Finally, despite the fact that the DCA analysis, used for the inference of statistical couplings, depends crucially on the effective number of sequences in the MSA, we observe robust and consistent results even for a few hundreds of sequences. For this reason, we believe that EDs, and therefore the topology of the network of coevolutionary couplings, are more robust with respect to the sample size than are the single interresidue couplings (41, 42). Importantly, this aspect widens de facto the scope of applicability of these inference methods beyond those cases for which thousands of sequences are available. In particular, this enables comparative studies in which homologous subfamilies, rather than the entire group, are studied separately, with the ultimate goal of highlighting the functionally features distinctive to each subgroup, as shown here for the challenging case of ion channels.

Materials and Methods

SI Appendix contains supplementary results, methods, and figures. The method introduced here is available as a software package and web server at spectrus.sissa.it/spectrus-evo_webserver.

Dataset.

We used the dataset of ref. 42 consisting of 813 MSAs. The latter were obtained with HHblits (92), a homology detection scheme, using sequences of target PDB entries as input queries. The MSAs in the dataset are heterogeneous for both the number of involved sequences (16 to 65,535) and positions (30 to 494). The PDB structures associated with the query sequences were used a posteriori to assess the structural and dynamical characteristics of the EDs inferred from the sole direct coupling analysis of the MSAs (39, 93). The MSA for adenylate kinase was obtained with the approach of ref. 42, while MSAs for the three ion channels were the same ones derived in refs. 74 and 52, based on curated phylogenetic reconstructions. All of the relative couplings were obtained using three DCA methods, described in SI Appendix.

EDs and DDs.

DDs were identified with the SPECTRUS algorithm (61). The method uses interresidue distance fluctuations as input data for a clustering procedure that optimally partitions protein structures into quasi-rigid domains. Interresidue distance fluctuations for adenylate kinase were obtained from atomistic MD trajectories, while, for the other considered instances, they were computed using the ENM of ref. 68.

In brief, the DD partitioning involves the following steps: (i) An auxiliary similarity matrix, $S_{ij}$, is derived from the distance fluctuations of all pairs of amino acids, $i$ and $j$; (ii) next, a spectral clustering scheme (61, 62, 94) is used to subdivide amino acids into an increasing number of domains, $Q$, from 2 to 10. For optimal domain discrimination, this spectral partitioning step is customarily performed with a k-medoids algorithm, after sparsifying the similarity matrix by retaining only the most significant couplings. Following ref. 61, we accordingly retained only entries corresponding to pairs of amino acids that were in contact in the reference PDB structures ($C_{\alpha }$ distances less than 10 Å). For robustness (62, 94), the stochastic k-medoids procedure was repeated 1,000 times for each value of $Q$, and we retained only the one with the best k-medoids score. Finally, (iii) for each partition into $Q=2,\mathrm{\dots },10$ domains, we computed a quality score, and used it to single out the top-most significant (top ranking) subdivision(s).

EDs were identified with exactly the same method, but with two differences. First, the $S_{ij}$ entries of the similarity matrix were derived from the DCA pairwise couplings. Specifically, the couplings were first additively shifted to remove negative values and then squared to increase the contrast between weak and strong couplings. The second change concerns the sparsification of the similarity matrix in step ii, which was necessary because the structural (contact) criterion used for DDs could not be used in the sequence-based context of EDs. As the simplest choice, we adopted the symmetric $k$-nearest neighbor criterion, where, for each residue, only the $k$ strongest couplings are kept; see Optimization of the k-Nearest Neighbor Network. To ensure the connectivity of the network associated with the $S$ matrix, a requisite for meaningful subdivisions, we always retained entries corresponding to consecutive residues. We evaluated the robustness of the ED assignment procedure with respect to (i) the size of the MSA dataset (see SI Appendix, Figs. S17 and S18), (ii) the “purity” of EDs (that is, their variability over independent instances of the k-medoids assignment; see SI Appendix, Fig. S19), (iii) the specific sparsification strategy applied to the DCA-based similarity matrix (see SI Appendix, Figs. S20–S23), and (iv) the DCA method used (see SI Appendix, Figs. S24–S29). In the latter case, we also tested the domain assignment variability upon omitting residues with the weakest couplings in the network; see SI Appendix, Fig. S23. We surmise that, in future developments of the current method, an optimization on the protocol for omitting such residues could improve EDs resolution.

Optimization of the k-Nearest Neighbor Network.

To set $k$, we profiled the clustering coefficient $C$ (95), or “cliqueness,” of the network of $k$-nearest neighboring residues for various values of $k$. The clustering coefficient measures the probability that two neighbors of a node in the network (i.e., a residue) are themselves neighbors. The local clustering coefficient of node $i$ is defined as $C_i=2t_i/[n_i(n_i-1)]$, where $t_i$ is the number of links between the $n_i$ neighbors of $i$. The global clustering coefficient is obtained by averaging $C_i$ over all nodes in the network with $n_i>1$. In this paper, we used a generalized, weighted definition of clustering coefficient, which takes into account the weights associated with each link (63).

A commonly used term of reference is a random graph, for which $C_{\text{rand}}=\overline{k}/(N-1)$, where $N$ is the number of nodes and $\overline{k}$ is the average number of neighbors per node (96). Here we use this quantity to profile the $k$ dependence of the clustering propensity of the network derived from the DCA. Specifically, for each of the 813 MSA entries, we computed $\mathrm{\Delta }C=C-C_{\text{rand}}$ for $k\in \{3,5,7,10,15,20,25,30,40,55\}$. We then identified the value of $k$ yielding the largest $\mathrm{\Delta }C$ for each entry. The distribution of such optimal values of $k$ is shown in Fig. 2. The distribution is visibly peaked at $k=7$, which we then used for the ED analysis. The peak location is robust with respect to the specific DCA method used and with respect to the MSA size (see SI Appendix, Fig. S3). The use of a suboptimal graph, anyway, leads basically to the same subdivisions (see SI Appendix, Fig. S29). Accordingly, in Results and Discussion, we always set $k=7$, making our method parameter-free.

Structural Compactness.

The spatial compactness of EDs was assessed a posteriori by establishing whether the individual EDs consisted of two or more subdomains that are $>\mathrm{\hspace{0.25em}10}$ Å apart. We mapped each ED $q$ to a graph where the $n_q$ nodes (residues) were linked only if their $C_{\alpha }$s were within 10 Å. We then considered all $n_q(n_q-1)$ distinct pairings of the nodes and checked whether or not they can be connected by a path on the network of links. The degree of disconnectedness of the domain is then measured as $d_q=b_q/(n_q-1)$, where $b_q$ is the number of residue pairs without a connecting path. The overall compactness of a subdivision into $Q$ domains is then defined as

$${\mathrm{\Omega }}^Q=1-\frac{1}{N}\sum _{q=1}^Q{d}_q,$$ [1]

where $N$ is the total number of nodes/residues. For a physical interpretation of $\mathrm{\Omega }$, see SI Appendix, Fig. S6.