Chiral intertwined spirals and magnetic transition dipole moments dictated by cylinder helicity

Significance

Defining unique properties of anomalous molecular entities is one of the most important roles of chemistry. Revealed by discovery of carbon nanotubes, rolled sheets of graphitic carbons are among such molecular structures possessing unique chirality. Although the chirality in nanotubes is attracting renewed interest in physical science, our understanding as well as exploration of its utilities is still in its infancy due to scarcity of chiral congeners with discrete structures. In this paper, chirality-originated properties of tubular molecules have been disclosed. The chirality in the cylindrical molecular structure results in chiral double helices in crystals and in extremely large dissymmetry factors associated with circularly polarized light. Cylinder chirality would be characteristic features to be explored in materials science of tubular structures.

Abstract

The presence of anomalous chirality in a roll of graphitic carbon sheets has been recognized since the discovery of carbon nanotubes, which are becoming available in higher quantities through the isolation of chiral single-wall congeners with high purity. Exploration of the properties arising from cylinder chirality is expected to expand the scope of tubular entities in the future. By studying molecular fragments of helical carbon nanotubes, we herein reveal interesting properties that arise from this chirality. The chirality of nanoscale cylinders resulted in chirality of larger dimensions in the form of a double-helix assembly. Cylinder chirality in solution gave rise to a large dissymmetry factor of metal-free entities in circular polarized luminescence. Theoretical investigations revealed the pivotal role of cylindrical shapes in enhancing magnetic dipole transition moments to yield extreme rotatory strength. Unique effects of cylinder chirality in this study may prompt the development of tubular entities, for instance, toward chiroptical applications.

Since the discovery of carbon nanotubes in 1991, the anomalous chirality of cylindrical entities has attracted much interest (1). This chirality originates from unique helical arrangements of sp²-hybridized carbon atoms, i.e., helicity (2, 3), and fundamental properties of enantiomers of single-wall carbon nanotubes (SWNTs) are currently being revealed through the isolation of enantiomers (4–6). For instance, chiroptical properties including circular dichroism (CD) have been reported, and an improved purity of the specimens recently allowed for the proposal of an analytic correlation of the CD spectra with cylinder helicity through corrected electric transition dipole moments (ETDMs) (7). Although the nondiscrete nature of SWNTs intrinsically precludes definite conclusions on the structural origins of chirality-related properties, relevant information derived from discrete, segmental molecular models of SWNTs can deepen such a structural understanding. We have previously reported the synthesis of segmental molecules of helical SWNTs with stereochemical rigidity and revealed a few important features of these cylindrical molecules possessing chiral isomeric structures (8, 9) (Fig. 1). In this study, we investigated properties associated with the helicity of the nanoscale cylinders and found unique roles in their assembly and optical properties. The helicity dictated the chiral packings of the cylinders and resulted in the assembly of double-helical, spiral-stair packings in the crystal. In solution, the cylinder helicity played a determinant role to generate large magnetic transition dipole moments (MTDMs), which led to observations of anomalous dissymmetry factors with CD and circular polarized luminescence (CPL) spectroscopy (10). Notably, the nanoscale cylinders afforded an anomalously large luminescence dissymmetry factor (g_lum) for metal-free, organic molecules. The recorded g_lum value reached 10⁻¹, which is one order of magnitude greater than those of previously reported molecules (11).

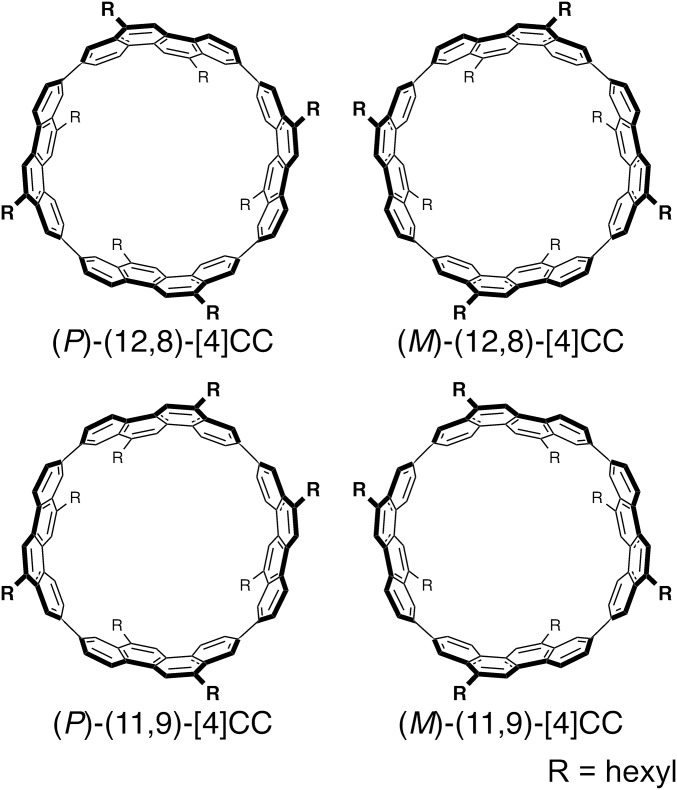
Fig. 1.

Chiral cylindrical molecules.

Results and Discussion

Chiral Intertwined Spirals of Helical Cylinders.

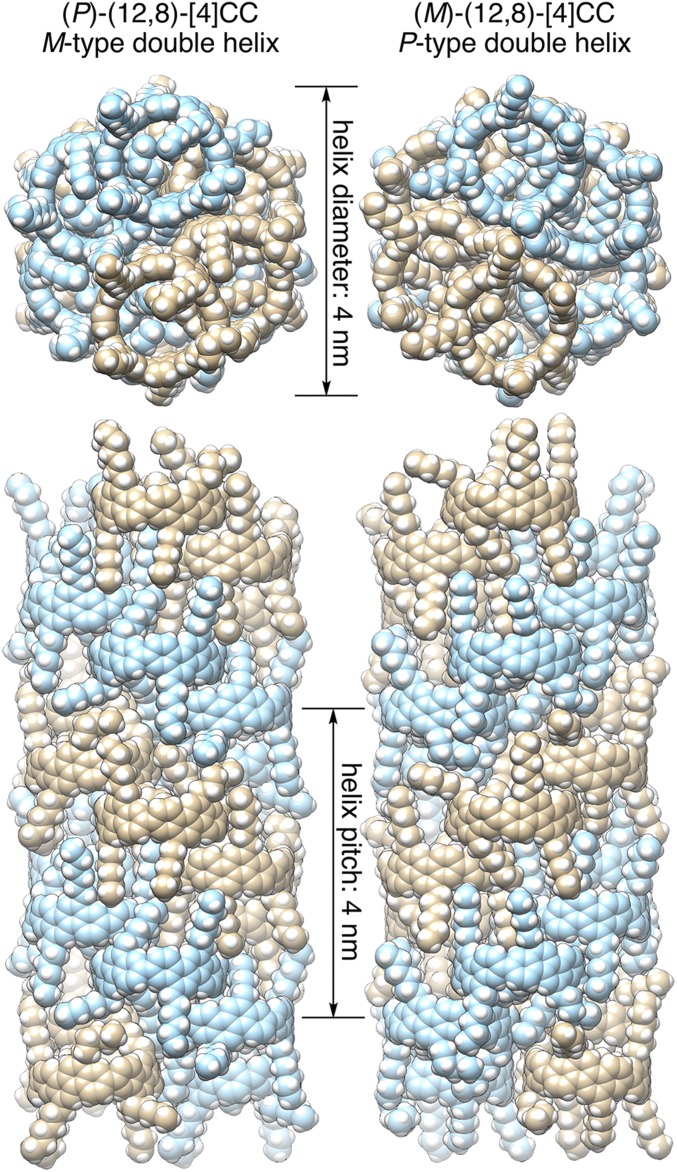
The cylindrical, segmental SWNT molecule used in this study was [4]cyclo-2,8-chrysenylene ([4]CC) (8, 12) (Fig. 1), and the effects of cylinder helicity on the crystal packings were investigated with (12,8) isomers. A single crystal was grown with an enantiomerically pure isomer, (P)-(12,8)-[4]CC, and was subjected to crystallographic analysis. As was the case with a racemate of (P)/(M) isomers (13), a thread-in-bead entanglement between alkyl chains and cylinders was observed as a basic motif in the crystal packings of the (P)-(12,8)-[4]CC molecules (SI Appendix, Fig. S1). The thread-in-bead entanglement of the (P)/(M) racemate resulted in a 2D, brick-wall-like network of molecules in an achiral Ccca space group (13), but the same thread-in-bead entanglement of the (P) isomer resulted in a twisted orientation of adjacent stacks to form a chiral 3D network of molecules. The space group of this (P)-(12,8)-[4]CC crystal was hexagonal P6₅, which revealed the presence of helical chirality in the crystal packings. Unexpectedly, the nanoscale cylinders formed two spiral-staircase stacks in the crystal, creating an intertwined double helix of the helical cylinders (Fig. 2). A single turn of the double helix was composed of six cylinders, which formed a left-handed, M-type helix with a pitch of 4 nm. The van der Waals diameter of the double helix measured 4 nm. A single crystal of the enantiomer, (M)-(12,8)-[4]CC, was also obtained as an enantiomorphic crystal with a P6₁ space group. Although structural differences such as molecular orientations, chain conformations, and solvent structures were present, the overall packing of the (M) isomer mirrored that of the (P) isomer, resulting in a right-handed, P-type double helix. This result showed that the helicity of the double-helix assembly in the crystals was dictated by the helicity of the nanoscale cylinders. A helical assembly of molecules is often observed with proteins, such as actin filaments, that are assembled by sophisticated hydrogen-bonding networks (14), and it is interesting to find that pure, nondirectional van der Waals interactions between hydrogen and carbon atoms can induce such chiral double-helical assemblies (15). The transmission of molecular chirality to nanoscale crystalline chirality has been demonstrated, which may be important for the development of nanocarbon materials in future (16).

Fig. 2.

Crystal structures of (P)- and (M)-(12,8)-[4]CC. The two intertwined spirals are shown in different colors. Disordered structures of one substituent with a minor population and solvent molecules were omitted for clarity.

CD.

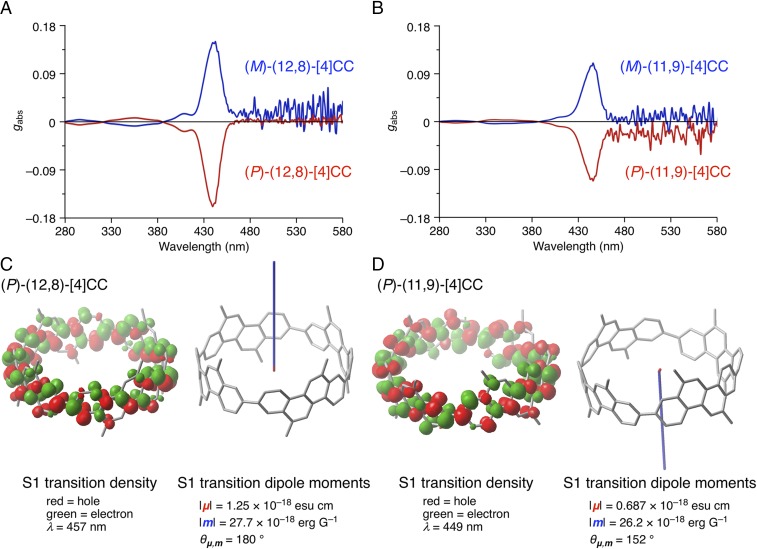
Interesting effects arising from cylinder helicity were observed in the solution-phase chiroptical measurements. Considering recent advances in the study of chiral SWNT congeners (6, 7), we carefully investigated the CD spectra of our system. Kataura and coworkers (6) recently succeeded in obtaining high-purity chiral SWNT specimens and investigating CD spectra in depth. With these spectra, an analytic and numerical procedure to predict CD spectra from a given enantiomeric cylinder was also proposed (7). In short, the analytic method used the corrected ETDM to predict the CD signals. Independently, in our previous studies with segmental [4]CC cylinders, we adopted time-dependent density-functional theory (TDDFT) to correlate CD spectra with enantiomeric structures (8), which was later confirmed to be valid by experimentally determined crystal structures of enantiomers (13). In this study, we further investigated the origin of the representative CD signals using theoretical analyses and observed several unique chiroptical features in nanoscale cylinders. Experimentally, CD spectra of (P)- and (M)-(12,8)-[4]CC in toluene showed exceptionally large absorption dissymmetry factors (10), g_abs = −0.167 and +0.166, at 443 nm, respectively (Fig. 3A). The CD spectra of another set of enantiomers, (P)- and (M)-(11,9)-[4]CC, also showed large g_abs values of −0.111 and +0.110 at 446 nm (Fig. 3B). These |g_abs| values are extraordinarily large, as |g_abs| values of 10⁻³ are regarded as large for molecular entities (17).

Fig. 3.

Chiroptical properties of cylindrical molecules. (A) CD spectra of (P)- and (M)-(12,8)-[4]CC in toluene at 25 °C. (B) CD spectra of (P)- and (M)-(11,9)-[4]CC in toluene at 25 °C. (C) Transition density (Left) and transition dipole moments (Right) of methyl-substituted (P)-(12,8)-[4]CC. In the transition density isosurface, hole (green) and electron (red) distributions are shown at an isovalue of 0.0004. For the dipole moments, the ETDM vector is shown in red, and the MTDM vector is shown in blue. (D) Transition density (Left) and transition dipole moments (Right) of the methyl-substituted (P)-(11,9)-[4]CC. In the transition density isosurface, hole (green) and electron (red) distributions are shown at an isovalue of 0.0004. For the dipole moments, the ETDM vector is shown in red, and the MTDM vector is shown in blue.

Large Magnetic Dipole Transition Moments in Cylinders.

To deduce the origin of these anomalously large |g_abs| values, we performed TDDFT analyses with methyl-substituted [4]CC. We observed no concentration dependency of the CD/CPL spectra (SI Appendix, Fig. S9), which showed that the spectra were ascribed to monomeric, molecularly dispersed species in solution (18). The absence of assembly in solution was also indicated in previous studies of the nanoscale cylinders with NMR spectroscopy (15, 19, 20). The largest |g_abs| of (P)-(12,8)-[4]CC corresponded to the first S1 transition, which was predominantly ascribed to a single-electron excitation from the highest occupied molecular orbital to the lowest unoccupied molecular orbital with a coefficient of 0.69 (SI Appendix, Fig. S3 and Table S1). Details of the S1 transition were further analyzed using the transition density and transition dipole moments (21, 22). The transition density of the S1 excitation is shown in Fig. 3C. The red isosurface shows the “hole” distributions where the single electron leaves upon excitation, and the green isosurface shows the “electron” distributions where the excited electron goes after the excitation. Because this electronic transition occurs over the cylinder, the total ETDM (µ) was parallel to the cylinder axis (z axis, SI Appendix, Fig. S5). The cancellation of the ETDM in the other directions, i.e., the X- and Y components (µ_X and µ_Y), can be visually understood by the breakdown analysis of the ETDM density shown in SI Appendix, Fig. S5. Thus, the µ_X and µ_Y moments were distributed similarly on opposite sides of the cylinder’s wall but faced opposite directions (23) (blue vs. green in SI Appendix, Fig. S5). The cylindrical π-systems exhibited even more important features in the analysis. As shown in Fig. 3C, a large MTDM (m) was parallel to the cylinder axis. In principle, the MTDM is generated by the angular momentum operator due to single-electron movement during excitation (24) and therefore is a vector product of the distance vector r and the ETDM µ: m ∝ r × µ (25–27). The large, Z-oriented m of the present nanoscale cylinder was therefore generated by the local µ-vectors, distributed over the whole cylinder, together with the r vectors, which radiated toward the outside of the large, nanoscale molecule. The breakdown of the topological analysis of the MTDM is shown in SI Appendix, Fig. S6. Finally, these two transition dipole moments, µ and m, are oppositely oriented (i.e., with an angle of 180°), resulting in a large rotatory strength (R), which is defined as R = |µ|•|m|•cosθ. The breakdown analyses of the (P)-(11,9)-isomer also revealed a dominant contribution from m (Fig. 3D), which was again generated by the cylindrical conjugated systems (SI Appendix, Figs. S7 and S8). The g value is then derived as a combination of |m| and |µ| in a relationship of g ∝ (|m|/|µ|)•cosθ (28). Thus, unlike conventional organic molecules with negligible MTDM contributions (22, 24, 29), π-conjugated systems on nanoscale cylinders achieve extraordinarily large |g_abs| values due to unique MTDM along the cylinder axis. We believe that these chiroptical characteristics and dominant MTDM should also be observed in other cylindrical entities, including SWNT congeners (20), and that the recently reported numerical correlation method that solely adopts ETDM without consideration of MTDM should be interpreted with caution (6, 7).

CPL, Large |g_lum| Value.

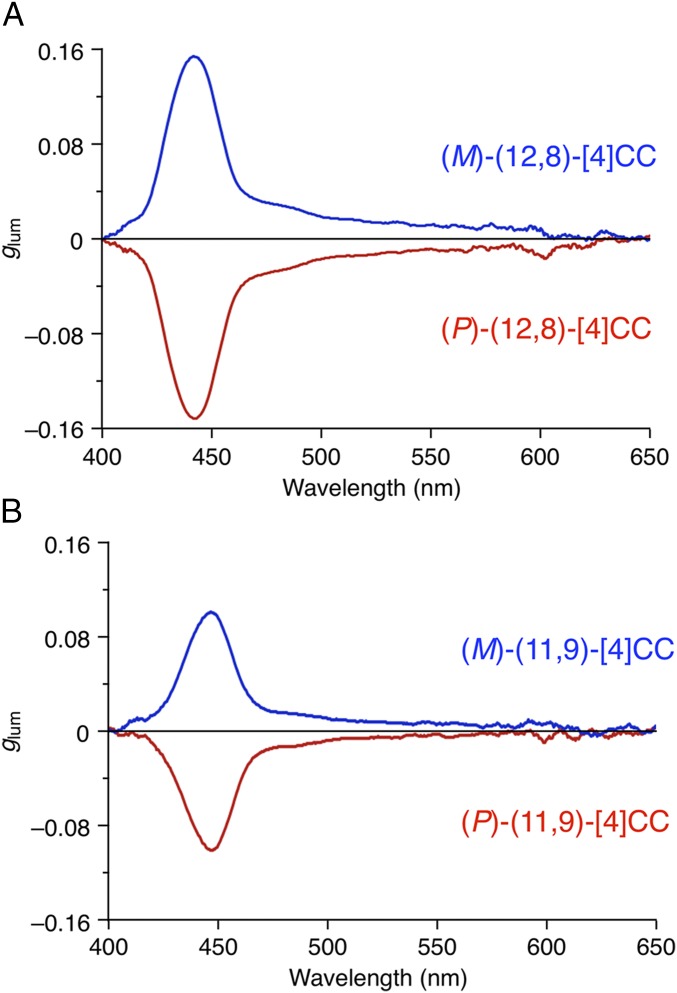
Finally, the helicity of the nanoscale cylinders resulted in a large luminescence dissymmetry factor g_lum with organic molecules. The intense photoluminescence (PL) of (P)-(12,8)-[4]CC was quantified, yielding a significantly high quantum yield of ϕ_PL = 0.80 in toluene, which prompted us to measure its CPL spectra (28). Achieving both a high ϕ_PL yield and a large g_lum factor is ideal for practical photonics applications such as CPL, and extensive efforts are currently being devoted to developing small molecules (11). However, achieving these two requirements simultaneously has been proven difficult. To the best of our knowledge, the highest |g_lum| value for organic molecules (0.035) was recorded with a chiral ketone derivative with a ϕ_PL = ∼0.001 (30). A comparable |g_lum| value of 0.032 was reported for a [6]helicene derivative with a much-improved yet moderate ϕ_PL yield of 0.296 (31). A significantly high ϕ_PL of 0.88 was achieved with a binaphthyl derivative, albeit with an inferior |g_lum| value of 0.003 (32). In this study of cylindrical molecules, an extraordinarily large g_lum value of −0.152 was recorded at 443 nm with (P)-(12,8)-[4]CC (Fig. 4) and, intriguingly, with a high ϕ_PL value, which suggests that organic molecules could rival lanthanide complexes in CPL performances (33). The other chiral isomers, (P)- and (M)-(11,9)-[4]CC, also achieved large g_lum values of −0.101 and +0.099, respectively, with a high ϕ_PL yield of 0.74.

Fig. 4.

CPL spectra in toluene. (A) (P)- and (M)-(12,8)-[4]CC. (B) (P)- and (M)-(11,9)-[4]CC.

Conclusions

Chirality originating solely from the anomalous arrangement of sp²-carbon networks gave rise to unique properties in nanoscale cylinders. Shape recognitions, driven only by van der Waals interactions, resulted in an intertwined, double-helix formation of the cylinders (15), and the helicity of the spiral stacks was dictated by the helicity of the cylinders. The occurrence of an extremely large |g_lum| value for organic molecules reveals an interesting design principle for CPL emitters: The π-conjugated systems distributed over a nanoscale cylinder possess an ideal topology for electric transitions that enhance MTDM and, consequently, dramatically increase the rotatory strength through R = |µ|•|m|•cosθ. Achieving large |m| without risking |µ| has been recognized as an ideal design for CPL emitters but also has been regarded as a paradoxical requirement for organic molecules (11, 27). This study unequivocally demonstrates that rigid nanoscale cylinders, including SWNT congeners, are promising CPL emitters that can fulfill such apparently paradoxical requirements. Taking advantage of other functional macrocylic molecules (34–36), we are currently investigating device applications of these hydrocarbon cylinders (11). Combinations of cylinders with aggregate/assembly-induced CPL enhancements in the solid state may be of practical interest (37).

Methods

Synthesis of [4]CC.

Compounds were synthesized, isolated, and characterized by a method reported in the literature (8).

Crystallographic Analysis.

Single crystals of (P)- and (M)-(12,8)-[4]CC were grown at 3 °C from a solution in CH₂Cl₂:methanol (1:1; 0.5 mg/mL) after filtration through a membrane filter (0.45-µm pore). A microseeding method effectively improved the reproducibility and crystal quality. X-ray diffraction analysis of single crystals was conducted on a Rigaku XtaLAB P200 diffractometer with multilayer mirror monochromated Cu_Κα radiation (λ = 1.54187) at −180 °C. A single crystal was mounted on a thin polymer tip with a cryoprotectant oil and frozen at −180 °C via flash-cooling. The collected diffraction data were processed with the CrysAlisPro software program (38). The structures were solved using a direct method in the SHELXD software program (39) and refined using a full-matrix least-squares method on F² in the SHELX program suite (36) running on the Yadokari-XG 2009 software program (40) and CrystalStructure (41). In the refinements, disordered alkyl groups and solvent molecules were restrained by SIMU and DFIX. The nonhydrogen atoms were analyzed anisotropically, and hydrogen atoms were input at calculated positions and refined with a riding model. Merohedral twinning was refined by TWIN. Cambridge Crystallographic Data Centre (CCDC) accession codes 1570803 and 1570804 contain the supplementary crystallographic data for this paper (SI Appendix, Fig. S2). These data can be obtained free of charge from the CCDC.

CD Spectroscopy.

CD spectroscopy was performed on JASCO J-1500 at 25 °C with a toluene solution. The error range of the CD measurement is ±5% (42), and the |g_abs| values of enantiomers can be considered identical within the error range. Measurements were performed with (P)-(12,8)-, (M)-(12,8)-, (P)-(11,9)-, and (M)-(11,9) isomers at the concentrations of 6.91 × 10⁻⁶, 6.13 × 10⁻⁶, 5.27 × 10⁻⁶ and 5.05 × 10⁻⁶ M, respectively.

Density-Functional Theory Calculations.

Theoretical calculations were performed at the density-functional theory (DFT) level with the B3LYP functional, the gradient correction of the exchange functional by Becke (43, 44) and the correlation functional by Lee et al. (45) on Gaussian 09 (46). The 6–31G(d,p) split valence plus polarization basis set was used (47–51). TDDFT calculations were performed for the first 30 singlet–singlet transitions with an additional keyword of IOP(9/40 = 2). Spectral analysis with the B3LYP functional agreed well with the ordering of the states in the experimental results but underestimated the excitation energy, affording slightly redshifted theoretical spectra (8, 52) (SI Appendix, Figs. S3 and S4 and Tables S1 and S2). TDDFT calculations at solvated states with polarizable continuum models were also performed, but we did not observe dramatic improvements particularly in the S1 transition of current interest (SI Appendix, Fig. S10 and Tables S3 and S4). Other sophisticated solvation models might improve minor discrepancies, which may provide interesting subjects for state-of-the-art theoretical studies (53, 54). DFT data were visualized and analyzed with the GaussView program.

Analyses of Transitions.

Transition density and transition dipole moments were generated through analyses of the DFT data with Multiwfn (19). The transition density was visualized with GaussView (Fig. 3), and the breakdown data of transition dipole moments were visualized with Multiwfn (SI Appendix, Figs. S5–S8).

CPL Spectroscopy.

CPL spectroscopy was performed on JASCO CPL-300. The error range, ±5%, is similar to that of the CD spectra. A solution of each specimen was prepared in toluene and degassed by a freeze–pump–thaw method before the measurements. The absolute quantum yield of the phosphorescence was separately measured in the same medium using a Hamamatsu PL quantum yield spectrometer C9920-02G. Measurements were performed with (P)-(12,8)-, (M)-(12,8)-, (P)-(11,9)-, and (M)-(11,9) isomers at the concentrations of 6.77 × 10⁻⁶, 4.90 × 10⁻⁶, 4.67 × 10⁻⁶, and 5.05 × 10⁻⁶ M, respectively.