Kinematics of flagellar swimming in Euglena gracilis: Helical trajectories and flagellar shapes

Significance

Active flagella provide the propulsion mechanism for a large variety of swimming eukaryotic microorganisms, from protists to sperm cells. Planar and helical beating patterns of these structures are recurrent and widely studied. The fast spinning motion of the locomotory flagellum of the alga Euglena gracilis constitutes a remarkable exception to these patterns. We report a quantitative description of the 3D flagellar beating in swimming E. gracilis. Given their complexity, these shapes cannot be directly imaged with current microscopy techniques. We show how to overcome these limitations by developing a method to reconstruct in full the 3D kinematics of the cell from conventional 2D microscopy images, based on the exact characterization of the helical motion of the cell body.

Abstract

The flagellar swimming of euglenids, which are propelled by a single anterior flagellum, is characterized by a generalized helical motion. The 3D nature of this swimming motion, which lacks some of the symmetries enjoyed by more common model systems, and the complex flagellar beating shapes that power it make its quantitative description challenging. In this work, we provide a quantitative, 3D, highly resolved reconstruction of the swimming trajectories and flagellar shapes of specimens of Euglena gracilis. We achieved this task by using high-speed 2D image recordings taken with a conventional inverted microscope combined with a precise characterization of the helical motion of the cell body to lift the 2D data to 3D trajectories. The propulsion mechanism is discussed. Our results constitute a basis for future biophysical research on a relatively unexplored type of eukaryotic flagellar movement.

Euglenids have long been used as model organisms for a broad range of biological studies, possibly because of their unique taxonomic position, which shows both animal-like and plant-like characteristics (1). Among the first microorganisms to be studied under a microscope (by van Leeuwenhoek, in the late 1600s), they still occupy center stage in contemporary research (2, 3), with new monographs soon to appear (4).

Studies on euglenid motility have recently focused on metaboly (5, 6), while flagellar swimming remains poorly investigated and understood, at least from the quantitative point of view. Qualitative observations have been made about the wiggling motion of the euglenid flagellum. Its characteristic movement has been dubbed “spinning lasso” or “figure eight.” A quantitative description of this peculiar movement, whose primary source of activation is the “9 + 2” axoneme common to most eukaryotes (7), is still lacking. Reconstruction of the flagellar motion and actuation of euglenids faces a major challenge: capturing the complex 3D configurations of the flagellum, which evades the inquiry of current microscopy techniques. Planar beats of flagella, easier to capture from image data, are otherwise widely studied (8–11).

A typical specimen of Euglena gracilis (Fig. 1A) is around $50\mathrm{\mu }$m in length. The flagellum they use for locomotion, which is slightly shorter than its body, beats by spinning at $\sim 40$ Hz in close proximity to the cell body (Movie S1). As for most flagellates, the swimming motion of E. gracilis is rototraslatory and inherently 3D. Whereas 3D tracking of swimming microorganisms is a long-standing experimental research field (12), and still developing, none of the current techniques is capable of capturing the flagellar swimming of euglenids in full detail. For example, stereomatching has been used to track euglenids and other protists (13, 14), but it lacks the spatial resolution to resolve the motion of both body and flagellum (the whole swimmer is a point). Confocal microscopy, a powerful tool for 3D imaging, does not have sufficient time resolution (15) to resolve flagellar beating. Digital holographic microscopy is capable of high resolution in both time and space (16), and it gives the possibility of multiple simultaneous tracking for high-throughput statistics (17, 18). However, to date it has been successful only up to the 3D reconstruction of trajectories and pitch of particle-like objects with a prolate shape (19) and of the helical beating of an isolated flagellar structure (20). The close proximity of Euglena’s flagellum to the cell body makes the simultaneous reconstruction of cell body and flagellar shape a challenge, even for this technique.

Fig. 1.

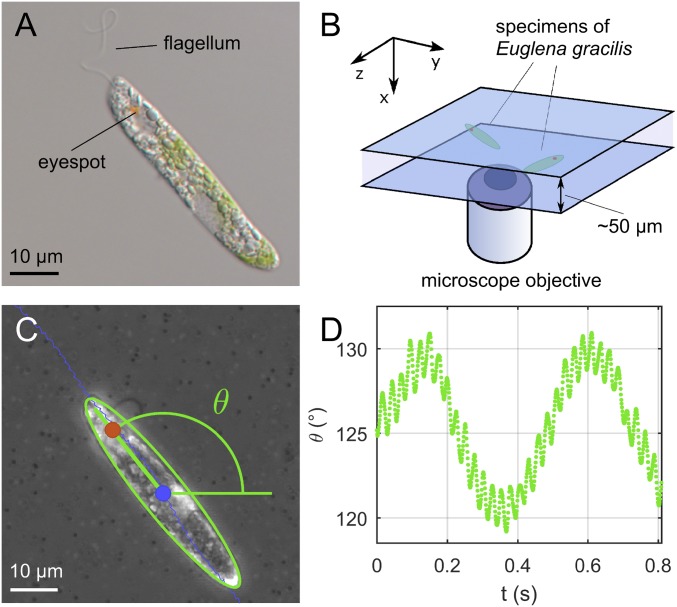
(A) Micrograph of a specimen of E. gracilis. The anterior flagellum is visible, together with the eyespot, a pigmented organelle that is part of the photosensory apparatus of the cell. (B) Schematic of the experimental setup: Euglenids swim between two microscope slides separated by ∼50 $\mathrm{\mu }$m. (C) Example of image segmentation results from high-speed videos: Position of the geometric body center (blue), position of the eyespot (red), and body orientation (green) are measured. (D) Projected body orientation $\theta$ as a function of time: A large amplitude oscillation is modulated by a smaller oscillation at flagellar beating time scale.

We are able to recover the flagellar kinematics of E. gracilis through a reconstruction strategy based on simple assumptions and on the physics governing the motion of the system. Our analysis is based on standard microscopy image sequences, recorded at high frame rate. This guarantees the appropriate spatiotemporal resolution (even though from a 2D perspective). We restrict our analysis to the case in which the Euglena flagellar beating is, to a good approximation, periodic in time (hence, no lateral steering).

In this case, the physics governing the system (low Reynolds number hydrodynamics) imposes restrictions on which trajectories and rotations of the cell are actually possible.

Swimming at Low Reynolds Number with Periodic Beats

Helical swimming trajectories are ubiquitous among microorganisms (21). Simple physical arguments can explain the prevalence of helical trajectories, as suggested in the seminal papers (22, 23). The homogeneity and isotropy of fluid–body hydrodynamic interactions, which hold true for a body isolated from boundaries or other objects, play a crucial role. In this case, the periodic beating of a swimmer results in periodic body frame components of its translational and angular velocities. See Supporting Information, section 1 for details. The time evolution of the center $𝐜$ and of the rotation $𝐑$ of the swimmer body frame are obtained, via time integration, from these periodic velocities (Eq. S7). The general solution of the swimming problem driven by periodic beats, with period $T_b$, is as follows. The position of the body center $𝐜(t)$ evolves in time according to

$$𝐜(t)={𝐜}_h(t)+{𝐑}_{𝐧}(\omega t){\stackrel{\sim }{𝐜}}_b(t)$$ [1]

while the rotation of the body is described by

$$𝐑(t)={𝐑}_{𝐧}(\omega t){\stackrel{\sim }{𝐑}}_b(t).$$ [2]

In the previous two formulas, the closed curve ${\stackrel{\sim }{𝐜}}_b$ and the rotation ${\stackrel{\sim }{𝐑}}_b$ are periodic functions, with period $T_b$, ${𝐑}_{𝐧}(\omega t)$ is a rotation with axis $𝐧$ and angle $\omega t$, and ${𝐜}_h$ describes a circular helix with axis $𝐧$ that closes a turn every $T=2\pi /|\omega |$ seconds. The details of the derivation of Eqs. 1 and 2 are given in the Supporting Information, section 1.

Two time scales emerge in defining the kinematics: the flagellar beating period $T_b$ and the time $T$ needed to close one turn of the smooth circular helix ${𝐜}_h$. In the swimming of Euglena, as for most microorganism, $T$ is much larger then $T_b$: It takes many beats to close a turn. The general trajectory can be seen as a smooth—and “slow”—helix perturbed by $T_b$-periodic “fast” swirls. Similarly, the orientation of the body can be seen as a slow rotation with constant angular velocity around $𝐧$, perturbed by fast $T_b$-periodic jerks.

Translational and rotational motions are coupled. For the sake of argument, suppose that $T=N{T}_b$ is a multiple of $T_b$. Then, fix a phase $\tau$ within one beat and consider times $t_k=\tau +k{T}_b$. The center moves according to $𝐜(t_k)$, and these points lie on a circular helix of axis $𝐧$ (a perturbed version of ${𝐜}_h$: a helix with the same pitch, but possibly different radius). Meanwhile, the body of the swimmer keeps rotating around the axis $𝐧$, each time by an angle $\omega T/N$. It follows that after $N$ beats, exactly when one turn of the helix is closed, the swimmer ends up in the same orientation (Movie S2).

Results from recent studies on 3D helical trajectories of microswimmers can be cast within the predictions of this model. Observed “chiral ribbon” trajectories in human sperm motility (18) fall precisely in the general expression given by Eq. 1. In the chiral ribbon case, the periodic ${\stackrel{\sim }{𝐜}}_b$ traces a line segment, a special and degenerate case of our more general ${\stackrel{\sim }{𝐜}}_b$, which describes a closed orbit. Rather than lying on a ribbon, the resulting Euglena’s trajectories are drawn on a “helically shaped tube” (a tubular neighborhood of the “backbone” helix ${𝐜}_h$). We emphasize that Eqs. 1 and 2 provide the general characterization for any motion driven by the periodic beating of a propulsive appendage. Special cases, where the backbone curve ${𝐜}_h$ of the trajectory in Eq. 1 is either a planar curve, or a straight line, follow when the rotation axis $𝐧$ is either orthogonal to the translation in one beat (as in the planar trajectories of sperm cells, when propelled by planar beating of their tails) or parallel to it (as in the case of bacteria propelled by rotating helical flagella).

Experimental Observations

We observed specimens of E. gracilis swimming in a water solution while confined between two microscope slides (Fig. 1B). The spacing between the slides was measured by focusing control beads attached to the respective walls (24) and was found to range between 40 and 60 $\mathrm{\mu }$m. The control beads were also used to check that the fluid was at rest during the experiments. We acquired high-speed micrographs of several cells at 1,000 frames per second (fps), selecting only specimens swimming with a regular, periodic beat (Fig. 1C). More details about the experimental setup can be found in Materials and Methods.

In these conditions, for time scales larger than the flagellar beat, the swimming trajectories follow a characteristic sinusoidal path, while the cell body undergoes an apparent “swinging” movement with the same period. At smaller time scales, finer features of the trajectories can be observed, together with a higher-frequency “swinging” motion of the cell body (Movie S1). The latter becomes evident by plotting the projected body orientation as a function of time (Fig. 1D): A fast oscillation with amplitude $\sim 1°$ and period $\sim 25$ ms is superimposed on a slower oscillation with amplitude $\sim 5°$ and period $\sim 0.5$ s. This is the typical footprint of a helical swimming motion projected on a 2D plane.

Cell Body Motion Reconstruction

Eqs. 1 and 2 can be applied to recover 3D kinematics from 2D image sequences. This can be achieved by fitting 2D projections of the 3D kinematics imposed by theory to experimental data. A similar idea has been pursued in refs. 25–27. In the following, we outline the main steps of our procedure.

We model Euglena’s body as an ellipsoid (in our experiments, the surface of the cell does not visibly deform during swimming). We consider the swimmer reference frame located at the geometric center of the body, with axes aligned with the symmetry axes of the ellipsoid. With optical aberrations and out-of-focus effects being negligible, microscopy images of the cell body can be assimilated to projections of the ellipsoid on the focal plane. Using image segmentation, we extract three relevant kinematic quantities from these projections (Fig. 1C): the projection $\mathrm{\Pi }𝐜$ of the body center (Fig. 2E), the projection $\mathrm{\Pi }𝐞$ of the eyespot position $𝐞$ (Fig. 2F), and the angle $\theta$, formed by the projection of the major axis of the ellipsoid with the horizontal (Fig. 2G).

Fig. 2.

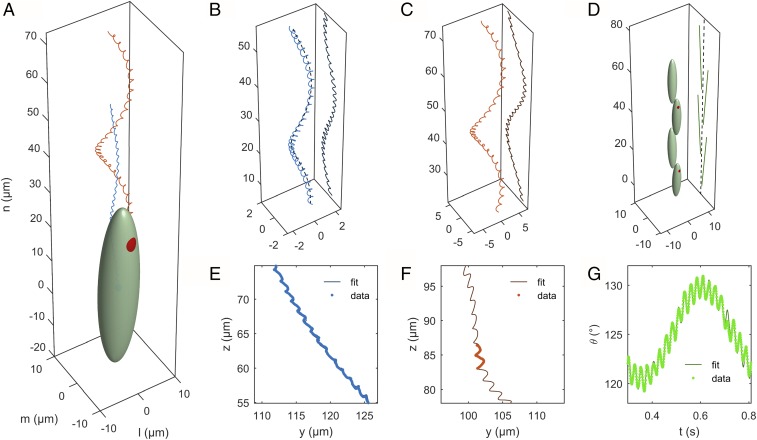
(A) Three-dimensional representation of Euglena’s body, with trajectories of the body center (blue) and of the eyespot (red) reconstructed from the fitting procedure. The reference axes $𝐥$, $𝐦$, and $𝐧$ are chosen such that $𝐧$ is the axis of the helical trajectory. (B) Projection of the centroid trajectory $\mathrm{\Pi }𝐜$ and (C) of the eyespot trajectory $\mathrm{\Pi }𝐞$ on the focal plane. (D) Projection of the major axis of the cell body $\mathrm{\Pi }𝐤=(\cos \theta ,\sin \theta )$ on the focal plane. (E–G) Comparison between experimental measurements and model best-fitting curves for the quantities $\mathrm{\Pi }𝐜$, $\mathrm{\Pi }𝐞$, and $\theta$. Note that the experimental data for $\mathrm{\Pi }𝐞$ are available only when the eyespot is visible.

We then consider the restrictions imposed by the theoretical model and obtain formulas for the observable quantities $\mathrm{\Pi }𝐜$, $\mathrm{\Pi }𝐞$, and $\theta$. They depend on a list of parameters $\xi$, which include, among others, the beating period $T_b$, the Fourier coefficients of the $T_b$-periodic functions in Eqs. 1 and 2, and the geometric parameters of the circular helix ${𝐜}_h$. For the full list $\xi$ of parameters, and their detailed expressions, we refer the reader to Supporting Information, section 2.

We recover the values of the parameters $\xi$ by finding the least-squares fit between theoretical observables and measured experimental data. That is, we find $\xi$ that minimizes

$$\begin{array}{c}\hfill \sum _j{\parallel \mathrm{\Pi }𝐜(\xi ,t_j^c)-\mathrm{\Pi }{𝐜}^{\ast }(t_j^c)\parallel }^2,\hfill \\ \hfill \sum _j{\parallel \mathrm{\Pi }𝐞(\xi ,t_j^e)-\mathrm{\Pi }{𝐞}^{\ast }(t_j^e)\parallel }^2,\hspace{0.17em}\text{and}\hspace{0.17em}\sum _j{\left|\theta (\xi ,t_j^{\theta })-{\theta }^{\ast }(t_j^{\theta })\right|}^2,\hfill \end{array}$$

where the $\xi$-dependent functions are the expression given by the theory for $\mathrm{\Pi }𝐜$, $\mathrm{\Pi }𝐞$, and $\theta$, while experimental data are denoted with an asterisk. Sums are taken over the time instants where tracking data are available.

The set of parameters $\xi$ so obtained is sufficient to determine the 3D expression for $𝐜$ and $𝐑$ as given by Eqs. 1 and 2, thus allowing us to recover the full 3D time evolution of the reference frame of the swimmer (Fig. 2A).

The fact that $\mathrm{\Pi }𝐜$, $\mathrm{\Pi }𝐞$, and $\theta$ contain all of the information needed to recover the 3D kinematics becomes evident when going through the details of the theory, for which we refer to Supporting Information, section 2. We mention here the key ideas behind this. The time evolution of $\mathrm{\Pi }𝐜$ alone is sufficient to recover the 3D trajectory of $𝐜$ (Fig. 2B). The “lift” $\mathrm{\Pi }𝐜\to 𝐜$ is possible thanks to the rotational symmetry imposed by Eq. 1. Similarly, the angle $\theta$ is sufficient to lift $\mathrm{\Pi }𝐤\to 𝐤$ the projection $\mathrm{\Pi }𝐤=(\cos \theta ,\sin \theta )$ of the unit vector $𝐤$ that determines the major symmetry axis of the cell body in 3D (Fig. 2D). The extra datum $\mathrm{\Pi }𝐞$ contains the information about the cell body rotation around $𝐤$. Together with $\theta$, the eyespot projection allows us then to recover the whole swimmer moving frame, that is, $(\theta ,\hspace{0.17em}\mathrm{\Pi }𝐞)\to 𝐑$.

Flagellar Shapes

We reconstruct the shapes of the flagellum, that is, the time history of a 3D deformable curve, from the knowledge of its (partial) projections given by microscopy images. The reconstruction consists of finding a curve minimizing a “projection error,” which quantifies the distance between experimental points and projections of the curve. We describe the method in more detail in the following.

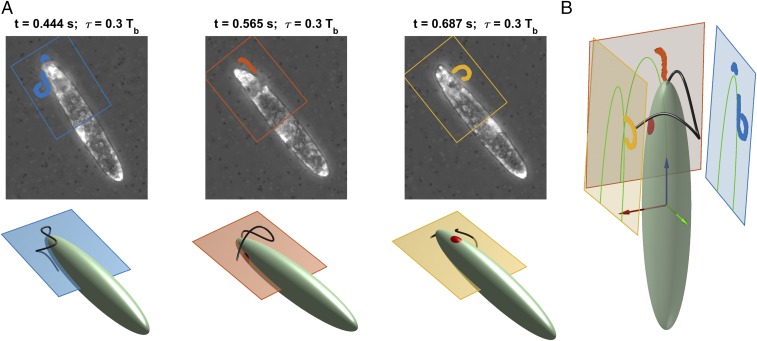
Fix a phase $\tau$ between 0 and $T_b$ (determined earlier) and consider images at times $t_k=\tau +k{T}_b$. At these instants, assuming beat periodicity, the flagellum lies in the same configuration with respect to the body frame. As the Euglena rotates, for different $t_k$ a different view of this configuration appears on the focal plane. The results of the previous section allow us to locate at every instant the focal plane with respect to the body frame. Image segmentation gives us a set of points where the flagellum projection on each plane must lie (Fig. 3A).

Fig. 3.

Stereographic reconstruction of the flagellum. (A) Fixed a phase $\tau$ between 0 and the beating period $T_b$, images taken at times $t_k=\tau +k{T}_b$, show the flagellum in the same configuration with respect to the cell body, but from different viewpoints (Top). At each instant the Euglena’s position and orientation with respect to the focal plane are known from 3D cell body motion reconstruction results (Bottom). (B) The flagellum is recovered by finding the 3D curve whose projections (on the respective planes) are the closest possible to the experimental projections.

We are able to locate $N_{pl}$ planes (11 to 19, depending on the experiment) together with a set of projection points $P_j^{\ast }$ for each plane $j=1,2,\dots ,N_{pl}$. The flagellum is recovered by finding the 3D curve whose projections are the closest possible to these sets of experimental points on the respective planes (Fig. 3B and Movie S3). The “closeness” of a curve $𝐫$ to the experimental points is determined by the projection error

$$Err(𝐫)=\sum _{j=1}^{N_{pl}}\sum _{{𝐩}^{\ast }\in P_j^{\ast }}\text{dist}{\left({𝐩}^{\ast },{\mathrm{\Pi }}_j𝐫\right)}^2,$$ [3]

where we denoted by ${\mathrm{\Pi }}_j$ the projection on the $j\text{th}$ plane. In the previous equation, the distance $\text{dist}\left({𝐩}^{\ast },{\mathrm{\Pi }}_j𝐫\right)$ between a point ${𝐩}^{\ast }$ and the projection ${\mathrm{\Pi }}_j𝐫$ is defined as the minimum with respect to the curve parameter $s$ of $\parallel {𝐩}^{\ast }-{\mathrm{\Pi }}_j𝐫(s)\parallel$. We use interpolating cubic spline curves

$$𝐫=Sp({𝐱}_1,\dots ,{𝐱}_{N_{sp}})$$ [4]

to parametrize the flagellum. The interpolated points ${𝐱}_1,\dots ,{𝐱}_{N_{sp}}$ are chosen as to minimize the projection error. Substituting Eq. 4 in Eq. 3 leads to the expression to be minimized. More details on the algorithmic implementation of the problem are given in Supporting Information, section 3.

Results

Motion Characteristics.

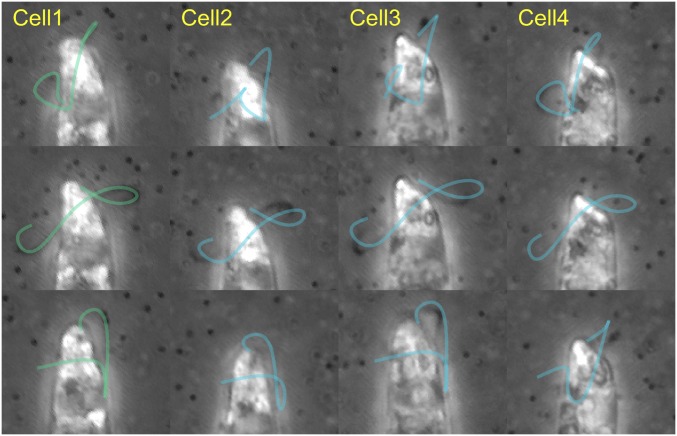
We applied our technique to multiple sets of experimental data, obtaining excellent agreement between experiments and theory (Fig. 2 E and F). We report here on the reconstruction of trajectories and flagellar shapes for one representative cell. Results for other cells are reported in Supporting Information, section 4, with comments on the variability of the results between different cells, and on the quantitative evaluation of the uncertainties of our reconstruction procedures. In particular (Fig. 4 and Movie S4), the history of flagellar shapes of our representative cell matches well with those of different specimens, suggesting the existence of a distinctive Euglena beat style, as described below.

Fig. 4.

Grid of experimental images from four different swimming cells (columns) taken at different times (rows). The reconstructed time history of flagellar shapes from cell 1 (green, first column), conveniently scaled in both space and time, is attached to the other cells’ bodies (blue). A good overlap between the projections of the attached flagella and the experimental images emerges (see Movie S4 and Supporting Information, section 4 for more details). This shows that the flagellar beat of cell 1, presented here in the main text, is a valid representative of a common beating style.

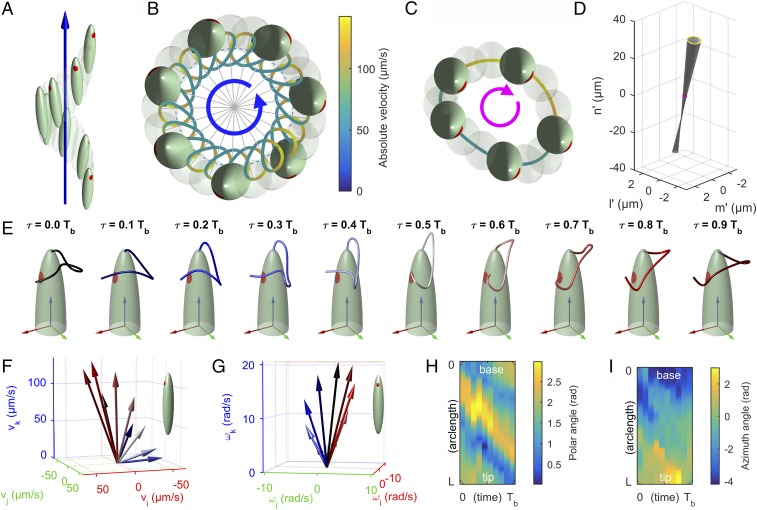
A side view of the reconstructed swimming kinematics is shown in Fig. 5A. For visualization purposes, the Euglena’s body is not to scale with the displacements. The trajectory of the body center evolves along a helix with right-handed orientation. The helix is actually quite narrow, with an average radius of ≈0.75 $\mathrm{\mu }$m, a small fraction of the Euglena’s width of ∼9.2 $\mathrm{\mu }$m. The pitch is ≈35.8 $\mathrm{\mu }$m, ∼0.7 times the length of the cell ∼50.8 $\mathrm{\mu }$m. The calculated beating period is $T_b\approx$ 24.3 ms. The Euglena closes a turn of the helix in $T\approx$ 0.5 s, so approximately after $N=21$ beats. In Fig. 5B a top view of the trajectory is shown. A color map on the trajectory displays the absolute velocity of the body center: The center moves by continuously accelerating and decelerating, with velocities ranging between 50 and 140 $\mathrm{\mu }$m/s. The cell body (full or transparent) is depicted at the beginning of each beat ($\tau =0$). It can be noticed that the eyespot points in the outward direction.

Fig. 5.

(A–D) Representation of Euglena’s kinematics. The dimensions of the cell body are not to scale with displacements for visualization purposes. (A) Side view. The Euglena follows a right-handed helical path. Full or transparent bodies are shown at the beginning of each beat. (B) Top view. The body center trajectory $𝐜(t)$ is rendered using a color map to highlight the absolute instantaneous velocity. (C) Body motion as seen from a reference frame of axes $𝐥\prime$, $𝐦\prime$, and $𝐧\prime$ moving on the circular helix ${𝐜}_h(t)$ while rotating by ${𝐑}_{𝐧}(\omega t)$ (top view). Full or transparent bodies are shown at instants equally spaced within one beat. (D) Quasi-conical surface spanned by the major symmetry axis of the cell during one beat. (E) Sequence of flagellar shapes for 10 consecutive instants (phases) within one beat. Each phase is labeled with a different color. Body reference axes $𝐢$, $𝐣$, and $𝐤$ are represented in red, green, and blue, respectively. (F) Translational velocity $𝐯$ and (G) angular velocity $𝝎$ of the cell, represented in body reference frame coordinates. Velocities are shown for each flagellar phase and color-coded accordingly. (H) Polar angle and (I) azimuth angle of the unit tangent vector to the flagellum, as functions of the arc length and time.

To have a closer picture of the periodic motion within one beat we consider the evolution of the system as seen by an observer moving with the backbone helix ${𝐜}_h(t)$ while rotating by ${𝐑}_{𝐧}(\omega t)$ (Eq. 1). In this view (Fig. 5C), the cell moves on a quasi-circular orbit in clockwise direction (opposite to the one of the backbone trajectory). As for the body orientation, it is interesting to note that the surface spanned by the major symmetry axis of the cell is roughly a cone (Fig. 5D): The projection of this motion in 2D translates into the “small amplitude swings” observed at the microscope. The rotation around its long axis (so to say its “rolling” motion) is negligible and the eyespot points always to the same direction.

Remarks on the Propulsion Mechanism.

A sequence of flagellar shapes for 10 consecutive instants (phases) within one beat is shown in Fig. 5E. In Fig. 5 F and G the resulting instantaneous translational and angular velocities are represented in body reference frame coordinates. Each phase is labeled with a different color. Bending waves emerge from the base of the flagellum and run through its whole length, fading at its tip. The flagellum bends while swinging around the cell body, with velocities that oscillate significantly both in magnitude and direction.

The propulsion mechanism of Euglena cannot be adequately summarized as a “backward beating of a flagellum to push the cell forward.” The flagellum beats laterally, spanning a complex sequence of nonplanar shapes: No obvious symmetries can be exploited to guess the way the body moves as a result of the flagellar beating. In fact, this motion entails spiraling trajectories coupled to body rotations. To confirm that the reconstructed flagellar shapes are consistent with the observed swimming motion, we calculated the kinematics that the reconstructed flagellar beat generates by imposing the hydrodynamic force balance on the swimmer. Using the local drag approximation (28) of resistive force theory (RFT), we obtained a good qualitative agreement by fitting the resistive coefficients for the flagellum to best match the experimental data, as done in ref. 9 (Supporting Information, section 5 and Fig. S6). Reproducing the experimental data in full quantitative detail will require a more detailed analysis.

RFT shows that the observed kinematics is consistent with the typical thrust mechanism of smooth flagella. Indeed, peaks in the translational velocity of the cell body are correlated with the flagellar wave propagating parallel to the major axis, in the direction opposite to the one of motion, while peaks in the rotational velocity occur during the flagellar swing around the body (see Movie S5 and Supporting Information, section 5 for more details). This seems to confirm the claim (29) that, for the euglenoid flagellum, the presence of soft (nontubular) mastigonemes does not affect the flagellar thrust mechanism in a major way, as it instead happens in other organisms (30).

Conclusions

We have presented a 3D kinematics reconstruction of euglenid flagellar motion. To accomplish this, we have introduced a technique to recover 3D kinematics from 2D microscopy images (Movie S6). This gives unprecedented detail, and it is applicable to other organisms.

As with other methods to reconstruct 3D information from 2D data (25–27), our approach is based on a model and on specific assumptions. In particular, we are limited to periodic beating and to motions confined to the narrow field of view of high-resolution microscopy. Even when these limitations will be overcome by new techniques capable of direct 3D imaging of flagellar and body kinematics (at comparable levels of spatiotemporal detail), the characterization of trajectories as generalized helices, on which our method is based, will stand. The biological significance of patterns emerging from the trajectories of flagellated unicellular swimmers has often been emphasized in the past (18). Here we show that, in fact, the geometric structure of the trajectories is exactly the signature of the periodic flagellar beating that generates them.

Our work paves the way for future studies of the flows induced in the surrounding fluid by flagellar beating and for the investigation of the mechanisms governing the internal actuation of the flagellum. E. gracilis can be seen as a first example for a large class of model organisms whose swimming strokes are less symmetric than those explored so far and for which quantitative data are not yet available.

Materials and Methods

Cell Culture.

Strain SAG 1224-5-27 of E. gracilis obtained from the SAG Culture Collection of Algae at the University of Göttingen was maintained axenic in liquid culture medium Eg (see the medium recipe from SAG) in sterile 16-mL polystyrene test tubes. Cultures were transferred weekly. They were kept in an incubator (IPP 110plus; Memmert) at 15 °C and at a light: dark cycle of 12:12 h under cold white LED illumination with an irradiance of about 50 $\mathrm{\mu }\text{mol}/({\text{m}}^2\text{s})$.

Experimental Setting.

For each experimental trial a dilute solution was prepared of E. gracilis and of 0.5 $\mathrm{\mu }$m in diameter polystyrene, fluorescent beads [(F8813; Life Technologies), volume fraction of ∼0.05%] in culture medium Eg. Swimming cells were imaged in phase contrast illumination by using an Olympus IX81 inverted microscope equipped with a LCAch 40× Ph2 objective (N.A. 0.55). The estimated depth of field for such arrangement is ∼2.3 $\mathrm{\mu }$m. Cells were confined between two microscope slides separated with a ∼50-$\mathrm{\mu }$m-thick double-sided adhesive spacer. Micrographs were recorded at a frame rate of 1,000 fps by using a high-speed complementary metal–oxide–semiconductor digital camera (FASTCAM Mini UX100; Photron).

Image Processing and Data Fitting.

Image processing and numerical fitting have been performed with programs developed in-house implemented in the MATLAB environment (MathWorks).