Pulsed evolution shaped modern vertebrate body sizes

Significance

The diversity of forms found among animals on Earth is striking. Despite decades of study, it has been difficult to reconcile the patterns of diversity seen between closely related species with those observed when studying single species on ecological timescales. We propose a set of models, called Lévy processes, to attempt to reconcile rapid evolution between species with the relatively stable distributions of phenotypes seen within species. These models, which have been successfully used to model stock market data, allow for long periods of stasis followed by bursts of rapid change. We find that many vertebrate groups are well fitted by Lévy models compared with models for which traits evolve toward a stationary optimum or evolve in an incremental and wandering manner.

Abstract

The relative importance of different modes of evolution in shaping phenotypic diversity remains a hotly debated question. Fossil data suggest that stasis may be a common mode of evolution, while modern data suggest some lineages experience very fast rates of evolution. One way to reconcile these observations is to imagine that evolution proceeds in pulses, rather than in increments, on geological timescales. To test this hypothesis, we developed a maximum-likelihood framework for fitting Lévy processes to comparative morphological data. This class of stochastic processes includes both an incremental and a pulsed component. We found that a plurality of modern vertebrate clades examined are best fitted by pulsed processes over models of incremental change, stationarity, and adaptive radiation. When we compare our results to theoretical expectations of the rate and speed of regime shifts for models that detail fitness landscape dynamics, we find that our quantitative results are broadly compatible with both microevolutionary models and observations from the fossil record.

A key debate in evolutionary biology centers around the seeming contradictions regarding the tempo and mode of evolution as seen in fossil data compared with ecological data. Fossil data often support models of stasis, in which little evolutionary change is seen within lineages over long timescales (1, 2), while ecological data show that rapid bursts of evolution are not only possible, but potentially common (3, 4). At face value, these observations seem to contradict one another, an observation known as the “paradox of stasis” (5). These observations are often reconciled through a descriptive model of pulsed evolution, entailing stasis interrupted by pulses of rapid change, as famously articulated by Simpson (6).

On macroevolutionary timescales, pulses of rapid change are expected to look roughly instantaneous. Only recently have statistical methods grown sophisticated enough to model pulsed evolution as a stochastic process, with advances showing that punctuation is detectable in some fossil time series (7) and between pairs of living and extinct taxa (8).

While these studies establish the existence of pulsed evolution, it is still unknown whether the evolutionary mode is common or rare. How many clades in the Tree of Life were shaped by abrupt pulses of rapid evolution? If these evolutionary pulses are common, then that should inform our expectations about how traits evolved for clades that left no fossils and the potential for vulnerable species to adapt rapidly to climate change (9). To this end, phylogenetic models—models of trait evolution that account for the shared ancestry of species—have played a vital role in measuring the relative support of competing Simpsonian modes of evolution.

A pioneering meta-analysis (10) fitted a collection of phylogenetic models to 49 animal clades, finding preference for modes of incremental, but not explosive, evolutionary change. That work predated the advent of phylogenetic models of pulsed evolution (11, 12), so its frequency could not have been measured. Moreover, there remains a concern that models of incremental and pulsed change leave similar patterns of trait variation in neontological data (13, 14). While recent methodological developments show that there is power in comparative data to identify pulsed evolution (11, 12, 15), little is known about the statistical properties of these methods, nor is much known about the prevalence of pulsed change throughout some of Earth’s most intensely studied clades.

Here, we examine evidence for pulsed evolution across vertebrate taxa, using a method for fitting Lévy processes to comparative data. These processes can capture both incremental and pulsed modes of evolution in a single, simple framework. We apply this method to analyze 66 vertebrate clades containing 8,323 extant species for evidence of pulsed evolution by comparing the statistical fit of several varieties of Lévy jump processes (modeling different types of pulsed evolution) to three models that emphasize alternative macroevolutionary dynamics. Under these models, the adaptive optimum of a lineage may wander incrementally and freely (Brownian motion), it may change incrementally but remain stationary (Ornstein–Uhlenbeck), or it may change most rapidly following the initial diversification of a clade while decelerating over time, e.g., during an adaptive radiation (early burst). Beyond simple model comparison, we show that the parameter estimates corresponding to the microevolutionary and macroevolutionary mechanisms of the model have biologically meaningful interpretations (2), illuminating previously hidden features of Simpson’s adaptive grid.

Results

Maximum-Likelihood Method Has Power to Distinguish Pulsed Evolution from Comparative Data.

We developed a maximum-likelihood method for fitting Lévy processes to phylogenetic comparative data using restricted maximum-likelihood estimation (REML), by analyzing the phylogenetically independent contrasts (16) (Materials and Methods). The Lévy processes we apply in this work consist of two components: a Brownian motion and a pure jump process. The Brownian motion is characterized by a rate parameter, ${\sigma }^2$, and the pure jump process is characterized by a Lévy measure, $\nu (\cdot )$, where $\nu (dx)dt$ can be thought of as the probability of a jump with a size in the interval $(x,x+dx)$ occurring in the short time $dt$. Note that this model does not couple pulses of evolution to cladogenesis, as in the classical theory of punctuated equilibrium (17). Instead, pulses may occur at any time, sometimes known as “punctuated anagenesis” (18).

Both Lévy processes with jumps and pure Brownian motion accumulate variance proportionally to time (SI Appendix), leading to speculation that it is impossible to distinguish between pulsed and certain incremental models from comparative data (13, 14). For simulations with moderately sized clades ($>100$ taxa), we had sufficient power to differentiate pulsed evolution from other Simpsonian modes of evolution. This is due to the impact of rare, large jumps resulting in a heavy-tailed distribution of trait change (SI Appendix). Moreover, we saw low false positive rates for identifying pulsed evolution, even in the presence of phylogenetic error (4% for clades with ∼100 taxa, 7% for clades with ∼300 taxa; SI Appendix).

Extant Vertebrate Body Sizes Evolved by Rapid Bursts.

We assembled comparative datasets from time-scaled tree estimates and body size measurements for 66 clades across five major vertebrate groups (Table 1). We computed the sample size-corrected Akaike information criteria weights (wAICc) (19, 20) for each dataset from a panel of models. We used a Brownian motion (BM) to model incremental phenotypic change, in which a lineage’s phenotype follows a wandering optimum. We used the Ornstein–Uhlenbeck (OU) model to model incremental evolution around a single stationary optimum and the early burst (EB) model to capture adaptive radiation, in which the tempo of evolution slows over time. We also compared two different types of jump processes: the compound Poisson with normally distributed jumps [jump normal (JN)] and the normal inverse Gaussian (NIG). The JN process waits for an exponentially distributed amount of time before jumping to a new value; we use this to represent stasis followed by large-scale shifts between adaptive zones. On the other hand, the NIG process is constantly jumping, with larger jumps requiring longer waiting times; this model captures the dynamics of constant phenotypic change, where the majority of change occurs within the width of an adaptive zone, but rare shifts between adaptive zones are still possible. Finally, we examined the combination of the Brownian and jump processes, BM+JN and BM+NIG. We further modeled intraspecific variation and sampling noise using a normal distribution. Examples of how each different Lévy process models trait evolution can be found in SI Appendix.

Table 1.

Vertebrate datasets

	Clade sizes
Group	No. clades	Mean	(min, max)	Phylogeny	Body size
Fish	12	105	(37, 251)	Collected (10, 45–53)	Length from fishbase.org
Amphibians	4	176	(103, 231)	Pruned from refs. 39 and 54	Length from ref. 55
Reptiles	24	127	(53, 220)	Pruned from refs. 56 and 57	Length from ref. 58
Birds	17	111	(56, 260)	Pruned from ref. 41	Mass from ref. 59
Mammals	9	158	(69, 229)	Collected (60–66)	Mass from ref. 67
Total	66	126	(37, 260)	—	—

Data were collected for N = 66 clades for 8,323 species records in total (mean 126 species per clade). The “Phylogeny” column indicates how phylogenies within each vertebrate group were generally acquired: by pruning from a large tree or by collecting independently estimated trees from the literature.

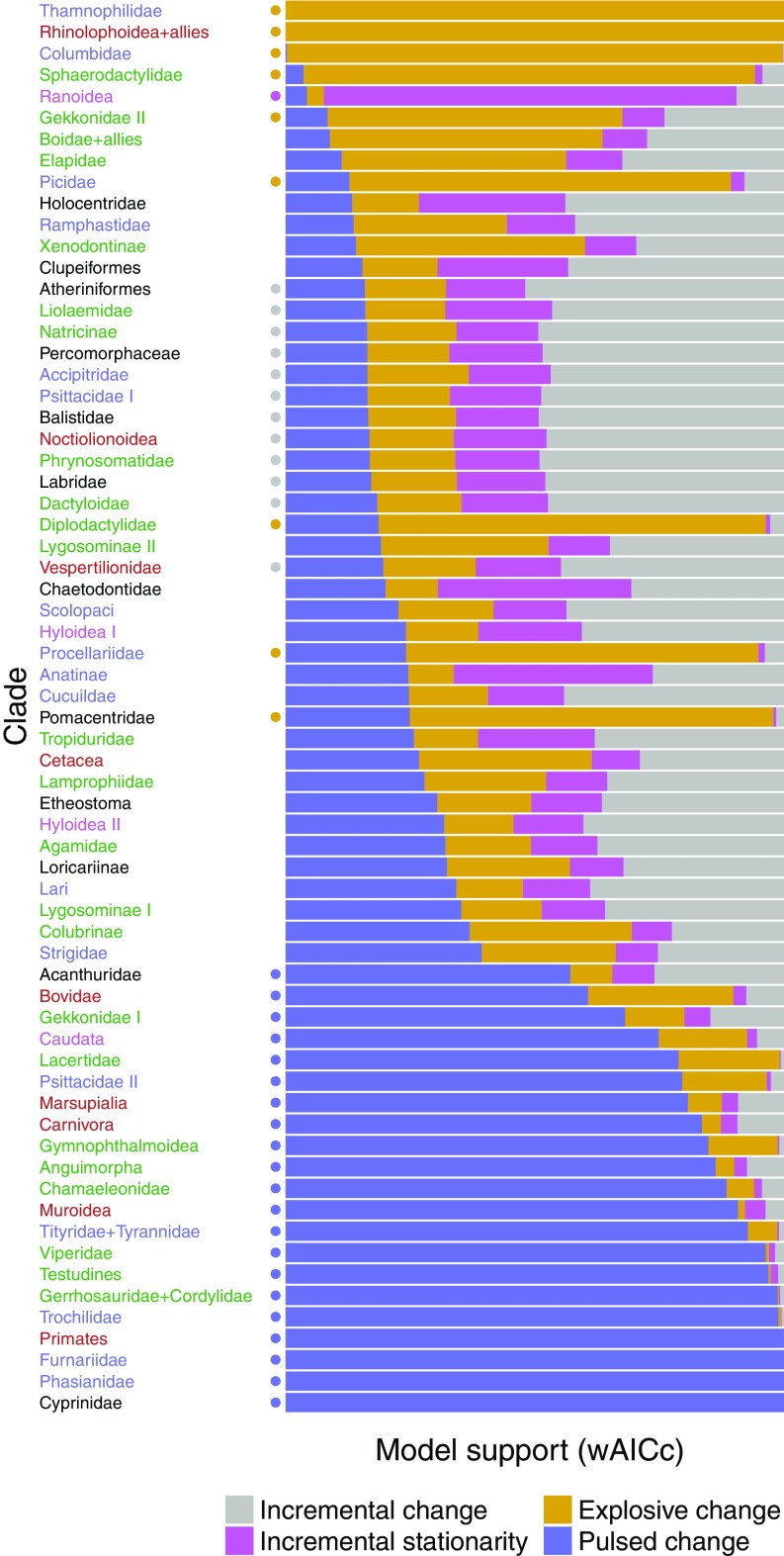
Fig. 1 shows that that 32% of clades were best fitted by models of pulsed evolution. BM, EB, and OU were each selected substantially less often (18%, 14%, and 2%, respectively). About 34% of clades lacked decisive support for any single mode of trait evolution. We did not find any evidence that a particular evolutionary mode is enriched in any of the five vertebrate groups (${\chi }^2$ test, $P\approx 0.10$). Lévy jump models and Brownian models fitted to any given clade yield nearly identical estimates of process variance (SI Appendix), indicating that the tempo and mode of evolution leave distinct patterns in comparative data.

Fig. 1.

Model selection profiles for 66 vertebrate clades. Clade colors indicate their order: black, fish; purple, amphibians; green, reptiles; blue, birds; and red, mammals. Each clade was fitted to seven models, classified into four groups: incremental change (BM), incremental stationarity (OU), explosive change (EB), and pulsed change (JN, NIG, BM+JN, BM+NIG). AICc weights were computed using only the best-fitting model within each class. A model class is selected only if its AICc weight is twice as large than that of any other model class (circles indicate selection counts: 12 incremental change, 1 incremental stationarity, 9 explosive change, 21 pulsed change, 23 ambiguous). Alternative model classifications are provided in SI Appendix.

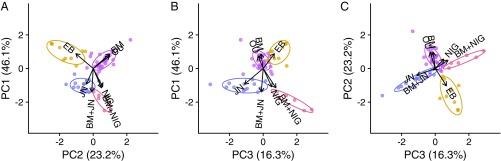
We speculated that clades would favor models that produced similar patterns in comparative data. To characterize this, we applied a principal components analysis to the vectors of wAICc scores of Fig. 1 and then clustered wAICc profiles using k-means (k = 4). The first three principal components explain 85.6% of the variance. Fig. 2 shows that four clusters form around clades that select models of incremental evolution (BM and OU), explosive evolution (EB), and the two models representing pulsed evolution (JN and NIG). Interestingly, the third component separates clades that favored the two different kinds of jump models we explored, with the most pulsed process (JN) running opposite to the infinitely active processes (NIG). This suggests that with more power it will be possible to choose among different models of pulsed evolution with greater confidence.

Fig. 2.

Empirical axes of trait evolution. Shown are the principal components and k-means clusters ($k=4$) for wAICc scores reported in Fig. 1. A–C plot the first three principal component axes as pairs, explaining 85.6% of the model-fit variance. Both principal components analysis (PCA) and the k-means clusters identify three major axes of trait evolution: incremental change and incremental stationarity (purple), explosive (gold), and pulsed models, with the pulsed axis being divisible into subtypes of jump processes with finite (blue) and infinite (red) activity.

Waiting Times to Transition Between Adaptive Zones.

Under a microevolutionary model of stabilizing selection, intraspecific variation is distributed normally around the adaptive optimum (21). This intraspecific variation in turn approximates the width of a given adaptive zone (6, 22). When fitting models of trait evolution, we inferred a parameter that corresponds to the SD of intraspecific variation. Because we have only one sample per species, this is a noisy measure of intraspecific variation that also includes measurement error. We therefore regressed our estimates of the intraspecific variation, using bird data with known phenotypic standard deviations, and used the regressed estimates as a measure of intraspecific variation, ${\sigma }_{\text{intra}}$ (Materials and Methods and SI Appendix).

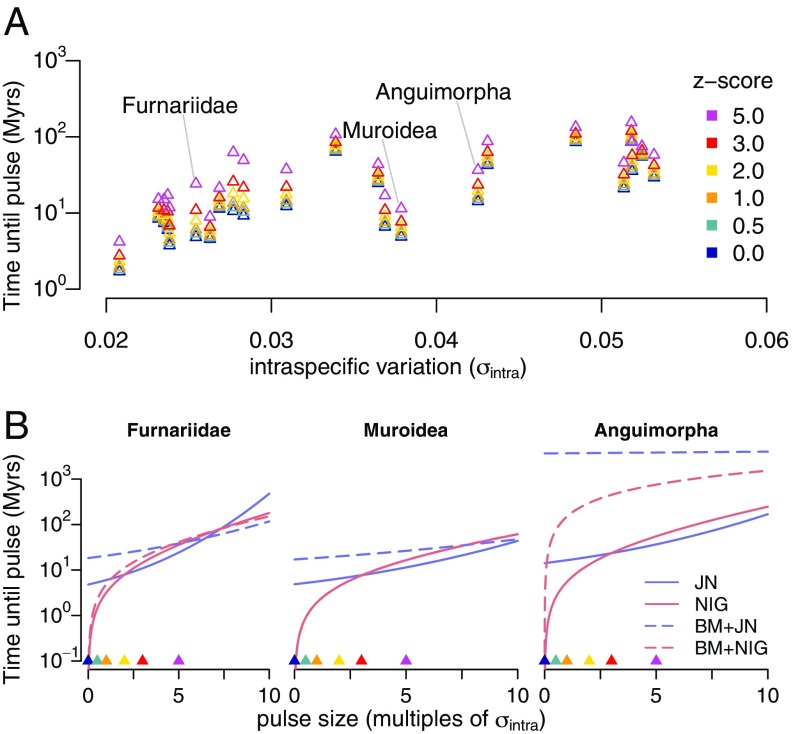
We sought to estimate the rate at which lineages escaped their current adaptive zones via shifts. To do so, we computed the expected waiting time, $\overline{t}(z{\sigma }_{\text{intra}})$, until the lineage jumps at least $z$ intraspecific standard deviations away from the current phenotype (Materials and Methods). Fig. 3A shows these waiting times for the pure Jump Normal process. The value at $z=0$ shows the waiting time for a jump of any size to occur, while we take $z\ge 2$ to be a jump outside of the current adaptive zone, which we define as the interval containing roughly 95% of intraspecific variation per lineage. We found that lineages waited between 1 million and 100 million y before shifting to new adaptive zones ($z\ge 2$), with a median waiting time of $2.5\times {10}^7$ y.

Fig. 3.

Expected waiting time to shift between adaptive zones. (A) Plot shows the expected waiting time needed to produce an evolutionary pulse that is at least $z$ times that of the SD of the intraspecific variance (${\sigma }_{\text{intra}}$). Times are shown for the pure JN process for those clades that select jump processes and ${\sigma }_{\text{intra}}>0$ by any amount. (B) Waiting times until pulses at least as large as a given size differ between the four fitted jump models for three clades shown in A. JN (blue) has finite activity and cannot easily produce small amounts of change quickly, unlike the NIG (red), which is infinitely active. The AIC selects pure jump models (solid lines) for Furnariidae (Left) and Muroidea (Center) and a jump-diffusion model (dashed lines) for Anguimorpha (Right).

The waiting time between adaptive shifts depends both on the magnitude of the shift and on the underlying jump model (Fig. 3B). Models with jumps differ in two ways: (i) the relative frequencies of jumps within and between adaptive zones (e.g., $z<2$ vs. $z\ge 2$) and (ii) whether the fitted model is a pure jump process or a jump-diffusion process. JN models experience long periods of stasis, and jumps tend to be large. Thus, small changes within a lineage’s adaptive zone occur on approximately the same timescale as jumps between adaptive zones. In contrast, infinitely active processes, as represented by NIG, jump continuously. Under these models, shifts within an adaptive zone occur frequently, which could reflect rapid adaptation to small-scale environmental perturbations, while larger shifts between adaptive zones occur on much longer timescales. Interestingly, we find that both finite and infinite activity pure jump models predict similar rates of shifting between adaptive zones, indicated by the fact that the solid curves are near each other for $z\ge 2$. When looking at a clade that is best fitted by a jump-diffusion model, such as Anguimorpha (Fig. 3B, Right), we find that they explain most of the morphological disparity among taxa via the BM component of the model, and we see that jumps occur extremely rarely compared with pure jump models. Jump-diffusion models with small diffusion components produce jump size–time curves that are essentially identical to the jump size–time curves for the corresponding pure jump model (compare NIG and BM+NIG for Muroidea).

Discussion

The pulses of rapid evolution proposed by Simpson (6) are evident in ecological (3, 4) and paleontological (23) observations. Because of their rapidity relative to geological timescales, such phenotypic “jumps” are difficult to observe directly (24, 25), but their lasting impressions are detectable in both simulated and empirical comparative phenotypic datasets (Fig. 1). Among Simpsonian modes of phenotypic macroevolution—including unconstrained incremental evolution, evolutionary stationarity, explosive evolution, and pulsed evolution—we found that pulsed evolution is not only detectable, but also a preferred explanation for how body sizes evolved among diverse vertebrate groups. Phenotypic variation accrues in time at a rate that is nearly identical when assuming models of nonstationary incremental evolution vs. pulsed evolution; that is, they differ in evolutionary mode rather than evolutionary tempo.

To test for the signatures of different modes of evolution, we assembled neontological comparative datasets for 66 vertebrate clades, composed of time-calibrated phylogenies and body size measurements (Table 1). Importantly, we undertook the call for “broad comprehensive sampling” that is necessary to characterize tempo and mode of evolution without bias (26). We developed a method to fit a model of phylogenetic evolution of continuous traits for processes that model macroevolutionary jumps by exploiting the mathematical properties of Lévy processes. Applying our method to the vertebrate dataset, we found that body size evolution was best explained by jump models in 32% of vertebrate clades when fitting incremental, stationary, and explosive models of evolution along with four flavors of jump processes. Taking a broader definition of support for models that concentrate, rather than evenly distribute, evolutionary change, pulsed and EB models are selected for 45% of all clades and for 70% among those clades with strong model preference of any kind. This suggests future work to explore the interaction of EB and pulsed models, in which the rate and/or magnitude of evolutionary pulses decay following the initial radiation of a clade.

Simulated datasets with phylogenetic error do not result in a systematic bias toward preferring Lévy processes over competing models (SI Appendix, Fig. S2). We found that, if anything, our data-filtering and model selection procedures tip the balance to incorrectly favor nonpulsed over pulsed models of evolution. The false positive rates seen in simulations are four to seven times lower than the rates of clades that are best fitted by Lévy processes in the empirical data, suggesting a very low false discovery rate. These findings contradicted concerns that incremental and pulsed models would be difficult to distinguish, because BM models and jump processes result in the same tempo of evolution (measured by the variance that the processes accumulate per unit time). Nonetheless, rare, large jumps result in heavy-tailed distributions of trait change along branches (quantified by the excess kurtosis of the trait change distribution), which can be distinguished from incremental evolution occurring at a similar tempo. In the empirical dataset, we found no support that certain model classes were overrepresented within a particular vertebrate group (SI Appendix, Table S2). One possibility is that the five vertebrate groups explore phenotypic space using the same palette of evolutionary modes in roughly equal proportion.

We did not replicate findings of weak support for EB (10). Several studies have reported that macroevolutionary models of continuous trait evolution may produce misleading results when intraspecific variation is ignored (27–30). Thus, we suspected that EB models that ignore intraspecific variation cannot simultaneously explain explosive variation between deeply diverged species in the clade alongside variation concentrated near the tips of the tree. When we forced the model to ignore intraspecific variation, we found OU to be better supported than EB or BM (SI Appendix, Table S3). This suggests that many findings of support for models of evolutionary stationarity over models of adaptive radiation may be due to model misspecification (either by ignoring intraspecific variation or by assuming a fixed value), rather than evidence for adaptive landscapes with single stationary peaks. We therefore suggest that modeling intraspecific variation is an essential component of analyses of comparative data, although more work is needed to understand the complicated interplay when modeling both intraspecific and evolutionary variation simultaneously (30, 31).

One possible microevolutionary explanation for pulses of rapid evolution may relate to Wright’s shifting-balance theory, in which small populations stochastically shift between adaptive zones (32). We estimate that the median waiting time to jump to new adaptive zones is on the order of ${10}^7$ y across clades, consistent with predictions for the time required to jump between adaptive peaks that are separated by fitness valleys via genetic drift in small populations (24). Under this model, the primary impediment to peak shifts is escaping the current adaptive zone; once escaped, transitions to new adaptive optima occur rapidly. With biologically reasonable parameters, shifts between adaptive zones are expected to occur every $\sim {10}^6-{10}^7$ generations, but take only $\sim {10}^2-{10}^3$ generations to complete once initiated. Alternatively, this waiting time may represent the timescale of changes of the adaptive landscape itself. Under this model, macroevolutionary jumps are precipitated by changing biotic or abiotic conditions (such as climate change). Quantitative genetic theory shows that adaptation to new, nearby optima can occur extremely rapidly, again on the order of $\sim {10}^2-{10}^3$ generations (25).

Our results may also be compatible to the classic theory of punctuated equilibrium, in which pulses of evolution are coincident with cladogenesis (17). In this scenario, apparent “punctuated anagenesis” in comparative data is due to speciation events corresponding to now-extinct lineages. While recent work showed that jointly modeling lineage dynamics and trait evolution has some power to detect classical punctuated equilibrium from comparative data (33), little is known about the power to distinguish strict punctuated equilibrium from more generic pulsed evolutionary models. If “hidden speciations” occur at an approximately constant rate across a phylogeny, it is likely that it would be difficult to disentangle these two models from neontological data alone. Instead, inhomogeneous speciation dynamics, such as logistic diversification (34), may provide a sufficiently strong signal to disentangle anagenetic and cladogenetic models of pulsed evolution.

We found that different kinds of jump processes, representing different modes of rapid evolution (constant rapid adaptation vs. long periods of stasis broken up by jumps between adaptive zones), leave faint, but unique, signatures in phylogenetic data. By integrating these models into fossil sequences, we suspect that further fine-scale details of macroevolution can be elucidated. Moreover, in quantitative finance, where the “fossil record” of stock prices through time is perfectly kept, fine-scale dynamics of jump processes can be inferred (35, 36), suggesting that such power exists for suitably densely sampled fossil sequences. Our approach, which uses only modern data but integrates them into a phylogenetic framework, represents an important step toward a fully integrative analysis of macroevolutionary processes.

Materials and Methods

Likelihoods Using Characteristic Functions.

Because most Lévy processes are known only by their characteristic function, we developed a REML algorithm that operates on characteristic functions. We computed the likelihood of the independent contrasts by proceeding from the tips to the root of the phylogeny. To do so, we recursively update the estimate of the trait at internal nodes as a linear combination of the trait value at the two daughter nodes. We also include an additional term to model the uncertainty in trait values at the tips of the tree due to both intraspecific variation and measurement error. Details of the algorithm can be found in SI Appendix.

Optimizing Model Fit Using REML.

To fit the model to data, we used the R programming language and relied on several R packages (37–39). Our package is available at https://github.com/Schraiber/pulsR. Optimal parameter values are obtained by maximizing the likelihood, using the Nelder–Mead simplex method (40). To ensure that we obtained true maximum-likelihood estimates, we performed multiple independent parameter searches (10 for empirical data, 4 for simulated data). In addition, we validated that all maximum-likelihood estimates agreed with model hierarchies; e.g., the maximum likelihood for OU must be greater than or equal to that for BM.

Simulation Study for Model Selection Power and Sensitivity.

We assessed the power and false positive rate of our method by manipulating tree size and phylogenetic error in a controlled simulation setting. Each dataset was simulated by sampling one tree from an empirical posterior distribution of trees (41) and then simulating trait data under each of the seven candidate models (BM, OU, EB, JN, NIG, BM+JN, BM+NIG). Simulation parameters are given in SI Appendix, Table S1. We then computed AIC weights for each of the seven datasets across the same seven candidate models, once under the originally sampled tree (the “true” tree) and then again under the maximum clade credibility tree that summarizes the posterior (the “consensus” tree). Repeating this procedure 100 times, we counted how often each model type is selected in the presence and absence of tree error. This experiment was conducted for two clades with sizes representative of our empirical datasets (Procellariidae with 106 taxa and Tityridae, Tyrannidae, and allies with 325 taxa). In total, we simulated 1,400 datasets and performed 39,200 maximum-likelihood fittings.

Vertebrate Dataset.

We compiled numerous phylogenetic and trait measurement resources to measure body size evolution (Table 1). The species relationships within each clade were represented using fixed phylogenies with branch lengths measured in millions of years. Body size data were represented by body length for fish, amphibians, and reptiles and, mass being a function of volume, by the cube root of body mass for mammals and birds. Trait measurements were then log transformed, under the assumption that trait evolution operates on a multiplicative scale (42). Handling the data in this manner permits the comparison of evolutionary parameters between clades because our body size and tree data share a common scale. Broadly, we applied the same data assembly strategy to all clades within each of the five vertebrate groups. Clades were generally either extracted from large, taxon-rich phylogenies (amphibians, reptiles, birds) or pooled across independently estimated phylogenies (fish, mammals). Availability and quality of trait data varied between vertebrate groups, each requiring special handling.

Fish.

Standard, fork, and total lengths were extracted from Fishbase, using RFishbase (43). For each fish clade, we used an allometric regression to convert all taxa to the most frequently observed length type (44).

Amphibians.

Mean female snout-vent lengths were used for the three Anuran clades (Ranoidea, Hyloidea I, and Hyloidea II). Caudata traits were drawn from ref. 39.

Reptiles.

Total lengths were used for all snake (Serpentes) clades. Maximum straight-line carapace lengths were used for turtles (Chelonia). Snout-vent lengths were used for all remaining reptile clades.

Mammals.

Adult unsexed body mass measurements were used.

Birds.

Adult sex-averaged mean body mass measurements were used.

Data treatment.

We corrected for two sources of measurement error that would potentially mislead model selection tests to favor Lévy processes. First, rounding error in the trait data caused some clades to contain contrasts that have the exact value of zero. Zero-valued contrasts artificially favor the JN process, which contains a singularity at 0. Second, grossly inaccurate measurements and/or phylogenetic error will drive some portion of contrasts to appear excessively large, fattening the tail density of the trait distribution. To mitigate such errors, we first pruned away any subclades with zero-valued contrasts for all clades. Then, assuming a BM model, we pruned away the subclade with the most extreme valued contrast for 63 of 66 clades. The three clades exempted from the second filtering step either had a large, but expected, contrast (Anguimorpha, involving the contrast containing Varanus komodoensis) or had the largest contrast fall near the base of the tree (Procellariidae and Thamnophilidae). The filtering procedures resulted in a 4.7% loss of data (8,323 of 8,729 taxa remained). SI Appendix contains further details regarding how the input data were processed.

Empirical Model Selection.

We computed sample size-corrected AIC weights (wAICc) for each clade across four model classes: BM, OU, EB, and Lévy processes (Fig. 1). The Lévy process with the highest AICc score was chosen to represent all Lévy processes within the class. Model selection required the model class to be at least twice as probable as any competing model class. With BM being a special case of the remaining six models, this threshold lies on the cusp of the maximum relative probability that it might receive under wAICc. Numerous alternative analyses under various model classifications and assumptions are located in SI Appendix.

Expected Waiting Time Between Adaptive Shifts.

For Lévy processes with a jump component, we are interested in the waiting time until a jump outside of the current adaptive zone occurs. Under the symmetric jump models we consider here, the waiting time for a jump larger than $x$ is

$$\overline{t}(x)=\frac{1}{2{\int }_x^{\mathrm{\infty }}\nu (ds)}.$$

We characterized the width of adaptive zones by the amount of intraspecific variation in a clade. To provide an accurate estimate of intraspecific variation for all clades, we regressed our observed values of ${\sigma }_{\text{tip}}$ against direct measurements of intraspecific SD in birds (59) ($n=16$, $P<0.005$, $R^2=0.53$, slope $=0.200$, intercept $=0.059$). Further details for this analysis and results using the uncorrected ${\sigma }_{\text{tip}}$ estimates are given in SI Appendix.