Fluid-driven origami-inspired artificial muscles

Significance

Artificial muscles are flexible actuators with capabilities similar to, or even beyond, natural muscles. They have been widely used in many applications as alternatives to more traditional rigid electromagnetic motors. Numerous studies focus on rapid design and low-cost fabrication of artificial muscles with customized performances. Here, we present an architecture for fluidic artificial muscles with unprecedented performance-to-cost ratio. These artificial muscles can be programed to produce not only a single contraction but also complex multiaxial actuation, and even controllable motion with multiple degrees of freedom. Moreover, a wide variety of materials and fabrication processes can be used to build the artificial muscles with other functions beyond basic actuation.

Abstract

Artificial muscles hold promise for safe and powerful actuation for myriad common machines and robots. However, the design, fabrication, and implementation of artificial muscles are often limited by their material costs, operating principle, scalability, and single-degree-of-freedom contractile actuation motions. Here we propose an architecture for fluid-driven origami-inspired artificial muscles. This concept requires only a compressible skeleton, a flexible skin, and a fluid medium. A mechanical model is developed to explain the interaction of the three components. A fabrication method is introduced to rapidly manufacture low-cost artificial muscles using various materials and at multiple scales. The artificial muscles can be programed to achieve multiaxial motions including contraction, bending, and torsion. These motions can be aggregated into systems with multiple degrees of freedom, which are able to produce controllable motions at different rates. Our artificial muscles can be driven by fluids at negative pressures (relative to ambient). This feature makes actuation safer than most other fluidic artificial muscles that operate with positive pressures. Experiments reveal that these muscles can contract over 90% of their initial lengths, generate stresses of ∼600 kPa, and produce peak power densities over 2 kW/kg—all equal to, or in excess of, natural muscle. This architecture for artificial muscles opens the door to rapid design and low-cost fabrication of actuation systems for numerous applications at multiple scales, ranging from miniature medical devices to wearable robotic exoskeletons to large deployable structures for space exploration.

Artificial muscles (1, 2) are a long-sought class of actuators for applications in industrial robots, wearable devices, and medical instruments (3–10). Numerous transduction methods have been proposed, including the use of thermal energy, electric fields, and pressurized fluids. Shape-memory alloys (SMAs) can generate a large contractile stress (>200 MPa) when they are heated above their (solid-state) phase transition temperature but at the cost of hysteresis and slow cycle times (11). Low-cost polymer fibers, such as a twisted fishing line and sewing thread, have been demonstrated to generate impressively large stresses up to 140 MPa (4.5% stroke) and significant tensile strokes up to 49% (1 MPa load). Similar to SMAs, this twisted fiber-based muscle is thermally driven; thus, its energy conversion efficiency is low (<2%) relative to natural muscles (40%) (12). Electroactive polymers (EAPs), either ionic (13) or dielectric (14–16), are widely investigated materials for building artificial muscles due to their relatively high efficiency (≈30%), light weight, and structural compliance (elastic modulus <1 MPa) (1, 17). Polymer-based actuators have material properties that closely mimic muscle and can produce substantial deformations in the presence of an external electric field (18, 19). However, often extremely high voltages (typically >1 kV for dielectric elastomer actuators) or hermetic encapsulation (in the case of ionic polymer–metal composites) is required (13), posing barriers to practical applications. Electrically driven hydrogels are able to produce reversible actuation at small scales (20), however their responses are relatively slow (from seconds to hours) compared with other artificial muscles (1, 21). Phase-change materials (both liquid–gas and solid–liquid transitions) have been used to build electrically driven elastomeric artificial muscles (22, 23). These muscles exhibit very promising performances in terms of high strain (up to 900%) and high stress (up to 29 MPa), while their energy efficiencies are similar to SMAs and their actuation speeds are relatively slow.

Fluid-driven actuators are the most widely used artificial muscles due to their simplicity, large actuation stress and deformation, high energy efficiency, and low cost (24–28). The McKibben actuator is one of the most popular fluidic artificial muscles (29, 30). A linear contraction and large force can be produced when a positive fluidic pressure is applied to a bladder inside an anisotropic outer mesh. This kind of artificial muscle can be driven either pneumatically or hydraulically. However, a high-pressure (>100 kPa) fluid is needed where the pressure is determined by the constituent material properties and desired force and displacement. Related actuators such as pouch motors (31) and Peano muscles (32, 33) have a simple planar architecture compared with the standard McKibben actuator. These artificial muscles can generate both linear contraction and torsional motion at a relatively low air pressure (10 kPa). The contraction ratios of these muscles are limited to ∼36% due the cylindrical geometry of their inflated membranes. Vacuum-actuated muscle-inspired pneumatic structures (VAMPs) are elastomeric actuators that exhibit similar reversible behaviors and mechanical performances as those of natural skeletal muscles (34). Planar linear contraction and torsional motion can be generated by VAMPs through the buckling of their elastomeric beams caused by negative pressure (relative to ambient). Negative-pressure operation offers greater safety, compactness, and robustness compared with other fluidic artificial muscles driven by positive pressure, yet the maximum actuation stress (65 kPa) and contraction (45%) that VAMPs can generate are limited by the negative pressure (vacuum) and the buckling strength of their elastomeric structures (35).

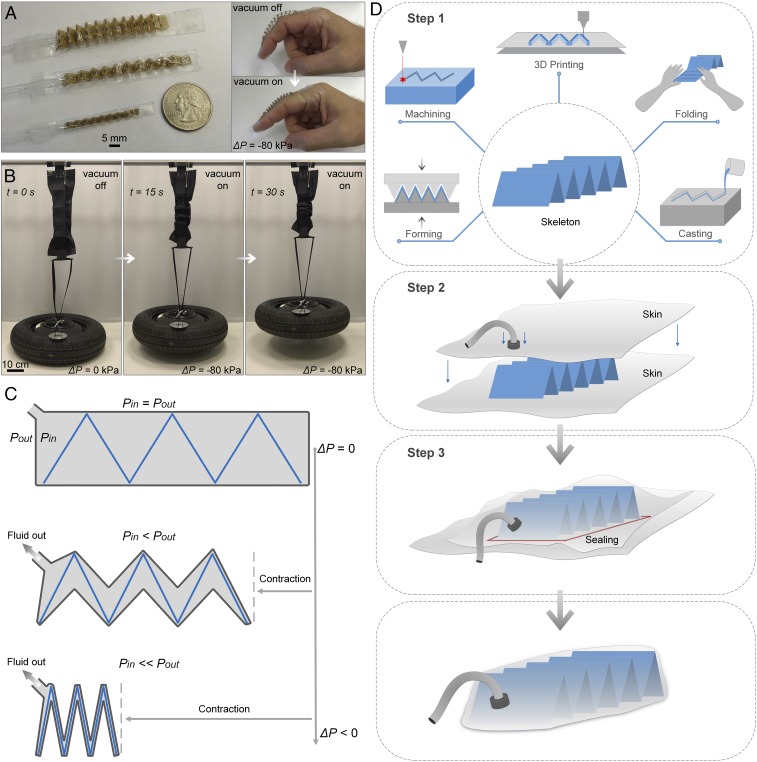
Although significant progress has been achieved, there remains a long-standing scientific challenge for the development of high-performance artificial muscles with low-cost fabrication, complex actuation, easy operation, and scalable implementation. Inspired by the cold gas-pressure folding idea (36), here we propose the design and fabrication methods for an architecture of fluid-driven origami-inspired artificial muscles (FOAMs). This architecture allows us to program artificial muscles with multiaxial complex motions as well as controllable motions at different rates. These artificial muscles are fast, powerful, and energy efficient, and they can be fabricated at multiple scales using a variety of materials at very low costs (Fig. 1 A and B).

Fig. 1.

Design, fabrication, and resulting multiscale actuators. (A) Miniature linear actuators use polyether ether ketone (PEEK) zigzag origami structures as the skeletons and PVC films as the skins. These biocompatible materials make the actuators suitable for medical and wearable applications. (B) A large-scale high-power actuator is assembled using a zigzag skeleton composed of nylon plates (fold width = 10 cm). The skin is made of thermoplastic polyurethane (TPU)-coated nylon fabric. A car wheel (diameter ≈75 cm, weight ≈22 kg) is lifted to 20 cm within 30 s (Movie S3). (C) Principle of operation of the actuators. Contraction is mainly driven by the tension force of the skin. This force is produced by the pressure difference between the internal and external fluids. Removing fluid from the actuator will temporarily decrease the internal pressure. (D) Fabrication process. A standard actuator can be quickly fabricated in three simple steps: (step 1) skeleton construction using any of a number of techniques, (step 2) skin preparation, and (step 3) fluid-tight sealing.

Principle of Operation and Modeling

Our artificial muscle system consists of three fundamental components: a compressible solid skeletal structure, a flexible fluid-tight skin, and a fluid medium. In this system, the skin is sealed as a bag covering the internal components. The fluid medium fills the internal space between the skeleton and the skin. In the initial equilibrium state, the pressures of the internal fluid and the external fluid are equal. However, as the volume of the internal fluid is changed, a new equilibrium is achieved. A pressure difference between the internal and external fluids induces tension in the flexible skin. This tension will act on the skeleton, driving a transformation that is regulated by its structural geometry (Fig. 1C and Movie S1).

A simplified mechanical model is developed to describe the interaction of the three components of the artificial muscle (SI Appendix, Fig. S1). In this model, each structural void on a skeleton is abstracted as two connected rigid plates/beams. This connection is modeled as a compression spring (stiffness: $k_s$) for the void with two parallel plates/beams. If the void has two hinged plates/beams, then the hinge can be modeled as a torsional spring, or as two cantilever springs, with an initial opening angle and a bending stiffness $k_s$. The skin is modeled as a massless, flexible, and nonstretchable membrane between two plates/beams, forming a cylindrical void. This membrane’s geometry is approximated as a parabolic surface, and the skin’s elongation and bending deformation are both neglected in this model. If the internal pressure $P_{in}$ is lower than the external pressure $P_{out}$ (a negative pressure difference, $\mathrm{\Delta }P<0$), the membrane deforms inwards toward the void. Under tension, the void will be driven to contract. In this study, we focus primarily on negative pressure-driven artificial muscles due to their large contracting ratios and ease of fabrication. The membrane’s tension force, $T$, is produced by the pressure difference $\mathrm{\Delta }P$. This force is estimated based on the Laplace Law as $T=\mathrm{\Delta }P\times R\times W$, where $R$ is the radius of curvature of the membrane and $W$ is the width of the void. Based on our model, the void’s force–contraction interaction can be predicted using the principle of virtual work. We validated this model by experimenting with a group of linear zigzag-type actuators. The results show that our model could predict the output force and free contraction with maximum errors of ∼7% and 11% (at $\mathrm{\Delta }P=$ −70 kPa), respectively. The details for the theoretical modeling and the experimental validations are described in SI Appendix. Given this accuracy of prediction, our model can be used to design the artificial muscles to desired performances.

Fabrication Method and Material Choices

As shown in Fig. 1D and Movie S2, fabrication of the proposed artificial muscles follows three basic steps: construction of the deformable skeletal structure, preparation of the outer skin, and then assembly and sealing. The skeleton can be a spring, an origami-like folded structure, or any solid structure with hinged or elastic voids. To construct the skeleton with a given design, a number of different fabrication techniques can be used, such as 3D printing, machining, casting, forming, and even manual folding. Once the skeleton and skin are prepared, the skeleton is enclosed by sealing the skin. The sealing process is dictated by the skin material and can include heat-pressing, gluing, welding, zippering, and sewing. It should be noted that if a positive pressure is used to drive the artificial muscle, then the skin needs to be fixed at specific locations on the skeleton to produce tension to deform the skeleton (SI Appendix, Fig. S3 A–C and Movie S4). For the negative pressure case, the skin–skeleton fixation step is not necessary, as the skin will be tightly confined onto the skeleton’s surface.

Using this fabrication method, a wide variety of materials can be used to construct artificial muscles for particular applications, deformation patterns, and force-displacement requirements (Fig. 2, Movie S5, and SI Appendix, Fig. S7). The material used for constructing the skeleton needs to have a certain rigidity to support the axial compressive force from the skin tension. Although an artificial muscle can still work even after its skeleton is buckled, the contraction ratio and force production will be substantially reduced. We experimented with two vacuum-driven muscles with different wall thicknesses of their skeletons (1 mm and 3 mm, respectively). A 20% reduction in blocked force and a 50% decrease in free contraction were observed after the thinner skeleton was buckled at −70 kPa (SI Appendix, Fig. S4 A, D, and G). For the case of discrete folds, the skeleton’s hinges have to be compliant to allow the desired structural transformation. For repeatable actuation, skeleton elasticity is also required to bring the skeleton back to its initial configuration after each actuation. To enhance fluid circulation and avoid jamming, the skeleton should have several channels through its structure.

Fig. 2.

Linear zigzag actuators made of a variety of materials using different fabrication methods. (A) A transparent actuator lifts a clear acrylic plate. Skeleton material ($SkeM$): 0.254 mm transparent polyester sheet. Fabrication method ($FM$): laser cutting and manual folding. Skin material ($SkiM$): 0.102 mm transparent PVC film (Vinyl). Driving fluid ($DF$): air. (B) A soft linear actuator contracts well even when it is confined into a metal screw nut. $SkeM$: silicone rubber (M4601). $FM$: casting. $SkiM$: 0.24 mm TPU film. $DF$: air. (C) A vacuum-driven water-soluble actuator is dissolved in hot water (≈ 70 °C) within 5 min. $SkeM$: polyvinyl alcohol (PVA). $FM$: 3D printing. $SkiM$: 0.025 mm PVA film. $DF$: air. (D) A water pump-driven hydraulic actuator pulls an underwater object for 3.5 cm in 20 s. $SkeM$: 0.254 mm stainless steel (316). $FM$: manual forming. $SkiM$: 0.24 mm TPU film. $DF$: water.

In general, the skin must be resistant to both the fluids inside and outside of the skin. However, to demonstrate the flexibility in materials choices for these artificial muscles, a PVA-based actuator can be fully dissolved in hot water (≈ 70 °C) within 5 min (Fig. 2C and Movie S5). Flexibility is also required to allow easy bending during actuation. An ideal inextensible thin film material can avoid undesired elongating and bending deformations on the skin when a pressure is applied. Such skin deformations will reduce the system’s performances and make the actuation difficult to control. In the comparison shown in SI Appendix, Fig. S4 F and I, a linear actuator with 0.24 mm TPU-based skin (tensile modulus: 25 MPa) produced ∼60% less contractile force compared with using an actuator with 0.34 mm nylon fabric skin (tensile modulus: 460 MPa). Sufficient skin tensile strength must be maintained to effectively transfer the tension force induced by the fluidic pressure. In addition, the skin material has to be amenable to a convenient sealing method.

The choice of the fluid depends on the working environment and performance requirements. In addition, the fluid medium has to be compatible with the materials used in the skeleton, skin, and sealing process. In our current study, we focus on using the available fluid surrounding the artificial muscle. In this case, the internal fluid and the external fluid are homogeneous, although using a different internal fluid is also possible for the artificial muscle. As demonstrated in SI Appendix, Fig. S3D and Movie S5, a 1 kg weight can be easily lifted in the air by a cylindrical muscle using water as the internal fluid (flow rate: 80 mL/min). A fluid with low viscosity is ideal for achieving a rapid and energy-efficient actuation. Air is the most accessible fluid for making a lightweight artificial muscle, and the surrounding water can be directly used for actuation in an underwater environment (Fig. 2D and Movie S5).

A variety of jamming-based mechanisms have been successfully developed for universal grippers (37, 38) and stiffness-tunable robots (39–41). Similar granular materials or layered structures can be used in FOAMs to enhance the functionalities of stiffness tuning and object manipulation (e.g., rigidify when an object is grasped). These are appealing features given the compatibility with the FOAM concept both in terms of structures and materials and with the use of negative pressure.

Programmable Motions

A variety of motions can be achieved by programing the geometry of the skeleton (SI Appendix, Fig. S8 and Movie S6). Assuming the fluid pressure is constant everywhere within the skin, the skeleton’s shape transformation is determined by a combination of the contractions from each individual structural void. Identical voids can be distributed over the skeleton using different arrangements for generating various synchronous contractions. A 90% linear contraction can be produced by an origami skeleton using a symmetrical zigzag geometry (Fig. 3A). A skeleton using a standard Miura-ori origami pattern is able to generate a 2D surface contraction (92% contraction ratio) when a vacuum is applied (Fig. 3B). A 3D skeleton using the water-bomb origami pattern can transform a spherical structure to a cylindrical structure (91% contraction ratio) (Fig. 3C). Using an asymmetrical arrangement of the voids, a bending motion can be produced on a beam-shaped skeleton (Fig. 3D). A flasher origami skeleton can generate a rotation (>90°) and a 54% contraction simultaneously using a single vacuum supply (Fig. 3E).

Fig. 3.

Various basic actuation motions and programmable pseudosequential actuation with multiple degrees of freedom. (A) A 19 cm-long linear zigzag actuator contracts to a compressed structure shorter than 2 cm. The 1D contraction ratio is ∼90%. (B) A 2D origami skeleton using the Miura-ori patterns (area: $11\times 10$ cm²) can contract to a dense bar-shaped structure (area: $9\times 1$ cm²). The 2D area contraction ratio approaches 92%. (C) A 3D “magic-ball” origami using the water-bomb pattern (radius: 3.5 cm) contracts to a compacted cylindrical structure (radius: 0.9 cm; height: 6.5 cm). The 3D volume decreases 91% after this contraction. (D) Bending motion can be achieved by using an asymmetrical beam structure as the skeleton. (E) Using a flasher origami pattern as the skeleton, the actuator rotates more than 90 degrees around its center, and its 2D surface contracts by 54% simultaneously. (F) A complex out-of-plane motion combining torsion and contraction can be programed through a 2D Miura-ori origami pattern with select folds weakened. (G) Three fingers on a robotic hand are actuated at different rates using a single control of the internal air pressure. The skeletal structure of this robotic hand is 3D printed from nylon. Different hinge strengths inside the structural voids are designed for these three fingers, which produce significantly different bending stiffnesses: $k_{s1}(red)<k_{s2}(green)<k_{s3}(blue)$. The bending stiffness of each finger determines its own bending angle at a certain internal pressure level. (H) A bottle of water is gripped, lifted, and twisted by a single-channel vacuum-driven robotic arm. The robotic arm has a modular structure including a cup-shaped gripper and a cylindrical lifter. The gripper uses a polyester magic-ball origami as its skeleton, while a much stiffer compression spring (302 stainless steel) is used as the lifter’s skeleton. When the internal pressure decreases smoothly, the gripping motion will always start first, then the lifting and twisting motions start later as the internal pressure reduces further.

In addition to the programmable arrangement for identical voids, voids with different hinge stiffnesses can also be used to achieve differential contractions. This principle can generate asymmetrical out-of-plane motions. For example, a 2D Miura-ori origami skeleton with some hinges weakened can realize a complex motion that combines both torsion and contraction (Fig. 3F). Furthermore, if the hinge or connection stiffnesses $k_s$ are significantly distinct, then a controllable pseudosequential motion can be generated by the artificial muscle (Movie S6). For example, three fingers on a robotic hand (Fig. 3G and SI Appendix, Fig. S8G), with a bending–stiffness ratio $k_{s1}:k_{s2}:k_{s3}\approx 1:2:3$, can be actuated at different rates using a single pressure control. In a second example, a pneumatically driven robotic arm can first grip an object, then lift and twist the gripped object. This pseudosequential multiaxial manipulation is achieved by a single control pressure. In this case, the gripper’s plastic skeleton (polyester, elastic modulus ≈5 GPa) is much more compliant than the metal skeleton (302 stainless steel, elastic modulus ≈190 GPa) in the “arm” (Fig. 3H and SI Appendix, Fig. S8H. Although this motion is not strictly sequential, we believe sequential motion is possible, if the response is tuned to be nonlinear, for example using a group of distinct snap-through hinges integrated into the skeleton (42, 43).

Performance Characterization

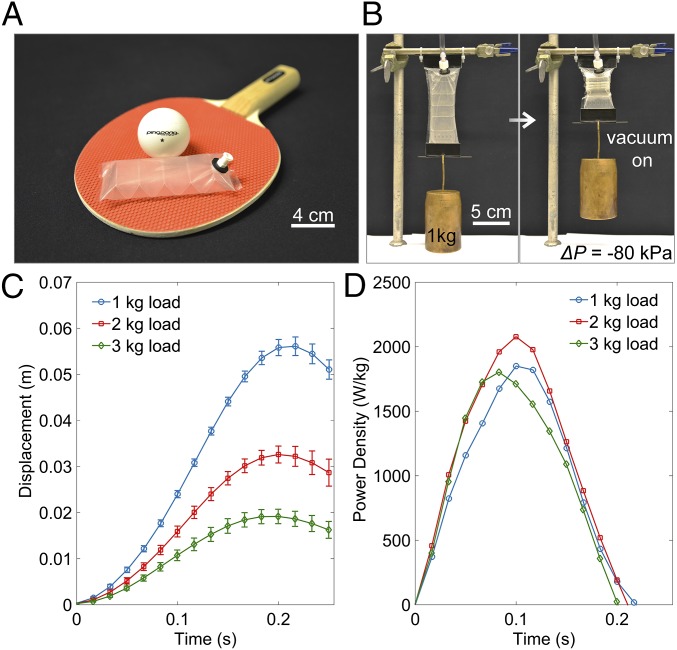
We characterized the force and contraction performances of the proposed artificial muscles through a series of quasi-static experiments. A group of linear zigzag actuators with nylon skins were fabricated with different fold angles of their skeletons (SI Appendix, Figs. S1E and S2I). A blocked force of ∼428 N was generated using a regulated −90 kPa vacuum supply. This indicates that this nylon-based linear artificial muscle can provide an actuation stress of ∼600 kPa (approximately six times greater than the sustainable stress of mammalian skeletal muscle) (1). The peak free-contraction ratio was ∼50% without prestretching (SI Appendix, Fig. S2I). The maximum contraction ratio also depends on the thickness of the skeleton materials, a contraction ratio over 90% is possible using a thinner zigzag skeleton as shown in Fig. 3A. The effects of hysteresis, as observed from our experiments, were negligible compared with an air cylinder (SI Appendix, Fig. S2 D and F), enhancing controllability when using the muscle either as a force source or to control displacement (SI Appendix, Fig. S5 C and D). To characterize the dynamic performances including power density, energy conversion efficiency, and bandwidth, we performed a group of load-lifting experiments using a polyester-based lightweight artificial muscle (Fig. 4A and Movie S7). This 10 cm-long linear actuator was fabricated within 10 min, with materials costing less than $1. This actuator weighs 2.6 g, and it can lift a 3 kg object within 0.2 s using a −80 kPa vacuum. The open-loop control bandwidth of this actuator was ∼1.1 Hz (with a 0.5 kg load; see SI Appendix, Fig. S5E). The peak output power density obtained from our experiments was over 2 kW/kg (Fig. 4C and SI Appendix, Fig. S6E; the weight of the pressure source and associated plumbing are not included), more than six times the peak power density of mammalian skeletal muscles (0.3 kW/kg) (1). The mechanical-to-mechanical energy conversion efficiencies of the actuators were ∼23% (1 kg load, pneumatically driven) and 59% (0.5 kg load, hydraulically driven) in our load-lifting experiments (SI Appendix, Fig. S6D). However, the electrical-to-mechanical energy efficiencies were ∼2% to 5%, when miniature electric vacuum pumps were included into the systems (SI Appendix, Fig. S6C). We should note that the actuators used for characterization have not been optimized for force, displacement, bandwidth, or energy/power. Our experimental result reveals that the proposed artificial muscles are powerful, fast, and energy efficient.

Fig. 4.

Dynamic characterization of a lightweight actuator. (A) A miniature linear zigzag actuator (weight ≈ 2.6 g, volume ≈ 32 cm³) and a common ping-pong ball (weight ≈ 2.5 g, volume ≈ 33.5 cm³). The actuator is primarily made of polyester sheets (skeleton thickness: 0.254 mm; skin thickness: 0.038 mm). (B) It can lift objects several orders of magnitude more massive using a negative internal air pressure (−80 kPa). (C and D) Dynamic performance in load-lifting tests. The actuator can lift a 1 kg load to 5.5 cm within 0.2 s (C). This indicates an average power density of ∼1.04 kW/kg. A peak power density over 2 kW/kg was obtained during the 2 kg load-lifting tests (D).

Conclusions

In this study, we have demonstrated a concept of FOAMs. These muscles can be easily made from a large variety of materials, and they are able to generate powerful, efficient, and programmable multidimensional actuation. This technique allows us to quickly program, fabricate, and implement actuation systems for very specific working environments at multiple scales, such as active metamaterials (44), miniature surgical devices (45, 46), wearable robotic exoskeletons (47), transformable architecture, as well as deep-sea manipulation (48) and large deployable structures for space exploration (49, 50). The use of negative pressure offers a safer way of actuation for FOAMs compared with artificial muscles driven by highly pressurized fluids. This is a promising feature for future applications in wearable devices and human–robot interactions.

Materials and Methods

The blocked force and free contraction were obtained using a universal testing machine (Instron 5544A, Instron Corporation). A laser displacement sensor (LK-031 and LK-2001, Keyence Corporation) was used to measure the skin deformation (SI Appendix, Fig. S1 F and G). The muscle’s load-lifting motion was recorded by a camera and then analyzed (speed and height) using image-analyzing software in each test. A laser cutter was used to cut thin-sheet skeletons, and most of the other skeletons were built by 3D printers using different materials (e.g., nylon, TPU, etc.). A variety of thin-sheet materials, such as TPU, PVC, polyester, and TPU-coated nylon fabric, were used to make the skins. The majority of the skins were directly sealed by an impulse heat sealer (AIE-410FL, American International Electric, Inc.) using proper sealing times for the different skin materials (SI Appendix, Table S1). More details can be found in SI Appendix.