Vertebrate body size jumps the Wright way

Fossil data provide copious evidence that anatomical (morphological) change within individual lineages is not constant: short bursts of great change commonly separate long durations of little change (1, 2). Despite this, most models of morphological change assume that probabilities of morphological character change are the same from one generation to the next: even if rates change over time—such as in “Cambrian explosion” or “early burst” models, where high disparity among anatomies evolves early—then it is still assumed that fast rates of continuous character change gave way to slow rates of continuous change (3). In statistical parlance, early bursts usually are modeled as nonstationary processes (usually lognormal for continuous data such as size, or Poisson for discrete characters, such as presence/absence of structures) in which some instantaneous rate of change declines over time. In contrast, null hypotheses are modeled as stationary processes in which the instantaneous rate does not shift over time. However, both null and test models assume that the processes underlying anatomical change are continuous-time processes, with instantaneous probabilities of change or amounts of change.

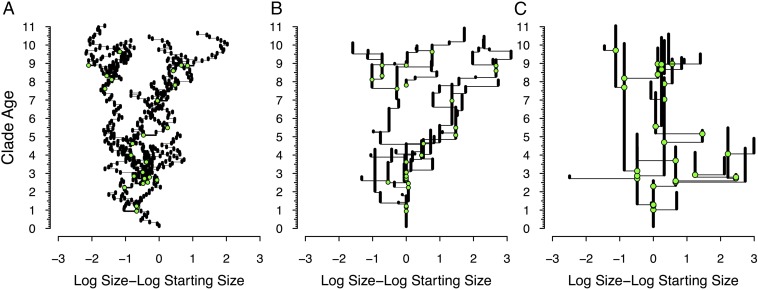
In PNAS, Landis and Schraiber (4) put continuous-time models of anatomical evolution to the test. Although numerous studies do this using fossil data (1, 2, 5), Landis and Schraiber (4) do this using size data and phylogenetic estimates from extant taxa only. Under their model, anatomical change happens in pulses, with a probability of some time t between pulses given by a Lévy process. Suppose that we simulate phylogenetic evolution and change for some continuous trait, such as size, under both continuous time and Lévy processes. Under a continuous-time model, our computer generates some number between 0 and 1 for each lineage at each time step, which we then use to determine some small amount of change following, for example, a lognormal distribution. This creates a Brownian motion “drift” of size (Fig. 1A). Under the Lévy process, our computer generates some number between 0 and 1 that determines a waiting time t before size changes. Assuming that the waiting time is less than the remaining lifetime of a lineage, we then generate a second number between 0 and 1 to determine change, but using a distribution with much higher variance than in our simple Brownian motion model. This would be repeated after each pulse. What we now have is a different random walk model, where the “generation time” varies exponentially across and within lineages, and where both the average generation time and the average amount of absolute change are much greater than under a standard Brownian motion model (Fig. 1B).

Fig. 1.

Three models of continuous change on the same phylogeny, with cladogenetic events (green circles) and lineage lifetimes following exponential distributions. The x axis gives the (log) difference between the original body size and the derived size. Note that the actual phylogeny is identical in all three figures. (A) Brownian motion. Here, each “generation” shows some shift following a lognormal distribution. (B) Jump (pulsed) model. Here, shifts are exponentially distributed over time within lineages and follow a lognormal distribution with larger log-variance. (C) Punctuated equilibrium. Here, shifts coincide with cladogenesis and follow a lognormal distribution with still larger log-variance.

Unless we have a directional change [i.e., a driven trend (6)] in which, for example, size increases are more probable than are size decreases, the single most-probable outcome is no net change under either model (1). However, a key difference is that it will be much easier to “accidentally” get large amounts of change over short periods of time given pulsed change. First, when pulsed change happens, then it (probably) will be absolutely greater than under Brownian motion. Thus, closely related species can be quite different from each other. Second, if we “accidentally” get two pulses over a short period of time, then we might get considerable change that would be almost impossible to achieve under simple Brownian motion. Thus, “bursts” (early or late) should be fairly common given pulsed change even with rates of change (both in frequencies of pulses and amounts of change per pulse or “jump”).

Landis and Schraiber (4) analyze body size evolution in 66 vertebrate clades based on phylogenies of living species, using Brownian motion, Ornstein-Uhlenbeck [where some attractor constrains shifts, mimicking stabilizing selection (1)], early burst [i.e., Brownian motion with decreasing step sizes over time (3)], and different jump (equals pulsed) models with periodic change. Notably, some include a Brownian motion component, so both “phyletic gradualism” (5) and pulses occur. In the 43 clades for which the data best fit any considered model or class of models, 23 best fit one of the pulsed models, with 13 best fitting one of the two incremental models and 9 best-fitting the early burst model. Thus, without fossil data suggesting prolonged periods of stasis or limited change within lineages, Landis and Schraiber (4) still find support for the notion that much change in vertebrate body size occurs in short pulses rather than continuously.

As so often is the case, the numerous theoretical and methodological implications to Landis and Schraiber’s study (4) are as important as the basic results themselves. One theoretical implication concerns the intensity of selection when fixing changes in anatomy. For example, Lande (7) estimates that observed trends in tooth evolution in horses required about two deaths per million individuals per generation due to insufficiently thick teeth. However, if we remodel this using a jump process between shifts in horse teeth, then we would require a far stronger selective gradient during the short intervals of time over which it really mattered. Combining existing models for examining directional change (1) with Landis and Schraiber’s (4) model thus might provide much more realistic descriptions of the strength of natural selection following the models of Wright (8, 9) rather than of Fisher (10).

Methodologically, Landis and Schraiber’s (4) study presents a new wrinkle for “tip-dating” methods that combine morphological and molecular data when estimating divergence times (11). Such analyses typically use discrete character data rather than continuous data, such as size, and thus assume waiting times for each individual character. However, they also assume that each character has its own waiting time, rather than there being a waiting time before any character can change (12). If we recast this so that there is a waiting time for any character change and then some probability that any individual character changes, then we have a jump model of discrete character change (13). This probably is not an issue for temporally long branches: as Landis and Schraiber (4) note, we expect similar amounts of change along, for example, the branch leading to tuataras, whether change is continuous or pulsed, particularly if the pulses themselves follow continuous processes. However, for short divergences, allowing for pulses makes it plausible that branches accrued considerable change over short periods of time. Along these same lines, it will be interesting to apply jump models to molecular data too, as some studies suggest that processes thought to underlie pulsed models, such as allopatry (5), also affect molecular evolution (14).

It bears emphasizing that Landis and Schraiber’s (4) model differs in a key way from Eldredge and Gould’s (5) punctuated equilibrium model: evolutionary change is not tied to cladogenesis (Fig. 1C). Instead, Landis and Schraiber’s (4) method models punctuated anagenesis, where an ancestral morphospecies (equaling “species” insofar as fossil data are concerned) is rapidly replaced by a derived morphospecies (15). Thus, (and as the authors note), Landis and Schraiber’s (4) pulsed model is similar to Sewall Wright’s original shifting balance models (8, 9), in which populations (“demes”) rendered morphologically distinct by combinations of local selection and genetic/phenotypic drift occasionally achieve higher adaptive peaks than achieved by related populations and thus supplant those populations. Thus, rather than continuous anagenetic change within lineages, we have punctuated anagenetic change instead. [Although Wright’s (8, 9) models are easily adapted to explain Eldredge and Gould’s (5) model by making demic shifts induce cladogenesis as well as phenotypic change, this was not Wright’s original intent (16)].

We could modify Landis and Schraiber’s (4) methods to accommodate punctuated equilibrium models. If we add a 50% chance of a pulse at each branching and then use a Lévy process to model expected “lost” speciation events causing additional jumps/pulses, then we effectively model punctuated equilibrium (13). Note, that it is only 50%, because both the modified descendant and the static ancestor give rise to extant sister clades under this model. Note also that because of extinction, we expect only some of the branching events in a clade to have extant daughters (17); thus, there will be pulses now identical to anagenesis. Molecular trees often imply a concentration of divergences early in clade histories (18). Suppose such a clade also shows an early burst of change. If the number of nodes informs the number of jumps, then jump models might better explain apparent early bursts driven by elevated speciation but constant rates of change (19) than standard early burst models. This could also affect the type of pulsed model that is favored, given many closely related but morphologically distinct species. Without speciational change, jump + Brownian motion models should be favored over pure jump models in such cases, as pure jump models would expect most closely related species to be identical. However, if half of the “recent” branching events are given jumps, then the differences are explained without incremental change.

In short, Landis and Schraiber’s (4) approach only scratches the surface of how we should model anatomical evolution among living organisms. However, this is a very important (and, some paleobiologists might say, long overdue) scratch! Relevant work using fossil data suggests that morphological evolution often is more complex than any single model allows (20). Landis and Schraiber (4) themselves begin the “mix and match” game by combining jump models with continuous-change models. I expect this to be a stepping stone to combining pulsed models with speciational, early burst, driven trends, and numerous other models in the next few years. In doing so, we should capture a better idea of the relative contributions of pertinent processes to overall evolution while not assuming that any one need predominate.